2-6. НЕКОТОРЫЕ ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЯ И ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ

Предварительные замечания. Результат измерения состоит из оценки измеряемой величины (ее действительного значения) и погрешности измерения, характеризующей точность измерения. Полученные числа должны оканчиваться цифрами одинаковых разрядов. Погрешность выражается числом с одной или двумя значащими цифрами. Две значащие цифры оставляют при более точных измерениях и при цифре старшего разряда, равной или меньшей трех. Такое представление погрешностей основано на том, что они определяют лишь интервал, в котором заключено истинное значение измеряемой величины. Для приведения окончания полученных чисел к одинаковым разрядам эти числа округляются. Напомним основные правила округления.

1. Если первая из отбрасываемых цифр а за ней есть значащие цифры, то последнюю из сохраняемых цифр увеличивают на единицу. Например, округляя число 28,754 до трех значащих цифр, напишем 28,8.

2. Если отбрасывается цифра 5, а за ней нет значащих цифр, то последнюю сохраняемую цифру оставляют неизменной, если она четная, и увеличивают на единицу, если она нечетная. Предполагается, что избыточность и недостаточность при многих округлениях взаимно компенсируется. Например, округляя число 28,75 до трех значащих цифр, напишем 28,8. Для числа 28,65 округленное значение — 28,6.

3. Если первая из отбрасываемых цифр то последнюю сохраняемую цифру не изменяют. Например, округляя число 218,74 до четырех значащих цифр, напишем 218,7.

Технические измерения. Прежде чем приступить к измерению, нужно отнести его к определенному виду по точности. Точность измерения должна быть соотнесена с его задачей.

Наиболее распространены технические измерения, которые выполняют однократно, и их погрешность определяется погрешностью измерительного прибора. Здесь могут быть два случая. В первом случае измерение выполняется имеющимся в наличии прибором, класс точности которого Максимальная погрешность прибора где конечное значение шкалы прибора. Результат измерения записывают в форме показание прибора.

Пример 1. Измеряют напряжение сети щитовым вольтметром типа Показание вольтметра Вычисляют Дмакс Результат измерения: .

Во втором случае измерение должно быть выполнено с погрешностью, не превышающей заданную (допустимую) Ддоп. Выбирают соответствующий измерительный прибор, погрешность которого и при помощи однократного измерения получают результат:

Пример 2. Нужно измерить сопротивление резистора, номинал которого 910 Ом; допустимая погрешность измерения Ддоп Ом. Выбирают мост постоянного тока, например типа основная относительная погрешность которого на пределе измерения до 108 Ом Уравновесив мост, отсчитывают значение сопротивления Ом. Максимальная погрешность Ом. Результат измерения: Ом.

Следует иметь в виду, что определяемая при технических измерениях погрешность является суммарной, т. е.

Понятие о контрольно-поверочных измерениях. Отнесем к этому виду все измерения, в которых случайная составляющая погрешности имеет существенное значение и ее нужно оценить и уменьшить. Точность таких измерений задается доверительным интервалом и доверительной вероятностью. Контрольно-поверочные измерения выполняются с помощью многократных наблюдений. Систематическая составляющая погрешности, по возможности, устраняется предварительно.

Порядок выполнения измерений и их оценки: производят наблюдений измеряемой величины и получают ряд ее значений

находят действительное значение А как среднее арифметическое х по формуле (2-11); вычисляют разности

проверяют (просматривают) разности с целью исключения грубых погрешностей;

вычисляют по формуле (2-12) оценку среднеквадратического отклонения отдельных наблюдений;

определяют по формуле (2-13) оценку среднеквадратического отклонения среднего арифметического;

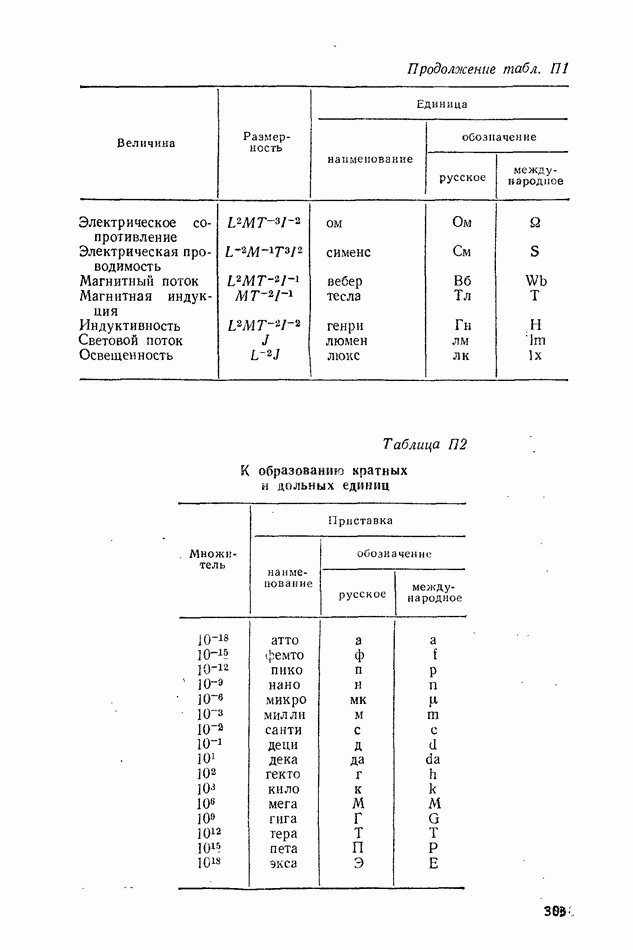
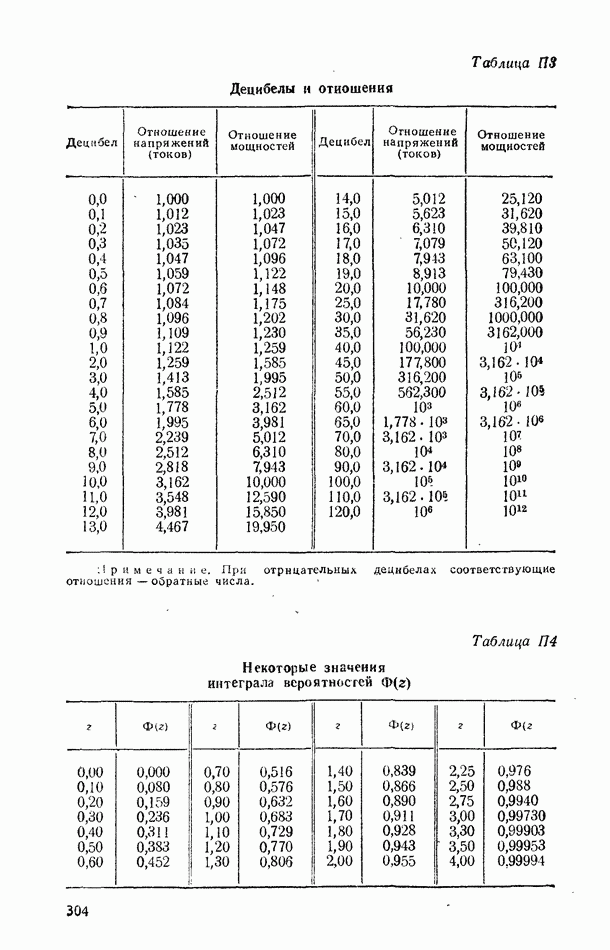
находят доверительный интервал по установленной доверительной вероятности (или наоборот), пользуясь интегралом вероятности или плотностью распределения Стьюдента (см. табл. П4, П5).

Пример 3. Рассмотрим измерение сопротивления резистора, предназначенного для аттенюатора. Данные наблюдений и последующие вычисления сведены в таблицу 2-й.

Таблица 2-2 (см. скан)

Семнадцатое наблюдение резко отличается от остальных. Проверим, не является ли оно грубой погрешностью. По условию С вероятностью 0,997 результат семнадцатого наблюдения не является грубой погрешностью. Найдем оценку среднеквадратического отклонения среднего арифметического: Ом. Доверительный интервал определим при доверительной вероятности 0,99. По

значению интеграла вероятности находим Границы интервала Ом. Результат измерения записываем в такой форме: Ом;

Пример 4. Рассмотрим измерение сопротивления того же резистора, но ограниченное первыми пятью наблюдениями. Среднее арифметическое равно 593 Ом. Оценка среднеквадратического отклонения наблюдения Ом. Оценка среднеквадратического отклонения среднего арифметического Ом.

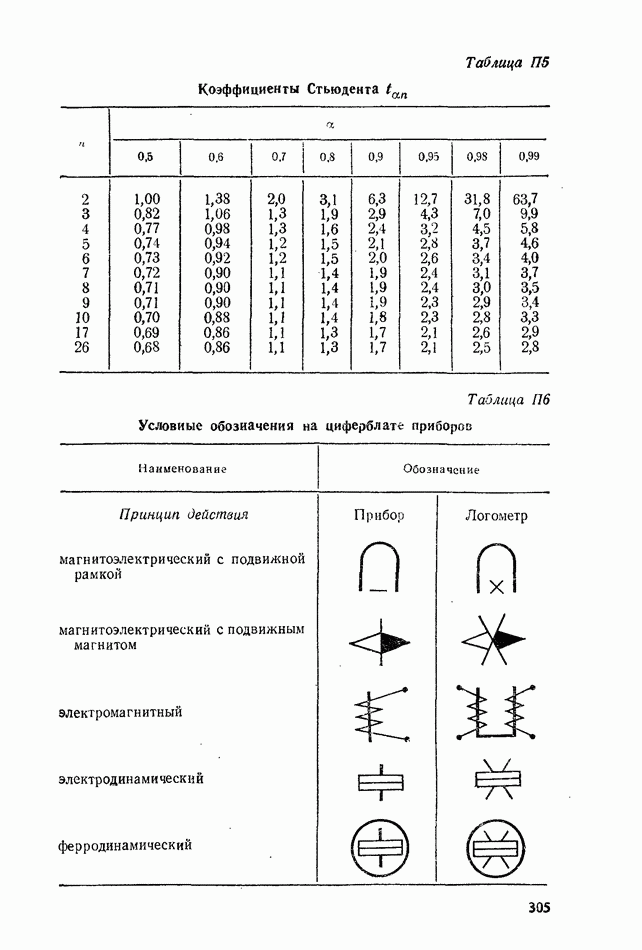
Для определения доверительного интервала нужно воспользоваться коэффициентом Стьюдента (см. табл. П5). При той же доверительной вероятности Следовательно, границы интервала Ом. Округляем до одной значащей цифры: Результат измерения записываем так: Ом;

Если в измерении имеется неисключенная систематическая погрешность и значение ее теоретически или экспериментально определено, то можно найти необходимое число наблюдений, при выполнении которых случайная погрешность не будет определяющей.

Пример 5. Установлено значение систематической погрешности Ом. Находим Подставляя а из примера 4, находим: По табл. 2-3 для находим .

ГОСТ 8.011-72 устанавливает количественные показатели точности измерений, способы их выражения и формы представления результатов измерений. Выбор способов регламентируется соответствующими документами.

Таблица 2-3 (см. скан)