| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2-3. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
Случайные погрешности измерений возникают вследствие одновременного воздействия на объект измерения нескольких независимых величин, изменения которых носят флуктуационный характер. Определенный вклад в случайную погрешность измерения вносит и случайная погрешность средства измерения.
Будем полагать, что систематическая составляющая погрешности измерения исключена и  Случайная погрешность, как случайная величина, полностью
Случайная погрешность, как случайная величина, полностью
характеризуется плотностью распределения вероятностей (иначе, плотностью вероятности)  где
где  функция распределения. Следовательно, определяется не численное значение случайной погрешности, а лишь вероятность того, что она заключена в некотором интервале или не превышает некоторого значения. Если известен закон распределения, то известны
функция распределения. Следовательно, определяется не численное значение случайной погрешности, а лишь вероятность того, что она заключена в некотором интервале или не превышает некоторого значения. Если известен закон распределения, то известны  и
и  Вероятность
Вероятность  нахождения случайной погрешности в заданном интервале от
нахождения случайной погрешности в заданном интервале от  до
до  находится по формуле
находится по формуле

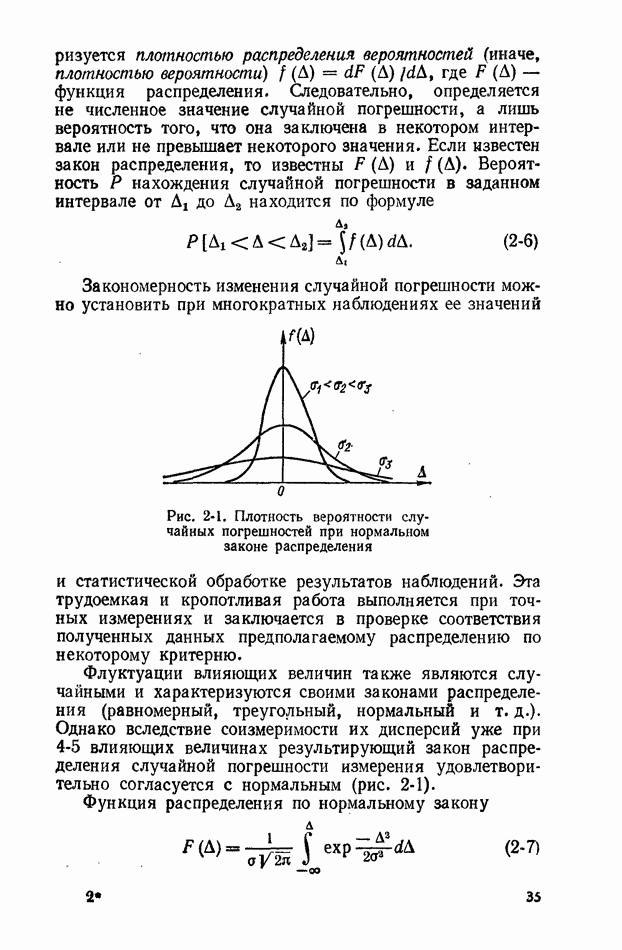
Закономерность изменения случайной погрешности можно установить при многократных наблюдениях ее значений и статистической обработке результатов наблюдений.

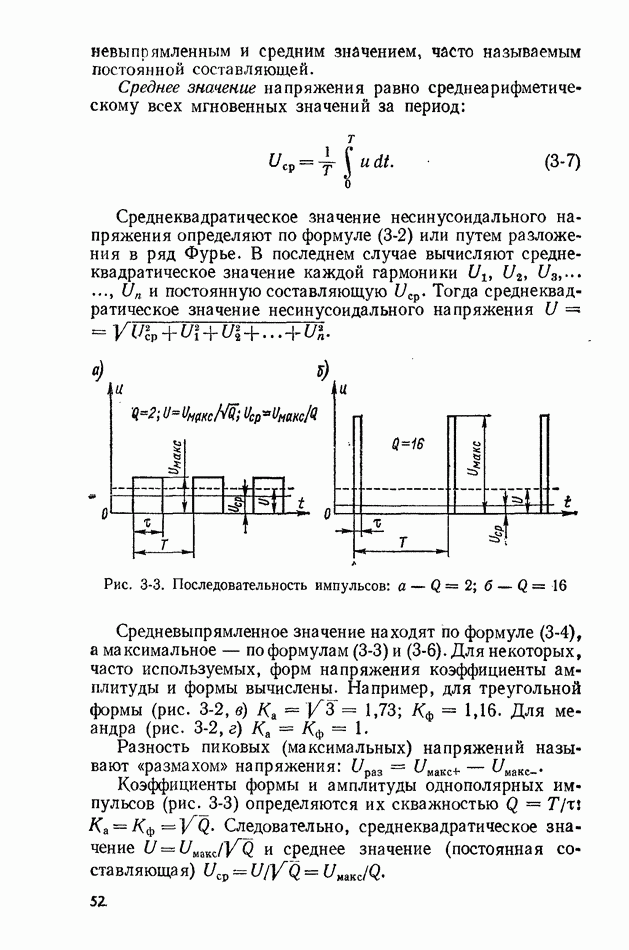
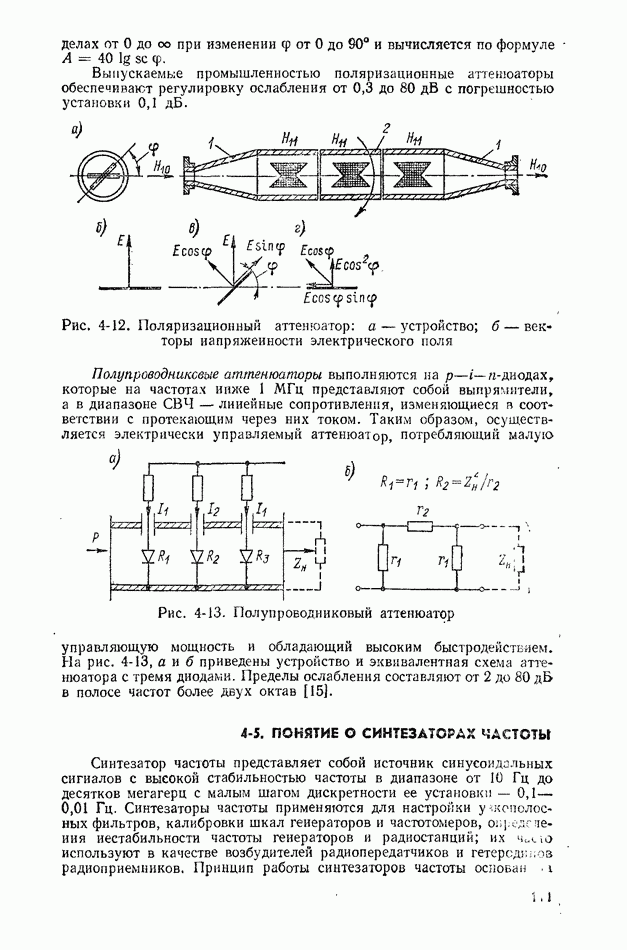
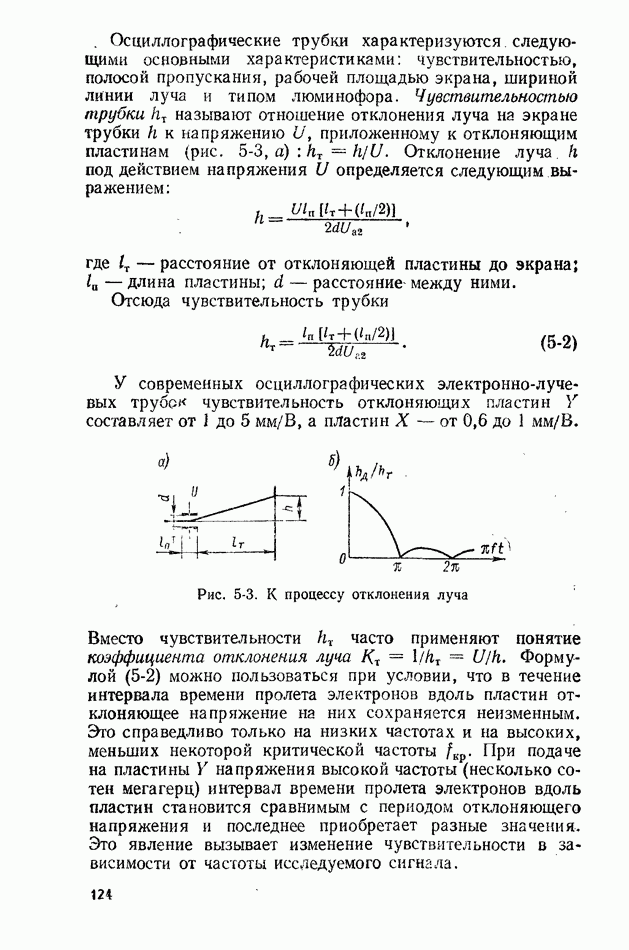
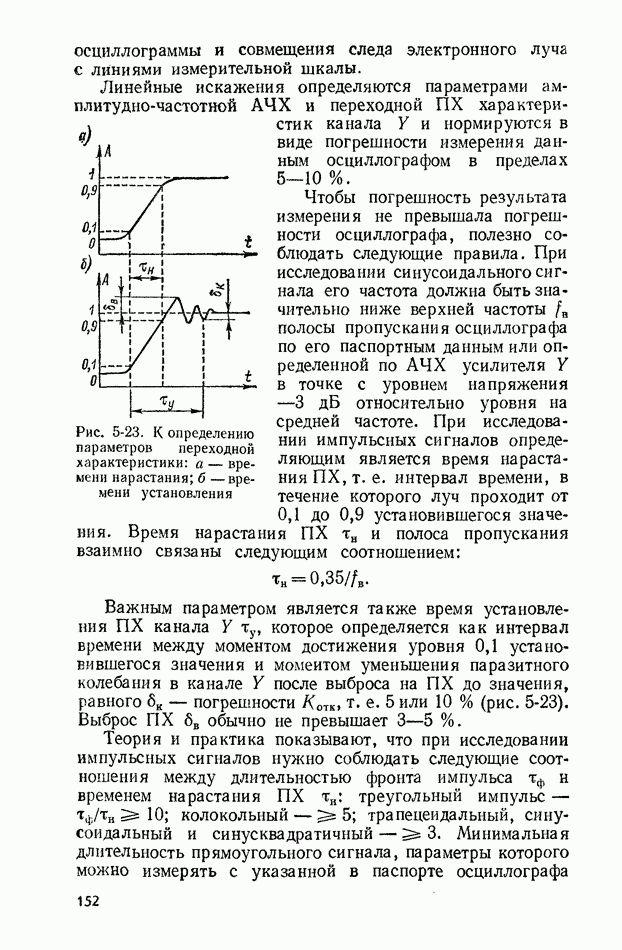
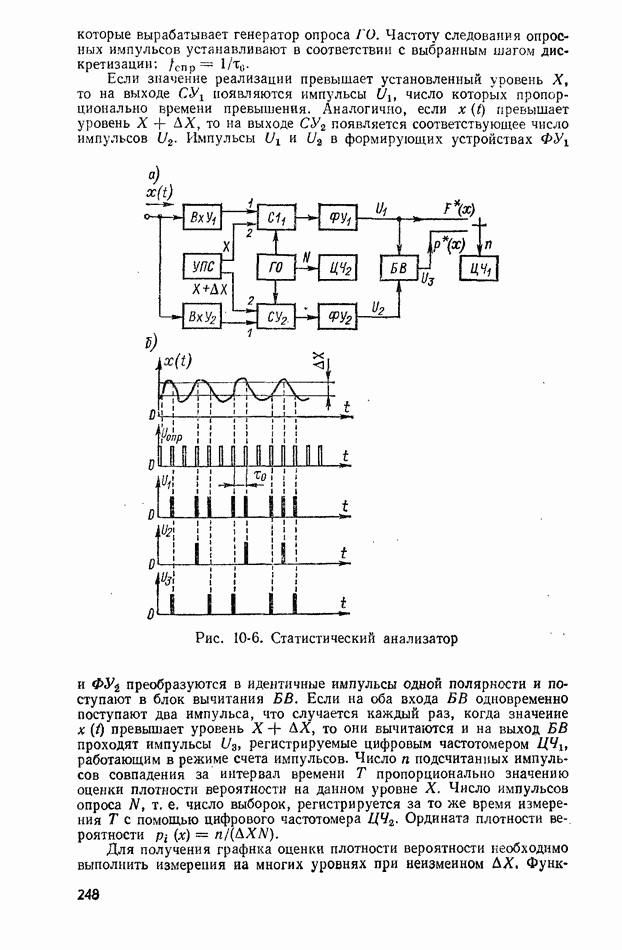
Рис. 2-1. Плотность вероятности случайных погрешностей при нормальном законе распределения
Эта трудоемкая и кропотливая работа выполняется при точных измерениях и заключается в проверке соответствия полученных данных предполагаемому распределению по некоторому критерию.
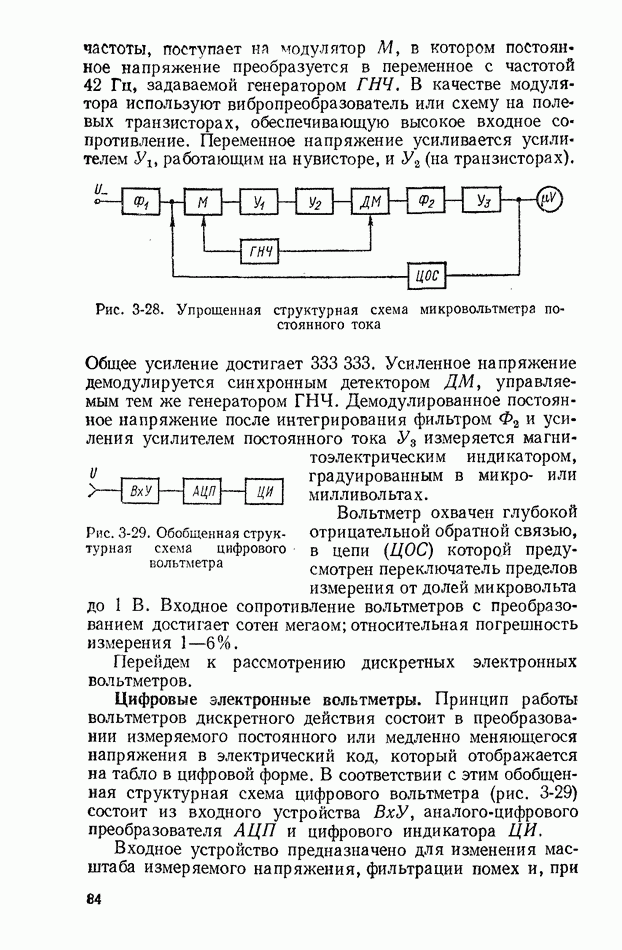
Флуктуации влияющих величин также являются случайными и характеризуются своими законами распределения (равномерный, треугольный, нормальный и т. д.). Однако вследствие соизмеримости их дисперсий уже при 4-5 влияющих величинах результирующий закон распределения случайной погрешности измерения удовлетворительно согласуется с нормальным (рис. 2-1).
Функция распределения по нормальному закону

и плотность вероятности

где  дисперсия, характеризующая рассеивание случайной погрешности относительно центра распределения, а
дисперсия, характеризующая рассеивание случайной погрешности относительно центра распределения, а  ее среднеквадратическое отклонение.
ее среднеквадратическое отклонение.
Дисперсия и среднеквадратическое отклонение характеризуют точность измерения: чем больше  тем меньше точность. В практике измерений преимущественно используется среднеквадратическое отклонение с, так как оно выражается в тех же единицах, что и измеряемая величина.
тем меньше точность. В практике измерений преимущественно используется среднеквадратическое отклонение с, так как оно выражается в тех же единицах, что и измеряемая величина.

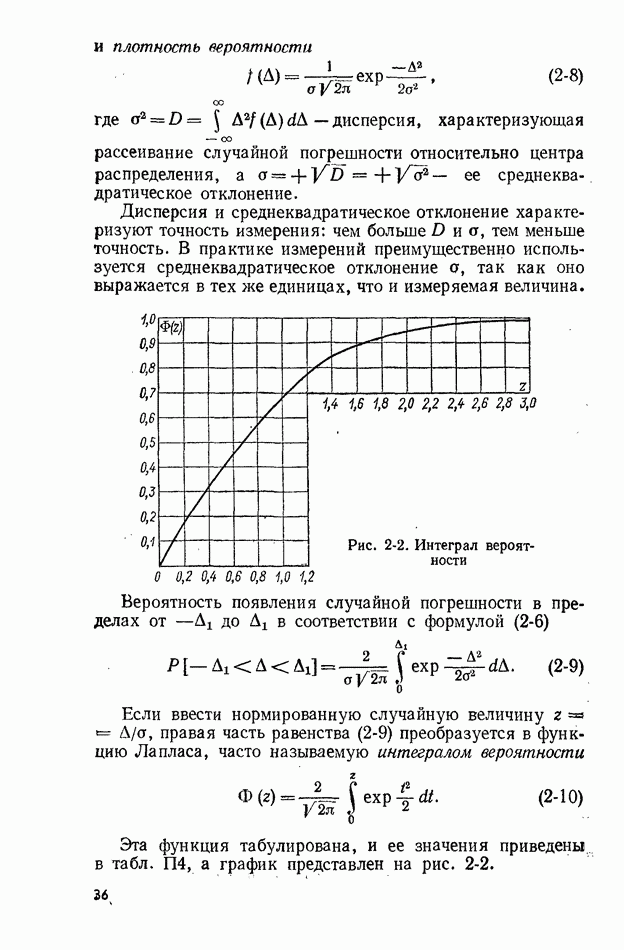
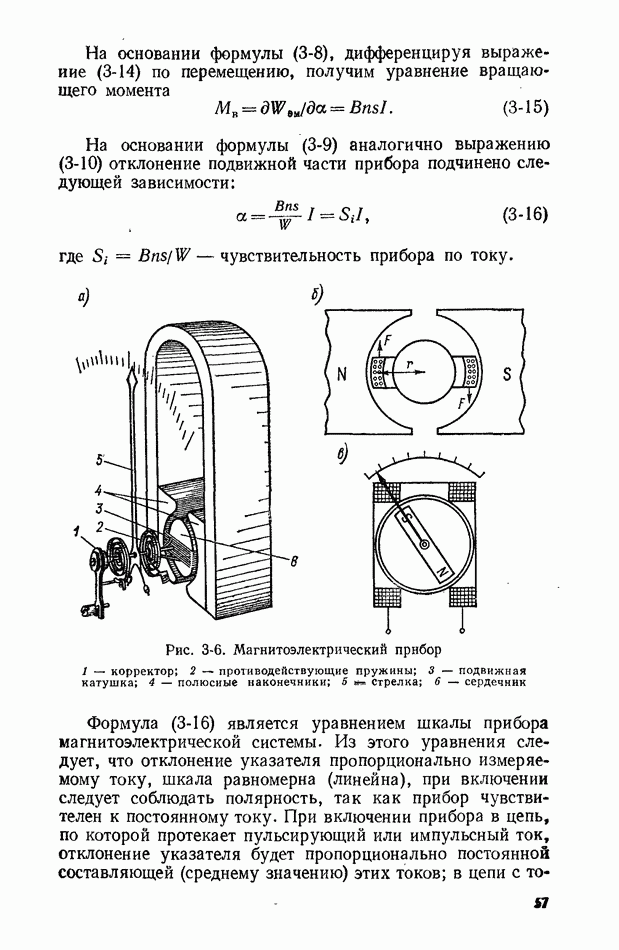
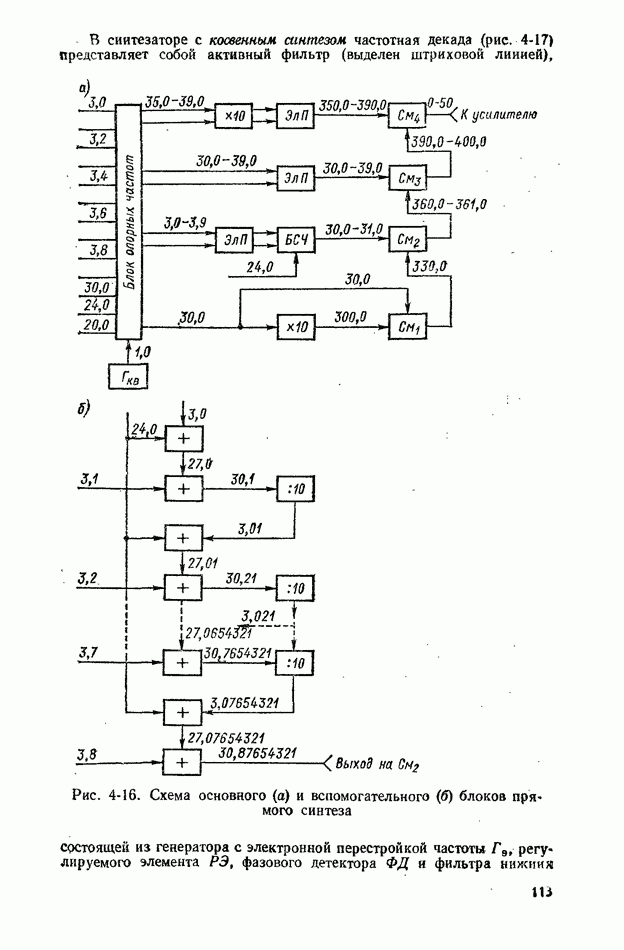
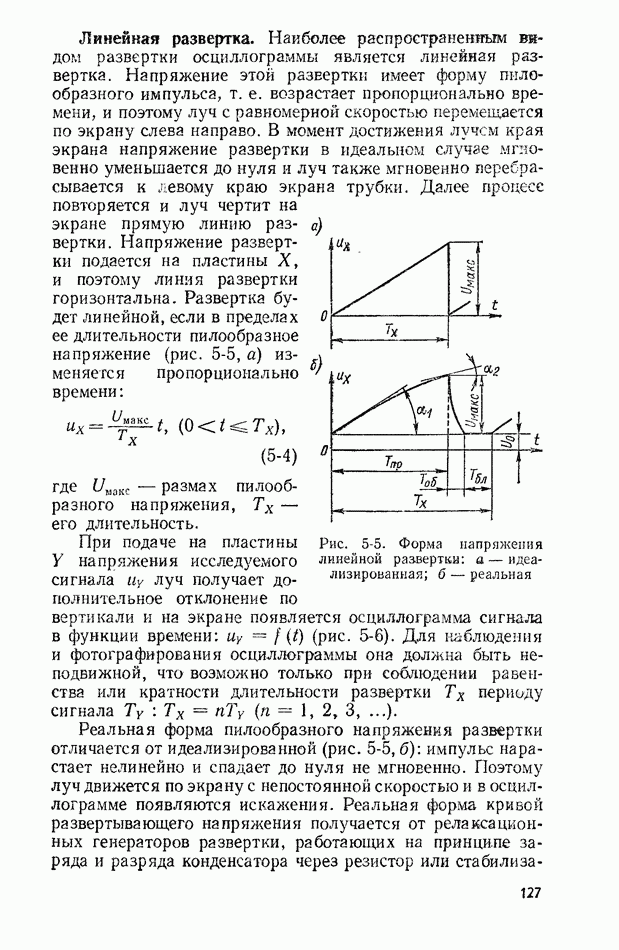
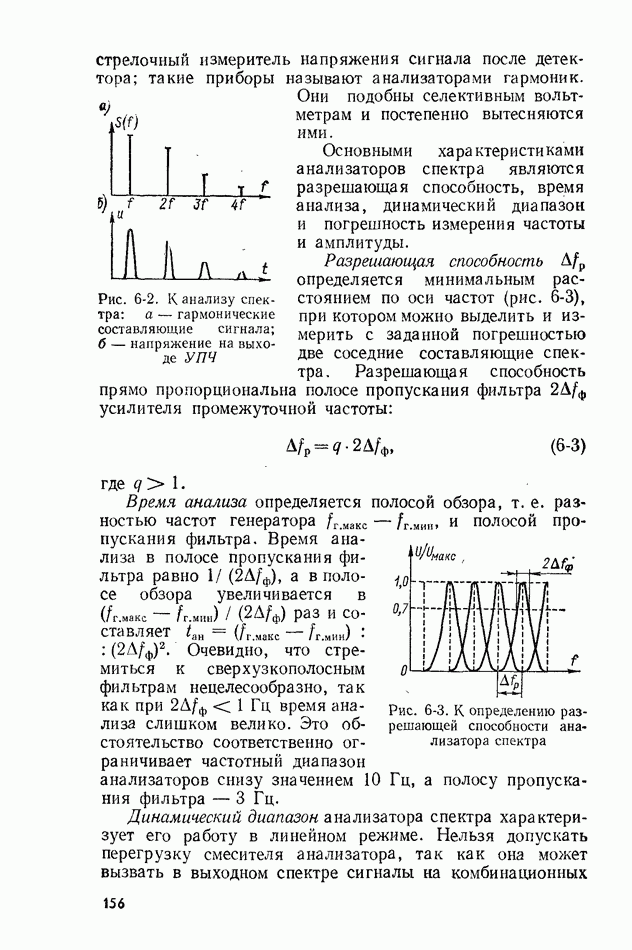
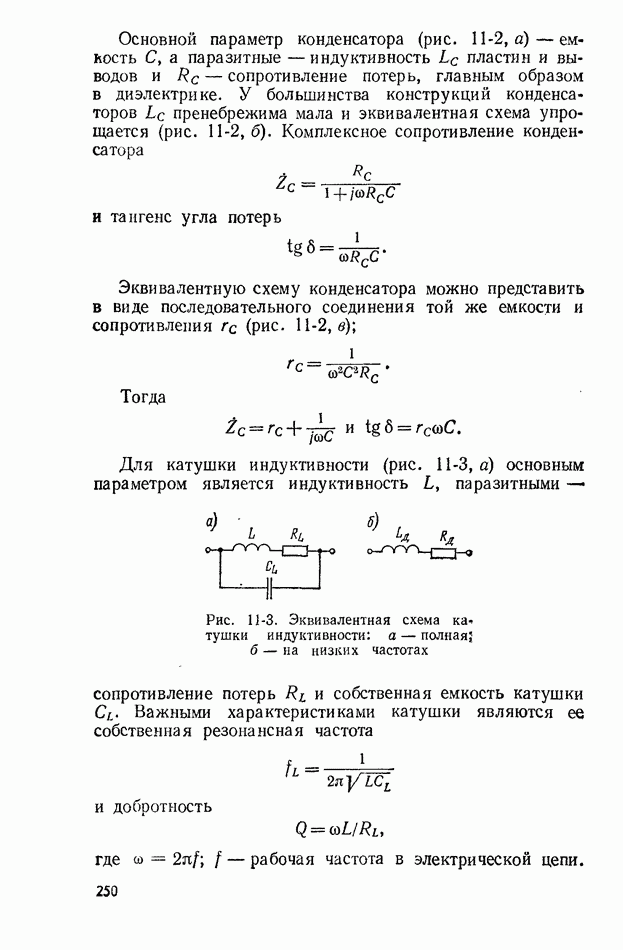
Рис. 2-2. Интеграл вероятности
Вероятность появления случайной погрешности в пределах от  до
до  в соответствии с формулой
в соответствии с формулой 

Если ввести нормированную случайную величину  правая часть равенства
правая часть равенства  преобразуется в функцию Лапласа, часто называемую интегралом вероятности
преобразуется в функцию Лапласа, часто называемую интегралом вероятности

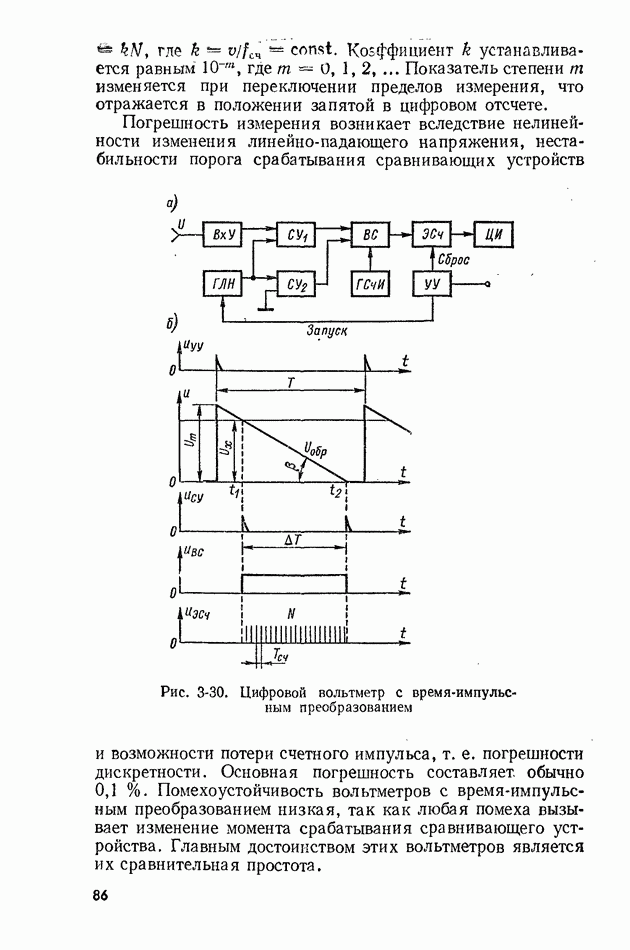
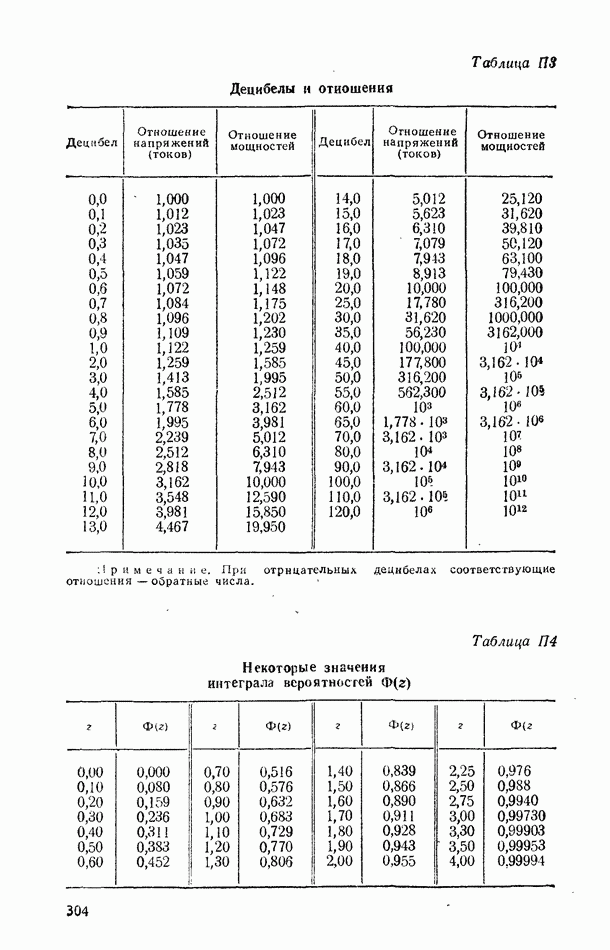
Эта функция табулирована, и ее значения приведены, в табл.  а график представлен на рис. 2-2.
а график представлен на рис. 2-2.
Если задана некоторая вероятность а  то, найдя
то, найдя  можно определить
можно определить  При нормальном законе распределения максимальную погрешность Дмакс принимают равной
При нормальном законе распределения максимальную погрешность Дмакс принимают равной  что соответствует вероятности появления погрешности, превышающей
что соответствует вероятности появления погрешности, превышающей  Это означает, что в 369 из 370 наблюдений с вероятностью 0,9973 погрешность заключена в интервале ±3а и лишь в одном наблюдении может выйти за его пределы.
Это означает, что в 369 из 370 наблюдений с вероятностью 0,9973 погрешность заключена в интервале ±3а и лишь в одном наблюдении может выйти за его пределы.

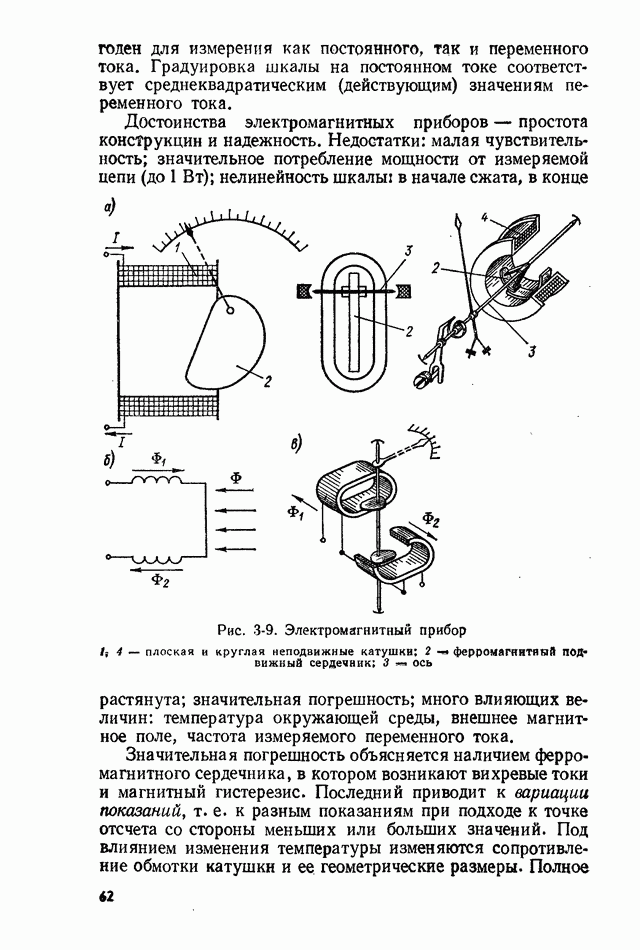
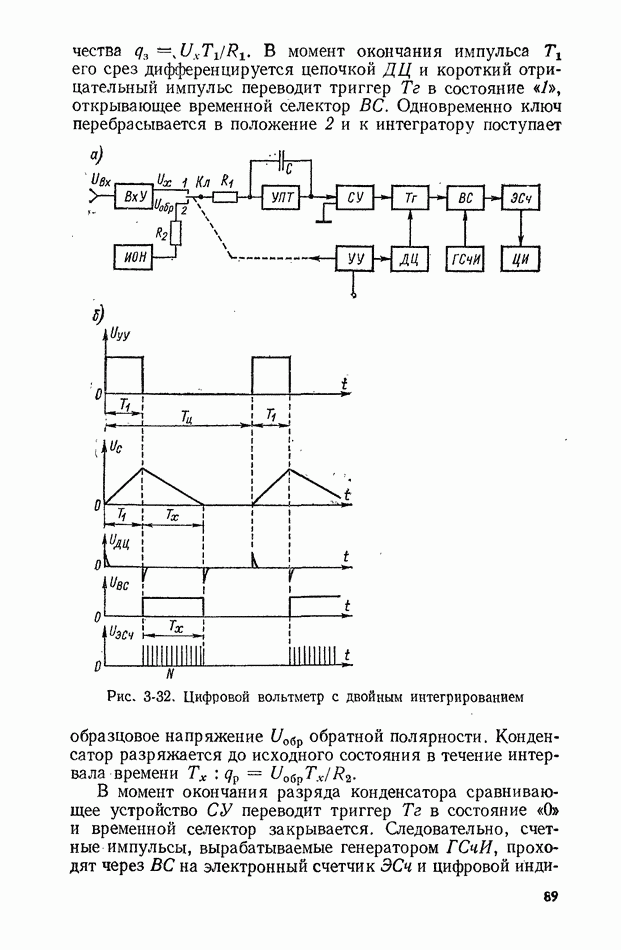
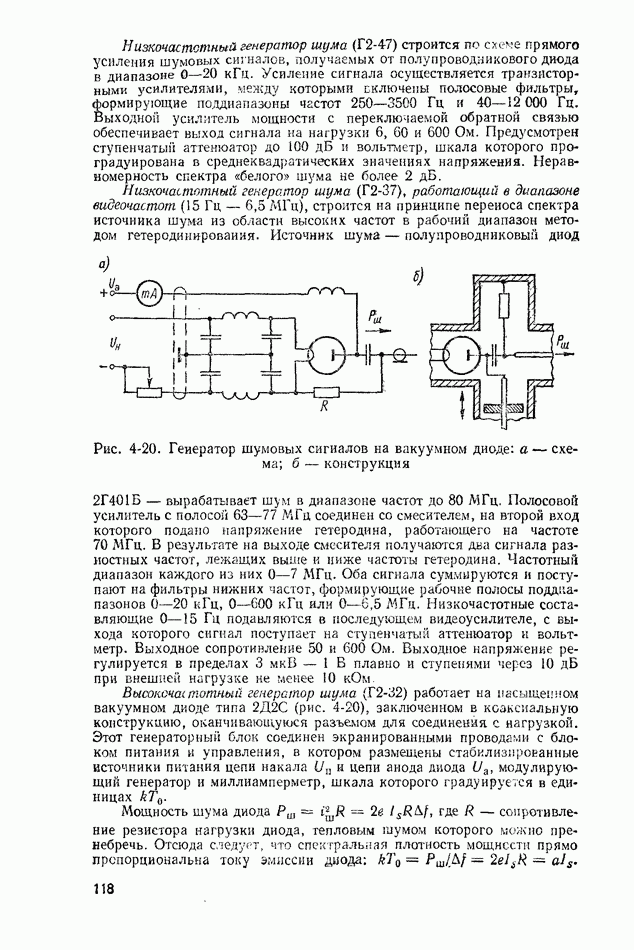
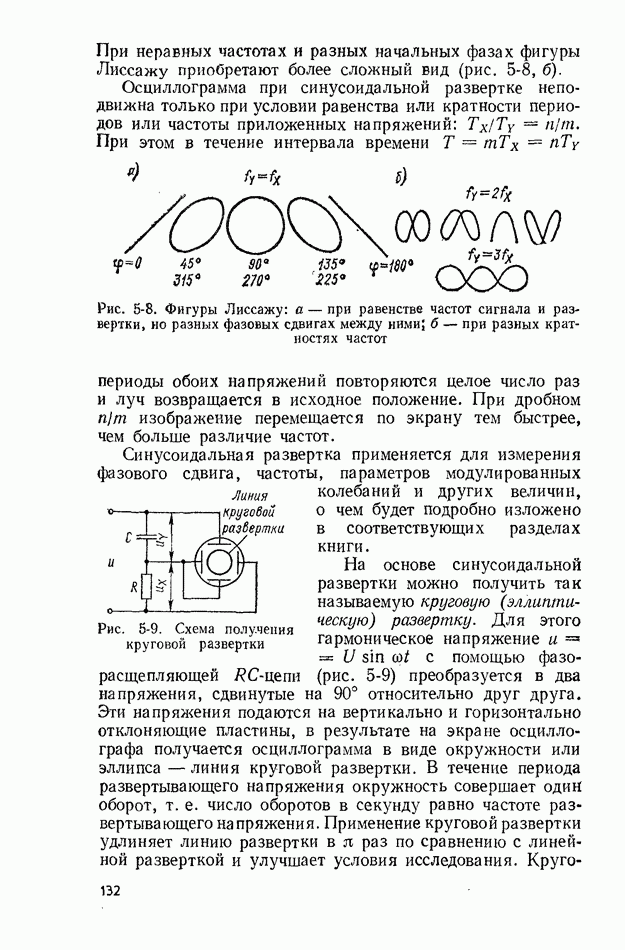
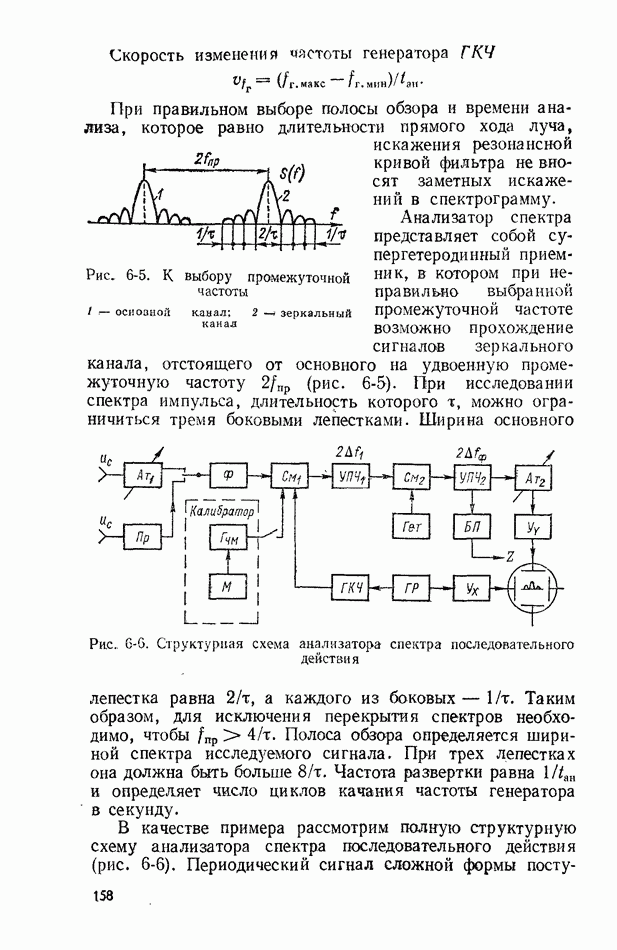
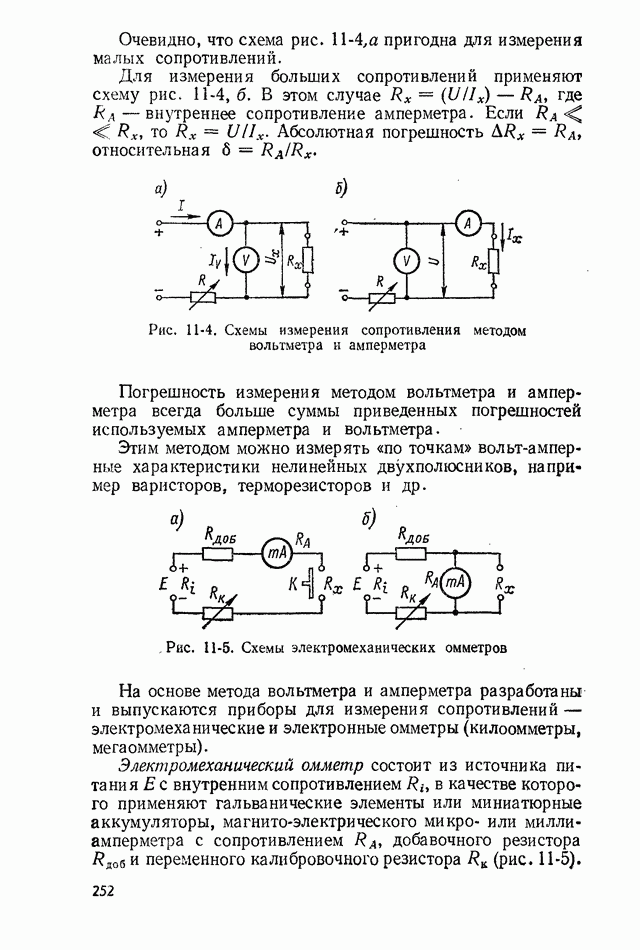
Рис. 2-3. Плотность вероятности случайных погрешностей при равномерном законе распределения
Равномерный закон распределения также встречается в измерениях. В частности, он характерен для измерения непрерывных величин методом дискретного счета. Плотность вероятности погрешности в интервале от  до
до  (рис. 2-3) записывается в следующем виде;
(рис. 2-3) записывается в следующем виде;

Следовательно, дисперсия

и среднеквадратическое отклонение

Например, погрешность квантования, которая обычно заключена в пределах единицы младшего разряда (от —1/2 до 1/2), характеризуется среднеквадратическим отклонением 
Вернемся к закону нормального распределения. Этот закон характеризуется численными параметрами: математическим ожиданием и дисперсией. Точное определение этих параметров практически невозможно, так как для этого нужно иметь бесконечно большое число значений случайной величины, т. е. выполнить  наблюдений при
наблюдений при  . В практике измерений
. В практике измерений  всегда конечно, поэтому вычисленные в результате эксперимента значения называют
всегда конечно, поэтому вычисленные в результате эксперимента значения называют
оценками математического ожидания и среднеквадратичен ского отклонения.
Рассмотрим процедуру статистического измерения некоторой величины, истинное значение которой  Производят
Производят  однократных наблюдений, в результате которых получают ряд случайных значений измеряемой величины
однократных наблюдений, в результате которых получают ряд случайных значений измеряемой величины  . В каждом
. В каждом  абсолютная погрешность 1-го наблюдения
абсолютная погрешность 1-го наблюдения  Определить значение этой погрешности невозможно, так как
Определить значение этой погрешности невозможно, так как  неизвестно.
неизвестно.
За оценку математического ожидания (истинного значения) принимают среднее арифметическое значение

которое называют действительным значением А измеряемой величины  при
при 
Теперь можно вычислить абсолютное отклонение  каждого результата наблюдения относительно среднего значения:
каждого результата наблюдения относительно среднего значения:  Очевидно, что
Очевидно, что  при
при  Для контроля правильности вычислений можно использовать свойства отклонений результатов наблюдений от среднего арифметического: сумма отклонений равна нулю
Для контроля правильности вычислений можно использовать свойства отклонений результатов наблюдений от среднего арифметического: сумма отклонений равна нулю  и сумма их квадратов минимальна:
и сумма их квадратов минимальна: 
Оценка  среднеквадратического отклонения абсолютных отклонений
среднеквадратического отклонения абсолютных отклонений  каждого из однократных
каждого из однократных  наблюдений определяется по формуле
наблюдений определяется по формуле

Точность результата  измерений будет выше. Она характеризуется оценкой
измерений будет выше. Она характеризуется оценкой  среднеквадратического отклонения среднего арифметического (действительного) значения:
среднеквадратического отклонения среднего арифметического (действительного) значения:

С увеличением числа измерений  (при независимых результатах) точность увеличивается пропорционально
(при независимых результатах) точность увеличивается пропорционально  Казалось бы, что увеличением
Казалось бы, что увеличением  можно получить любое увеличение точности. Однако здравый смысл и практика измерений подсказывают, что
можно получить любое увеличение точности. Однако здравый смысл и практика измерений подсказывают, что  приносит мало пользы, так как сама измеряемая величина может измениться за время измерения.
приносит мало пользы, так как сама измеряемая величина может измениться за время измерения.
Доверительный интервал и доверительная вероятность. В результате  наблюдений измеряемой величины
наблюдений измеряемой величины  получаем оценку ее действительного значения А, равного среднему арифметическому X, в соответствии с формулой (2-11). Эта оценка также случайная величина; ее среднеквадратическое отклонение а - определяется по формуле (2-13), т. е. результат измерения содержит неопределенность. Требуется выяснить, в каких пределах может изменяться действительное значение А при повторных измерениях (статистических) величины
получаем оценку ее действительного значения А, равного среднему арифметическому X, в соответствии с формулой (2-11). Эта оценка также случайная величина; ее среднеквадратическое отклонение а - определяется по формуле (2-13), т. е. результат измерения содержит неопределенность. Требуется выяснить, в каких пределах может изменяться действительное значение А при повторных измерениях (статистических) величины  в одних и тех же условиях, т. е. нужно найти интервал значений, который с заданной вероятностью «накрывает» истинное значение измеряемой величины. Такой интервал называют доверительным, а заданную (установленную) вероятность — доверительной. Доверительный интервал и доверительная вероятность характеризуют неопределенность результата измерения. Аналитически это записывается следующим образом:
в одних и тех же условиях, т. е. нужно найти интервал значений, который с заданной вероятностью «накрывает» истинное значение измеряемой величины. Такой интервал называют доверительным, а заданную (установленную) вероятность — доверительной. Доверительный интервал и доверительная вероятность характеризуют неопределенность результата измерения. Аналитически это записывается следующим образом:

Выражение (2-14) читается так: истинное значение измеренной величины  заключено в пределах доверительного интервала от
заключено в пределах доверительного интервала от  до
до  с доверительной вероятностью а.
с доверительной вероятностью а.
Аналогично для случайной погрешности

Случайная погрешность измерения заключена в пределах доверительного интервала от  до
до  с доверительной вероятностью а.
с доверительной вероятностью а.
В зависимости от целей измерения доверительную вероятность устанавливают равной  . В выражениях (2-14) и (2-15) доверительные интервалы симметричны. Половину доверительного интервала называют предельной (максимальной, допустимой) погрешностью при доверительной вероятности а. Иногда доверительный интервал несимметричен и имеет вид
. В выражениях (2-14) и (2-15) доверительные интервалы симметричны. Половину доверительного интервала называют предельной (максимальной, допустимой) погрешностью при доверительной вероятности а. Иногда доверительный интервал несимметричен и имеет вид 
Предельную погрешность и доверительный интервал выражают через среднеквадратическое отклонение. Для нормального закона распределения доверительный интервал по заданной доверительной вероятности (и наоборот) определяют при помощи таблицы интеграла вероятности (табл. П4). Задаются доверительной вероятностью  например 0,95. По таблице находят
например 0,95. По таблице находят  и значение
и значение  которое в данном случае равно 2. Так как
которое в данном случае равно 2. Так как  то
то  и доверительный интервал
и доверительный интервал 
Очевидно, что и доверительный интервал, и доверительная вероятность связаны с числом наблюдений  так как
так как  Чем больше
Чем больше  тем уже интервал. Однако, как уже было сказано выше, в практике измерений
тем уже интервал. Однако, как уже было сказано выше, в практике измерений  встречается редко. Для числа наблюдений
встречается редко. Для числа наблюдений  доверительный интервал определяется не через
доверительный интервал определяется не через  а через некоторый коэффициент
а через некоторый коэффициент  который зависит от числа наблюдений
который зависит от числа наблюдений  и доверительной вероятности а. Закон изменения коэффициента
и доверительной вероятности а. Закон изменения коэффициента  определяется распределением Стьюдента нормированной случайной величины
определяется распределением Стьюдента нормированной случайной величины  вычисленного для
вычисленного для  с нормальным распределением. Коэффициент
с нормальным распределением. Коэффициент  определяется с помощью следующей формулы:
определяется с помощью следующей формулы:

где  доверительная вероятность;
доверительная вероятность;  плотность вероятности распределения Стьюдента при 2.
плотность вероятности распределения Стьюдента при 2.
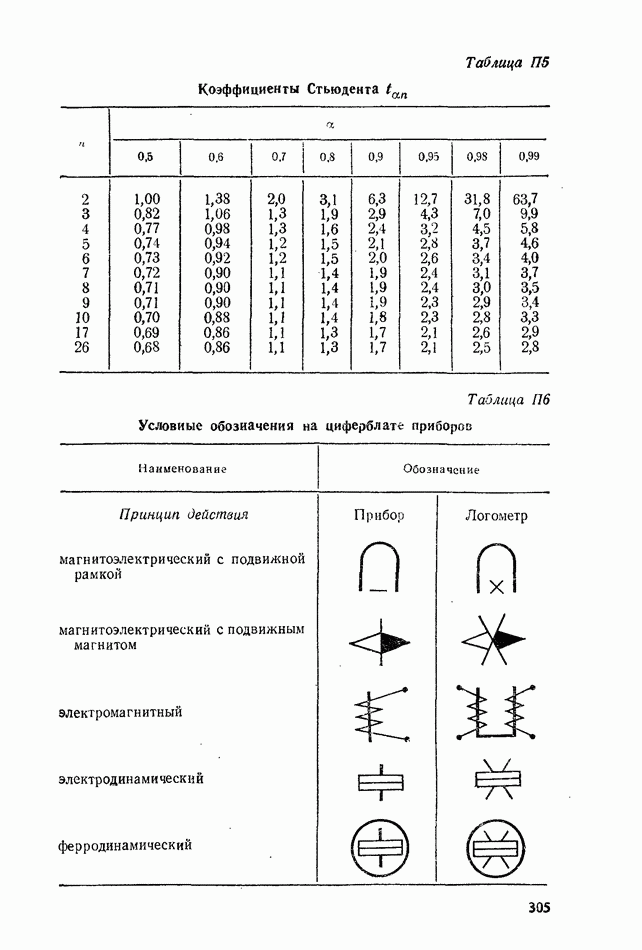
Интеграл  табулирован (см. табл. П5). При
табулирован (см. табл. П5). При  распределение Стьюдента стремится к нормальному. Доверительный интервал находят по заданной вероятности и числу наблюдений. Например:
распределение Стьюдента стремится к нормальному. Доверительный интервал находят по заданной вероятности и числу наблюдений. Например:  Из табл.
Из табл.  находят значение
находят значение  Тогда
Тогда 
Легко убедиться, что при использовании распределения Стьюдента доверительный интервал расширяется при той же самой доверительной вероятности.
Грубые погрешности. При статистических измерениях результаты каждого наблюдения отличаются друг от друга. Нередко случается, что одно или два значения отличаются более резко, чем остальные. Если можно утверждать, что
это не промахи, т. е. не явные ошибки, допущенные оператором, то необходимо установить, не являются ли они грубыми погрешностями, которые так же нужно исключить из обработки, как и промахи. Исключение грубой погрешности без достаточных оснований приводит к необоснованному улучшению результата измерений. С другой стороны, неисключение грубой погрешности, в особенности при малом числе наблюдений, исказит как действительное значение измеренной величины, так и границы доверительного интервала. Следовательно, грубые погрешности необходимо обнаруживать и исключать.
Простейшим способом обнаружения грубой погрешности при нормальном законе распределения является сравнение абсолютной погрешности «подозрительного» наблюдения  с максимальной погрешностью
с максимальной погрешностью  Если
Если  то этот результат следует отбросить и вновь вычислить значения
то этот результат следует отбросить и вновь вычислить значения  Этот способ основан на том, что вероятность появления значения, отклоняющегося от среднего арифметического более чем на
Этот способ основан на том, что вероятность появления значения, отклоняющегося от среднего арифметического более чем на  равна всего лишь 0,003.
равна всего лишь 0,003.
Однако следует помнить, что при небольшом числе наблюдений  хотя и с малой вероятностью, но возможно, что отброшенное число является не грубой погрешностью, а естественным статистическим отклонением данной величины. Поэтому в ответственных случаях определение грубой погрешности производится на основе теории вероятности
хотя и с малой вероятностью, но возможно, что отброшенное число является не грубой погрешностью, а естественным статистическим отклонением данной величины. Поэтому в ответственных случаях определение грубой погрешности производится на основе теории вероятности  . Устанавливается, при каком числе измерений
. Устанавливается, при каком числе измерений  с заданной вероятностью а можно отбросить результат наблюдения, превышающий заданное число или заданные границы.
с заданной вероятностью а можно отбросить результат наблюдения, превышающий заданное число или заданные границы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 1-2. МЕРЫ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 1-3. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 1-4. ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 1-5. ИЗМЕРИТЕЛЬНЫЕ УСТАНОВКИ И СИСТЕМЫ
- 1-6. ОСНОВНЫЕ СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЯ
- 1-7. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
- ГЛАВА ВТОРАЯ. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-2. СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
- 2-3. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
- 2-4. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- 2-5. ПОГРЕШНОСТЬ КОСВЕННЫХ ИЗМЕРЕНИЯ
- 2-6. НЕКОТОРЫЕ ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЯ И ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ
- ГЛАВА ТРЕТЬЯ. ИЗМЕРЕНИЕ ТОКА И НАПРЯЖЕНИЯ
- 3-2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АМПЕРМЕТРЫ И ВОЛЬТМЕТРЫ
- 3-3. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
- ГЛАВА ЧЕТВЕРТАЯ. ГЕНЕРАТОРЫ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ
- 4-2. ГЕНЕРАТОРЫ СИГНАЛОВ ИНФРАНИЗКИХ И НИЗКИХ ЧАСТОТ
- 4-3. ГЕНЕРАТОРЫ СИГНАЛОВ ВЫСОКИХ И УЛЬТРАВЫСОКИХ ЧАСТОТ
- 4-4. ГЕНЕРАТОРЫ СИГНАЛОВ СВЕРХВЫСОКИХ ЧАСТОТ
- 4-5. ПОНЯТИЕ О СИНТЕЗАТОРАХ ЧАСТОТЫ
- 4-6. ГЕНЕРАТОРЫ ИМПУЛЬСНЫХ СИГНАЛОВ
- 4-7. ГЕНЕРАТОРЫ ШУМОВЫХ СИГНАЛОВ
- ГЛАВА ПЯТАЯ. ЭЛЕКТРОННО-ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 5-2. ЭЛЕКТРОННО-ЛУЧЕВЫЕ ТРУБКИ
- 5-3. ОСЦИЛЛОГРАФИЧЕСКИЕ РАЗВЕРТКИ
- 5-4. КАНАЛЫ УПРАВЛЕНИЯ ЛУЧОМ
- 5-5. КАЛИБРАТОРЫ АМПЛИТУДЫ И ДЛИТЕЛЬНОСТИ
- 5-6. СТРОБОСКОПИЧЕСКИЕ ОСЦИЛЛОГРАФЫ
- 5-7. НЕКОТОРЫЕ ОСОБЕННОСТИ ОСЦИЛЛОГРАФИЧЕСКИХ ИЗМЕРЕНИЙ
- ГЛАВА ШЕСТАЯ. ИЗМЕРЕНИЕ СПЕКТРА И ФОРМЫ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 6-2. АНАЛИЗАТОРЫ СПЕКТРА ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- 6-3. АНАЛИЗ СПЕКТРА В РЕАЛЬНОМ ВРЕМЕНИ
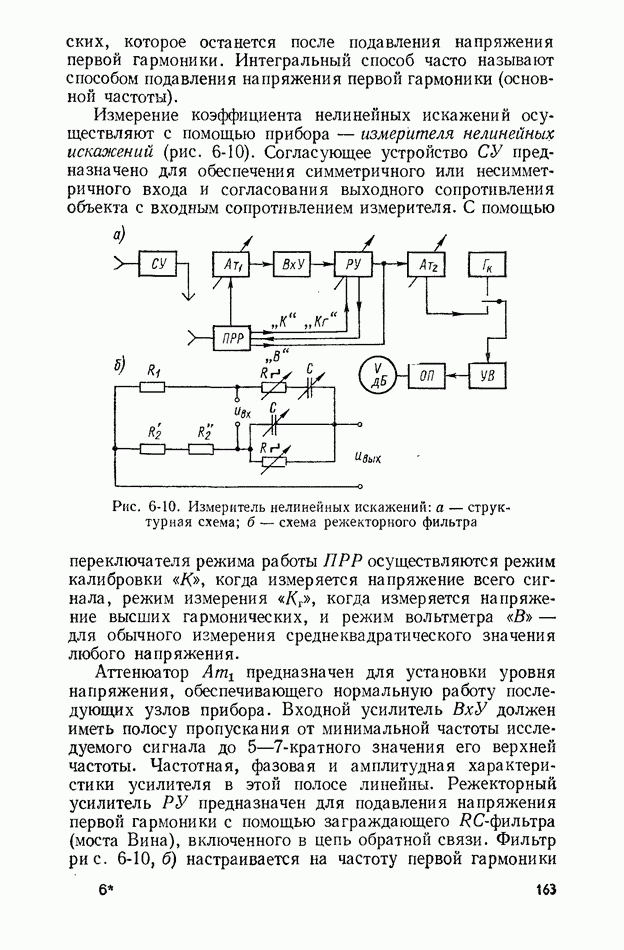
- 6-4. ИЗМЕРЕНИЕ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
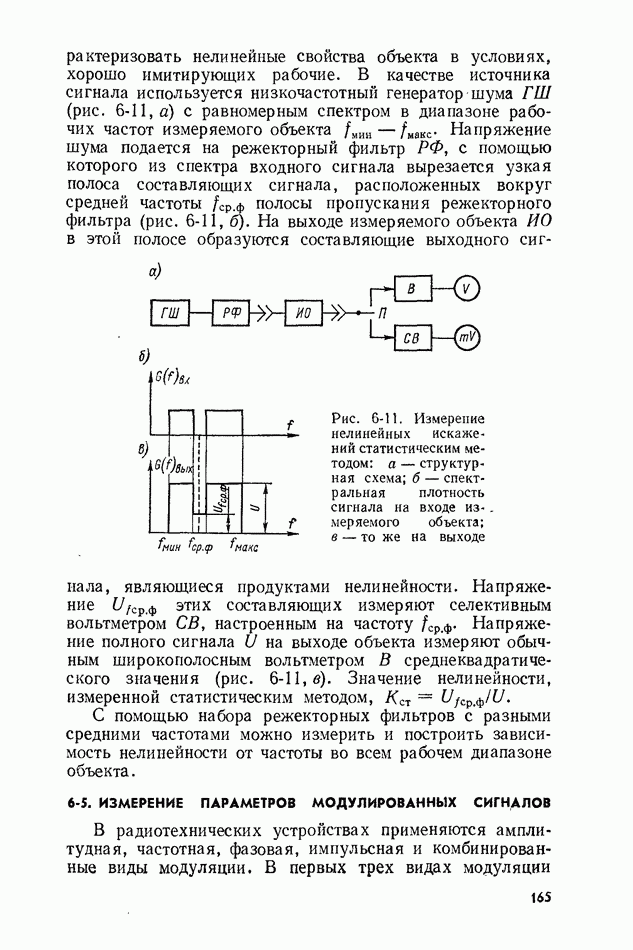
- 6-5. ИЗМЕРЕНИЕ ПАРАМЕТРОВ МОДУЛИРОВАННЫХ СИГНАЛОВ
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ФАЗОВОГО СДВИГА
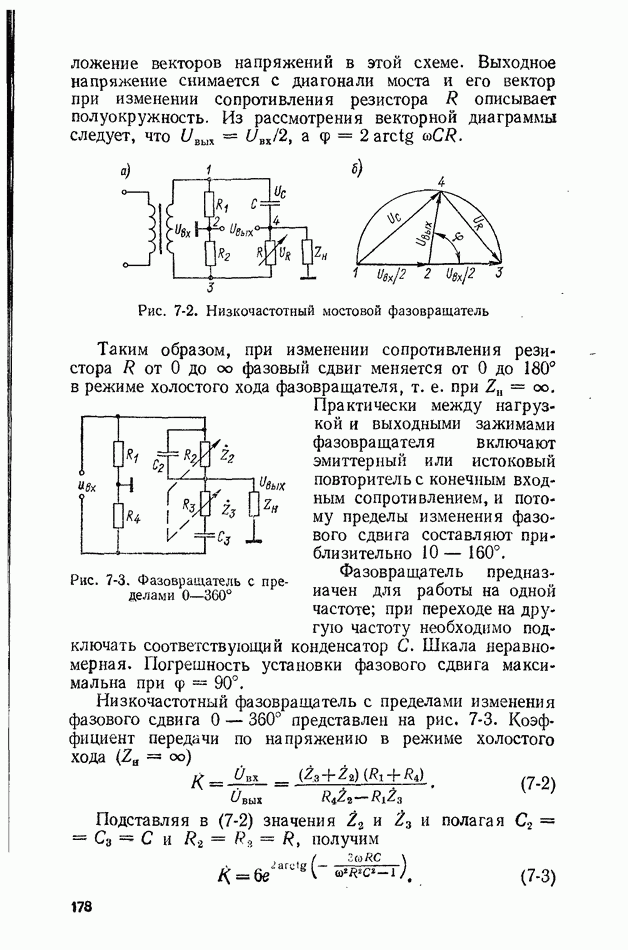
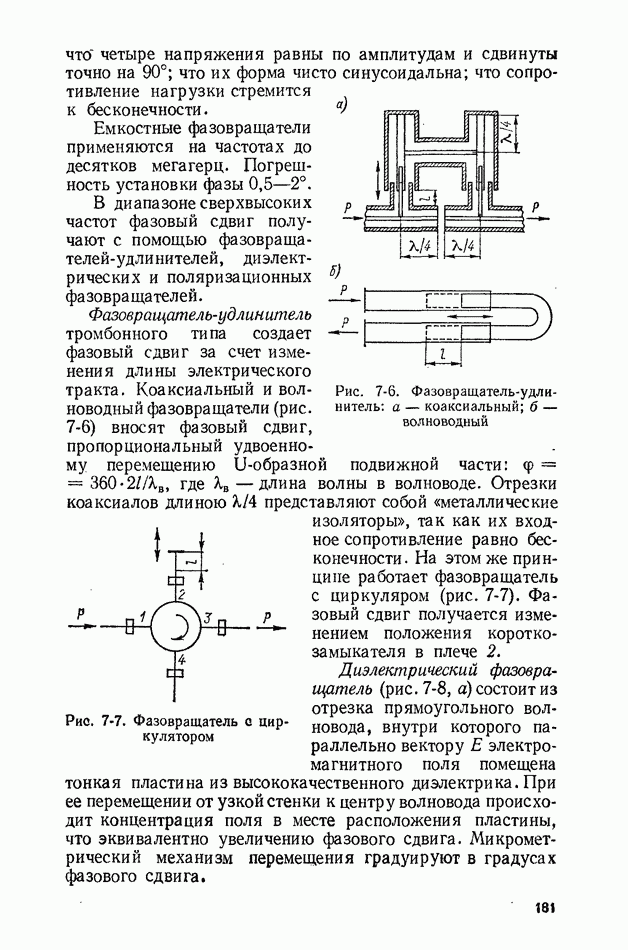
- 7-2. ФАЗОВРАЩАТЕЛИ
- 7-3. ОСЦИЛЛОГРАФИЧЕСКИЙ МЕТОД
- 7-4. КОМПЕНСАЦИОННЫЙ МЕТОД
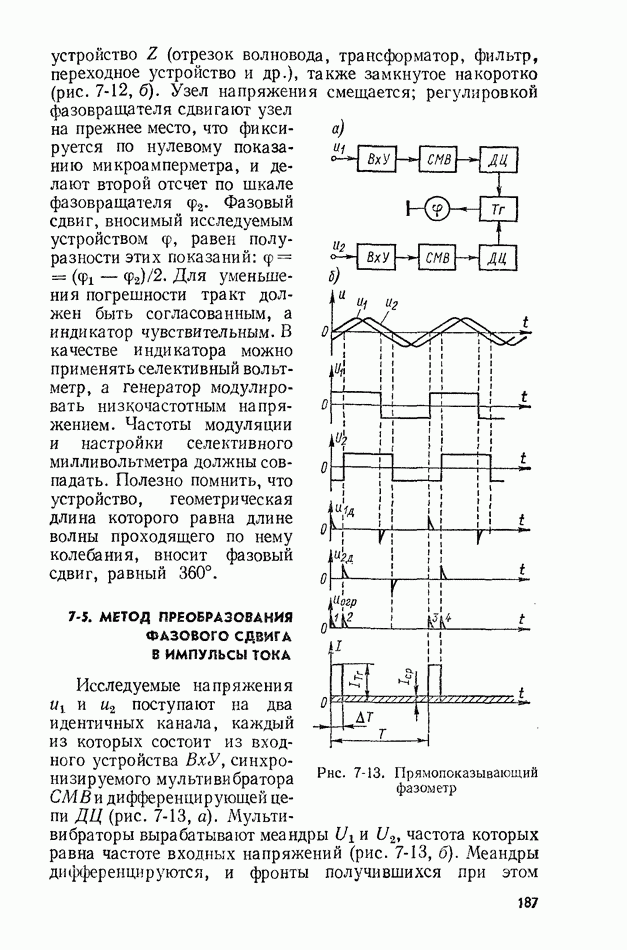
- 7-5. МЕТОД ПРЕОБРАЗОВАНИЯ ФАЗОВОГО СДВИГА В ИМПУЛЬСЫ ТОКА
- 7-6. МЕТОД ДИСКРЕТНОГО СЧЕТА
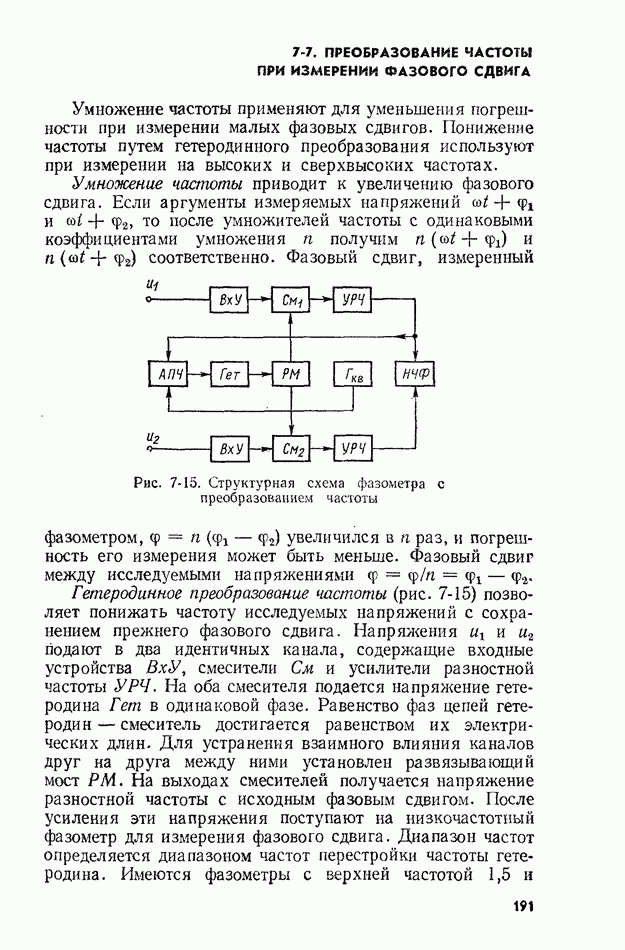
- 7-7. ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ ПРИ ИЗМЕРЕНИИ ФАЗОВОГО СДВИГА
- ГЛАВА ВОСЬМАЯ. ИЗМЕРЕНИЕ ЧАСТОТЫ И ИНТЕРВАЛОВ ВРЕМЕНИ
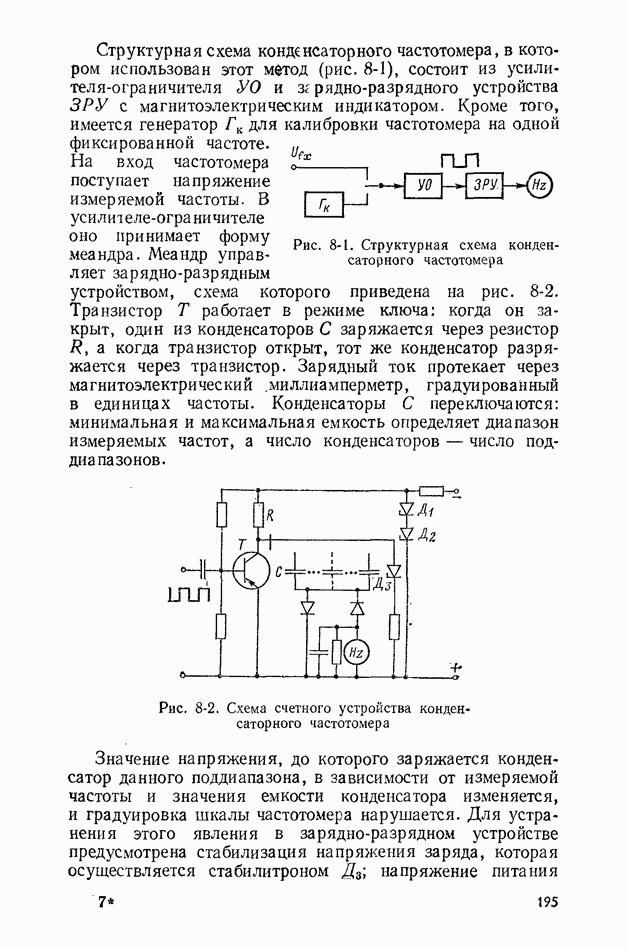
- 8-2. МЕТОД ПЕРЕЗАРЯДА КОНДЕНСАТОРА
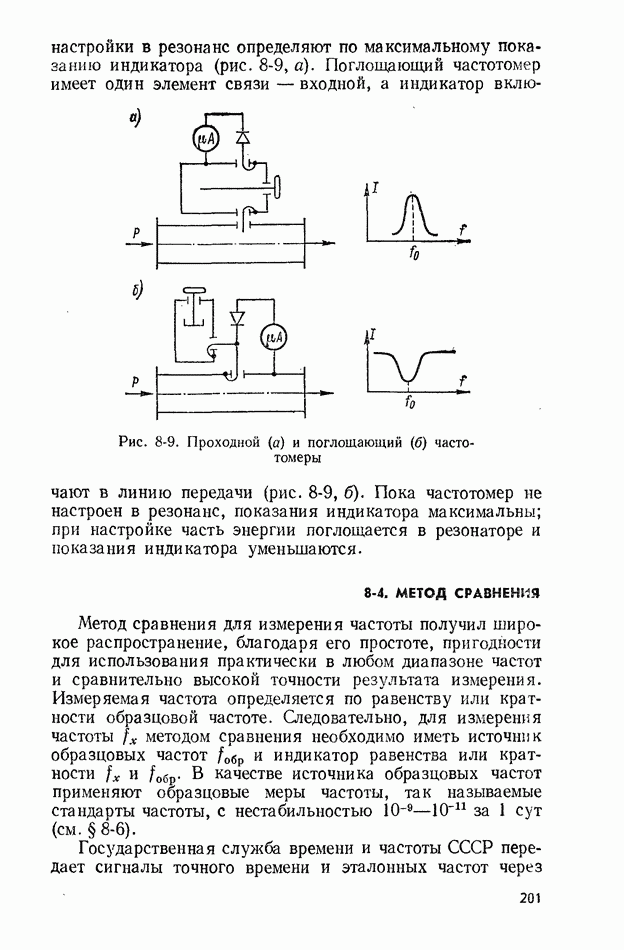
- 8-3. РЕЗОНАНСНЫЙ МЕТОД
- 8-4. МЕТОД СРАВНЕНИЯ
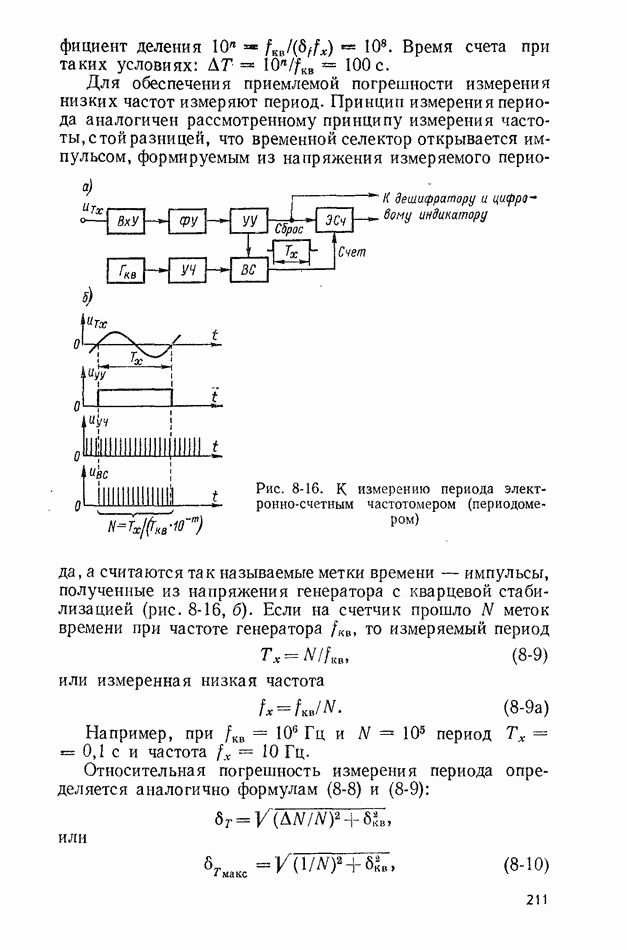
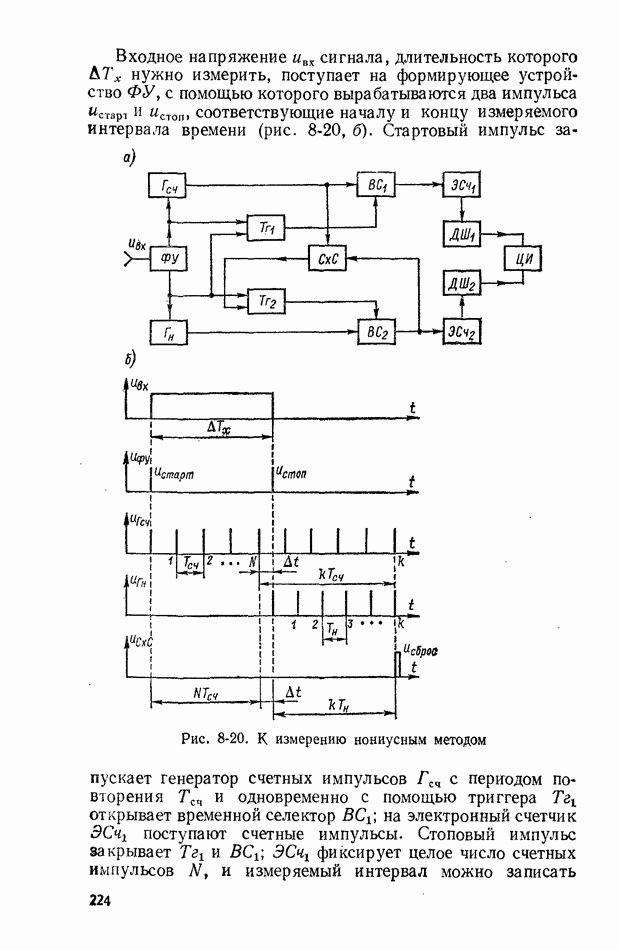
- 8-5. МЕТОД ДИСКРЕТНОГО СЧЕТА
- 8-6. ПОНЯТИЕ О СТАНДАРТАХ ЧАСТОТЫ И ВРЕМЕНИ
- 8-7. ПРЕЦИЗИОННОЕ ИЗМЕРЕНИЕ ЧАСТОТЫ И ВРЕМЕНИ
- ГЛАВА ДЕВЯТАЯ. ИЗМЕРЕНИЕ МОЩНОСТИ
- 9-2. ИЗМЕРЕНИЕ ПОГЛОЩАЕМОЙ МОЩНОСТИ
- 5-3. ИЗМЕРЕНИЕ ПРОХОДЯЩЕЙ МОЩНОСТИ
- 9-4. ИЗМЕРЕНИЕ ВЕСЬМА МАЛОЙ МОЩНОСТИ
- ГЛАВА ДЕСЯТАЯ. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ СИГНАЛОВ
- 10-2. ИЗМЕРЕНИЕ МОМЕНТОВ
- 10-3. ИЗМЕРЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ
- 10-4. ИЗМЕРЕНИЕ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА
- 10-5. ИЗМЕРЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТИ ВЕРОЯТНОСТИ
- ГЛАВА ОДИННАДЦАТАЯ. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЭЛЕМЕНТОВ ЭЛЕКТРИЧЕСКИХ И РАДИОТЕХНИЧЕСКИХ УСТРОЙСТВ
- 11-2. МЕТОД ВОЛЬТМЕТРА И АМПЕРМЕТРА
- 11-3. МОСТОВОЙ МЕТОД
- 11.4. РЕЗОНАНСНЫЙ МЕТОД
- 11-5. МЕТОД ДИСКРЕТНОГО СЧЕТА
- 11-6. ИЗМЕРЕНИЕ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 11-7. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ИНТЕГРАЛЬНЫХ СХЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЦЕПЕЙ СВЕРХВЫСОКИХ ЧАСТОТ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ ЛИНИИ
- 12-3. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА СТОЯЧЕЙ ВОЛНЫ И КОЭФФИЦИЕНТА ОТРАЖЕНИЯ
- 12-4. ИЗМЕРЕНИЕ ПОЛНОГО СОПРОТИВЛЕНИЯ
- 12-5. ИЗМЕРЕНИЕ НЕОДНОРОДНОСТИ
- ГЛАВА ТРИНАДЦАТАЯ. ИЗМЕРЕНИЕ ОСЛАБЛЕНИЯ
- 13-2. ИЗМЕРЕНИЕ ВНОСИМОГО ОСЛАБЛЕНИЯ
- 13-3. ИЗМЕРЕНИЕ СОБСТВЕННОГО ОСЛАБЛЕНИЯ
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЕ П1
- ПРИЛОЖЕНИЕ 2. КЛАССИФИКАЦИЯ РАДИОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ