| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА ДЕСЯТАЯ. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ СИГНАЛОВ
10-1. ОПРЕДЕЛЕНИЯ ИЗМЕРЯЕМЫХ ВЕЛИЧИН
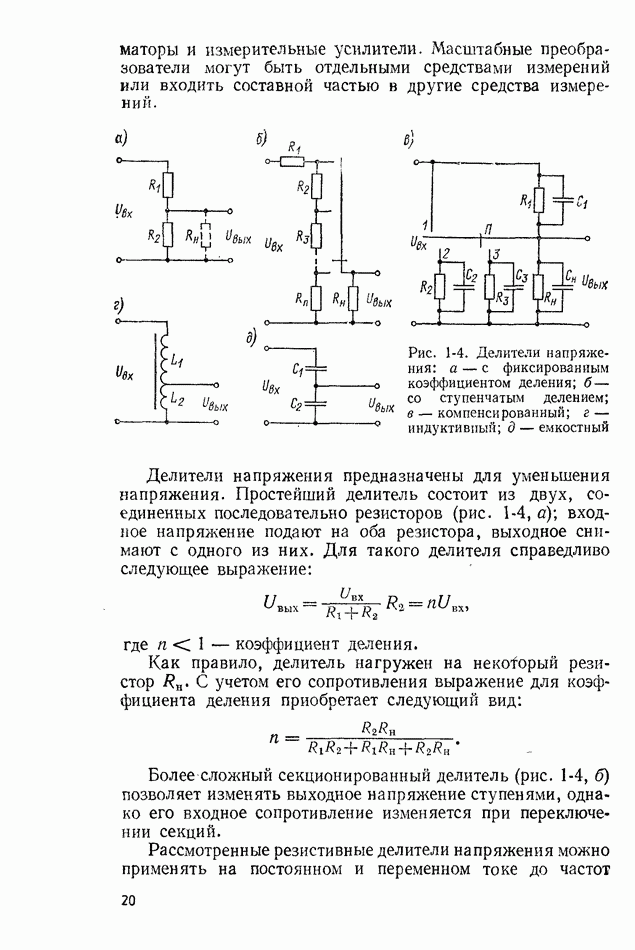
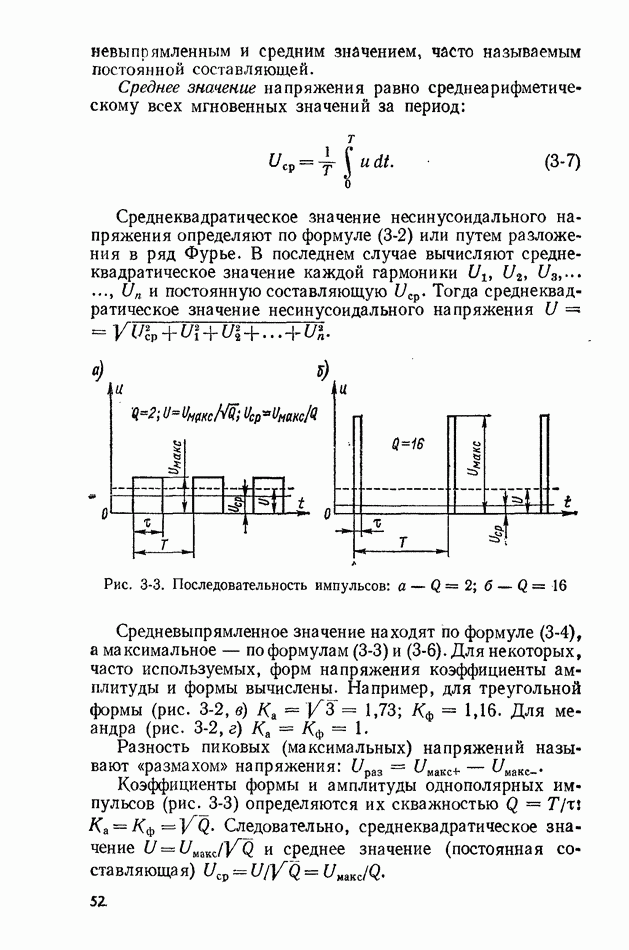
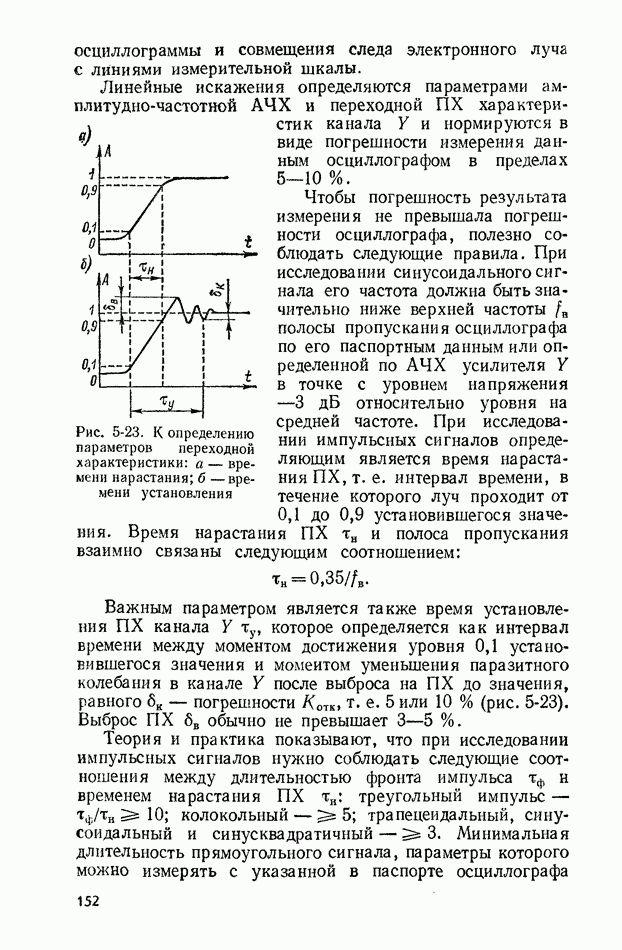
Случайный (вероятностный, или стохастический) сигнал может принимать различные значения в зависимости от случая, и его изменения точно предсказать невозможно (рис. 10-1). Случайные сигналы подразделяют на стационарные и нестационарные. Случайный сигнал называется стационарным., если плотность вероятности любой совокупности его мгновенных значений не изменяется при любом сдвиге этой совокупности во времени, т. е.

Нестационарным называется случайный сигнал, у которого Плотность вероятности некоторой совокупности его мгновенных значений изменяется при сдвиге этой совокупности во времени, т. е. в выражении (10-1) должен стоять знак неравенства.
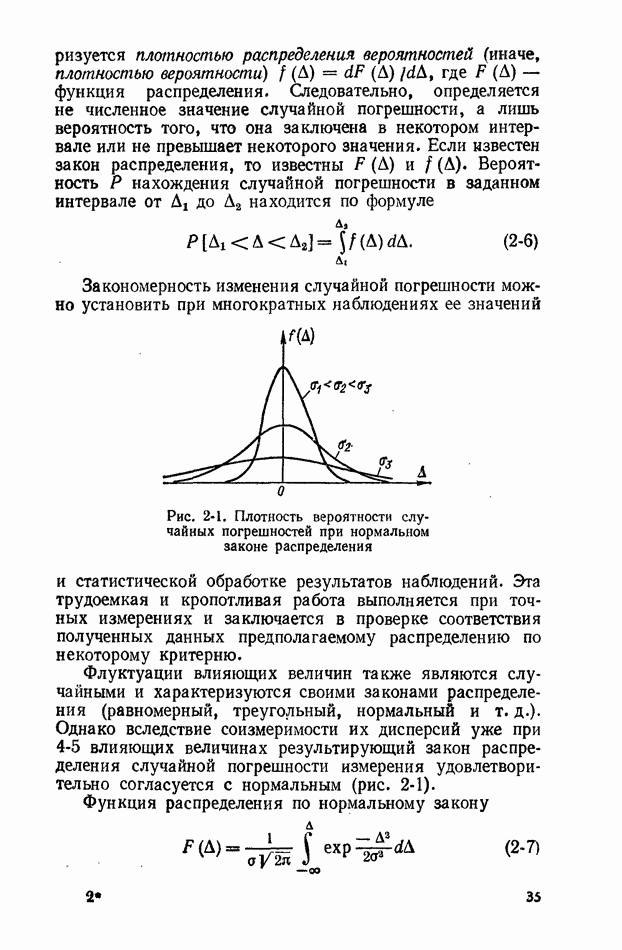
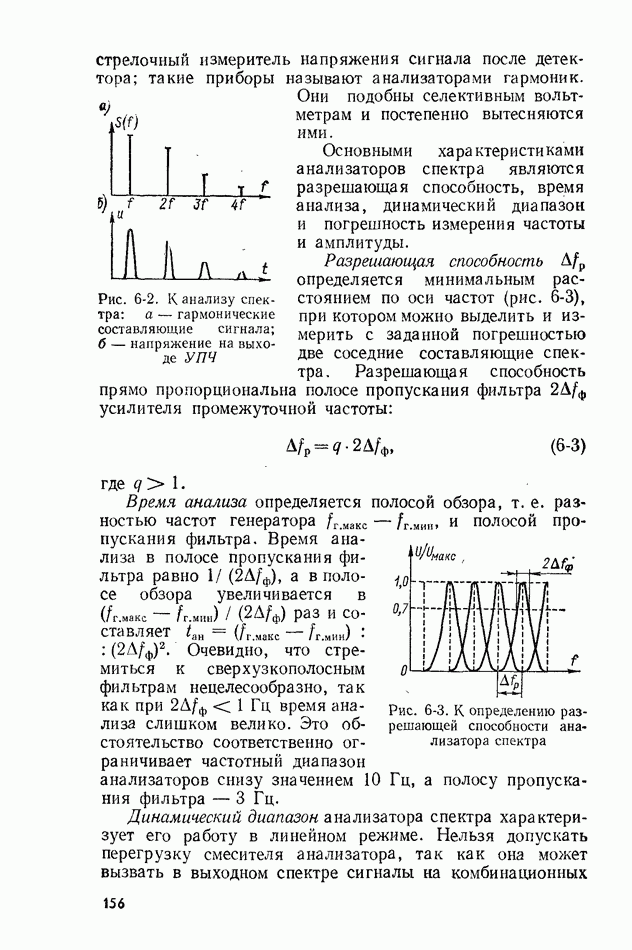
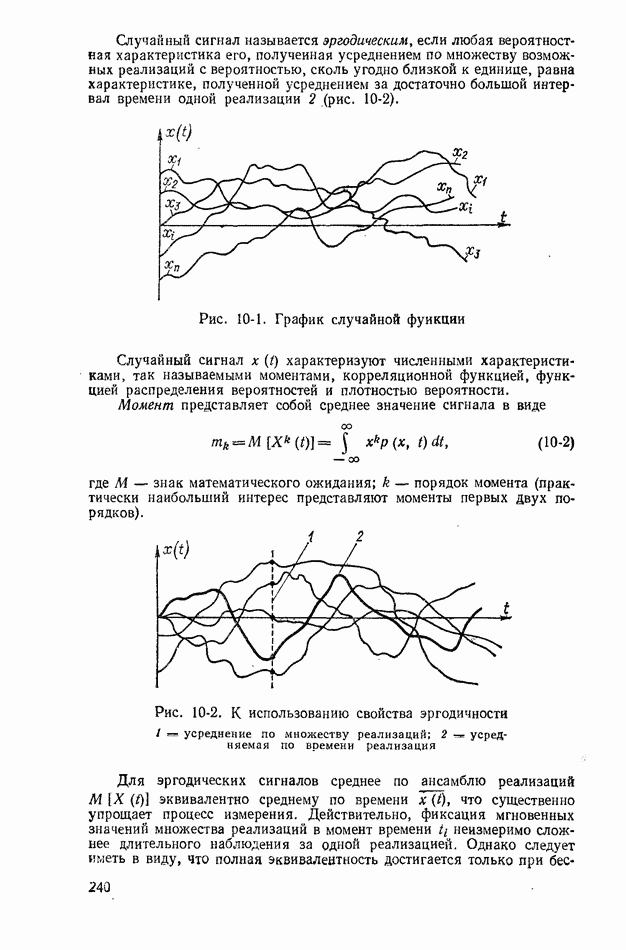
Случайный сигнал называется зргодическим, если любая вероятностная характеристика его, полученная усреднением по множеству возможных реализаций с вероятностью, сколь угодно близкой к единице, равна характеристике, полученной усреднением за достаточно большой интервал времени одной реализации 2 (рис. 10-2).

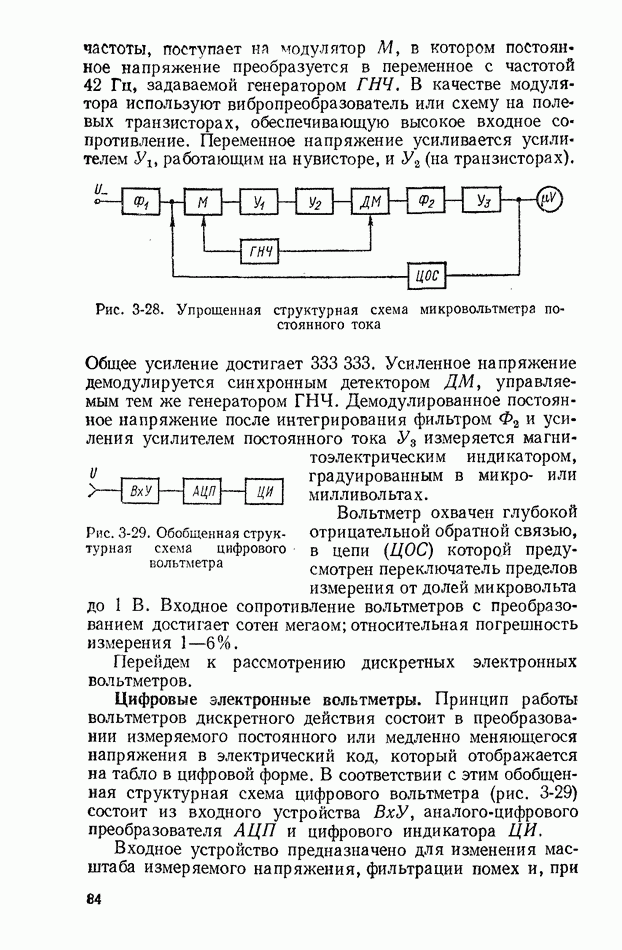
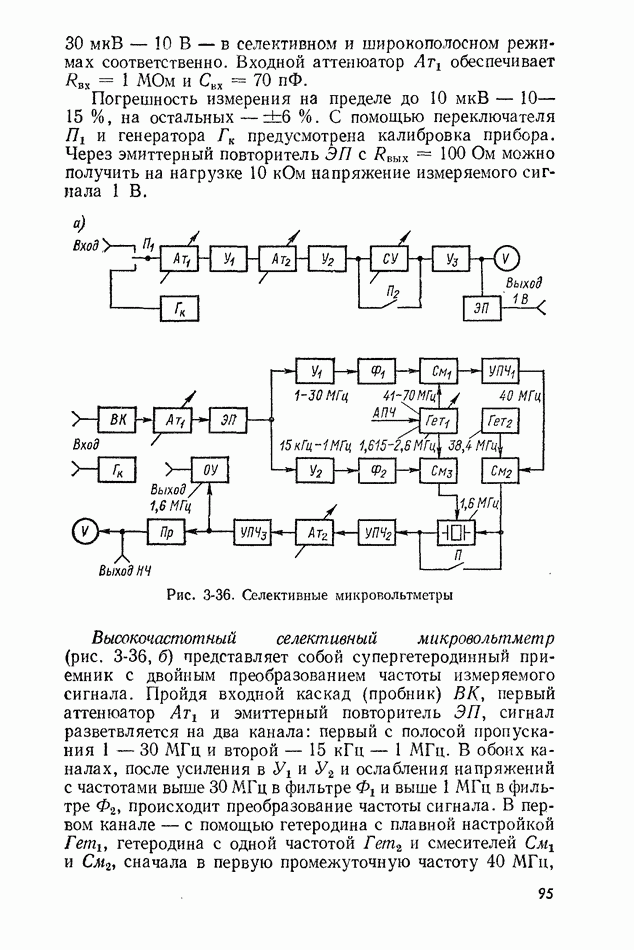
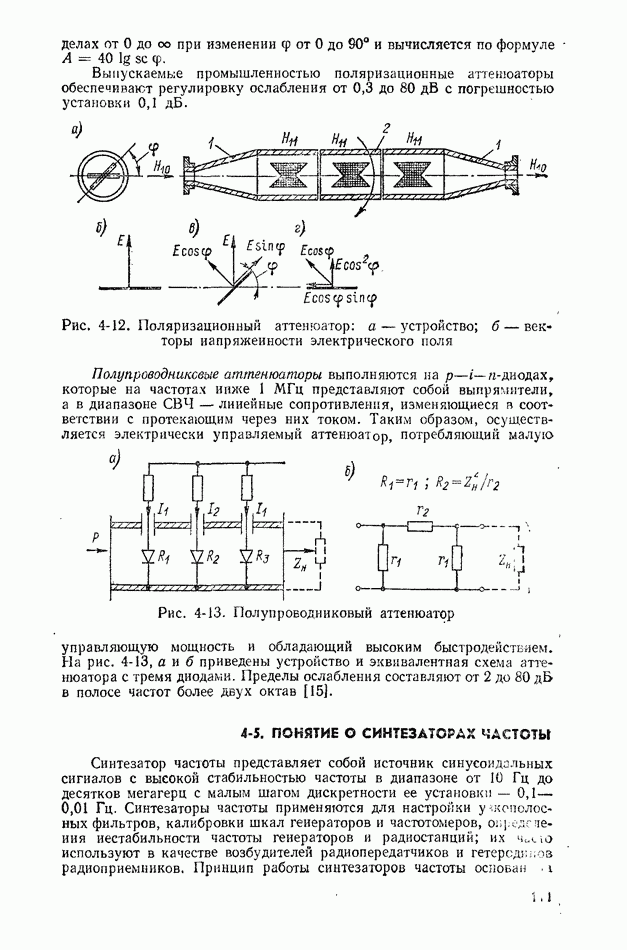
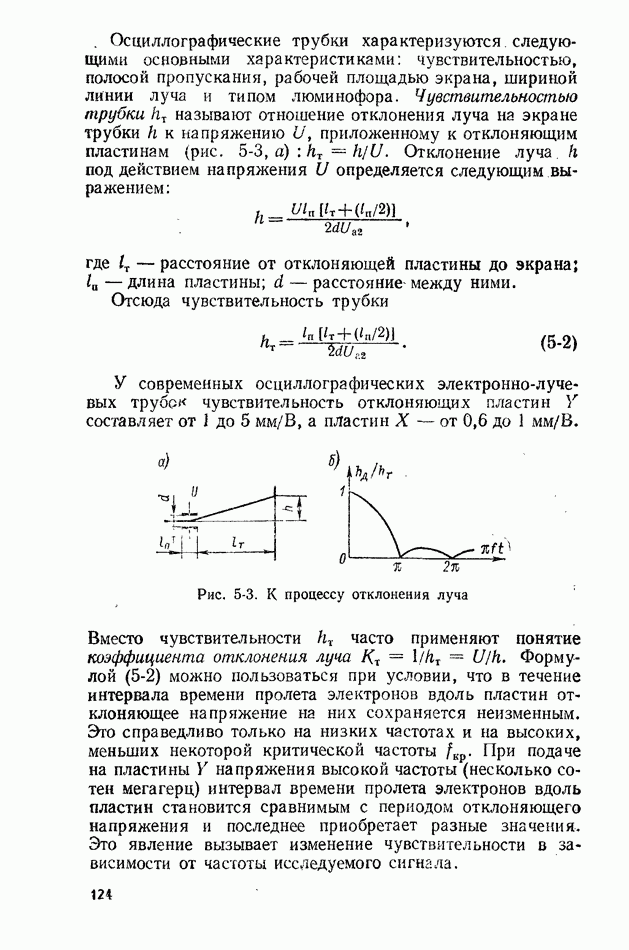
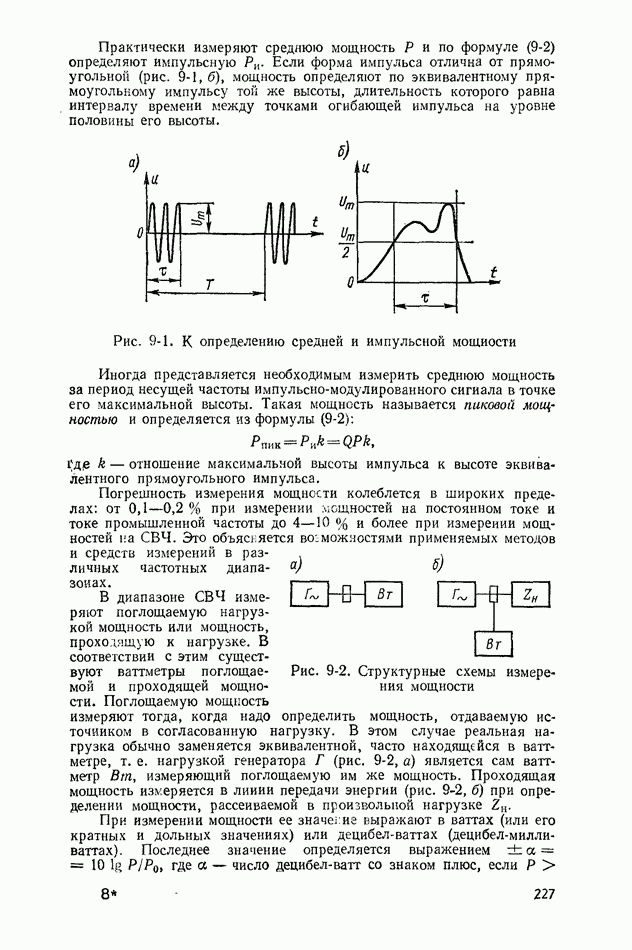
Рис. 10-1. График случайной функции
Случайный сигнал  характеризуют численными характеристиками, так называемыми моментами, корреляционной функцией, функцией распределения вероятностей и плотностью вероятности.
характеризуют численными характеристиками, так называемыми моментами, корреляционной функцией, функцией распределения вероятностей и плотностью вероятности.
Момент представляет собой среднее значение сигнала в виде

где  знак математического ожидания;
знак математического ожидания;  порядок момента (практически наибольший интерес представляют моменты первых двух порядков).
порядок момента (практически наибольший интерес представляют моменты первых двух порядков).

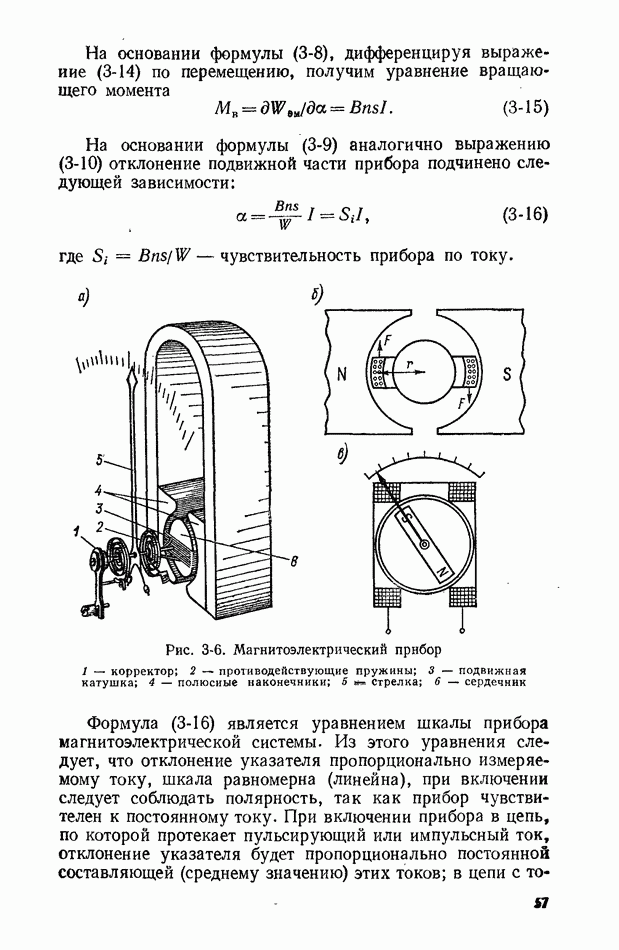
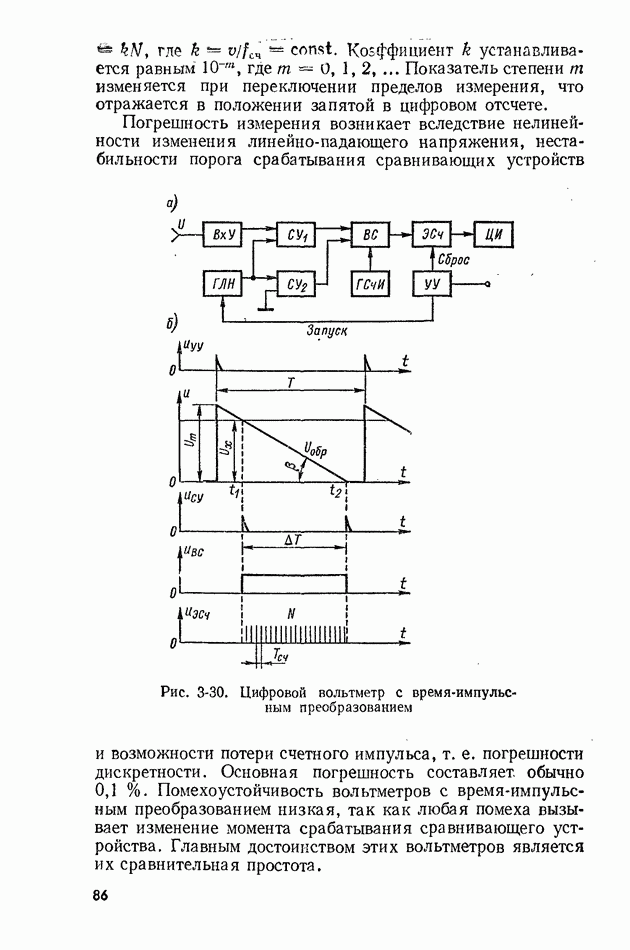
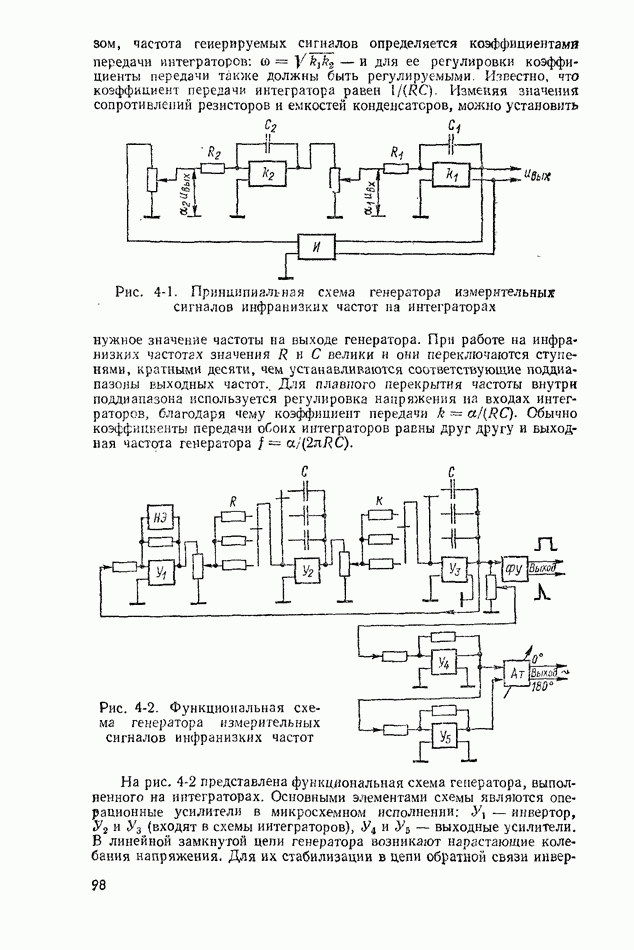
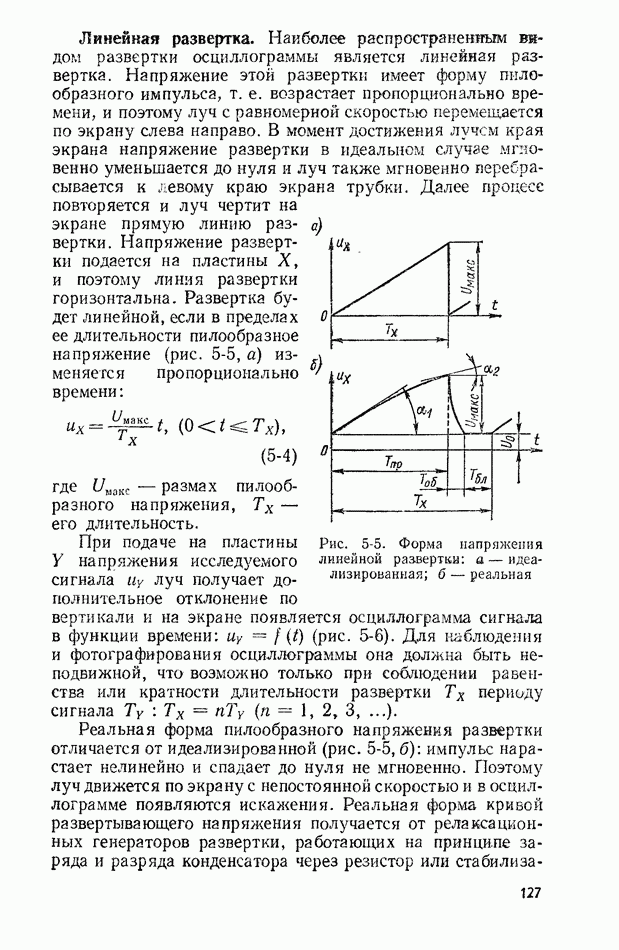
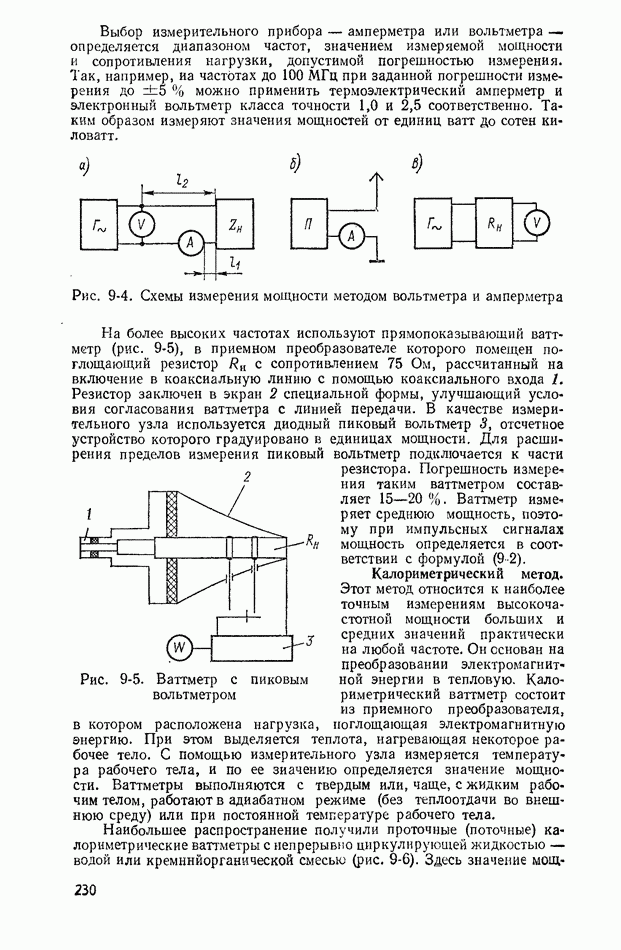
Рис. 10-2. К использованию свойства эргодичности 1 - усреднение по множеству реализаций; 2 - усредняемая по времени реализация
Для эргодических сигналов среднее по ансамблю реализаций  эквивалентно среднему по времени
эквивалентно среднему по времени  что существенно упрощает процесс измерения. Действительно, фиксация мгновенных значений множества реализаций в момент времени
что существенно упрощает процесс измерения. Действительно, фиксация мгновенных значений множества реализаций в момент времени  неизмеримо сложнее длительного наблюдения за одной реализацией. Однако следует иметь в виду, что полная эквивалентность достигается только при
неизмеримо сложнее длительного наблюдения за одной реализацией. Однако следует иметь в виду, что полная эквивалентность достигается только при
бесконечном времени наблюдения, а так как эксперимент всегда выполняется за конечный интервал времени, то его результат дает приближенные значения. Полученные в таких условиях характеристики называют статистическими характеристиками, или оценками, которые сами являются случайными величинами с погрешностями статистического характера.
Момент, первого порядка одномерного стационарного эргодического сигнала на основании формулы (10-2) имеет следующий вид:

( интервал времени усреднения) — и численно равен среднему значению (постоянной составляющей) случайного сигнала
интервал времени усреднения) — и численно равен среднему значению (постоянной составляющей) случайного сигнала  Момент второго порядка
Момент второго порядка

численно равен средней мощности сигнала, выделяемой на сопротивлении 1 Ом.
Случайный сигнал состоит из постоянной и переменной - составляющих:  Подставляя это выражение в формулу (10-4), получаем
Подставляя это выражение в формулу (10-4), получаем

где

— среднее значение квадрата переменной составляющей — дисперсия.
Напомним, что среднеквадратическое отклонение а, характеризующее рассеивание реализации случайного сигнала, равно положительному корню квадратному из дисперсии: 
Корреляционная функция  случайного сигнала
случайного сигнала  численно равна среднему значению произведения переменной составляющей сигнала в мрмент
численно равна среднему значению произведения переменной составляющей сигнала в мрмент  и такой же составляющей в момент
и такой же составляющей в момент  где
где  определенный интервал времени запаздывания:
определенный интервал времени запаздывания:

Функция  характеризует статистическую связь между мгновенными значениями случайного сигнала, разделенными заданным интервалом времени.
характеризует статистическую связь между мгновенными значениями случайного сигнала, разделенными заданным интервалом времени.
Нормированная корреляционная функция является отношением корреляционной функции сигнала к его дисперсии:

Взаимно-корреляционная функция характеризует статистическую связь между мгновенными значениями двух случайных сигналов,
разделенных заданным интервалом времени. Численно она равна среднему значению произведения переменных составляющих случайных сигналов, одна из которых запаздывает относительно другой на определенный интервал времени 

Энергетический спектр случайного сигнала выражает среднюю мощность сигнала (10-4), приходящуюся на единицу полосы частот. Энергетический спектр и корреляционная функция одного и того же стационарного случайного сигнала математически связаны формулами Винера-Хинчина:

Более полными, но и более сложными являются функция распределения  и плотность вероятности
и плотность вероятности  где
где  символ вероятности.
символ вероятности.
Нестационарные случайные сигналы нельзя исследовать на одной реализации, так же, как и стационарные неэргодические сигналы. Для исследования таких сигналов предварительно записывают, например на магнитную ленту, некоторое число реализаций. Затем считывают значения всех реализаций в одном «сечении» в интересующий момент времени и полученные данные записывают вновь в некотором масштабе условного времени в виде дискретных значений. Полученную новую зависимость принимают за реализацию стационарного эргодического сигнала.
При исследовании погрешностей статистических измерений важную роль играет интервал корреляции тк случайного сигнала, который определяется по формуле  (Корреляция имеет место между значениями случайного сигнала в интервалах времени, приблизительно равных тк). Введено понятие максилгального интервала корреляции
(Корреляция имеет место между значениями случайного сигнала в интервалах времени, приблизительно равных тк). Введено понятие максилгального интервала корреляции  за пределами которого выборки значений сигнала можно считать некоррелированными. Значение функции
за пределами которого выборки значений сигнала можно считать некоррелированными. Значение функции  где
где  наперед заданное малое число, например 0,05.
наперед заданное малое число, например 0,05.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ОСНОВНЫЕ СВЕДЕНИЯ О СРЕДСТВАХ ИЗМЕРЕНИЙ
- 1-2. МЕРЫ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 1-3. ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 1-4. ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 1-5. ИЗМЕРИТЕЛЬНЫЕ УСТАНОВКИ И СИСТЕМЫ
- 1-6. ОСНОВНЫЕ СВОЙСТВА СРЕДСТВ ИЗМЕРЕНИЯ
- 1-7. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
- ГЛАВА ВТОРАЯ. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- 2-2. СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
- 2-3. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
- 2-4. СУММИРОВАНИЕ ПОГРЕШНОСТЕЙ
- 2-5. ПОГРЕШНОСТЬ КОСВЕННЫХ ИЗМЕРЕНИЯ
- 2-6. НЕКОТОРЫЕ ПРАВИЛА ВЫПОЛНЕНИЯ ИЗМЕРЕНИЯ И ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ
- ГЛАВА ТРЕТЬЯ. ИЗМЕРЕНИЕ ТОКА И НАПРЯЖЕНИЯ
- 3-2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АМПЕРМЕТРЫ И ВОЛЬТМЕТРЫ
- 3-3. ЭЛЕКТРОННЫЕ ВОЛЬТМЕТРЫ
- ГЛАВА ЧЕТВЕРТАЯ. ГЕНЕРАТОРЫ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ
- 4-2. ГЕНЕРАТОРЫ СИГНАЛОВ ИНФРАНИЗКИХ И НИЗКИХ ЧАСТОТ
- 4-3. ГЕНЕРАТОРЫ СИГНАЛОВ ВЫСОКИХ И УЛЬТРАВЫСОКИХ ЧАСТОТ
- 4-4. ГЕНЕРАТОРЫ СИГНАЛОВ СВЕРХВЫСОКИХ ЧАСТОТ
- 4-5. ПОНЯТИЕ О СИНТЕЗАТОРАХ ЧАСТОТЫ
- 4-6. ГЕНЕРАТОРЫ ИМПУЛЬСНЫХ СИГНАЛОВ
- 4-7. ГЕНЕРАТОРЫ ШУМОВЫХ СИГНАЛОВ
- ГЛАВА ПЯТАЯ. ЭЛЕКТРОННО-ЛУЧЕВЫЕ ОСЦИЛЛОГРАФЫ
- 5-2. ЭЛЕКТРОННО-ЛУЧЕВЫЕ ТРУБКИ
- 5-3. ОСЦИЛЛОГРАФИЧЕСКИЕ РАЗВЕРТКИ
- 5-4. КАНАЛЫ УПРАВЛЕНИЯ ЛУЧОМ
- 5-5. КАЛИБРАТОРЫ АМПЛИТУДЫ И ДЛИТЕЛЬНОСТИ
- 5-6. СТРОБОСКОПИЧЕСКИЕ ОСЦИЛЛОГРАФЫ
- 5-7. НЕКОТОРЫЕ ОСОБЕННОСТИ ОСЦИЛЛОГРАФИЧЕСКИХ ИЗМЕРЕНИЙ
- ГЛАВА ШЕСТАЯ. ИЗМЕРЕНИЕ СПЕКТРА И ФОРМЫ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 6-2. АНАЛИЗАТОРЫ СПЕКТРА ПОСЛЕДОВАТЕЛЬНОГО ДЕЙСТВИЯ
- 6-3. АНАЛИЗ СПЕКТРА В РЕАЛЬНОМ ВРЕМЕНИ
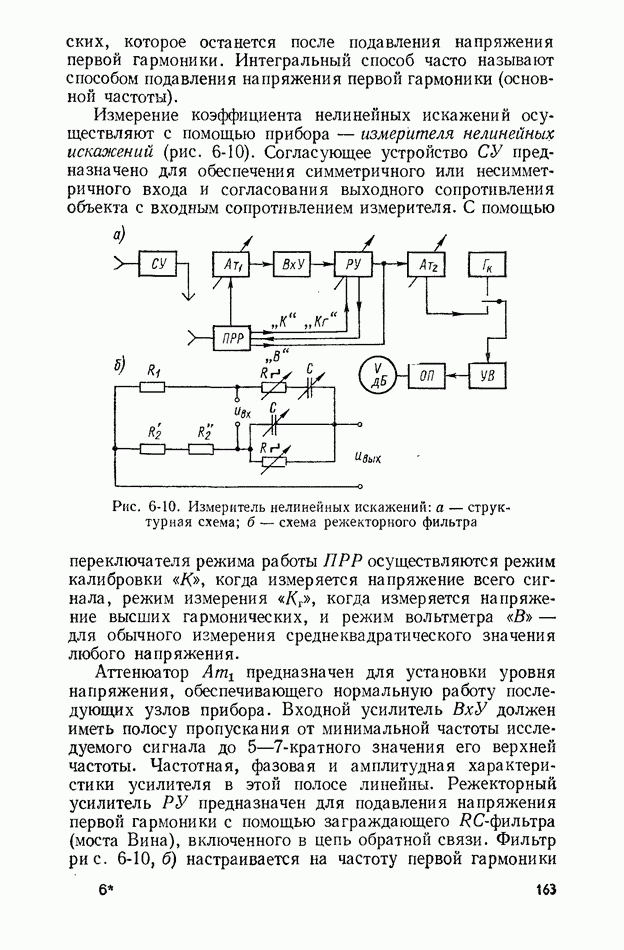
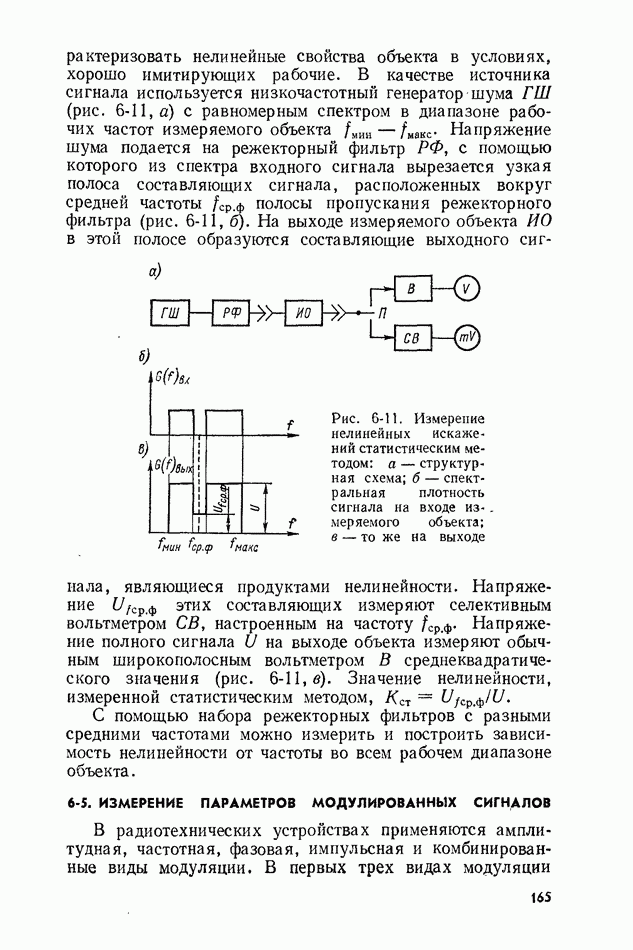
- 6-4. ИЗМЕРЕНИЕ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ
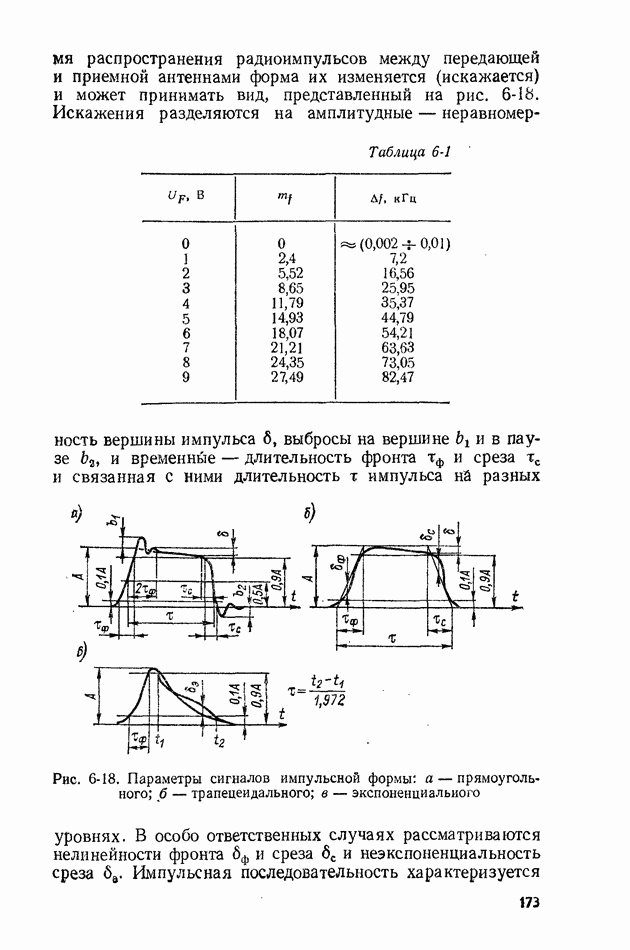
- 6-5. ИЗМЕРЕНИЕ ПАРАМЕТРОВ МОДУЛИРОВАННЫХ СИГНАЛОВ
- ГЛАВА СЕДЬМАЯ. ИЗМЕРЕНИЕ ФАЗОВОГО СДВИГА
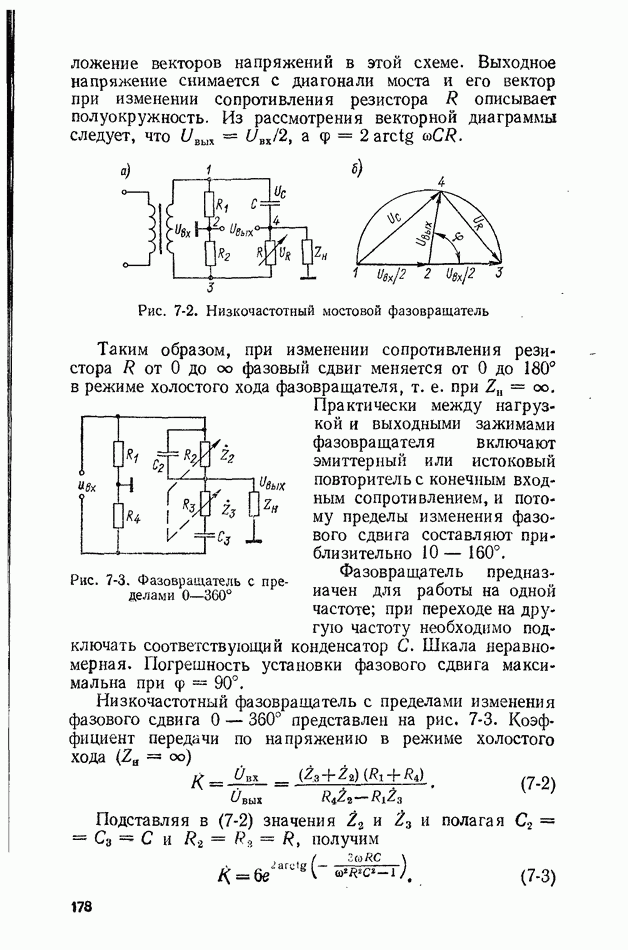
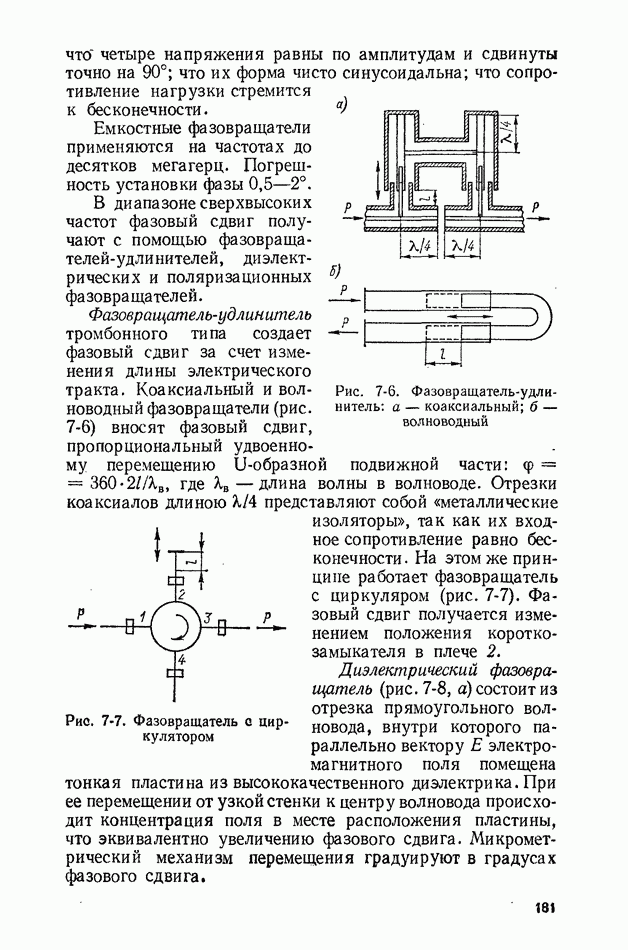
- 7-2. ФАЗОВРАЩАТЕЛИ
- 7-3. ОСЦИЛЛОГРАФИЧЕСКИЙ МЕТОД
- 7-4. КОМПЕНСАЦИОННЫЙ МЕТОД
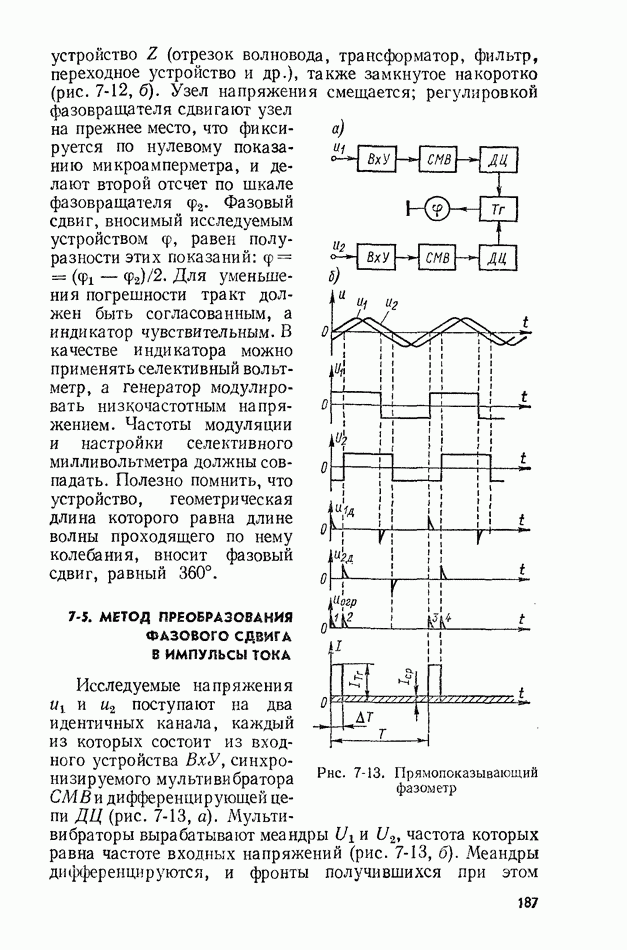
- 7-5. МЕТОД ПРЕОБРАЗОВАНИЯ ФАЗОВОГО СДВИГА В ИМПУЛЬСЫ ТОКА
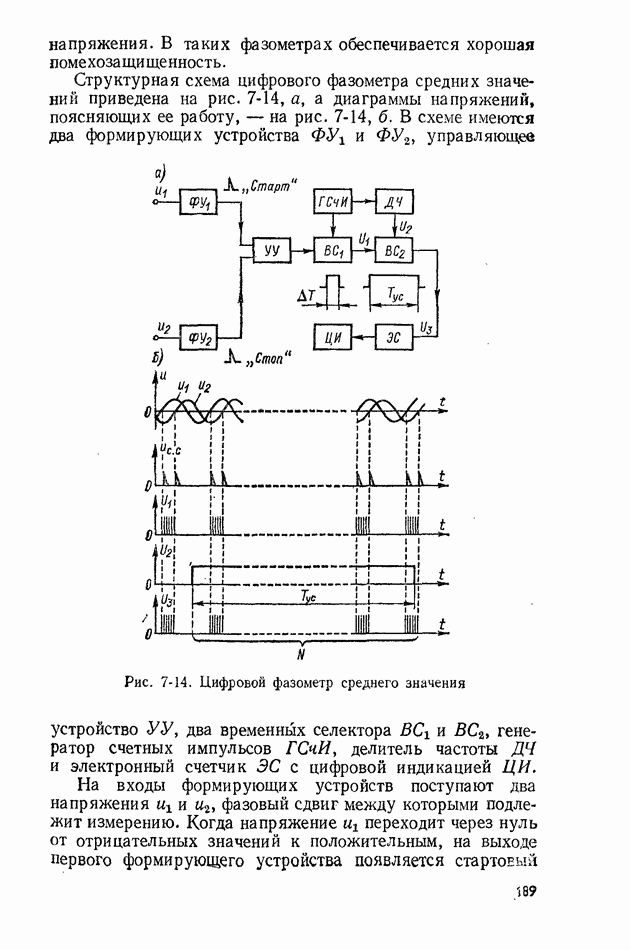
- 7-6. МЕТОД ДИСКРЕТНОГО СЧЕТА
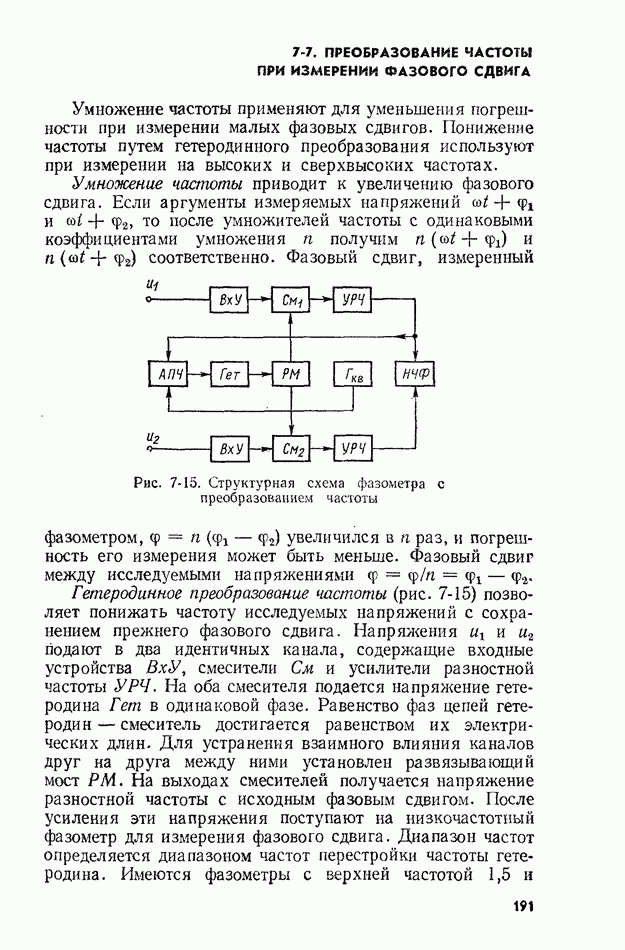
- 7-7. ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ ПРИ ИЗМЕРЕНИИ ФАЗОВОГО СДВИГА
- ГЛАВА ВОСЬМАЯ. ИЗМЕРЕНИЕ ЧАСТОТЫ И ИНТЕРВАЛОВ ВРЕМЕНИ
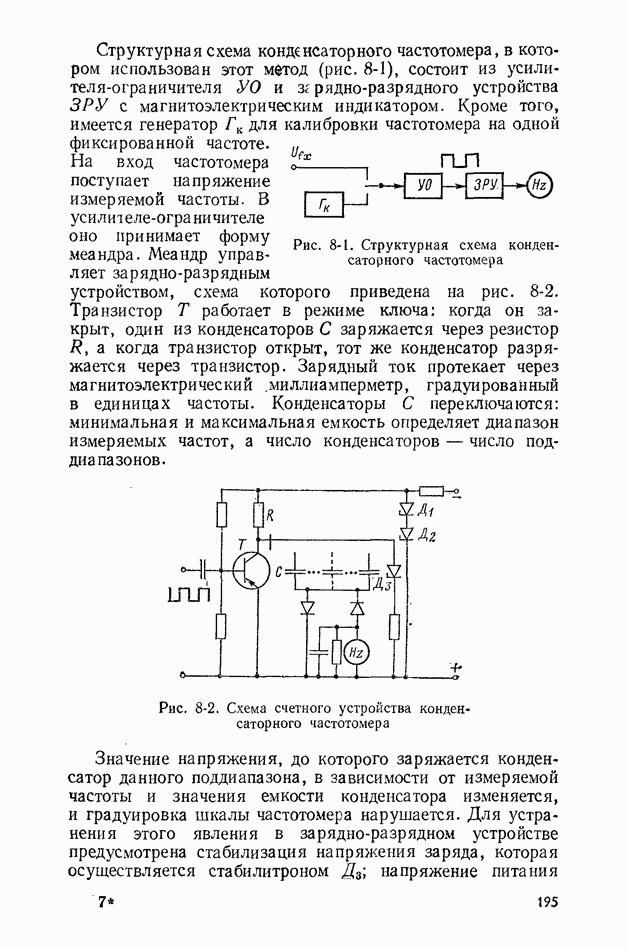
- 8-2. МЕТОД ПЕРЕЗАРЯДА КОНДЕНСАТОРА
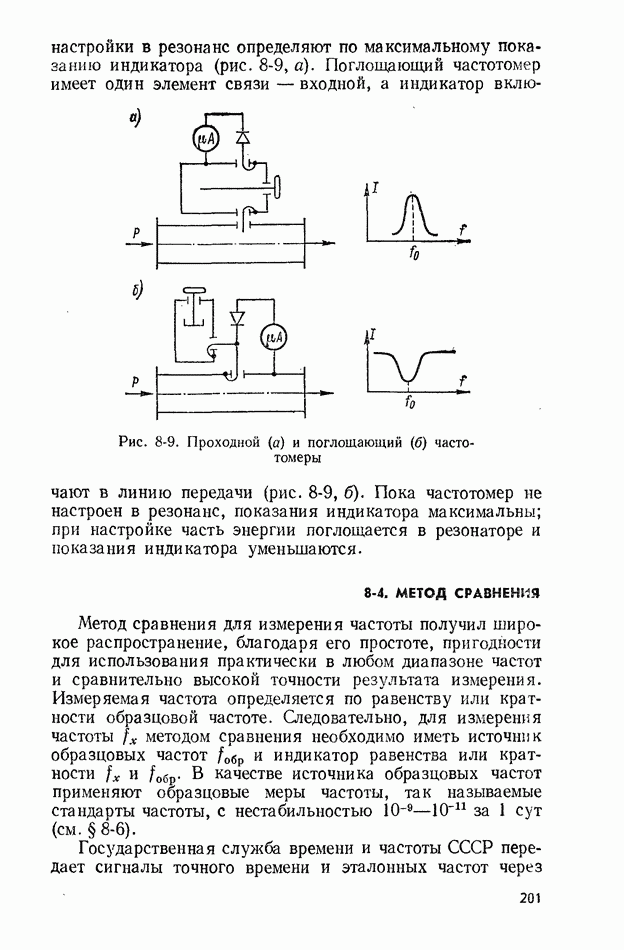
- 8-3. РЕЗОНАНСНЫЙ МЕТОД
- 8-4. МЕТОД СРАВНЕНИЯ
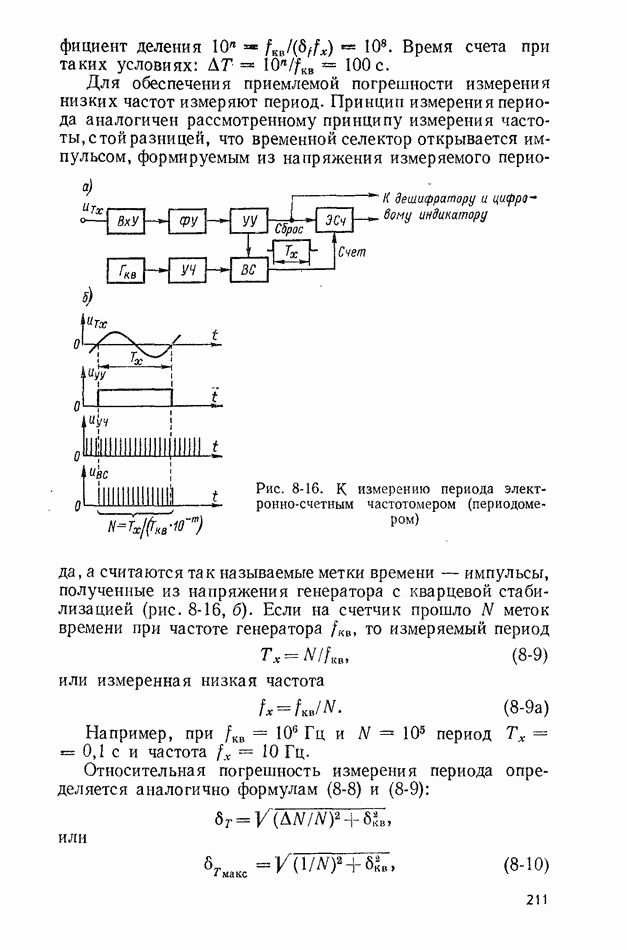
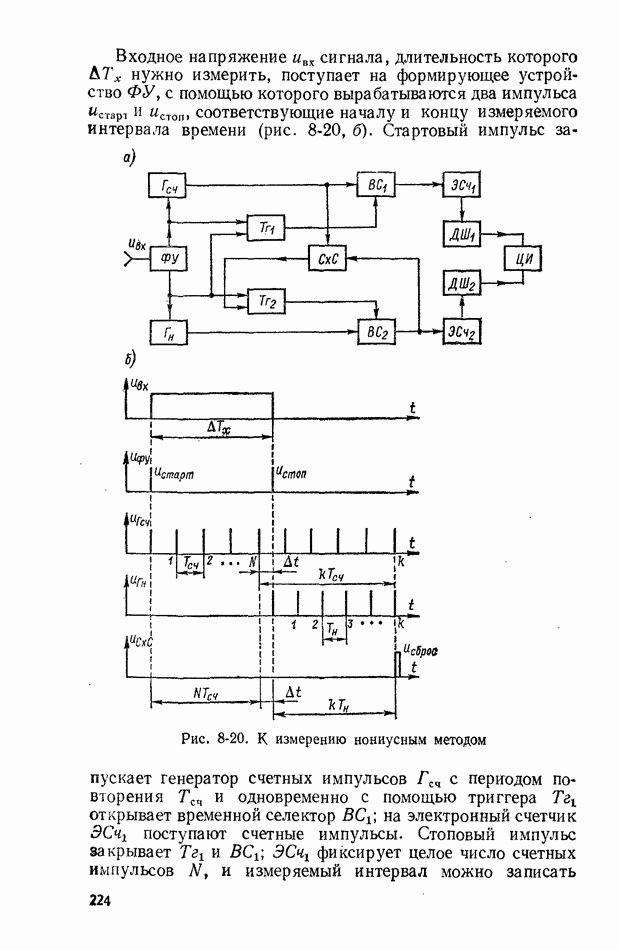
- 8-5. МЕТОД ДИСКРЕТНОГО СЧЕТА
- 8-6. ПОНЯТИЕ О СТАНДАРТАХ ЧАСТОТЫ И ВРЕМЕНИ
- 8-7. ПРЕЦИЗИОННОЕ ИЗМЕРЕНИЕ ЧАСТОТЫ И ВРЕМЕНИ
- ГЛАВА ДЕВЯТАЯ. ИЗМЕРЕНИЕ МОЩНОСТИ
- 9-2. ИЗМЕРЕНИЕ ПОГЛОЩАЕМОЙ МОЩНОСТИ
- 5-3. ИЗМЕРЕНИЕ ПРОХОДЯЩЕЙ МОЩНОСТИ
- 9-4. ИЗМЕРЕНИЕ ВЕСЬМА МАЛОЙ МОЩНОСТИ
- ГЛАВА ДЕСЯТАЯ. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ СИГНАЛОВ
- 10-2. ИЗМЕРЕНИЕ МОМЕНТОВ
- 10-3. ИЗМЕРЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ
- 10-4. ИЗМЕРЕНИЕ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА
- 10-5. ИЗМЕРЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТИ ВЕРОЯТНОСТИ
- ГЛАВА ОДИННАДЦАТАЯ. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЭЛЕМЕНТОВ ЭЛЕКТРИЧЕСКИХ И РАДИОТЕХНИЧЕСКИХ УСТРОЙСТВ
- 11-2. МЕТОД ВОЛЬТМЕТРА И АМПЕРМЕТРА
- 11-3. МОСТОВОЙ МЕТОД
- 11.4. РЕЗОНАНСНЫЙ МЕТОД
- 11-5. МЕТОД ДИСКРЕТНОГО СЧЕТА
- 11-6. ИЗМЕРЕНИЕ АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- 11-7. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ИНТЕГРАЛЬНЫХ СХЕМ
- ГЛАВА ДВЕНАДЦАТАЯ. ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЦЕПЕЙ СВЕРХВЫСОКИХ ЧАСТОТ
- 12-2. ИЗМЕРИТЕЛЬНЫЕ ЛИНИИ
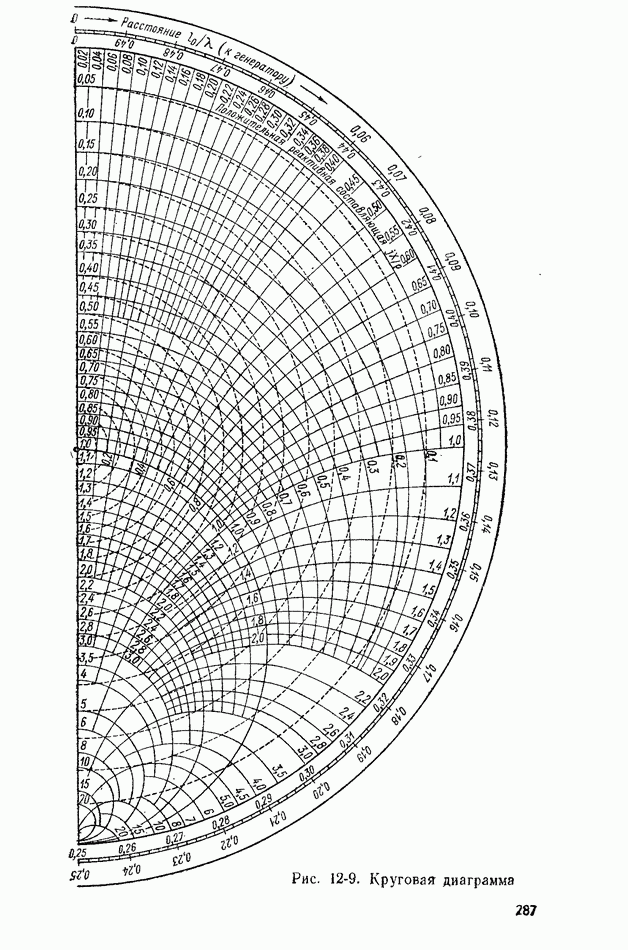
- 12-3. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА СТОЯЧЕЙ ВОЛНЫ И КОЭФФИЦИЕНТА ОТРАЖЕНИЯ
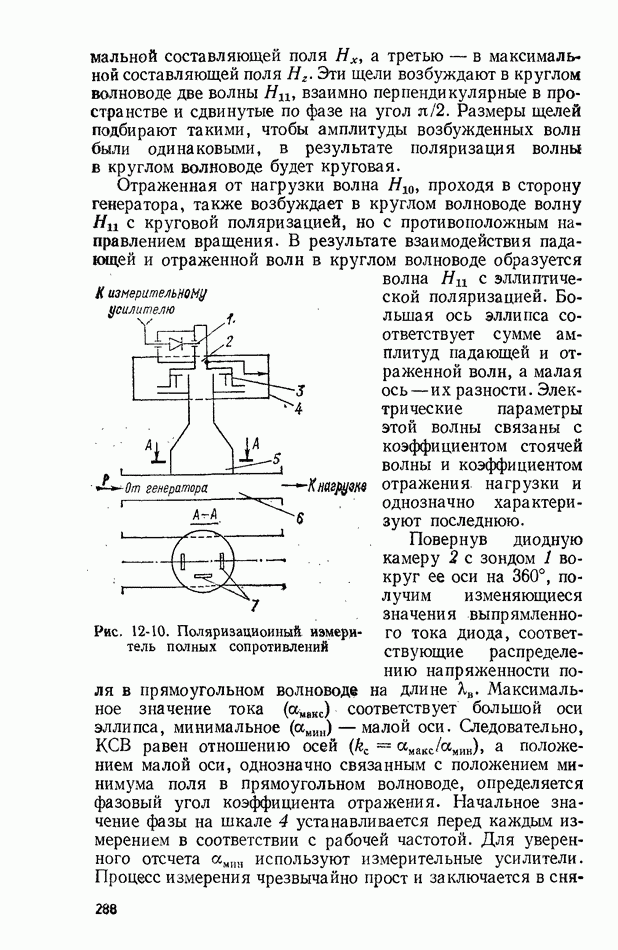
- 12-4. ИЗМЕРЕНИЕ ПОЛНОГО СОПРОТИВЛЕНИЯ
- 12-5. ИЗМЕРЕНИЕ НЕОДНОРОДНОСТИ
- ГЛАВА ТРИНАДЦАТАЯ. ИЗМЕРЕНИЕ ОСЛАБЛЕНИЯ
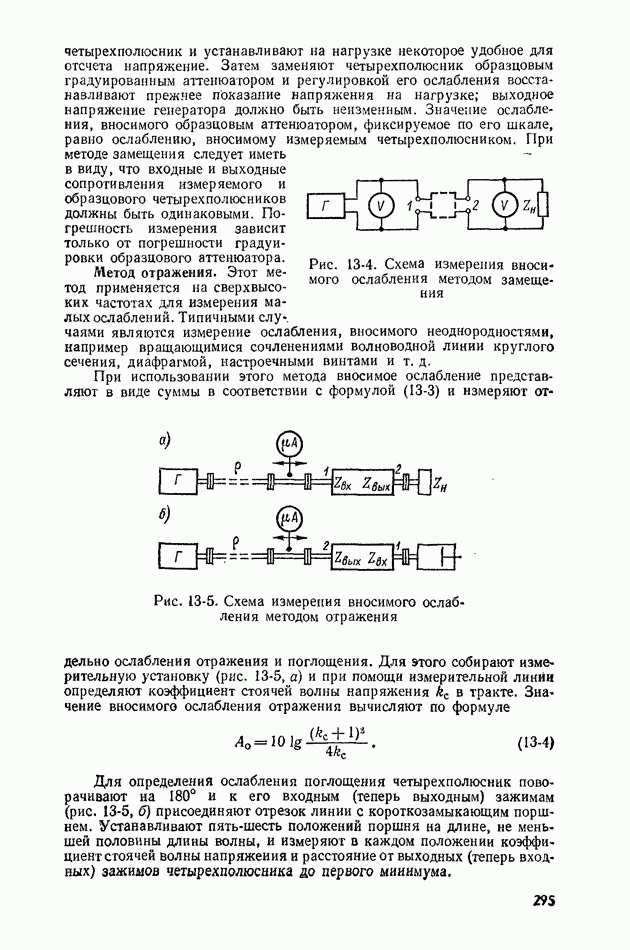
- 13-2. ИЗМЕРЕНИЕ ВНОСИМОГО ОСЛАБЛЕНИЯ
- 13-3. ИЗМЕРЕНИЕ СОБСТВЕННОГО ОСЛАБЛЕНИЯ
- ЗАКЛЮЧЕНИЕ
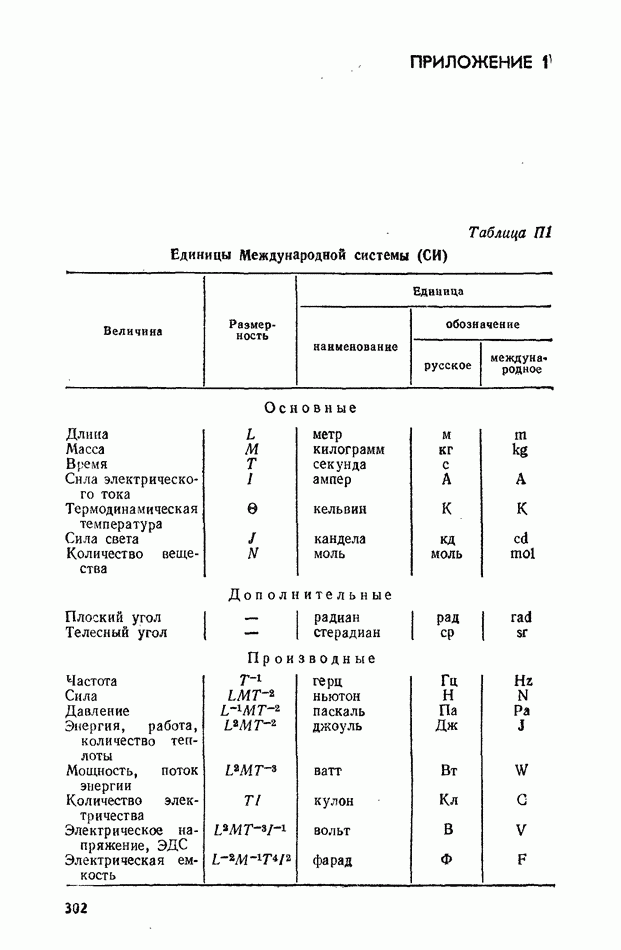
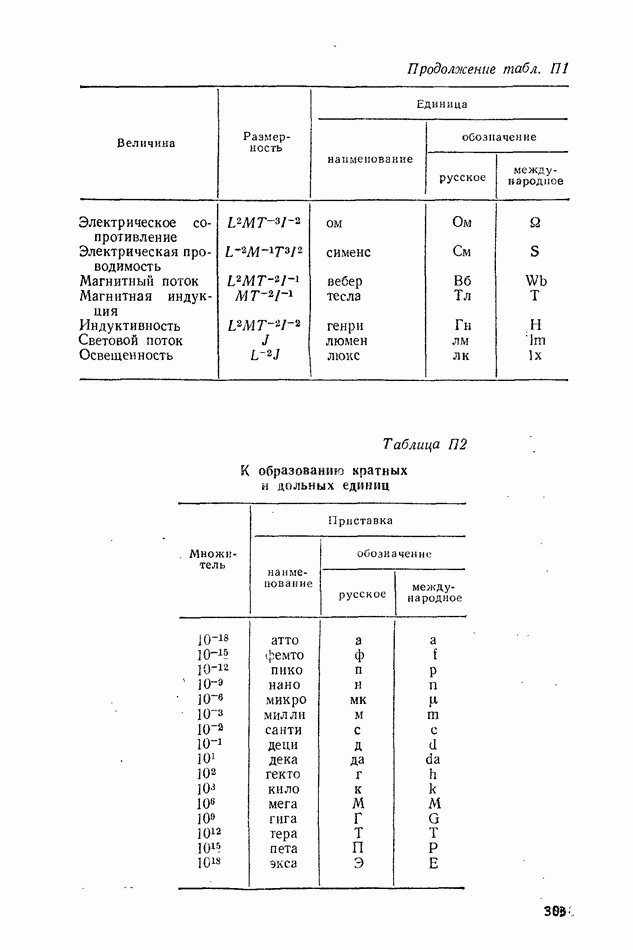
- ПРИЛОЖЕНИЕ П1
- ПРИЛОЖЕНИЕ 2. КЛАССИФИКАЦИЯ РАДИОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ