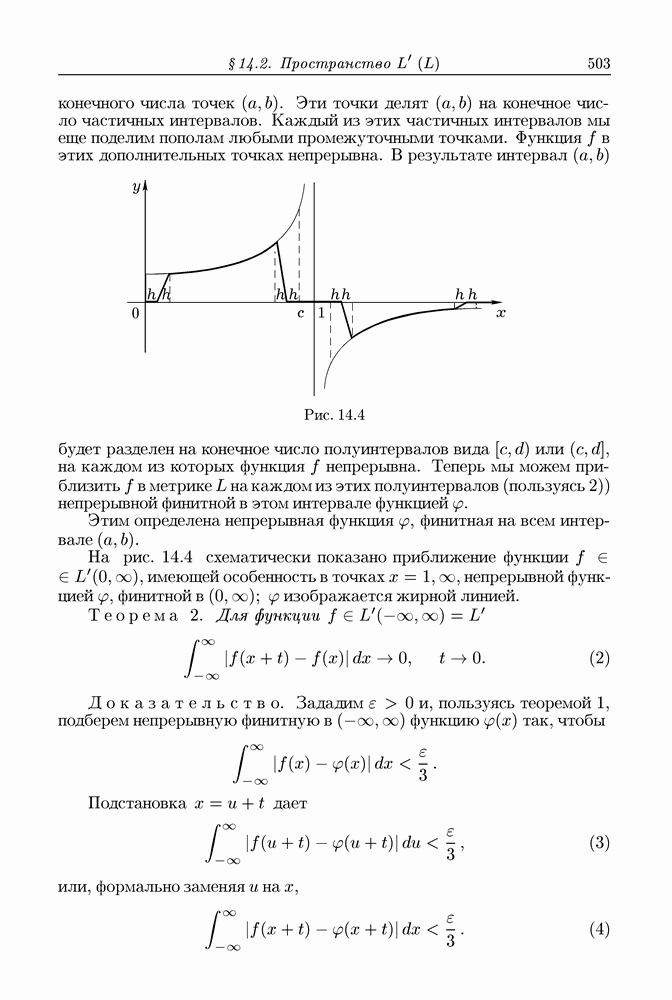
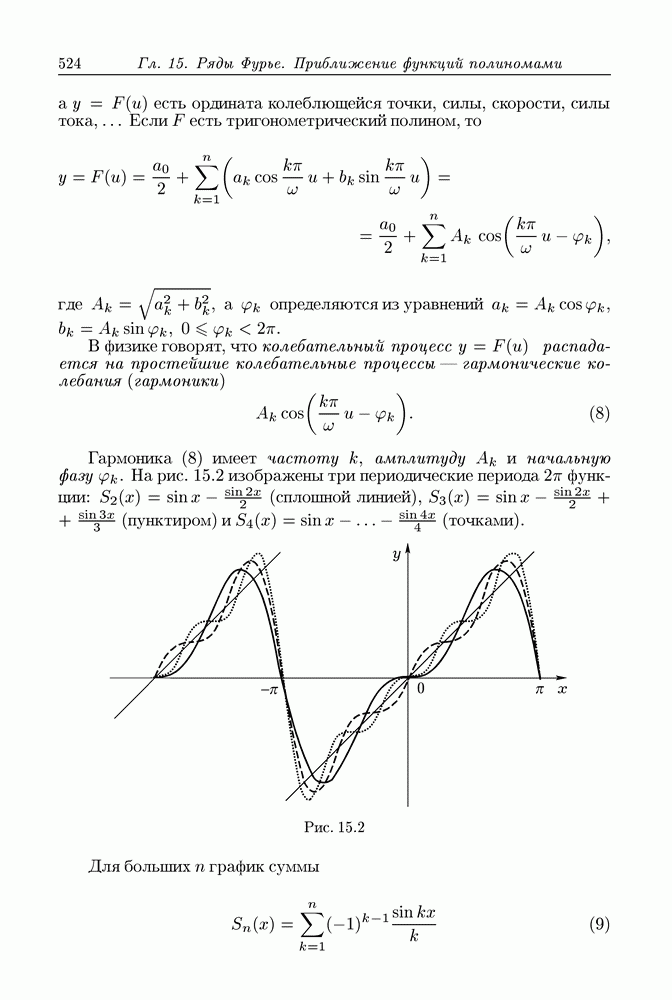
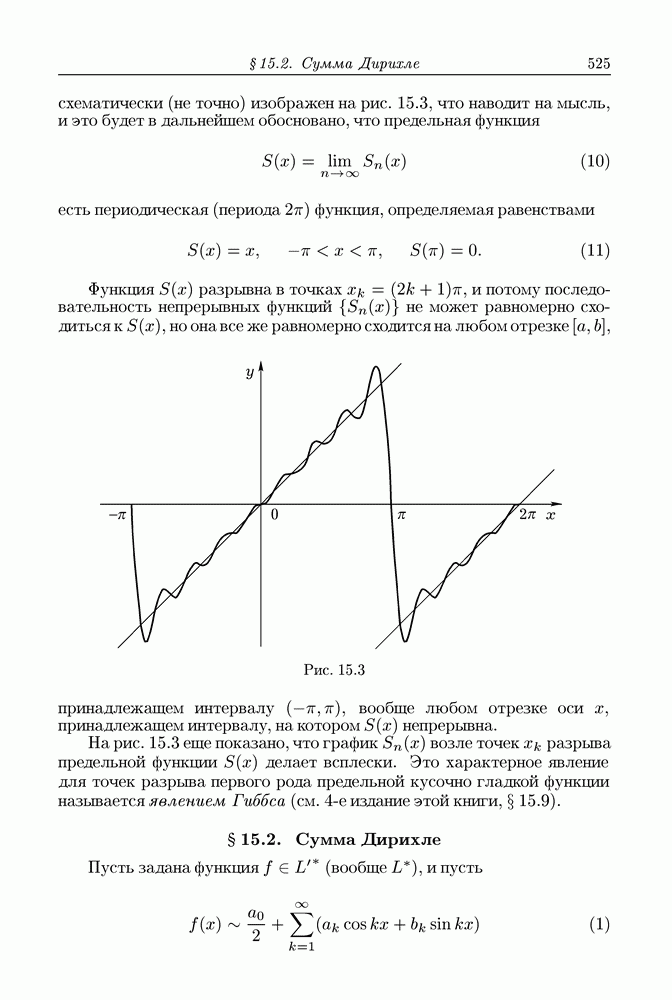
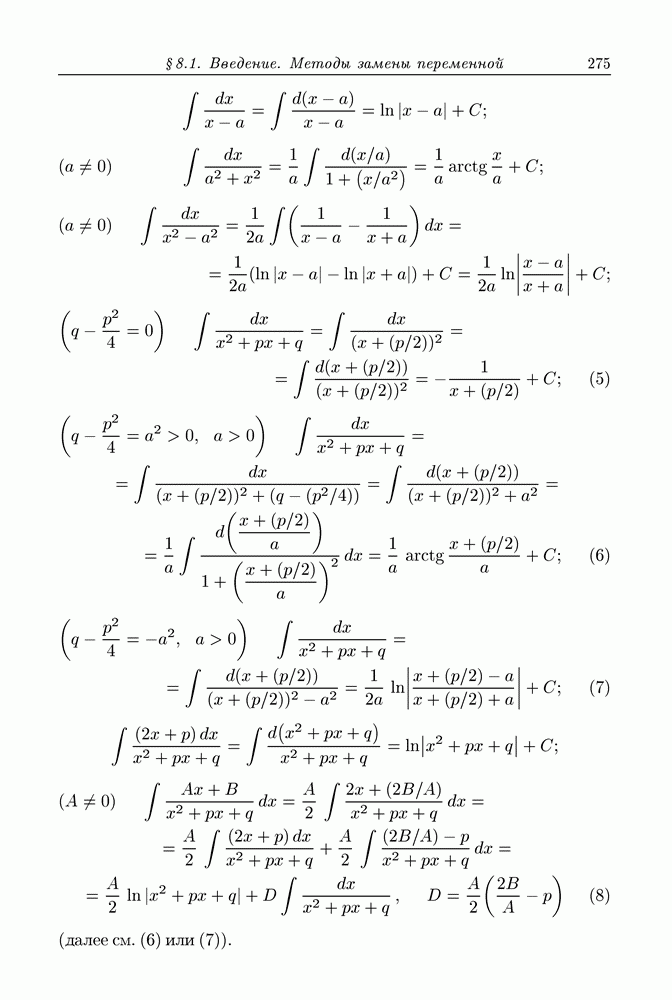| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
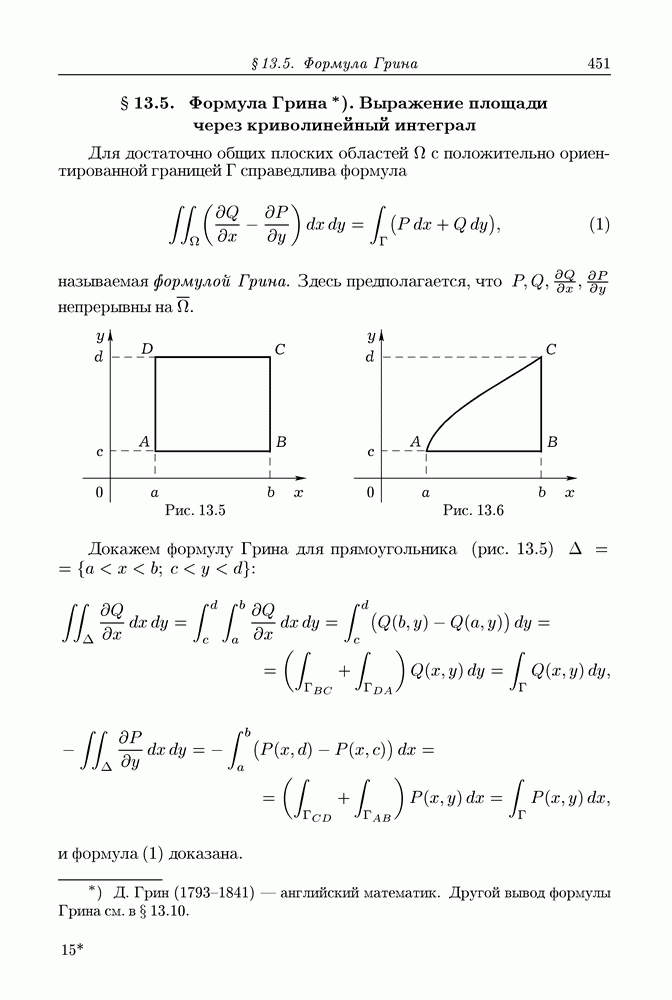
§ 13.3. Поле потенциала
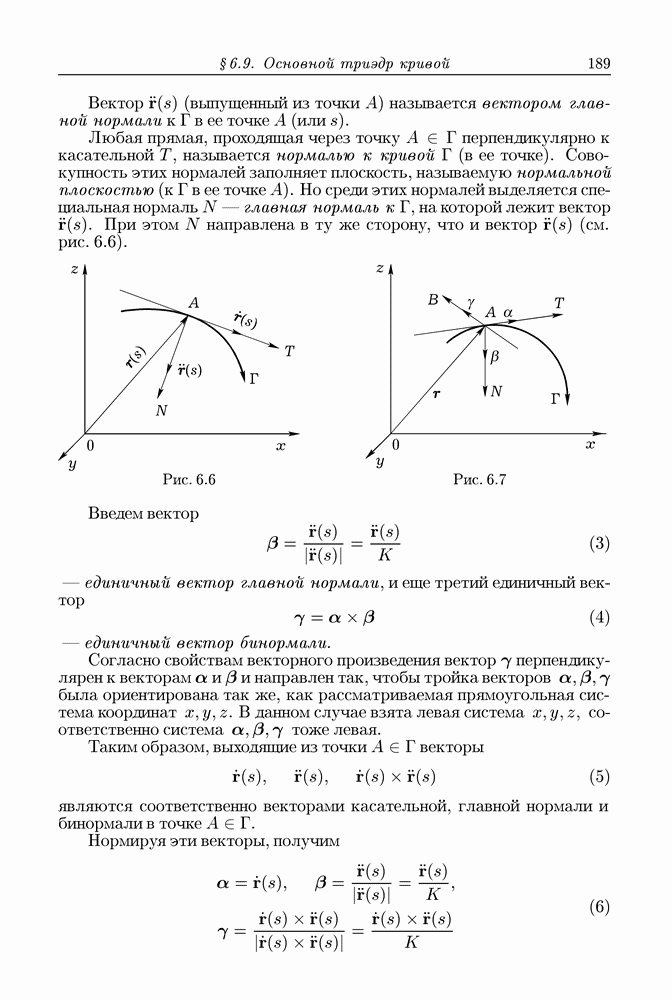
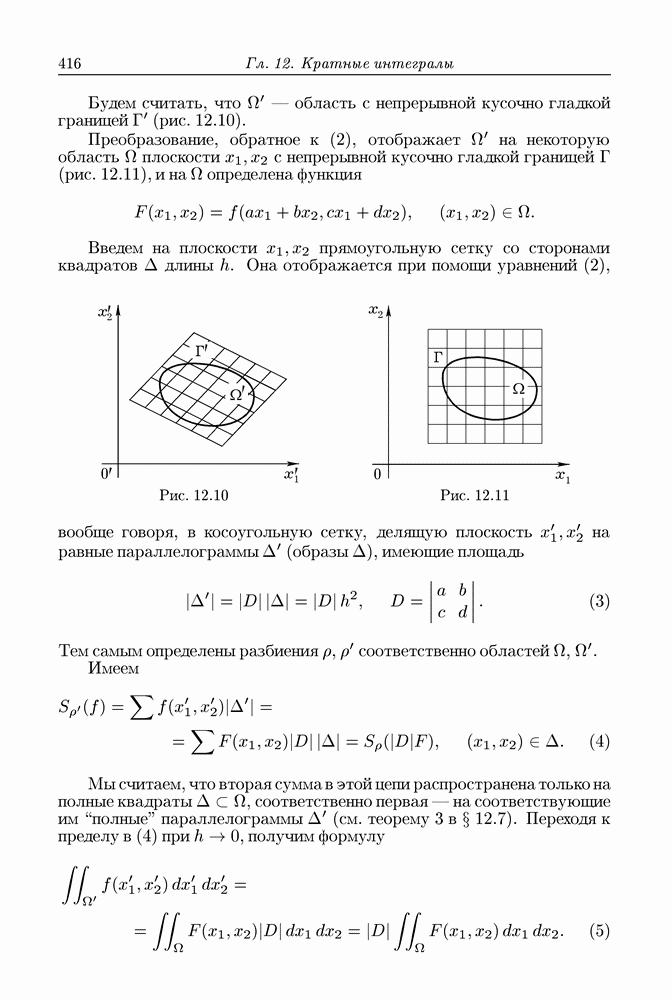
Очень важным случаем поля вектора  является тот, когда на области
является тот, когда на области  где задано поле, существует функция
где задано поле, существует функция  имеющая непрерывные частные производные, для которых выполняются равенства
имеющая непрерывные частные производные, для которых выполняются равенства

Такую функцию  называют потенциальной функцией вектора
называют потенциальной функцией вектора  . Говорят еще (см. § 7.6), что вектор
. Говорят еще (см. § 7.6), что вектор  есть градиент функции
есть градиент функции  и пишут
и пишут

Докажем теорему.
Теорема 1. Пусть на области  задано поле вектора
задано поле вектора  , непрерывного на
, непрерывного на  Следующие утверждения эквивалентны:
Следующие утверждения эквивалентны:
1) существует на  однозначная функция
однозначная функция  имеющая непрерывные частные производные, для которой на
имеющая непрерывные частные производные, для которой на  выполняется равенство
выполняется равенство 
2) интеграл от  по любому замкнутому непрерывному кусочно гладкому контуру С, принадлежащему
по любому замкнутому непрерывному кусочно гладкому контуру С, принадлежащему  равен нулю:
равен нулю:

3) если  определенная фиксированная точка
определенная фиксированная точка  то интеграл
то интеграл  по любой ориентированной кусочно гладкой кривой
по любой ориентированной кусочно гладкой кривой  с началом в
с началом в  и с концом в А зависит от
и с концом в А зависит от  но не зависит от ее формы; таким образом, при фиксированной точке
но не зависит от ее формы; таким образом, при фиксированной точке 

Функция  есть потенциальная функция вектора а на
есть потенциальная функция вектора а на  (однозначная). Она отличается от
(однозначная). Она отличается от  на константу.
на константу.
Доказательство. Из утверждения 1) следует 3). В самом деле, пусть на  существует функция
существует функция  потенциальная для а.
потенциальная для а.
Зададим на  определенную точку
определенную точку  и переменную точку
и переменную точку  Соединим
Соединим  с А непрерывной кусочно гладкой кривой
с А непрерывной кусочно гладкой кривой  определенной уравнениями
определенной уравнениями

Таким образом, значениям  параметра
параметра  соответствуют точки и А.
соответствуют точки и А.
Если подставить в  вместо x, y, z соответственно функции
вместо x, y, z соответственно функции  то
то  будет непрерывной кусочно гладкой функцией от
будет непрерывной кусочно гладкой функцией от  На основании теоремы о производной сложной функции в точках гладкости С (где С имеет касательную)
На основании теоремы о производной сложной функции в точках гладкости С (где С имеет касательную)

Отсюда следует, что

т. е. криволинейный интеграл при фиксированной точке  зависит только от положения точки
зависит только от положения точки  но не от пути, по которому она достигается из точки
но не от пути, по которому она достигается из точки 

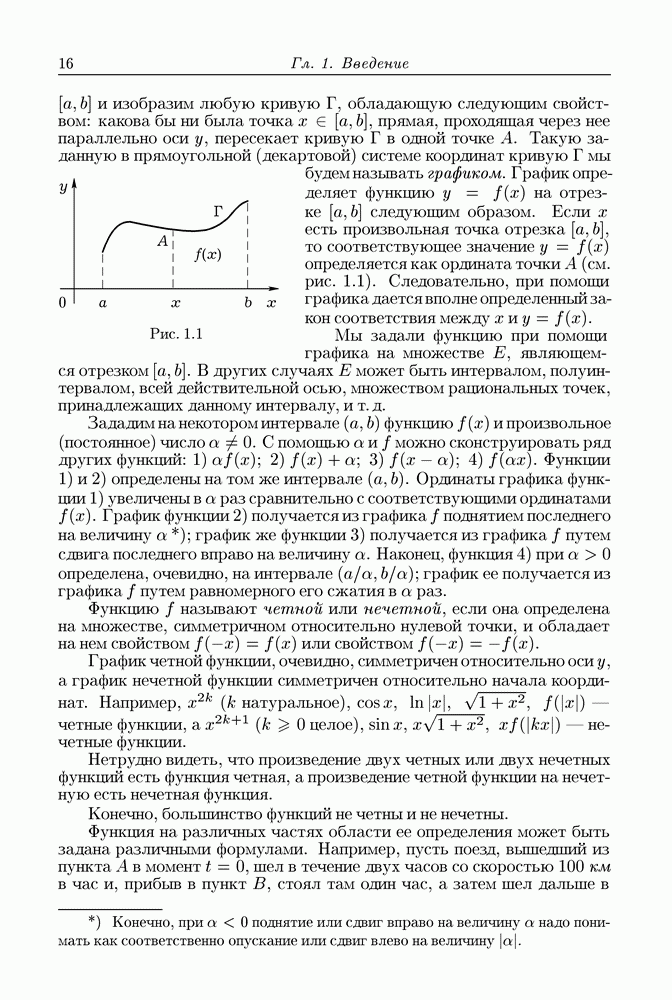
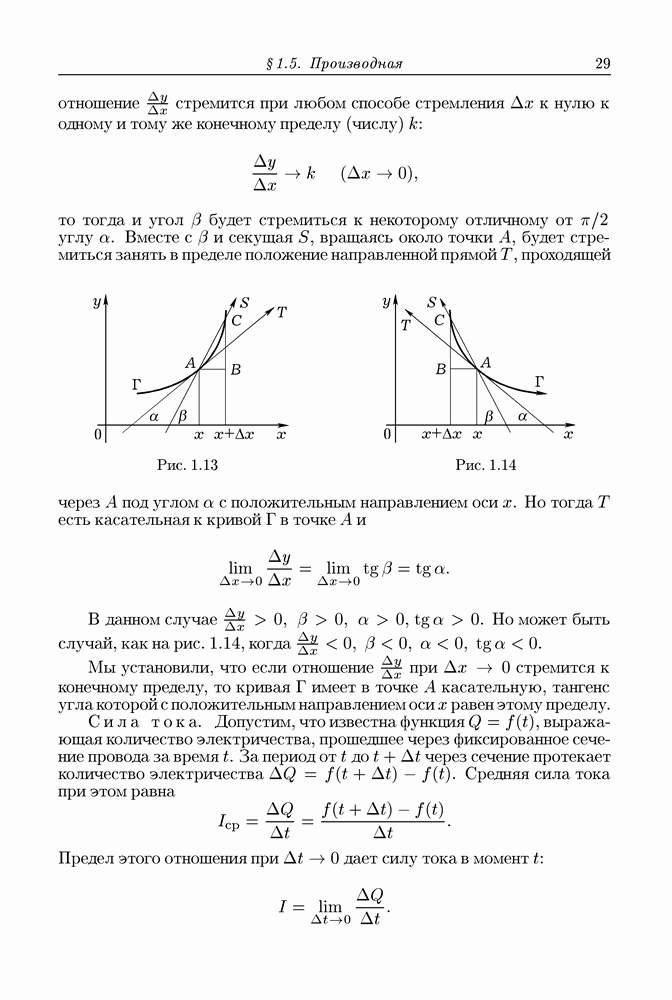
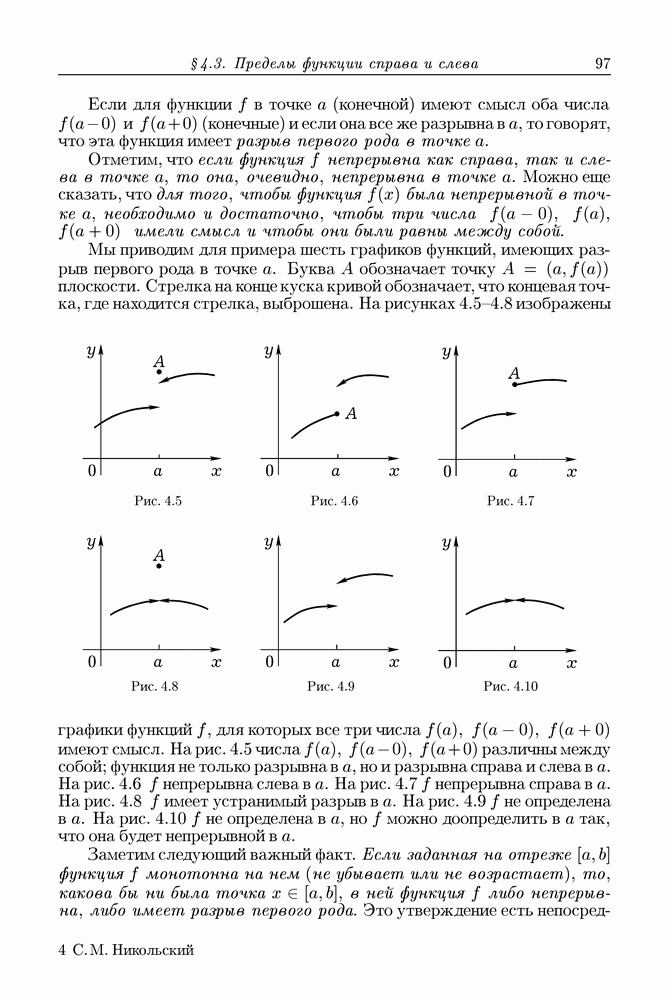
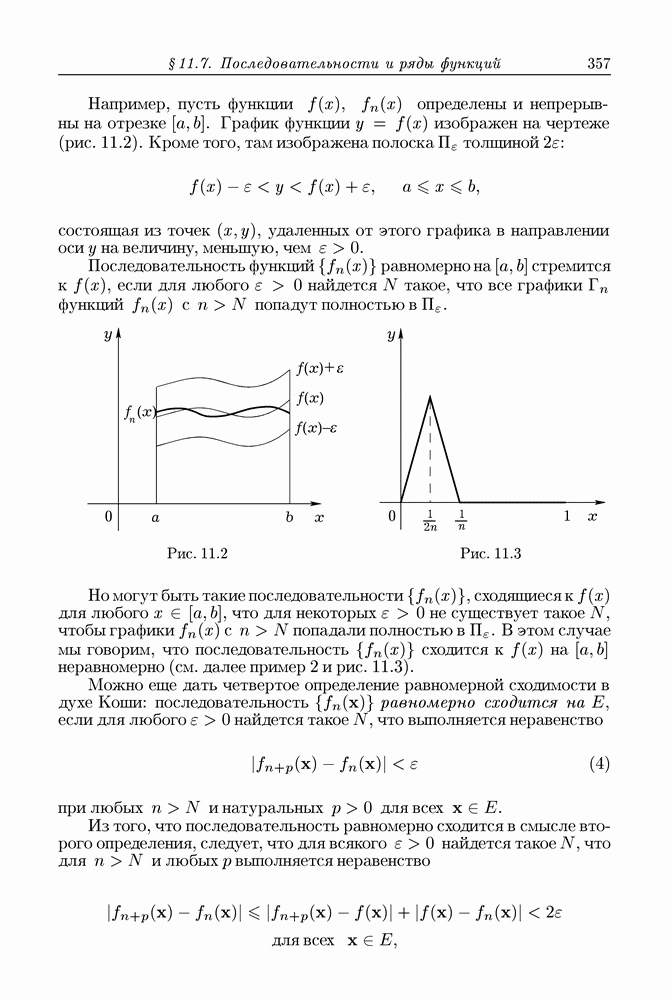
Рис. 13.1
Наоборот, из 3) следует 1). В самом деле, зададим фиксированную точку  Пусть известно, что данное поле вектора
Пусть известно, что данное поле вектора  таково, что криволинейный интеграл по любой кусочно гладкой кривой, соединяющей
таково, что криволинейный интеграл по любой кусочно гладкой кривой, соединяющей  с произвольной точкой
с произвольной точкой  не зависит от этой кривой, а зависит только от точки А. Таким образом, существует функция
не зависит от этой кривой, а зависит только от точки А. Таким образом, существует функция  такая, что
такая, что

Чтобы доказать, что  в точке
в точке  принадлежащей
принадлежащей  будем рассуждать следующим образом. В пределах области
будем рассуждать следующим образом. В пределах области  проведем отрезок
проведем отрезок  параллельный оси
параллельный оси  где
где  Соединим
Соединим  произвольной непрерывной кусочно гладкой ориентированной в направлении от
произвольной непрерывной кусочно гладкой ориентированной в направлении от 
кривой  и обозначим через С отрезок
и обозначим через С отрезок  ориентированный от
ориентированный от  к А. Тогда
к А. Тогда  (рис. 13.1) и
(рис. 13.1) и

так как очевидно, что 
Кривая  в дальнейшем рассуждении не будет изменяться, и потому первый интеграл в правой части (1) можно считать константой, которую мы обозначим через К. Таким образом,
в дальнейшем рассуждении не будет изменяться, и потому первый интеграл в правой части (1) можно считать константой, которую мы обозначим через К. Таким образом,

Функция  непрерывна, в частности, непрерывна по
непрерывна, в частности, непрерывна по  поэтому
поэтому  и мы доказали нужное равенство. Аналогично докажем равенства
и мы доказали нужное равенство. Аналогично докажем равенства

строя специальные, соединяющие точки  кривые, заканчивающиеся при подходе к
кривые, заканчивающиеся при подходе к  отрезком, в первом случае параллельным оси у, и во втором — оси
отрезком, в первом случае параллельным оси у, и во втором — оси  Мы доказали 1) при
Мы доказали 1) при 
Эквивалентность 2) и 3) тривиальна. В самом деле, пусть имеет место 2) и  два принадлежащих
два принадлежащих  пути, соединяющих точки
пути, соединяющих точки  Тогда
Тогда  замкнутый контур и
замкнутый контур и

т. е. выполняется 3). Наоборот, если имеет место 3) и С с  замкнутый контур, то, представив его в виде суммы
замкнутый контур, то, представив его в виде суммы  каких-либо контуров, получим
каких-либо контуров, получим

так как  соединяют одну и ту же пару точек. Если определенный на открытом множестве
соединяют одну и ту же пару точек. Если определенный на открытом множестве  вектор
вектор

является не только непрерывным, но и имеет непрерывные частные производные, то имеет смысл вектор

называемый ротором вектора  .
.
Если для вектора  выполняется одно из утверждений 2) или 3) предыдущей теоремы, то на основании этой теоремы на
выполняется одно из утверждений 2) или 3) предыдущей теоремы, то на основании этой теоремы на  можно определить однозначную (потенциальную) функцию
можно определить однозначную (потенциальную) функцию  имеющую непрерывные частные производные, так что
имеющую непрерывные частные производные, так что 
В таком случае если функции  имеют на
имеют на  непрерывные частные производные, то
непрерывные частные производные, то  имеет непрерывные частные производные второго порядка и имеют место равенства
имеет непрерывные частные производные второго порядка и имеют место равенства

Мы пришли к следующей теореме.
Теорема 2. Если поле вектора а, имеющего на открытом множестве  непрерывные частные производные, обладает тем свойством, что для любого ориентированного кусочно гладкого замкнутого контура
непрерывные частные производные, обладает тем свойством, что для любого ориентированного кусочно гладкого замкнутого контура 

то

Обратная теорема для произвольного, пусть даже связного, множества  не верна. Но она верна во всяком случае, если
не верна. Но она верна во всяком случае, если  есть прямоугольный параллелепипед.
есть прямоугольный параллелепипед.
В этом случае для определенного на  непрерывно дифференцируемого вектора а, имеющего
непрерывно дифференцируемого вектора а, имеющего  эффективно строится его потенциал по формуле
эффективно строится его потенциал по формуле

где  произвольная фиксированная точка и
произвольная фиксированная точка и  произвольная константа. В самом деле (пояснения ниже),
произвольная константа. В самом деле (пояснения ниже),

где мы применили формулу Ньютона-Лейбница, свойство (3) и, кроме того, дифференцирование под знаком интеграла. То, что последнее в данном случае законно, будет обосновано позже (в § 13.12). Аналогично доказывается, что  Таким образом,
Таким образом,  следовательно, выполняются равенства (2) для любого ориентированного (замкнутого) контура
следовательно, выполняются равенства (2) для любого ориентированного (замкнутого) контура 
Заметим, что правая часть (4) без последнего члена представляет собой криволинейный интеграл от вектора вдоль трехзвенной ломаной. Но имеет место более общая
Теорема 3. Пусть область  односвязна, т. е. такова, что любой принадлежащий ей кусочно гладкий контур можно стянуть в точку
односвязна, т. е. такова, что любой принадлежащий ей кусочно гладкий контур можно стянуть в точку  так, что в процессе стягивания он будет находиться в
так, что в процессе стягивания он будет находиться в  Тогда из того, что определенный на
Тогда из того, что определенный на  непрерывно дифференцируемый вектор а имеет
непрерывно дифференцируемый вектор а имеет  следует выполнение равенства (2) для любого ориентированного замкнутого контура
следует выполнение равенства (2) для любого ориентированного замкнутого контура 
Таким образом, из теоремы 3 следует существование определенной на  однозначной функции, потенциальной для вектора а на
однозначной функции, потенциальной для вектора а на 
Область, находящаяся между двумя концентрическими шаровыми поверхностями, удовлетворяет условию теоремы, между тем как область, представляющая собой все пространство без оси  не удовлетворяет этому условию, и в этом последнем случае можно указать пример (см. ниже) поля вектора, для которого теорема 3 не верна.
не удовлетворяет этому условию, и в этом последнем случае можно указать пример (см. ниже) поля вектора, для которого теорема 3 не верна.
Все понятия и теоремы, о которых была речь выше, легко переносятся на плоский случай. В плоскости  рассматриваются произвольные кусочно гладкие ориентированные кривые
рассматриваются произвольные кусочно гладкие ориентированные кривые

принадлежащие заданной области  На
На  задается поле непрерывного вектора
задается поле непрерывного вектора 
Криволинейный интеграл от  по кривой С определяется в точности так же, как в трехмерном случае. Его можно рассматривать как частный случай (см. § 13.2, (3)), полагая
по кривой С определяется в точности так же, как в трехмерном случае. Его можно рассматривать как частный случай (см. § 13.2, (3)), полагая

Таким образом,

Теперь уже потенциальная функция  вектора а, если она существует на
вектора а, если она существует на  есть однозначная, определенная на
есть однозначная, определенная на  функция
функция  от двух переменных. Ее градиент равен:
от двух переменных. Ее градиент равен:

Таким образом, в плоском случае теоремы 1-3 могут быть сформулированы следующим образом.
Теорема 1. Для поля  непрерывного вектора
непрерывного вектора  следующие утверждения равносильны:
следующие утверждения равносильны:
1)  для любого (непрерывного кусочно гладкого) замкнутого контура
для любого (непрерывного кусочно гладкого) замкнутого контура 
2) интеграл  зависит только от конечных точек
зависит только от конечных точек 
3) на  для вектора а существует потенциальная функция
для вектора а существует потенциальная функция 
Теорема 2. Если вектор а непрерывно дифференцируем на  и имеет на
и имеет на  потенциал, то
потенциал, то

Это вытекает из равенства

Теорема 3. Если область  односвязна и на ней выполняется тождественно (5), то вектор а имеет на
односвязна и на ней выполняется тождественно (5), то вектор а имеет на  потенциал.
потенциал.
Это утверждение есть частный случай теоремы 3, доказываемой ниже. Ее можно также наглядным образом получать из доказываемой ниже теоремы Грина.
Пример 1. Вектор а с компонентами

имеет непрерывные частные производные на области С, представляющей собой плоскость с выкинутой нулевой точкой. Легко проверить, что  на
на  Область
Область  не удовлетворяет условию теоремы 3, и сама теорема в данном случае неверна.
не удовлетворяет условию теоремы 3, и сама теорема в данном случае неверна.
В самом деле, введем область С, полученную выкидыванием из плоскости  отрицательного луча
отрицательного луча  оси х. На С согласно теореме 3 существует функция
оси х. На С согласно теореме 3 существует функция  . Ее можно определить в переменной точке
. Ее можно определить в переменной точке  , например, как криволинейный интеграл от а по любому пути
, например, как криволинейный интеграл от а по любому пути  , соединяющему фиксированную точку, пусть
, соединяющему фиксированную точку, пусть 

Однако эта функция не может быть продолжена с С на всю плоскость так, чтобы она была там однозначной и непрерывной.
В самом деле, значение  в произвольной точке
в произвольной точке  окружности радиуса 1 с центром в нулевой точке равно
окружности радиуса 1 с центром в нулевой точке равно

Чтобы прийти в точку  (лежащую на выкинутом луче), мы можем двигаться по нашей окружности, увеличивая в до
(лежащую на выкинутом луче), мы можем двигаться по нашей окружности, увеличивая в до  или уменьшая в до
или уменьшая в до  первом случае предельное значение
первом случае предельное значение  будет равно
будет равно  , а во втором
, а во втором  т.е. функция
т.е. функция  не может быть продолжена нужным образом на всю плоскость.
не может быть продолжена нужным образом на всю плоскость.
Так как произвольная потенциальная для а на  функция должна отличаться от рассмотренной функции
функция должна отличаться от рассмотренной функции  на постоянную, то доказано, что вообще не существует определенной на
на постоянную, то доказано, что вообще не существует определенной на  однозначной функции, которая была бы потенциальной для вектора а (всюду на
однозначной функции, которая была бы потенциальной для вектора а (всюду на 
Мы сознательно провели сравнительно длинное рассуждение, чтобы обосновать это утверждение. Его можно заменить следующим, более кратким. Существуют замкнутые, принадлежащие  гладкие контуры такие, что интегралы от нашего вектора а по ним не равны нулю. Например, таким контуром является окружность радиуса 1 с центром в нулевой точке — для нее
гладкие контуры такие, что интегралы от нашего вектора а по ним не равны нулю. Например, таким контуром является окружность радиуса 1 с центром в нулевой точке — для нее

Но тогда на  не может быть определена однозначная функция
не может быть определена однозначная функция  потенциальная для а (всюду на
потенциальная для а (всюду на  ), потому что существование такой функции противоречило бы теореме 1.
), потому что существование такой функции противоречило бы теореме 1.
Доказательство теоремы 3. Оно основано на том, что она верна, если  есть куб.
есть куб.
Зададим произвольный замкнутый кусочно гладкий контур 

Здесь параметр и пробегает отрезок [0,1], что, очевидно, не уменьшает общности. Тот факт, что контур  указанным в теореме 3 образом стягивается в точку, описывается так: существует поверхность
указанным в теореме 3 образом стягивается в точку, описывается так: существует поверхность  описываемая функциями
описываемая функциями

непрерывными, дифференцируемыми по  на треугольнике А и кусочно гладкими непрерывными по
на треугольнике А и кусочно гладкими непрерывными по  на
на  и такими, что
и такими, что

Так как  ограничена и замкнута,
ограничена и замкнута,  открыто и
открыто и  то найдется число
то найдется число  такое, что, какова бы ни была точка
такое, что, какова бы ни была точка  любой покрывающий ее куб с ребром длины
любой покрывающий ее куб с ребром длины  принадлежит
принадлежит 
Будем обозначать через  кубы, принадлежащие
кубы, принадлежащие 
Будем говорить, что множество  есть образ множества
есть образ множества  с А, если
с А, если  есть совокупность точек, полученных как отображения точек
есть совокупность точек, полученных как отображения точек  при помощи трех функций (5).
при помощи трех функций (5).

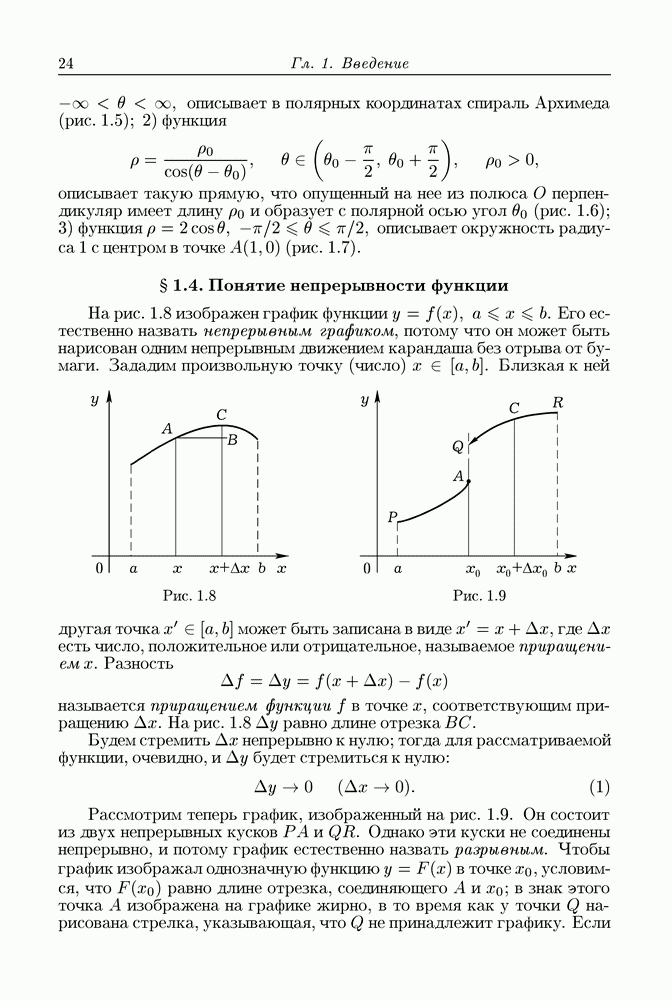
Рис. 13.2
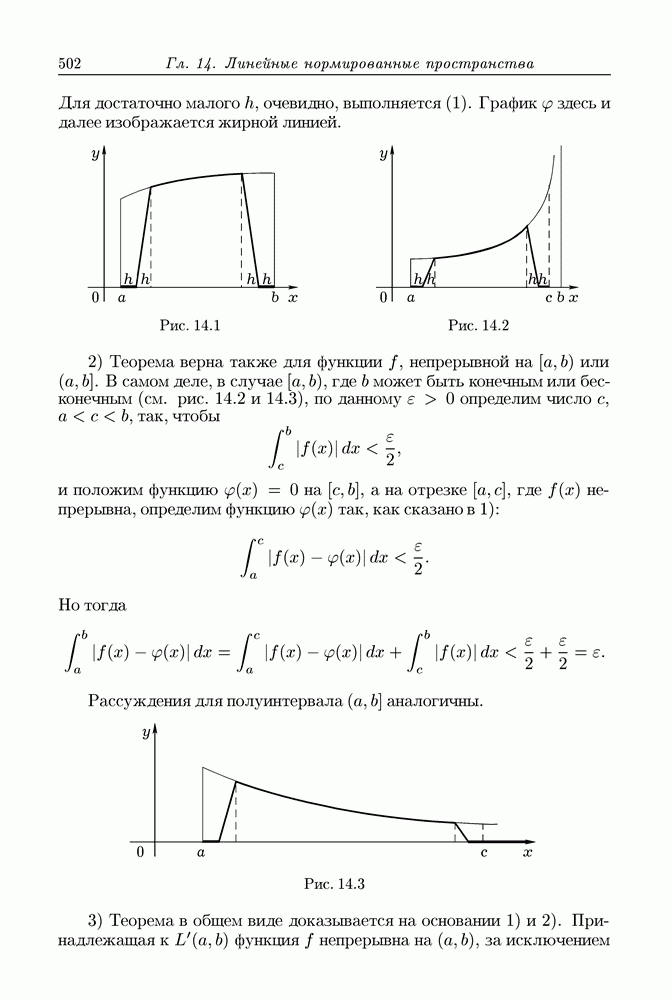
Рассечем А прямоугольной сеткой (рис. 13.2), настолько густой, чтобы образы  полученных частиц
полученных частиц  помещались в кубах а с ребром
помещались в кубах а с ребром  Ориентируем соответственно границы
Ориентируем соответственно границы  частиц
частиц  (рис. 13.2). Им соответствуют замкнутые непрерывные кусочно гладкие кривые
(рис. 13.2). Им соответствуют замкнутые непрерывные кусочно гладкие кривые  Каждая из них принадлежит некоторому кубу
Каждая из них принадлежит некоторому кубу  поэтому
поэтому

Сумма всех таких интегралов равна нулю:

потому что  и
и  обозначают одну и ту же кривую, ориентированную противоположно.
обозначают одну и ту же кривую, ориентированную противоположно.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.2. Множество. Интервал, отрезок
- § 1.3. Функция
- § 1.4. Понятие непрерывности функции
- § 1.5. Производная
- § 1.6. Первообразная. Неопределенный интеграл
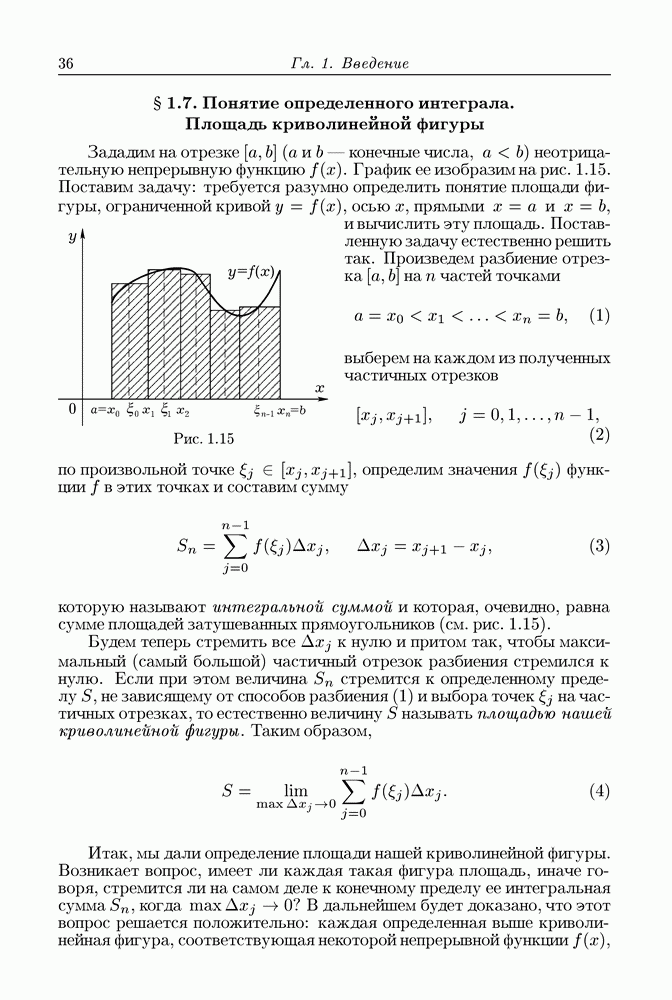
- § 1.7. Понятие определенного интеграла. Площадь криволинейной фигуры
- Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
- § 2.1. Рациональные и иррациональные числа
- § 2.2. Определение неравенства
- § 2.3. Основная лемма. Определение арифметических действий
- § 2.4. Основные свойства действительных чисел
- § 2.5. Изоморфизм различных представлений действительных чисел. Физические величины
- § 2.6. Неравенства для абсолютных величин
- § 2.7. Точные верхняя и нижняя грани множества
- § 2.8. Символика математической логики
- Глава 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 3.1. Понятие предела последовательности
- § 3.2. Арифметические действия с пределами
- § 3.3. Бесконечно малая и бесконечно большая величины
- § 3.4. Существование предела у монотонной ограниченной последовательности
- § 3.5. Число е
- § 3.6. Леммы о вложенных отрезках, существовании точных граней множества и сечения во множестве действительных чисел
- § 3.7. Теорема Больцано-Вейерштрасса. Верхний и нижний пределы
- § 3.8. Критерий Коши существования предела
- § 3.9. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 4. ПРЕДЕЛ ФУНКЦИИ
- § 4.1. Понятие предела функции
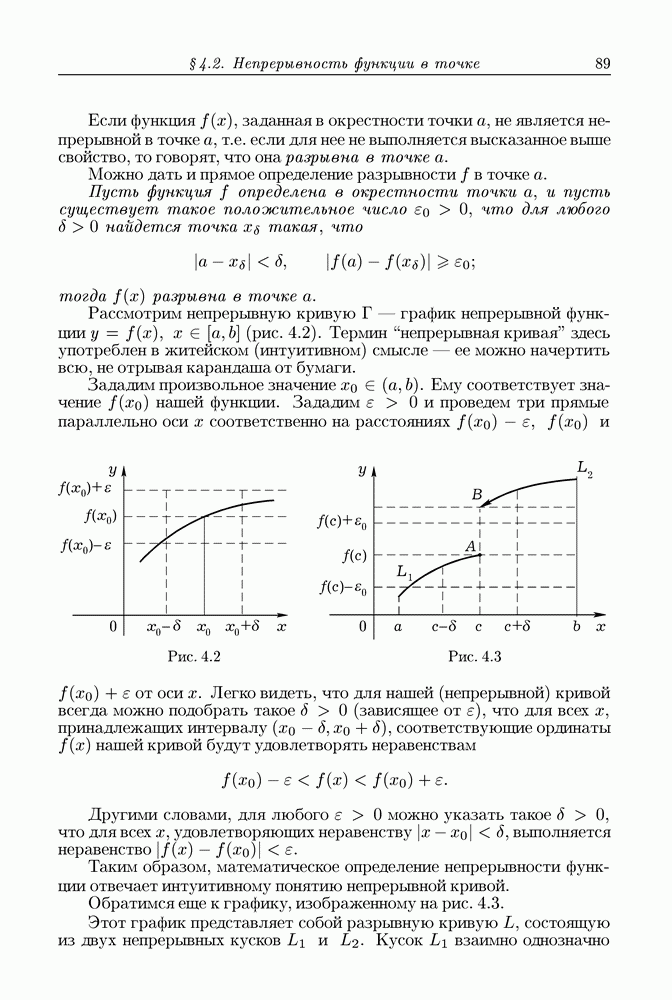
- § 4.2. Непрерывность функции в точке
- § 4.3. Пределы функции справа и слева. Монотонная функция
- § 4.4. Функции, непрерывные на отрезке
- § 4.5. Обратная функция
- § 4.6. Показательная и логарифмическая функции
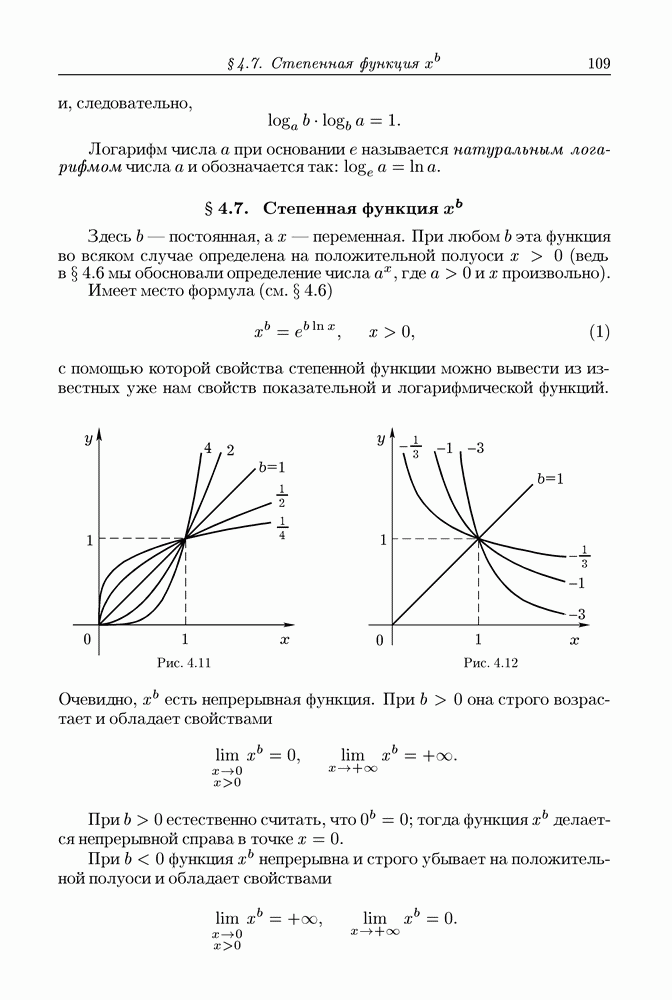
- § 4.7. Степенная функция x^b
- § 4.8. Еще о числе е
- § 4.9. lim sin oo/oo
- § 4.10. Порядок переменной, эквивалентность (асимптотика)
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- § 5.1. Производная
- § 5.2. Дифференциал функции
- § 5.3. Производная функции от функции
- § 5.4. Производная обратной функции
- § 5.6. Производные и дифференциалы высшего порядка
- § 5.7. Возрастание и убывание функции на интервале и в точке. Локальный экстремум
- § 5.8. Теоремы о среднем значении. Критерии возрастания и убывания функции на интервале. Достаточные критерии локальных экстремумов
- § 5.9. Формула Тейлора
- § 5.10. Формулы Тейлора для важнейших элементарных функций
- § 5.11. Ряд Тейлора
- § 5.12. Выпуклость кривой в точке. Точка перегиба
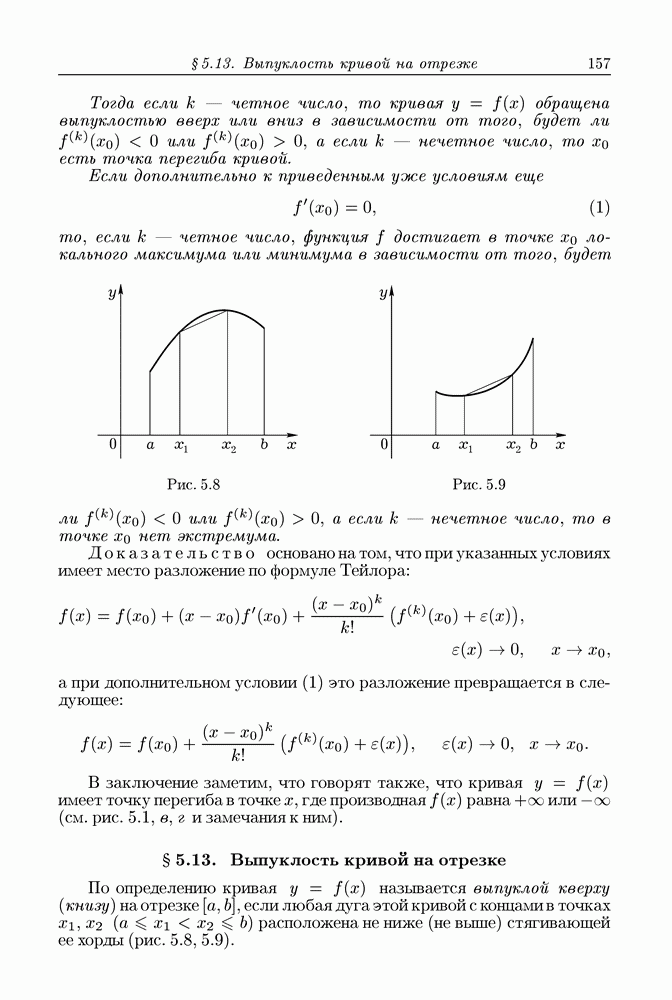
- § 5.13. Выпуклость кривой на отрезке
- § 5.14. Раскрытие неопределенностей
- § 5.15. Асимптота
- § 5.16. Схема построения графика функции
- § 5.17. Кусочно непрерывные и кусочно гладкие функции
- Глава 6. n-МЕРНОЕ ПРОСТРАНСТВО. ГЕОМЕТРИЯ КРИВОЙ
- § 6.1. n-мерное пространство. Линейное множество
- § 6.2. Евклидово n-мерное пространство. Пространство со скалярным произведением
- § 6.3. Линейное нормированное пространство
- § 6.4. Вектор-функция в n-мерном евклидовом пространстве
- § 6.5. Непрерывная кривая. Гладкая кривая
- § 6.6. Геометрический смысл производной вектор-функции
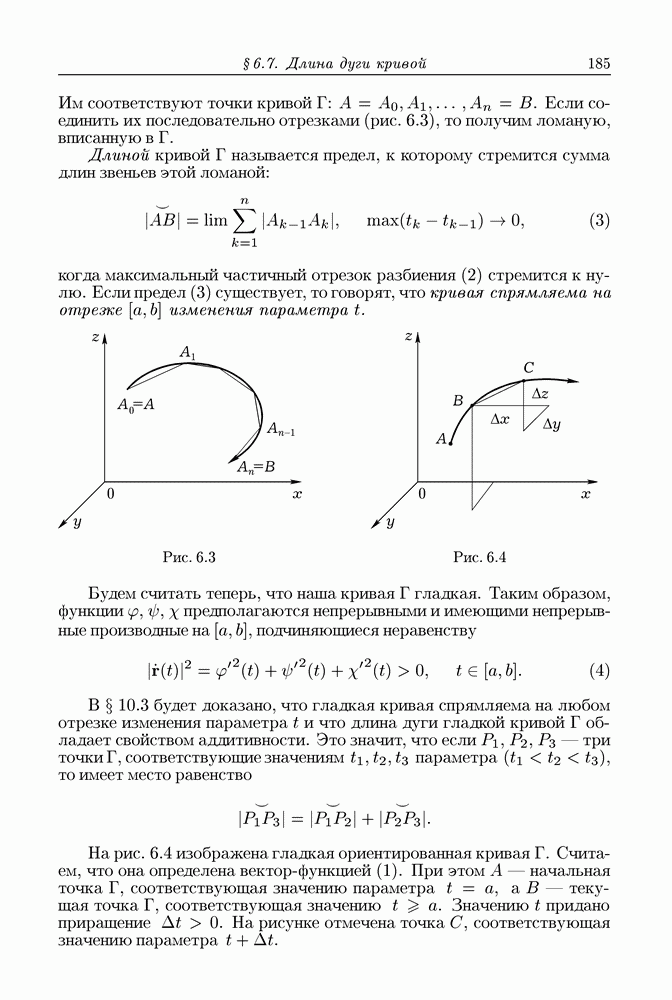
- § 6.7. Длина дуги кривой
- § 6.8. Касательная
- § 6.9. Основной триэдр кривой
- § 6.10. Соприкасающаяся плоскость
- § 6.11. Кривизна и радиус кривизны кривой
- § 6.12. Эволюта
- § 6.13. Формулы Френе. Свойства эволюты
- Глава 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 7.1. Открытое множество
- § 7.2. Предел функции
- § 7.3. Непрерывная функция
- § 7.4. Частные производные и производная по направлению
- § 7.5. Дифференцируемая функция. Касательная плоскость
- § 7.6. Производная сложной функции. Производная по направлению. Градиент
- § 7.7. Независимость от порядка дифференцирования
- § 7.8. Дифференциал функции. Дифференциал высшего порядка
- § 7.9. Теорема Больцано-Вейерштрасса
- § 7.10. Замкнутые и открытые множества
- § 7.11. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве
- § 7.12. Лемма о вложенных прямоугольниках и лемма Бореля
- § 7.13. Формула Тейлора
- § 7.14. локальный (абсолютный) экстремум функции
- § 7.15. Теоремы существования неявной функции
- § 7.16. Теорема существования решения системы уравнений
- § 7.17. Отображения
- § 7.18. Гладкая поверхность
- § 7.19. Дифференциалы неявных функций. Линеаризация
- § 7.20. Локальный относительный экстремум
- § 7.21. Замена переменных в частных производных
- § 7.22. Система зависимых функций
- Глава 8. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. АЛГЕБРА МНОГОЧЛЕНОВ
- § 8.1. Введение. Методы замены переменной и интегрирования по частям
- § 8.2. Комплексные числа
- § 8.3. Комплексные функции
- § 8.4. Многочлены
- § 8.5. Разложение рациональной функции на простейшие дроби
- § 8.6. Интегрирование рациональных дробей
- § 8.7. Интегрирование алгебраических иррациональностей
- § 8.8. Подстановки Эйлера
- § 8.9. Биномиальные дифференциалы. Теорема Чебышева
- § 8.10. Интегрирование тригонометрических выражений
- § 8.11. Тригонометрические подстановки
- § 8.12. Несколько важных интегралов, не выражаемых в элементарных функциях
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
- § 9.2. Ограниченность интегрируемой функции
- § 9.3. Суммы Дарбу
- § 9.4. Основная теорема
- § 9.5. Теоремы о существовании интеграла от непрерывной и монотонной функции на [a, b]
- § 9.6. Аддитивные и однородные свойства интеграла
- § 9.7. Неравенства и теорема о среднем
- § 9.8. Интеграл как функция верхнего предела. Теорема Ньютона-Лейбница
- § 9.9. Вторая теорема о среднем
- § 9.10. Видоизменение функции
- § 9.11. Несобственные интегралы
- § 9.12. Несобственные интегралы от неотрицательных функций
- § 9.13. Интегрирование по частям
- § 9.14. Несобственный интеграл и ряд
- § 9.15. Несобственные интегралы с особенностями в нескольких точках
- § 9.16. Формула Тейлора с остатком в интегральной форме
- § 9.17. Формулы Валлиса и Стирлинга
- Глава 10. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- § 10.1. Площадь в полярных координатах
- § 10.2. Объем тела вращения
- § 10.3. Длина дуги гладкой кривой
- § 10.4. Площадь поверхности тела вращения
- § 10.5. Интерполяционный многочлен Лагранжа
- § 10.6. Квадратурные формулы прямоугольников
- § 10.7. Формула Симпсона
- Глава 11. РЯДЫ
- § 11.1. Понятие ряда
- § 11.2. Действия с рядами
- § 11.3. Ряды с неотрицательными членами
- § 11.4. Ряд Лейбница
- § 11.5. Абсолютно сходящиеся ряды
- § 11.6. Условно и безусловно сходящиеся ряды с действительными членами
- § 11.7. Последовательности и ряды функций. Равномерная сходимость
- § 11.8. Интегрирование и дифференцирование равномерно сходящихся рядов на отрезке
- § 11.9. Кратные ряды. Перемножение абсолютно сходящихся рядов
- § 11.10. Суммирование рядов и последовательностей методом средних арифметических
- § 11.11. Степенные ряды
- § 11.12. Дифференцирование и интегрирование степенных рядов
- § 11.13. Степенные ряды функций e^z, cos z, sinz комплексной переменной
- Глава 12. КРАТНЫЕ ИНТЕГРАЛЫ
- § 12.2. Мера Жордана
- § 12.3. Важные примеры квадрируемых по Жордану множеств
- § 12.4. Еще один критерий измеримости множества. Полярные координаты
- § 12.5. Другие случаи измеримости
- § 12.6. Понятие кратного интеграла
- § 12.7. Верхняя и нижняя интегральные суммы. Основная теорема
- § 12.8. Интегрируемость непрерывной функции на замкнутом измеримом множестве. Другие критерии
- § 12.9. Свойства кратных интегралов
- § 12.10. Сведение кратного интеграла к интегрированию по отдельным переменным
- § 12.11. Непрерывность интеграла по параметру
- § 12.12. Геометрическая интерпретация знака определителя
- § 12.13. Замена переменных в кратном интеграле. Простейший случай
- § 12.14. Замена переменных в кратном интеграле
- § 12.15. Доказательство леммы 1 § 12.14
- § 12.16. Полярные координаты в плоскости
- § 12.17. Полярные и цилиндрические координаты в пространстве
- § 12.18. Гладкая поверхность
- § 12.19. Площадь поверхности
- Глава 13. ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- § 13.1. Криволинейный интеграл первого рода
- § 13.2. Криволинейный интеграл второго рода
- § 13.3. Поле потенциала
- § 13.4. Ориентация плоской области
- § 13.5. Формула Грина. Выражение площади через криволинейный интеграл
- § 13.6. Интеграл по поверхности первого рода
- § 13.7. Ориентация поверхностей
- § 13.8. Интеграл по ориентированной плоской области
- § 13.9. Поток вектора через ориентированную поверхность
- § 13.10. Дивергенция. Теорема Гаусса-Остроградского
- § 13.11. Ротор вектора. Формула Стокса
- § 13.12. Дифференцирование интеграла по параметру
- § 13.13. Несобственный интеграл
- § 13.14. Равномерная сходимость несобственного интеграла
- § 13.15. Равномерно сходящийся интеграл для неограниченной области
- Глава 14. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ
- § 14.2. Пространство L'(L)
- § 14.3. Пространство L2 (L2)
- § 14.4. Пространство …
- § 14.5. Полнота системы элементов в банаховом пространстве
- § 14.6. Ортогональная система в пространстве со скалярным произведением
- § 14.7. Ортогонализация системы
- § 14.8. Полнота системы функций в …
- Глава 15. РЯДЫ ФУРЬЕ. ПРИБЛИЖЕНИЕ ФУНКЦИЙ ПОЛИНОМАМИ
- § 15.2. Сумма Дирихле
- § 15.3. Формулы для остатка ряда Фурье
- § 15.4. Теоремы об осцилляции
- § 15.5. Критерий сходимости рядов Фурье. Полнота тригонометрической системы функций
- § 15.6. Комплексная форма записи ряда Фурье
- § 15.7. Дифференцирование и интегрирование рядов Фурье
- § 15.8. Оценка остатка ряда Фурье
- § 15.9. Алгебраические многочлены. Многочлены Чебышева
- § 15.10. Теорема Вейерштрасса
- § 15.11. Многочлены Лежандра
- Глава 16. ИНТЕГРАЛ ФУРЬЕ. ОБОБЩЕННЫЕ ФУНКЦИИ
- § 16.1. Понятие интеграла Фурье
- § 16.2. Сходимость простого интеграла Фурье к порождающей его функции
- § 16.3. Преобразование Фурье. Повторный интеграл Фурье. Косинус- и синус-преобразования Фурье
- § 16.4. Производная преобразования Фурье
- § 16.5. Обобщенные функции в смысле D
- § 16.6. Пространство S
- § 16.7. Пространство S обобщенных функций