| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1.5. Производная
Понятие производной возникло как результат многовековых усилий, направленных на решение таких задач, как задача о проведении касательной к кривой или о вычислении скорости неравномерного движения. Подобные задачи и задача о вычислении площади криволинейной фигуры интересовали математиков с древних времен. В XVII веке в работах Ньютона и Лейбница эта деятельность получила определенное теоретическое завершение. Ньютон и Лейбниц создали общие методы дифференцирования и интегрирования функций и доказали важную теорему, носящую их имя, устанавливающую тесную связь между операциями дифференцирования и интегрирования. Надо, однако, иметь в виду, что современное изложение этих вопросов существенно отличается от того, как они излагались во времена Ньютона и Лейбница. В рассуждениях и понятиях, которыми оперировали в то время, с нашей точки зрения можно найти много неясного; да и сами математики того времени это сознавали, о чем свидетельствуют ожесточенные дискуссии, которые происходили по этим вопросам между ними.
Современный математический анализ базируется на понятии предела, которое выкристаллизовалось в четкую формулировку не так уж давно — в первой половине девятнадцатого столетия. Большая заслуга в этом принадлежит французскому математику Коши.
Понятие предела существенно используется в определениях понятий непрерывности функции, производной, интеграла.
Мгновенная скорость. Пусть точка движется по прямой и функция  выражает зависимость от времени
выражает зависимость от времени  ее расстояния (с учетом знака)
ее расстояния (с учетом знака)  до некоторой начальной точки О прямой. В момент времени
до некоторой начальной точки О прямой. В момент времени  точка находится на расстоянии
точка находится на расстоянии  от О. В момент же времени
от О. В момент же времени  она находится на расстоянии
она находится на расстоянии  от О. Средняя скорость ее на промежутке времени
от О. Средняя скорость ее на промежутке времени  равна
равна

Мгновенную или истинную скорость  точки в момент времени
точки в момент времени  естественно определить как предел, к которому стремится
естественно определить как предел, к которому стремится  при
при  т.е.
т.е. 

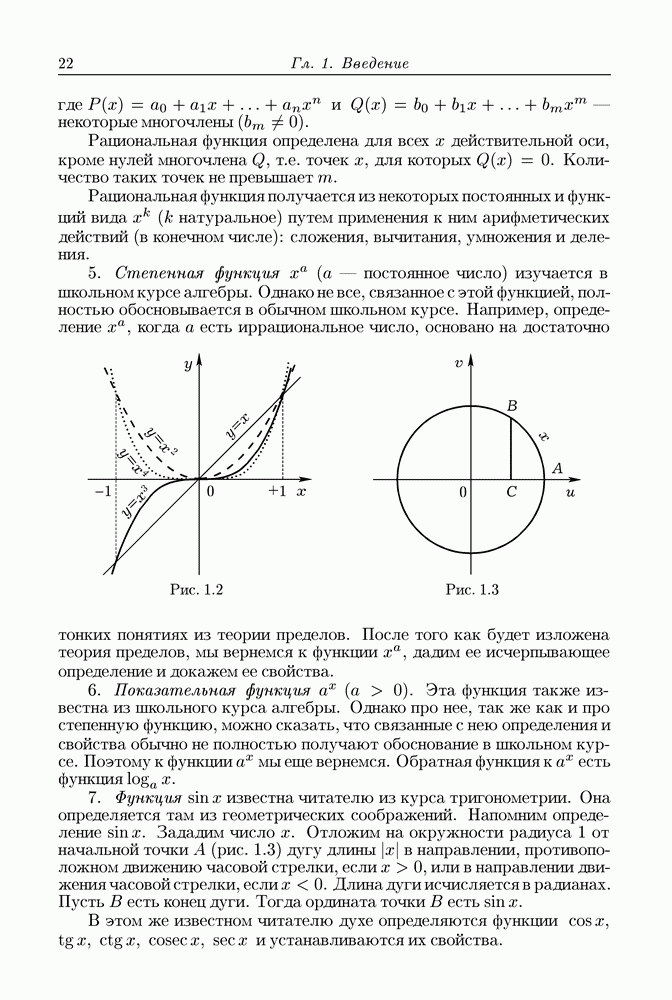
Касательная к кривой. Рассмотрим какую-нибудь непрерывную кривую  в плоскости или пространстве (рис. 1.11).
в плоскости или пространстве (рис. 1.11).
Пусть А — лежащая на ней точка и А — другая лежащая на  точка. Прямую
точка. Прямую  проходящую через
проходящую через  будем называть секущей (кривую
будем называть секущей (кривую  Будем теперь точку А двигать непрерывно по
Будем теперь точку А двигать непрерывно по  неограниченно приближая к А. Тогда секущая
неограниченно приближая к А. Тогда секущая  будет вращаться относительно А. Может случиться, что при этом
будет вращаться относительно А. Может случиться, что при этом  будет стремиться занять в пределе положение вполне определенной (проходящей, очевидно, через А) прямой, которую мы обозначили через
будет стремиться занять в пределе положение вполне определенной (проходящей, очевидно, через А) прямой, которую мы обозначили через  Если это будет иметь место, то говорят, что кривая
Если это будет иметь место, то говорят, что кривая  имеет в точке А касательную. Именно прямую
имеет в точке А касательную. Именно прямую  называют касательной к
называют касательной к  в точке А.
в точке А.

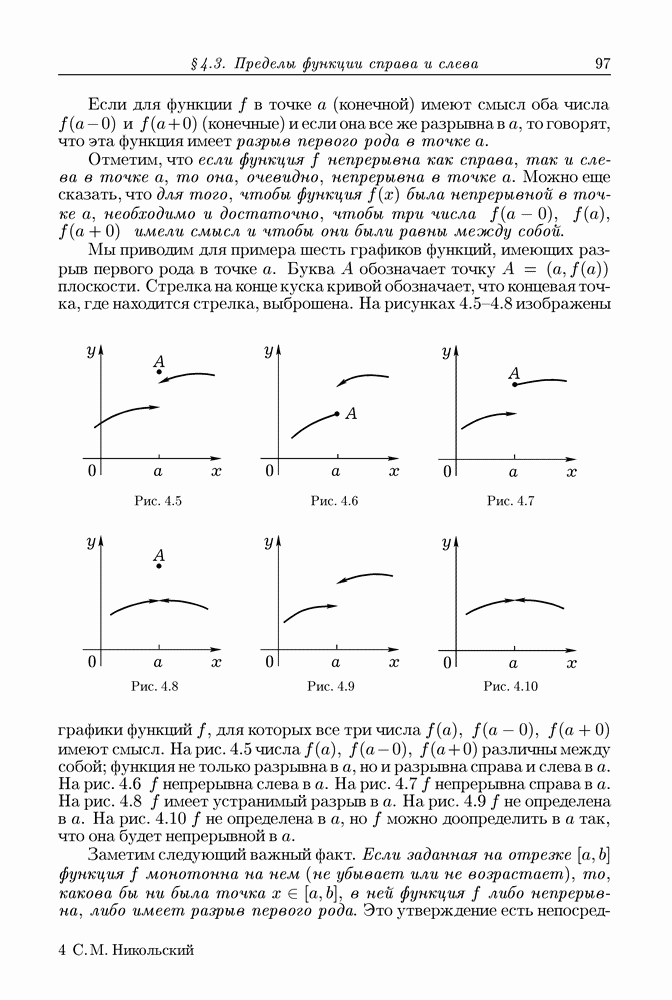
Рис. 1.11

Рис. 1.12
Не всякая непрерывная кривая в любой ее точке имеет касательную. Тривиальным примером этого может служить кривая, изображенная на рис. 1.12. Она состоит из двух гладких кусков  соединенных в точке А "под углом". На рисунке на кривой отмечены две другие точки,
соединенных в точке А "под углом". На рисунке на кривой отмечены две другие точки,  соответственно лежащие на
соответственно лежащие на  через
через  обозначены проходящие через
обозначены проходящие через  и А секущие.
и А секущие.
Очевидно, что если  двигаясь соответственно по
двигаясь соответственно по  будут приближаться к А, то секущие
будут приближаться к А, то секущие  будут стремиться занять в пределе положение двух разных прямых
будут стремиться занять в пределе положение двух разных прямых  Поэтому рассматриваемая кривая не имеет касательной в точке А. Впрочем, можно было бы, развивая введенное определение, сказать, что наша кривая имеет в точке А две односторонние касательные, но об этом речь сейчас не идет.
Поэтому рассматриваемая кривая не имеет касательной в точке А. Впрочем, можно было бы, развивая введенное определение, сказать, что наша кривая имеет в точке А две односторонние касательные, но об этом речь сейчас не идет.
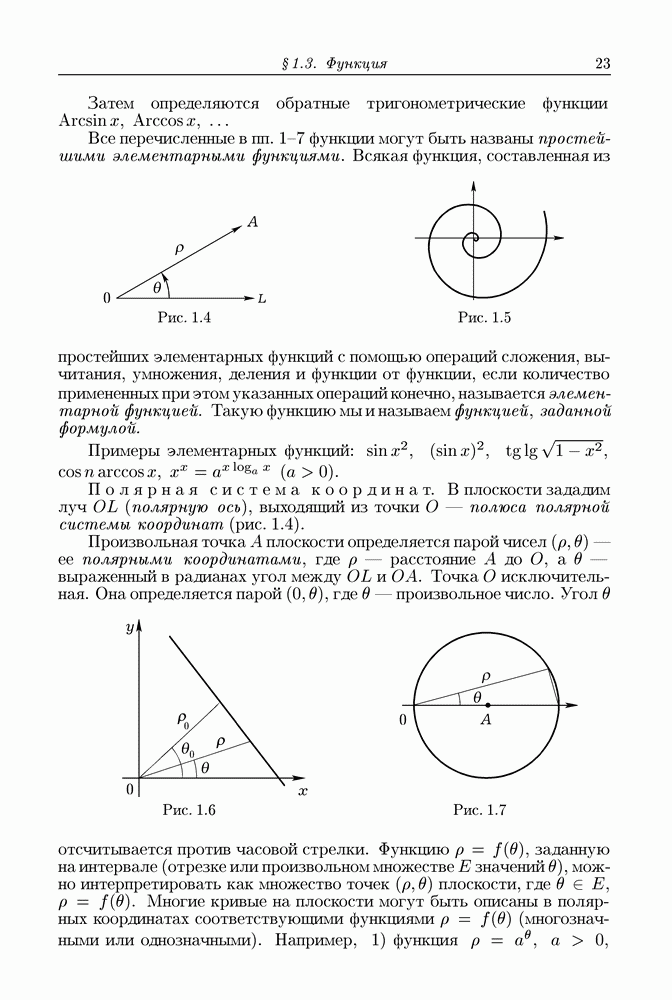
Пусть теперь кривая  есть график непрерывной на
есть график непрерывной на  функции (рис. 1.13)
функции (рис. 1.13) 
Зададим на  точку А, имеющую абсциссу
точку А, имеющую абсциссу  и другую точку С, имеющую абсциссу
и другую точку С, имеющую абсциссу  Через эти точки проведем прямую
Через эти точки проведем прямую  секущую. На ней отметим стрелкой положительное направление (соответствующее возрастанию
секущую. На ней отметим стрелкой положительное направление (соответствующее возрастанию  Угол между этим направлением и положительной осью х обозначим через
Угол между этим направлением и положительной осью х обозначим через  . В данном случае
. В данном случае  Очевидно,
Очевидно,

Будем  стремить к нулю; тогда вследствие непрерывности
стремить к нулю; тогда вследствие непрерывности  будет также и А у стремиться к нулю, и точка С, двигаясь по
будет также и А у стремиться к нулю, и точка С, двигаясь по  будет стремиться к точке А. Если окажется (этого может и не быть), что при этом
будет стремиться к точке А. Если окажется (этого может и не быть), что при этом
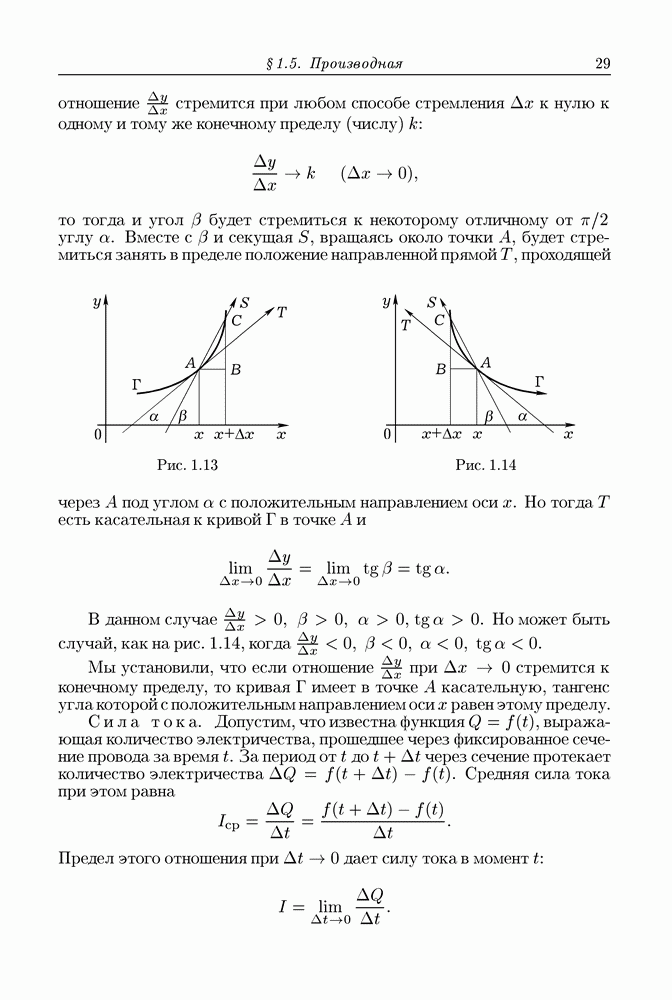
отношение стремится при любом способе стремления  к нулю к одному и тому же конечному пределу (числу) k:
к нулю к одному и тому же конечному пределу (числу) k:

то тогда и угол  будет стремиться к некоторому отличному от
будет стремиться к некоторому отличному от  углу а. Вместе с
углу а. Вместе с  и секущая
и секущая  вращаясь около точки А, будет стремиться занять в пределе положение направленной прямой
вращаясь около точки А, будет стремиться занять в пределе положение направленной прямой  проходящей через А под углом а с положительным направлением оси
проходящей через А под углом а с положительным направлением оси 

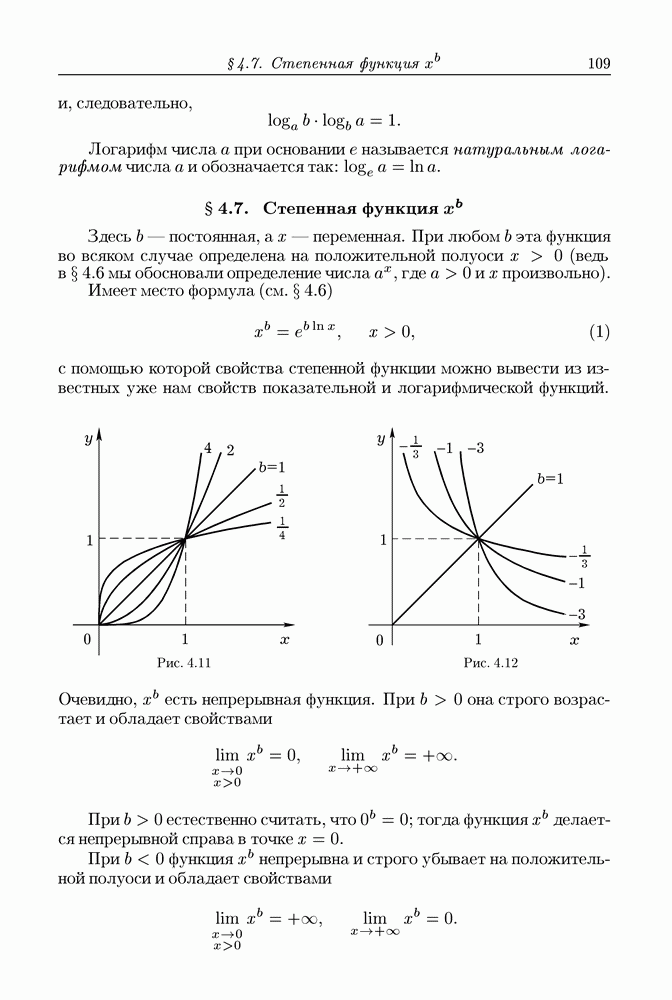
Рис. 1.13

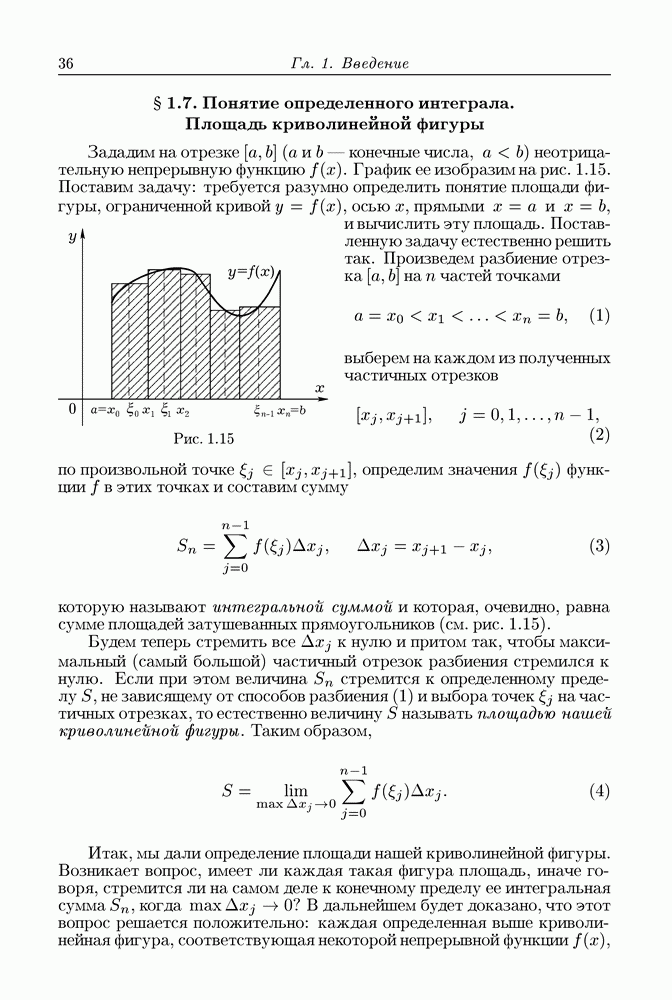
Рис. 1.14
Но тогда  есть касательная к кривой
есть касательная к кривой  в точке А и
в точке А и

В данном случае  Но может быть случай, как на рис. 1.14, когда
Но может быть случай, как на рис. 1.14, когда  .
.
Мы установили, что если отношение  при
при  стремится к конечному пределу, то кривая
стремится к конечному пределу, то кривая  имеет в точке А касательную, тангенс угла которой с положительным направлением оси х равен этому пределу.
имеет в точке А касательную, тангенс угла которой с положительным направлением оси х равен этому пределу.
Сила тока. Допустим, что известна функция  выражающая количество электричества, прошедшее через фиксированное сечение провода за время
выражающая количество электричества, прошедшее через фиксированное сечение провода за время  За период от
За период от  до
до  через сечение протекает количество электричества
через сечение протекает количество электричества  Средняя сила тока при этом равна
Средняя сила тока при этом равна

Предел этого отношения при  дает силу тока в момент t:
дает силу тока в момент t:

Производная. Все три рассмотренные задачи, несмотря на то, что они относятся к различным областям человеческого знания: механике, геометрии, теории электричества, — привели к одной и той же математической операции, которую нужно произвести над некоторой функцией. Надо найти предел отношения приращения функции к соответствующему приращению аргумента, когда последнее стремится к нулю. Мы могли бы как угодно увеличить число задач, решение которых приводится к подобной операции. К ней приводит задача о скорости химической реакции, о плотности неравномерно распределенной массы и др.
Естественно, что эта операция получила в математике специальное название. Она называется операцией дифференцирования функции. Результат ее называется производной.
Итак, производной от функции  заданной на некотором интервале
заданной на некотором интервале  в точке х этого интервала, называется предел, к которому стремится отношение приращения функции
в точке х этого интервала, называется предел, к которому стремится отношение приращения функции  в этой точке к соответствующему приращению аргумента, когда последнее стремится к нулю. Производную принято обозначать так:
в этой точке к соответствующему приращению аргумента, когда последнее стремится к нулю. Производную принято обозначать так:

Но широко употребляются и другие обозначения: Удобство того или иного из них читатель впоследствии оценит сам.
Результаты рассмотренных примеров теперь можно сформулировать так:
Скорость в момент  движущейся по числовой прямой точки, координата которой
движущейся по числовой прямой точки, координата которой  есть функция
есть функция  от времени равна производной от этой функции
от времени равна производной от этой функции 
Тангенс угла  между касательной к кривой, описываемой функцией
между касательной к кривой, описываемой функцией  в точке, имеющей абсциссу
в точке, имеющей абсциссу  и положительным направлением оси х равен производной
и положительным направлением оси х равен производной 
Сила тока I в проводе в момент если функция  выражает количество электричества, прошедшее за время
выражает количество электричества, прошедшее за время  через сечение провода, равна производной
через сечение провода, равна производной 
Некоторые формулы. При натуральном 

В самом деле, считая  будем иметь
будем иметь

где мы снова пользуемся элементарными свойствами пределов, которые будут обоснованы в дальнейшем (см. ниже замечание). Справедливы также формулы:

где  — константа. Докажем первое равенство, доказательство второго предоставляем читателю. При
— константа. Докажем первое равенство, доказательство второго предоставляем читателю. При 

Мы воспользовались свойством  и тем фактом, что функция
и тем фактом, что функция  непрерывна. Оба эти утверждения будут обоснованы далее (см. § 4.2 и § 4.9). При
непрерывна. Оба эти утверждения будут обоснованы далее (см. § 4.2 и § 4.9). При  равенства (2) и (3) выражают, что производная от постоянной равна нулю (см. ниже (4)).
равенства (2) и (3) выражают, что производная от постоянной равна нулю (см. ниже (4)).
Производная от функции  есть в свою очередь функция
есть в свою очередь функция  Если производная от
Если производная от  существует, то она называется второй производной от
существует, то она называется второй производной от  и обозначается так:
и обозначается так: 
Подобным же образом определяются высшие производные  от
от  порядка
порядка  где
где  любое натуральное число.
любое натуральное число.
Вторая производная от функции  выражающей закон движения точки на прямой, равна, очевидно, ускорению этой точки в момент времени
выражающей закон движения точки на прямой, равна, очевидно, ускорению этой точки в момент времени 
Уже из сказанного видно, что понятие производной имеет громадное значение в прикладных вопросах, но оно является фундаментальным и в самой математике. Это будет видно из дальнейшего.
Отметим, что постоянное число С, рассматриваемое как функция от х (см. § 1.3), имеет производную, равную нулю тождественно (т.е. равную нулю для всех  . В самом деле,
. В самом деле,

Обратное утверждение также верно: если о функции известно, что ее производная равна нулю тождественно,  то она есть постоянная. Это простое утверждение, чтобы его доказать строго математически, требует уже достаточно серьезного аппарата, с которым мы познакомимся позднее (см. § 5.8). С другой стороны, из механических соображений оно совершенно очевидно. В самом деле, пусть функция
то она есть постоянная. Это простое утверждение, чтобы его доказать строго математически, требует уже достаточно серьезного аппарата, с которым мы познакомимся позднее (см. § 5.8). С другой стороны, из механических соображений оно совершенно очевидно. В самом деле, пусть функция  выражает закон движения точки по прямой, причем ее скорость тождественно равна нулю:
выражает закон движения точки по прямой, причем ее скорость тождественно равна нулю:  Тогда точка стоит на месте и расстояние
Тогда точка стоит на месте и расстояние  ее до начальной точки О равно постоянной при любом
ее до начальной точки О равно постоянной при любом  Тот факт, что в этом рассуждении мы х заменили на
Тот факт, что в этом рассуждении мы х заменили на  не имеет значения — время тоже можно обозначать через х.
не имеет значения — время тоже можно обозначать через х.
Отметим еще, что если функции  имеют в некоторой точке х производную и
имеют в некоторой точке х производную и  постоянные числа, то функция
постоянные числа, то функция

также имеет производную, равную

В самом деле,

Во втором равенстве в этой цепочке равенств мы воспользовались тем фактом, что предел суммы равен сумме пределов, и в третьем, — что постоянную законно вынести за знак предела.
По индукции можно доказать более общее утверждение:

где  постоянные числа, а о функциях
постоянные числа, а о функциях  предполагается, что они имеют производные.
предполагается, что они имеют производные.
В частности, получим производную от многочлена:

( - постоянные).
- постоянные).
Замечание. Формулу  можно доказать по индукции. При
можно доказать по индукции. При  имеем
имеем

Если теперь допустить, что формула  верна, то получим (см. § 5.1, (5))
верна, то получим (см. § 5.1, (5))

Отметим формулы  § 5.1 и таблицу § 5.5, которые могут оказаться полезными читателю еще до того, как он дойдет до них, изучая предмет систематически.
§ 5.1 и таблицу § 5.5, которые могут оказаться полезными читателю еще до того, как он дойдет до них, изучая предмет систематически.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.2. Множество. Интервал, отрезок
- § 1.3. Функция
- § 1.4. Понятие непрерывности функции
- § 1.5. Производная
- § 1.6. Первообразная. Неопределенный интеграл
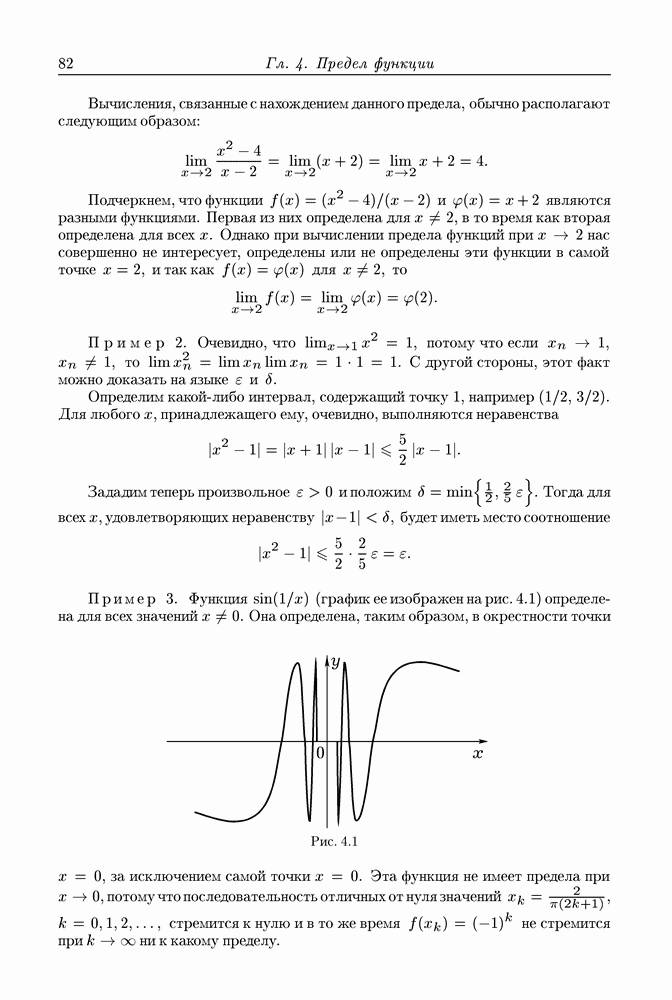
- § 1.7. Понятие определенного интеграла. Площадь криволинейной фигуры
- Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
- § 2.1. Рациональные и иррациональные числа
- § 2.2. Определение неравенства
- § 2.3. Основная лемма. Определение арифметических действий
- § 2.4. Основные свойства действительных чисел
- § 2.5. Изоморфизм различных представлений действительных чисел. Физические величины
- § 2.6. Неравенства для абсолютных величин
- § 2.7. Точные верхняя и нижняя грани множества
- § 2.8. Символика математической логики
- Глава 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
- § 3.1. Понятие предела последовательности
- § 3.2. Арифметические действия с пределами
- § 3.3. Бесконечно малая и бесконечно большая величины
- § 3.4. Существование предела у монотонной ограниченной последовательности
- § 3.5. Число е
- § 3.6. Леммы о вложенных отрезках, существовании точных граней множества и сечения во множестве действительных чисел
- § 3.7. Теорема Больцано-Вейерштрасса. Верхний и нижний пределы
- § 3.8. Критерий Коши существования предела
- § 3.9. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 4. ПРЕДЕЛ ФУНКЦИИ
- § 4.1. Понятие предела функции
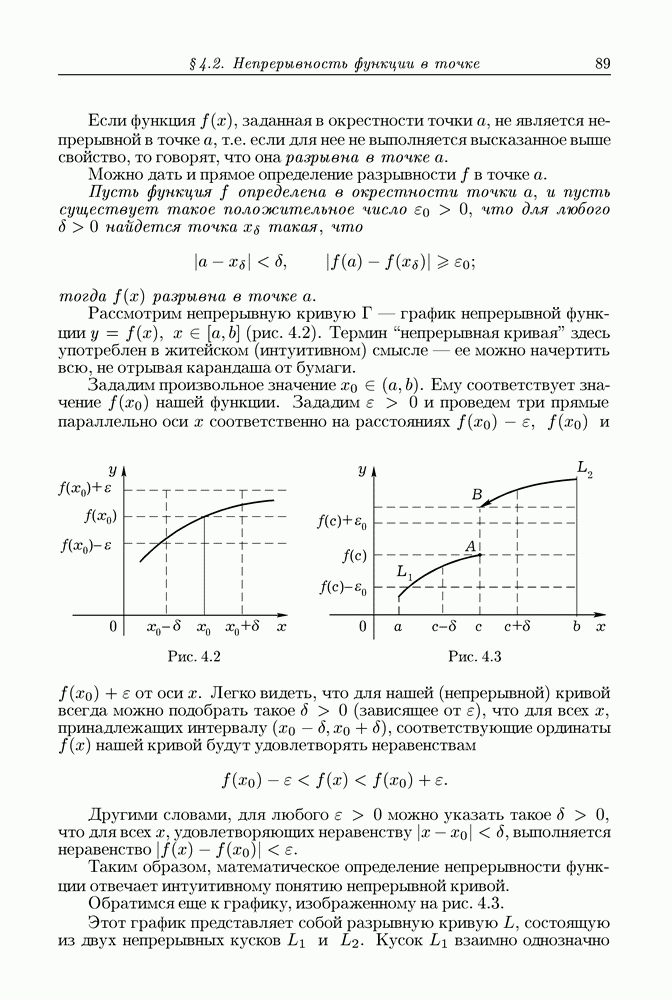
- § 4.2. Непрерывность функции в точке
- § 4.3. Пределы функции справа и слева. Монотонная функция
- § 4.4. Функции, непрерывные на отрезке
- § 4.5. Обратная функция
- § 4.6. Показательная и логарифмическая функции
- § 4.7. Степенная функция x^b
- § 4.8. Еще о числе е
- § 4.9. lim sin oo/oo
- § 4.10. Порядок переменной, эквивалентность (асимптотика)
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- § 5.1. Производная
- § 5.2. Дифференциал функции
- § 5.3. Производная функции от функции
- § 5.4. Производная обратной функции
- § 5.6. Производные и дифференциалы высшего порядка
- § 5.7. Возрастание и убывание функции на интервале и в точке. Локальный экстремум
- § 5.8. Теоремы о среднем значении. Критерии возрастания и убывания функции на интервале. Достаточные критерии локальных экстремумов
- § 5.9. Формула Тейлора
- § 5.10. Формулы Тейлора для важнейших элементарных функций
- § 5.11. Ряд Тейлора
- § 5.12. Выпуклость кривой в точке. Точка перегиба
- § 5.13. Выпуклость кривой на отрезке
- § 5.14. Раскрытие неопределенностей
- § 5.15. Асимптота
- § 5.16. Схема построения графика функции
- § 5.17. Кусочно непрерывные и кусочно гладкие функции
- Глава 6. n-МЕРНОЕ ПРОСТРАНСТВО. ГЕОМЕТРИЯ КРИВОЙ
- § 6.1. n-мерное пространство. Линейное множество
- § 6.2. Евклидово n-мерное пространство. Пространство со скалярным произведением
- § 6.3. Линейное нормированное пространство
- § 6.4. Вектор-функция в n-мерном евклидовом пространстве
- § 6.5. Непрерывная кривая. Гладкая кривая
- § 6.6. Геометрический смысл производной вектор-функции
- § 6.7. Длина дуги кривой
- § 6.8. Касательная
- § 6.9. Основной триэдр кривой
- § 6.10. Соприкасающаяся плоскость
- § 6.11. Кривизна и радиус кривизны кривой
- § 6.12. Эволюта
- § 6.13. Формулы Френе. Свойства эволюты
- Глава 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- § 7.1. Открытое множество
- § 7.2. Предел функции
- § 7.3. Непрерывная функция
- § 7.4. Частные производные и производная по направлению
- § 7.5. Дифференцируемая функция. Касательная плоскость
- § 7.6. Производная сложной функции. Производная по направлению. Градиент
- § 7.7. Независимость от порядка дифференцирования
- § 7.8. Дифференциал функции. Дифференциал высшего порядка
- § 7.9. Теорема Больцано-Вейерштрасса
- § 7.10. Замкнутые и открытые множества
- § 7.11. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве
- § 7.12. Лемма о вложенных прямоугольниках и лемма Бореля
- § 7.13. Формула Тейлора
- § 7.14. локальный (абсолютный) экстремум функции
- § 7.15. Теоремы существования неявной функции
- § 7.16. Теорема существования решения системы уравнений
- § 7.17. Отображения
- § 7.18. Гладкая поверхность
- § 7.19. Дифференциалы неявных функций. Линеаризация
- § 7.20. Локальный относительный экстремум
- § 7.21. Замена переменных в частных производных
- § 7.22. Система зависимых функций
- Глава 8. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. АЛГЕБРА МНОГОЧЛЕНОВ
- § 8.1. Введение. Методы замены переменной и интегрирования по частям
- § 8.2. Комплексные числа
- § 8.3. Комплексные функции
- § 8.4. Многочлены
- § 8.5. Разложение рациональной функции на простейшие дроби
- § 8.6. Интегрирование рациональных дробей
- § 8.7. Интегрирование алгебраических иррациональностей
- § 8.8. Подстановки Эйлера
- § 8.9. Биномиальные дифференциалы. Теорема Чебышева
- § 8.10. Интегрирование тригонометрических выражений
- § 8.11. Тригонометрические подстановки
- § 8.12. Несколько важных интегралов, не выражаемых в элементарных функциях
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
- § 9.2. Ограниченность интегрируемой функции
- § 9.3. Суммы Дарбу
- § 9.4. Основная теорема
- § 9.5. Теоремы о существовании интеграла от непрерывной и монотонной функции на [a, b]
- § 9.6. Аддитивные и однородные свойства интеграла
- § 9.7. Неравенства и теорема о среднем
- § 9.8. Интеграл как функция верхнего предела. Теорема Ньютона-Лейбница
- § 9.9. Вторая теорема о среднем
- § 9.10. Видоизменение функции
- § 9.11. Несобственные интегралы
- § 9.12. Несобственные интегралы от неотрицательных функций
- § 9.13. Интегрирование по частям
- § 9.14. Несобственный интеграл и ряд
- § 9.15. Несобственные интегралы с особенностями в нескольких точках
- § 9.16. Формула Тейлора с остатком в интегральной форме
- § 9.17. Формулы Валлиса и Стирлинга
- Глава 10. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- § 10.1. Площадь в полярных координатах
- § 10.2. Объем тела вращения
- § 10.3. Длина дуги гладкой кривой
- § 10.4. Площадь поверхности тела вращения
- § 10.5. Интерполяционный многочлен Лагранжа
- § 10.6. Квадратурные формулы прямоугольников
- § 10.7. Формула Симпсона
- Глава 11. РЯДЫ
- § 11.1. Понятие ряда
- § 11.2. Действия с рядами
- § 11.3. Ряды с неотрицательными членами
- § 11.4. Ряд Лейбница
- § 11.5. Абсолютно сходящиеся ряды
- § 11.6. Условно и безусловно сходящиеся ряды с действительными членами
- § 11.7. Последовательности и ряды функций. Равномерная сходимость
- § 11.8. Интегрирование и дифференцирование равномерно сходящихся рядов на отрезке
- § 11.9. Кратные ряды. Перемножение абсолютно сходящихся рядов
- § 11.10. Суммирование рядов и последовательностей методом средних арифметических
- § 11.11. Степенные ряды
- § 11.12. Дифференцирование и интегрирование степенных рядов
- § 11.13. Степенные ряды функций e^z, cos z, sinz комплексной переменной
- Глава 12. КРАТНЫЕ ИНТЕГРАЛЫ
- § 12.2. Мера Жордана
- § 12.3. Важные примеры квадрируемых по Жордану множеств
- § 12.4. Еще один критерий измеримости множества. Полярные координаты
- § 12.5. Другие случаи измеримости
- § 12.6. Понятие кратного интеграла
- § 12.7. Верхняя и нижняя интегральные суммы. Основная теорема
- § 12.8. Интегрируемость непрерывной функции на замкнутом измеримом множестве. Другие критерии
- § 12.9. Свойства кратных интегралов
- § 12.10. Сведение кратного интеграла к интегрированию по отдельным переменным
- § 12.11. Непрерывность интеграла по параметру
- § 12.12. Геометрическая интерпретация знака определителя
- § 12.13. Замена переменных в кратном интеграле. Простейший случай
- § 12.14. Замена переменных в кратном интеграле
- § 12.15. Доказательство леммы 1 § 12.14
- § 12.16. Полярные координаты в плоскости
- § 12.17. Полярные и цилиндрические координаты в пространстве
- § 12.18. Гладкая поверхность
- § 12.19. Площадь поверхности
- Глава 13. ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- § 13.1. Криволинейный интеграл первого рода
- § 13.2. Криволинейный интеграл второго рода
- § 13.3. Поле потенциала
- § 13.4. Ориентация плоской области
- § 13.5. Формула Грина. Выражение площади через криволинейный интеграл
- § 13.6. Интеграл по поверхности первого рода
- § 13.7. Ориентация поверхностей
- § 13.8. Интеграл по ориентированной плоской области
- § 13.9. Поток вектора через ориентированную поверхность
- § 13.10. Дивергенция. Теорема Гаусса-Остроградского
- § 13.11. Ротор вектора. Формула Стокса
- § 13.12. Дифференцирование интеграла по параметру
- § 13.13. Несобственный интеграл
- § 13.14. Равномерная сходимость несобственного интеграла
- § 13.15. Равномерно сходящийся интеграл для неограниченной области
- Глава 14. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ
- § 14.2. Пространство L'(L)
- § 14.3. Пространство L2 (L2)
- § 14.4. Пространство …
- § 14.5. Полнота системы элементов в банаховом пространстве
- § 14.6. Ортогональная система в пространстве со скалярным произведением
- § 14.7. Ортогонализация системы
- § 14.8. Полнота системы функций в …
- Глава 15. РЯДЫ ФУРЬЕ. ПРИБЛИЖЕНИЕ ФУНКЦИЙ ПОЛИНОМАМИ
- § 15.2. Сумма Дирихле
- § 15.3. Формулы для остатка ряда Фурье
- § 15.4. Теоремы об осцилляции
- § 15.5. Критерий сходимости рядов Фурье. Полнота тригонометрической системы функций
- § 15.6. Комплексная форма записи ряда Фурье
- § 15.7. Дифференцирование и интегрирование рядов Фурье
- § 15.8. Оценка остатка ряда Фурье
- § 15.9. Алгебраические многочлены. Многочлены Чебышева
- § 15.10. Теорема Вейерштрасса
- § 15.11. Многочлены Лежандра
- Глава 16. ИНТЕГРАЛ ФУРЬЕ. ОБОБЩЕННЫЕ ФУНКЦИИ
- § 16.1. Понятие интеграла Фурье
- § 16.2. Сходимость простого интеграла Фурье к порождающей его функции
- § 16.3. Преобразование Фурье. Повторный интеграл Фурье. Косинус- и синус-преобразования Фурье
- § 16.4. Производная преобразования Фурье
- § 16.5. Обобщенные функции в смысле D
- § 16.6. Пространство S
- § 16.7. Пространство S обобщенных функций