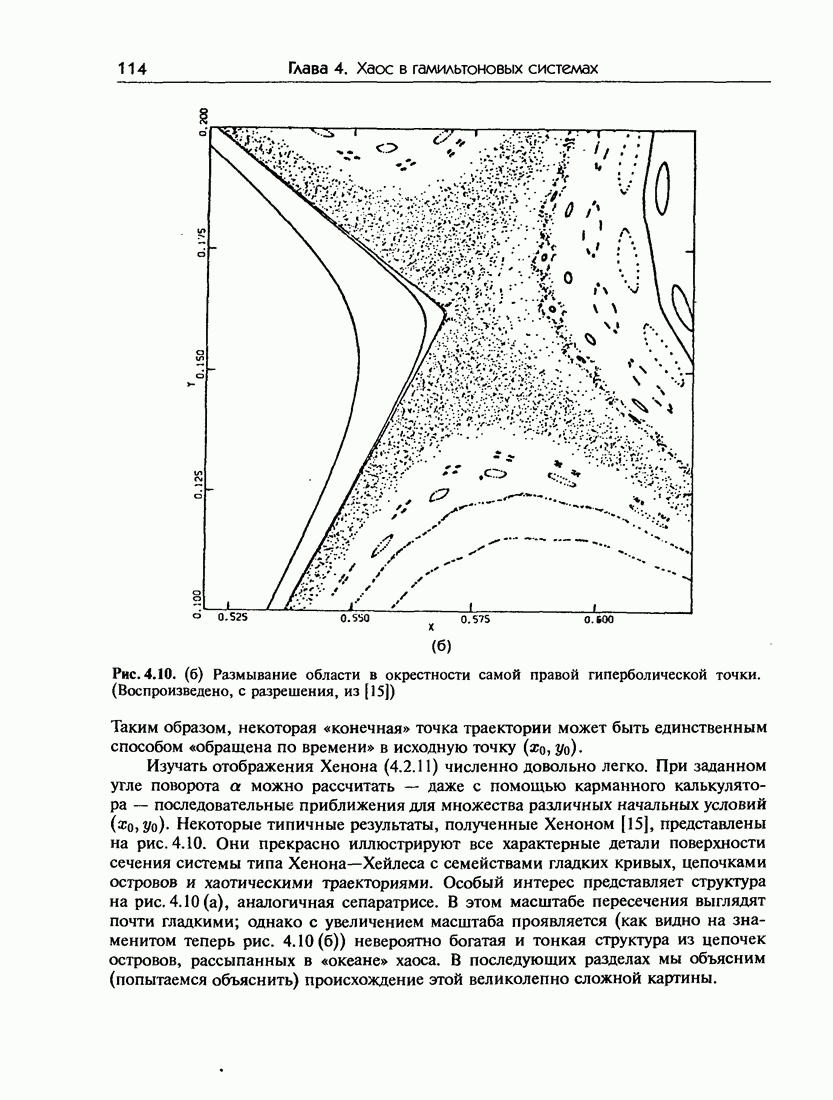
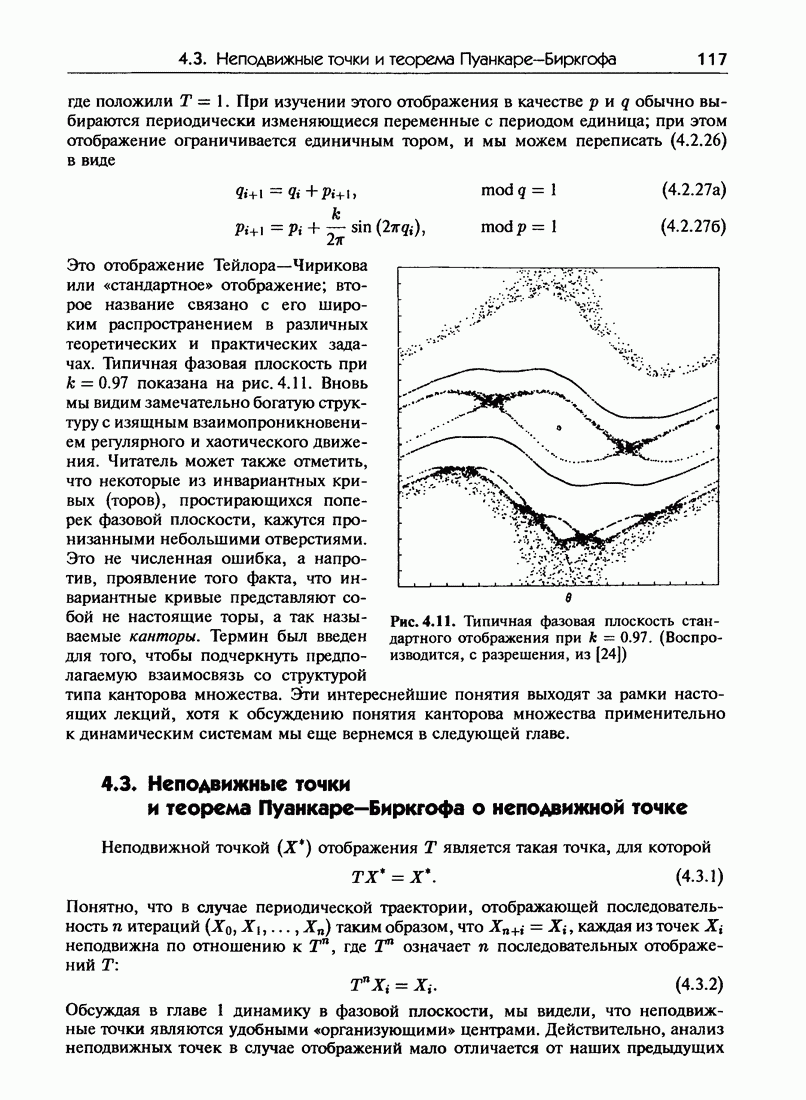
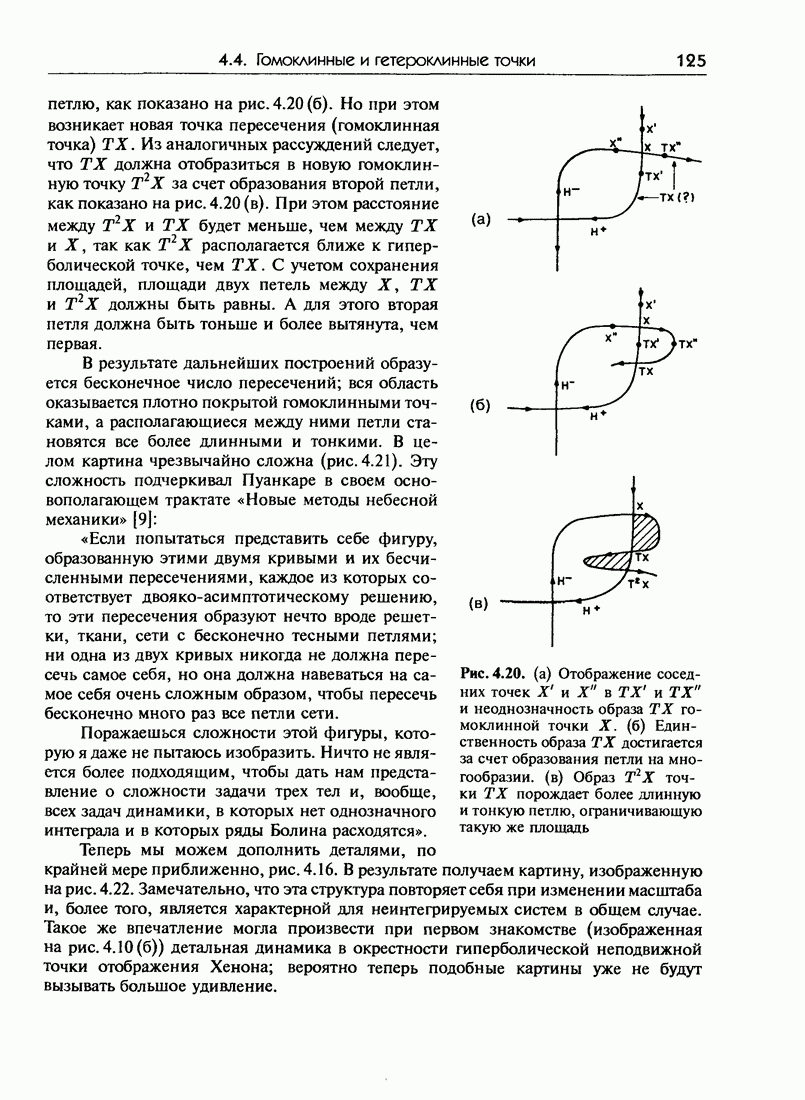
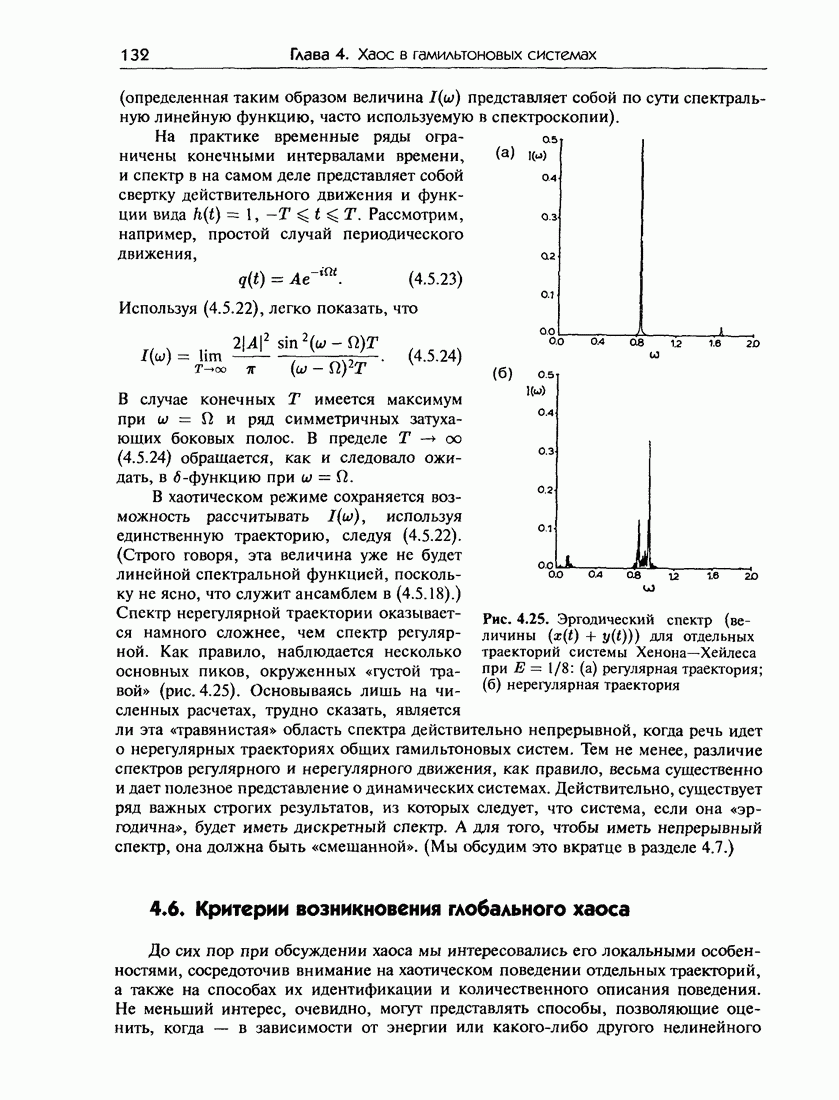
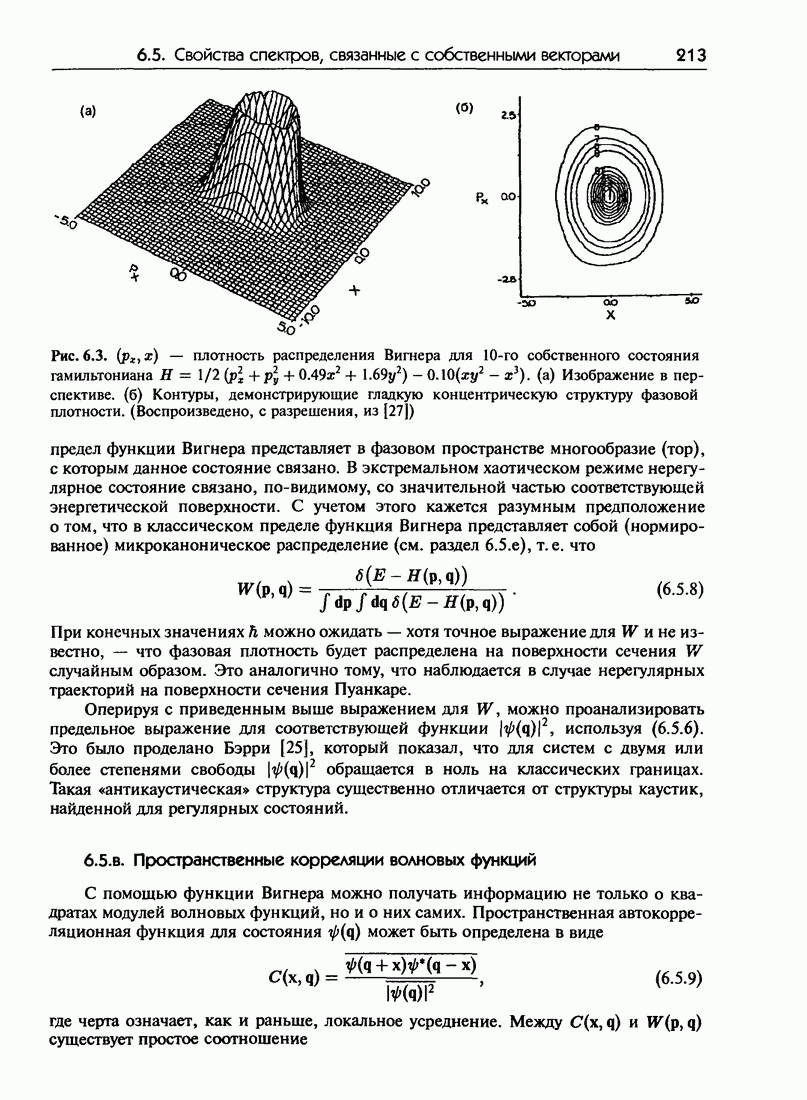
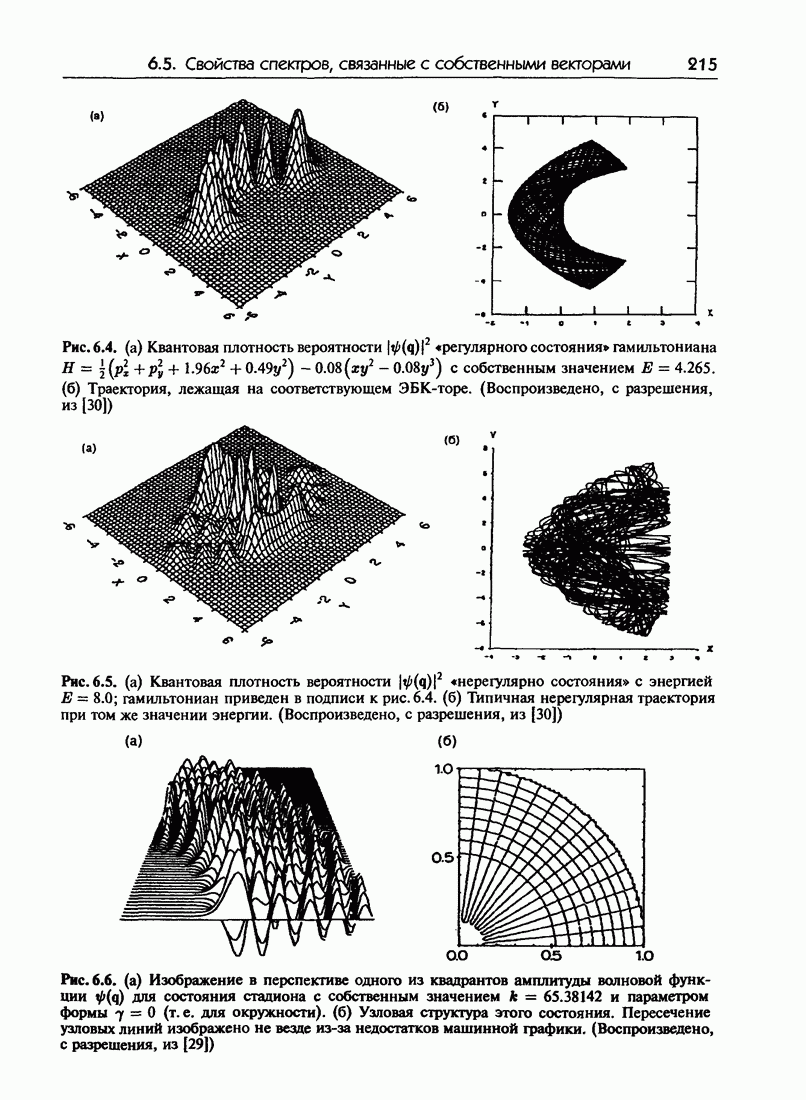
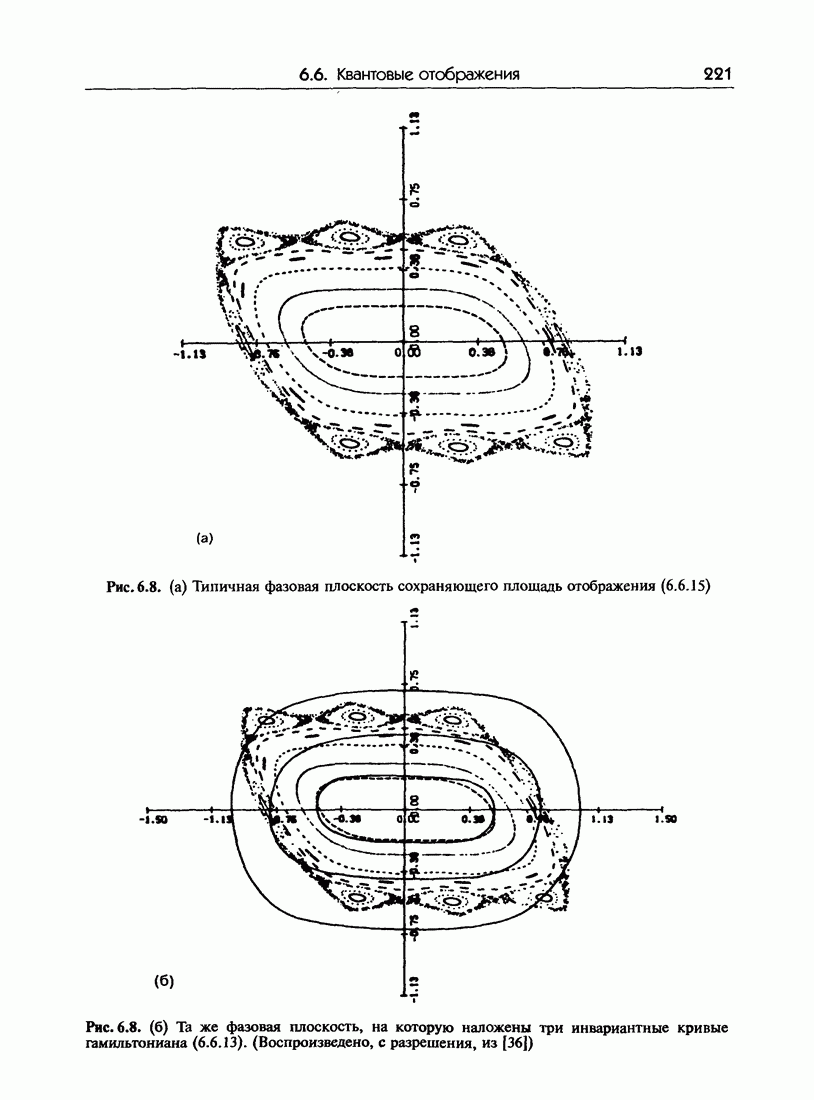
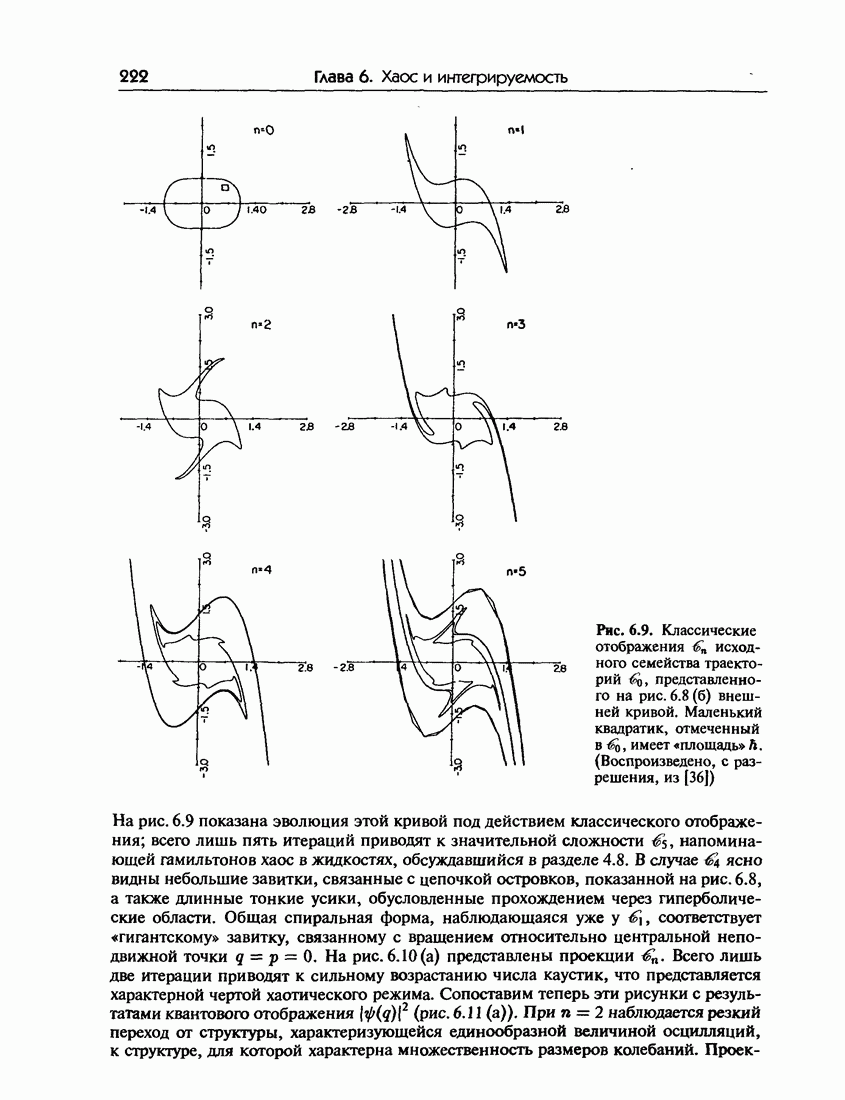
| Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Предисловие
Цель данного вводного курса состоит в том, чтобы обеспечить переход от традиционных курсов по дифференциальным уравнениям и классической механике к быстро развивающимся областям нелинейной динамики и хаоса и представить «старые» и «новые» концепции в едином широком контексте.
Такой подход к изложению обусловлен тем, что многие студенты физических и инженерных специальностей (с соответствующим базовым образованием по дифференциальным уравнениям и классической механике), стремящиеся освоить новые интересные результаты, связанные с хаосом в динамических системах, склонны иногда считать, что эта «новая» область знаний существенно отличается от «старых» курсов. Я полагаю, что более полное понимание «новых» идей может быть достигнуто, если рассматривать их как естественное развитие «старых». Один из способов подчеркнуть эту преемственность основан на использовании уравнений движения Гамильтона. Эти фундаментальные уравнения классической механики создают естественную основу для обсуждения динамики (в фазовом пространстве) систем дифференциальных уравнений, которые могут проявлять как регулярное, так и хаотическое поведение. Большое внимание уделено концепции интегрируемости, поскольку прочное ее усвоение существенно углубляет понимание динамики неинтегрируемых систем и значение фундаментальной КАМ-теоремы. Эта концепция лежит также в основе изложения интегрируемых дифференциальных уравнений в частных производных и динамики солитонов в заключительных главах книги.
Первые четыре главы, а именно «Динамика дифференциальных уравнений», «Динамика гамильтоновых систем», «Классическая теория возмущений» и «Хаос в гамильтоновых системах и сохраняющие площадь отображения» составляют ядро книги; уровень изложения вполне доступен способным студентам старших курсов и начинающим аспирантам и предполагает наличие знаний, лишь немного выходящих за рамки стандартных курсов по дифференциальным уравнениям и классической механике. Конечно, определенную часть материала, составляющего содержание этих глав, можно найти в других книгах и обзорах, но цель (и надежда на ее достижение) состояла в том, чтобы изложить «старые» и «новые» понятия с единой точки зрения. При этом гамильтонова динамика изложена во второй главе хотя и «традиционным» образом, но с определенным «геометрическим» уклоном. Для этого в главу включено приложение «Геометрические представления в классической механике», связанное с основным текстом посредством ряда подстрочных примечаний. Оно призвано помочь студентам по возможности безболезненно перейти (если они хотят этого) от «традиционного» к «геометрическому» формализму механики.
Основное содержание большинства недавно появившихся прекрасных книг по хаосу и нелинейной динамике составляют диссипативные динамические системы. По приведенным выше соображениям данный курс посвящен в основном хаосу в гамильтоновых системах. Тем не менее для полноты изложения в книгу включена одна глава (глава 5), посвященная диссипативной динамике. По возможности подчеркнута взаимосвязь с динамическими концепциями предыдущих глав, а также с реальными задачами гидродинамики.
Последние три главы представляют собой попытку показать широту и разнообразие проблем нелинейной динамики. Уровень изложения по сравнению с
предыдущими главами несколько повышается; предполагаются знания в рамках курсов элементарной квантовой механики (главы 6 и 7) и теории функций комплексной переменной (глава 8). Глава 6 служит введением в современное изучение возможных взаимосвязей между классическим хаосом и соответствующим квантовомеханическим поведением систем в «квазиклассическом пределе». Глава 7 посвящена динамике нелинейных дифференциальных уравнений в частных производных, в том числе и интегрируемых уравнений, обладающих солитонными решениями. На первый взгляд может показаться, что изучение хаоса и солитонов взаимно исключает друг друга, поскольку в первом случае речь идет о свойствах неинтегрируемых, тогда как во втором — о свойствах интегрируемых систем. Мне, однако, представляется весьма важным совместное изучение этих концепций. Существенно продвинуться в понимании реальных физических задач, связанных с пространственно-временным хаосом (таких, как гидродинамическая турбулентность) можно, лишь изучая одновременно хаос и интегрируемость как в случае обыкновенных дифференциальных уравнений, так и в случае дифференциальных уравнений в частных производных.
Последняя глава «Аналитическая структура динамических систем» вводит читателя в круг идей другой современной области исследований, связанной с попытками отыскать общность в труднообозримом разнообразии свойств обыкновенных дифференциальных уравнений и дифференциальных уравнений в частных производных — независимо от того, интегрируемы они или нет — путем анализа особенностей их решений в комплексной области.
Книга может быть использована для чтения двухсеместрового курса, в котором материал общего характера первых четырех или пяти глав излагается в первом семестре; второй семестр посвящается более специальным темам, изложенным в последних трех главах. При этом необходимо учитывать, что по своему замыслу книга в значительной степени рассчитана на прочтение в целом. Разделы и подразделы, помеченные звездочкой, содержат более сложный материал или технические детали и при первом чтении могут быть опущены, что не нарушит связности изложения.
Необходимо подчеркнуть, что книга не является исчерпывающим, даже с современной точки зрения, обзором по хаосу. В соответствии с этим я старался включать в рассмотрение только хорошо обоснованные физические модели и соответствующие ссылки. Число публикаций чрезвычайно возросло за последние годы, и я не пытался составить полную библиографию (задача на данном этапе практически нереальная). Поэтому я приношу свои извинения тем многочисленным авторам, чьи блестящие работы здесь не упомянуты.
Мне особенно приятно поблагодарить моих аспирантов Франка Кариелло, Джоел Чекен и Грегори Левина за их существенную помощь в подготовке рукописи. Ни одну из глав я не считал завершенной без их скрупулезного анализа и конструктивной критики. Если окажется, что в глазах студенческой аудитории эта книга имеет какие-либо достоинства, то в немалой степени этому способствовали их старания.
Наконец, я хочу поблагодарить В. Г. Льюиса за помощь в подготовке рисунков и Луизу Винтер за героические усилия по переписке рукописи.
М. Табор Нью-Йорк Ноябрь 1988
| Следующий параграф >> |
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
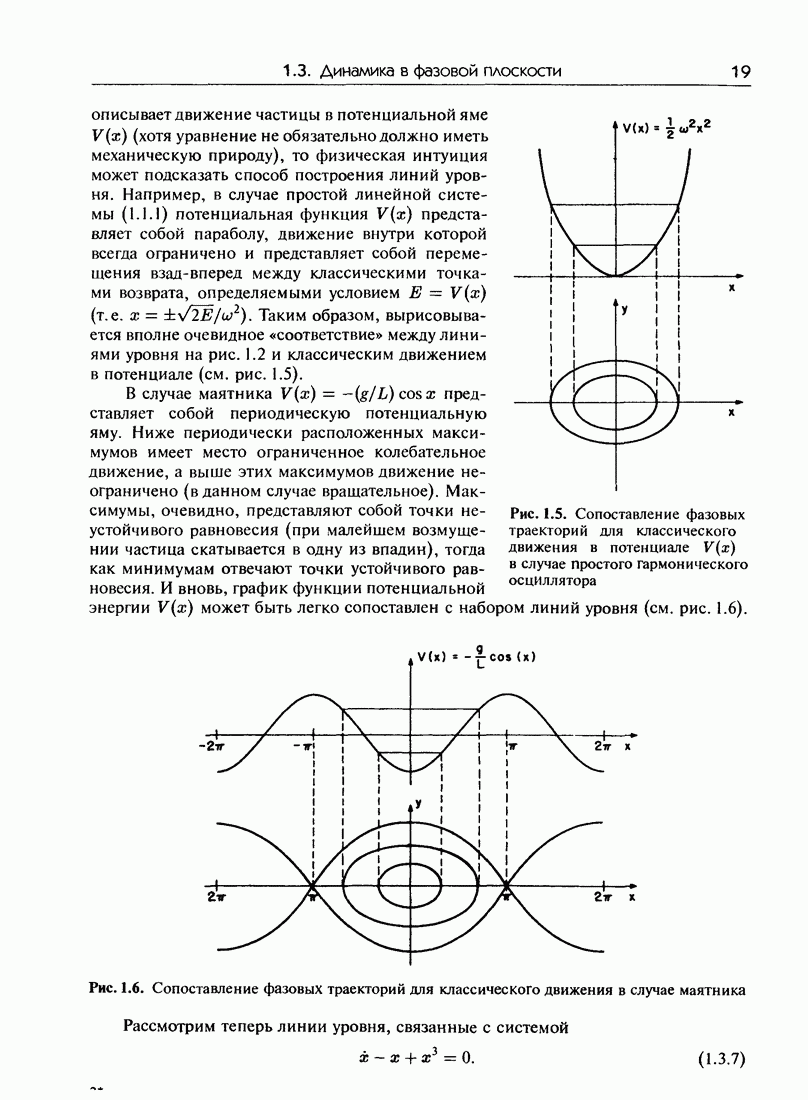
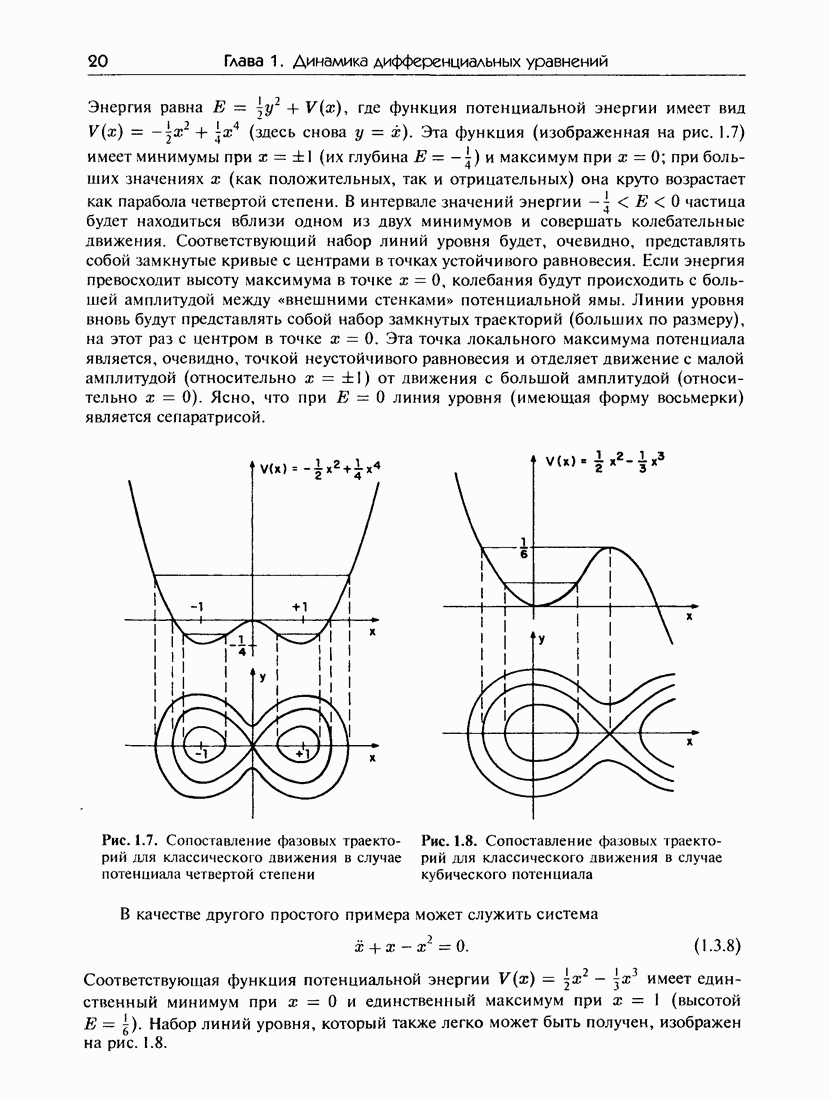
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
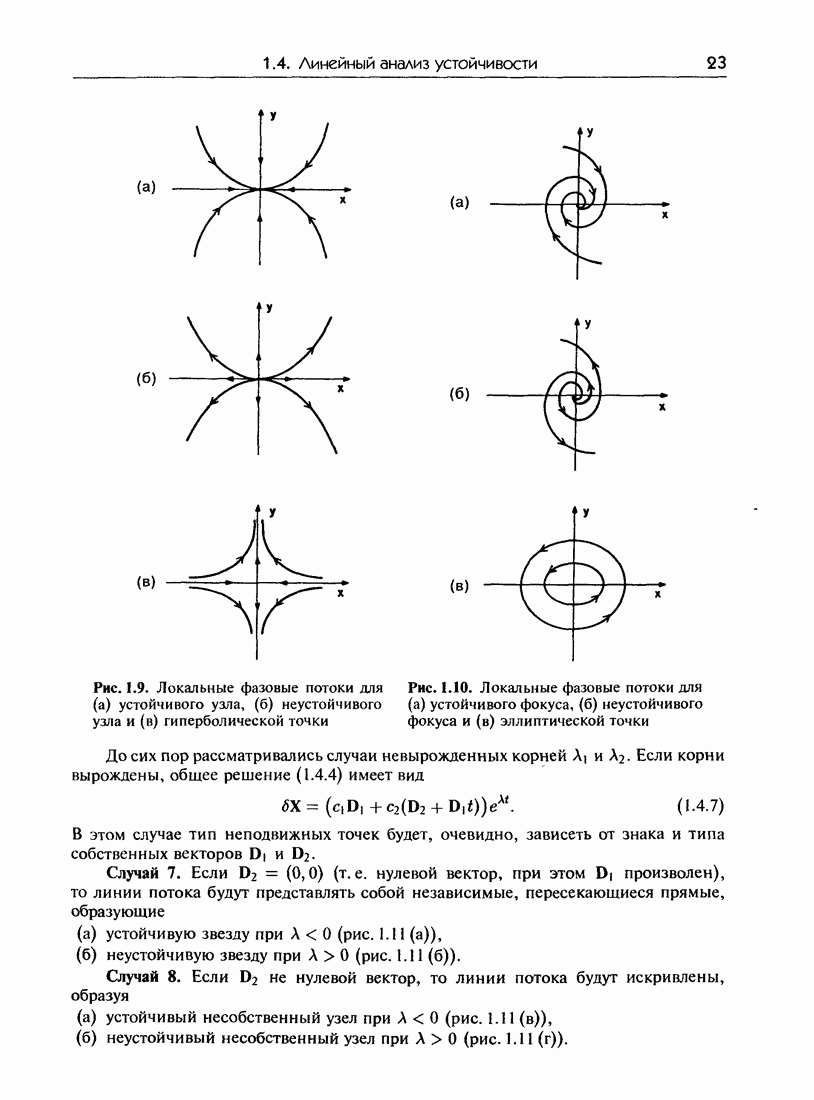
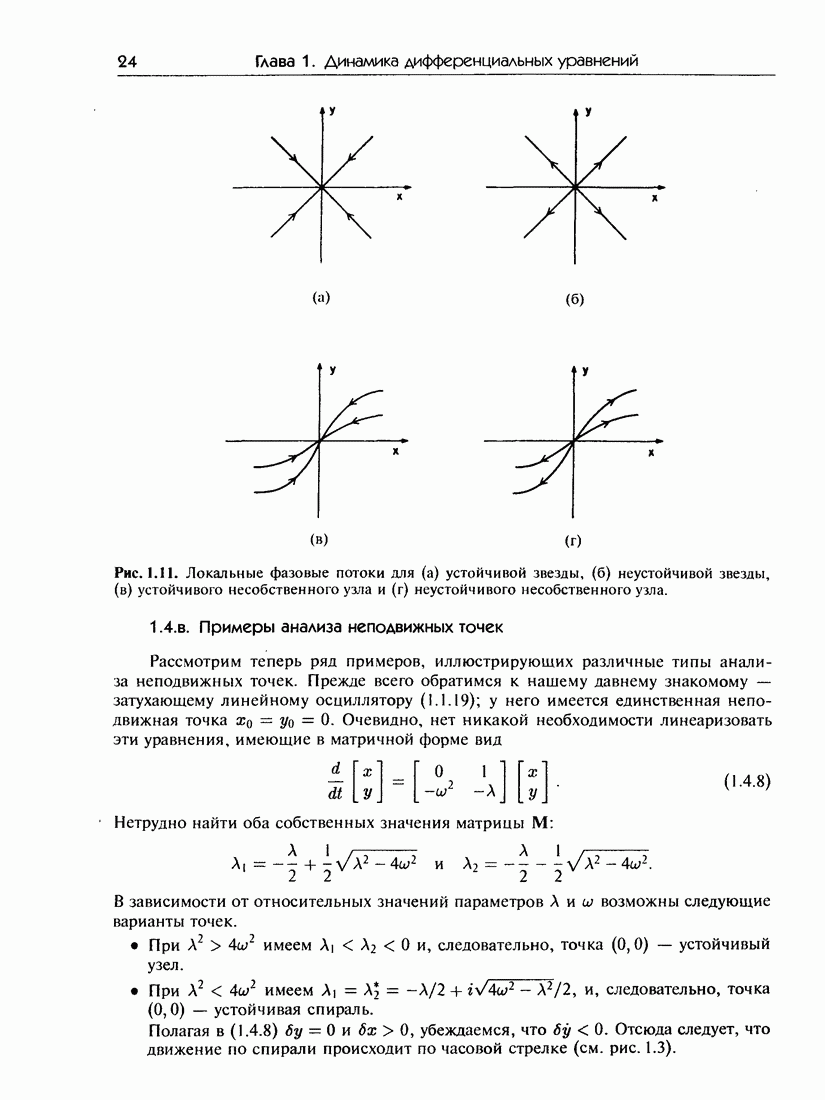
- 1.4. Линейный анализ устойчивости
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
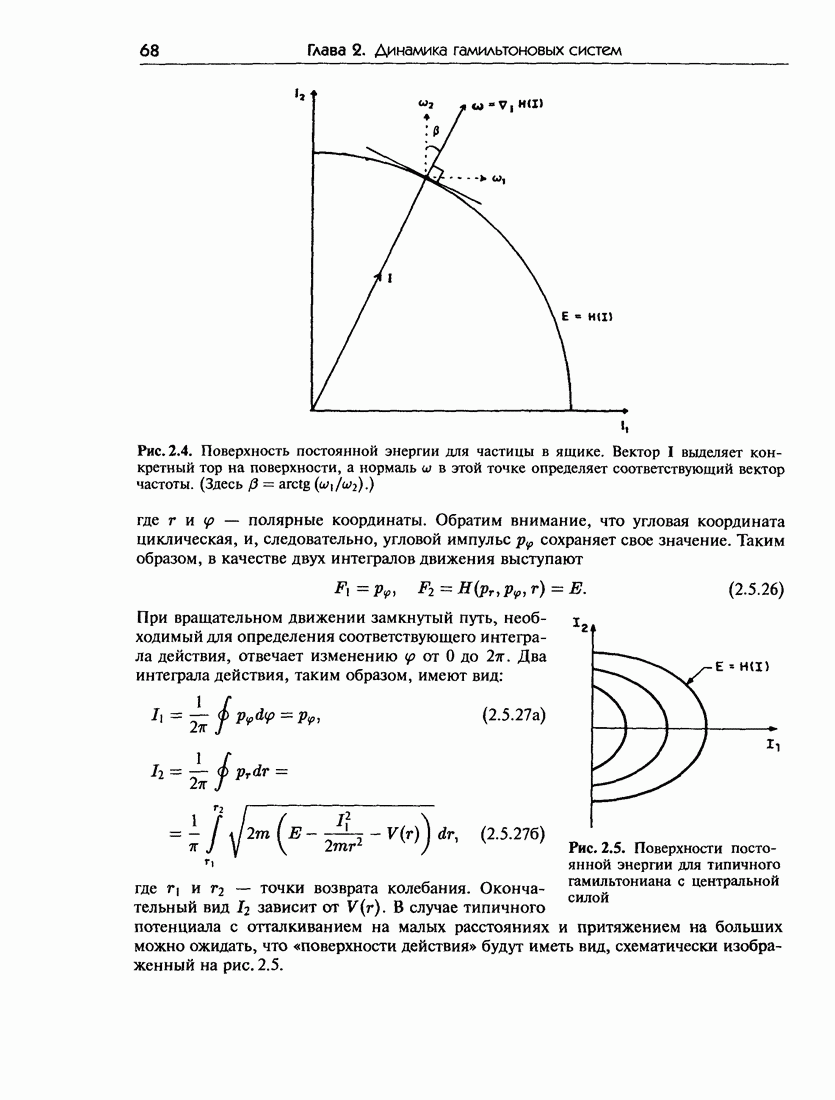
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
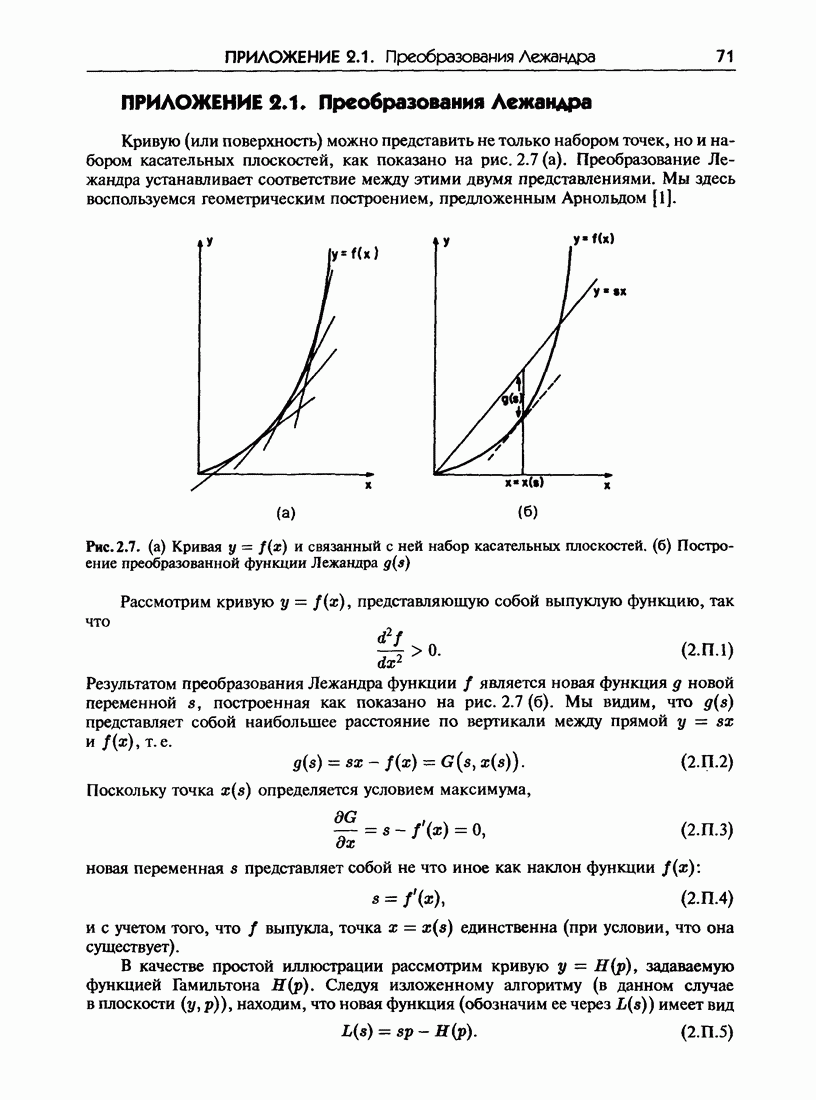
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
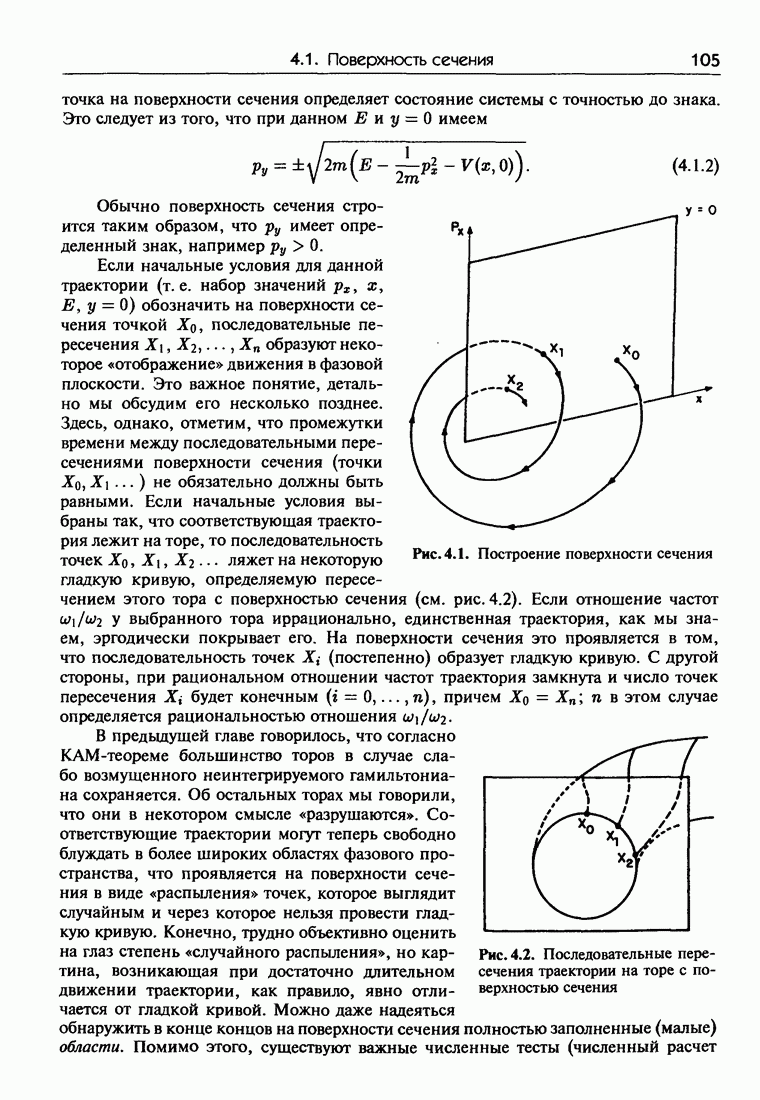
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
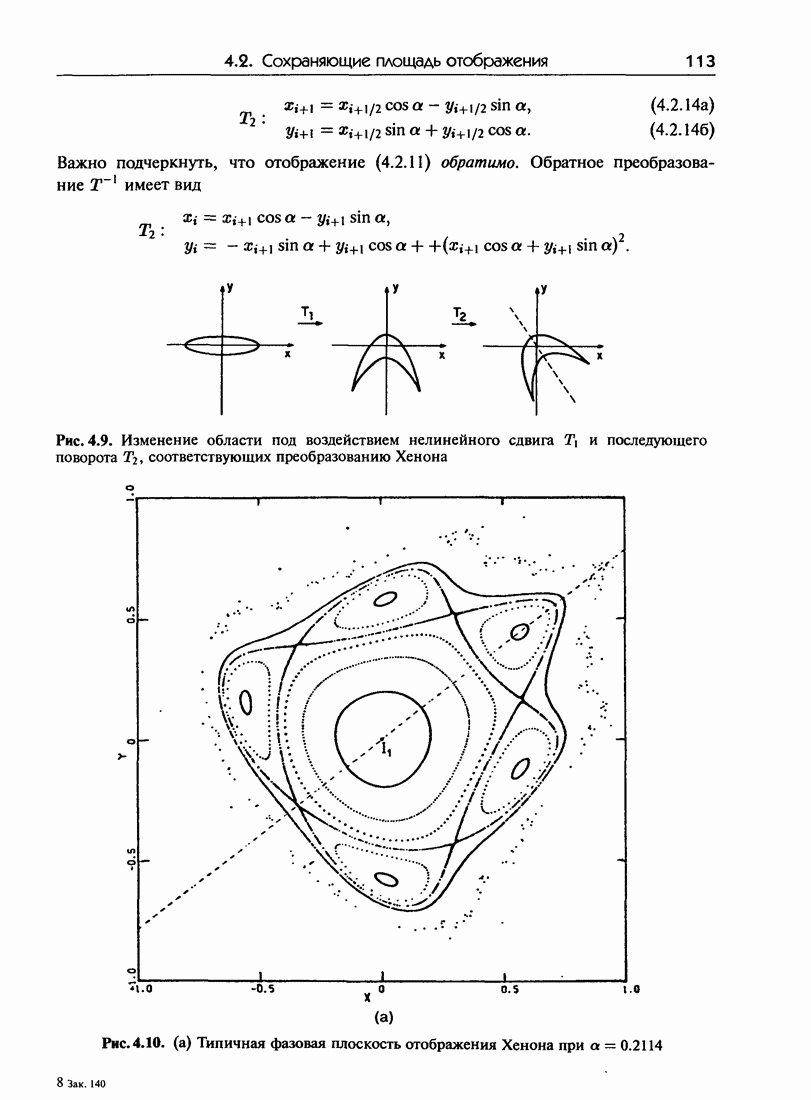
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
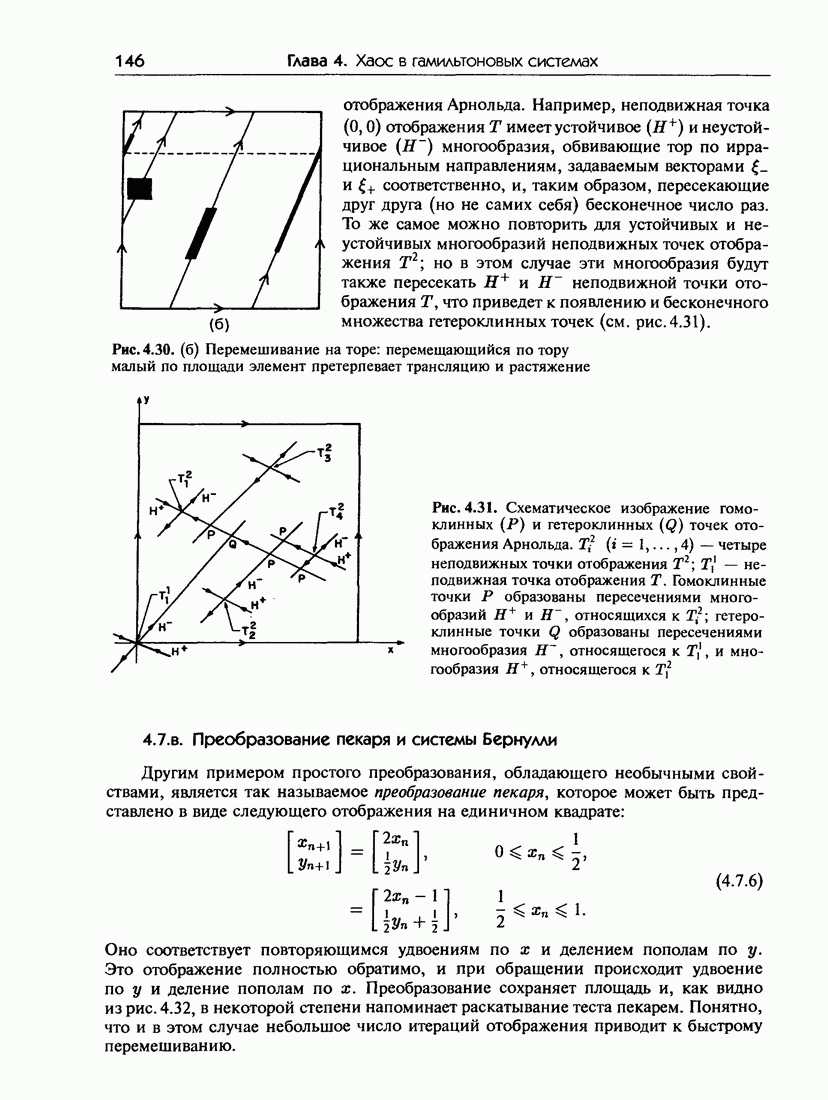
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
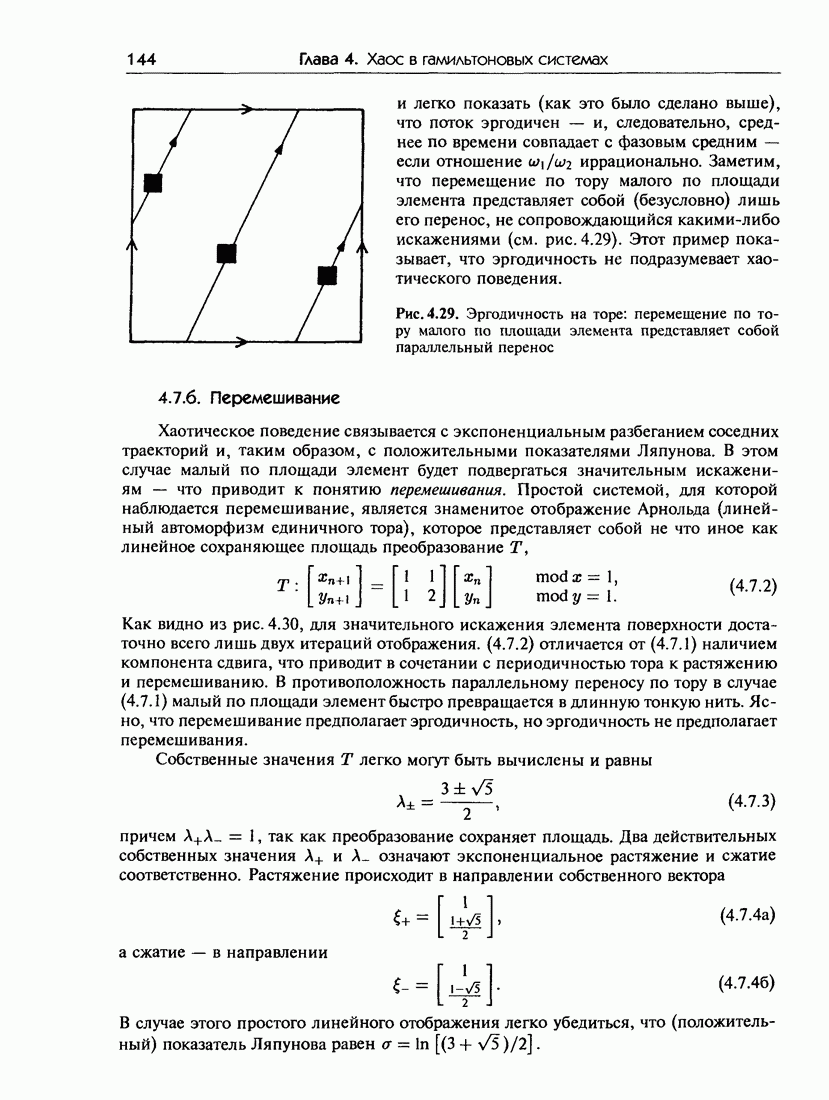
- 4.7.б. Перемешивание
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
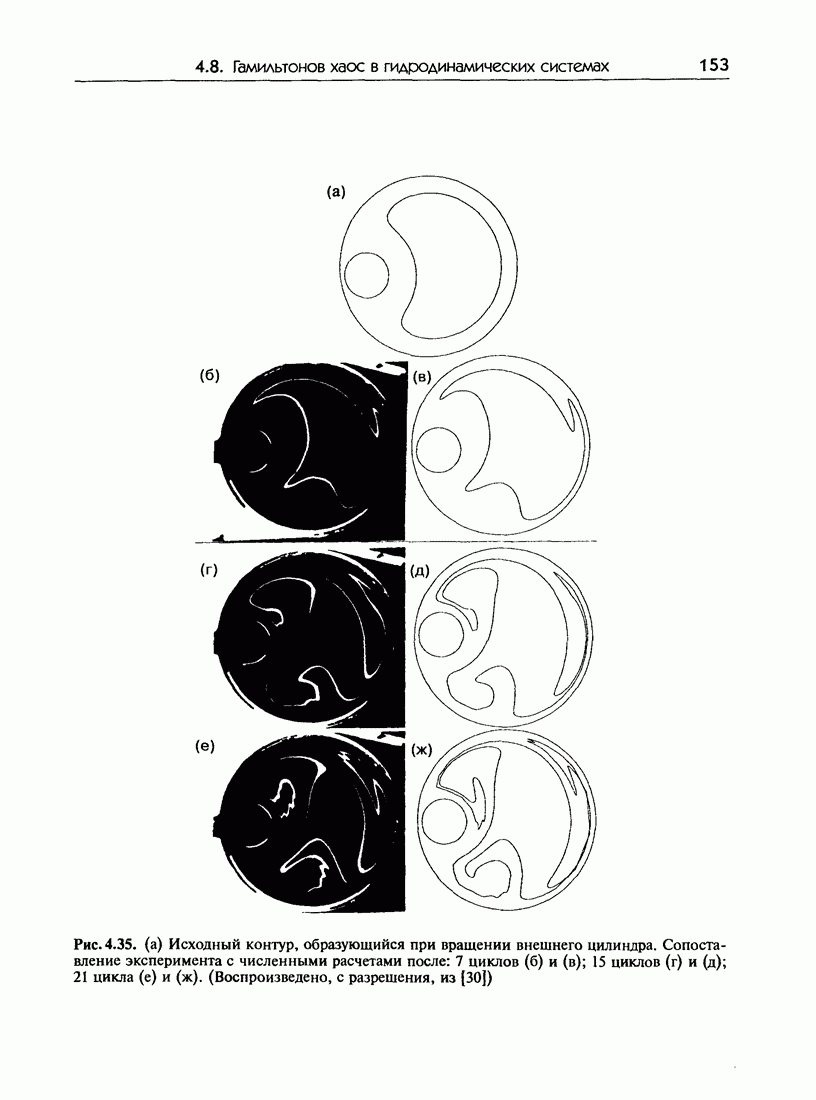
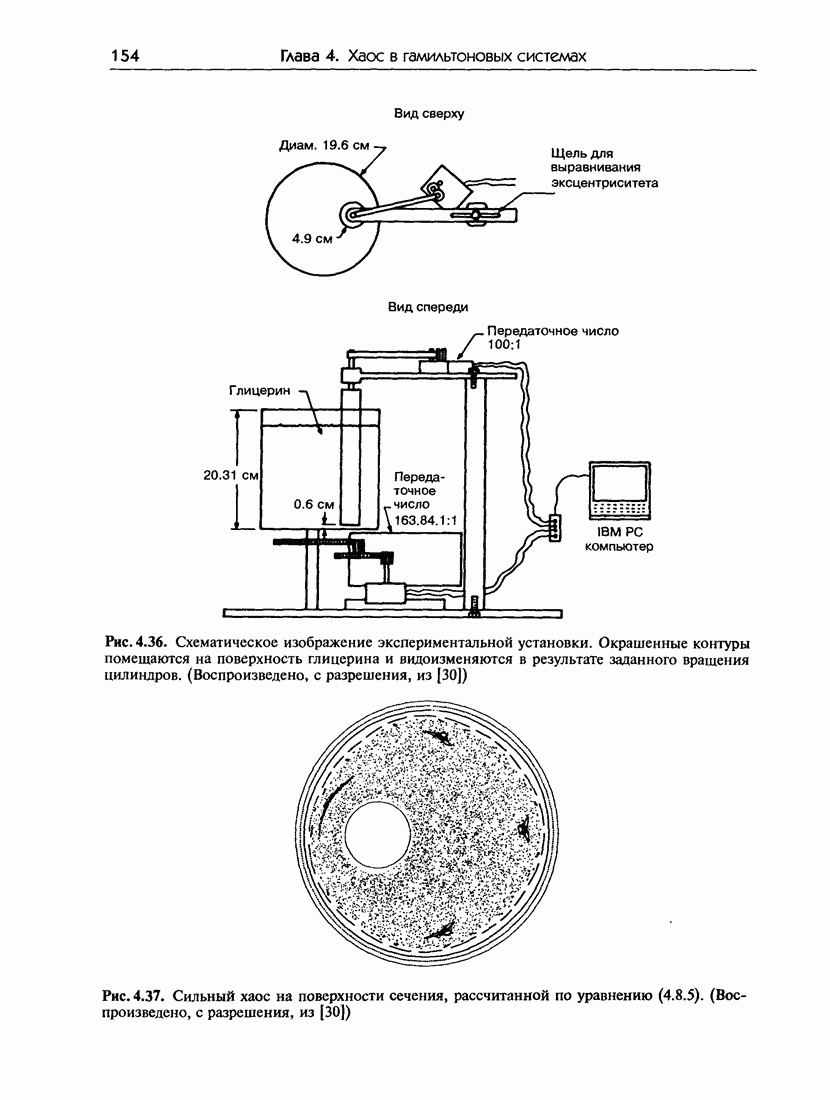
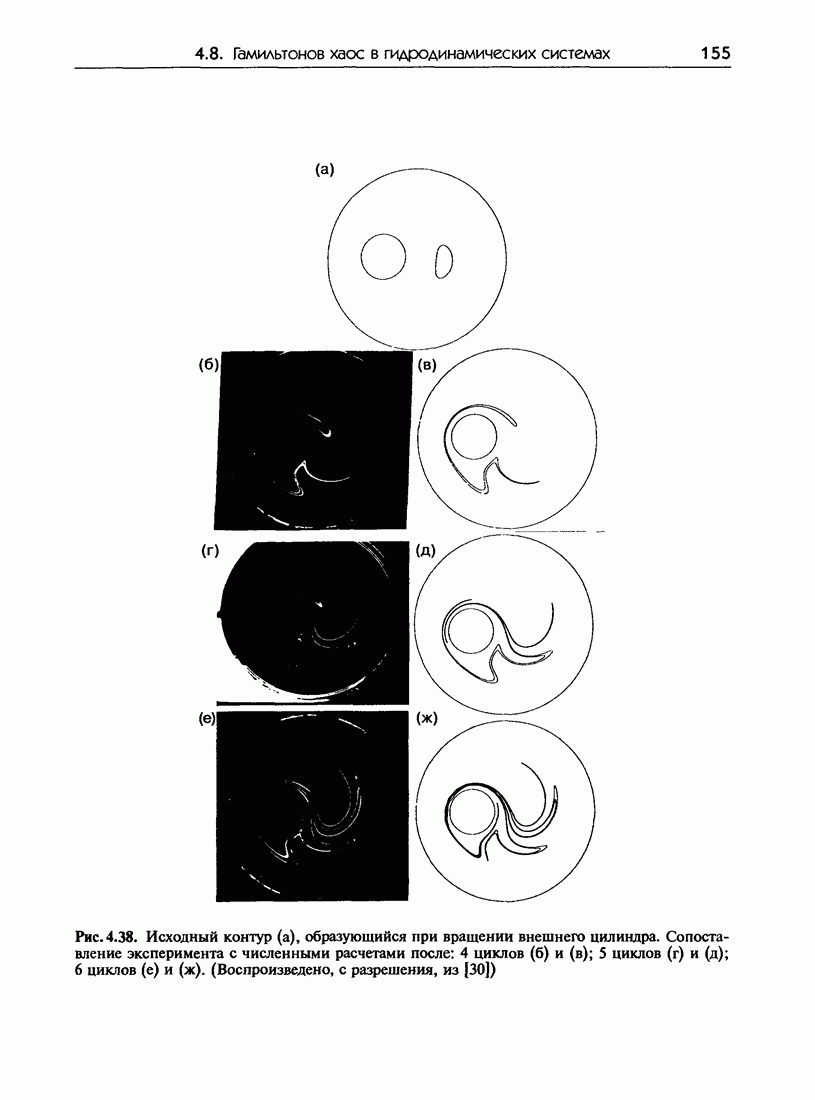
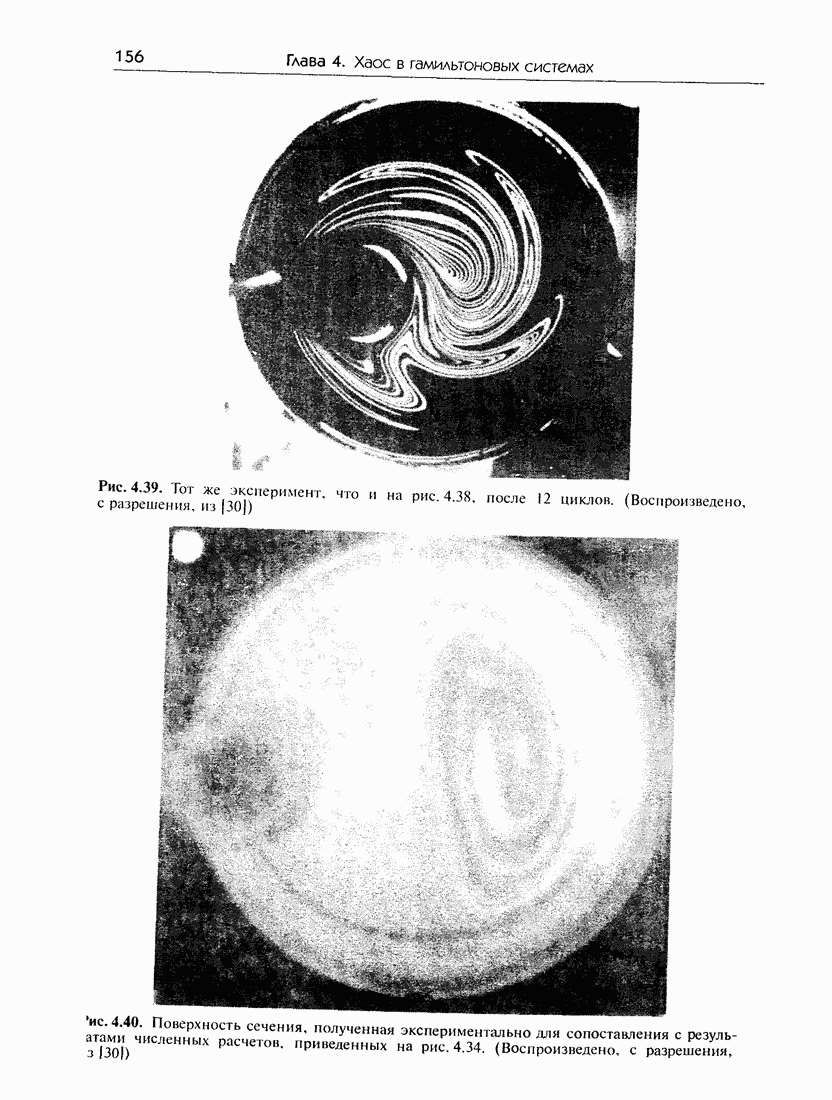
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
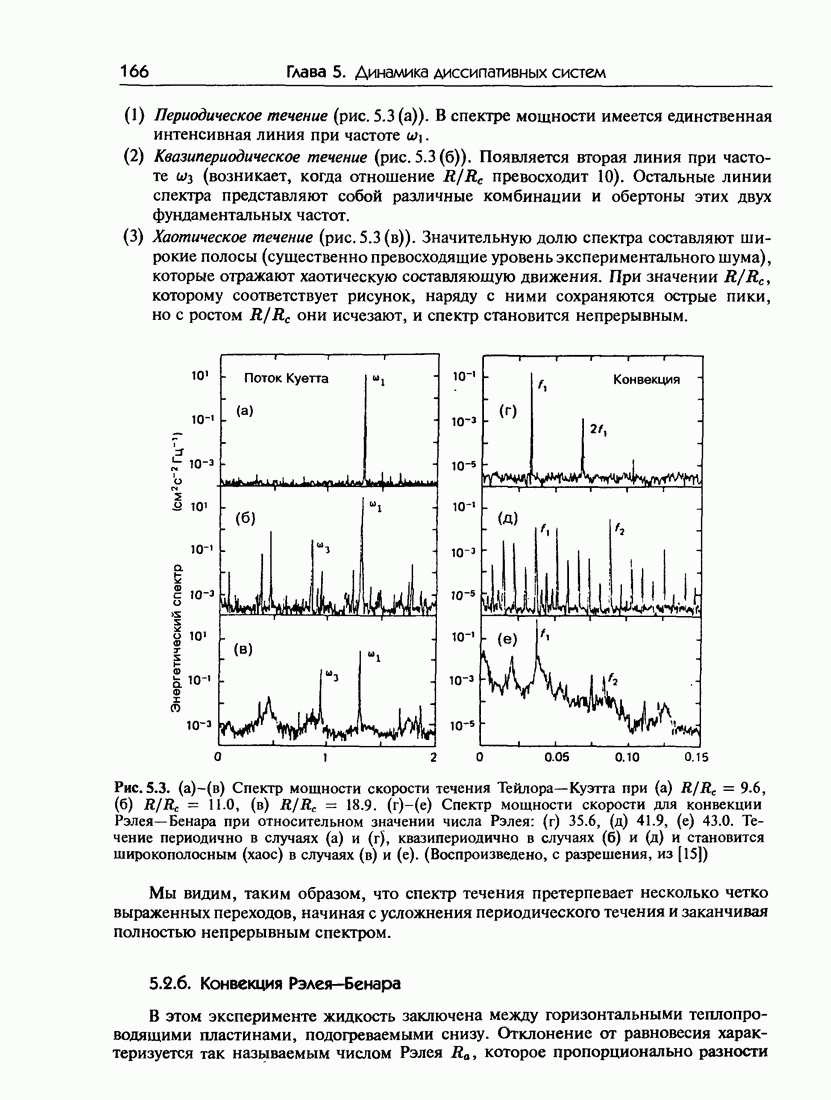
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
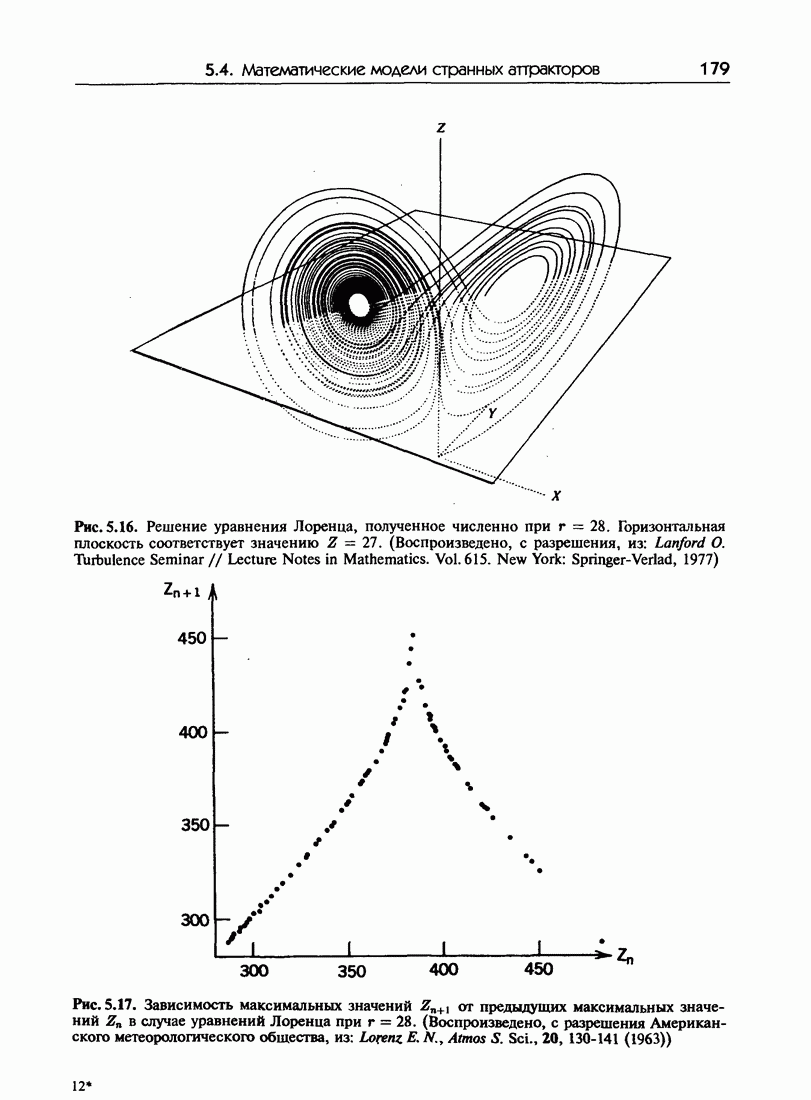
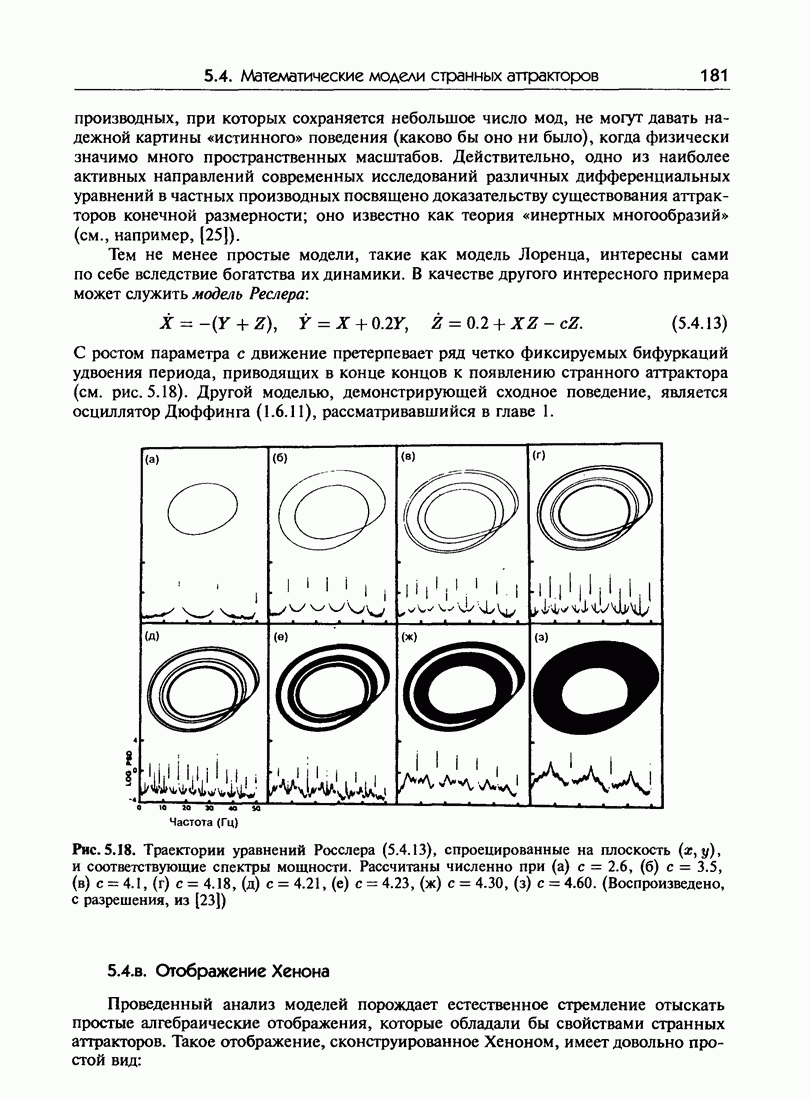
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
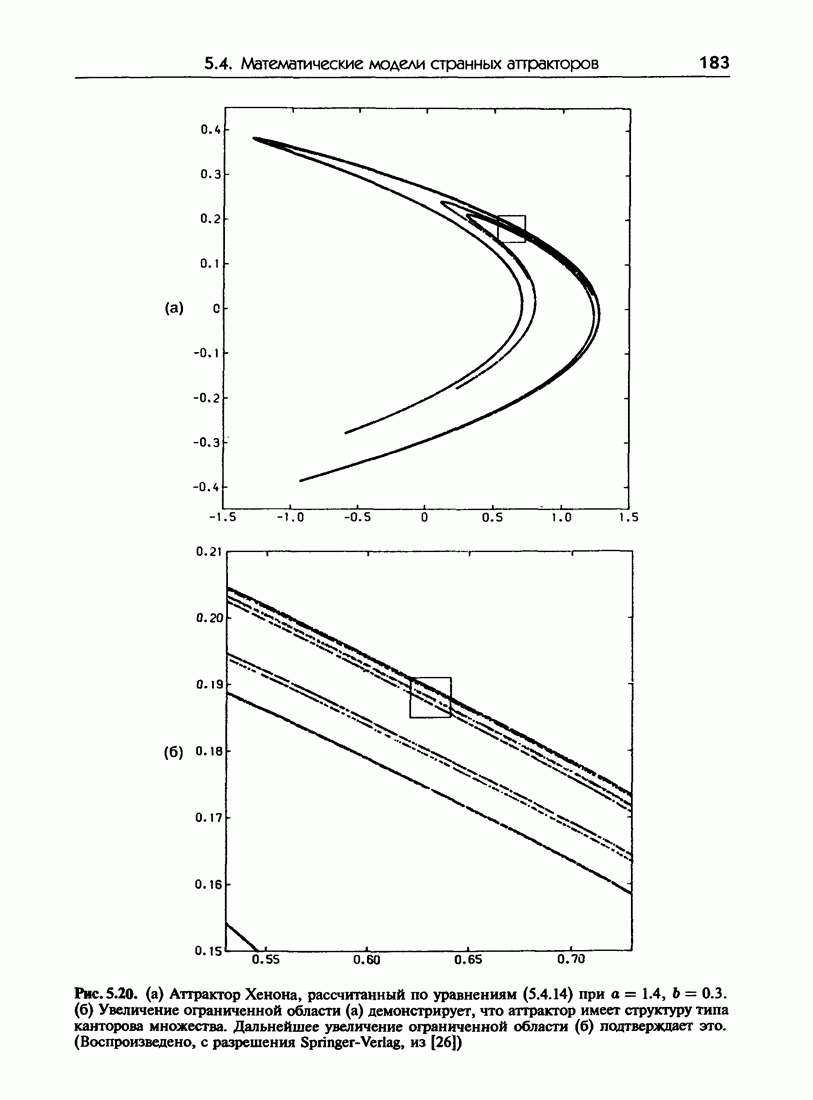
- 5.4.в. Отображение Хенона
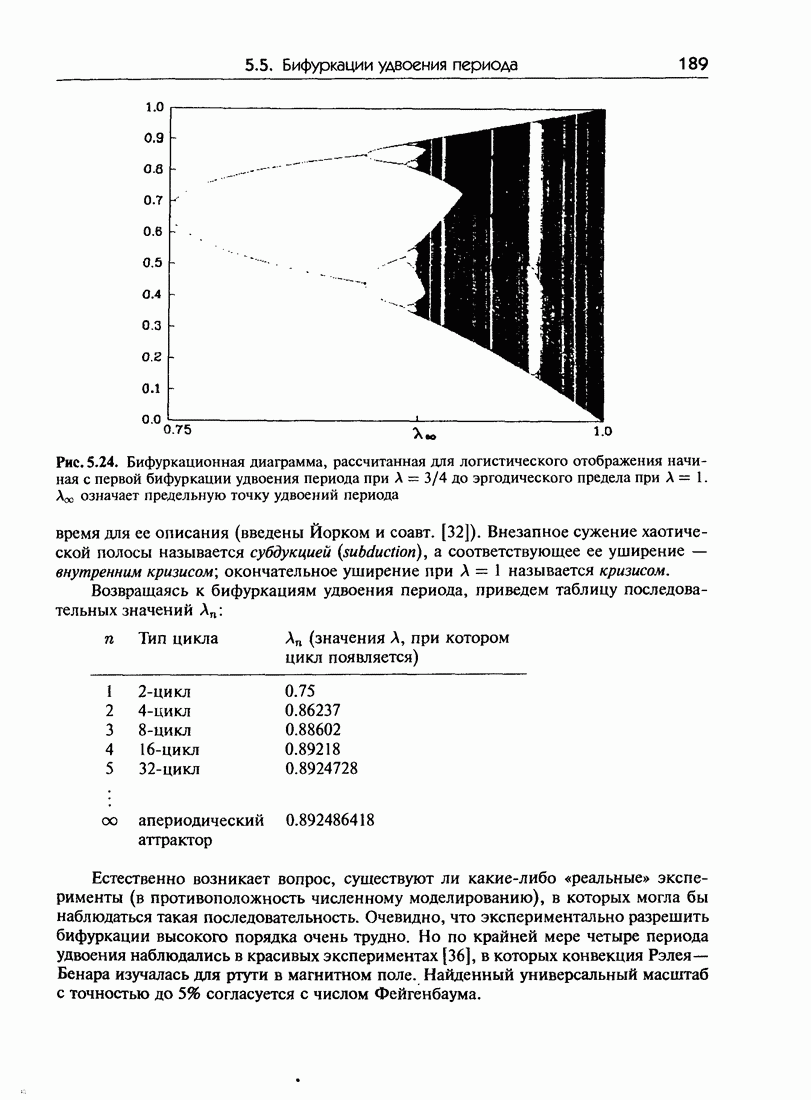
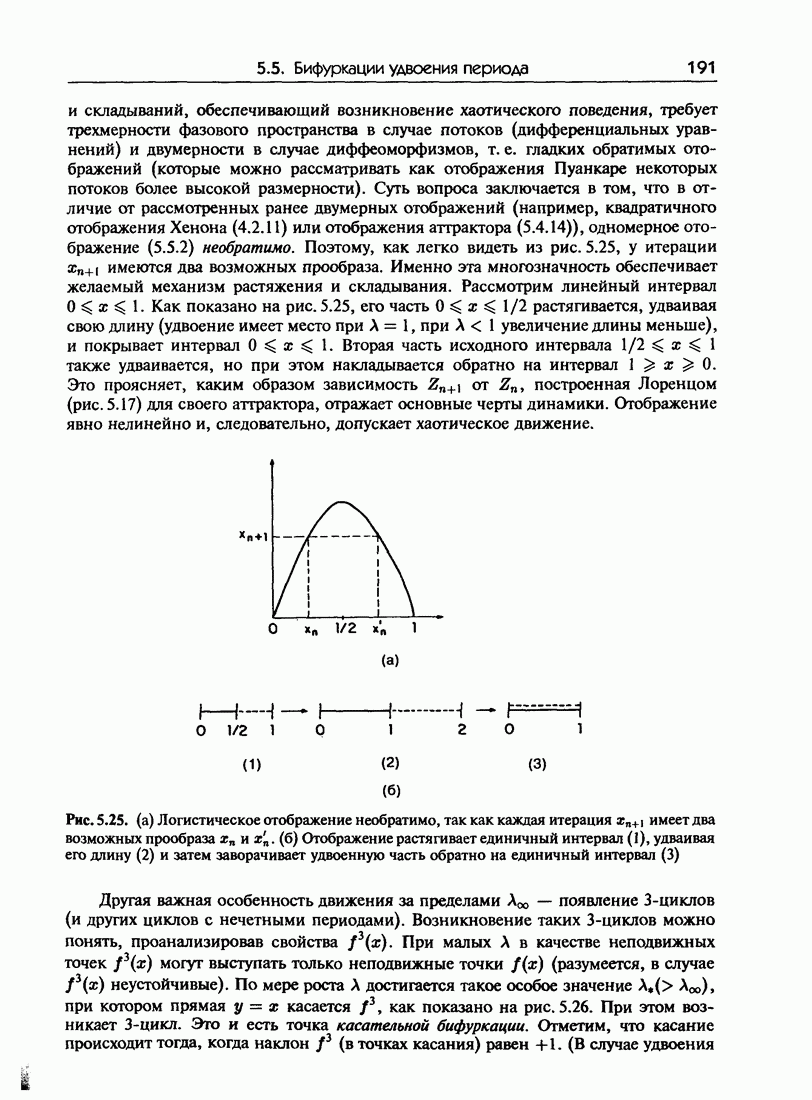
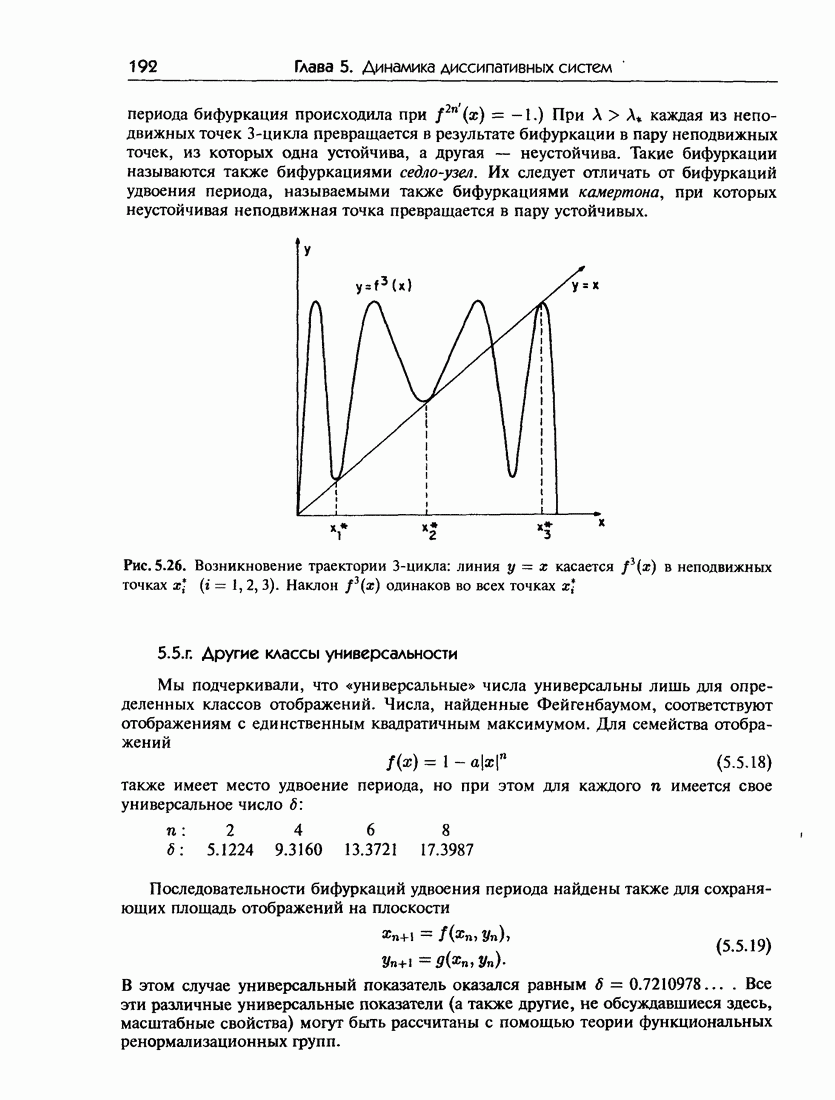
- 5.5. Бифуркации удвоения периода
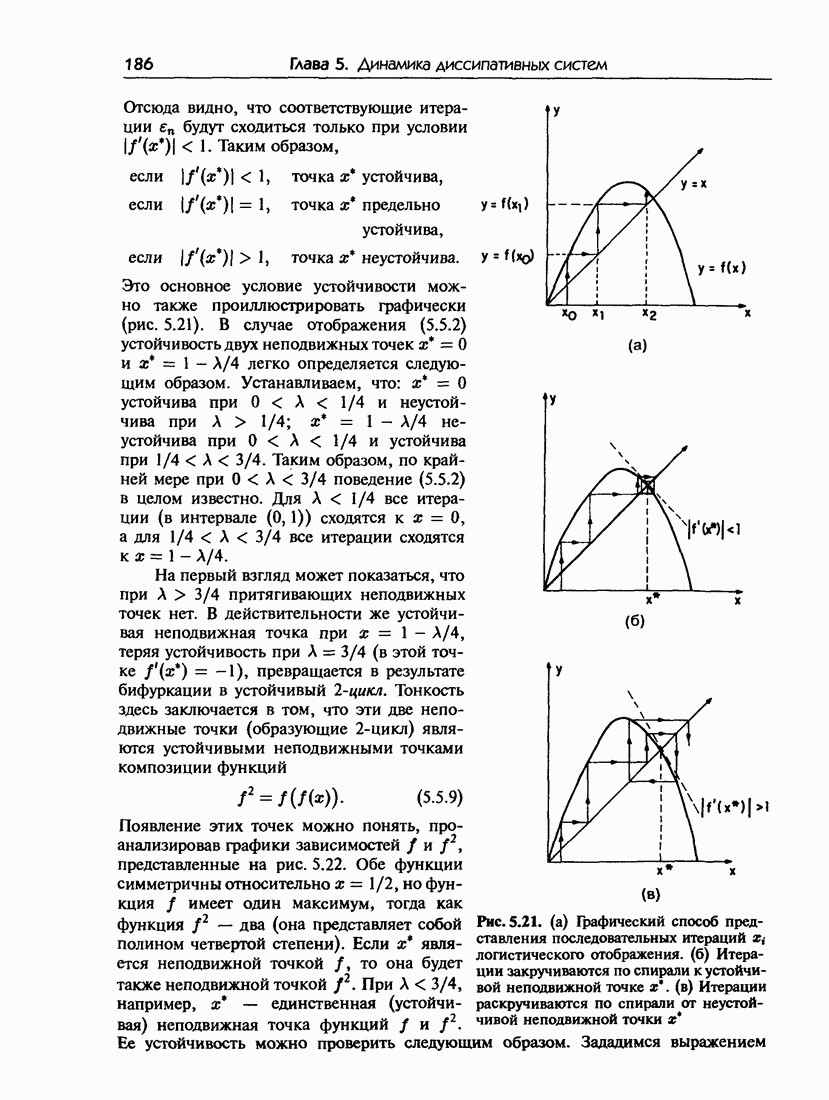
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
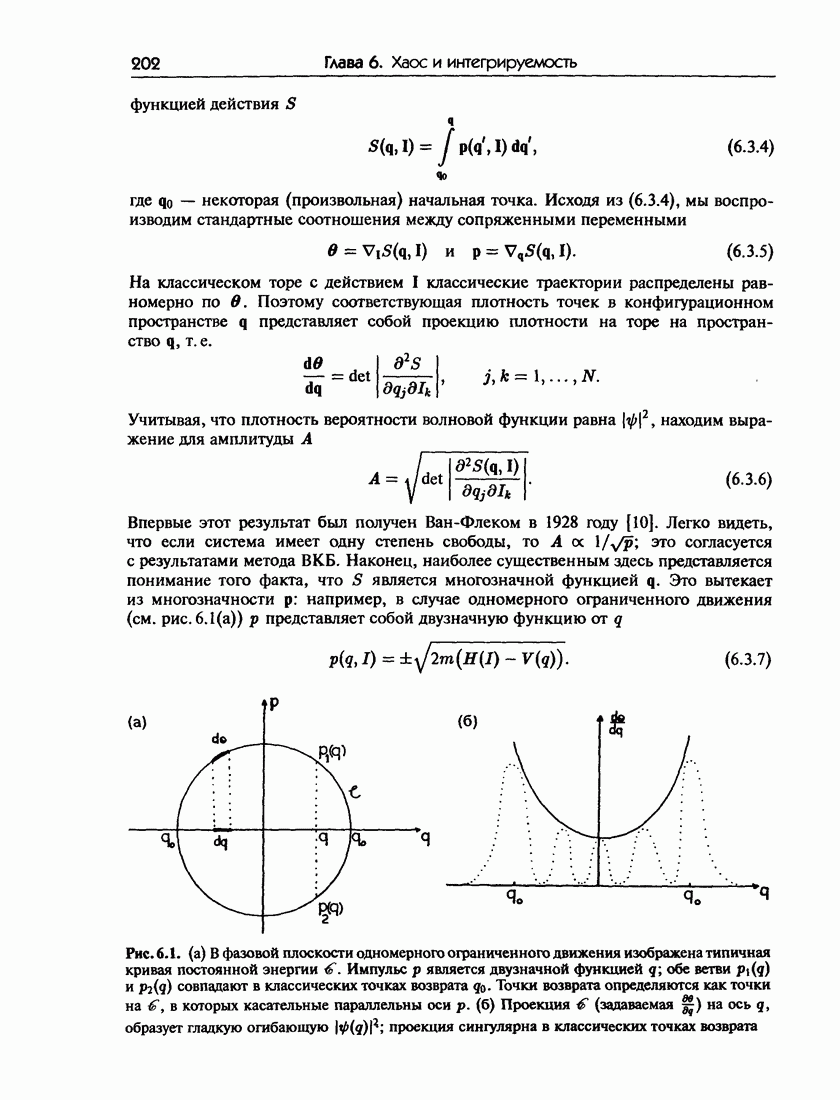
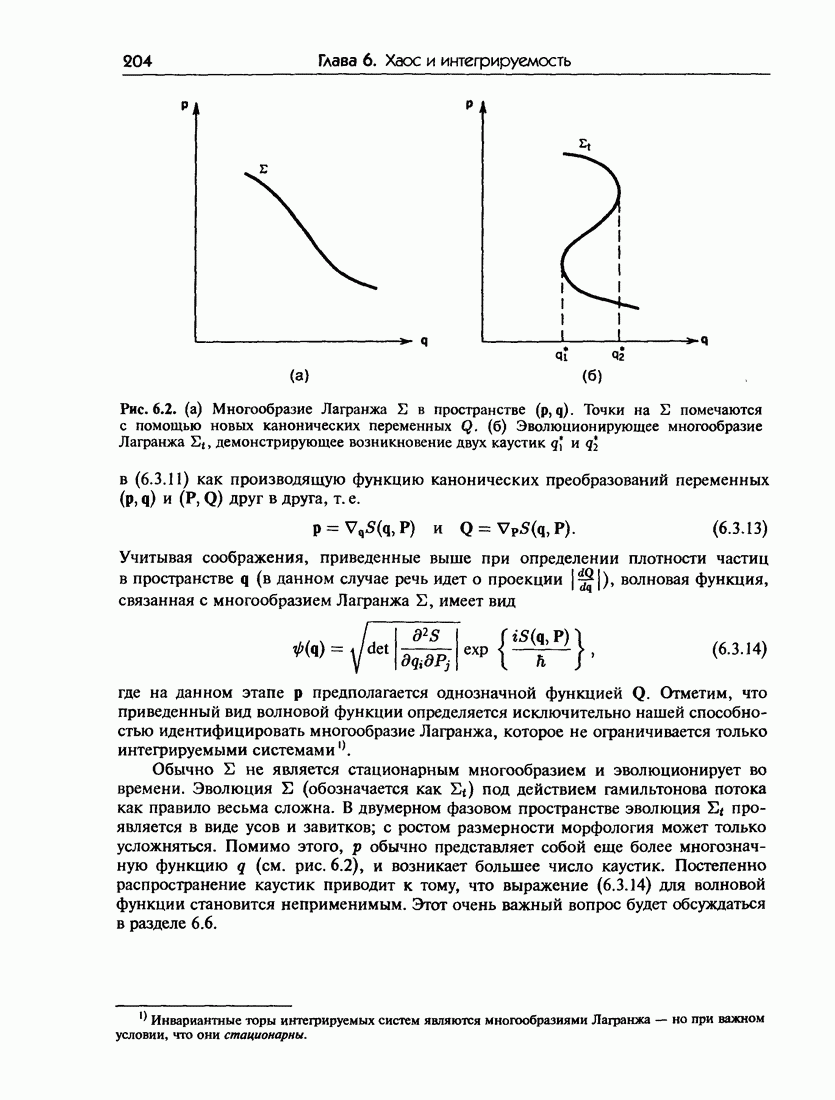
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
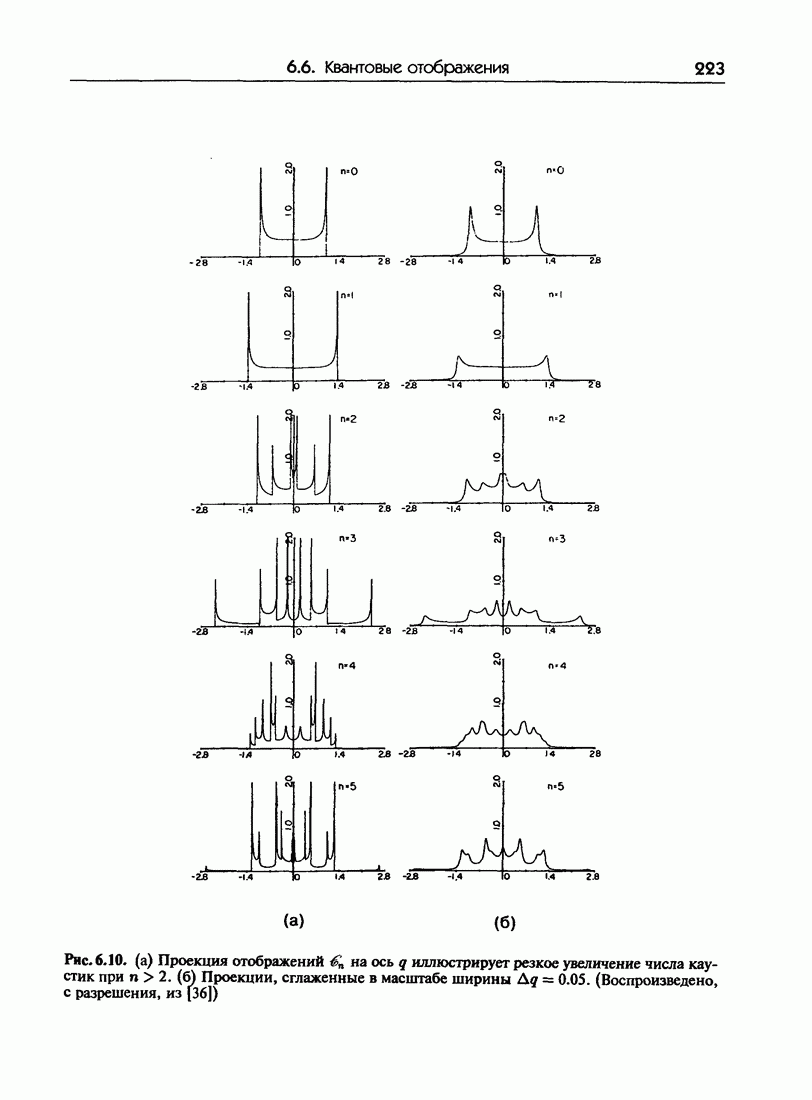
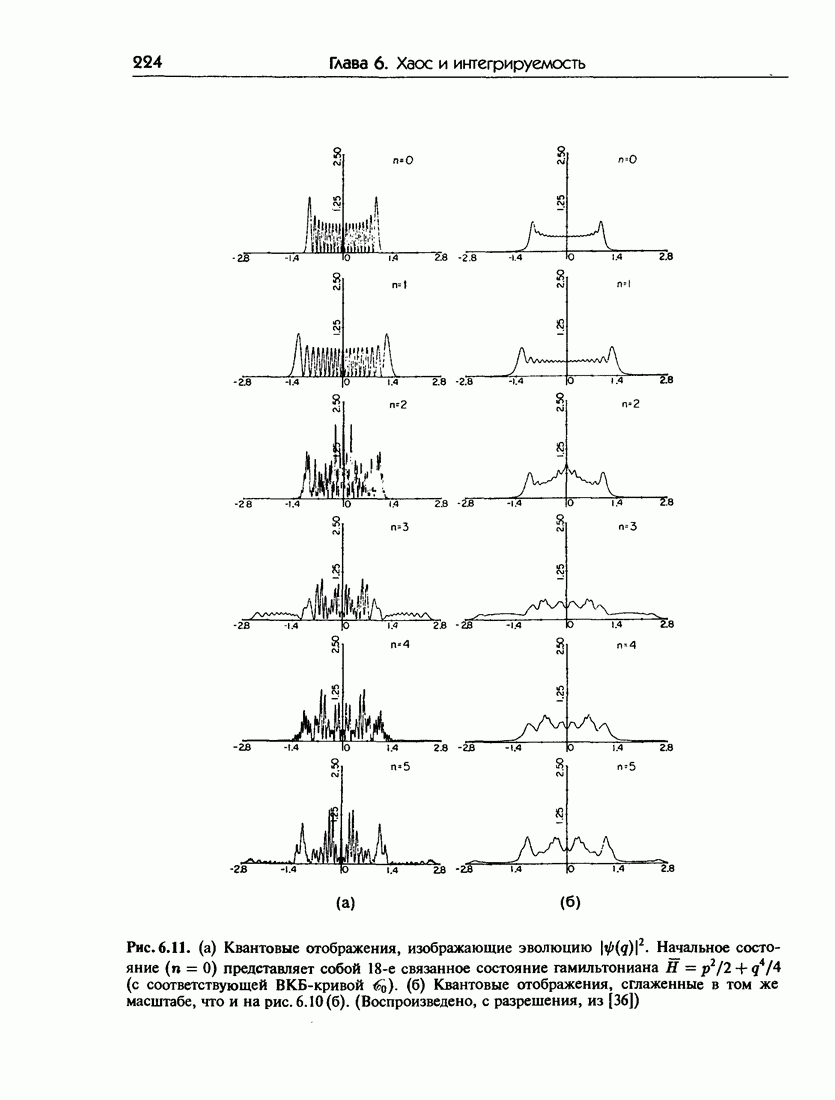
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
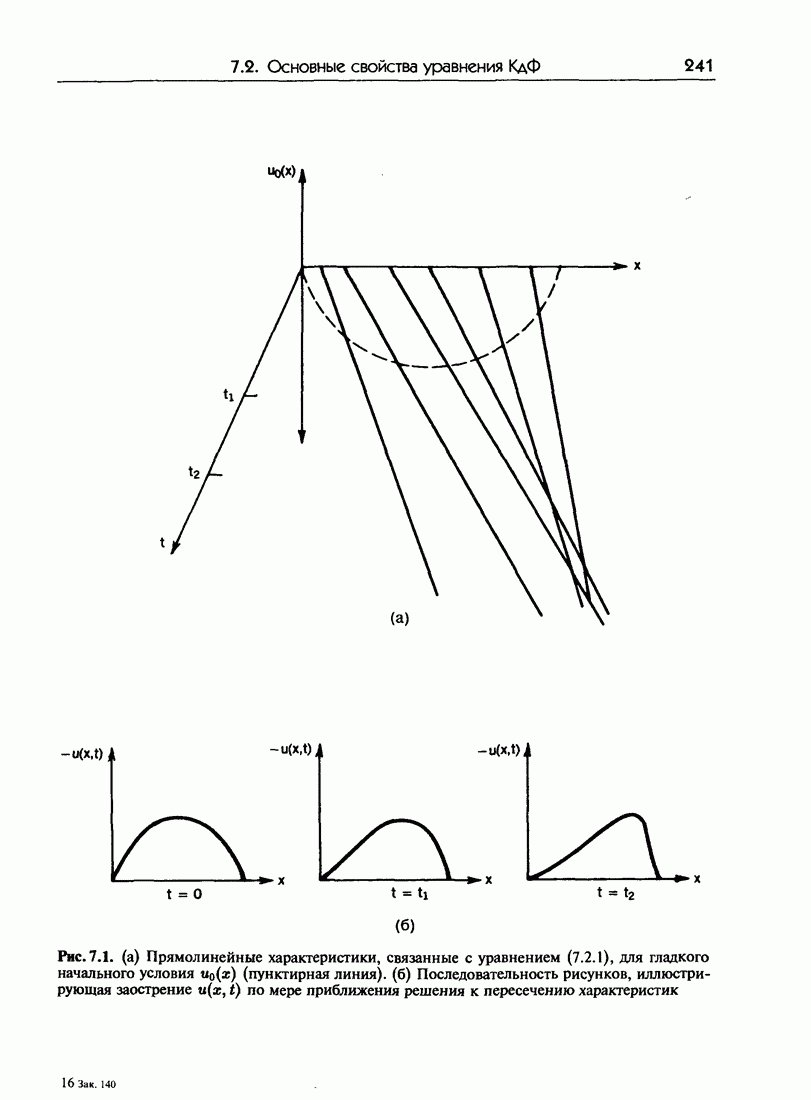
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
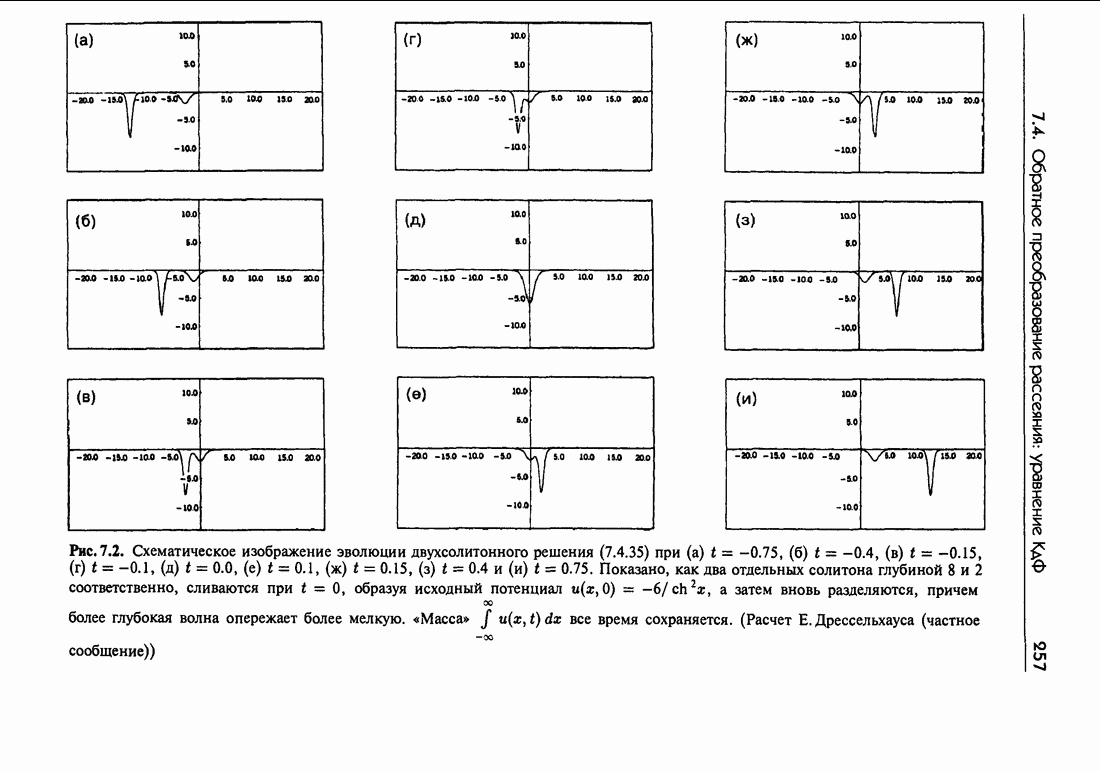
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда