| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
Как отмечалось в разделе 6.4, для неинтегрируемых гамильтонианов не существует «прямых» условий квантования типа условий ЭБК. Однако разработан альтернативный квазиклассический метод, основанный на использовании классических замкнутых траекторий системы, начало которому было положено в работе [41]. Его изложение для гамильтоновых систем общего вида представляет собой значительные сложности. С этой точки зрения квантовые отображения служат простой основой для обсуждения основных идей. Вначале мы дадим обзор необходимых квантовомеханических предпосылок.
6.7.а. Предварительные сведения из квантовой механики
Частица с массой  в потенциальном поле
в потенциальном поле  удовлетворяет уравнению Шрёдингера
удовлетворяет уравнению Шрёдингера

где  образуют полный набор собственных функций (занумерованных с помощью некоторого вектора квантовых чисел, обозначенного через
образуют полный набор собственных функций (занумерованных с помощью некоторого вектора квантовых чисел, обозначенного через  с соответствующими собственными значениями
с соответствующими собственными значениями  Квантовомеханическая плотность состояний определяется соотношением
Квантовомеханическая плотность состояний определяется соотношением

т. е. каждому собственному значению соответствует пик  -функции. Функция Грина (пропагатор) для (6.7.1) удовлетворяет уравнению
-функции. Функция Грина (пропагатор) для (6.7.1) удовлетворяет уравнению

и может быть представлена в «билинейном виде»

Вычисляя «след» функции Грина (т.е. полагая  равным
равным  и интегрируя по всем
и интегрируя по всем  находим
находим

Воспользовавшись формальным соотношением

(где — главное значение Коши), запишем

тогда переход к пределу  дает
дает

Ниже мы увидим, что в квазиклассическом пределе  можно представить в терминах классических путей, соединяющих
можно представить в терминах классических путей, соединяющих  и что операция вычисления следа «отбирает» только замкнутые траектории системы.
и что операция вычисления следа «отбирает» только замкнутые траектории системы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
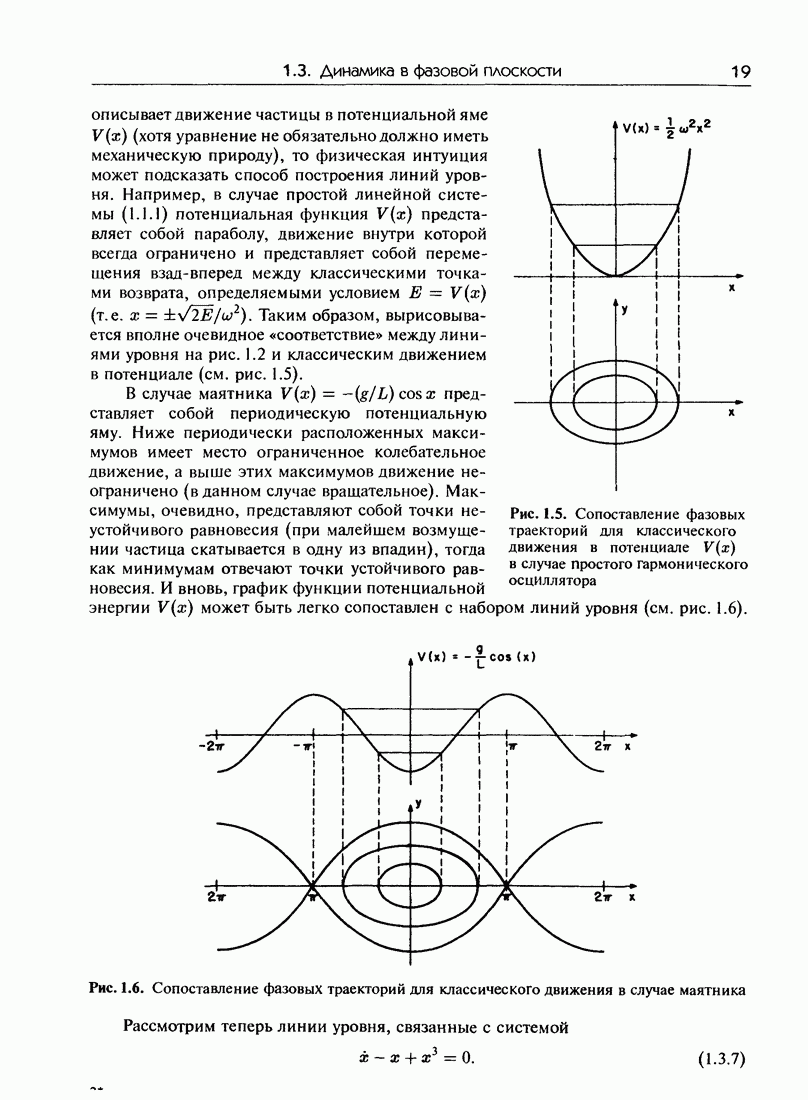
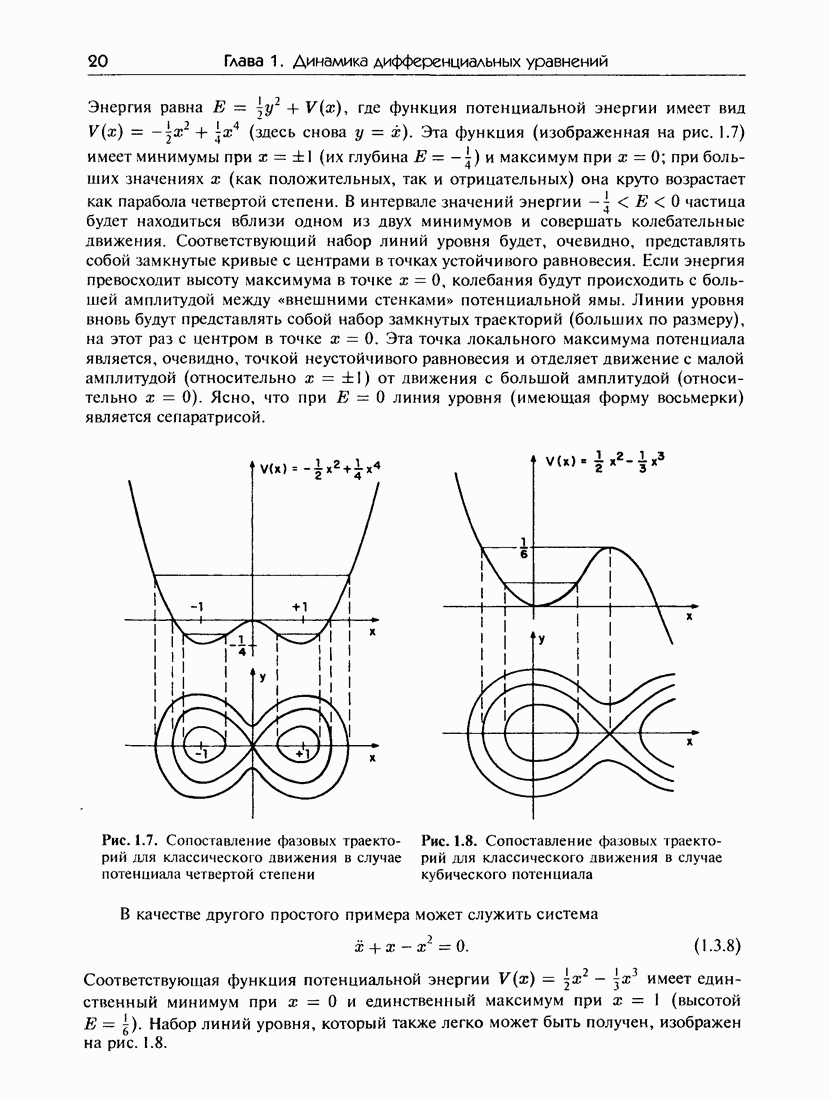
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
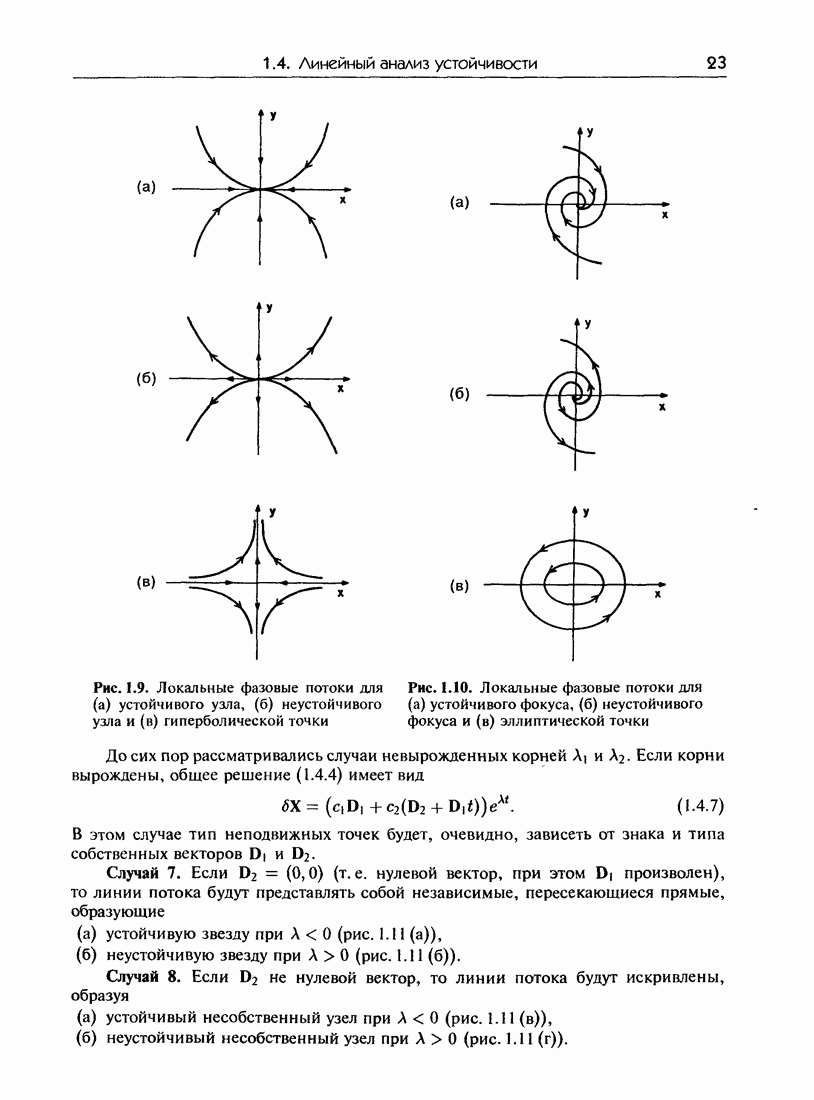
- 1.4. Линейный анализ устойчивости
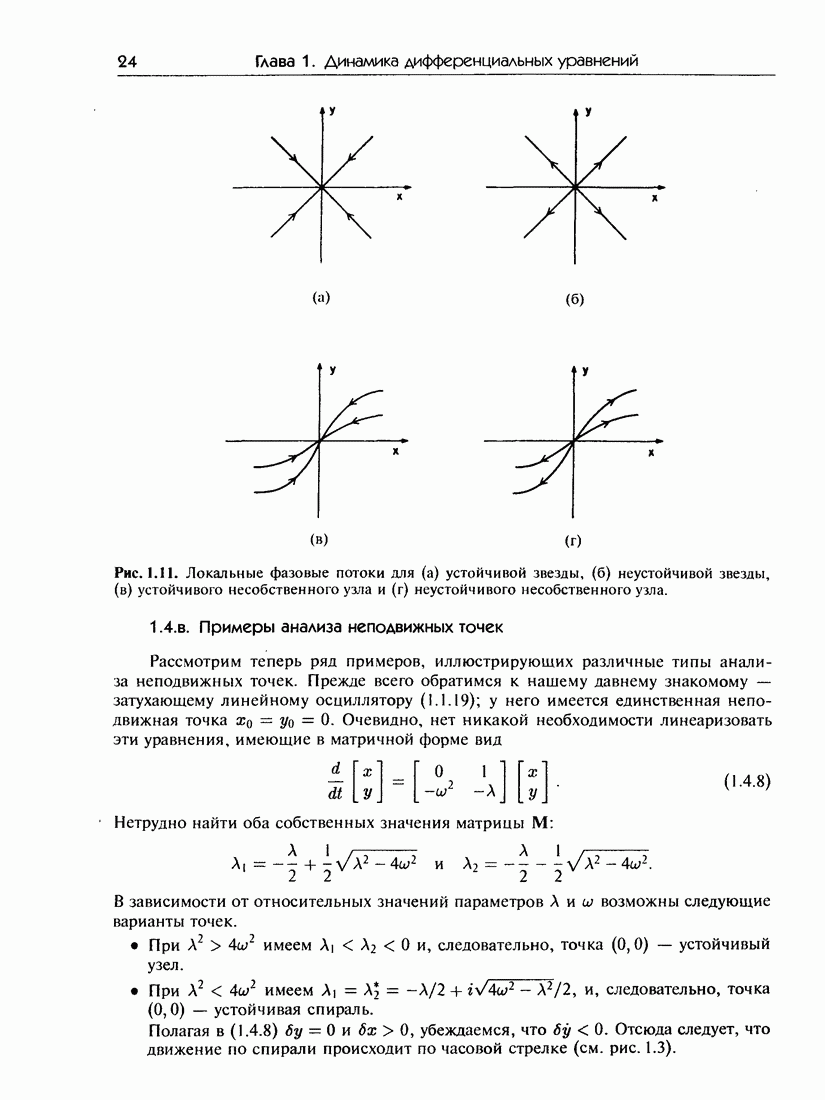
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
- 4.7.б. Перемешивание
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
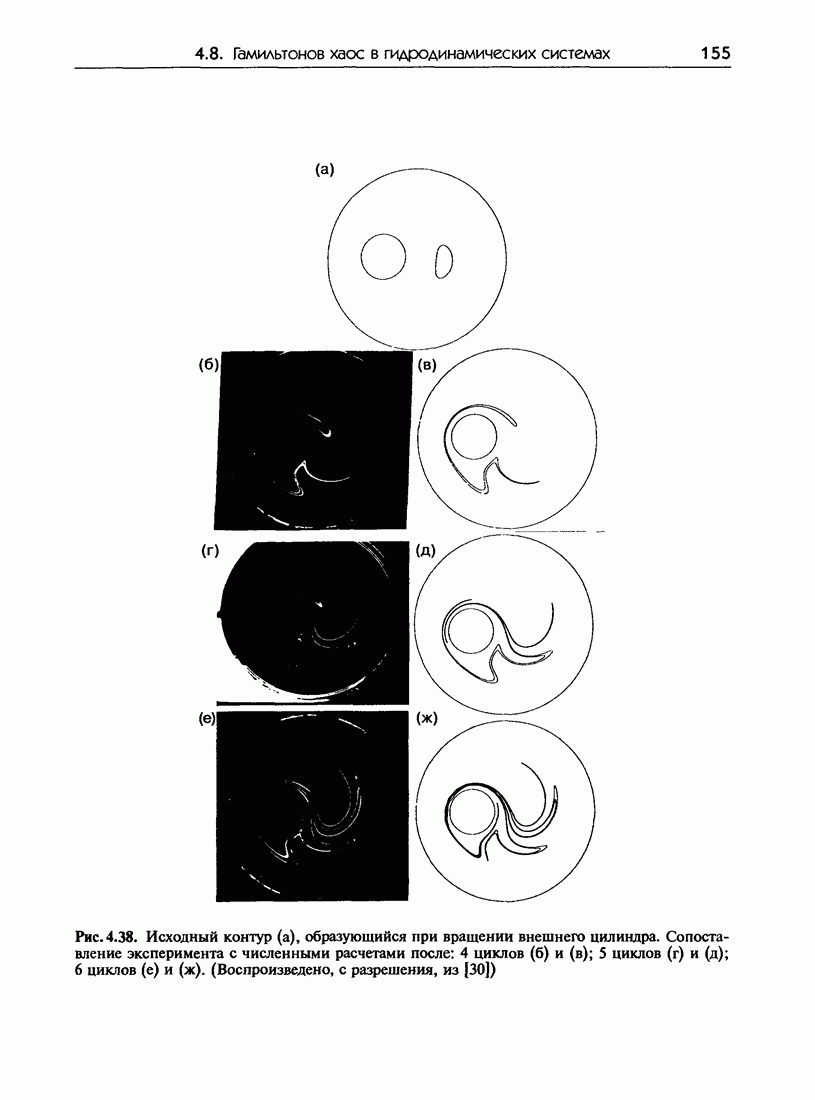
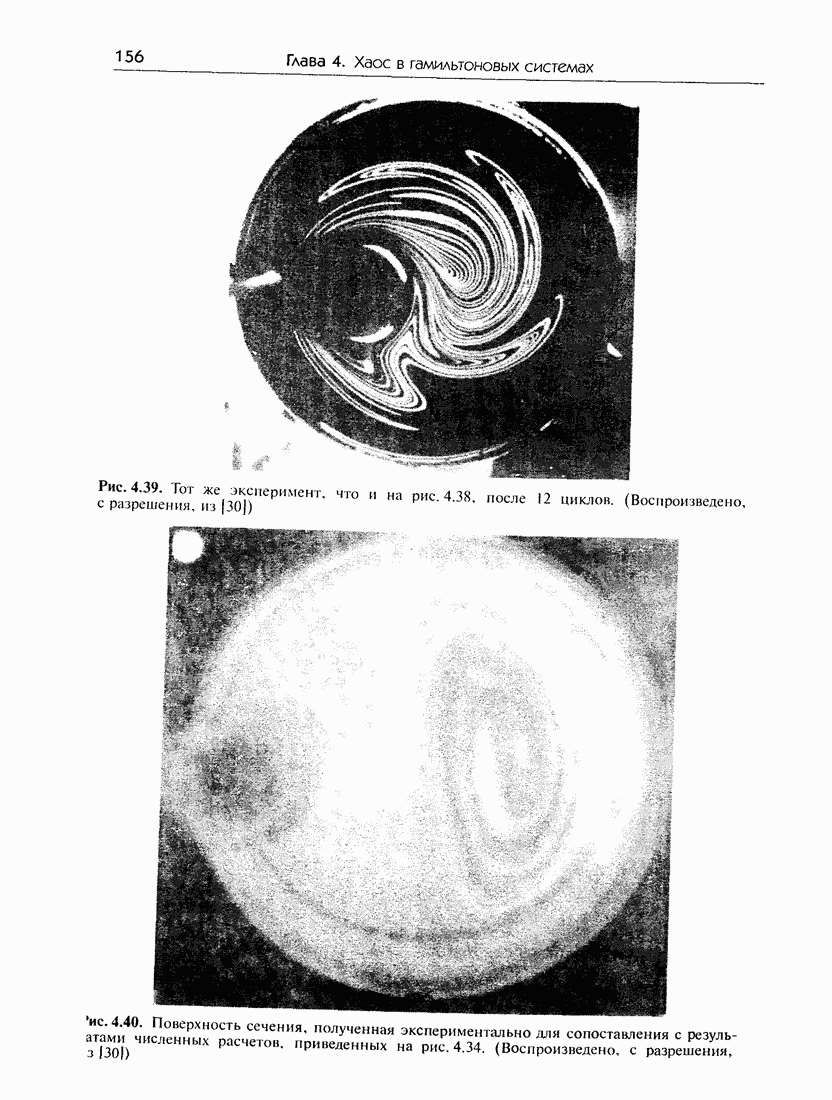
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
- 5.2. Экспериментальные наблюдения возникновения турбулентности
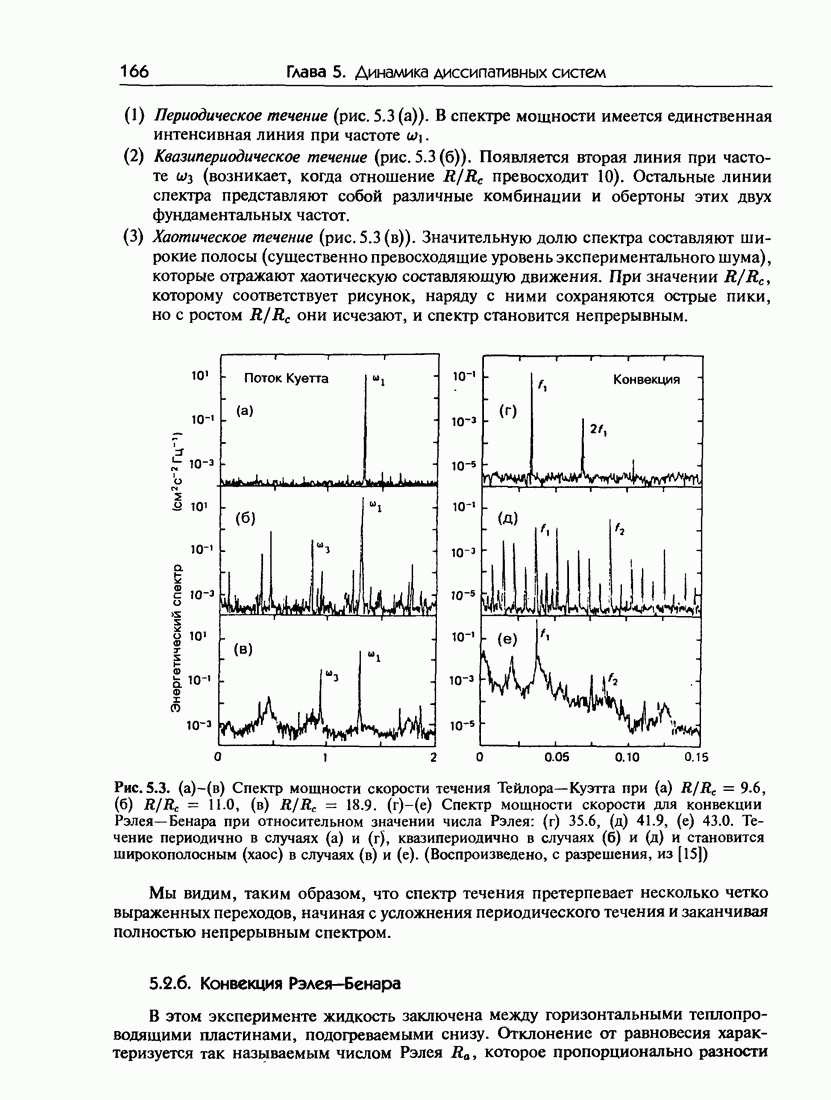
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
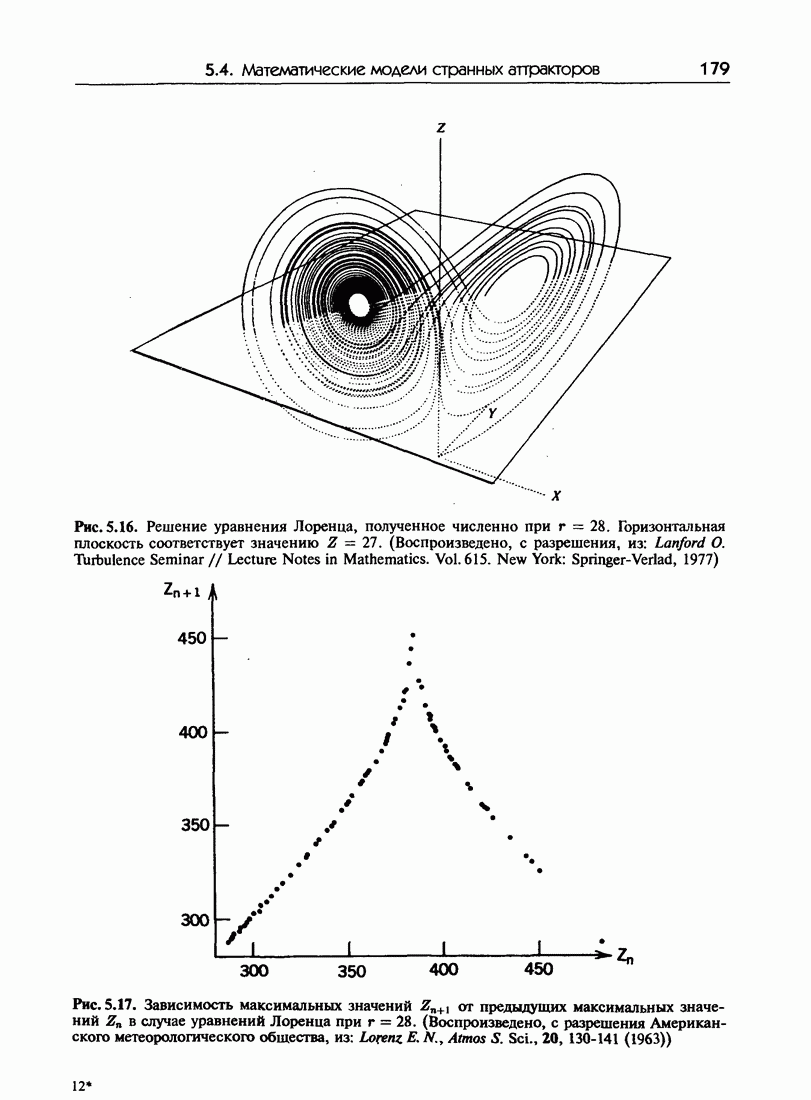
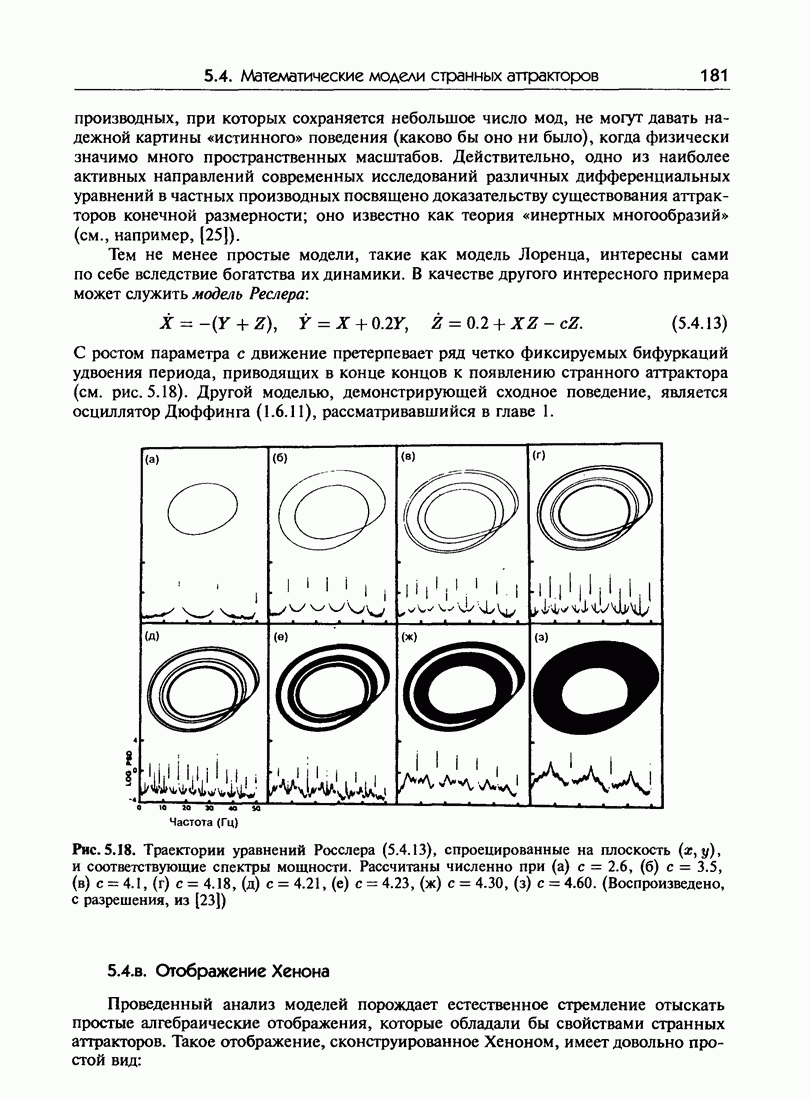
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
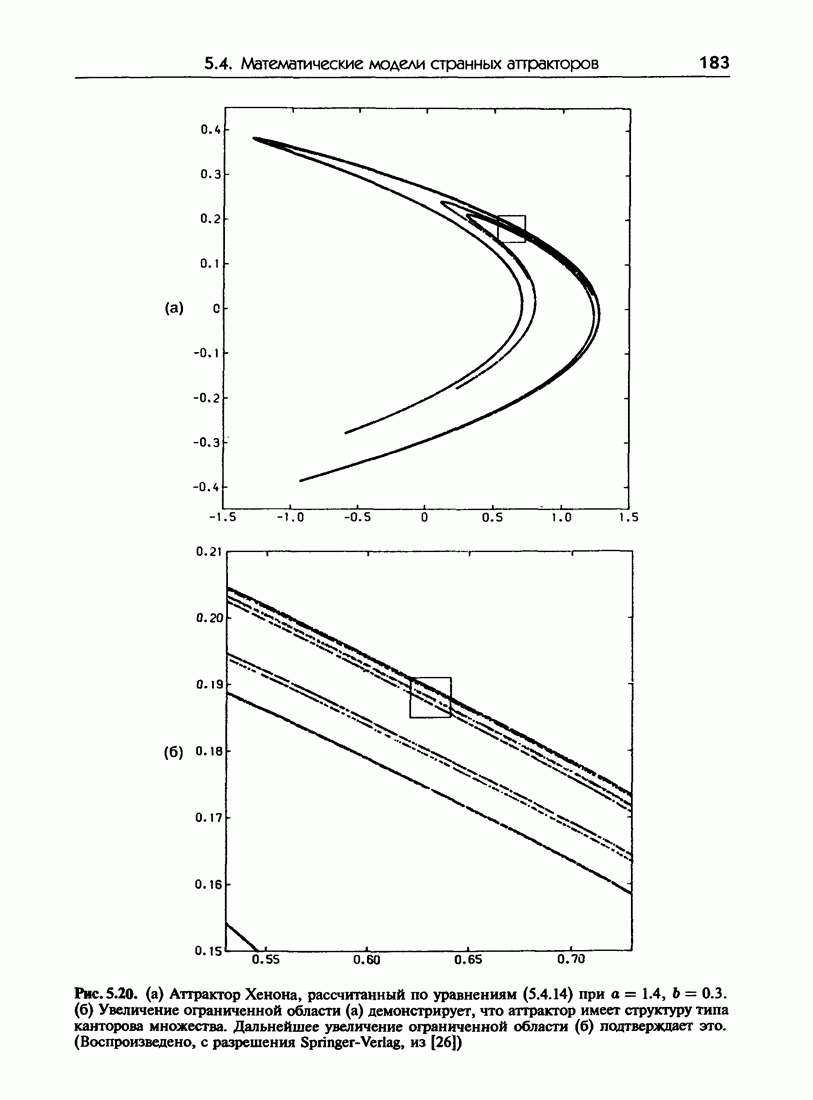
- 5.4.в. Отображение Хенона
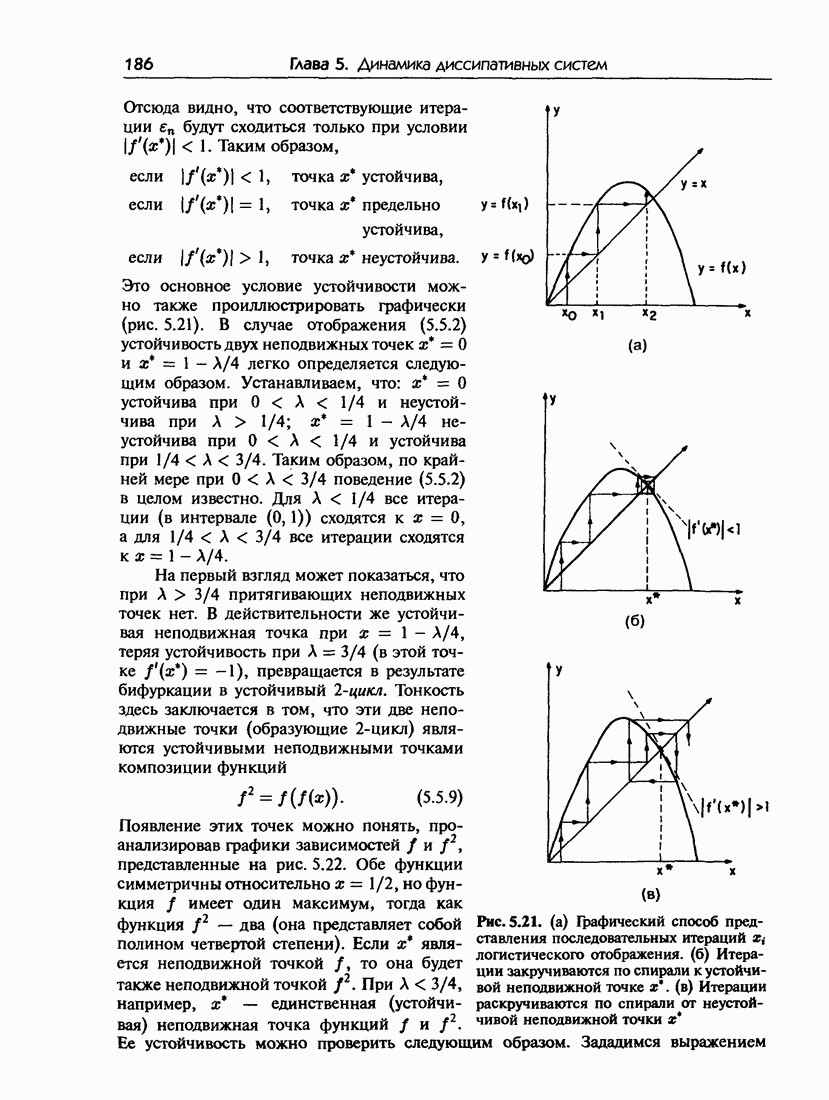
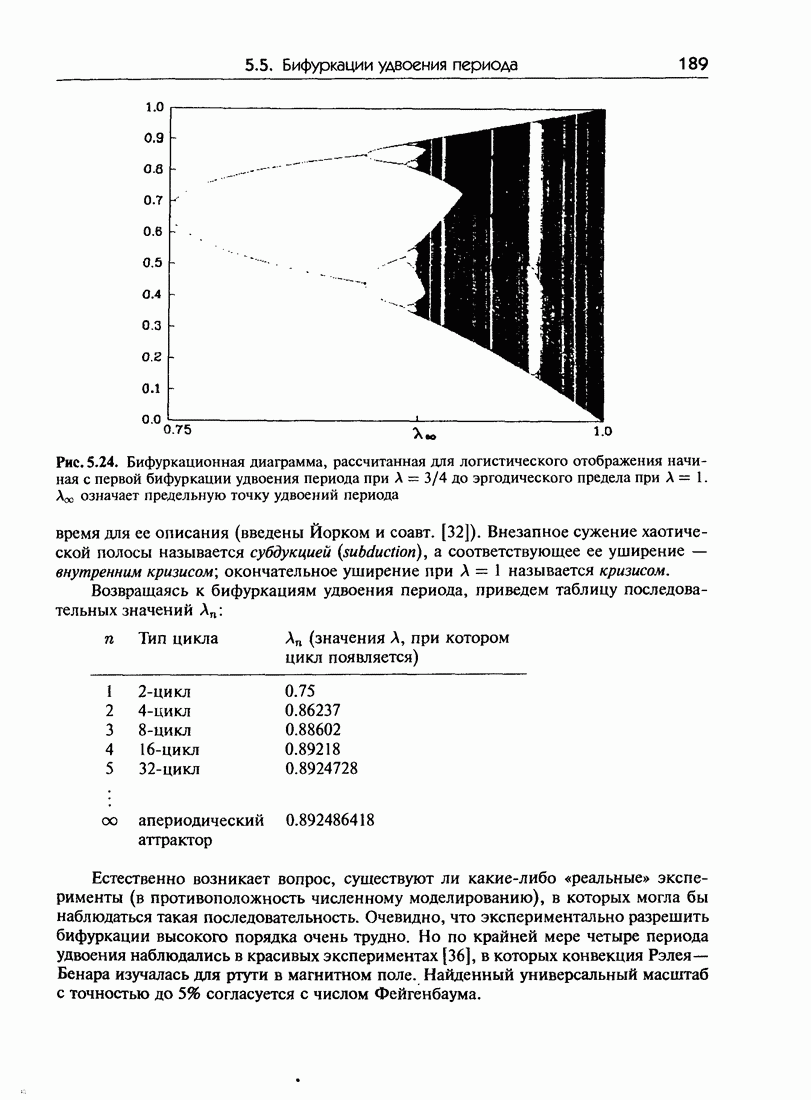
- 5.5. Бифуркации удвоения периода
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда