| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.4.8.1. Преобразование и квантование остаточных блоков 4х4 (0-15, 18-25)
Это преобразование оперирует с блоками 4x4 остаточных данных (они помечены 0 - 15 и 18 - 25 на рис. 6.37) после прогноза компенсации движения или прогноза intra. Преобразование в стандарте H.264 [3] основано на DCT, но имеет ряд фундаментальных отличий.

Рис. 6.37. Порядок сканирования блоков макроблока.
1. Оно является целочисленным (все операции могут быть выполнены с помощью целочисленной арифметики без потери точности при декодировании).
2. Оно гарантирует идентичность результатов обратных преобразований, выполняемых кодером и декодером (при использовании целочисленной арифметики).
3. Ядро алгоритма преобразования можно реализовать, используя только операцию сложения и сдвига.
4. Масштабирование (одна из функций преобразования) интегрировано в квантователь, что сокращает общее число операций умножения.
Процедуры обратного квантования и обратного преобразования могут быть выполнены с помощью арифметики над целыми 16 битными числами (за исключением некоторых аномальных остаточных данных), причем с использованием всего одного умножения на один коэффициент без потери точности.
Приближенное DCT блоков 4x4. Напомним (см. гл. 3), что преобразование DCT матриц 4x4 задается формулой:
 (6.1)
(6.1)
где
![]()
Это произведение матриц можно представить в следующей удобной форме [3]:
 (6.2)
(6.2)
Здесь ![]() «базовое»
двухмерное преобразование. Матрица
«базовое»
двухмерное преобразование. Матрица ![]() состоит из масштабных множителей, а
символ
состоит из масштабных множителей, а
символ ![]() обозначает
поэлементное умножение матрицы
обозначает
поэлементное умножение матрицы ![]() на масштабные множители матрицы
на масштабные множители матрицы ![]() с теми же
координатами (это умножение скаляров, а не матриц). Константы
с теми же
координатами (это умножение скаляров, а не матриц). Константы ![]() и
и ![]() определены выше, a
определены выше, a ![]() равно
равно ![]() (примерно
0,414).
(примерно
0,414).
Для
упрощения реализации преобразования величину ![]() приближают
числом 0,5. Чтобы соблюсти ортогональность преобразования, необходимо
подправить число
приближают
числом 0,5. Чтобы соблюсти ортогональность преобразования, необходимо
подправить число ![]() :
:
![]()
Вторую и
четвертую строки матрицы ![]() , а также второй и четвертый столбец
матрицы
, а также второй и четвертый столбец
матрицы ![]() необходимо
увеличить в два раза, а матрицу
необходимо
увеличить в два раза, а матрицу ![]() для компенсации, наоборот,
перемасштабировать вдвое. При этом сокращается наполовину число умножений при
«базовом» преобразовании
для компенсации, наоборот,
перемасштабировать вдвое. При этом сокращается наполовину число умножений при
«базовом» преобразовании ![]() , которые могли бы привести к потере
точности при использовании целочисленной арифметики. Окончательное прямое
преобразование примет следующий вид:
, которые могли бы привести к потере
точности при использовании целочисленной арифметики. Окончательное прямое
преобразование примет следующий вид:
 (6.3)
(6.3)
Это
преобразование является приближением настоящего преобразования DCT матриц 4x4, поскольку в нем изменены коэффициенты ![]() и
и ![]() .
Его
результат не тождествен применению DCT.
.
Его
результат не тождествен применению DCT.
|
Пример Сравните выход построенного приближенного преобразования матрицы 4 х 4 с результатом «истинного» DCT применительно к входному блоку X:
Выход DCT:
Выход приближенного преобразования:
Их разность:
|
Итак,
имеется явное различие выходных коэффициентов, которые зависят от ![]() и
и ![]() .
В
контексте кодека Н.264 приближенное преобразование имеет почти такую же
степень сжатия, что и DCT. Однако при этом имеется ряд существенных
достоинств. «Базовую» часть преобразования
.
В
контексте кодека Н.264 приближенное преобразование имеет почти такую же
степень сжатия, что и DCT. Однако при этом имеется ряд существенных
достоинств. «Базовую» часть преобразования ![]() можно совершить целочисленной
арифметикой с использованием только сложений, вычитаний и поразрядных сдвигов.
Область операций преобразований такова, что в ней можно применять целые 16
разрядные переменные (за исключением некоторых аномальных блоков), поскольку
входные данные находятся в пределах ±255. Масштабирующий оператор
можно совершить целочисленной
арифметикой с использованием только сложений, вычитаний и поразрядных сдвигов.
Область операций преобразований такова, что в ней можно применять целые 16
разрядные переменные (за исключением некоторых аномальных блоков), поскольку
входные данные находятся в пределах ±255. Масштабирующий оператор ![]() тратит по одному
умножению на каждый коэффициент. Эту функцию можно встроить в модуль
квантователя (см. далее).
тратит по одному
умножению на каждый коэффициент. Эту функцию можно встроить в модуль
квантователя (см. далее).
Обратное преобразование задается формулой (6.4). Стандарт Н.264 [1] определяет это преобразование явно в виде последовательности арифметических операций:
 (6.4)
(6.4)
В
этой формуле каждый коэффициент блока ![]() умножается на соответствующий весовой
множитель матрицы
умножается на соответствующий весовой
множитель матрицы ![]() .
Отметим, что умножение на числа ±1/2 можно реализовать в виде сдвигов разрядов
вправо на один шаг без существенной потери точности, так как коэффициенты
.
Отметим, что умножение на числа ±1/2 можно реализовать в виде сдвигов разрядов
вправо на один шаг без существенной потери точности, так как коэффициенты ![]() уже были
перемасштабированы.
уже были
перемасштабированы.
Прямое
и обратное преобразования удовлетворяют тождеству ![]() .
.
Квантование. Стандарт Н.264
использует скалярное квантование (см. гл. 3). Механизм прямого и обратного
квантования усложняется следующими требованиями: избегать деления и/или арифметические
операции с плавающей запятой и встроить в него операции масштабирования и
обратного масштабирования с использованием матриц ![]() и
и ![]() , описанных выше.
, описанных выше.
Основная операция квантователя [3] имеет вид
![]()
где ![]() коэффициенты
заданного выше преобразования,
коэффициенты
заданного выше преобразования, ![]() шаг
квантования и
шаг
квантования и ![]() квантованные
коэффициенты. Функция round (здесь и далее)
не обязательно должна совпадать с округлением до ближайшего целого. Например,
операция взятия целой части (округление до ближайшего целого, не
превосходящего данного числа) может дать ощутимое улучшение качества.
квантованные
коэффициенты. Функция round (здесь и далее)
не обязательно должна совпадать с округлением до ближайшего целого. Например,
операция взятия целой части (округление до ближайшего целого, не
превосходящего данного числа) может дать ощутимое улучшение качества.
Стандарт
задает 52 возможных значения шага ![]() , которые
проиндексированы параметром квантователя
, которые
проиндексированы параметром квантователя ![]() (см. табл. 6.5). Шаг
(см. табл. 6.5). Шаг ![]() удваивается при
изменении
удваивается при
изменении
![]() в шесть раз.
Широкие пределы шага квантователя дают возможность гибко контролировать
соотношение битовой скорости и качества. Значения
в шесть раз.
Широкие пределы шага квантователя дают возможность гибко контролировать
соотношение битовой скорости и качества. Значения ![]() могут быть
различными для компонент яркости и хроматичности. Оба параметра находятся в
пределах 0 - 51, и по умолчанию для параметра хроматичности установлено
значение
могут быть
различными для компонент яркости и хроматичности. Оба параметра находятся в
пределах 0 - 51, и по умолчанию для параметра хроматичности установлено
значение
![]() , которое
выводится из
, которое
выводится из
![]() так, что
так, что![]() меньше
меньше ![]() при
при ![]() . Устанавливаемое
пользователем соотношение между
. Устанавливаемое
пользователем соотношение между ![]() и
и ![]() отображается во множестве параметров
снимка.
отображается во множестве параметров
снимка.
Таблица 6.5. Размеры шага квантователя кодека Н.264.
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
... |
|
|
0,625 |
0,6875 |
0,8125 |
0,875 |
1 |
1,125 |
1,25 |
1,375 |
1,625 |
1,75 |
2 |
2,25 |
2,5 |
|
|
|
... |
18 |
... |
24 |
... |
30 |
... |
36 |
... |
42 |
... |
48 |
... |
51 |
|
|
|
5 |
|
10 |
|
20 |
|
40 |
|
80 |
|
160 |
|
224 |
Множители
обратного квантования ![]() ,
, ![]() или
или ![]() (см. уравнение (6.3)) встроены в
прямой квантователь. Сначала входной блок
(см. уравнение (6.3)) встроены в
прямой квантователь. Сначала входной блок ![]() , преобразуется, и получается блок
, преобразуется, и получается блок ![]() . Затем каждый
коэффициент
. Затем каждый
коэффициент ![]() квантуется и
масштабируется за одну операцию
квантуется и
масштабируется за одну операцию
![]() (6.5)
(6.5)
где переменная
![]() - это
- это ![]() ,
, ![]() или
или ![]() в зависимости от
значения индексов
в зависимости от
значения индексов ![]() (см. уравнение (6.3)):
(см. уравнение (6.3)):
|
Индексы |
|
|
|
(0,0), (2,0), (0,2) |
или (2,2) |
|
|
(1,1), (1,3), (3,1) |
или (3,3) |
|
|
Все остальные |
|
|
В
целях упрощения вычислений множитель ![]() реализован в справочной модели
программного обеспечения [4] в виде умножения на MF и правого сдвига
без использования операции деления:
реализован в справочной модели
программного обеспечения [4] в виде умножения на MF и правого сдвига
без использования операции деления:
![]()
где
![]()
и
![]() (6.6)
(6.6)
В целочисленной арифметике уравнение (6.6) реализуется в следующем виде:
![]()
![]() (6.7)
(6.7)
где >>
обозначает сдвиг двоичных разрядов вправо. В справочной программе ![]() равно
равно ![]() для блоков в
моде intra и
для блоков в
моде intra и ![]() в моде inter.
в моде inter.
|
Пример
|
Первые шесть
значений коэффициента MF (для всех пар
координат ![]() ),
применяемых
кодером справочной программы Н.264, приведены в табл. 6.6. Второй и третий
столбец этой таблицы (множители
),
применяемых
кодером справочной программы Н.264, приведены в табл. 6.6. Второй и третий
столбец этой таблицы (множители ![]() и
и ![]() ) были слегка модифицированы с учетом
уравнения (6.6).
) были слегка модифицированы с учетом
уравнения (6.6).
При
![]() множитель
MF не изменяется,
но делитель
множитель
MF не изменяется,
но делитель ![]() увеличивается в два раза при
каждом шестикратном увеличении
увеличивается в два раза при
каждом шестикратном увеличении ![]() . Например,
величина
. Например,
величина ![]() при
при
![]() ,
, ![]() при
при ![]() и т.д.
и т.д.
Таблица 6.6. Множители MF.
|
|
Индексы |
Индексы |
|
|
QP |
(0, 0), (2, 0), (0, 2), (2, 2) |
(1,1), (1,3), (3,1), (3,3) |
Все остальные |
|
0 |
13 107 |
5 243 |
8 066 |
|
1 |
11 916 |
4 660 |
7 490 |
|
2 |
10 082 |
4 194 |
6 554 |
|
3 |
9 362 |
3 647 |
5 825 |
|
4 |
8 192 |
3 355 |
5 243 |
|
5 |
7 282 |
2 893 |
4 559 |
Обратное квантование. Базовая операция масштабирования (обратного квантования) имеет вид
![]() . (6.8)
. (6.8)
Масштабирующие
множители обратного преобразования (из матрицы ![]() , содержащей числа
, содержащей числа ![]() ,
, ![]() и
и ![]() в
зависимости от значений индексов
в
зависимости от значений индексов ![]() )
встроены
в эту операцию вместе с постоянным множителем масштаба 64 для избежания ошибок
округления:
)
встроены
в эту операцию вместе с постоянным множителем масштаба 64 для избежания ошибок
округления:
![]() . (6.9)
. (6.9)
Коэффициенты ![]() преобразуются
базовым обратным преобразованием
преобразуются
базовым обратным преобразованием ![]() , (уравнение (6.4)). Выход обратного
преобразования делится на 64 для сокращения множителя масштаба (эта процедура
реализуется только сложением и правым сдвигом). Стандарт Н.264 не специфицирует
явно числа
, (уравнение (6.4)). Выход обратного
преобразования делится на 64 для сокращения множителя масштаба (эта процедура
реализуется только сложением и правым сдвигом). Стандарт Н.264 не специфицирует
явно числа ![]() и
и ![]() .
Вместо
этого определяется параметр
.
Вместо
этого определяется параметр ![]() при
при ![]() для каждой пары
координат
для каждой пары
координат ![]() , так что операция
масштабирования принимает вид:
, так что операция
масштабирования принимает вид:
![]() . (6.10)
. (6.10)
|
Пример
|
Величины ![]() определяются
стандартным образом при
определяются
стандартным образом при ![]() . Они приведены в табл. 6.7.
. Они приведены в табл. 6.7.
Таблица
6.7. Множители ![]() .
.
|
|
Индексы |
Индексы |
|
|
QP |
(0, 0), (2, 0), (0, 2), (2, 2) |
(1, 1), (1, 3), (3, 1), (3, 3) |
Все остальные |
|
0 |
10 |
16 |
13 |
|
1 |
11 |
18 |
14 |
|
2 |
13 |
20 |
16 |
|
3 |
14 |
23 |
18 |
|
4 |
16 |
25 |
20 |
|
5 |
18 |
29 |
23 |
В
уравнении (6.10) стоит множитель ![]() по причине увеличения вдвое выхода
масштабирования при каждом шестикратном возрастании параметра QP.
по причине увеличения вдвое выхода
масштабирования при каждом шестикратном возрастании параметра QP.
| << Предыдущий параграф | Следующий параграф >> |
- Пролог
- Предисловие
- Об авторе
- Глава 1. Введение
- 1.1. Сцена
- 1.2. Видеосжатие
- 1.3. MPEG-4 и Н.264
- 1.4. Об этой книге
- 1.5. Полезные ссылки
- ГЛАВА 2. ФОРМАТЫ ВИДЕО И ЕГО КАЧЕСТВО
- 2.1. Введение
- 2.2. Естественные видеосцены
- 2.3. Захват кадра
- 2.3.1. Пространственное сэмплирование
- 2.3.2. Временное сэмплирование
- 2.3.3. Кадры и полукадры
- 2.4. Цветовые пространства
- 2.4.1. RGB
- 2.4.2. YCbCr
- 2.4.3. Форматы сэмплирования YCbCr
- 2.5. Видеоформаты
- 2.6. Качество
- 2.6.1. Субъективное измерение качества
- 2.6.1.1. Факторы субъективного восприятия
- 2.6.1.2. ITU-R 500
- 2.6.2. Объективное измерение качества
- 2.7. Выводы
- 2.8. Полезные ссылки
- ГЛАВА 3. ОСНОВЫ ВИДЕОКОДИРОВАНИЯ
- 3.1. Введение
- 3.2. Видеокодек
- 3.3. Временная модель
- 3.3.1. Прогноз по предыдущему видеокадру
- 3.3.2. Изменения вследствие движения
- 3.3.3. Оценка и компенсация движения на основе блоков
- 3.3.4. Прогноз макроблока с компенсированным движением
- 3.3.5. Размер блока компенсации движения
- 3.3.6. Подпиксельная компенсация движения
- 3.3.7. Компенсация движения на основе областей
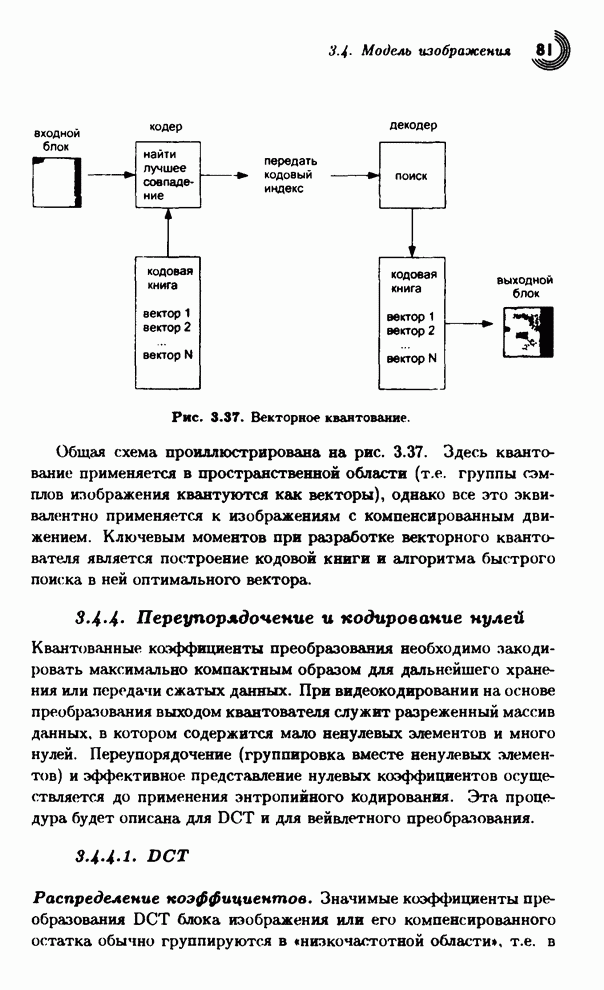
- 3.4. Модель изображения
- 3.4.1. Кодирование изображений с предсказанием
- 3.4.2. Кодирование преобразованием
- 3.4.2.1. Обзор
- 3.4.2.2. DCT
- 3.4.2.3. Вейвлеты
- 3.4.3. Квантование
- 3.4.4. Переупорядочение и кодирование нулей
- 3.4.4.1. DCT
- 3.4.4.2. Вейвлет
- 3.5. Энтропийный кодер
- 3.5.1. Коды с предсказанием
- 3.5.2. Коды переменной длины
- 3.5.2.1. Коды Хаффмана
- 3.5.2.2. Кодирование Хаффмана с предварительными вычислениями
- 3.5.2.3. Другие коды переменной длины
- 3.5.3. Арифметическое кодирование
- 3.5.3.1. Арифметическое кодирование с контекстом
- 3.6. Гибридная модель DPCM/DCT видеокодека
- 3.6.1. Пример работы кодека
- 3.7. Выводы
- 3.8. Полезные ссылки
- ГЛАВА 4 СТАНДАРТЫ MPEG-4 и Н.264
- 4.1. Введение
- 4.2. Развитие стандартов
- 4.2.1. ISO MPEG
- 4.2.2. ITU-T VCEG
- 4.2.3. JVT
- 4.2.4. История развития
- 4.2.5. Решение о содержании стандарта
- 4.3. Использование стандарта
- 4.3.1. Что кодирует стандарт
- 4.3.2. «Декодирование» стандартов
- 4.3.3. Подчинение стандартам
- 4.4. Обзор MPEG-4 Visual (Part2)
- 4.5. Обзор Н.264 (MPEG-4 Part 10)
- 4.6. Сравнение MPEG-4 Visual и Н.264
- 4.7. Родственные стандарты
- 4.7.1. JPEG и JPEG2000
- 4.7.2. MPEG-1 и MPEG-2
- 4.7.3. Н.261 и Н.263
- 4.7.4. Другие части MPEG-4
- 4.8. Выводы
- 4.9. Полезные ссылки
- ГЛАВА 5. MPEG-4 VISUAL
- 5.1. Введение
- 5.2. Обзор MPEG-4 Visual
- 5.2.1. Основные особенности
- 5.2.2. Инструменты, объекты, профили и уровни
- 5.2.3. Видеообъекты
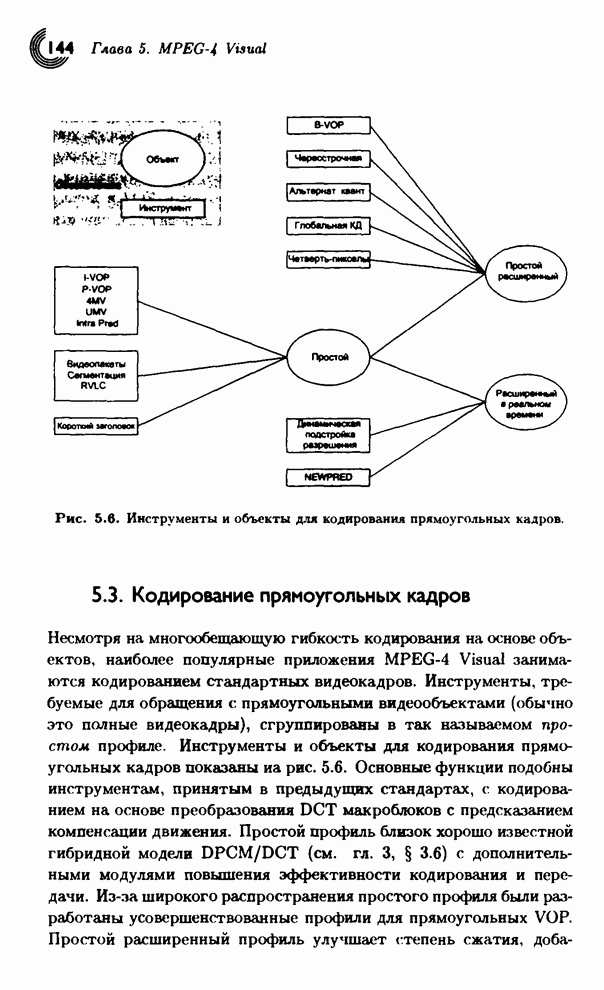
- 5.3. Кодирование прямоугольных кадров
- 5.3.1. Входные и выходные видеоформаты
- 5.3.2. Простой профиль
- 5.3.2.1. Видеоядро для низкой битовой скорости
- 5.3.2.2. Вазовые инструменты кодирования
- 5.3.2.3. Инструменты эффективного кодирования
- 5.3.2.4. Инструменты эффективной передачи
- 5.3.3. Простой расширенный профиль
- 5.3.4. Простой расширенный профиль в реальном времени
- 5.4. Кодирование областей произвольной формы
- 5.4.1. Базовый профиль
- 5.4.1.1. Бинарное кодирование формы
- 5.4.1.2. Кодирование VOP произвольной формы с компенсацией движения
- 5.4.1.3. Кодирование текстуры граничных макроблоков
- 5.4.2. Основной профиль
- 5.4.2.1. Градуированное кодирование формы
- 5.4.2.2. Статическое кодирование «спрайтов»
- 5.4.3. Профиль повышенной степени сжатия
- 5.4.4. N-битовый профиль
- 5.5. Масштабируемое видеокодирование
- 5.5.1. Пространственное масштабирование
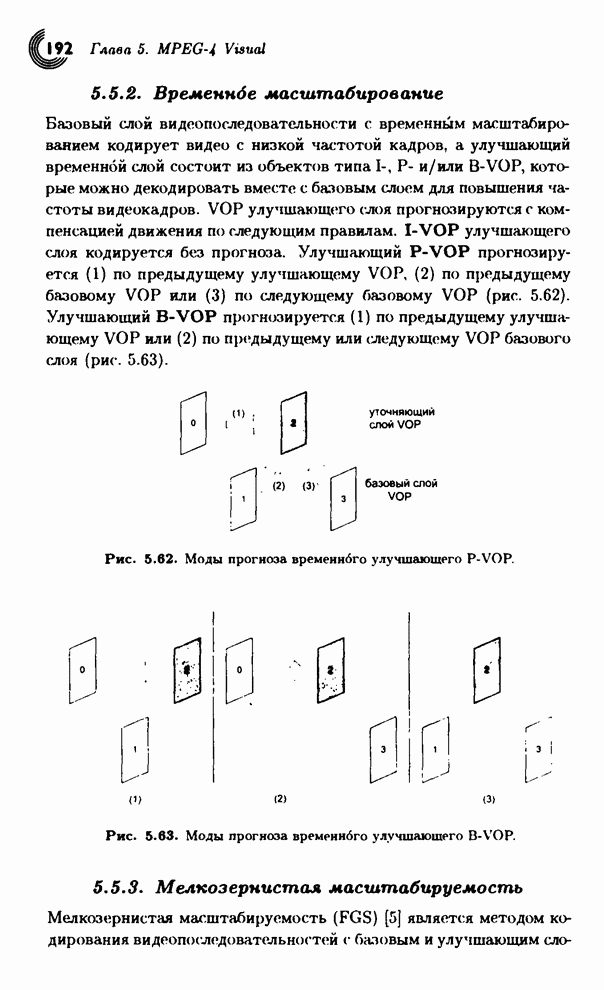
- 5.5.2. Временное масштабирование
- 5.5.3. Мелкозернистая масштабируемость
- 5.5.4. Простой масштабируемый профиль
- 5.5.5. Базовый масштабируемый профиль
- 5.5.6. Профиль мелкозернистой масштабируемости
- 5.6. Кодирование текстуры
- 5.6.1. Профиль масштабируемых текстур
- 5.6.2. Расширенный профиль масштабируемых текстур
- 5.7. Кодирование видео студийного качества
- 5.7.1. Простой студийный профиль
- 5.7.2. Базовый студийный профиль
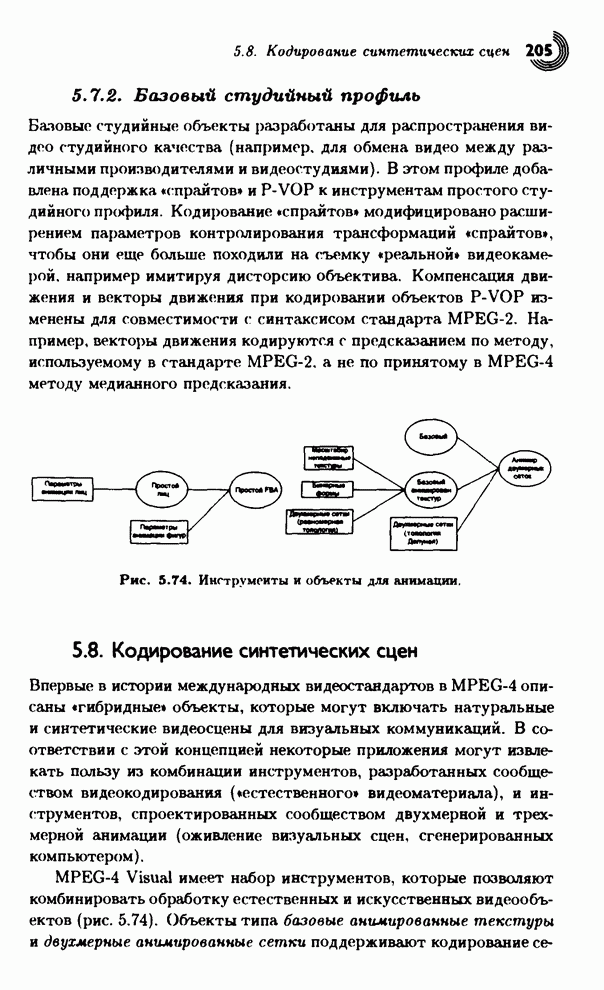
- 5.8. Кодирование синтетических сцен
- 5.8.1. Анимированное сеточное кодирование
- 5.8.2. Анимация лиц и фигур
- 5.9. Выводы
- 5.10. Полезные ссылки
- ГЛАВА 6. H.264/MPEG-4 Part 10
- 6.1. Введение
- 6.2. Кодек Н.264
- 6.3. Структура Н.264
- 6.3.1. Профили и уровни
- 6.3.2. Видеоформат
- 6.3.3. Формат закодированных данных
- 6.3.4. Ссылочные снимки
- 6.3.5. Слои
- 6.3.6. Макроблоки
- 6.4. Базовый профиль
- 6.4.1. Обзор
- 6.4.2. Организация ссылочных снимков
- 6.4.3. Слои
- 6.4.4. Прогнозирование макроблоков
- 6.4.5. Прогнозирование в моде inter
- 6.4.5.1. Древовидная структура компенсации движения
- 6.4.5.2. Векторы движения
- 6.4.5.3. Предсказание векторов движения
- 6.4.6. Прогноз в моде intra
- 6.4.6.1. Моды прогноза блоков яркости 4х4
- 6.4.6.2. Моды прогноза макроблоков яркости 16х16
- 6.4.6.3. Моды прогноза макроблоков хроматичности 8×8
- 6.4.6.4. Индикация мод прогнозирования intra
- 6.4.7. Деблочный фильтр
- 6.4.8. Преобразование и квантование
- 6.4.8.1. Преобразование и квантование остаточных блоков 4х4 (0-15, 18-25)
- 6.4.9. Коэффициенты DC преобразования и квантования блоков яркости 4×4 (только для моды intra 16х16)
- 6.4.10. Коэффициенты DC преобразования и квантования блоков хроматичности размером 2×2
- 6.4.11. Полный процесс прямого и обратного преобразования и квантования
- 6.4.12. Переупорядочивание
- 6.4.13. Энтропийное кодирование
- 6.5. Основной профиль
- 6.5.1. В-слои
- 6.5.2. Взвешенный прогноз
- 6.5.3. Чересстрочная развертка
- 6.5.4. Контекстно-адаптивное арифметическое кодирование (CABАС)
- 6.6. Расширенный профиль
- 6.6.1. Слои SP и SI
- 6.6.2. Слои деления данных
- 6.7. Транспортный механизм Н.264
- 6.8. Выводы
- 6.9. Полезные ссылки
- ГЛАВА 7. ДИЗАЙН И ПРОИЗВОДИТЕЛЬНОСТЬ
- 7.1. Введение
- 7.2. Функциональный дизайн
- 7.2.1. Сегментация
- 7.2.2. Оценка движения
- 7.2.2.1. Оценка движения на основе блоков
- 7.2.2.2. Оценка движения на основе объектов
- 7.2.3. Преобразование DCT/IDCT
- 7.2.3.1. DCT 8×8
- 7.2.3.2. Преобразование DCT 4х4 в Н.264
- 7.2.3.3. Границы объектов
- 7.2.4. Вейвлетное преобразование
- 7.2.5. Квантование и деквантование
- 7.2.6. Энтропийное кодирование
- 7.3. Вход и выход
- 7.3.1. Сопряжение процессов
- 7.3.2. Предварительная обработка
- 7.3.3. Последующая обработка
- 7.4. Производительность
- 7.4.1. Критерии
- 7.4.2. Субъективная производительность
- 7.4.3. Соотношение скорость/искажение
- 7.4.4. Вычислительная производительность
- 7.4.5. Оптимизация по производительности
- 7.5. Контроль битовой скорости
- 7.6. Транспортировка и хранение
- 7.6.1. Механизмы транспортировки
- 7.6.2. Форматы файлов
- 7.6.3. Кодирование и транспортные выпуски
- 7.7. Выводы
- 7.8. Полезные ссылки
- ГЛАВА 8. ПРОДУКТЫ И ПЕРСПЕКТИВЫ
- 8.1. Введение
- 8.2. Приложения
- 8.3. Платформы
- 8.4. Выбор кодека
- 8.5. Коммерческие детали
- 8.6. Что в перспективе
- 8.7. Заключение
- Литература