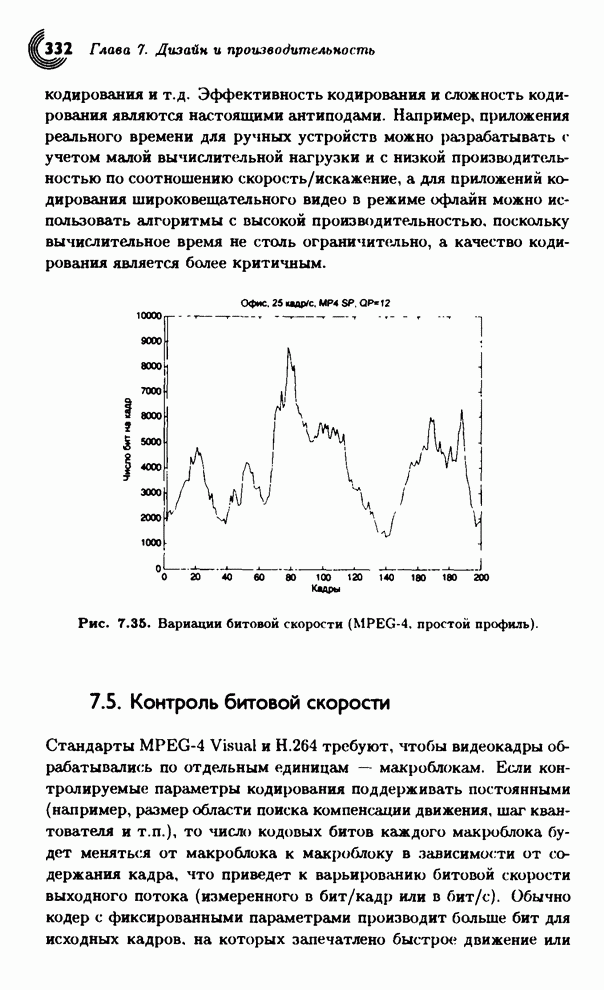
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.5.2. Коды переменной длины
Метод кодирования переменной длины сопоставляет потоку входных символов определенную последовательность кодовых слов (коды переменной длины, VLC, Variable Length Codes). Каждый символ отображается в кодовое слово, которое может иметь переменную длину, но каждое из них имеет целое число бит. Символы, встречающиеся чаще, представляются более короткими словами VLC, а редко встречающиеся символы кодируются более длинными словами VLC. Эффект сжатия данных начинает проявляться после кодирования достаточно большого числа входных символов.
3.5.2.1. Коды Хаффмана
Метод кодирования Хаффмана присваивает каждому символу код VLC, исходя из вероятности появления этого символа. В соответствии со схемой, предложенной Хаффманом в 1952 году [7], следует предварительно вычислить вероятность появления каждого символа и построить множество кодовых слов переменной длины. Этот процесс будет проиллюстрирован на двух примерах.
|
Пример Кодирование
Хаффмана, последовательность № 1 векторов перемещения. Необходимо закодировать
данные, содержащие разности векторов движения для видеопоследовательности
(последовательность №1). В табл. 3.2 перечислены вероятности Таблица 3.2. Вероятности векторов движения в последовательности № 1.
Рис. 3.45. Построение дерева Хаффмана (последовательность №1). 1. Построение дерева Хаффмана. Чтобы построить таблицу кодов Хаффмана для этого множества элементов, следует совершить итеративную процедуру: 1. упорядочить элементы по возрастанию вероятностей; 2. объединить два элемента с наименьшими вероятностями в один узел и присвоить этому узлу суммарную вероятность этих элементов; 3. переупорядочить оставшиеся элементы и узлы по возрастанию юс вероятностей и повторить шаг 2. Процедура повторяется до тех пор, пока не останется только один «корень», содержащий все остальные узлы и элементы. Эта процедура проиллюстрирована на рис. 3.45.
Таблица 3.3. Коды Хаффмана для векторов движения последовательности №1.
Таблица 3.4. Вероятности векторов движения в последовательности №2.
2. Кодирование. Каждому листу двоичного дерева ставится в соответствие код переменной длины. Для нахождения этого кода следует пройтись по дереву, начиная от корня (узел D) и двигаясь в сторону выбранного листа (элемента списка). При проходе каждой ветви к коду добавляются двоичные цифры 0 или 1; 0 соответствует верхней ветви, а 1 — нижней (они показаны на рис. 3.45). Полученное множество кодов приведено в табл. 3.3. Кодирование состоит в передаче соответствующего кода вместо вектора. Отметим, что дерево Хаффмана строится один раз и полученные коды можно хранить в поисковой таблице. Элементам,
имеющим большие вероятности, присваиваются короткие коды (например, код 1
присвоен вектору 0, который появляется чаще других). Векторам (-2, +2, -1,
+1) присвоены коды из 3 бит (несмотря на то что векторы -1 и +1 имеют большую
вероятность, чем -2 и +2). Длины кодов Хаффмана (целые числа) не совпадают с
идеальными длинами, задаваемыми формулой 3. Декодирование. Для декодирования данных декодер должен иметь копию дерева Хаффмана (или таблицу кодов). Эту таблицу можно передать отдельно, а можно переслать список элементов вместе с их вероятностями перед передачей кодированных данных. Каждый однозначно декодируемый код позволяет восстановить исходные данные, например: 011 декодируется в (1), 1 декодируется в (0), 000 декодируется в (2). |
|
Пример Кодирование Хаффмана, последовательность №2 векторов перемещения. Применение описанной выше процедуры к последовательности №2 с другим распределением вероятностей векторов приводит к другим кодам Хаффмана. Новые вероятности приведены в табл. 3.4. Отметим, что в этом примере нулевой вектор встречается существенно чаще (это соответствует видеопоследовательности с медленным движением). Таблица З.5. Коды Хаффмана для векторов движения последовательности N2.
На рис. 3.46 построено соответствующее дерево Хаффмана. Заметим, что «форма» дерева претерпела некоторые изменения (в силу изменения распределения вероятностей), и это, в свою очередь, породило новые коды Хаффмана (табл. 3.5). У дерева по-прежнему четыре узла, на один меньше числа элементов (пять), что характерно для любого дерева Хаффмана. |

Рис. 3.46. Дерево Хаффмана (последовательность №2).
Если распределение вероятностей хорошо соответствует частотам появления символов, то кодирование Хаффмана дает достаточно компактное представление исходных данных. В этих примерах вектор (0) с наибольшей вероятностью представляется кодом длиной в 1 бит. Однако для достижения оптимального сжатия необходимо использовать разные таблицы для этих последовательностей, имеющих разные распределения вероятностей векторов. Определенное снижение эффективности сжатия при использовании кодов с целочисленной длиной отчетливо видно при кодировании вектора (0) последовательности №2, так как оптимальное число бит (информационная емкость) для этого вектора равно 0,32 бит, однако лучшее, что может обеспечить код Хаффмана, это 1 бит.
| << Предыдущий параграф | Следующий параграф >> |
- Пролог
- Предисловие
- Об авторе
- Глава 1. Введение
- 1.1. Сцена
- 1.2. Видеосжатие
- 1.3. MPEG-4 и Н.264
- 1.4. Об этой книге
- 1.5. Полезные ссылки
- ГЛАВА 2. ФОРМАТЫ ВИДЕО И ЕГО КАЧЕСТВО
- 2.1. Введение
- 2.2. Естественные видеосцены
- 2.3. Захват кадра
- 2.3.1. Пространственное сэмплирование
- 2.3.2. Временное сэмплирование
- 2.3.3. Кадры и полукадры
- 2.4. Цветовые пространства
- 2.4.1. RGB
- 2.4.2. YCbCr
- 2.4.3. Форматы сэмплирования YCbCr
- 2.5. Видеоформаты
- 2.6. Качество
- 2.6.1. Субъективное измерение качества
- 2.6.1.1. Факторы субъективного восприятия
- 2.6.1.2. ITU-R 500
- 2.6.2. Объективное измерение качества
- 2.7. Выводы
- 2.8. Полезные ссылки
- ГЛАВА 3. ОСНОВЫ ВИДЕОКОДИРОВАНИЯ
- 3.1. Введение
- 3.2. Видеокодек
- 3.3. Временная модель
- 3.3.1. Прогноз по предыдущему видеокадру
- 3.3.2. Изменения вследствие движения
- 3.3.3. Оценка и компенсация движения на основе блоков
- 3.3.4. Прогноз макроблока с компенсированным движением
- 3.3.5. Размер блока компенсации движения
- 3.3.6. Подпиксельная компенсация движения
- 3.3.7. Компенсация движения на основе областей
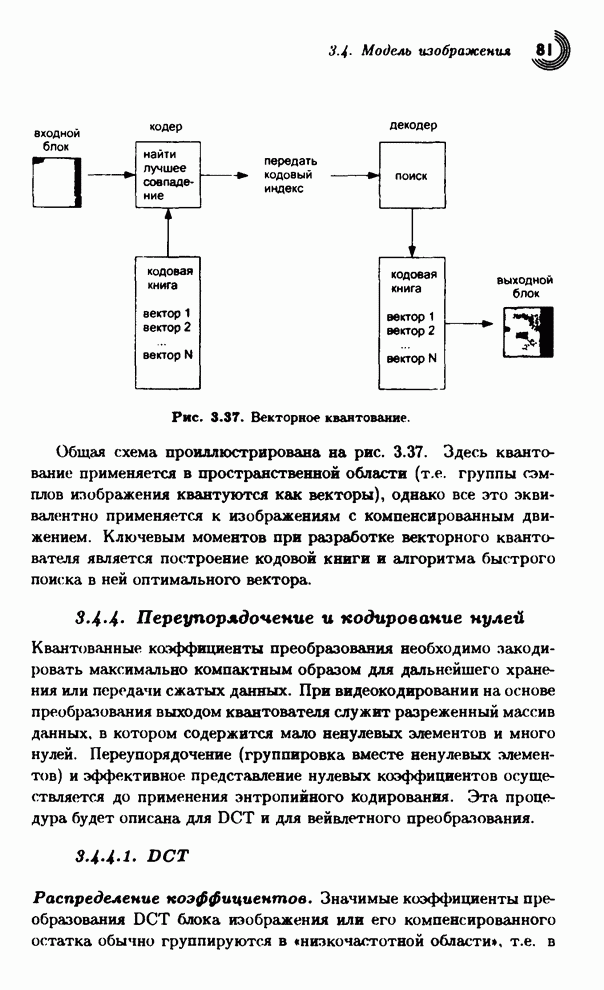
- 3.4. Модель изображения
- 3.4.1. Кодирование изображений с предсказанием
- 3.4.2. Кодирование преобразованием
- 3.4.2.1. Обзор
- 3.4.2.2. DCT
- 3.4.2.3. Вейвлеты
- 3.4.3. Квантование
- 3.4.4. Переупорядочение и кодирование нулей
- 3.4.4.1. DCT
- 3.4.4.2. Вейвлет
- 3.5. Энтропийный кодер
- 3.5.1. Коды с предсказанием
- 3.5.2. Коды переменной длины
- 3.5.2.1. Коды Хаффмана
- 3.5.2.2. Кодирование Хаффмана с предварительными вычислениями
- 3.5.2.3. Другие коды переменной длины
- 3.5.3. Арифметическое кодирование
- 3.5.3.1. Арифметическое кодирование с контекстом
- 3.6. Гибридная модель DPCM/DCT видеокодека
- 3.6.1. Пример работы кодека
- 3.7. Выводы
- 3.8. Полезные ссылки
- ГЛАВА 4 СТАНДАРТЫ MPEG-4 и Н.264
- 4.1. Введение
- 4.2. Развитие стандартов
- 4.2.1. ISO MPEG
- 4.2.2. ITU-T VCEG
- 4.2.3. JVT
- 4.2.4. История развития
- 4.2.5. Решение о содержании стандарта
- 4.3. Использование стандарта
- 4.3.1. Что кодирует стандарт
- 4.3.2. «Декодирование» стандартов
- 4.3.3. Подчинение стандартам
- 4.4. Обзор MPEG-4 Visual (Part2)
- 4.5. Обзор Н.264 (MPEG-4 Part 10)
- 4.6. Сравнение MPEG-4 Visual и Н.264
- 4.7. Родственные стандарты
- 4.7.1. JPEG и JPEG2000
- 4.7.2. MPEG-1 и MPEG-2
- 4.7.3. Н.261 и Н.263
- 4.7.4. Другие части MPEG-4
- 4.8. Выводы
- 4.9. Полезные ссылки
- ГЛАВА 5. MPEG-4 VISUAL
- 5.1. Введение
- 5.2. Обзор MPEG-4 Visual
- 5.2.1. Основные особенности
- 5.2.2. Инструменты, объекты, профили и уровни
- 5.2.3. Видеообъекты
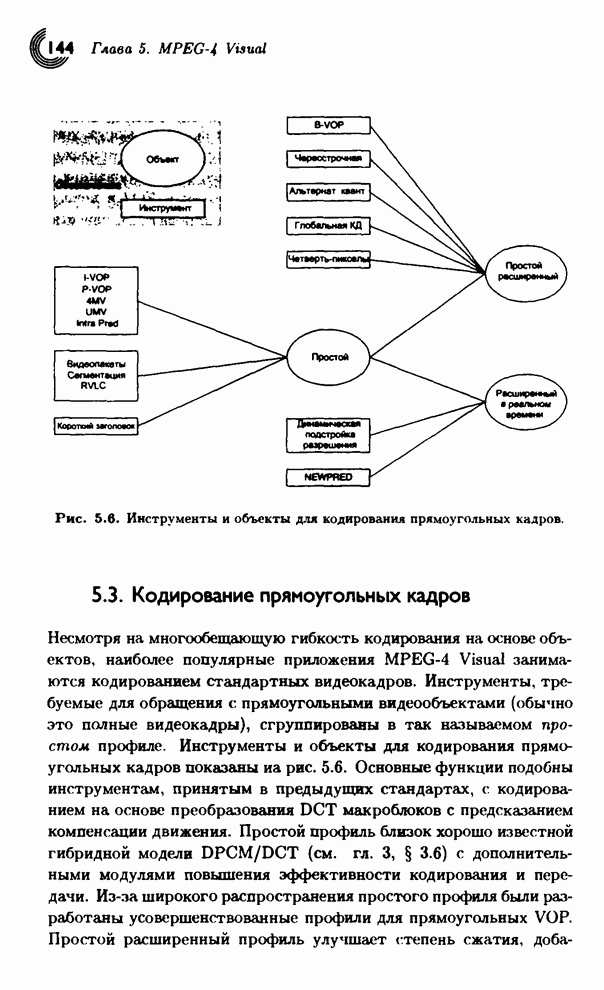
- 5.3. Кодирование прямоугольных кадров
- 5.3.1. Входные и выходные видеоформаты
- 5.3.2. Простой профиль
- 5.3.2.1. Видеоядро для низкой битовой скорости
- 5.3.2.2. Вазовые инструменты кодирования
- 5.3.2.3. Инструменты эффективного кодирования
- 5.3.2.4. Инструменты эффективной передачи
- 5.3.3. Простой расширенный профиль
- 5.3.4. Простой расширенный профиль в реальном времени
- 5.4. Кодирование областей произвольной формы
- 5.4.1. Базовый профиль
- 5.4.1.1. Бинарное кодирование формы
- 5.4.1.2. Кодирование VOP произвольной формы с компенсацией движения
- 5.4.1.3. Кодирование текстуры граничных макроблоков
- 5.4.2. Основной профиль
- 5.4.2.1. Градуированное кодирование формы
- 5.4.2.2. Статическое кодирование «спрайтов»
- 5.4.3. Профиль повышенной степени сжатия
- 5.4.4. N-битовый профиль
- 5.5. Масштабируемое видеокодирование
- 5.5.1. Пространственное масштабирование
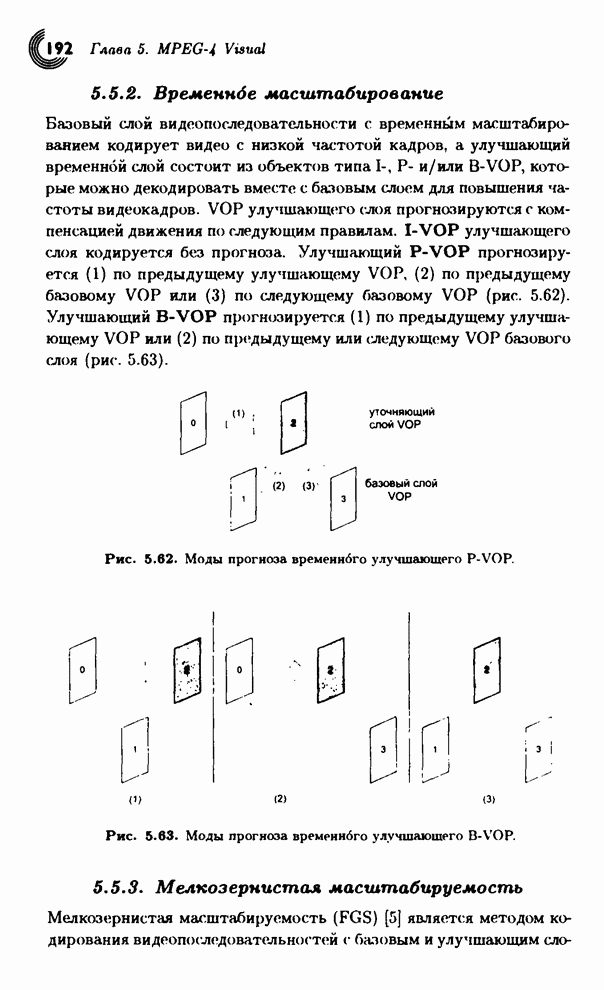
- 5.5.2. Временное масштабирование
- 5.5.3. Мелкозернистая масштабируемость
- 5.5.4. Простой масштабируемый профиль
- 5.5.5. Базовый масштабируемый профиль
- 5.5.6. Профиль мелкозернистой масштабируемости
- 5.6. Кодирование текстуры
- 5.6.1. Профиль масштабируемых текстур
- 5.6.2. Расширенный профиль масштабируемых текстур
- 5.7. Кодирование видео студийного качества
- 5.7.1. Простой студийный профиль
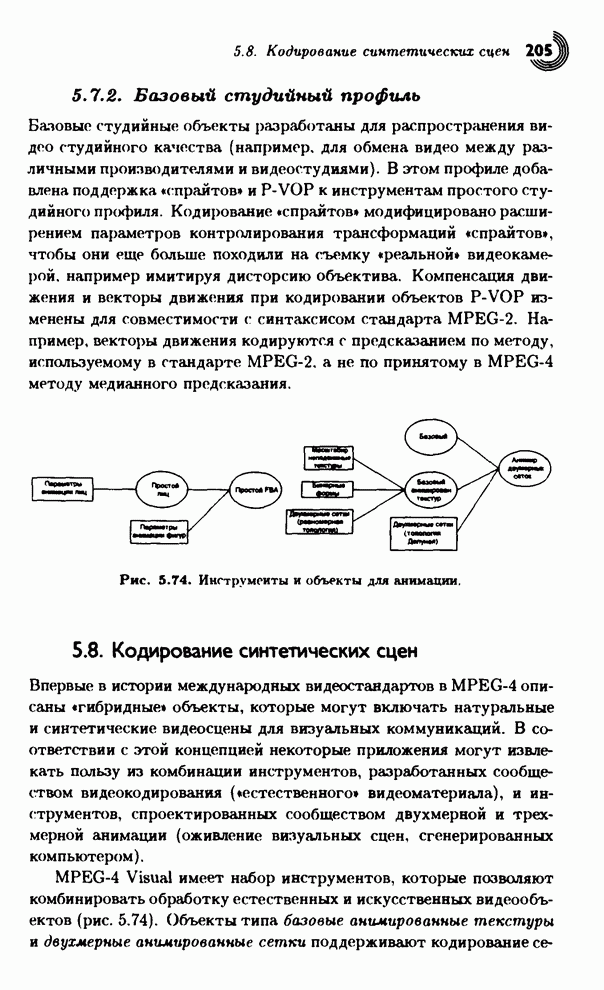
- 5.7.2. Базовый студийный профиль
- 5.8. Кодирование синтетических сцен
- 5.8.1. Анимированное сеточное кодирование
- 5.8.2. Анимация лиц и фигур
- 5.9. Выводы
- 5.10. Полезные ссылки
- ГЛАВА 6. H.264/MPEG-4 Part 10
- 6.1. Введение
- 6.2. Кодек Н.264
- 6.3. Структура Н.264
- 6.3.1. Профили и уровни
- 6.3.2. Видеоформат
- 6.3.3. Формат закодированных данных
- 6.3.4. Ссылочные снимки
- 6.3.5. Слои
- 6.3.6. Макроблоки
- 6.4. Базовый профиль
- 6.4.1. Обзор
- 6.4.2. Организация ссылочных снимков
- 6.4.3. Слои
- 6.4.4. Прогнозирование макроблоков
- 6.4.5. Прогнозирование в моде inter
- 6.4.5.1. Древовидная структура компенсации движения
- 6.4.5.2. Векторы движения
- 6.4.5.3. Предсказание векторов движения
- 6.4.6. Прогноз в моде intra
- 6.4.6.1. Моды прогноза блоков яркости 4х4
- 6.4.6.2. Моды прогноза макроблоков яркости 16х16
- 6.4.6.3. Моды прогноза макроблоков хроматичности 8×8
- 6.4.6.4. Индикация мод прогнозирования intra
- 6.4.7. Деблочный фильтр
- 6.4.8. Преобразование и квантование
- 6.4.8.1. Преобразование и квантование остаточных блоков 4х4 (0-15, 18-25)
- 6.4.9. Коэффициенты DC преобразования и квантования блоков яркости 4×4 (только для моды intra 16х16)
- 6.4.10. Коэффициенты DC преобразования и квантования блоков хроматичности размером 2×2
- 6.4.11. Полный процесс прямого и обратного преобразования и квантования
- 6.4.12. Переупорядочивание
- 6.4.13. Энтропийное кодирование
- 6.5. Основной профиль
- 6.5.1. В-слои
- 6.5.2. Взвешенный прогноз
- 6.5.3. Чересстрочная развертка
- 6.5.4. Контекстно-адаптивное арифметическое кодирование (CABАС)
- 6.6. Расширенный профиль
- 6.6.1. Слои SP и SI
- 6.6.2. Слои деления данных
- 6.7. Транспортный механизм Н.264
- 6.8. Выводы
- 6.9. Полезные ссылки
- ГЛАВА 7. ДИЗАЙН И ПРОИЗВОДИТЕЛЬНОСТЬ
- 7.1. Введение
- 7.2. Функциональный дизайн
- 7.2.1. Сегментация
- 7.2.2. Оценка движения
- 7.2.2.1. Оценка движения на основе блоков
- 7.2.2.2. Оценка движения на основе объектов
- 7.2.3. Преобразование DCT/IDCT
- 7.2.3.1. DCT 8×8
- 7.2.3.2. Преобразование DCT 4х4 в Н.264
- 7.2.3.3. Границы объектов
- 7.2.4. Вейвлетное преобразование
- 7.2.5. Квантование и деквантование
- 7.2.6. Энтропийное кодирование
- 7.3. Вход и выход
- 7.3.1. Сопряжение процессов
- 7.3.2. Предварительная обработка
- 7.3.3. Последующая обработка
- 7.4. Производительность
- 7.4.1. Критерии
- 7.4.2. Субъективная производительность
- 7.4.3. Соотношение скорость/искажение
- 7.4.4. Вычислительная производительность
- 7.4.5. Оптимизация по производительности
- 7.5. Контроль битовой скорости
- 7.6. Транспортировка и хранение
- 7.6.1. Механизмы транспортировки
- 7.6.2. Форматы файлов
- 7.6.3. Кодирование и транспортные выпуски
- 7.7. Выводы
- 7.8. Полезные ссылки
- ГЛАВА 8. ПРОДУКТЫ И ПЕРСПЕКТИВЫ
- 8.1. Введение
- 8.2. Приложения
- 8.3. Платформы
- 8.4. Выбор кодека
- 8.5. Коммерческие детали
- 8.6. Что в перспективе
- 8.7. Заключение
- Литература