| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3.4.4.2. Вейвлет
Распределение коэффициентов. На рис. 3.35 дано типичное распределение двухмерных вейвлетных коэффициентов. Значения многих коэффициентов, относящиеся к высокочастотной подполосе (внизу справа на рисунке), близки к нулю, и их можно проквантовать нулем без существенной потери качества изображения. Ненулевые коэффициенты формируют структуры изображения. Например, наклон скрипки проявляется в виде четкой горизонтальной структуры на горизонтальных и диагональных подполосах. Когда коэффициент в низкочастотной области не равен нулю, то с большой вероятностью коэффициенты в соответствующих позициях высокочастотных подполос также будут ненулевыми. Можно рассмотреть дерево ненулевых квантованных коэффициентов с корнем в низкочастотной области. На рис. 3.43 показана эта концепция. Единственный коэффициент в области LL первого слоя имеет по одному соответствующему коэффициенту во всех других областях данного слоя (т.е. все четыре коэффициента соответствуют одной и той же области исходного изображения). Позиция коэффициента слоя 1 отображается на 4 соответствующие дочерние позиции каждой подполосы слоя 2 (напомним, что подполоса слоя 2 имеет двойное разрешение по горизонтали и вертикали по сравнению со слоем 1).

Рис. 3.43. Вейвлетный коэффициент и его «потомки».
Кодирование нулевого дерева. Желательно кодировать ненулевые вейвлетные коэффициенты компактным образом до применения энтропийного кодера [6]. Эффективный метод решения этой задачи состоит в кодировании каждого дерева ненулевых коэффициентов начиная с самого низкого (корневого) уровня разложения. Кодируется коэффициент на самом нижним уровнем, за ним следует коэффициент дочерней позиции более высокого уровня и т.д. Процесс кодирования продолжается до тех пор, пока дерево не достигнет нулевого коэффициента. Коэффициенты на следующих уровнях, скорее всего, также будут нулевыми, поэтому имеет смысл представлять их единственным кодом, который обозначает дерево из одних нулей (нулевое дерево). Декодер реконструирует карту коэффициентов начиная с корня каждого дерева. Сначала декодируются и восстанавливаются ненулевые коэффициенты, а по достижении кода нулевого дерева все оставшиеся «потомки» полагаются равными нулю. Это построение лежит в основе метода вложенных нулевых деревьев (EZW, Embedded Zero Tree) кодирования вейвлетных коэффициентов. В процесс кодирования включена дополнительная возможность, когда за нулевым коэффициентом следует нулевое дерево (как раньше) или ненулевой дочерний коэффициент. Во втором случае происходит достаточно редко, однако качество восстанавливаемого изображения несколько улучшится, если алгоритм будет обслуживать такие возможности.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Пролог
- Предисловие
- Об авторе
- Глава 1. Введение
- 1.1. Сцена
- 1.2. Видеосжатие
- 1.3. MPEG-4 и Н.264
- 1.4. Об этой книге
- 1.5. Полезные ссылки
- ГЛАВА 2. ФОРМАТЫ ВИДЕО И ЕГО КАЧЕСТВО
- 2.1. Введение
- 2.2. Естественные видеосцены
- 2.3. Захват кадра
- 2.3.1. Пространственное сэмплирование
- 2.3.2. Временное сэмплирование
- 2.3.3. Кадры и полукадры
- 2.4. Цветовые пространства
- 2.4.1. RGB
- 2.4.2. YCbCr
- 2.4.3. Форматы сэмплирования YCbCr
- 2.5. Видеоформаты
- 2.6. Качество
- 2.6.1. Субъективное измерение качества
- 2.6.1.1. Факторы субъективного восприятия
- 2.6.1.2. ITU-R 500
- 2.6.2. Объективное измерение качества
- 2.7. Выводы
- 2.8. Полезные ссылки
- ГЛАВА 3. ОСНОВЫ ВИДЕОКОДИРОВАНИЯ
- 3.1. Введение
- 3.2. Видеокодек
- 3.3. Временная модель
- 3.3.1. Прогноз по предыдущему видеокадру
- 3.3.2. Изменения вследствие движения
- 3.3.3. Оценка и компенсация движения на основе блоков
- 3.3.4. Прогноз макроблока с компенсированным движением
- 3.3.5. Размер блока компенсации движения
- 3.3.6. Подпиксельная компенсация движения
- 3.3.7. Компенсация движения на основе областей
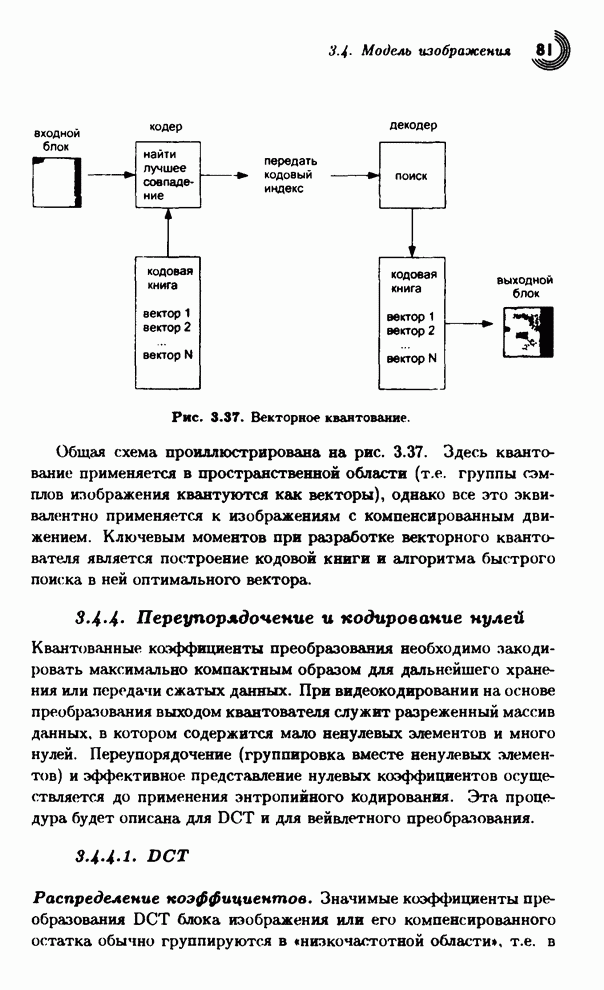
- 3.4. Модель изображения
- 3.4.1. Кодирование изображений с предсказанием
- 3.4.2. Кодирование преобразованием
- 3.4.2.1. Обзор
- 3.4.2.2. DCT
- 3.4.2.3. Вейвлеты
- 3.4.3. Квантование
- 3.4.4. Переупорядочение и кодирование нулей
- 3.4.4.1. DCT
- 3.4.4.2. Вейвлет
- 3.5. Энтропийный кодер
- 3.5.1. Коды с предсказанием
- 3.5.2. Коды переменной длины
- 3.5.2.1. Коды Хаффмана
- 3.5.2.2. Кодирование Хаффмана с предварительными вычислениями
- 3.5.2.3. Другие коды переменной длины
- 3.5.3. Арифметическое кодирование
- 3.5.3.1. Арифметическое кодирование с контекстом
- 3.6. Гибридная модель DPCM/DCT видеокодека
- 3.6.1. Пример работы кодека
- 3.7. Выводы
- 3.8. Полезные ссылки
- ГЛАВА 4 СТАНДАРТЫ MPEG-4 и Н.264
- 4.1. Введение
- 4.2. Развитие стандартов
- 4.2.1. ISO MPEG
- 4.2.2. ITU-T VCEG
- 4.2.3. JVT
- 4.2.4. История развития
- 4.2.5. Решение о содержании стандарта
- 4.3. Использование стандарта
- 4.3.1. Что кодирует стандарт
- 4.3.2. «Декодирование» стандартов
- 4.3.3. Подчинение стандартам
- 4.4. Обзор MPEG-4 Visual (Part2)
- 4.5. Обзор Н.264 (MPEG-4 Part 10)
- 4.6. Сравнение MPEG-4 Visual и Н.264
- 4.7. Родственные стандарты
- 4.7.1. JPEG и JPEG2000
- 4.7.2. MPEG-1 и MPEG-2
- 4.7.3. Н.261 и Н.263
- 4.7.4. Другие части MPEG-4
- 4.8. Выводы
- 4.9. Полезные ссылки
- ГЛАВА 5. MPEG-4 VISUAL
- 5.1. Введение
- 5.2. Обзор MPEG-4 Visual
- 5.2.1. Основные особенности
- 5.2.2. Инструменты, объекты, профили и уровни
- 5.2.3. Видеообъекты
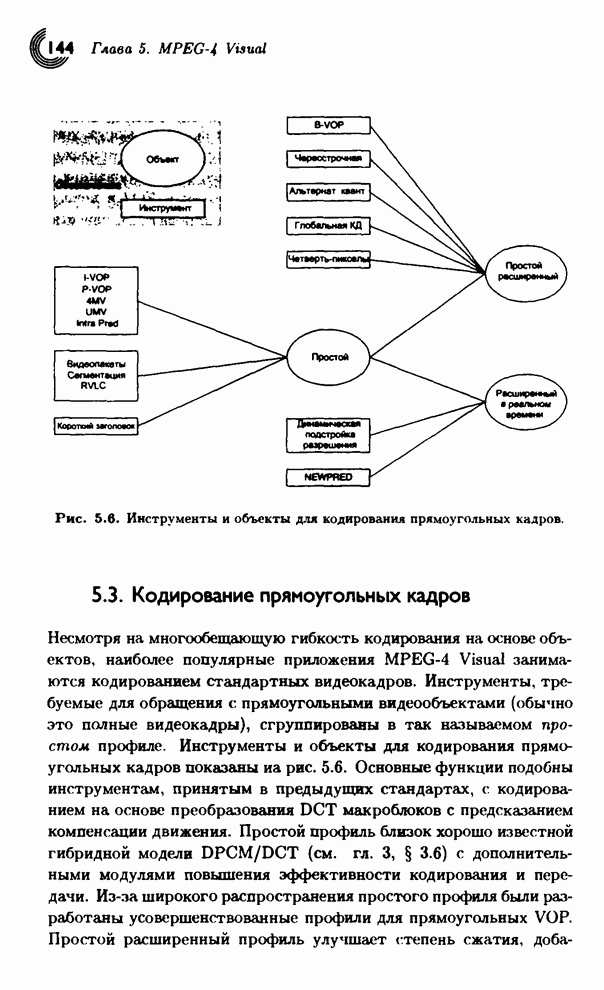
- 5.3. Кодирование прямоугольных кадров
- 5.3.1. Входные и выходные видеоформаты
- 5.3.2. Простой профиль
- 5.3.2.1. Видеоядро для низкой битовой скорости
- 5.3.2.2. Вазовые инструменты кодирования
- 5.3.2.3. Инструменты эффективного кодирования
- 5.3.2.4. Инструменты эффективной передачи
- 5.3.3. Простой расширенный профиль
- 5.3.4. Простой расширенный профиль в реальном времени
- 5.4. Кодирование областей произвольной формы
- 5.4.1. Базовый профиль
- 5.4.1.1. Бинарное кодирование формы
- 5.4.1.2. Кодирование VOP произвольной формы с компенсацией движения
- 5.4.1.3. Кодирование текстуры граничных макроблоков
- 5.4.2. Основной профиль
- 5.4.2.1. Градуированное кодирование формы
- 5.4.2.2. Статическое кодирование «спрайтов»
- 5.4.3. Профиль повышенной степени сжатия
- 5.4.4. N-битовый профиль
- 5.5. Масштабируемое видеокодирование
- 5.5.1. Пространственное масштабирование
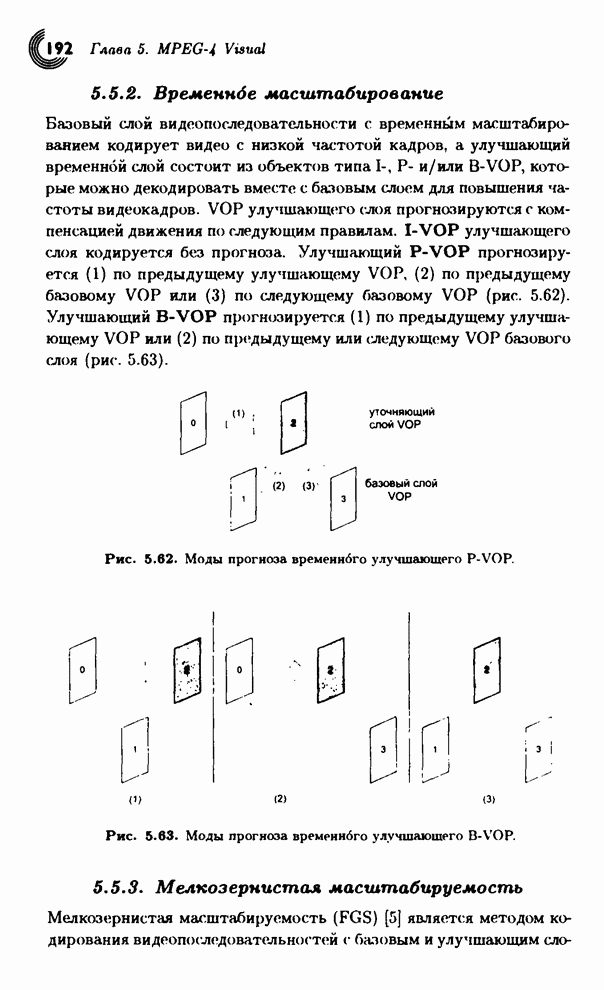
- 5.5.2. Временное масштабирование
- 5.5.3. Мелкозернистая масштабируемость
- 5.5.4. Простой масштабируемый профиль
- 5.5.5. Базовый масштабируемый профиль
- 5.5.6. Профиль мелкозернистой масштабируемости
- 5.6. Кодирование текстуры
- 5.6.1. Профиль масштабируемых текстур
- 5.6.2. Расширенный профиль масштабируемых текстур
- 5.7. Кодирование видео студийного качества
- 5.7.1. Простой студийный профиль
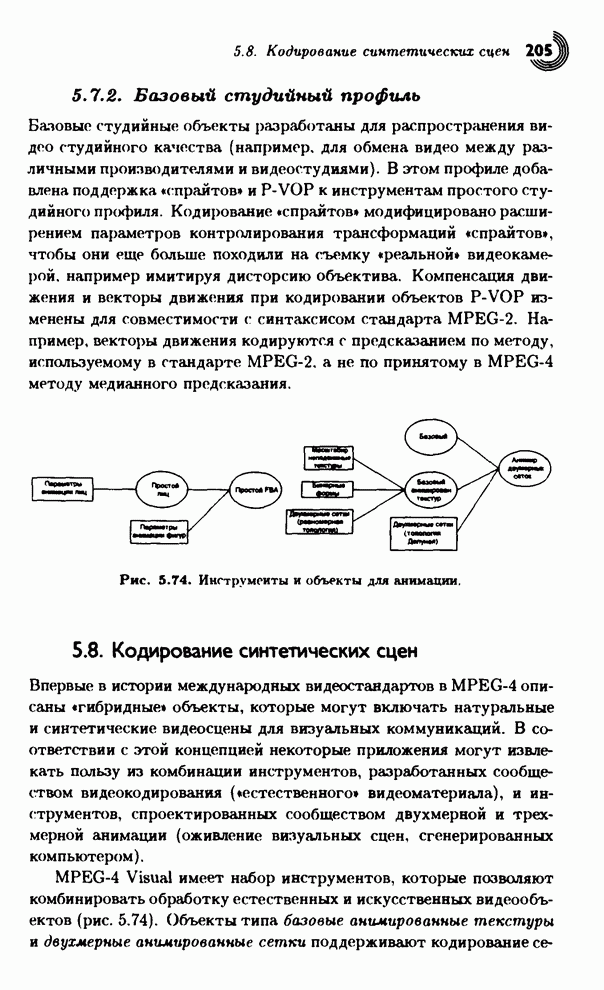
- 5.7.2. Базовый студийный профиль
- 5.8. Кодирование синтетических сцен
- 5.8.1. Анимированное сеточное кодирование
- 5.8.2. Анимация лиц и фигур
- 5.9. Выводы
- 5.10. Полезные ссылки
- ГЛАВА 6. H.264/MPEG-4 Part 10
- 6.1. Введение
- 6.2. Кодек Н.264
- 6.3. Структура Н.264
- 6.3.1. Профили и уровни
- 6.3.2. Видеоформат
- 6.3.3. Формат закодированных данных
- 6.3.4. Ссылочные снимки
- 6.3.5. Слои
- 6.3.6. Макроблоки
- 6.4. Базовый профиль
- 6.4.1. Обзор
- 6.4.2. Организация ссылочных снимков
- 6.4.3. Слои
- 6.4.4. Прогнозирование макроблоков
- 6.4.5. Прогнозирование в моде inter
- 6.4.5.1. Древовидная структура компенсации движения
- 6.4.5.2. Векторы движения
- 6.4.5.3. Предсказание векторов движения
- 6.4.6. Прогноз в моде intra
- 6.4.6.1. Моды прогноза блоков яркости 4х4
- 6.4.6.2. Моды прогноза макроблоков яркости 16х16
- 6.4.6.3. Моды прогноза макроблоков хроматичности 8×8
- 6.4.6.4. Индикация мод прогнозирования intra
- 6.4.7. Деблочный фильтр
- 6.4.8. Преобразование и квантование
- 6.4.8.1. Преобразование и квантование остаточных блоков 4х4 (0-15, 18-25)
- 6.4.9. Коэффициенты DC преобразования и квантования блоков яркости 4×4 (только для моды intra 16х16)
- 6.4.10. Коэффициенты DC преобразования и квантования блоков хроматичности размером 2×2
- 6.4.11. Полный процесс прямого и обратного преобразования и квантования
- 6.4.12. Переупорядочивание
- 6.4.13. Энтропийное кодирование
- 6.5. Основной профиль
- 6.5.1. В-слои
- 6.5.2. Взвешенный прогноз
- 6.5.3. Чересстрочная развертка
- 6.5.4. Контекстно-адаптивное арифметическое кодирование (CABАС)
- 6.6. Расширенный профиль
- 6.6.1. Слои SP и SI
- 6.6.2. Слои деления данных
- 6.7. Транспортный механизм Н.264
- 6.8. Выводы
- 6.9. Полезные ссылки
- ГЛАВА 7. ДИЗАЙН И ПРОИЗВОДИТЕЛЬНОСТЬ
- 7.1. Введение
- 7.2. Функциональный дизайн
- 7.2.1. Сегментация
- 7.2.2. Оценка движения
- 7.2.2.1. Оценка движения на основе блоков
- 7.2.2.2. Оценка движения на основе объектов
- 7.2.3. Преобразование DCT/IDCT
- 7.2.3.1. DCT 8×8
- 7.2.3.2. Преобразование DCT 4х4 в Н.264
- 7.2.3.3. Границы объектов
- 7.2.4. Вейвлетное преобразование
- 7.2.5. Квантование и деквантование
- 7.2.6. Энтропийное кодирование
- 7.3. Вход и выход
- 7.3.1. Сопряжение процессов
- 7.3.2. Предварительная обработка
- 7.3.3. Последующая обработка
- 7.4. Производительность
- 7.4.1. Критерии
- 7.4.2. Субъективная производительность
- 7.4.3. Соотношение скорость/искажение
- 7.4.4. Вычислительная производительность
- 7.4.5. Оптимизация по производительности
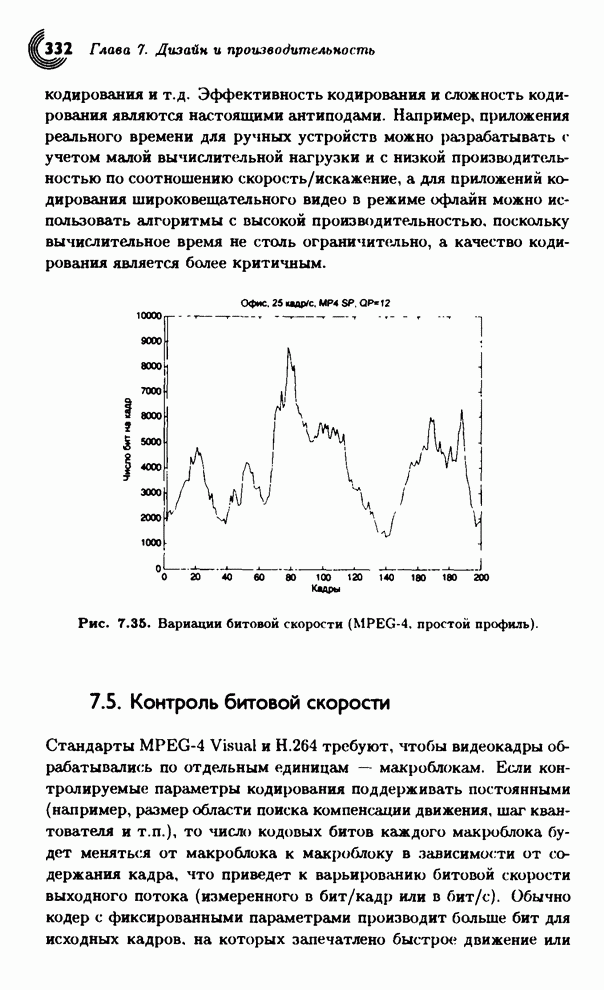
- 7.5. Контроль битовой скорости
- 7.6. Транспортировка и хранение
- 7.6.1. Механизмы транспортировки
- 7.6.2. Форматы файлов
- 7.6.3. Кодирование и транспортные выпуски
- 7.7. Выводы
- 7.8. Полезные ссылки
- ГЛАВА 8. ПРОДУКТЫ И ПЕРСПЕКТИВЫ
- 8.1. Введение
- 8.2. Приложения
- 8.3. Платформы
- 8.4. Выбор кодека
- 8.5. Коммерческие детали
- 8.6. Что в перспективе
- 8.7. Заключение
- Литература