| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4.3. Квантование
Квантователь
отображает числовой сигнал с областью значений ![]() в квантованный сигнал области
в квантованный сигнал области ![]() с уменьшенным числом значений.
Это дает возможность представить квантованные величины с меньшим числом бит по
сравнению с исходными неквантованными величинами. Скалярный квантователь
отображает один входной сэмпл в одно квантованное значение на выходе, а
векторный квантователь отображает группу сэмплов на входе (вектор) в
группу квантованных величин.
с уменьшенным числом значений.
Это дает возможность представить квантованные величины с меньшим числом бит по
сравнению с исходными неквантованными величинами. Скалярный квантователь
отображает один входной сэмпл в одно квантованное значение на выходе, а
векторный квантователь отображает группу сэмплов на входе (вектор) в
группу квантованных величин.
3.4.3.1. Скалярный квантователь
Простейшим примером скалярного квантователя может служить метод округления дробного числа до ближайшего целого, т.е. отображение из R в Z. Это процесс с частичной потерей информации (он необратим), так как невозможно установить точное значение исходного дробного числа по округленному целому числу.
Более общий метод равномерно квантования можно представить в виде формулы:
 (3.6)
(3.6)
где ![]() - это шаг квантования. Уровни
квантованных выходов расположены на одинаковых расстояниях
- это шаг квантования. Уровни
квантованных выходов расположены на одинаковых расстояниях ![]() друг от друга (это
проиллюстрировано в следующем примере).
друг от друга (это
проиллюстрировано в следующем примере).
|
Пример Квантованные
величины ) для сэмплов
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Рис. З.З6. Скалярные квантователи: линейный и нелинейный с нулевой мертвой зоной.
Рисунок 3.36 дает два примера скалярных квантователей: линейный квантователь (с линейным отображением входных значений в выходные) и нелинейный квантователь, в котором имеется «мертвая зона» вокруг нуля (здесь малые входные числа отображаются в нуль). В кодеке видеосжатия операция квантования состоит из двух частей: прямой квантователь FQ (Forward Quantiser) кодера и «обратный квантователь» IQ (Inverse Quantiser) декодера (на самом деле, квантование необратимо, поэтому правильнее говорить о «масштабировании» и «обратном масштабировании»). Критическим параметром служит размер шага квантования, т.е. расстояние между последовательными уровнями квантования. Если шаг квантования велик, то область значений квантования мала и ее можно эффективно представить (сильно сжать) при передаче, однако деквантованные величины будут грубыми приближениями исходных сигналов. Если шаг квантования мал, то деквантованные сигналы будут больше походить на исходные, но при этом потребуется больший размер области для квантованных величин, что понизит эффективность сжатия.
Квантование можно использовать для понижения точности изображения после применения кодирующего преобразования, например DCT или вейвлетного преобразования. Тем самым будет удалена часть незначимых величин и коэффициентов, близких к нулю. Прямой квантователь изображения или видео разработан так что он обнуляет несущественные значения коэффициентов, оставляя малое число существенных ненулевых коэффициентов. Типичным выходом прямого квантователя служит «разреженный» массив квантованных коэффициентов, в котором содержится много нулей.
3.4.3.2. Векторное квантование
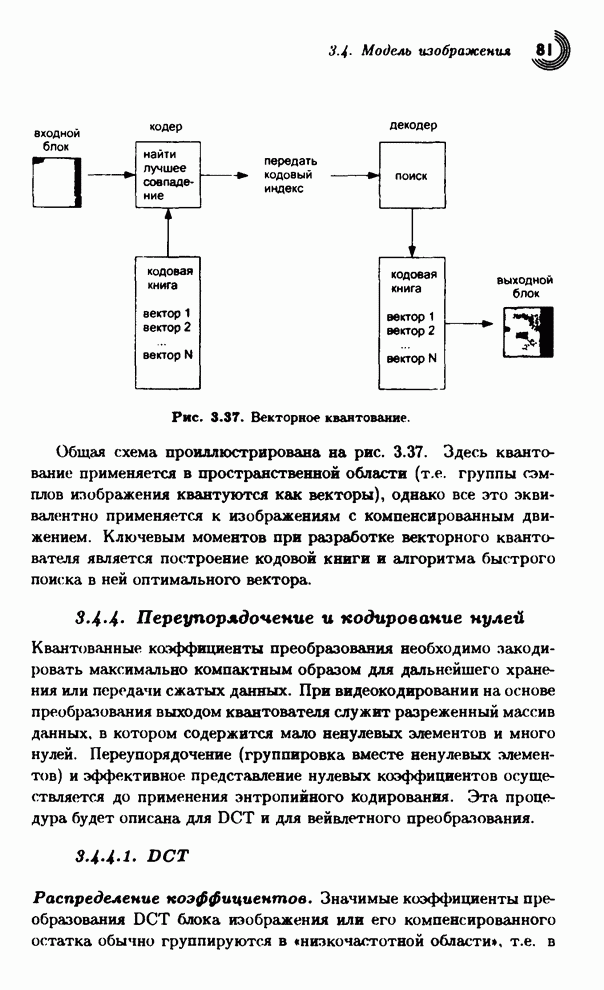
Векторный квантователь отображает множество входных данных (например, блок сэмплов) в один элемент (кодовое слово), а декодер каждому кодовому слову сопоставляет некоторое приближение к исходному множеству данных (вектору). Множество векторов хранится кодером и декодером в специальной кодовой книге. Типичная схема применения векторного квантования при сжатии изображений [5] состоит в следующем.
1. Разделить
исходное изображения на области (например, блоки пикселов размером ![]() ).
).
2. Выбрать в кодовой книге вектор, максимально близкий к текущей области.
3. Переслать декодеру индекс, идентифицирующий выбранный вектор.
4. На стороне декодера реконструировать приближенную копию области, используя выбранный вектор.

Рис. 3.37. Векторное квантование.
Общая схема проиллюстрирована на рис. 3.37. Здесь квантование применяется в пространственной области (т.е. группы сэмплов изображения квантуются как векторы), однако все это эквивалентно применяется к изображениям с компенсированным движением. Ключевым моментов при разработке векторного квантователя является построение кодовой книги и алгоритма быстрого поиска в ней оптимального вектора.
| << Предыдущий параграф | Следующий параграф >> |
- Пролог
- Предисловие
- Об авторе
- Глава 1. Введение
- 1.1. Сцена
- 1.2. Видеосжатие
- 1.3. MPEG-4 и Н.264
- 1.4. Об этой книге
- 1.5. Полезные ссылки
- ГЛАВА 2. ФОРМАТЫ ВИДЕО И ЕГО КАЧЕСТВО
- 2.1. Введение
- 2.2. Естественные видеосцены
- 2.3. Захват кадра
- 2.3.1. Пространственное сэмплирование
- 2.3.2. Временное сэмплирование
- 2.3.3. Кадры и полукадры
- 2.4. Цветовые пространства
- 2.4.1. RGB
- 2.4.2. YCbCr
- 2.4.3. Форматы сэмплирования YCbCr
- 2.5. Видеоформаты
- 2.6. Качество
- 2.6.1. Субъективное измерение качества
- 2.6.1.1. Факторы субъективного восприятия
- 2.6.1.2. ITU-R 500
- 2.6.2. Объективное измерение качества
- 2.7. Выводы
- 2.8. Полезные ссылки
- ГЛАВА 3. ОСНОВЫ ВИДЕОКОДИРОВАНИЯ
- 3.1. Введение
- 3.2. Видеокодек
- 3.3. Временная модель
- 3.3.1. Прогноз по предыдущему видеокадру
- 3.3.2. Изменения вследствие движения
- 3.3.3. Оценка и компенсация движения на основе блоков
- 3.3.4. Прогноз макроблока с компенсированным движением
- 3.3.5. Размер блока компенсации движения
- 3.3.6. Подпиксельная компенсация движения
- 3.3.7. Компенсация движения на основе областей
- 3.4. Модель изображения
- 3.4.1. Кодирование изображений с предсказанием
- 3.4.2. Кодирование преобразованием
- 3.4.2.1. Обзор
- 3.4.2.2. DCT
- 3.4.2.3. Вейвлеты
- 3.4.3. Квантование
- 3.4.4. Переупорядочение и кодирование нулей
- 3.4.4.1. DCT
- 3.4.4.2. Вейвлет
- 3.5. Энтропийный кодер
- 3.5.1. Коды с предсказанием
- 3.5.2. Коды переменной длины
- 3.5.2.1. Коды Хаффмана
- 3.5.2.2. Кодирование Хаффмана с предварительными вычислениями
- 3.5.2.3. Другие коды переменной длины
- 3.5.3. Арифметическое кодирование
- 3.5.3.1. Арифметическое кодирование с контекстом
- 3.6. Гибридная модель DPCM/DCT видеокодека
- 3.6.1. Пример работы кодека
- 3.7. Выводы
- 3.8. Полезные ссылки
- ГЛАВА 4 СТАНДАРТЫ MPEG-4 и Н.264
- 4.1. Введение
- 4.2. Развитие стандартов
- 4.2.1. ISO MPEG
- 4.2.2. ITU-T VCEG
- 4.2.3. JVT
- 4.2.4. История развития
- 4.2.5. Решение о содержании стандарта
- 4.3. Использование стандарта
- 4.3.1. Что кодирует стандарт
- 4.3.2. «Декодирование» стандартов
- 4.3.3. Подчинение стандартам
- 4.4. Обзор MPEG-4 Visual (Part2)
- 4.5. Обзор Н.264 (MPEG-4 Part 10)
- 4.6. Сравнение MPEG-4 Visual и Н.264
- 4.7. Родственные стандарты
- 4.7.1. JPEG и JPEG2000
- 4.7.2. MPEG-1 и MPEG-2
- 4.7.3. Н.261 и Н.263
- 4.7.4. Другие части MPEG-4
- 4.8. Выводы
- 4.9. Полезные ссылки
- ГЛАВА 5. MPEG-4 VISUAL
- 5.1. Введение
- 5.2. Обзор MPEG-4 Visual
- 5.2.1. Основные особенности
- 5.2.2. Инструменты, объекты, профили и уровни
- 5.2.3. Видеообъекты
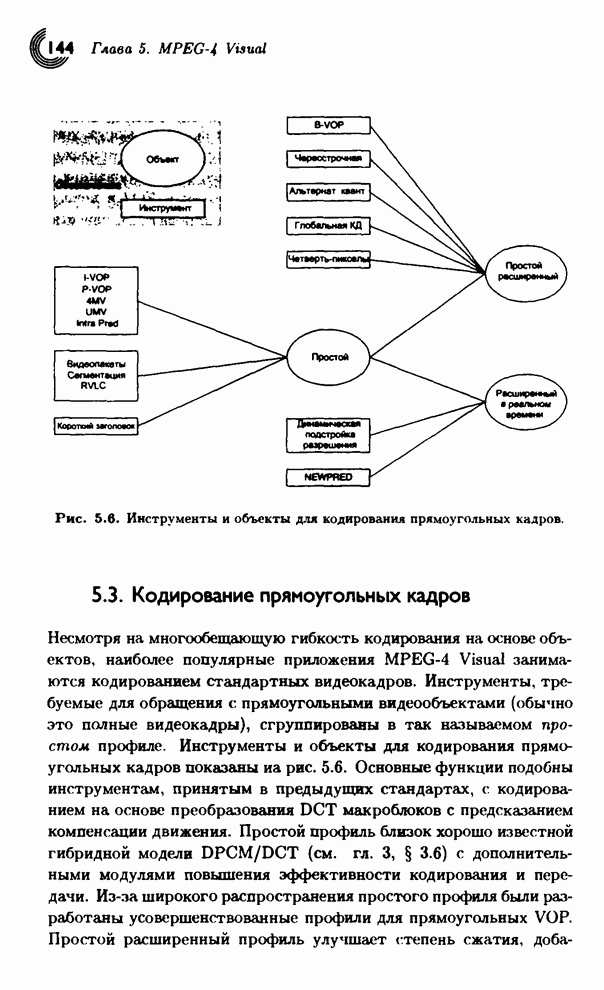
- 5.3. Кодирование прямоугольных кадров
- 5.3.1. Входные и выходные видеоформаты
- 5.3.2. Простой профиль
- 5.3.2.1. Видеоядро для низкой битовой скорости
- 5.3.2.2. Вазовые инструменты кодирования
- 5.3.2.3. Инструменты эффективного кодирования
- 5.3.2.4. Инструменты эффективной передачи
- 5.3.3. Простой расширенный профиль
- 5.3.4. Простой расширенный профиль в реальном времени
- 5.4. Кодирование областей произвольной формы
- 5.4.1. Базовый профиль
- 5.4.1.1. Бинарное кодирование формы
- 5.4.1.2. Кодирование VOP произвольной формы с компенсацией движения
- 5.4.1.3. Кодирование текстуры граничных макроблоков
- 5.4.2. Основной профиль
- 5.4.2.1. Градуированное кодирование формы
- 5.4.2.2. Статическое кодирование «спрайтов»
- 5.4.3. Профиль повышенной степени сжатия
- 5.4.4. N-битовый профиль
- 5.5. Масштабируемое видеокодирование
- 5.5.1. Пространственное масштабирование
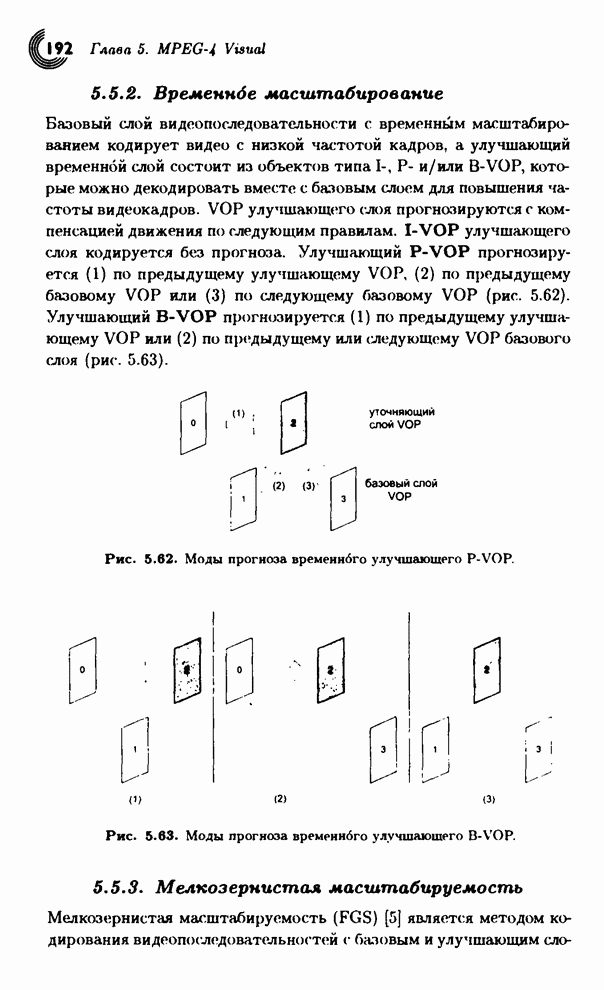
- 5.5.2. Временное масштабирование
- 5.5.3. Мелкозернистая масштабируемость
- 5.5.4. Простой масштабируемый профиль
- 5.5.5. Базовый масштабируемый профиль
- 5.5.6. Профиль мелкозернистой масштабируемости
- 5.6. Кодирование текстуры
- 5.6.1. Профиль масштабируемых текстур
- 5.6.2. Расширенный профиль масштабируемых текстур
- 5.7. Кодирование видео студийного качества
- 5.7.1. Простой студийный профиль
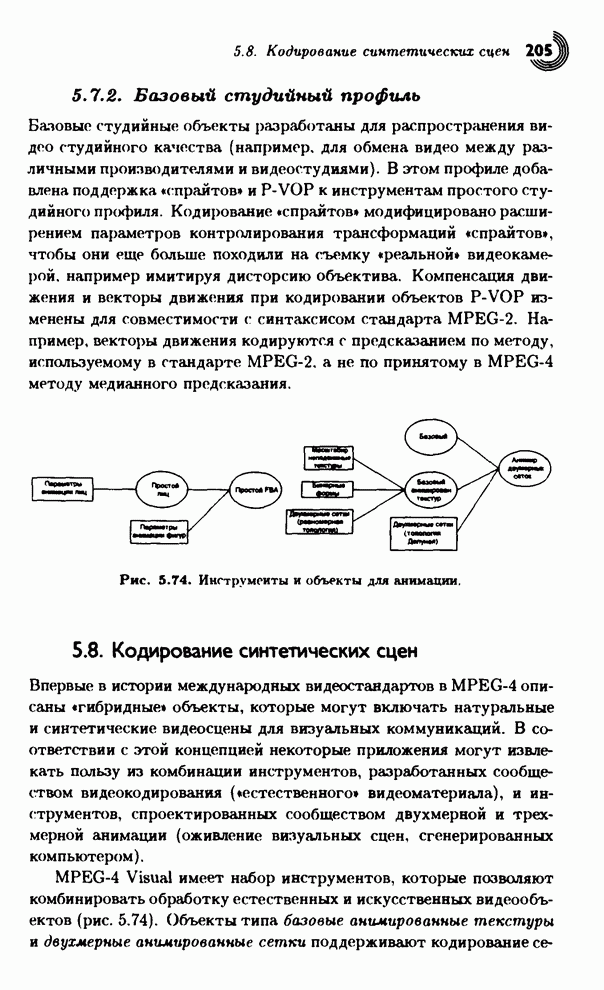
- 5.7.2. Базовый студийный профиль
- 5.8. Кодирование синтетических сцен
- 5.8.1. Анимированное сеточное кодирование
- 5.8.2. Анимация лиц и фигур
- 5.9. Выводы
- 5.10. Полезные ссылки
- ГЛАВА 6. H.264/MPEG-4 Part 10
- 6.1. Введение
- 6.2. Кодек Н.264
- 6.3. Структура Н.264
- 6.3.1. Профили и уровни
- 6.3.2. Видеоформат
- 6.3.3. Формат закодированных данных
- 6.3.4. Ссылочные снимки
- 6.3.5. Слои
- 6.3.6. Макроблоки
- 6.4. Базовый профиль
- 6.4.1. Обзор
- 6.4.2. Организация ссылочных снимков
- 6.4.3. Слои
- 6.4.4. Прогнозирование макроблоков
- 6.4.5. Прогнозирование в моде inter
- 6.4.5.1. Древовидная структура компенсации движения
- 6.4.5.2. Векторы движения
- 6.4.5.3. Предсказание векторов движения
- 6.4.6. Прогноз в моде intra
- 6.4.6.1. Моды прогноза блоков яркости 4х4
- 6.4.6.2. Моды прогноза макроблоков яркости 16х16
- 6.4.6.3. Моды прогноза макроблоков хроматичности 8×8
- 6.4.6.4. Индикация мод прогнозирования intra
- 6.4.7. Деблочный фильтр
- 6.4.8. Преобразование и квантование
- 6.4.8.1. Преобразование и квантование остаточных блоков 4х4 (0-15, 18-25)
- 6.4.9. Коэффициенты DC преобразования и квантования блоков яркости 4×4 (только для моды intra 16х16)
- 6.4.10. Коэффициенты DC преобразования и квантования блоков хроматичности размером 2×2
- 6.4.11. Полный процесс прямого и обратного преобразования и квантования
- 6.4.12. Переупорядочивание
- 6.4.13. Энтропийное кодирование
- 6.5. Основной профиль
- 6.5.1. В-слои
- 6.5.2. Взвешенный прогноз
- 6.5.3. Чересстрочная развертка
- 6.5.4. Контекстно-адаптивное арифметическое кодирование (CABАС)
- 6.6. Расширенный профиль
- 6.6.1. Слои SP и SI
- 6.6.2. Слои деления данных
- 6.7. Транспортный механизм Н.264
- 6.8. Выводы
- 6.9. Полезные ссылки
- ГЛАВА 7. ДИЗАЙН И ПРОИЗВОДИТЕЛЬНОСТЬ
- 7.1. Введение
- 7.2. Функциональный дизайн
- 7.2.1. Сегментация
- 7.2.2. Оценка движения
- 7.2.2.1. Оценка движения на основе блоков
- 7.2.2.2. Оценка движения на основе объектов
- 7.2.3. Преобразование DCT/IDCT
- 7.2.3.1. DCT 8×8
- 7.2.3.2. Преобразование DCT 4х4 в Н.264
- 7.2.3.3. Границы объектов
- 7.2.4. Вейвлетное преобразование
- 7.2.5. Квантование и деквантование
- 7.2.6. Энтропийное кодирование
- 7.3. Вход и выход
- 7.3.1. Сопряжение процессов
- 7.3.2. Предварительная обработка
- 7.3.3. Последующая обработка
- 7.4. Производительность
- 7.4.1. Критерии
- 7.4.2. Субъективная производительность
- 7.4.3. Соотношение скорость/искажение
- 7.4.4. Вычислительная производительность
- 7.4.5. Оптимизация по производительности
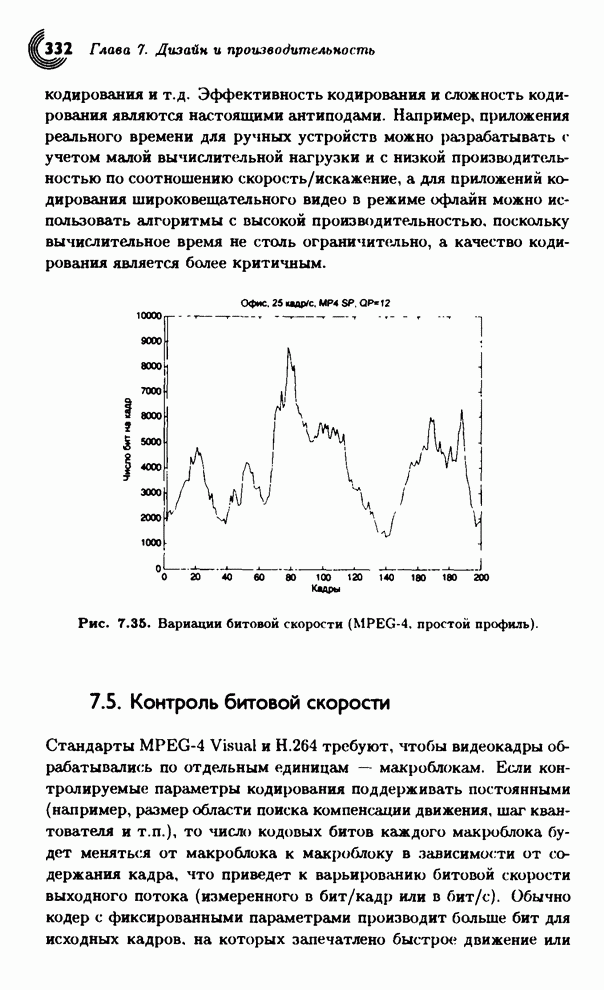
- 7.5. Контроль битовой скорости
- 7.6. Транспортировка и хранение
- 7.6.1. Механизмы транспортировки
- 7.6.2. Форматы файлов
- 7.6.3. Кодирование и транспортные выпуски
- 7.7. Выводы
- 7.8. Полезные ссылки
- ГЛАВА 8. ПРОДУКТЫ И ПЕРСПЕКТИВЫ
- 8.1. Введение
- 8.2. Приложения
- 8.3. Платформы
- 8.4. Выбор кодека
- 8.5. Коммерческие детали
- 8.6. Что в перспективе
- 8.7. Заключение
- Литература