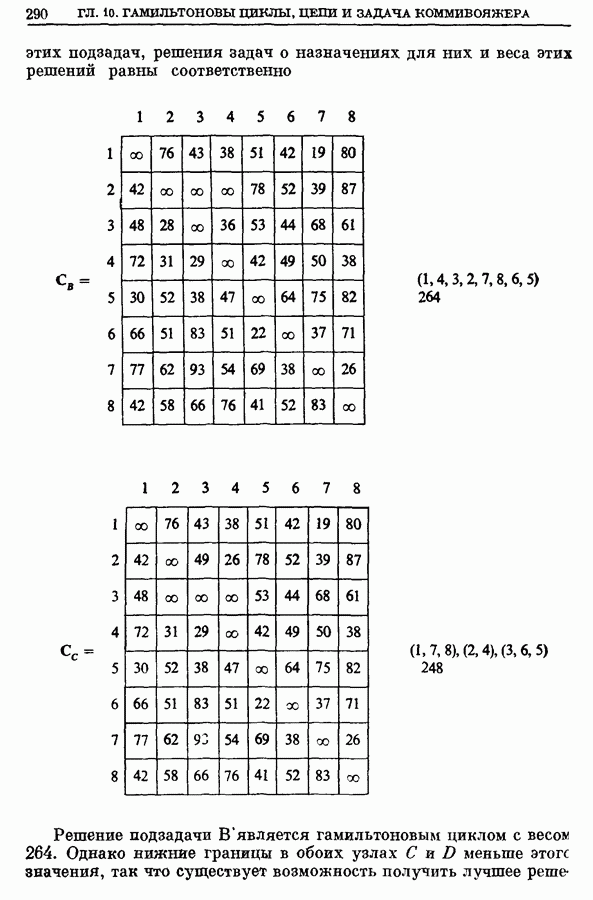
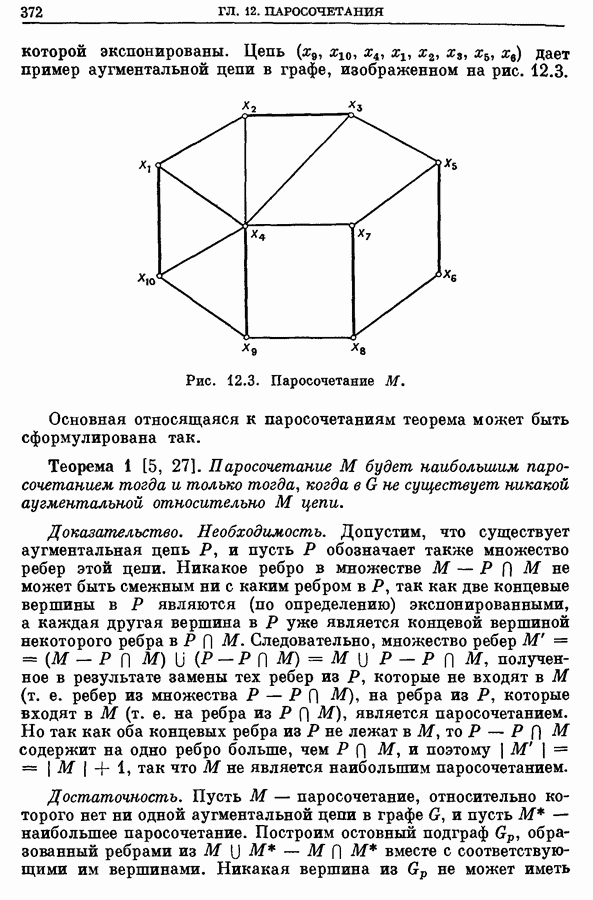
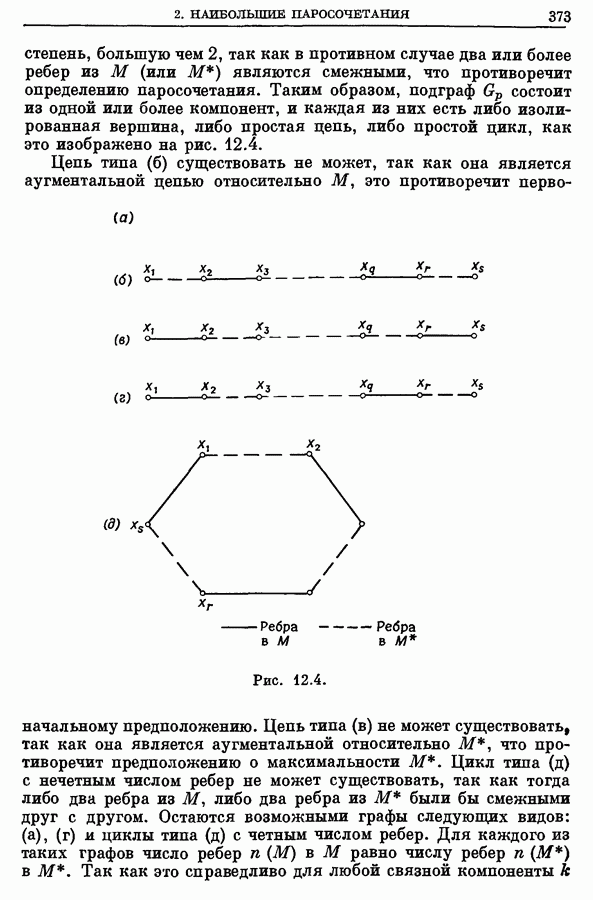
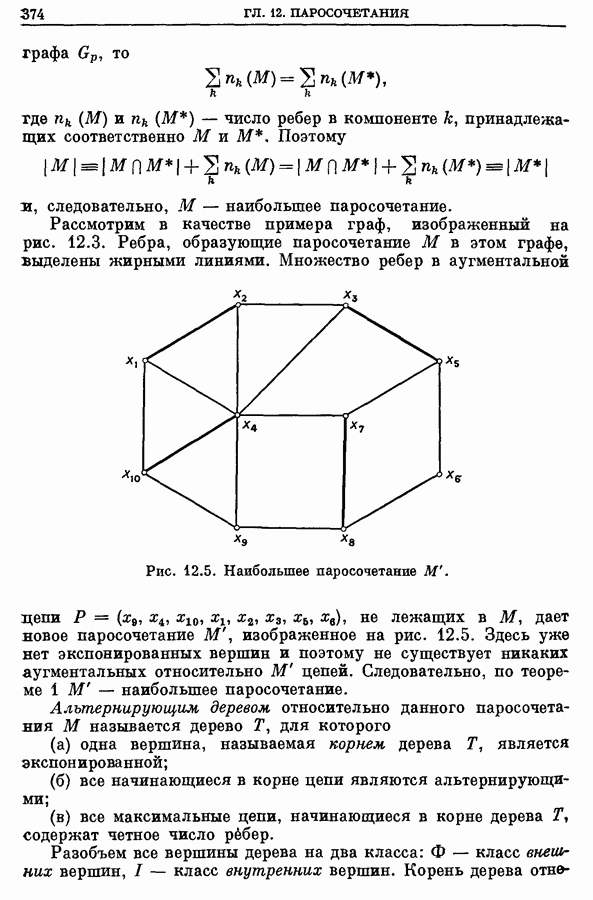
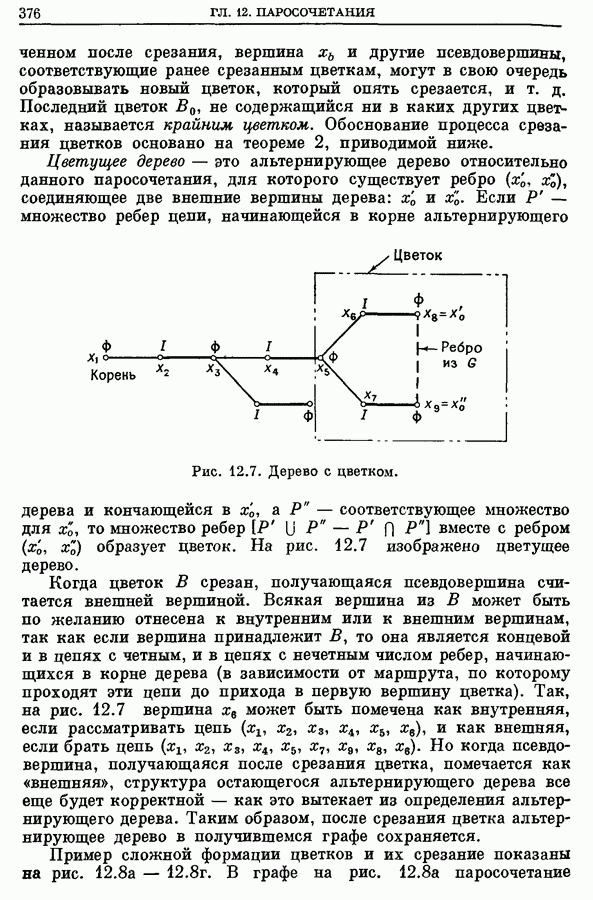
| << Предыдущий параграф | Следующий параграф >> |
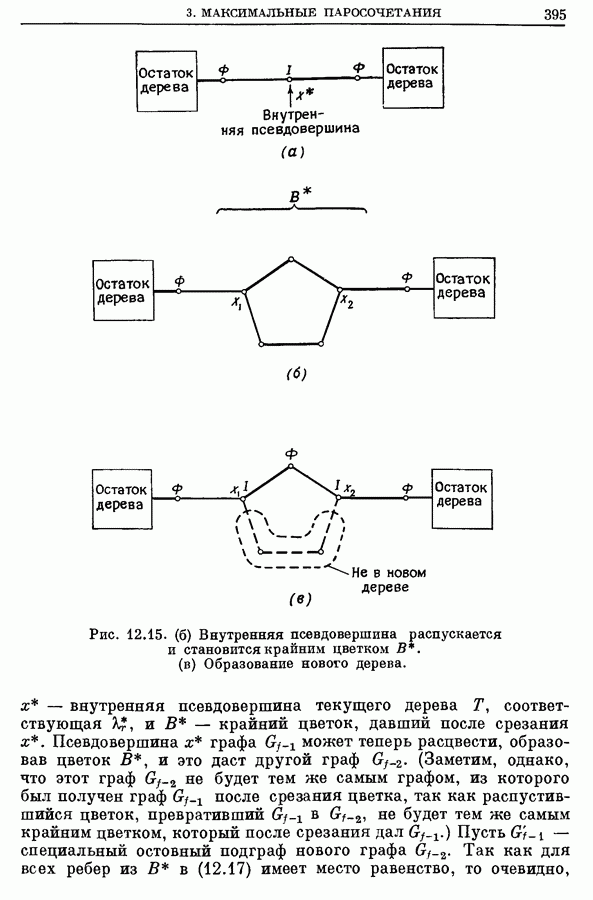
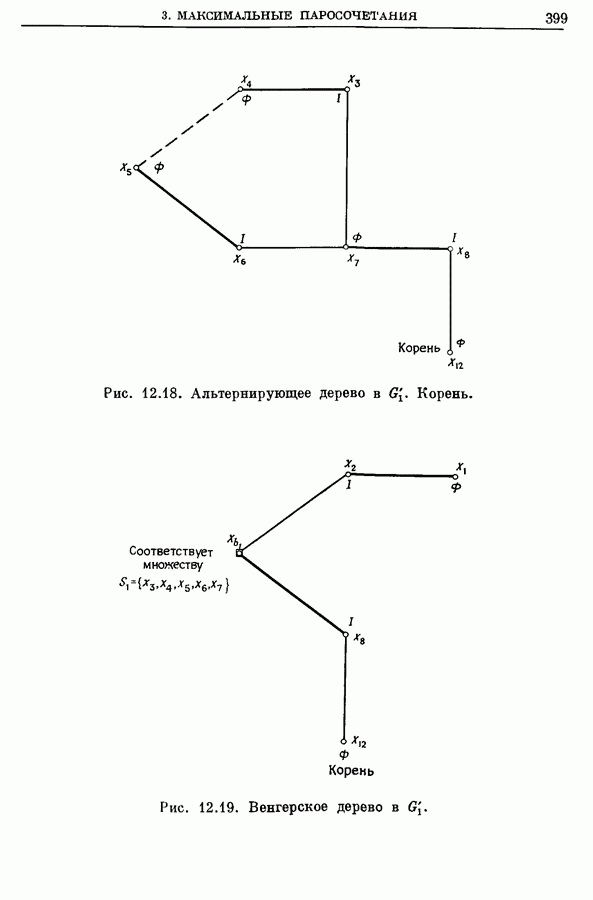
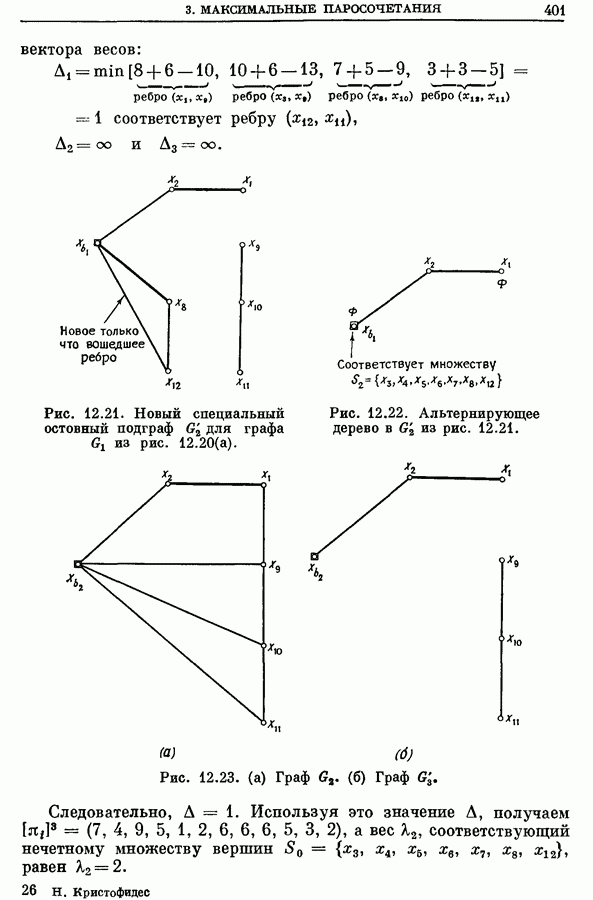
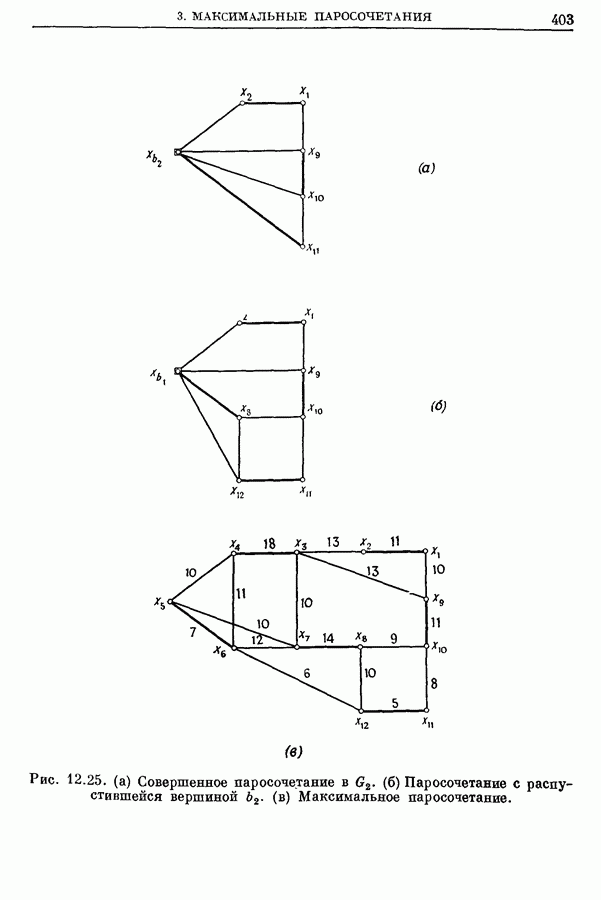
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
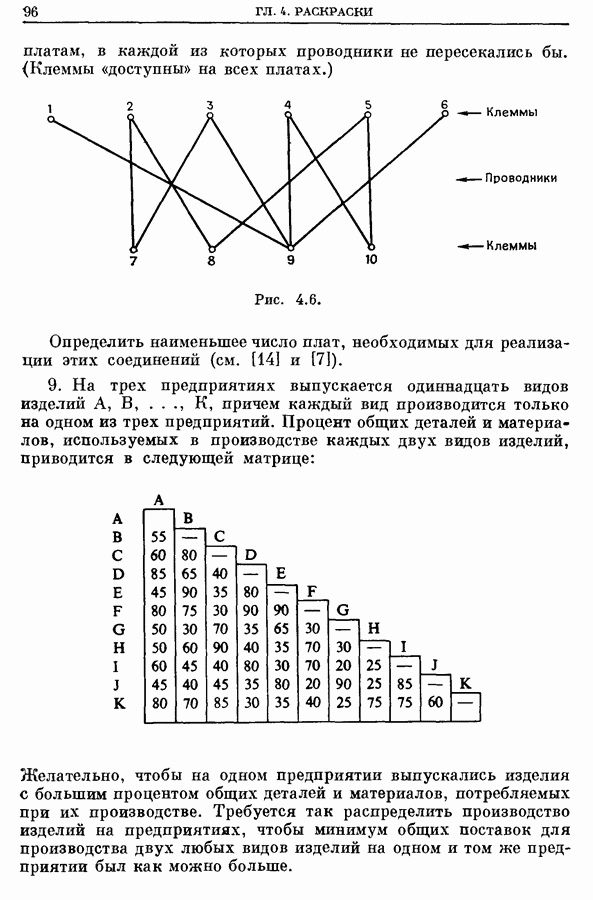
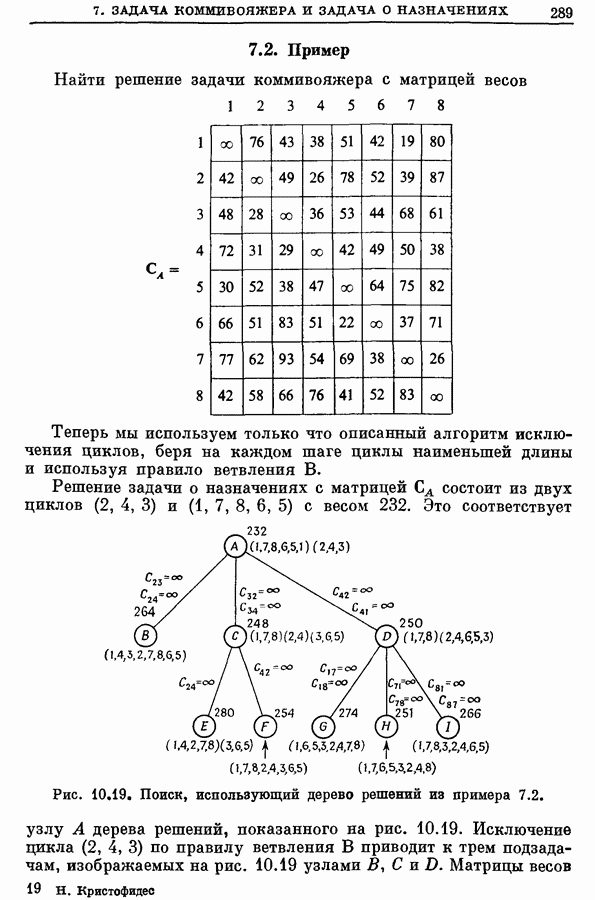
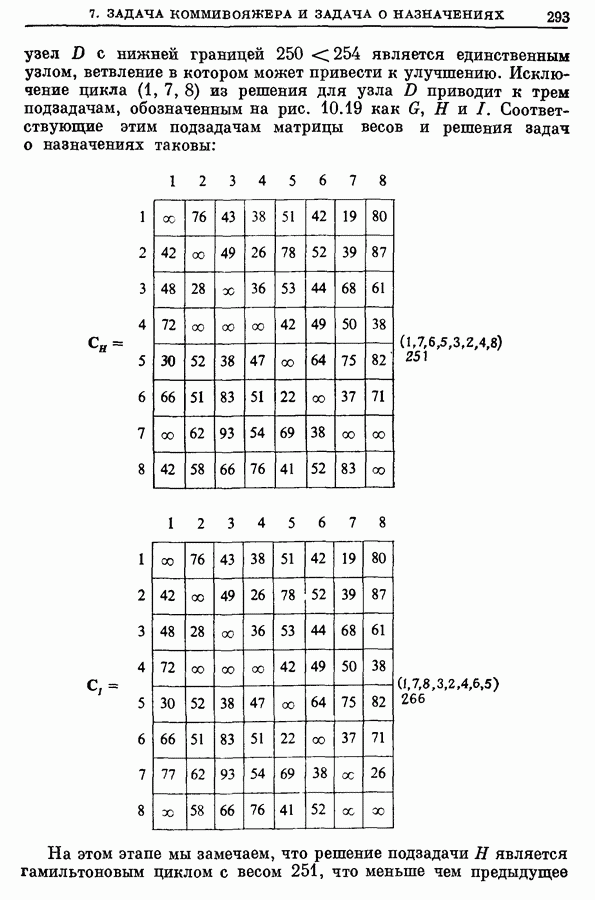
7. Задача коммивояжера и задача о назначениях
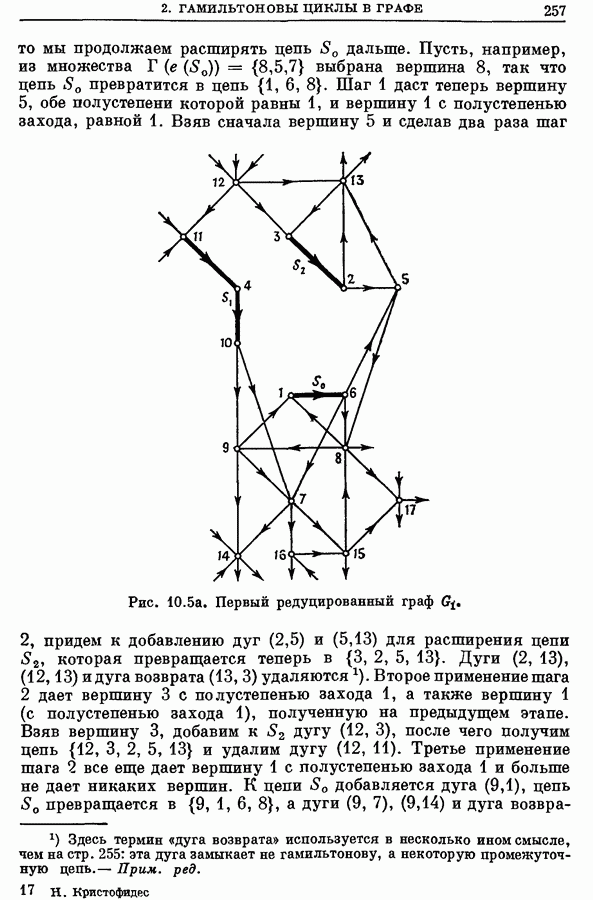
В разд. 5 было отмечено, что задача о назначениях, определяемая соотношениями (10.4), (10.5) и (10.6), может иметь решения, образованные некоторым числом непересекающихся циклов, и что соответствующий метод решения задачи коммивояжера требует наложения ограничений до тех пор, пока решение не будет состоять из единственного (гамильтонова) цикла. В настоящем разделе мы исследуем процедуры наложения этих ограничений в рамках алгоритма поиска, использующего дерево решений. Применяемая схема будет в основном такой же, как и в разд. 6.2 для алгоритма поиска, основанного на рассмотрении кратчайшего остова.
7.1. Алгоритм поиска, использующий дерево решений
Пусть решение задачи о назначениях с матрицей весов  образовано некоторым числом непересекающихся циклов. Так, например, если решение задачи с 8 вершинами имеет вид
образовано некоторым числом непересекающихся циклов. Так, например, если решение задачи с 8 вершинами имеет вид  для всех остальных пар
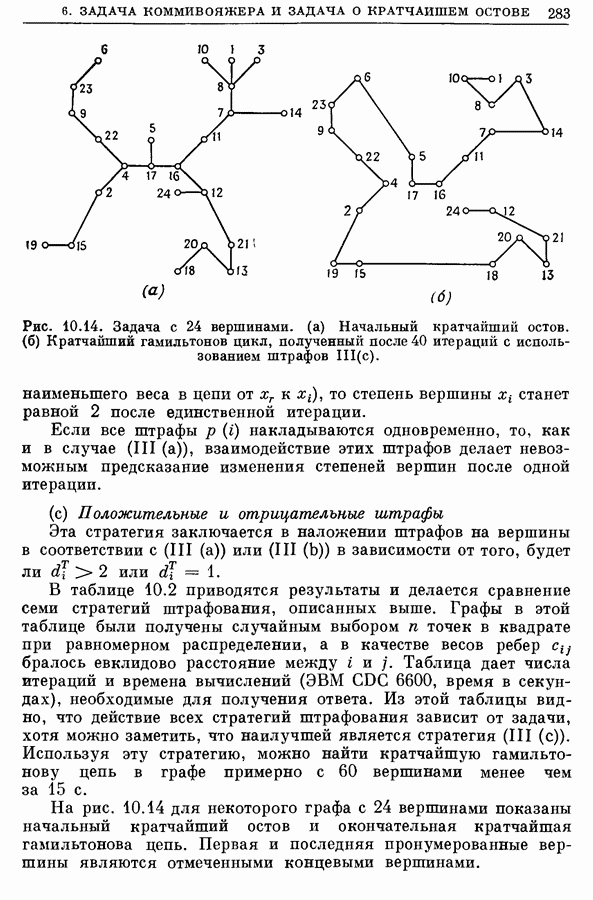
для всех остальных пар  то решение, отвечающее двум циклам, изображено на рис. 10.15 (а).
то решение, отвечающее двум циклам, изображено на рис. 10.15 (а).

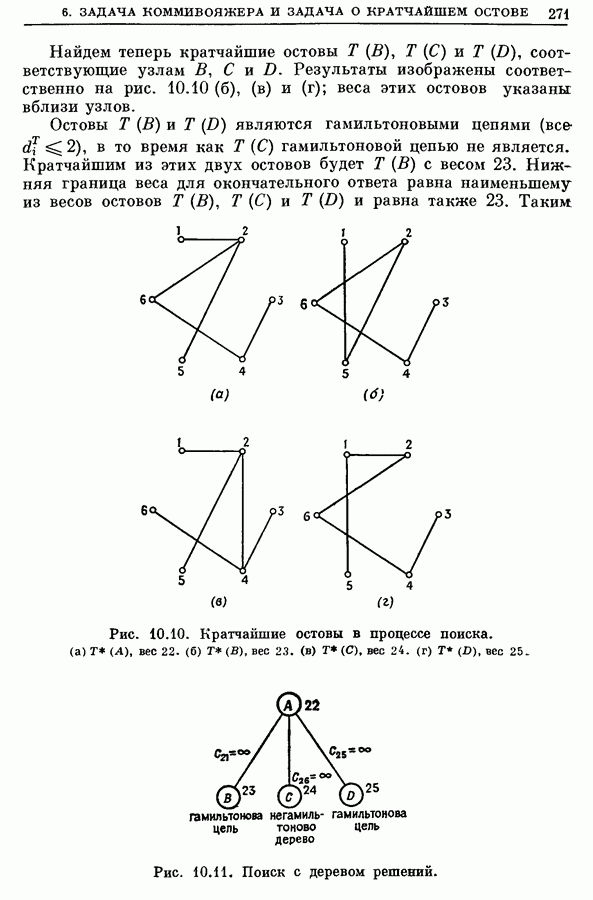
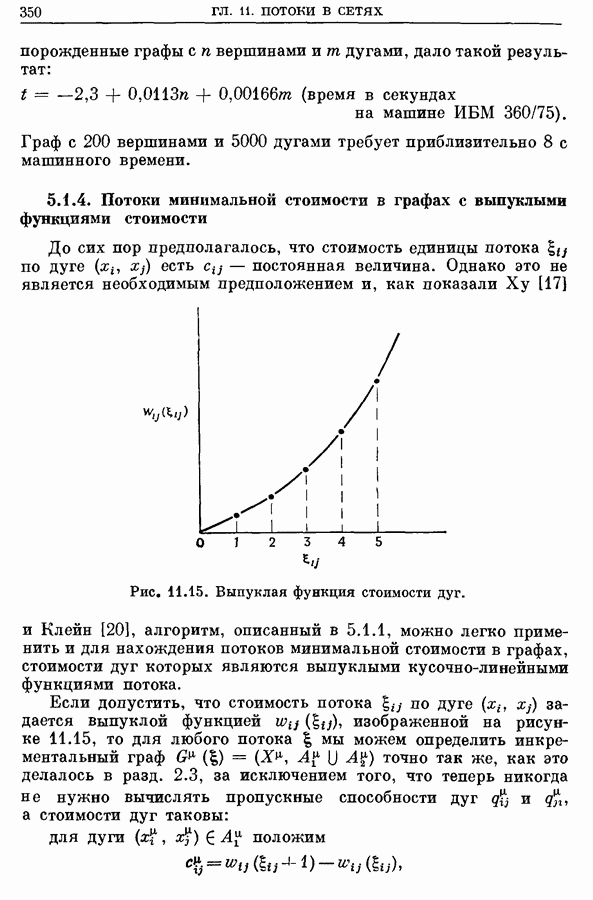
Рис. 10.15. Решение задач о назначениях, (а) Решение задачи  . (б) Решение задачи
. (б) Решение задачи 
Теперь необходимо сделать следующее — исключить данное решение вместе со многими другими такими же решениями, не потеряв решение задачи коммивояжера с той же матрицей весов. Так как решение задачи коммивояжера является гамильтоновым циклом, то мы будем пытаться исключить любое решение, состоящее более чем из одного цикла.
(А) Правило простого ветвления.
Пусть в общем случае решение задачи о назначениях содержит (не гамильтонов) цикл  длины k. Удаление этого цикла (и всех решений, его содержащих) из дальнейшего рассмотрения может быть произведено путем наложения требования, что по крайней мере одна из дуг
длины k. Удаление этого цикла (и всех решений, его содержащих) из дальнейшего рассмотрения может быть произведено путем наложения требования, что по крайней мере одна из дуг  не должна входить в решение. Это можно сделать совсем просто, если первоначальную задачу с матрицей весов
не должна входить в решение. Это можно сделать совсем просто, если первоначальную задачу с матрицей весов  разбить на к подзадач
разбить на к подзадач  . В задаче
. В задаче  полагается равным с», а все остальные
полагается равным с», а все остальные  остаются без изменения (т. е. такими же, как и в задаче
остаются без изменения (т. е. такими же, как и в задаче  в задаче
в задаче  и вообще в задаче
и вообще в задаче  Очевидно, что решение задачи
Очевидно, что решение задачи  не содержащее цикла
не содержащее цикла  является решением по крайней мере одной из задач
является решением по крайней мере одной из задач  следовательно, оптимальное решение задачи коммивояжера является решением одной или нескольких из зтих подзадач.
следовательно, оптимальное решение задачи коммивояжера является решением одной или нескольких из зтих подзадач.
Так, например, исключая на рис.  цикл длины 3, получим дерево решений, изображенное на рис. 10.16, в котором задачи
цикл длины 3, получим дерево решений, изображенное на рис. 10.16, в котором задачи  представлены узлами дерева, растущего из начальной задачи
представлены узлами дерева, растущего из начальной задачи  Пусть задачи
Пусть задачи  решены как задачи о назначениях, и пусть соответствующие веса будут
решены как задачи о назначениях, и пусть соответствующие веса будут  Так как
Так как  является нижней границей в задаче коммивояжера
является нижней границей в задаче коммивояжера
для  а также для
а также для  то число
то число  является нижней границей для веса решения первоначальной задачи коммив ояже
является нижней границей для веса решения первоначальной задачи коммив ояже 
Пусть, скажем,  (т. е.
(т. е.  ). Если решение задачи
). Если решение задачи  является гамильтоновым циклом, то оно будет решением первоначальной задачи коммивояжера. В противном случае пусть оно будет, скажем, таким, как на рис. 10.15 (б). Исключая цикл (1, 8, 2, 6, 1), мы снова составляем и решаем подзадачи
является гамильтоновым циклом, то оно будет решением первоначальной задачи коммивояжера. В противном случае пусть оно будет, скажем, таким, как на рис. 10.15 (б). Исключая цикл (1, 8, 2, 6, 1), мы снова составляем и решаем подзадачи  показанные на рис. 10.16.
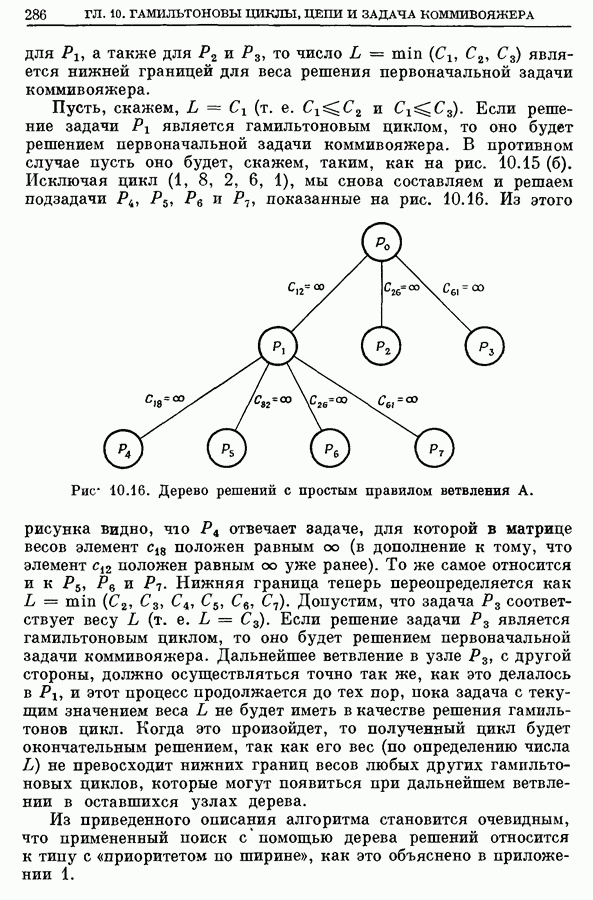
показанные на рис. 10.16.

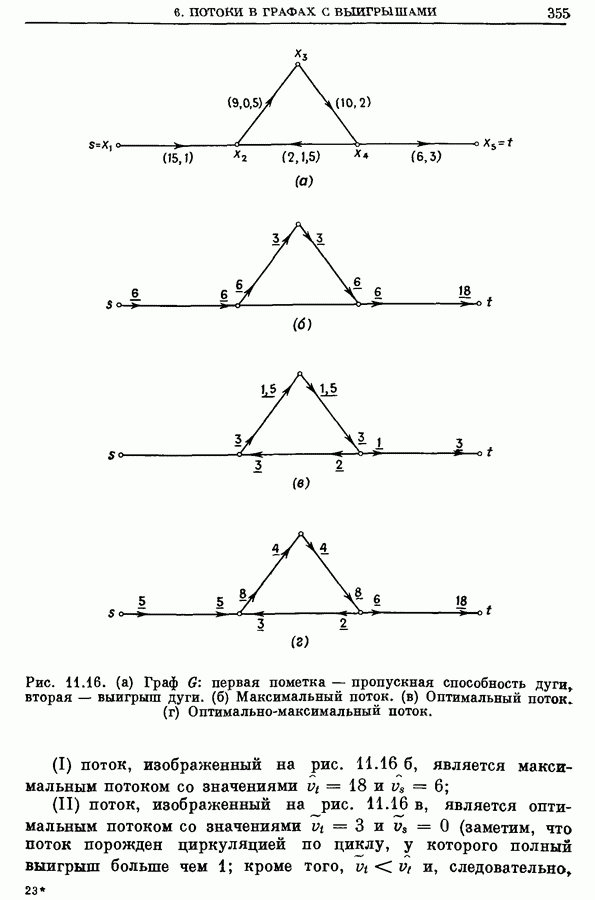
Рис. 10.16. Дерево решений с простым правилом ветвления А.
Из этого рисунка видно,  отвечает задаче, для которой в матрице весов элемент
отвечает задаче, для которой в матрице весов элемент  положен равным
положен равным  (в дополнение к тому, что элемент
(в дополнение к тому, что элемент  положен равным
положен равным  уже ранее). То же самое относится и к
уже ранее). То же самое относится и к  Нижняя граница теперь переопределяется как
Нижняя граница теперь переопределяется как  Допустим, что задача
Допустим, что задача  соответствует весу
соответствует весу  (т. е.
(т. е.  ). Если решение задачи
). Если решение задачи  является гамильтоновым циклом, то оно будет решением первоначальной задачи коммивояжера. Дальнейшее ветвление в узле
является гамильтоновым циклом, то оно будет решением первоначальной задачи коммивояжера. Дальнейшее ветвление в узле  с другой стороны, должно осуществляться точно так же, как это делалось в
с другой стороны, должно осуществляться точно так же, как это делалось в  и этот процесс продолжается до тех пор, пока задача с текущим значением веса
и этот процесс продолжается до тех пор, пока задача с текущим значением веса  не будет иметь в качестве решения гамильтонов цикл. Когда это произойдет, то полученный цикл будет окончательным решением, так как его вес (по определению числа
не будет иметь в качестве решения гамильтонов цикл. Когда это произойдет, то полученный цикл будет окончательным решением, так как его вес (по определению числа  не превосходит нижних границ весов любых других гамильтоновых циклов, которые могут появиться при дальнейшем ветвлении в оставшихся узлах дерева.
не превосходит нижних границ весов любых других гамильтоновых циклов, которые могут появиться при дальнейшем ветвлении в оставшихся узлах дерева.
Из приведенного описания алгоритма становится очевидным, что примененный поиск с помощью дерева решений относится к типу с «приоритетом по ширине», как это объяснено в приложении 1.
(Б) Правило исключающего ветвления.
Как объяснено в приложении 1, для хорошего ветвления при разбиении задачи  на подзадачи
на подзадачи  требуется только, чтобы каждое возможное решение задачи
требуется только, чтобы каждое возможное решение задачи  исключением удаляемых решений) было решением по крайней мере одной из подзадач. Однако, как отмечено в приложении, очень желательным свойством метода ветвления было бы разбиение возникающих подзадач на взаимно исключающие, коль скоро речь идет о возможных решениях задачи
исключением удаляемых решений) было решением по крайней мере одной из подзадач. Однако, как отмечено в приложении, очень желательным свойством метода ветвления было бы разбиение возникающих подзадач на взаимно исключающие, коль скоро речь идет о возможных решениях задачи  Иными словами, каждое допустимое решение задачи
Иными словами, каждое допустимое решение задачи  должно быть решением одной, и только одной из этих подзадач.
должно быть решением одной, и только одной из этих подзадач.
Ранее описанное правило ветвления основывалось на том факте, что цикл, такой, как  может быть удален посредством исключения одной из его дуг. Это, однако, не приводит в процессе ветвления к взаимно исключающим подзадачам. Так, в вышеприведенном примере решение задачи
может быть удален посредством исключения одной из его дуг. Это, однако, не приводит в процессе ветвления к взаимно исключающим подзадачам. Так, в вышеприведенном примере решение задачи  соответствующее циклам (1, 3, 6, 1) и (2, 5, 4, 7, 8, 2), является допустимым решением как подзадачи
соответствующее циклам (1, 3, 6, 1) и (2, 5, 4, 7, 8, 2), является допустимым решением как подзадачи  так и
так и 
Другим правилом ветвления, удаляющим цикл  и приводящим к взаимно исключающим подзадачам, является следующее:
и приводящим к взаимно исключающим подзадачам, является следующее:

где  достаточно большое отрицательное число, гарантирующее, что дуга, вес которой равен
достаточно большое отрицательное число, гарантирующее, что дуга, вес которой равен  входит в оптимальное решение.
входит в оптимальное решение.
Это правило ветвления наверняка приводит к взаимно исключающим подзадачам, так как для любых двух подзадач имеется по крайней мере одна дуга, исключенная из решения одной, но заведомо входящая в решение другой подзадачи. Легко также видеть, что ни одно возможное решение задачи  не будет потеряно, т. е. что любое решение первоначальной задачи
не будет потеряно, т. е. что любое решение первоначальной задачи  будет являться решением одной из подзадач. Это очевидно в силу того, что любое решение задачи
будет являться решением одной из подзадач. Это очевидно в силу того, что любое решение задачи  имеет некоторую последовательность дуг, выходящую из таких, как
имеет некоторую последовательность дуг, выходящую из таких, как  и первые
и первые  дуг должны совпадать с дугами цепи
дуг должны совпадать с дугами цепи  при некотором значении
при некотором значении  Значение
Значение  отвечает тому случаю, когда совпадения вообще нет,
отвечает тому случаю, когда совпадения вообще нет,  случаю, когда
случаю, когда  но
но 

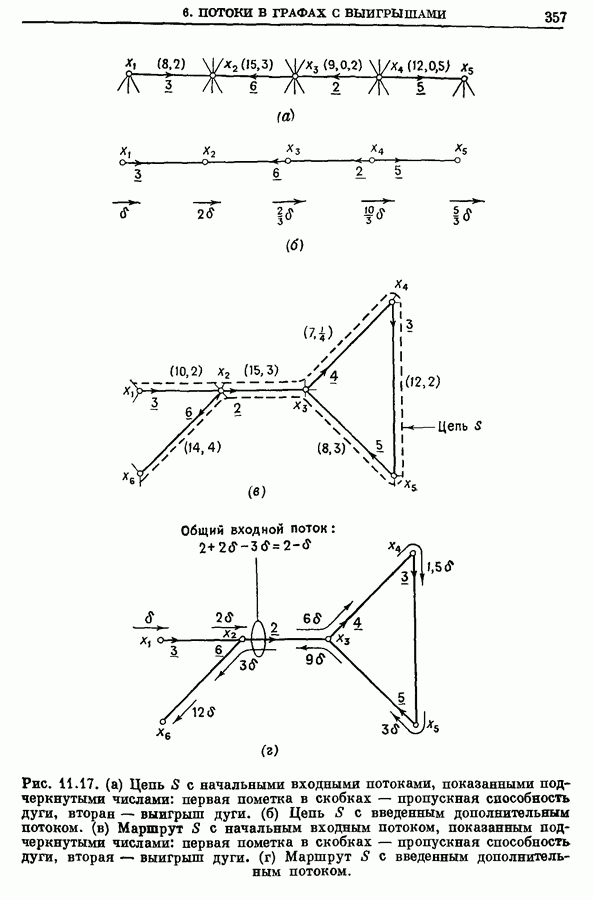
Рис. 10.17. Дерево решений с исключающим правилом ветвления Б.

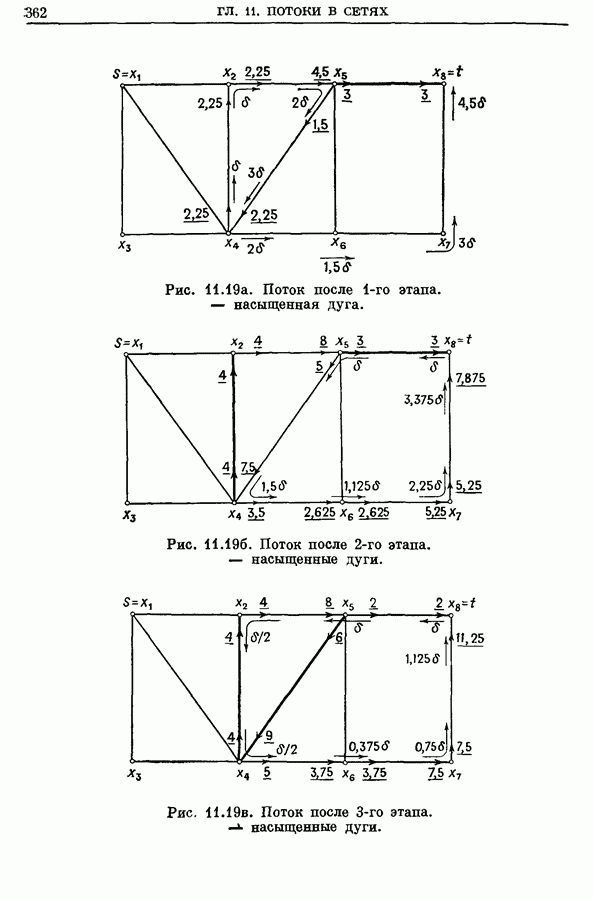
Рис. 10.18. Дерево решений с улучшенным правилом ветвления В.
В приведенном примере первоначальная задача  разбивалась бы на три подзадачи, показанные на рис. 10.17 (ср. с разбиением на первом уровне из рис. 10.16, полученным по предыдущему правилу ветвления).
разбивалась бы на три подзадачи, показанные на рис. 10.17 (ср. с разбиением на первом уровне из рис. 10.16, полученным по предыдущему правилу ветвления).
(В) Лучшее правило ветвления.
Оба предыдущих правила ветвления исключали (при каждом отдельном ветвлении) все решения, содержащие заданный цикл, такой, как  Очевидно, однако, что в решении задачи коммивояжера не только не должен не существовать такой цикл, но должна быть по крайней мере одна дуга, ведущая из множества вершин
Очевидно, однако, что в решении задачи коммивояжера не только не должен не существовать такой цикл, но должна быть по крайней мере одна дуга, ведущая из множества вершин  в множество вершин
в множество вершин  Действительно, существование какой-либо дуги, ведущей из
Действительно, существование какой-либо дуги, ведущей из  не только гарантирует исключение решений, содержащих цикл, принадлежащий множеству
не только гарантирует исключение решений, содержащих цикл, принадлежащий множеству  но также позволяет исключить решения, множества вершин которых лежат в 5 и которые состоят из нескольких циклов (а не только из одного). Таким образом, можно ожидать, что правило ветвления, основанное на требовании, чтобы существовала некоторая дуга из 5 в
но также позволяет исключить решения, множества вершин которых лежат в 5 и которые состоят из нескольких циклов (а не только из одного). Таким образом, можно ожидать, что правило ветвления, основанное на требовании, чтобы существовала некоторая дуга из 5 в  будет равномерно лучше, чем два предыдущие правила ветвления 2.
будет равномерно лучше, чем два предыдущие правила ветвления 2.
Так как дуга из 5 в  должна начинаться в некоторой вершине из
должна начинаться в некоторой вершине из  то задачу можно расщепить на к подзадач. В подзадаче
то задачу можно расщепить на к подзадач. В подзадаче  мы будем требовать, чтобы начальной вершиной дуги являлась
мы будем требовать, чтобы начальной вершиной дуги являлась  а конечной вершиной была некоторая вершина в
а конечной вершиной была некоторая вершина в  Это можно сделать, положив с
Это можно сделать, положив с  для всех
для всех  и оставив без изменения все другие веса. В решении получившейся задачи о назначениях мы наверняка бы имели дугу из
и оставив без изменения все другие веса. В решении получившейся задачи о назначениях мы наверняка бы имели дугу из  ведущую в
ведущую в  так как для всех других альтернатив их веса должны быть положены равными
так как для всех других альтернатив их веса должны быть положены равными 
В примере, данном выше, начальная задача  была бы в соответствии с настоящим правилом ветвления подразделена на три подзадачи, определенные, как показано на рис. 10.18. Дальнейшие ветвления происходят аналогично.
была бы в соответствии с настоящим правилом ветвления подразделена на три подзадачи, определенные, как показано на рис. 10.18. Дальнейшие ветвления происходят аналогично.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
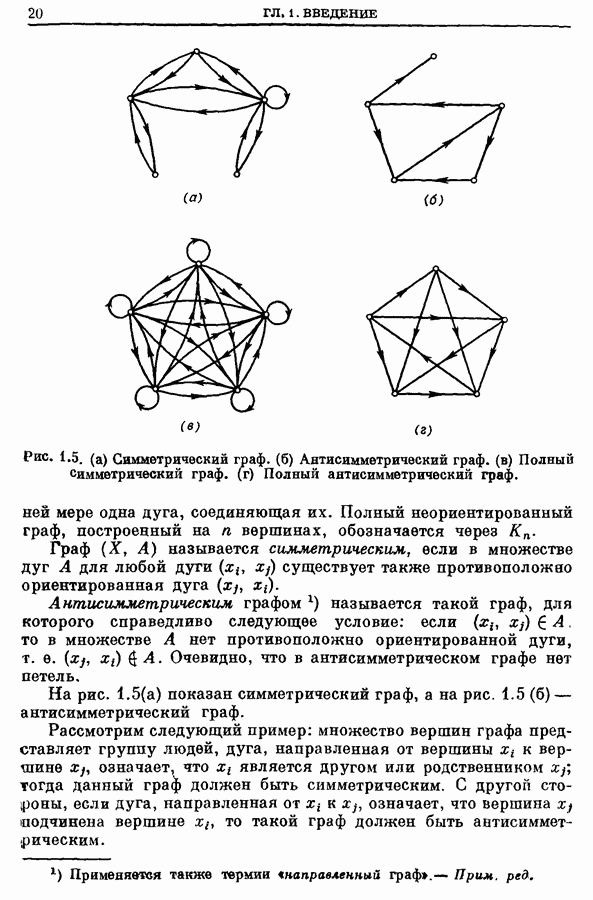
- 6. Типы графов
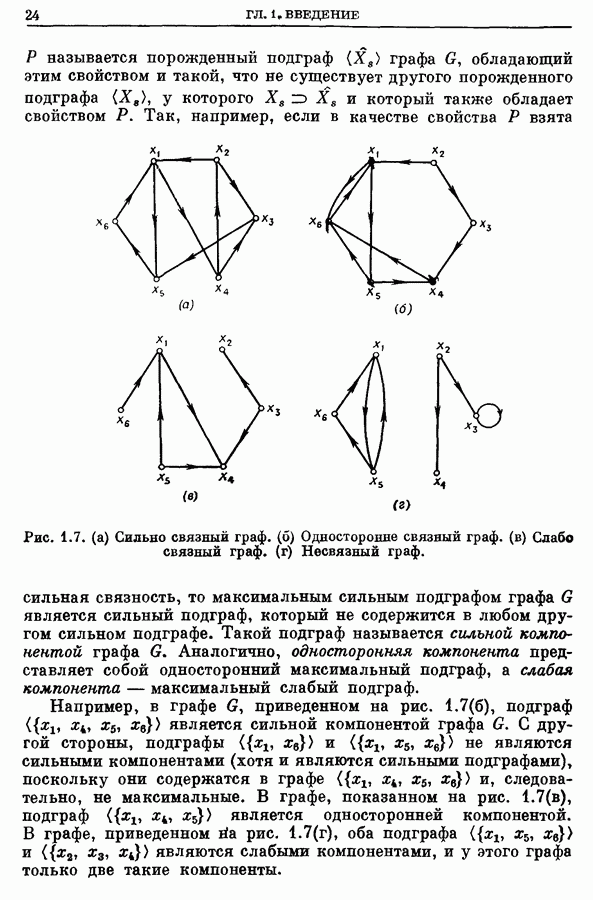
- 7. Сильно связные графы и компоненты графа
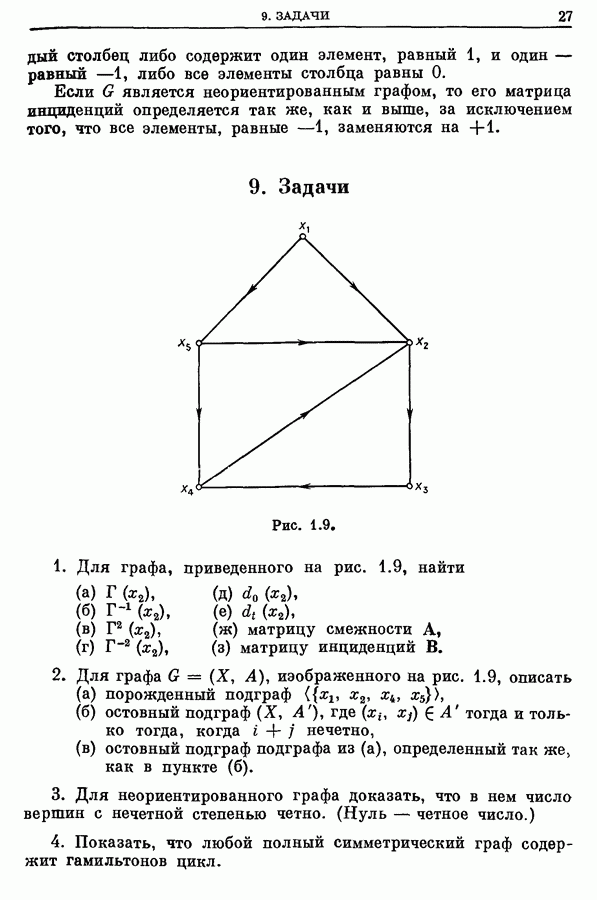
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
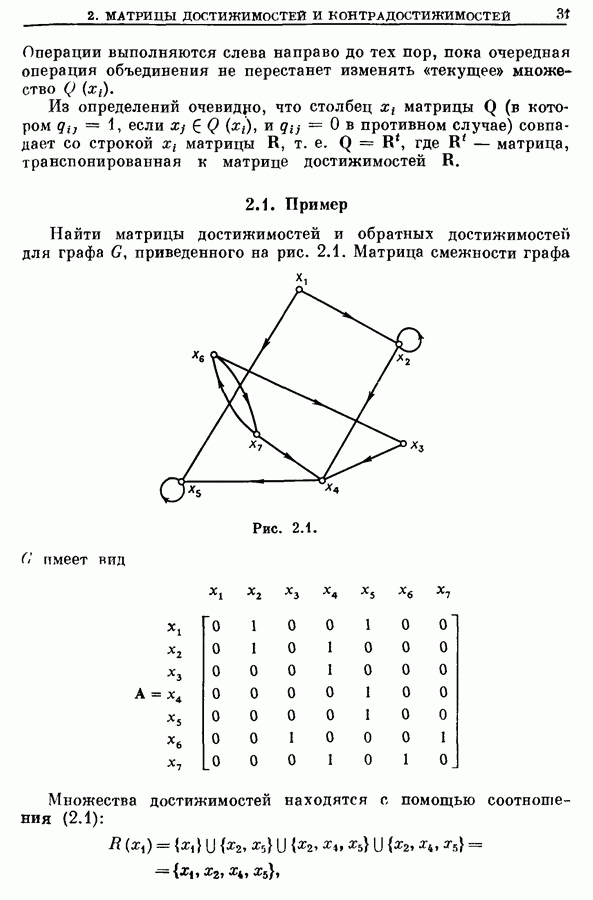
- 2. Матрицы достижимостеи и контрадостижимостей
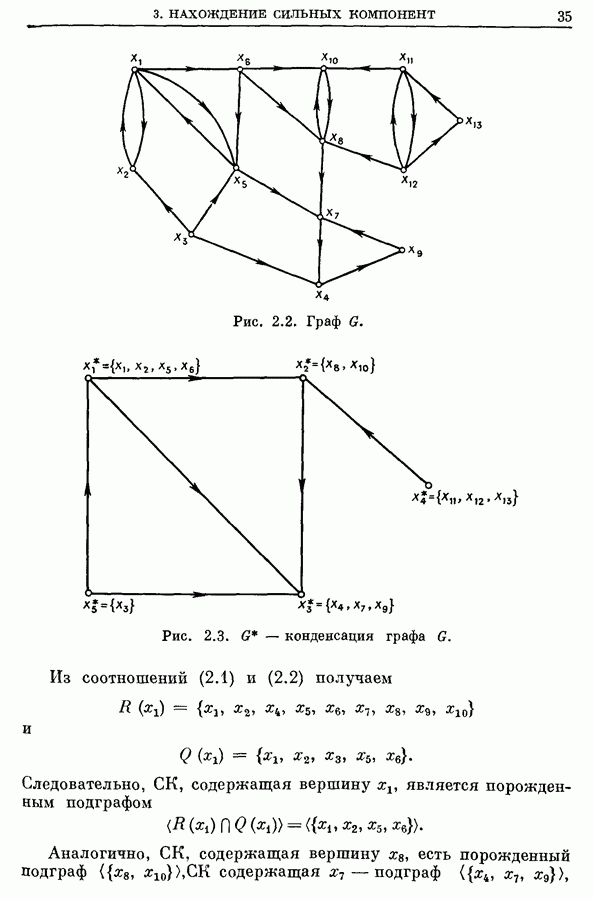
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
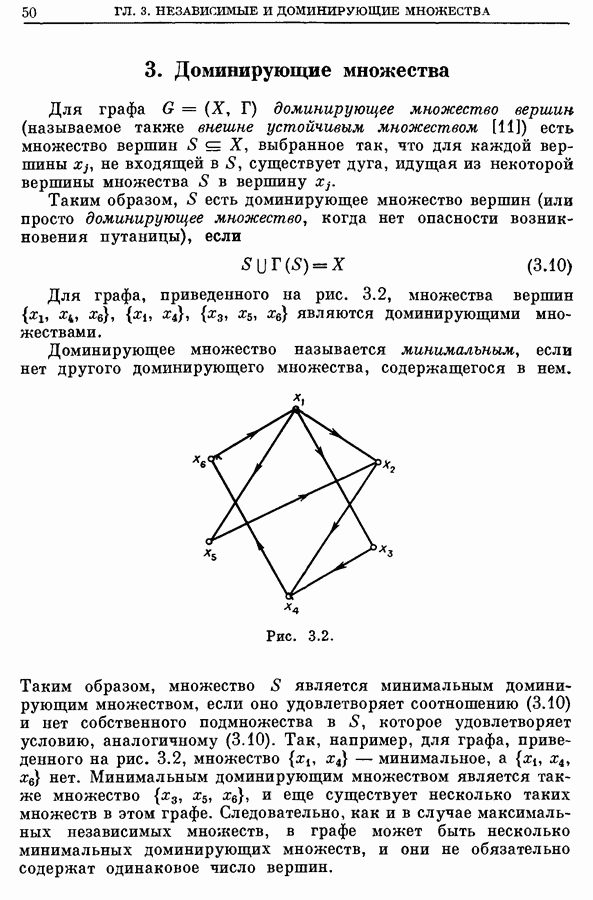
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
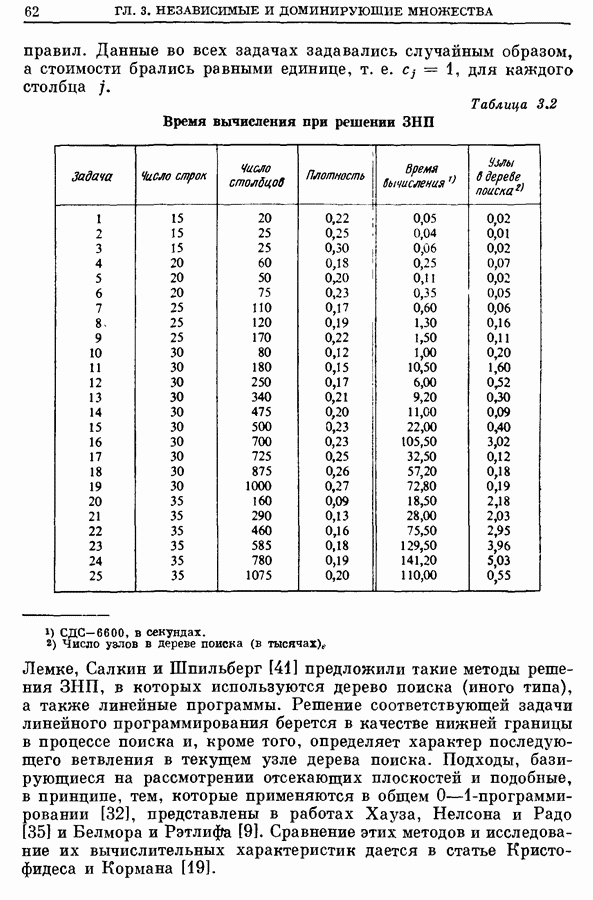
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
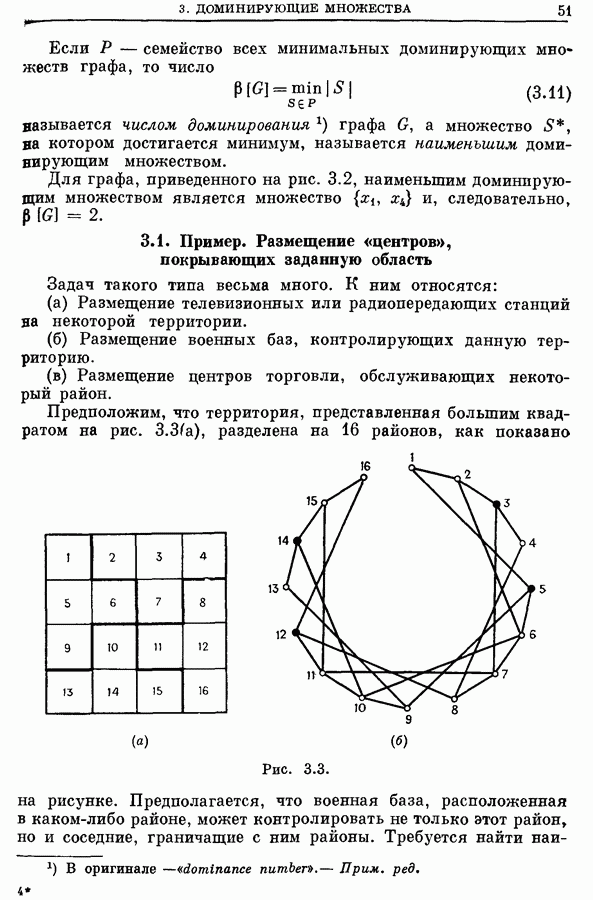
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
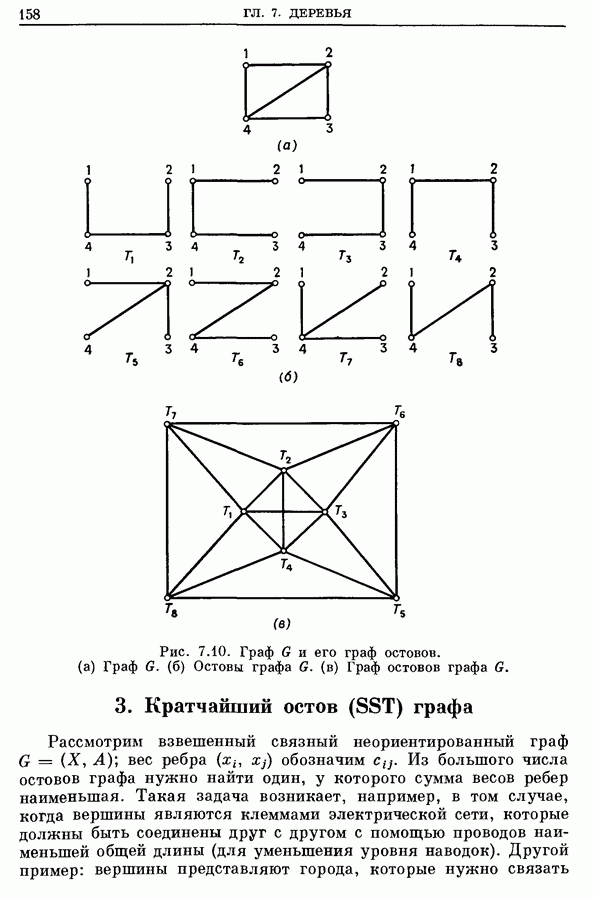
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
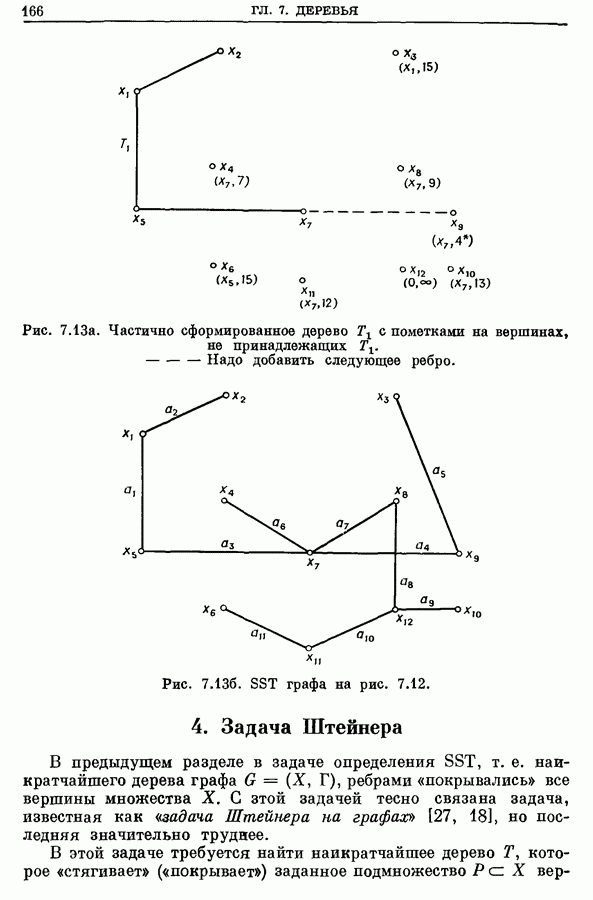
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
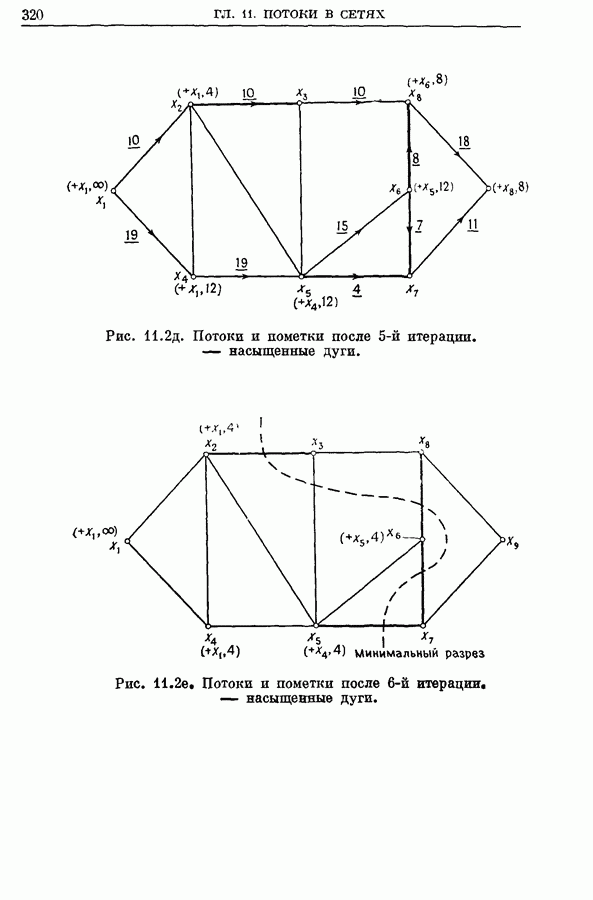
- Глава 11. ПОТОКИ В СЕТЯХ
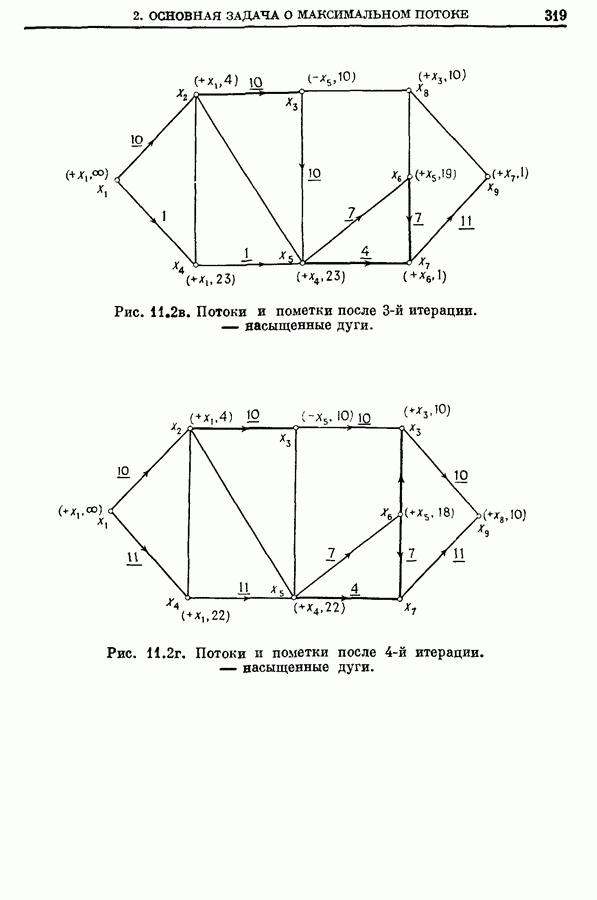
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
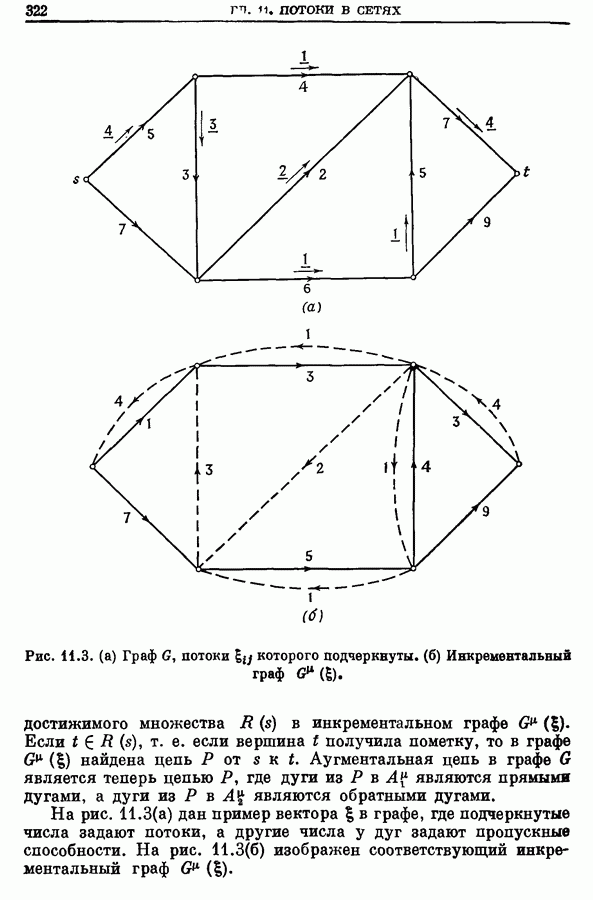
- 2.3. Инкрементальные графы
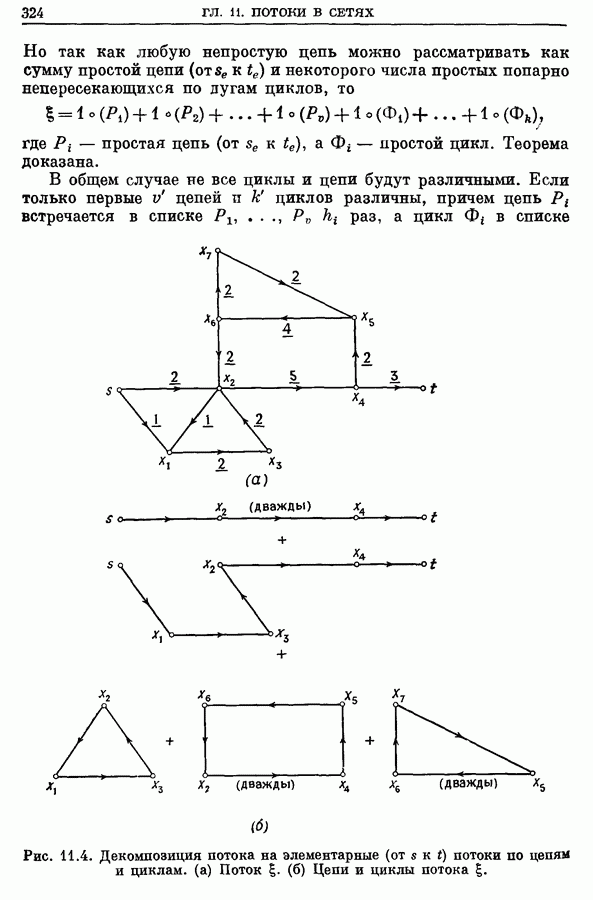
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
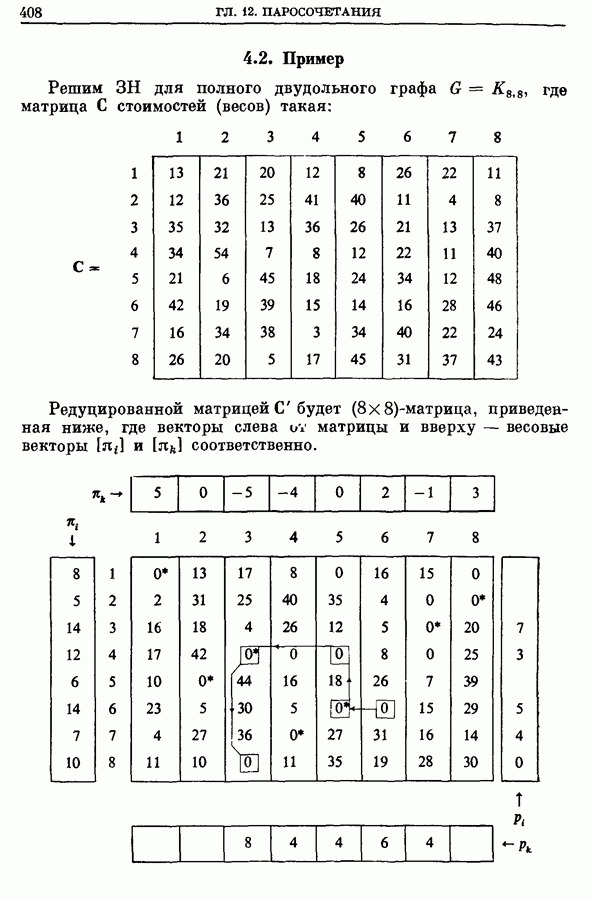
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
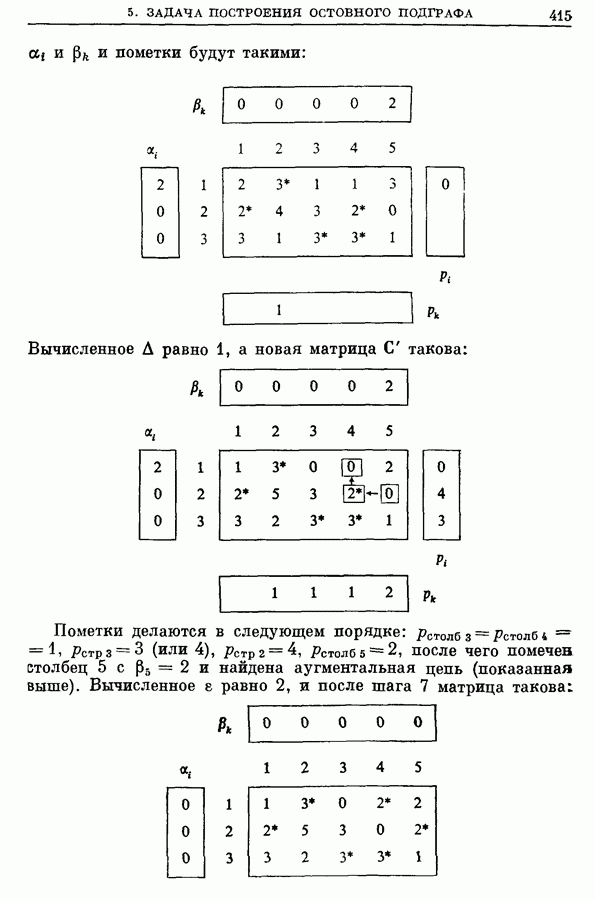
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
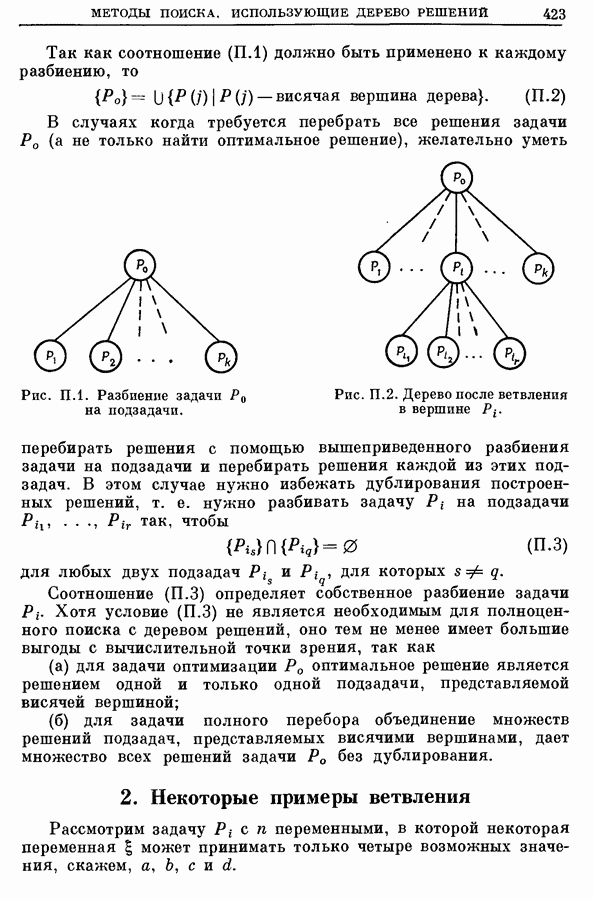
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
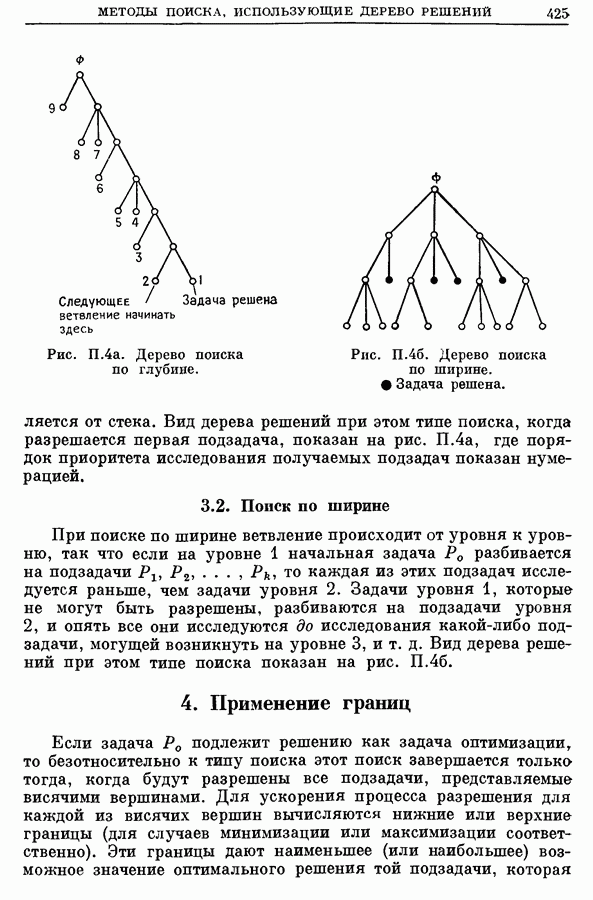
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления