| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Нахождейие К кратчайших путей между двумя заданными вершинами
В разд. 2 были даны методы нахождения в произвольном графе кратчайшего пути от  Но во многих практических приложениях требуется еще, чтобы кратчайший путь обладал некоторыми
Но во многих практических приложениях требуется еще, чтобы кратчайший путь обладал некоторыми
дополнительными свойствами. Эту задачу можно, конечно, рассматривать как задачу кратчайшего пути с некоторыми дополнительными ограничениями [4] или как многоцелевую задачу, в которой учитываются не только длина пути, но и другие  свойства. Но эти усложнения будут, вообще говоря, сильно увеличивать вычислительную работу, и с практической точки зрения более просто найти К кратчайших путей от
свойства. Но эти усложнения будут, вообще говоря, сильно увеличивать вычислительную работу, и с практической точки зрения более просто найти К кратчайших путей от  и выбрать среди них тот, который обладает нужными свойствами. Хотя такой метод и не эквивалентен прямому рассмотрению дополнительных свойств пути (пример этого будет дан в разд. 7 настоящей главы), но он применим даже в тех случаях, когда эти свойства сформулированы не строго или когда они по своей природе субъективны. В этом методе предполагается, что К кратчайших путей между
и выбрать среди них тот, который обладает нужными свойствами. Хотя такой метод и не эквивалентен прямому рассмотрению дополнительных свойств пути (пример этого будет дан в разд. 7 настоящей главы), но он применим даже в тех случаях, когда эти свойства сформулированы не строго или когда они по своей природе субъективны. В этом методе предполагается, что К кратчайших путей между  могут быть найдены достаточно эффективно. Именно это будет предметом изучения настоящей главы.
могут быть найдены достаточно эффективно. Именно это будет предметом изучения настоящей главы.
Мы будем здесь предполагать, что рассматриваются только простые цепи. И хотя кратчайший путь необходимо должен быть простой цепью (при условии, что граф не содержит циклов отрицательного веса), но второй, третий и т. д. кратчайшие пути не обязаны быть такими даже в случае, когда все  положительны. Задача нахождения К кратчайших путей без требования, что они являются простыми цепями, намного проще, и для ее решения Хоффман и Пэвли [20], Сакарович [32], Веллман и Калаба
положительны. Задача нахождения К кратчайших путей без требования, что они являются простыми цепями, намного проще, и для ее решения Хоффман и Пэвли [20], Сакарович [32], Веллман и Калаба  предложили итерационные методы, аналогичные описанным выше. Однако модифицирование этих методов с целью получения простых цепей осуществить не совсем легко, а так как почти во всех, практических приложениях алгоритма нахождения К кратчайших путей требуются именно простые цепи, то мы опишем метод, предложенный Иеном [35] и позволяющий находить К кратчайших простых цепей.
предложили итерационные методы, аналогичные описанным выше. Однако модифицирование этих методов с целью получения простых цепей осуществить не совсем легко, а так как почти во всех, практических приложениях алгоритма нахождения К кратчайших путей требуются именно простые цепи, то мы опишем метод, предложенный Иеном [35] и позволяющий находить К кратчайших простых цепей.
Пусть  кратчайший путь от у к
кратчайший путь от у к  где
где  соответственно 2-я,
соответственно 2-я,  вершины
вершины  кратчайшего пути. Пусть
кратчайшего пути. Пусть  «отклонение от пути;
«отклонение от пути;  в точке
в точке  Под этим понимается следующее:
Под этим понимается следующее:  кратчайший из путей, совпадающих с
кратчайший из путей, совпадающих с  от
от  до
до  вершины, а затем идущий к вершине, отличной от
вершины, а затем идущий к вершине, отличной от  вершин тех (ранее уже построенных) кратчайших путей
вершин тех (ранее уже построенных) кратчайших путей  , которые имеют те же самые начальные подпути от
, которые имеют те же самые начальные подпути от  вершине,
вершине,  приходит в вершину
приходит в вершину  по кратчайшему подпути, не проходящему ни через одну из вершин
по кратчайшему подпути, не проходящему ни через одну из вершин  участвующих в формировании первой части пути
участвующих в формировании первой части пути  Отсюда следует, что путь
Отсюда следует, что путь  необходимо должен быть простой цепью.
необходимо должен быть простой цепью.
Первый подпуть  (совпадающий с
(совпадающий с  ) пути
) пути  называется его корнем и
называется его корнем и
обозначается  второй подпуть
второй подпуть  пути
пути  называется ответвлением и обозначается через
называется ответвлением и обозначается через 
Алгоритм начинает работу с нахождения  с помощью алгоритма кратчайшего пути от
с помощью алгоритма кратчайшего пути от  описанного в разд. 2. Этот путь помещается в список
описанного в разд. 2. Этот путь помещается в список  (который должен содержать
(который должен содержать  кратчайшие пути). В общем случае для нахождения
кратчайшие пути). В общем случае для нахождения  нужно уже иметь кратчайшие пути
нужно уже иметь кратчайшие пути  Ниже приводится описание алгоритма.
Ниже приводится описание алгоритма.
5.1. Описание алгоритма
Присвоение начальных значений
Шаг 1. Найти  Положить
Положить  Если существует только один кратчайший путь
Если существует только один кратчайший путь  включить его в список
включить его в список  и перейти к шагу 2. Если таких путей несколько, но меньше, чем К, включить один из них в список
и перейти к шагу 2. Если таких путей несколько, но меньше, чем К, включить один из них в список  а остальные в список
а остальные в список  Перейти к шагу 2. Если существует К или более кратчайших путей
Перейти к шагу 2. Если существует К или более кратчайших путей  та задача решена. Останов.
та задача решена. Останов.
Нахождение всех отклонений
Шаг 2. Найти все отклонения  кратчайшего пути
кратчайшего пути  для всех
для всех  выполняя для каждого
выполняя для каждого  шаги с 3-го по 6-й.
шаги с 3-го по 6-й.
Шаг 3. Проверить, совпадает ли подпуть, образованный пер. выми  вершинами пути
вершинами пути  с подпутем, образованным первыми
с подпутем, образованным первыми  вершинами любого из путей
вершинами любого из путей  . Если
. Если  положить с
положить с  в противном случае ничего не изменять. (При выполнении алгоритма вершина Ху обозначается
в противном случае ничего не изменять. (При выполнении алгоритма вершина Ху обозначается  Перейти к шагу 4.
Перейти к шагу 4.
Шаг 4. Используя алгоритм кратчайшего пути, найти кратчайшие пути  от
от  исключая из рассмотрения вершины
исключая из рассмотрения вершины  Если существует несколько кратчайших путей, взять в качестве
Если существует несколько кратчайших путей, взять в качестве  один из них.
один из них.
Шаг 5. Построить  соединеняя
соединеняя  и поместить
и поместить  в список
в список 
Шаг 6. Заменить элементы матрицы весов, измененные на шаге их первоначальными значениями и возвратиться к шагу 3.
Выбор кратчайших отклонений
Шаг 7. Найти кратчайший путь в списке  Обозначить этот путь
Обозначить этот путь  и переместить его из
и переместить его из  Если
Если  то алгоритм
то алгоритм
заканчивает работу и  дает требуемый список К кратчайших путей. Если к
дает требуемый список К кратчайших путей. Если к  положить к — к 1 и вернуться к шагу 2.
положить к — к 1 и вернуться к шагу 2.
Если в  имеется более чем один кратчайший путь (скажем,
имеется более чем один кратчайший путь (скажем,  путей), то поместить в
путей), то поместить в  любой из них и продолжать, как и выше, до тех пор, пока увеличенное на
любой из них и продолжать, как и выше, до тех пор, пока увеличенное на  число путей, уже находящихся В
число путей, уже находящихся В  не совпадат с К или не превысит его. Тогда алгоритм завершает работу.
не совпадат с К или не превысит его. Тогда алгоритм завершает работу.
Обоснование вышеприведенного алгоритма основано на очевидном факте [11], [20]: путь  должен быть отклонением на
должен быть отклонением на  этапе (при некотором
этапе (при некотором  от одного из более коротких путей
от одного из более коротких путей  Поэтому необходимо просто построить все кратчайшие отклонения от каждого из
Поэтому необходимо просто построить все кратчайшие отклонения от каждого из  и просмотреть их для нахождения самого короткого отклонения. Это и будет путь
и просмотреть их для нахождения самого короткого отклонения. Это и будет путь  Следует заметить, что при
Следует заметить, что при  итерации все кратчайшие отклонения для
итерации все кратчайшие отклонения для  к — 2, уже включены в и нужно найти только одно отклонение от
к — 2, уже включены в и нужно найти только одно отклонение от  и пополнить им имеющийся список.
и пополнить им имеющийся список.
На шаге 3 мы полагаем с  для тех
для тех  начальные подпути которых, содержащие
начальные подпути которых, содержащие  вершин, совпадают с начальным
вершин, совпадают с начальным  -вершинным подпутем пути
-вершинным подпутем пути  Это делается для того, чтобы не получить снова
Это делается для того, чтобы не получить снова  в качестве отклонения (в точке
в качестве отклонения (в точке  ) от пути
) от пути  что вполне могло случиться, если бы мы действовали иначе, Так как при
что вполне могло случиться, если бы мы действовали иначе, Так как при  вес пути
вес пути  не больше веса пути
не больше веса пути 
Хотя на шаге 5 алгоритма каждый порожденйый путь  и помещается в список
и помещается в список  совершенно очевидно, что на
совершенно очевидно, что на  итерации этот список не должен содержать более К — к
итерации этот список не должен содержать более К — к  кратчайших отклонений
кратчайших отклонений  С вычислительной точки зрения наиболее сложным является шаг 4, где требуется
С вычислительной точки зрения наиболее сложным является шаг 4, где требуется  или
или  операций в зависимости от того, будут ли все
операций в зависимости от того, будут ли все  или
или  Так как этот шаг при
Так как этот шаг при  итерации выполняется
итерации выполняется  раз и так как
раз и так как  а число итераций равно К, то рассматриваемый алгоритм при нахождении кратчайших путей требует порядка
а число итераций равно К, то рассматриваемый алгоритм при нахождении кратчайших путей требует порядка  или
или  операций. Первая величина относится к графам с неотрицательными матрицами весов, а вторая — к графам с произвольными матрицами.
операций. Первая величина относится к графам с неотрицательными матрицами весов, а вторая — к графам с произвольными матрицами.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
- 2.3. Инкрементальные графы
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
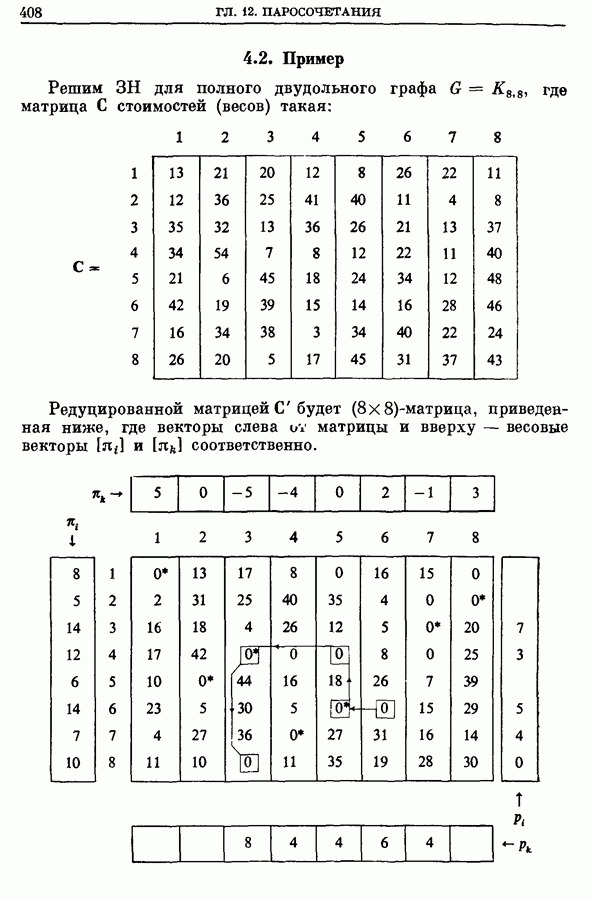
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
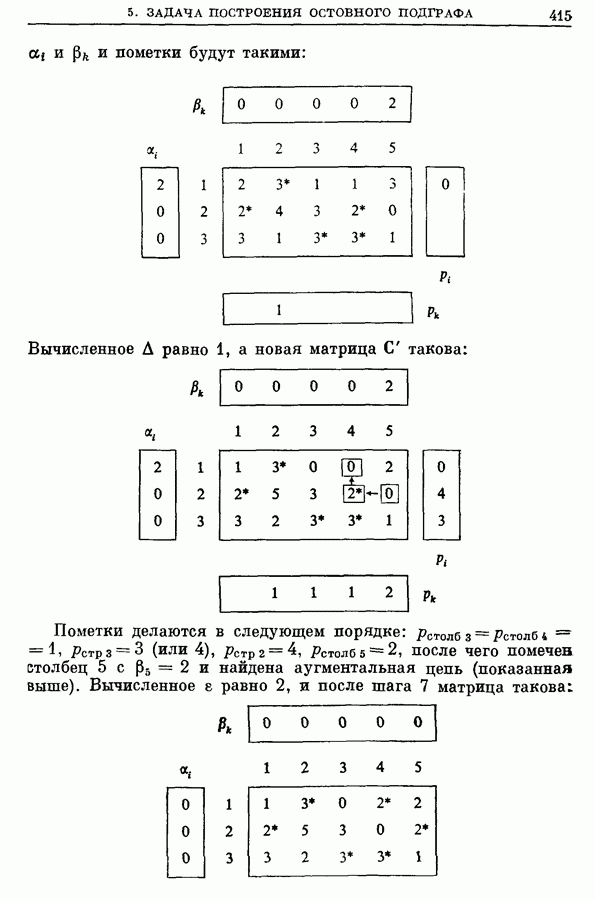
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления