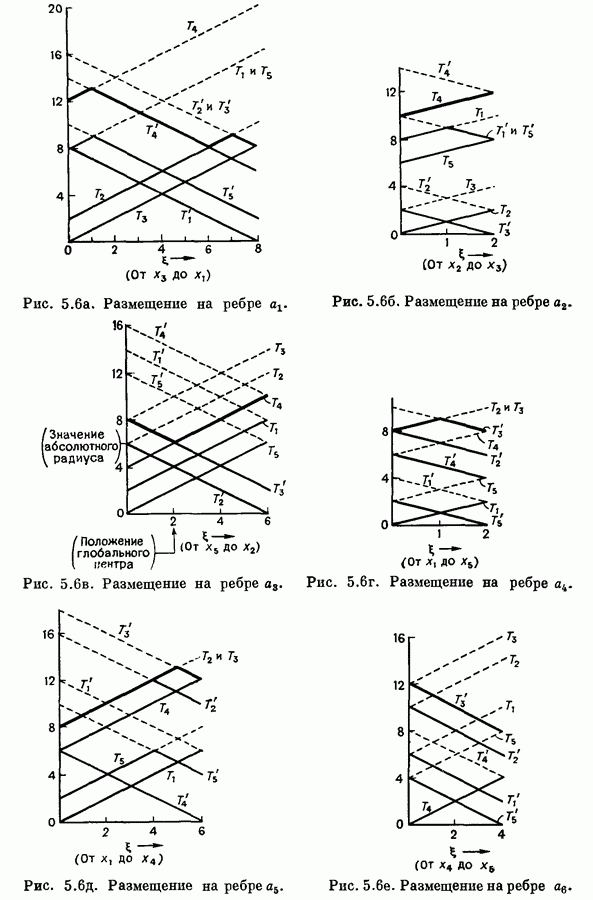
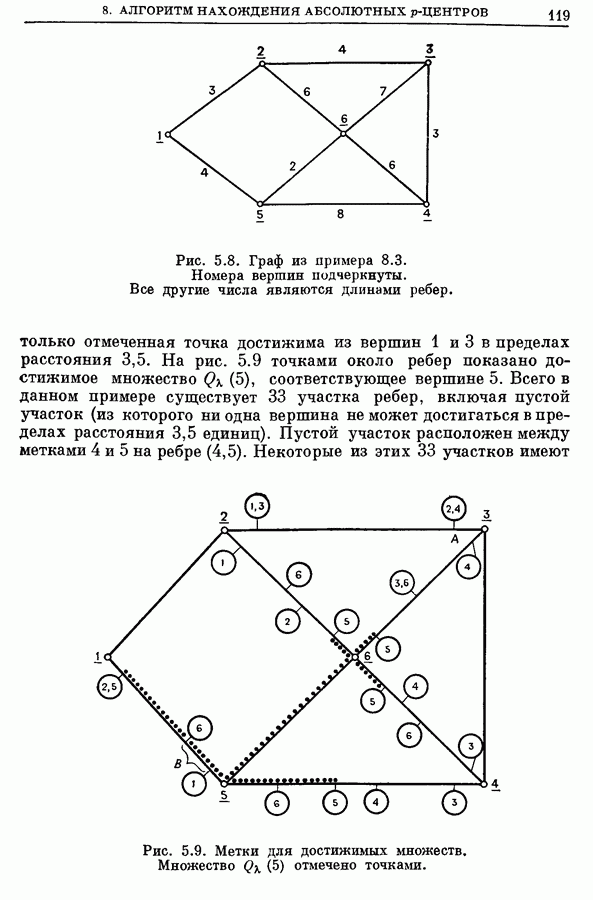
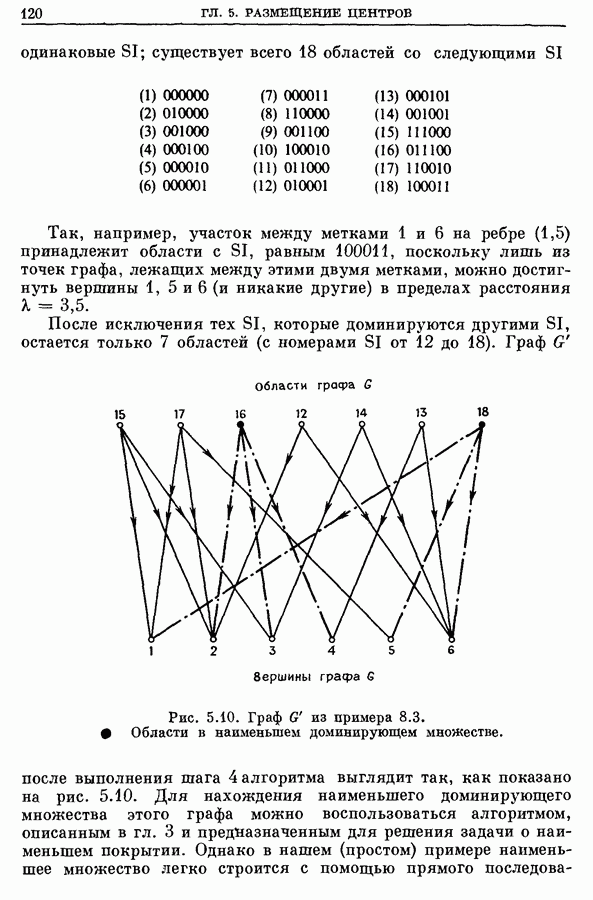
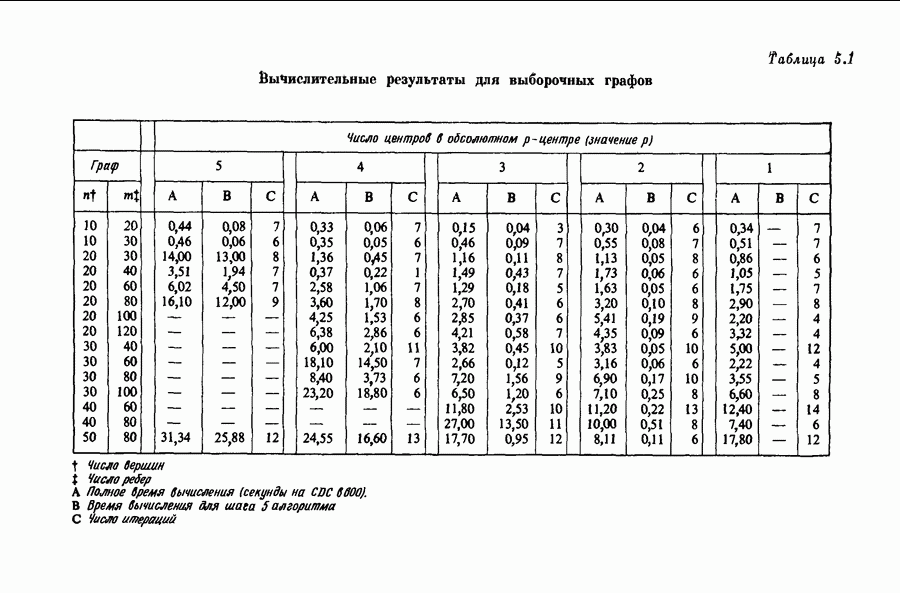
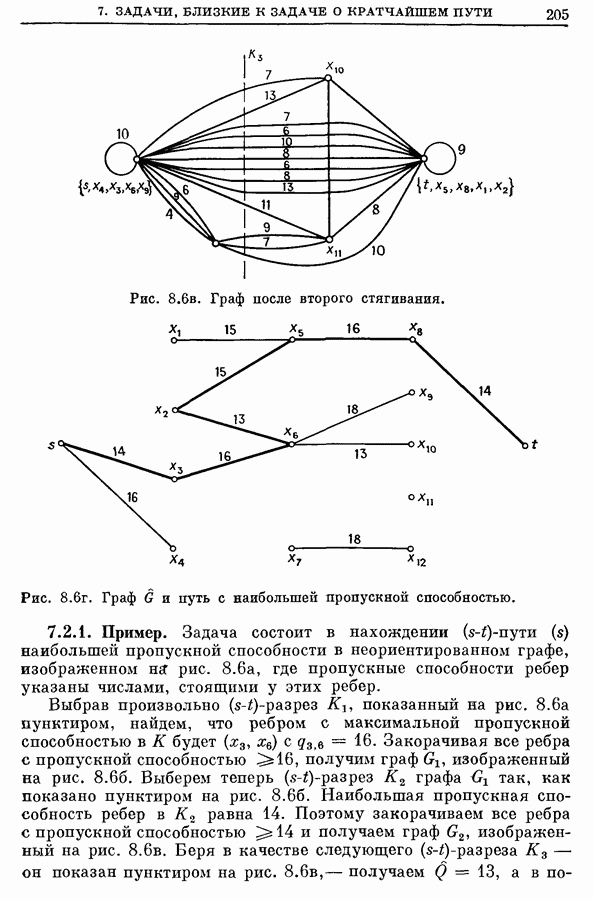
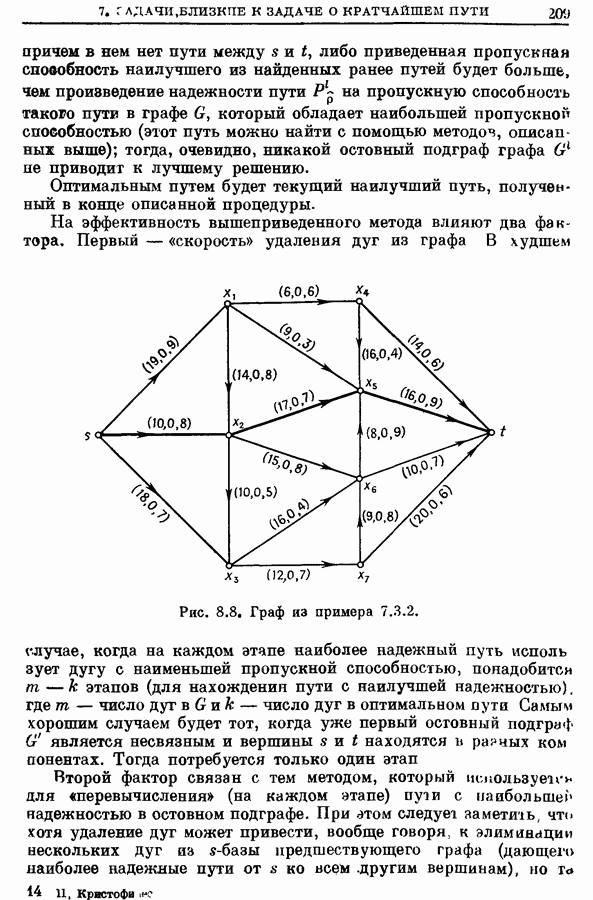
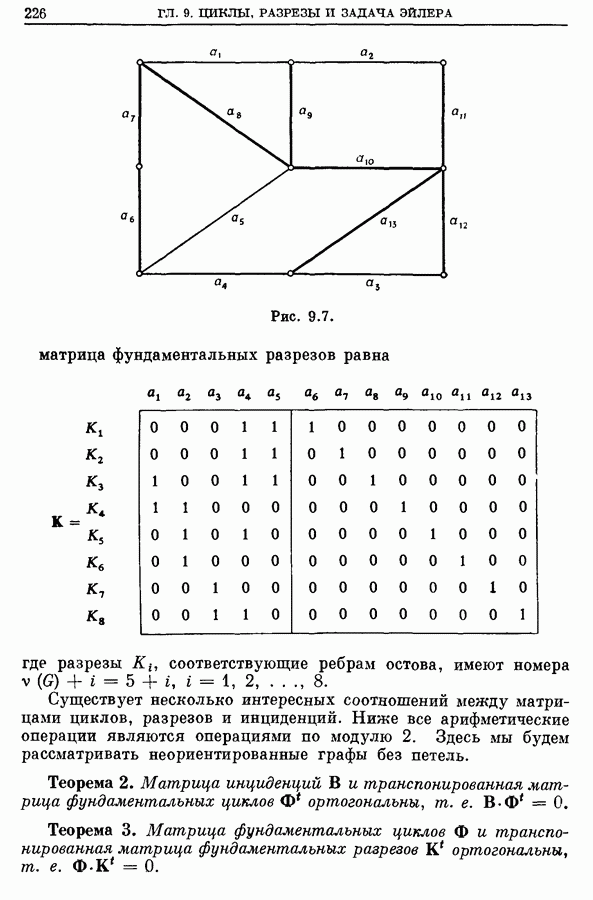
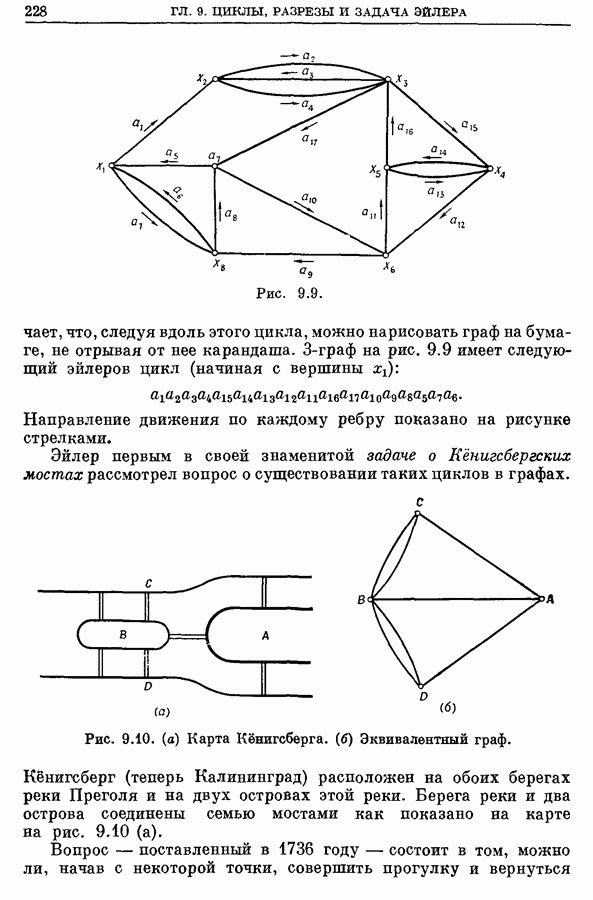
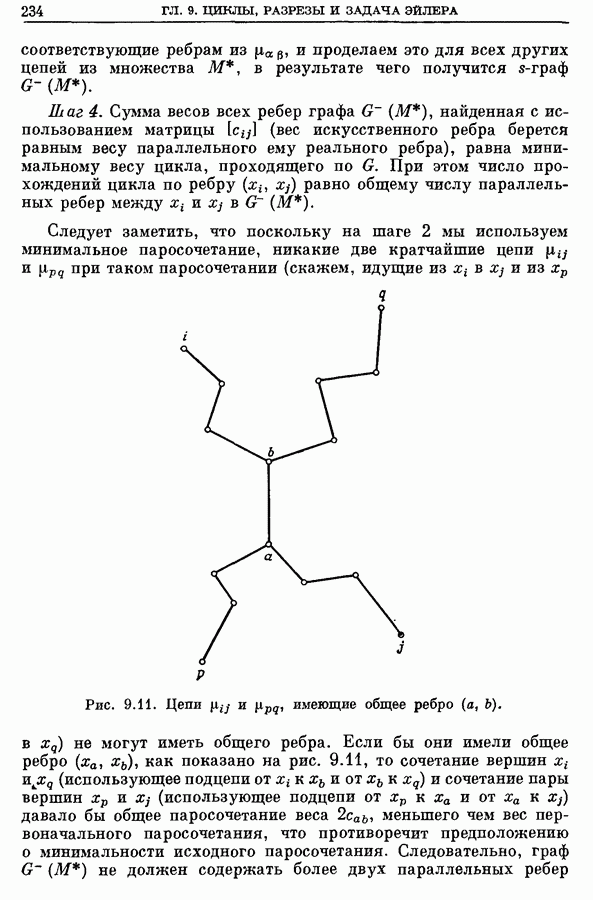
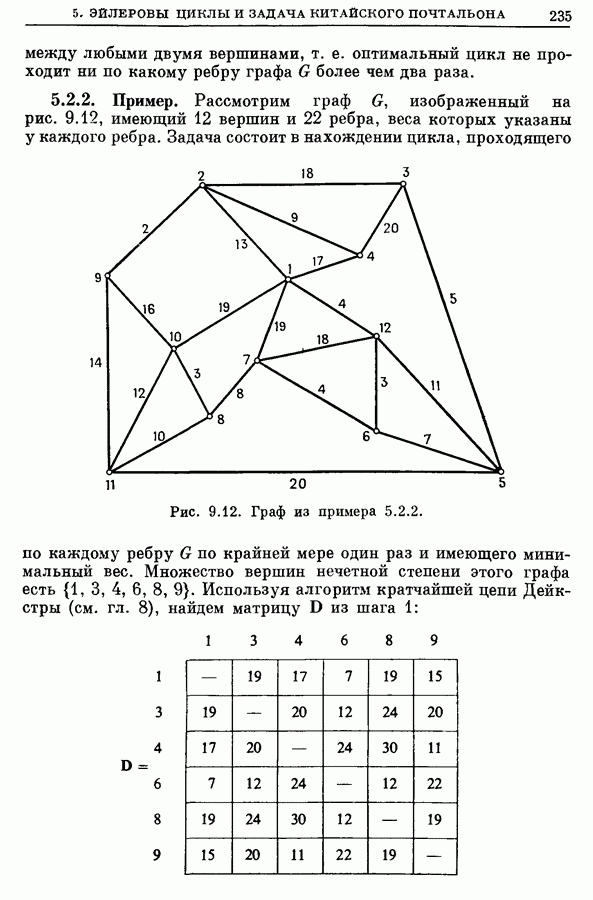
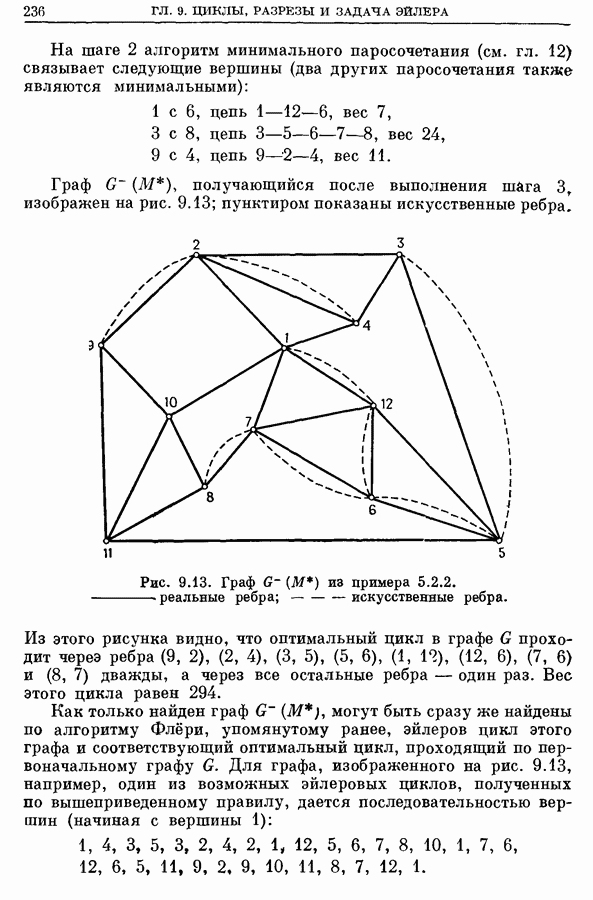
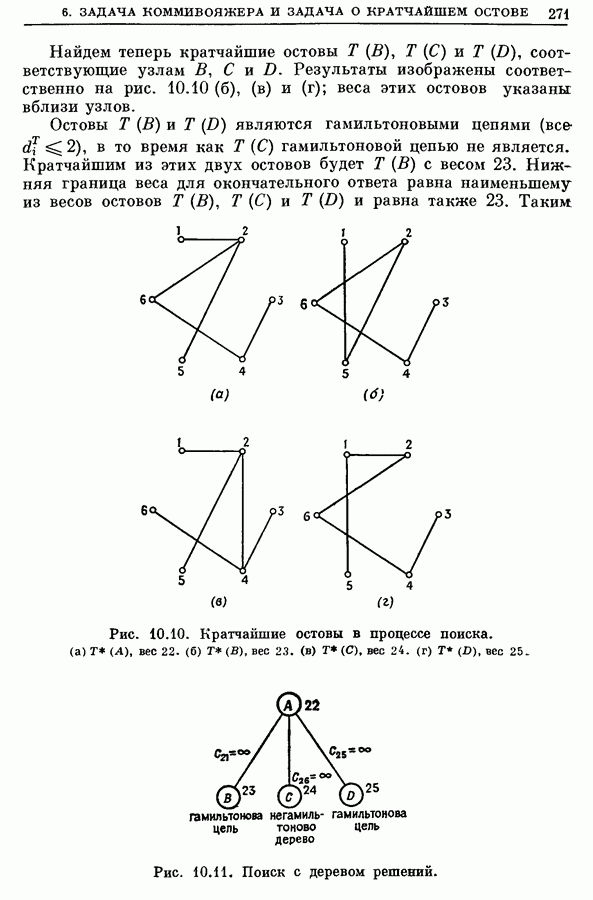
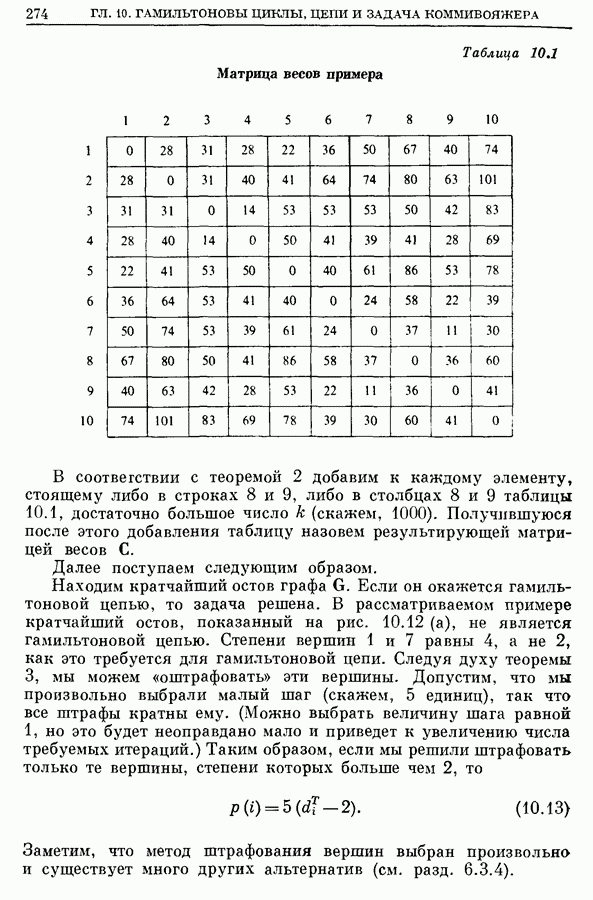
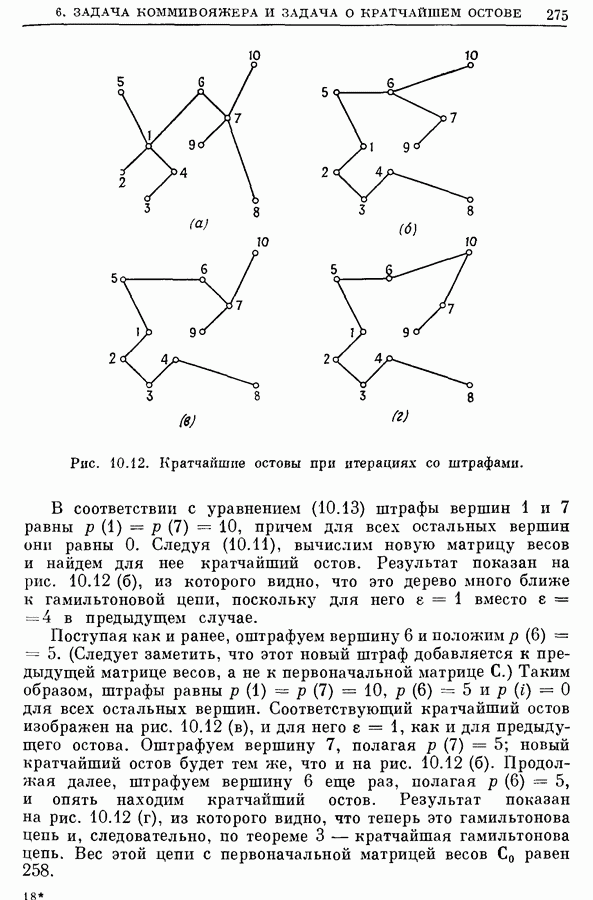
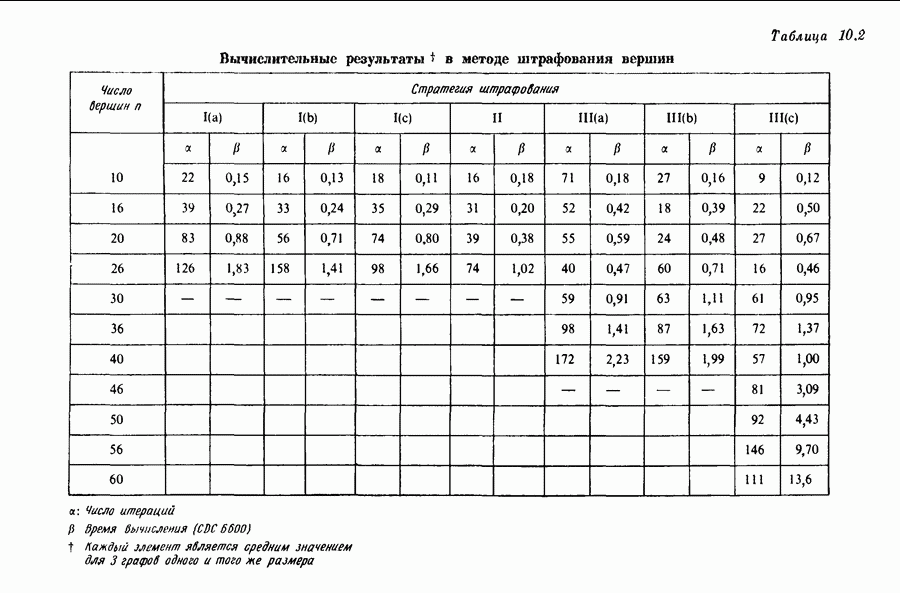
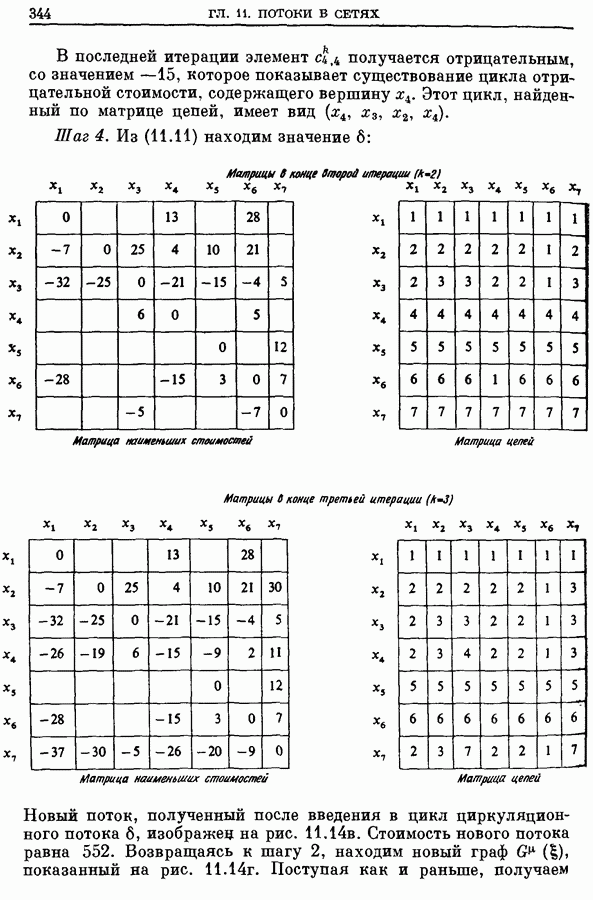
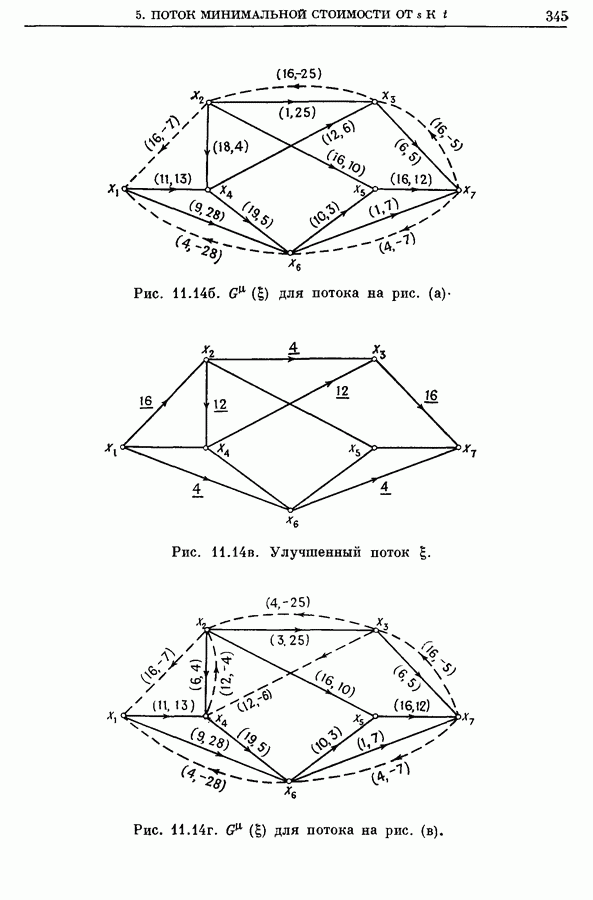
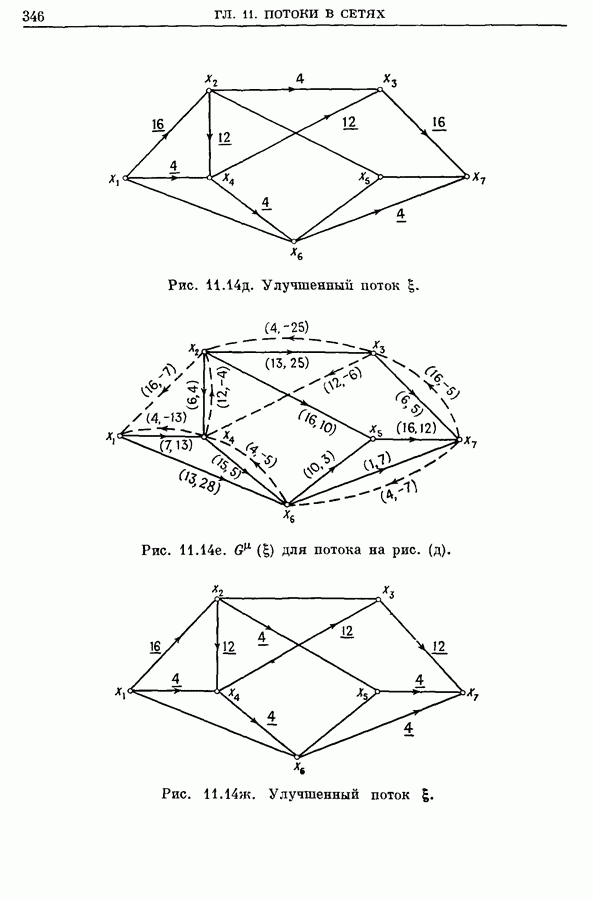
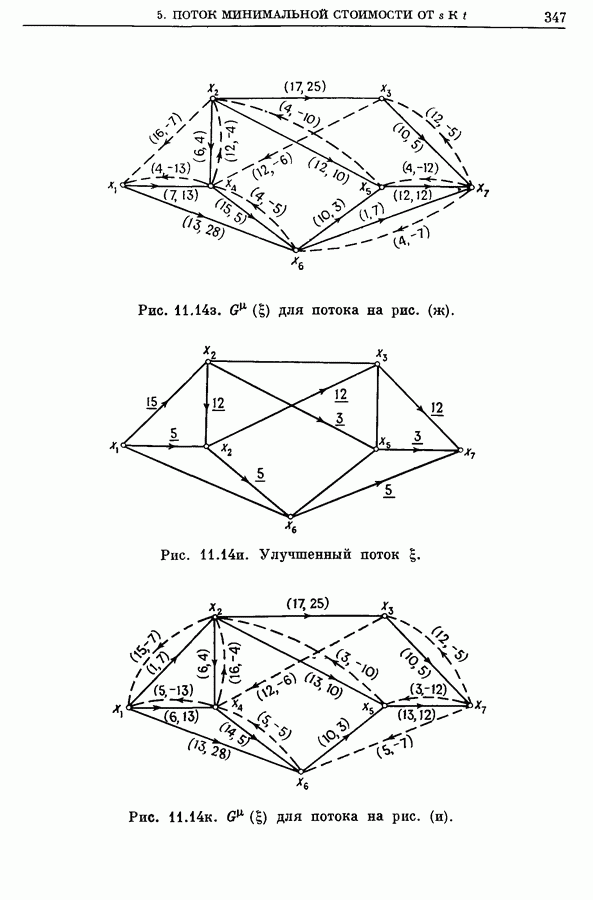
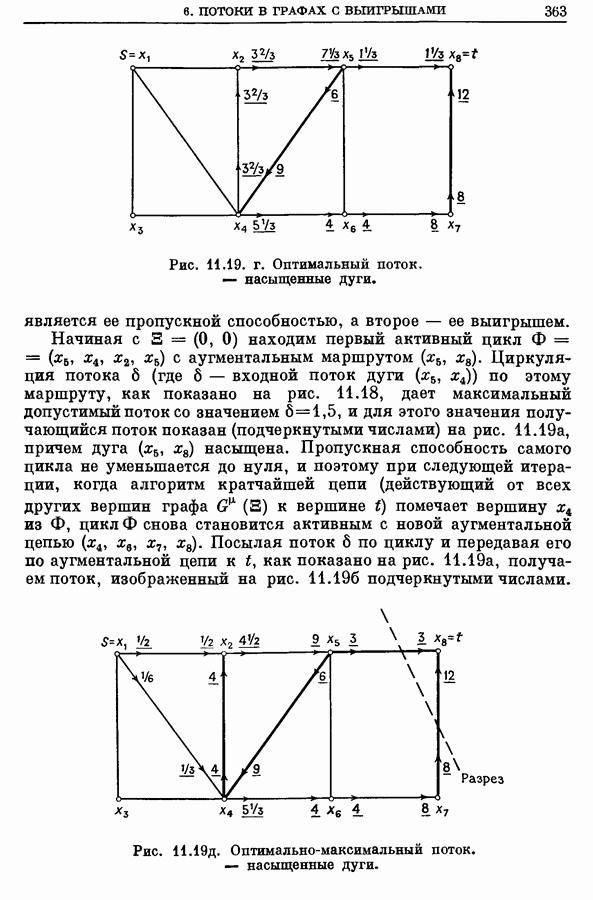
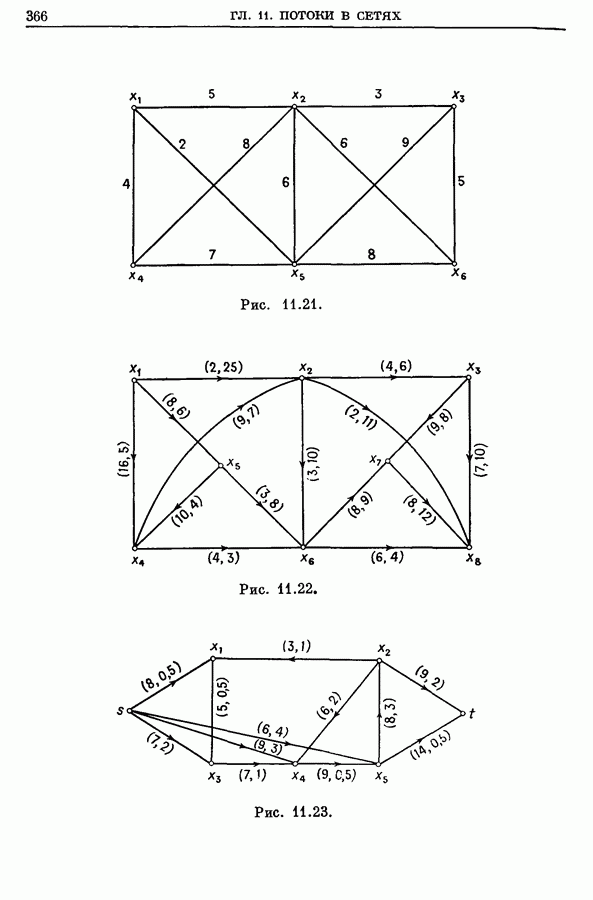
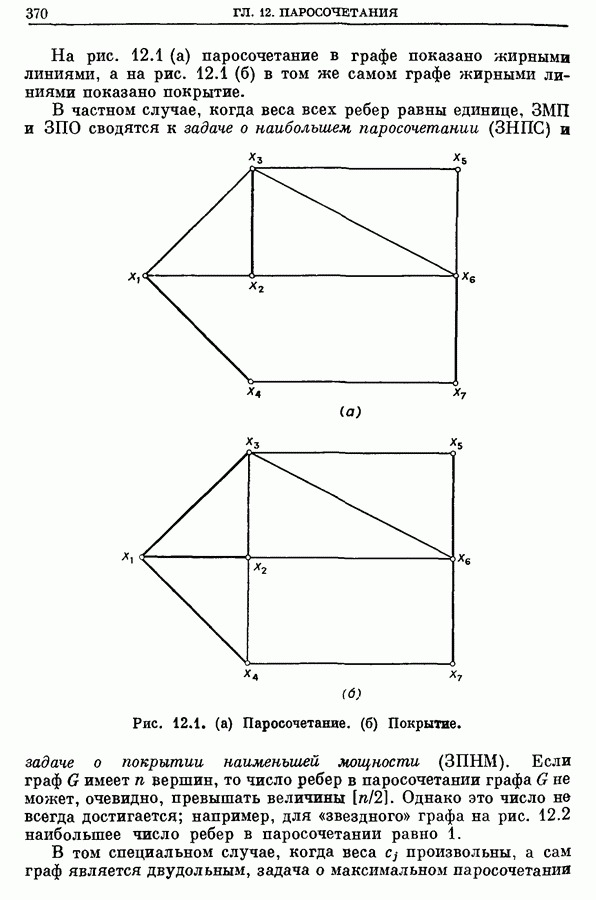
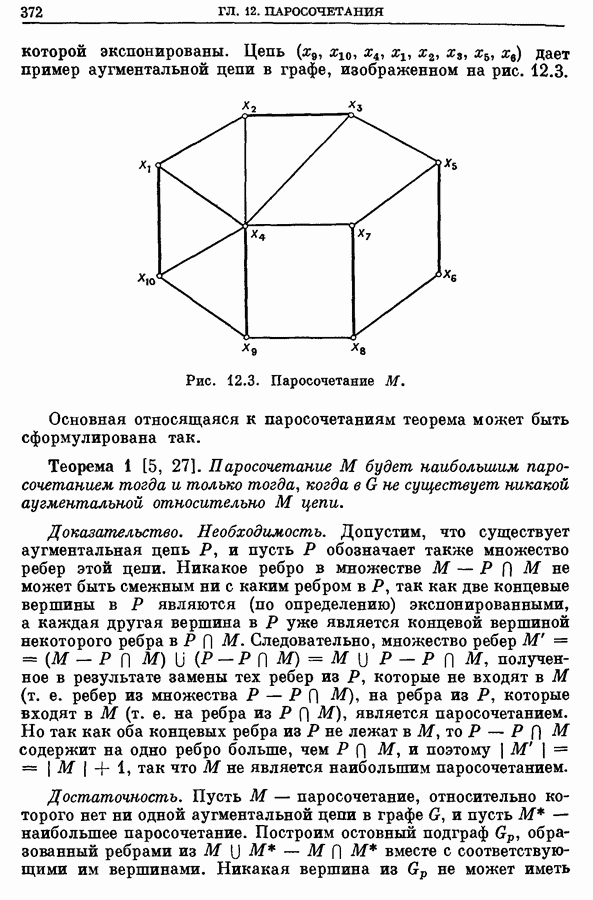
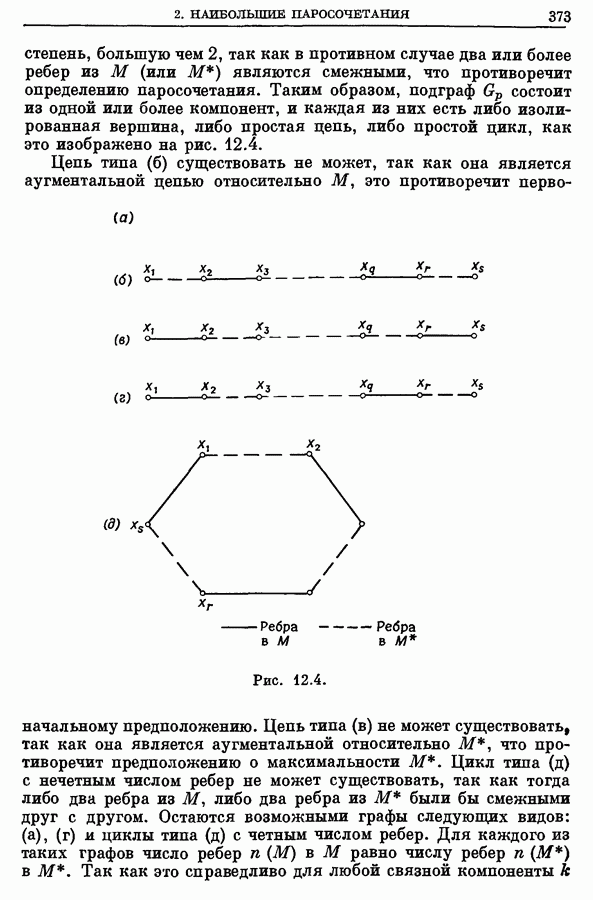
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
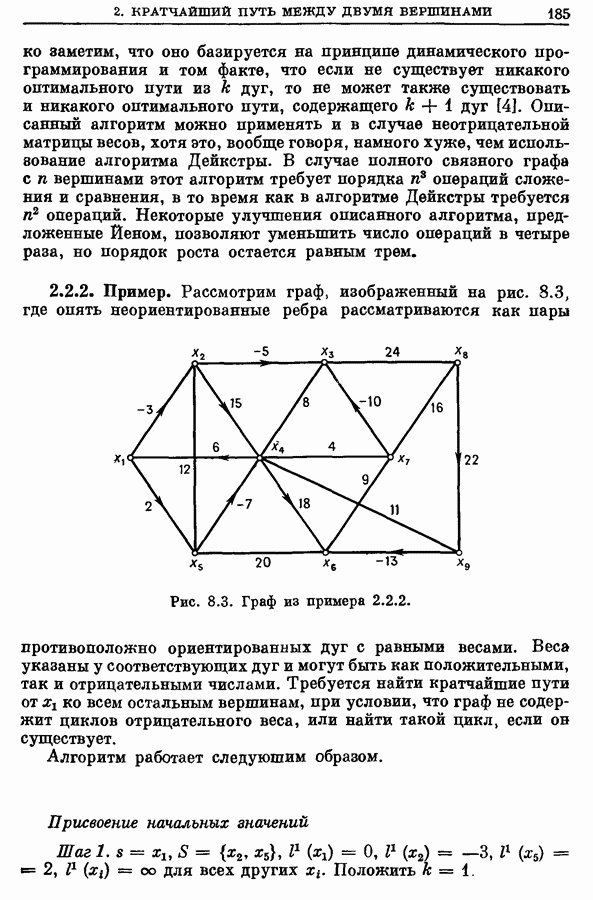
2.2. Цветки
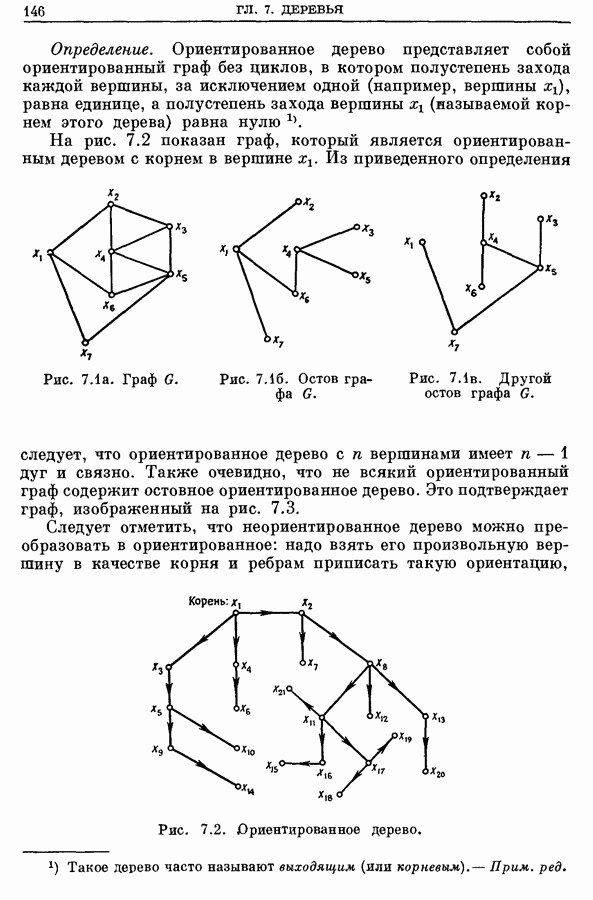
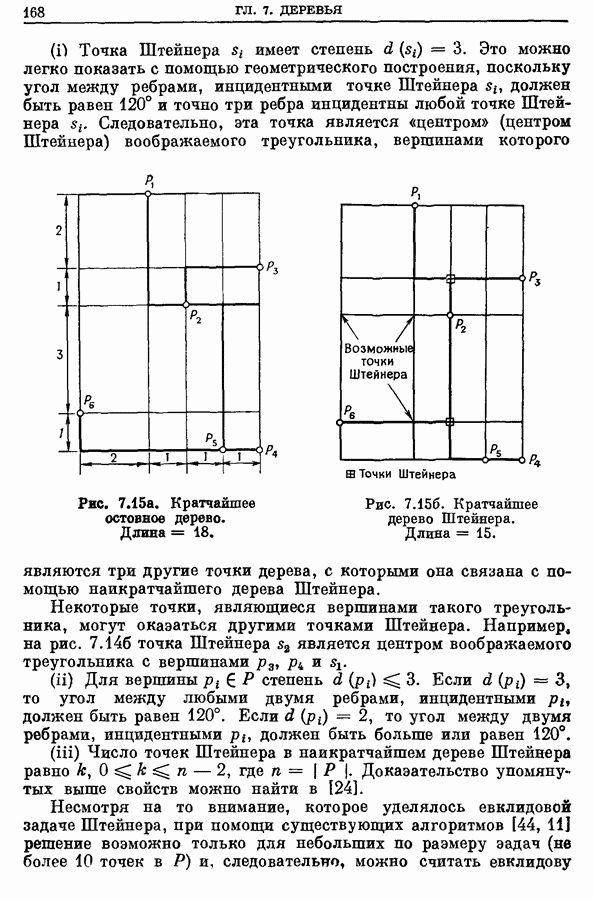
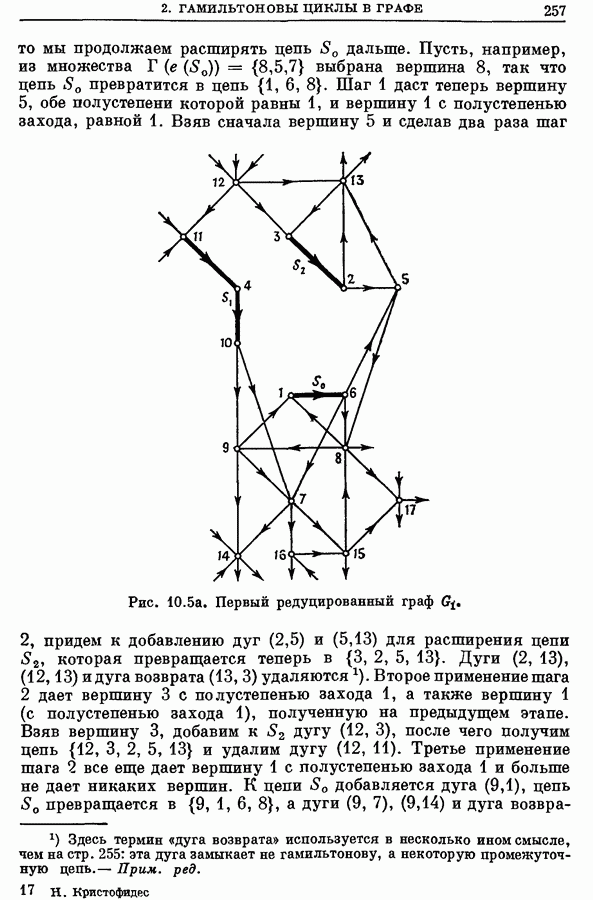
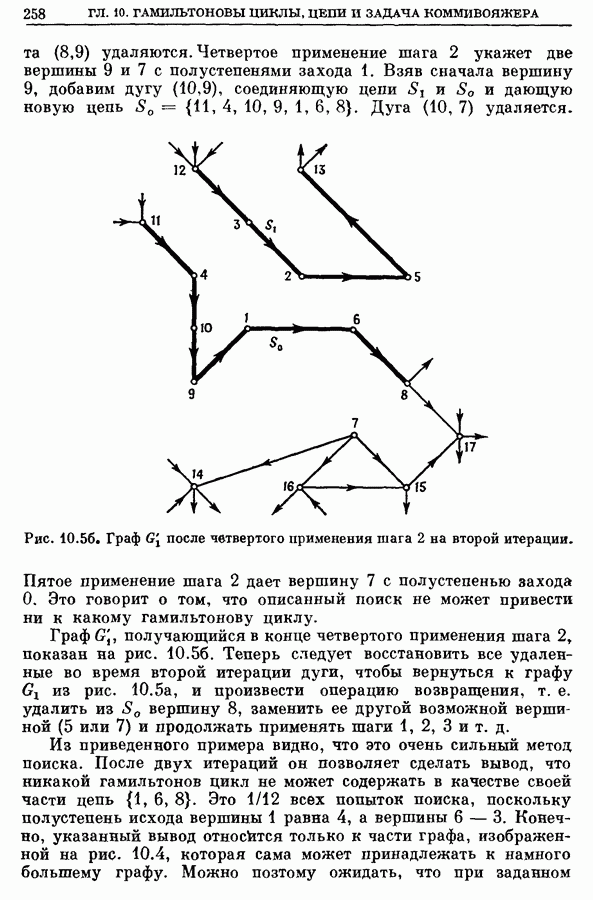
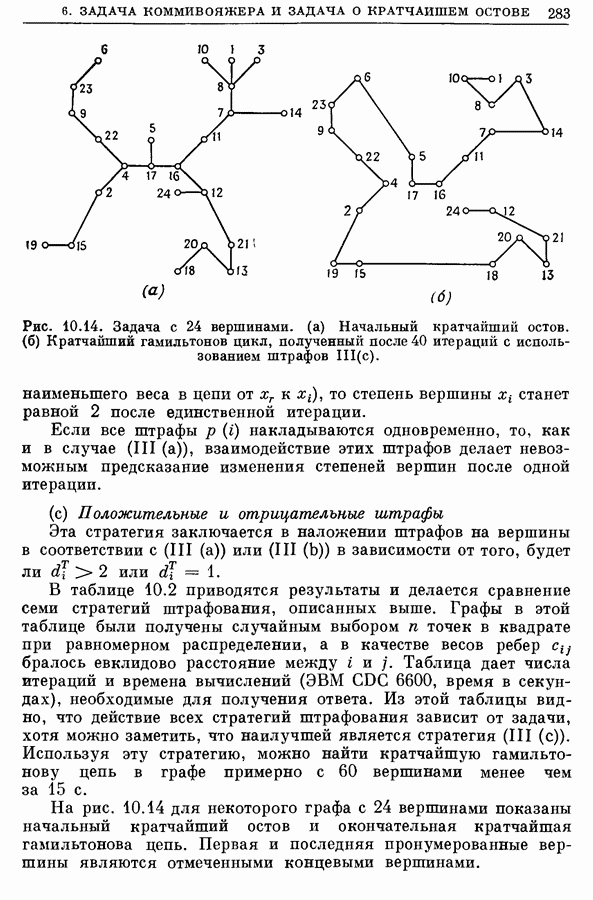
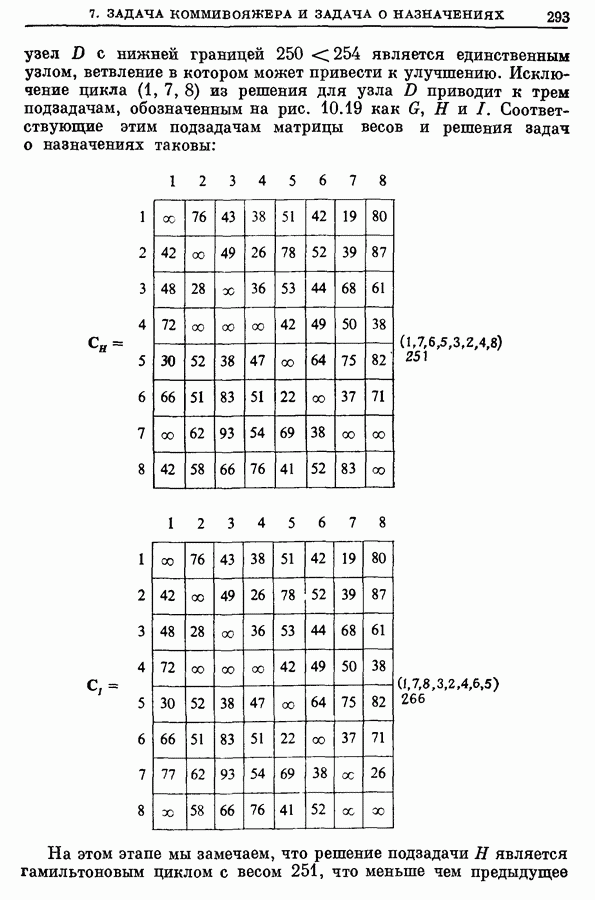
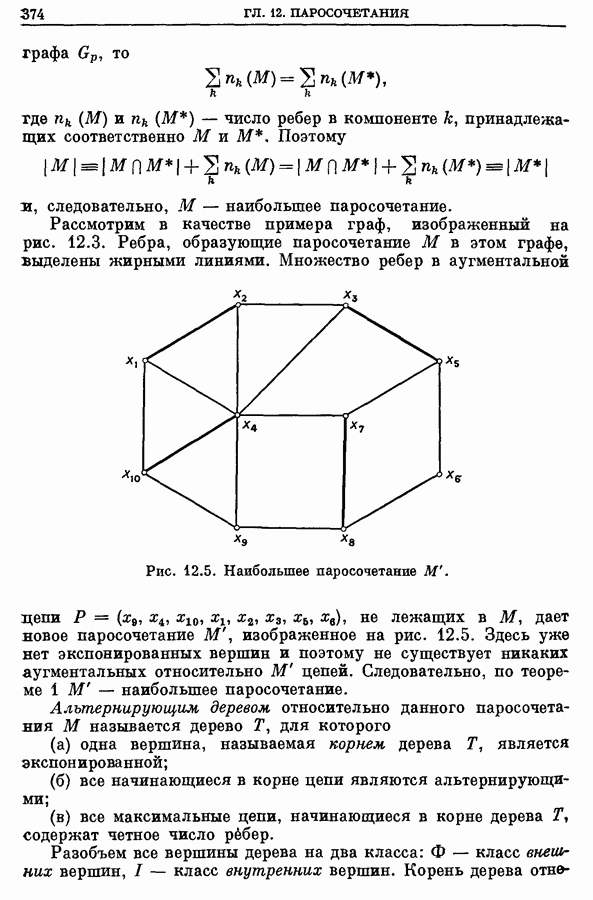
Цветком по отношению к паросочетанию  называется аугментальная цепь, начальная и конечная экспонированные вершины которой совпадают, т. е. эта цепь является циклом, так как число ребер этой цепи нечетно. На рис. 12.7 изображен цветок, образованный цепью с 5 ребрами.
называется аугментальная цепь, начальная и конечная экспонированные вершины которой совпадают, т. е. эта цепь является циклом, так как число ребер этой цепи нечетно. На рис. 12.7 изображен цветок, образованный цепью с 5 ребрами.
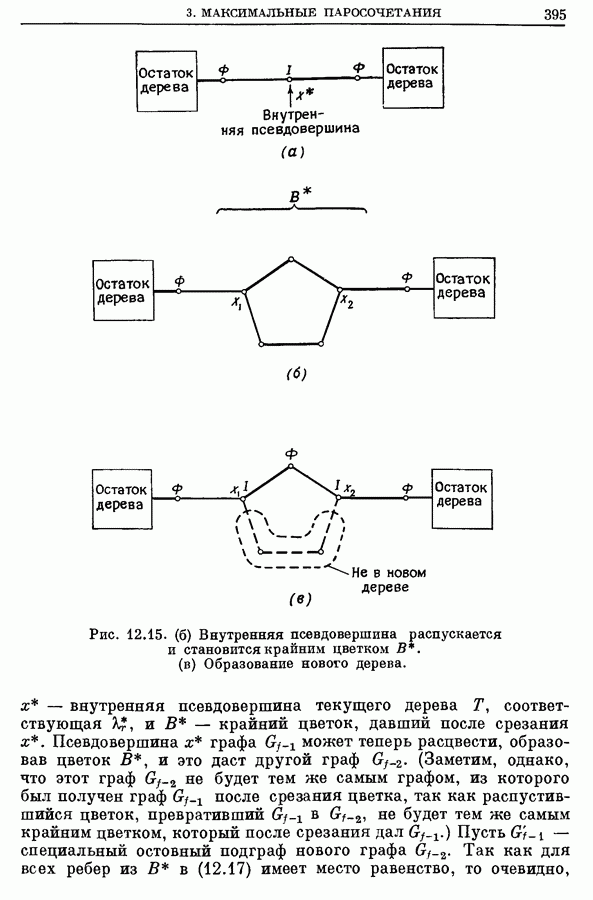
В алгоритмах для ЗМП и  описанных ниже, цветки срезают для того, чтобы получить более простой новый граф. Срезание цветка В состоит в замене всех вершин цветка В (скажем,
описанных ниже, цветки срезают для того, чтобы получить более простой новый граф. Срезание цветка В состоит в замене всех вершин цветка В (скажем,  одной новой псевдовершиной
одной новой псевдовершиной  Ребро
Ребро  добавляется всегда, когда существует ребро из некоторой вершины
добавляется всегда, когда существует ребро из некоторой вершины  к другой вершине
к другой вершине  В упрощенном графе,
В упрощенном графе,
полученном после срезания, вершина  и другие псевдовершины, соответствующие ранее срезанным цветкам, могут в свою очередь образовывать новый цветок, который опять срезается, и т. д. Последний цветок
и другие псевдовершины, соответствующие ранее срезанным цветкам, могут в свою очередь образовывать новый цветок, который опять срезается, и т. д. Последний цветок  не содержащийся ни в каких других цветках, называется крайним цветком. Обоснование процесса срезания цветков основано на теореме 2, приводимой ниже.
не содержащийся ни в каких других цветках, называется крайним цветком. Обоснование процесса срезания цветков основано на теореме 2, приводимой ниже.
Цветущее дерево — это альтернирующее дерево относительно данного паросочетания, для которого существует ребро  соединяющее две внешние вершины дерева:
соединяющее две внешние вершины дерева: 

Рис. 12.7. Дерево с цветком.
Если  множество ребер цепи, начинающейся в корне альтернирующего дерева и кончающейся в
множество ребер цепи, начинающейся в корне альтернирующего дерева и кончающейся в  а
а  соответствующее множество для
соответствующее множество для  то множество ребер
то множество ребер  вместе с ребром
вместе с ребром  образует цветок. На рис. 12.7 изображено цветущее дерево.
образует цветок. На рис. 12.7 изображено цветущее дерево.
Когда цветок В срезан, получающаяся псевдовершина считается внешней вершиной. Всякая вершина из В может быть по желанию отнесена к внутренним или к внешним вершинам, так как если вершина принадлежит В, то она является концевой и в цепях с четным, и в цепях с нечетным числом ребер, начинающихся в корне дерева (в зависимости от маршрута, по которому проходят эти цепи до прихода в первую вершину цветка). Так, на рис. 12.7 вершина  может быть помечена как внутренняя, если рассматривать цепь
может быть помечена как внутренняя, если рассматривать цепь  и как внешняя, если брать цепь
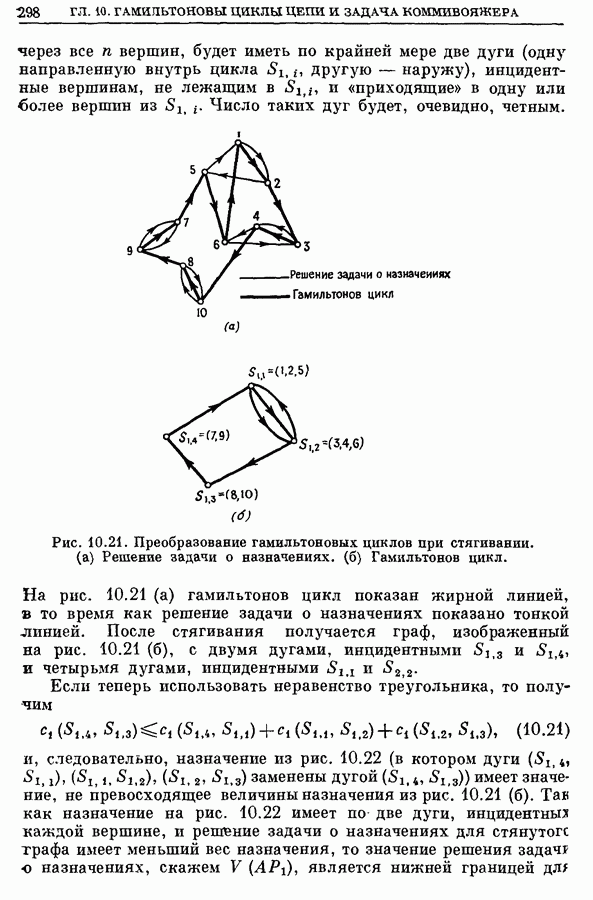
и как внешняя, если брать цепь  Но когда псевдовершина, получающаяся после срезания цветка, помечается как «внешняя», структура остающегося альтернирующего дерева все еще будет корректной — как это вытекает из определения альтернирующего дерева. Таким образом, после срезания цветка альтернирующее дерево в получившемся графе сохраняется.
Но когда псевдовершина, получающаяся после срезания цветка, помечается как «внешняя», структура остающегося альтернирующего дерева все еще будет корректной — как это вытекает из определения альтернирующего дерева. Таким образом, после срезания цветка альтернирующее дерево в получившемся графе сохраняется.
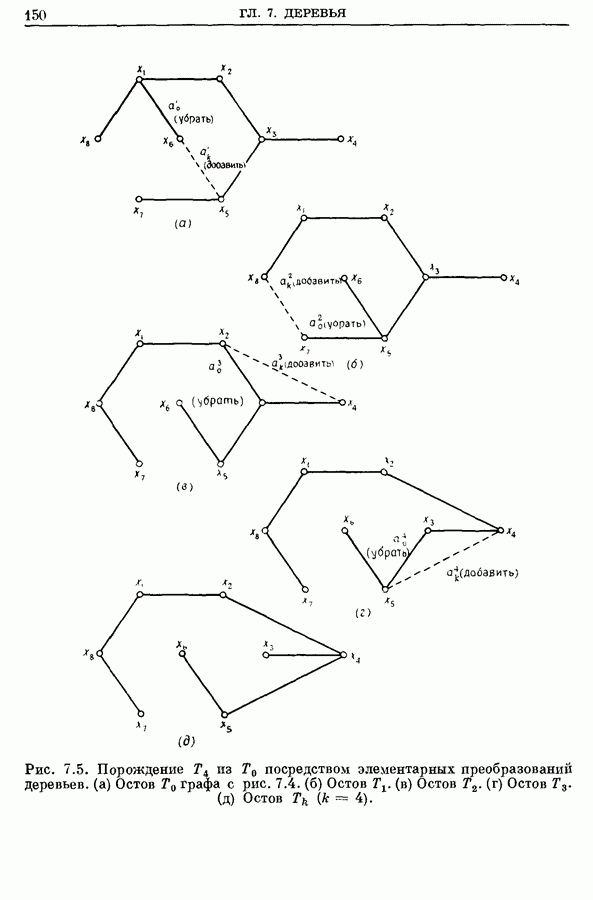
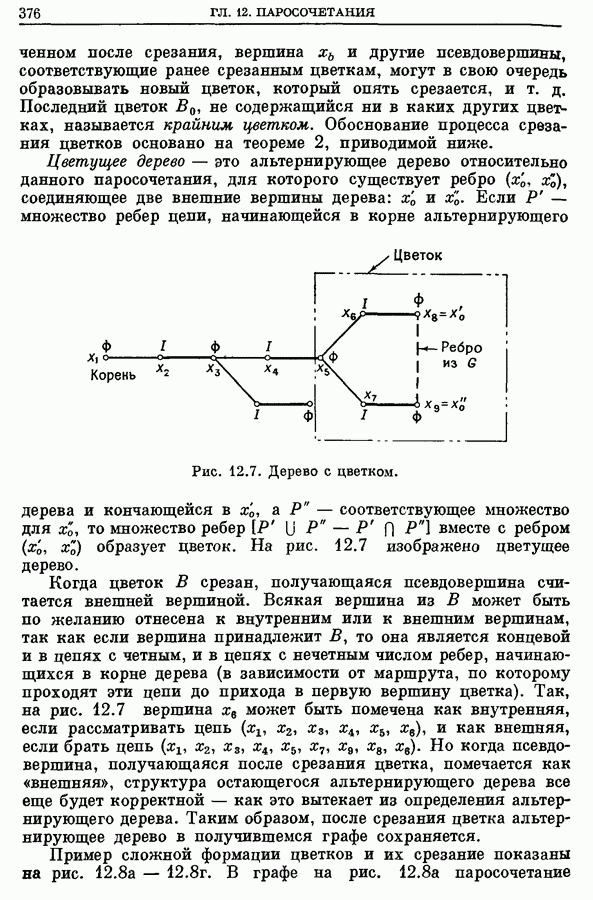
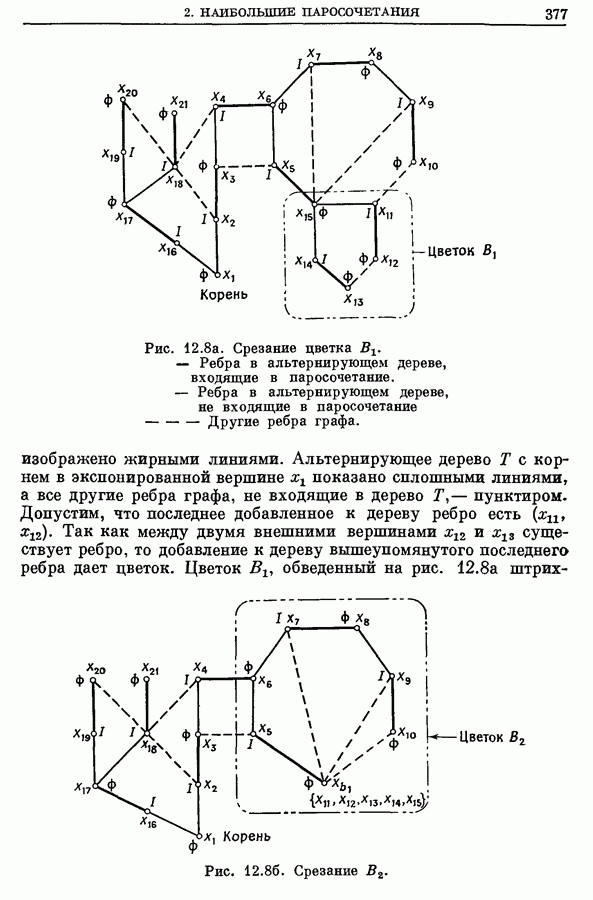
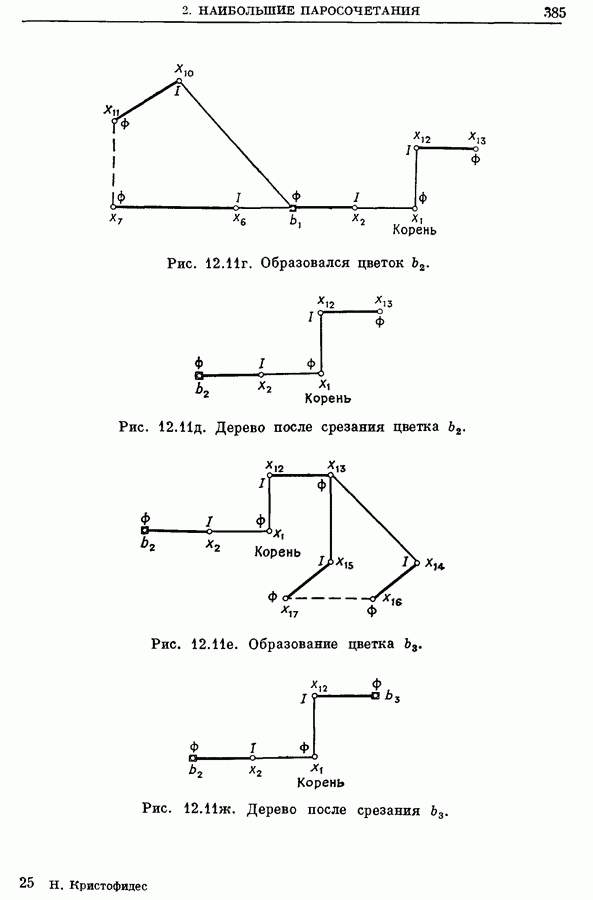
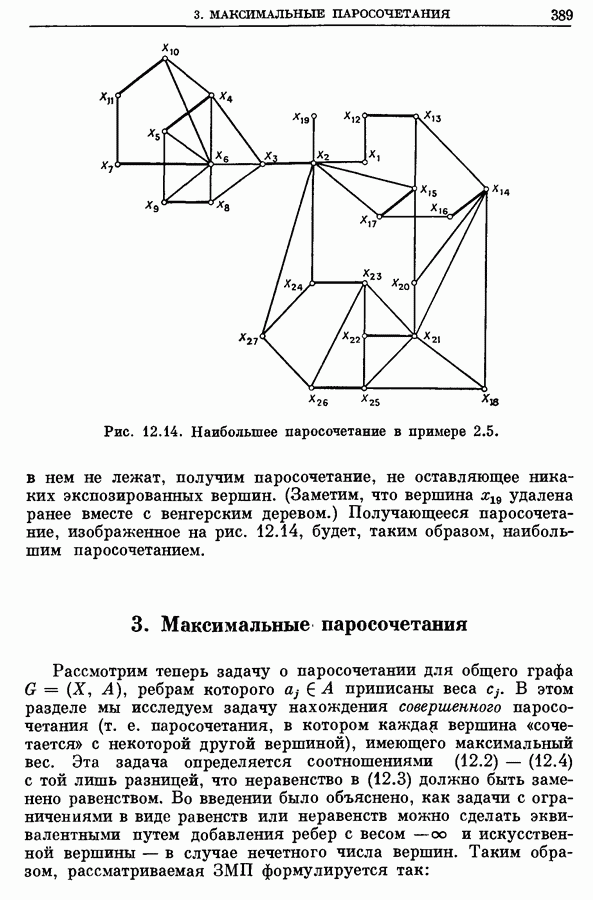
Пример сложной формации цветков и их срезание показаны на рис. 12.8а  графе на рис. 12.8а паросочетание
графе на рис. 12.8а паросочетание

Рис. 12.8а. Срезание цветка  Ребра в альтернирующем дереве, входящие в паросочетание. Ребра в альтернирующем дереве, не входящие в паросочетание
Ребра в альтернирующем дереве, входящие в паросочетание. Ребра в альтернирующем дереве, не входящие в паросочетание  Другие ребра графа.
Другие ребра графа.
изображено жирными линиями. Альтернирующее дерево  с корнем в экспонированной вершине
с корнем в экспонированной вершине  показано сплошными линиями, а все другие ребра графа, не входящие в дерево
показано сплошными линиями, а все другие ребра графа, не входящие в дерево  пунктиром. Допустим, что последнее добавленное к дереву ребро есть
пунктиром. Допустим, что последнее добавленное к дереву ребро есть  Так как между двумя внешними вершинами
Так как между двумя внешними вершинами  существует ребро, то добавление к дереву вышеупомянутого последнего ребра дает цветок. Цветок
существует ребро, то добавление к дереву вышеупомянутого последнего ребра дает цветок. Цветок  обведенный на рис. 12.8а
обведенный на рис. 12.8а

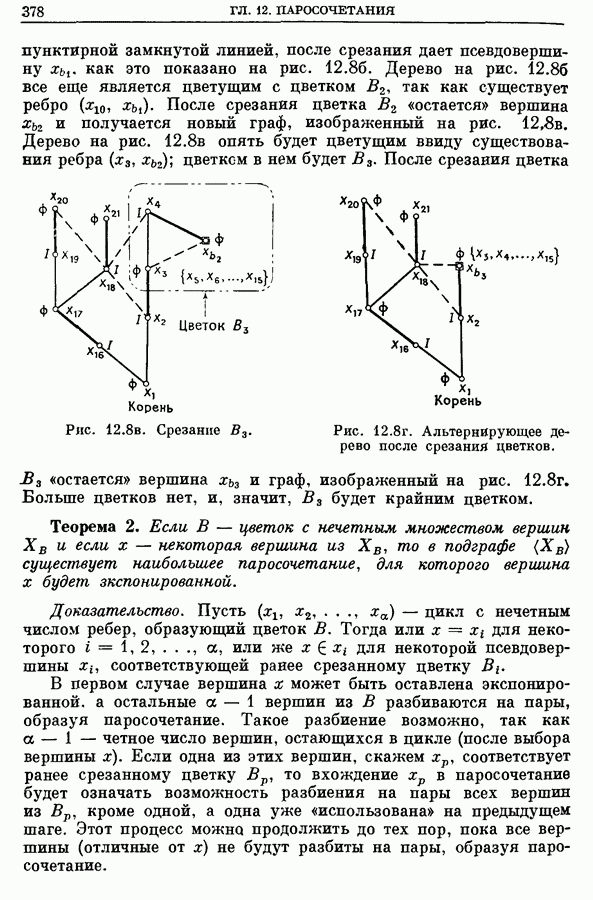
Рис. 12.86. Срезание 
штрих-пунктирной замкнутой линией, после срезания дает псевдовершину  как это показано на рис. 12.86. Дерево на рис. 12.86 все еще является цветущим с цветком
как это показано на рис. 12.86. Дерево на рис. 12.86 все еще является цветущим с цветком  так как существует ребро
так как существует ребро  После срезания цветка
После срезания цветка  «остается» вершина
«остается» вершина  и получается новый граф, изображенный на рис.
и получается новый граф, изображенный на рис.  Дерево на рис. 12.8в опять будет цветущим ввиду существования ребра
Дерево на рис. 12.8в опять будет цветущим ввиду существования ребра  цветком в нем будет
цветком в нем будет  После срезания цветка
После срезания цветка  «остается» вершина
«остается» вершина  и граф, изображенный на рис. 12.8г.
и граф, изображенный на рис. 12.8г.

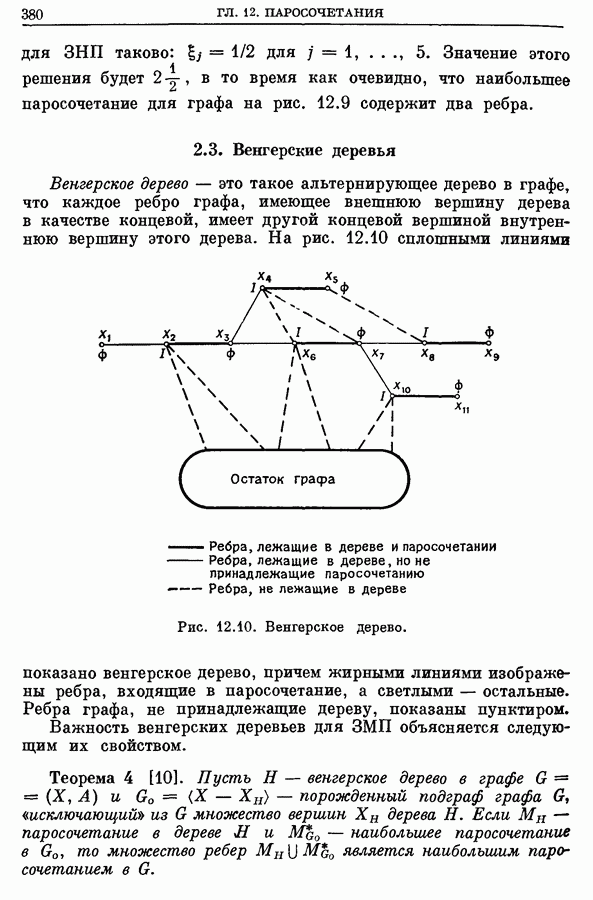
Рис. 12.8в. Срезание 

Рис. 12.8г. Альтернирующее дерево после срезания цветков.
Больше цветков нет, и, значит,  будет крайним цветком.
будет крайним цветком.
Теорема 2. Если В — цветок с нечетным множеством вершин  и если
и если  некоторая вершина из
некоторая вершина из  то в подграфе
то в подграфе  существует наибольшее паросочетание, для которого вершина х будет экспонированной.
существует наибольшее паросочетание, для которого вершина х будет экспонированной.
Доказательство. Пусть  цикл с нечетным числом ребер, образующий цветок В. Тогда или
цикл с нечетным числом ребер, образующий цветок В. Тогда или  для некоторого
для некоторого  или же
или же  для некоторой псевдовершины
для некоторой псевдовершины  соответствующей ранее срезанному цветку
соответствующей ранее срезанному цветку 
В первом случае вершина х может быть оставлена экспонированной. а остальные  вершин из В разбиваются на пары, образуя паросочетание. Такое разбиение возможно, так как
вершин из В разбиваются на пары, образуя паросочетание. Такое разбиение возможно, так как  четное число вершин, остающихся в цикле (после выбора вершины
четное число вершин, остающихся в цикле (после выбора вершины  Если одна из этих вершин, скажем
Если одна из этих вершин, скажем  соответствует ранее срезанному цветку
соответствует ранее срезанному цветку  то вхождение
то вхождение  в паросочетание будет означать возможность разбиения на пары всех вершин из
в паросочетание будет означать возможность разбиения на пары всех вершин из  кроме одной, а одна уже «использована» на предыдущем шаге. Этот процесс можно продолжить до тех пор, пока все вершины (отличные от х) не будут разбиты на пары, образуя паросочетание.
кроме одной, а одна уже «использована» на предыдущем шаге. Этот процесс можно продолжить до тех пор, пока все вершины (отличные от х) не будут разбиты на пары, образуя паросочетание.
В последнем из двух упомянутых случаев вершина  может быть оставлена экспонированной, а остальные
может быть оставлена экспонированной, а остальные  вершин из В разобьются на пары, порождая паросочетание, как и выше. Цветок
вершин из В разобьются на пары, порождая паросочетание, как и выше. Цветок  это цикл с нечетным числом ребер, и, следовательно, получается такая же самая ситуация относительно
это цикл с нечетным числом ребер, и, следовательно, получается такая же самая ситуация относительно  какая уже обсуждалась в случае цветка В, так что экспонированной в конце концов останется только вершина х.
какая уже обсуждалась в случае цветка В, так что экспонированной в конце концов останется только вершина х.
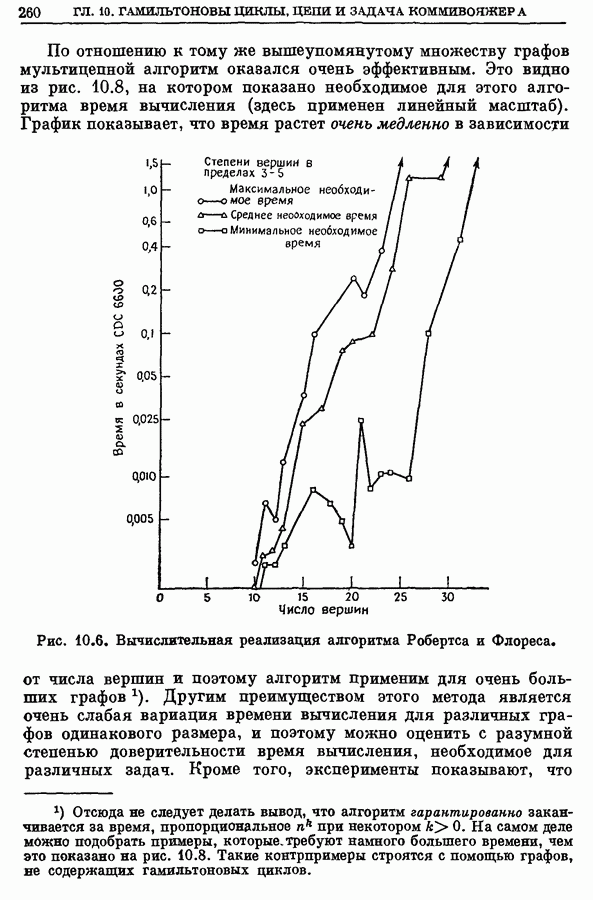
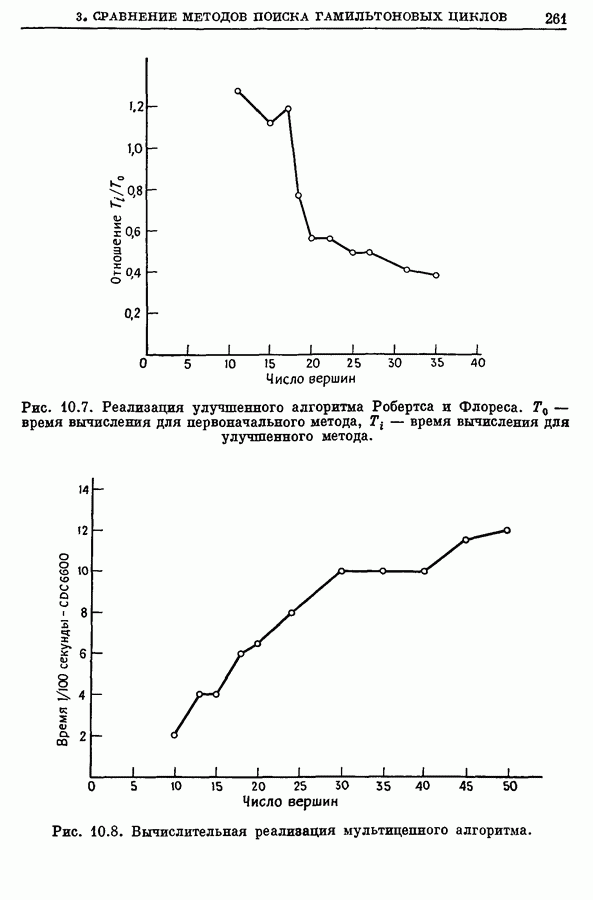
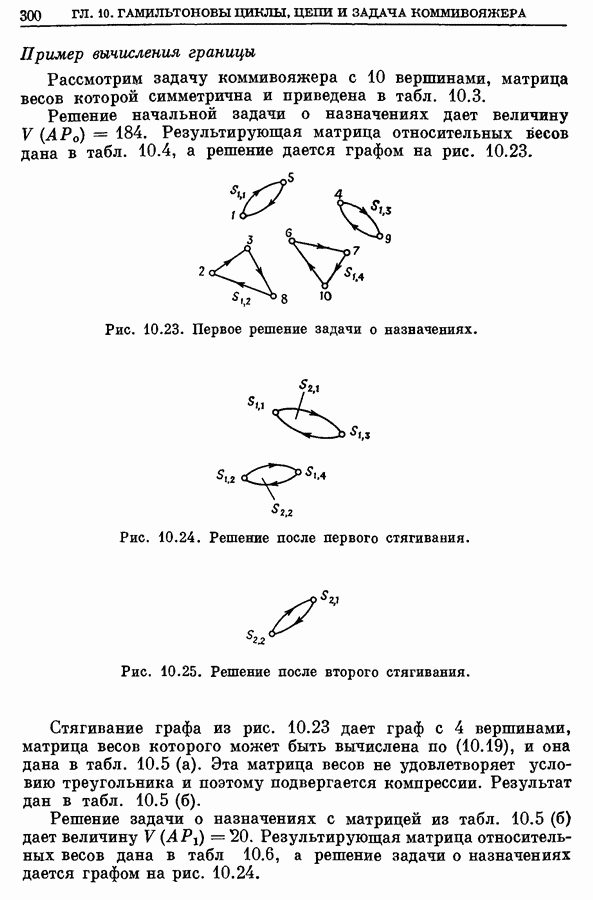
Важность цветков и циклов (цепей) с нечетным числом ребер в задачах о паросочетаниях можно оценить, анализируя следующий факт: при отсутствии таких циклов формулировка ЗМП на языке линейного программирования, даваемая соотношениями (12.2) и (12.3), приводит к собственно целочисленному решению, так что ограничения (12.4) становятся излишними [8, 16, 17]. Графы, не содержащие циклов с нечетным числом ребер, являются двудольными графами; они рассматриваются в последующих параграфах. Общие свойства полиэдров, определяемых соотношениями (12.3), содержатся в следующей теореме Балински [1].
Теорема 3. Все вершины, выпуклого полиэдра, задаваемого неравенствами

где  матрица инциденций графа, имеют координаты со значениями 0, 1/2 или 1.
матрица инциденций графа, имеют координаты со значениями 0, 1/2 или 1.
Случай нецелочисленных значений (а именно значения 1/2) отвечает циклам с нечетным числом ребер.

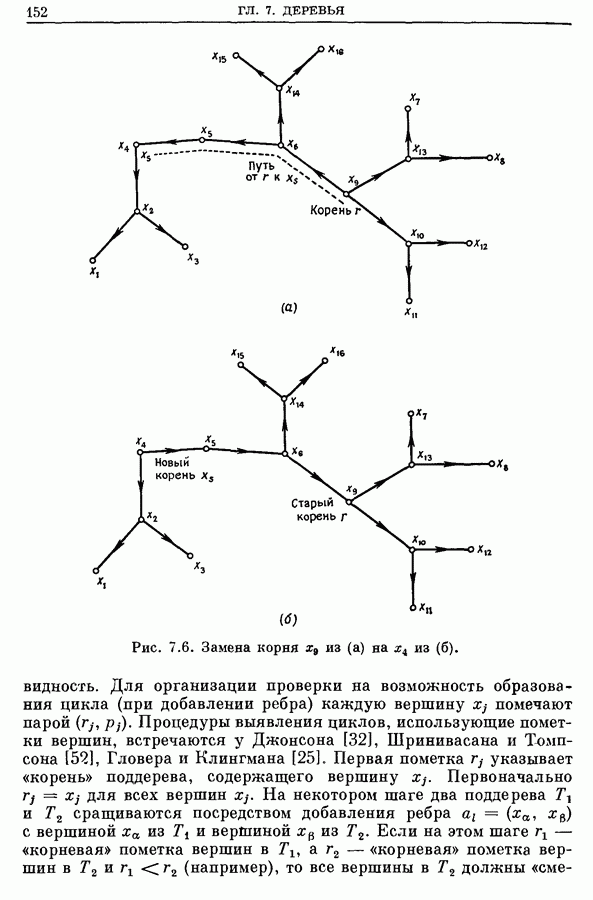
Рис. 12.9.
Если, например, граф состоит из единственного такого цикла, как показано на рис. 12.9, то решение задачи линейного программирования (12.2) и (12.3)
для ЗНП таково:  для
для  Значение этого решения будет 2 у, в то время как очевидно, что наибольшее паросочетание для графа на рис. 12.9 содержит два ребра.
Значение этого решения будет 2 у, в то время как очевидно, что наибольшее паросочетание для графа на рис. 12.9 содержит два ребра.
| << Предыдущий параграф | Следующий параграф >> |
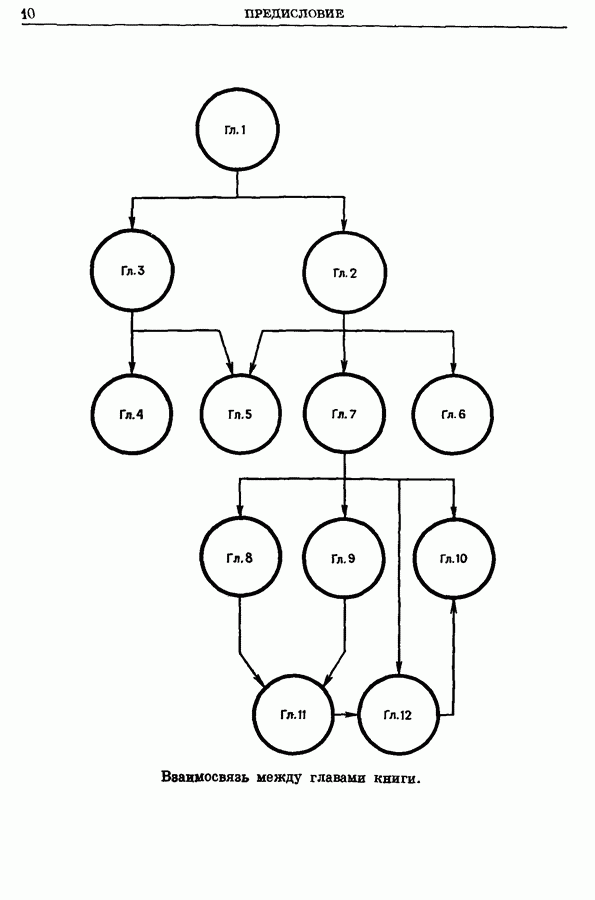
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
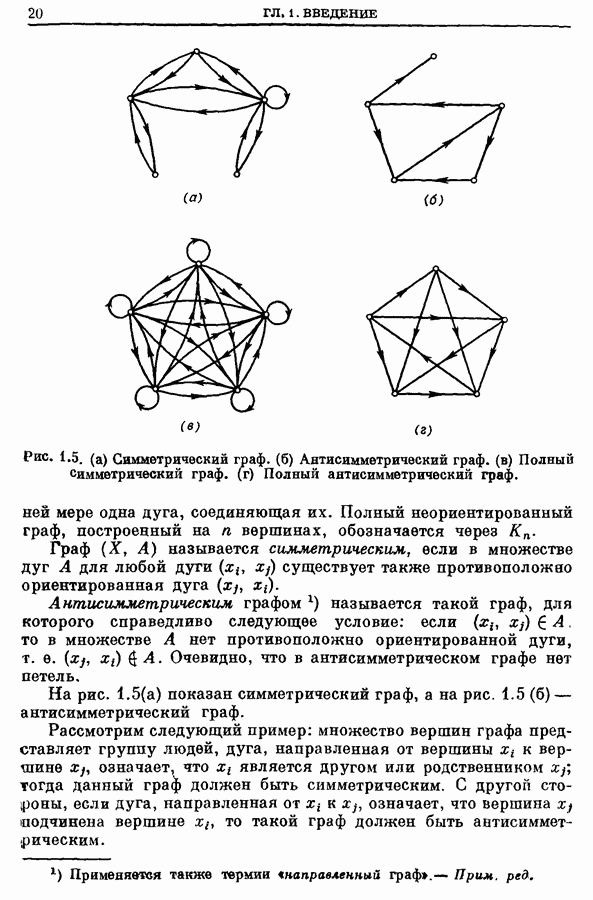
- 6. Типы графов
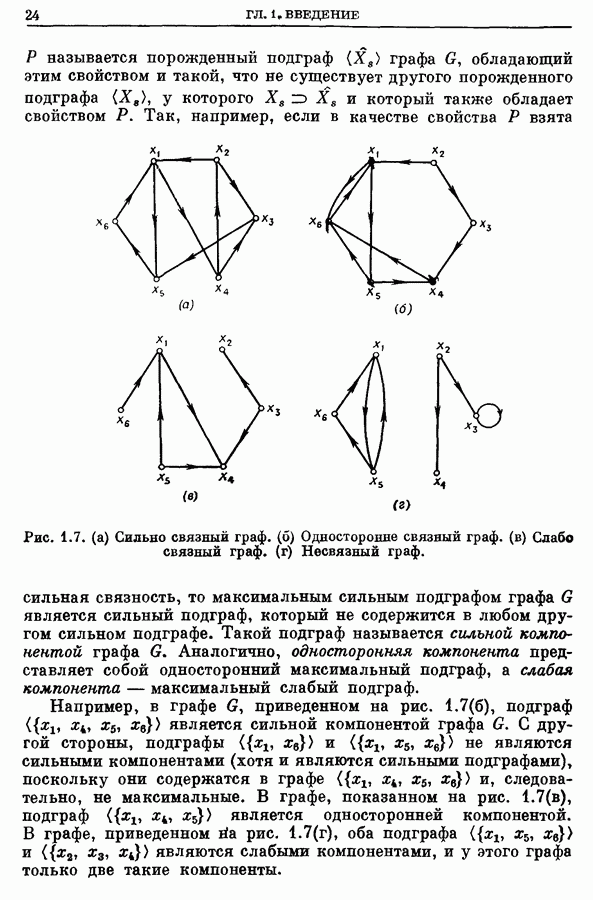
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
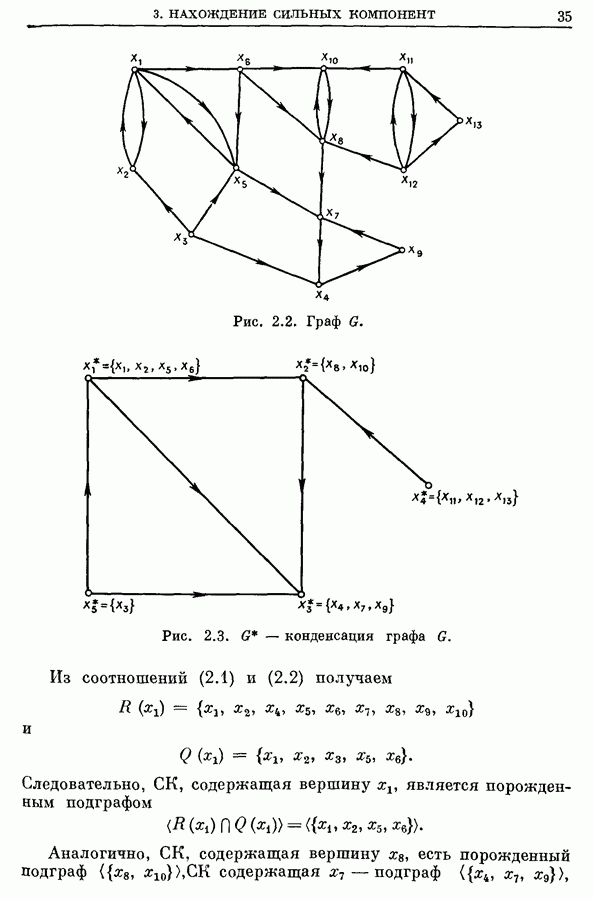
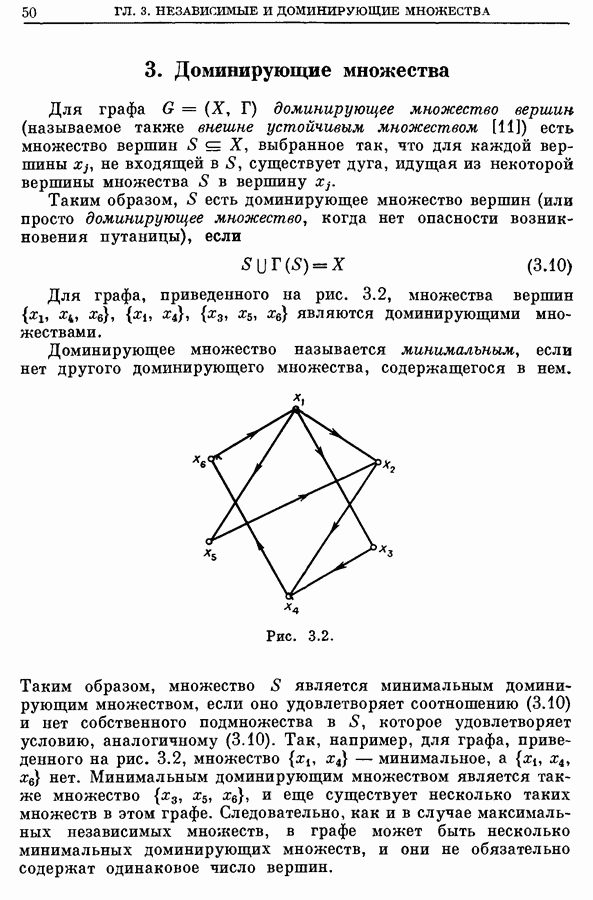
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
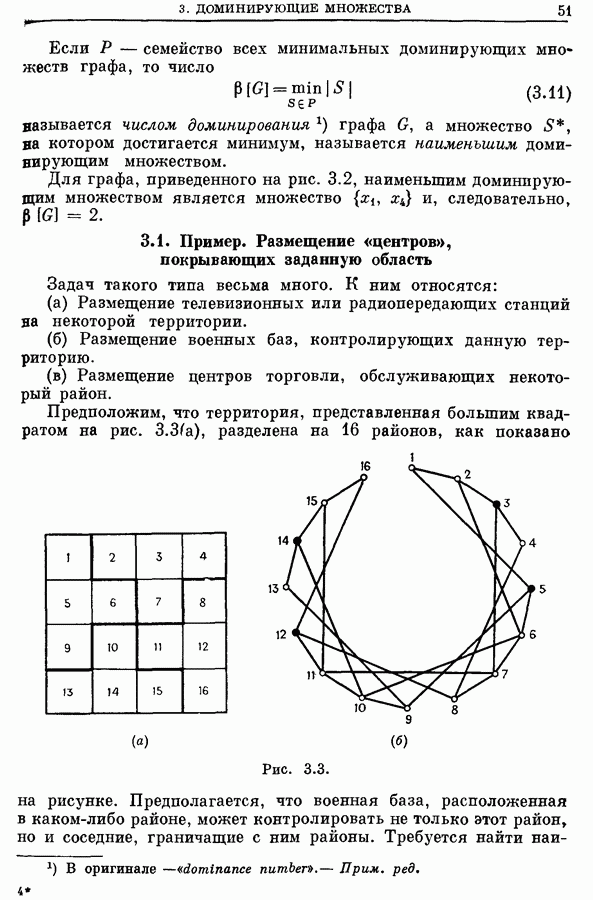
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
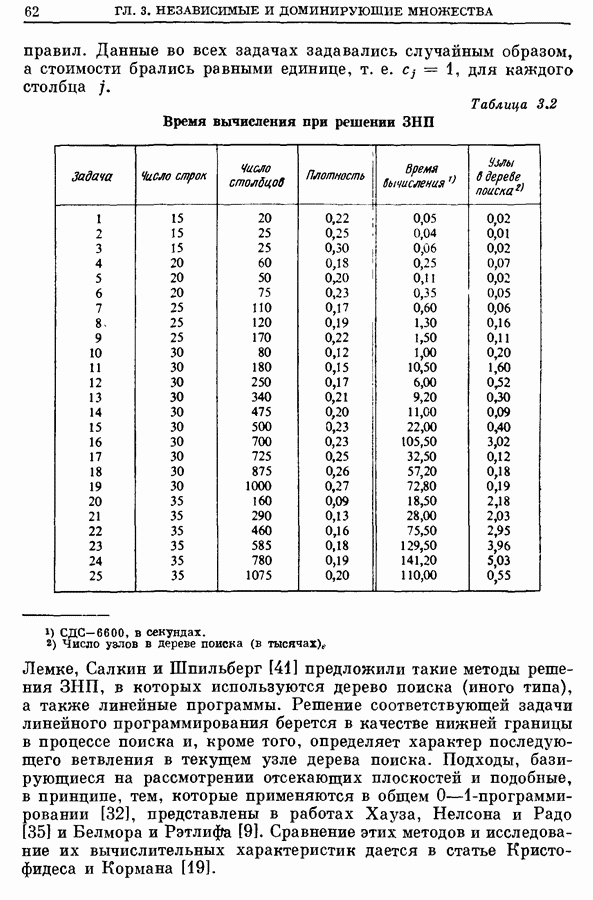
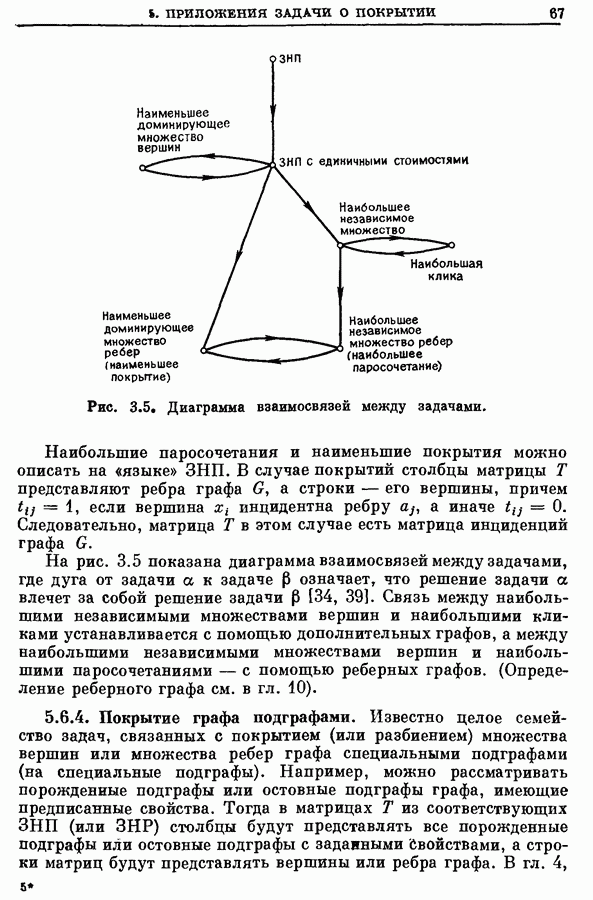
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
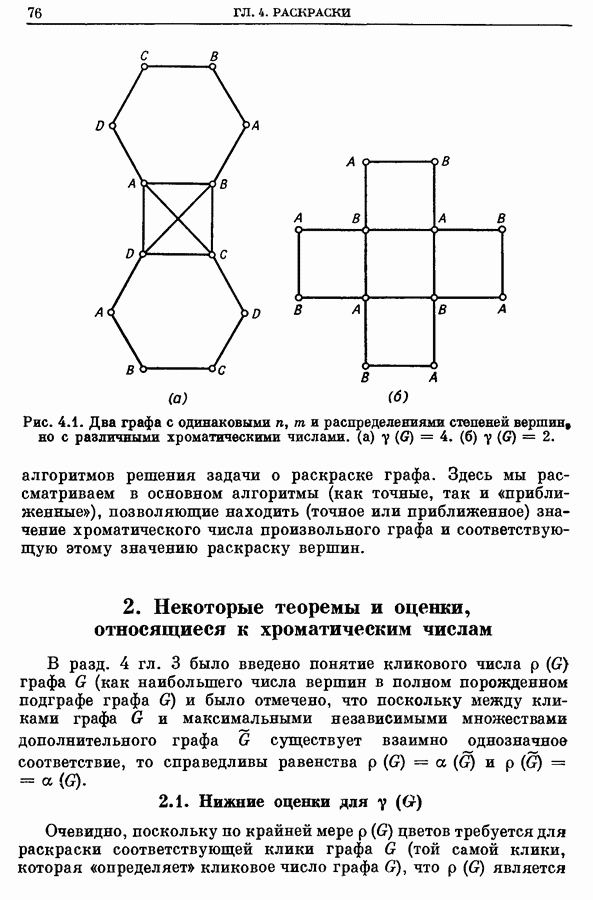
- Глава 4. РАСКРАСКИ
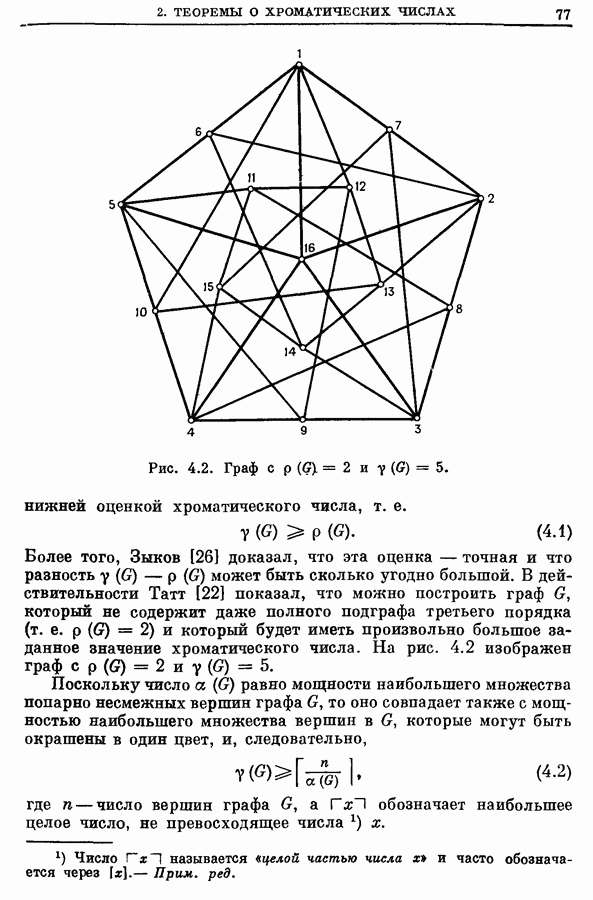
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
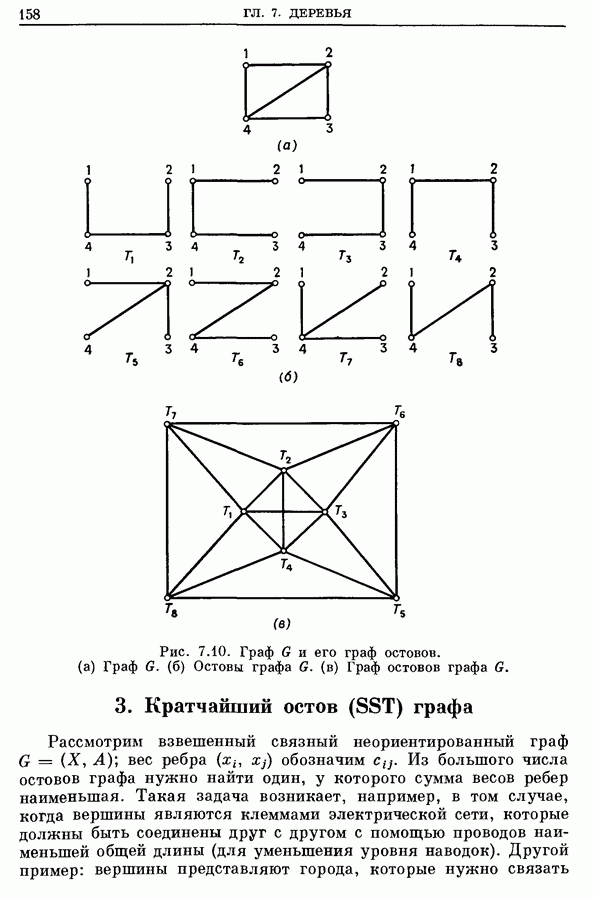
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
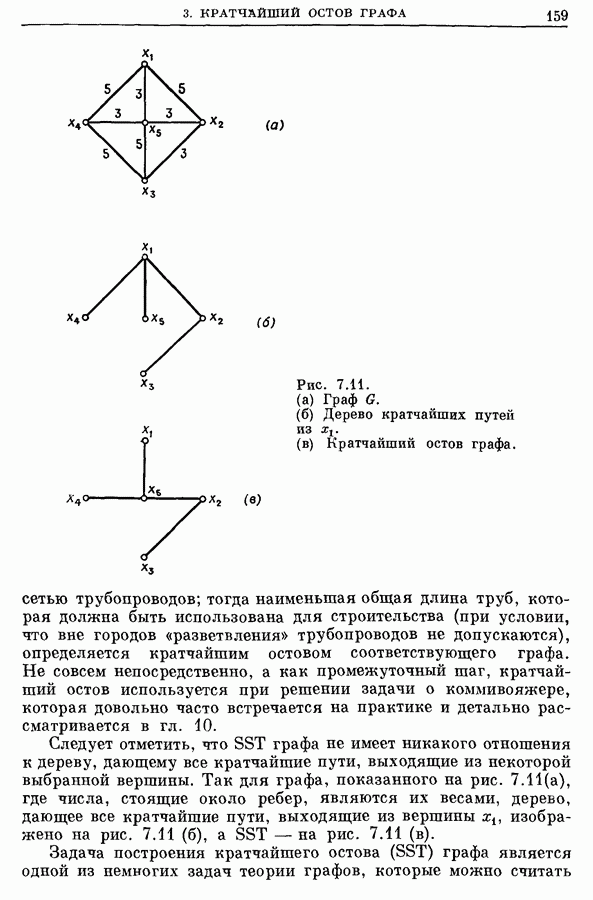
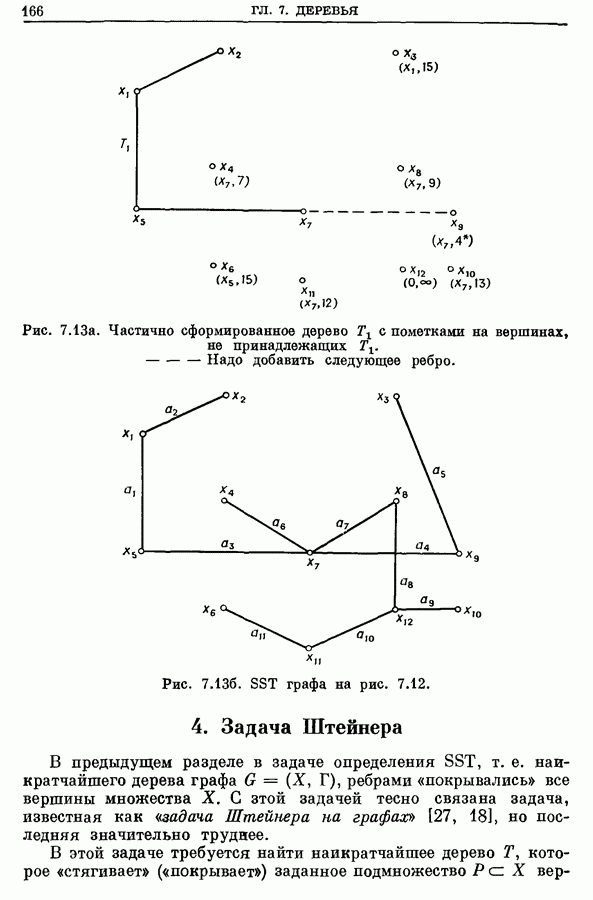
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
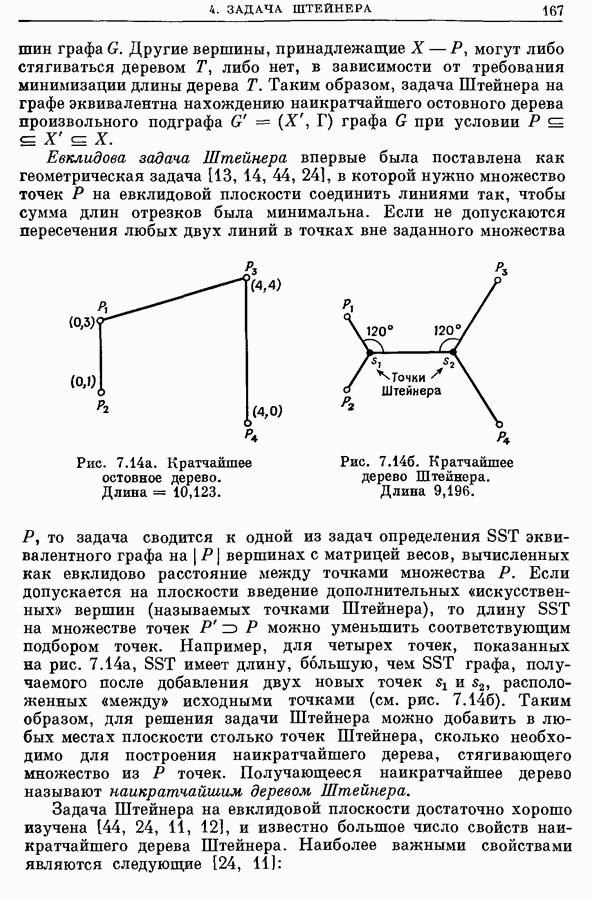
- 4. Задача Штейнера
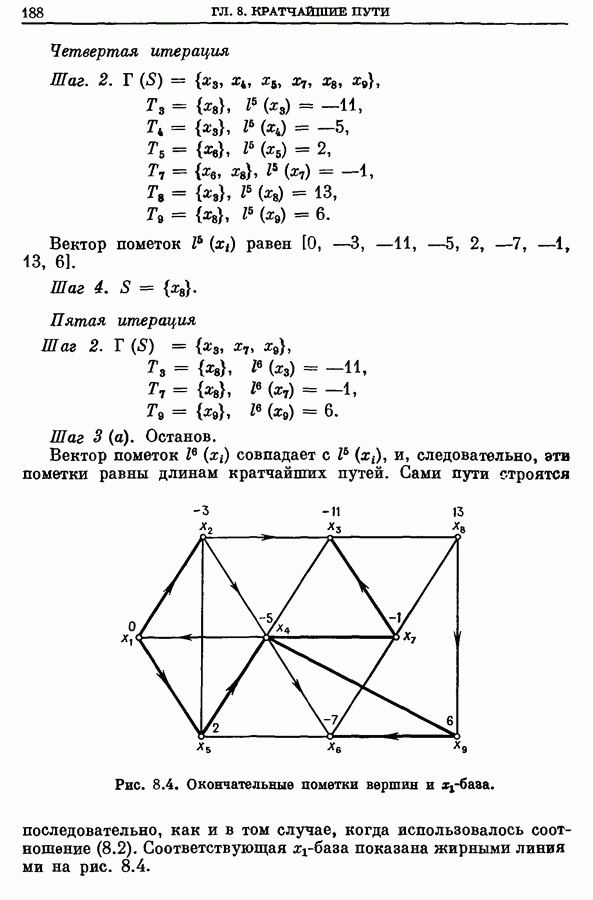
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
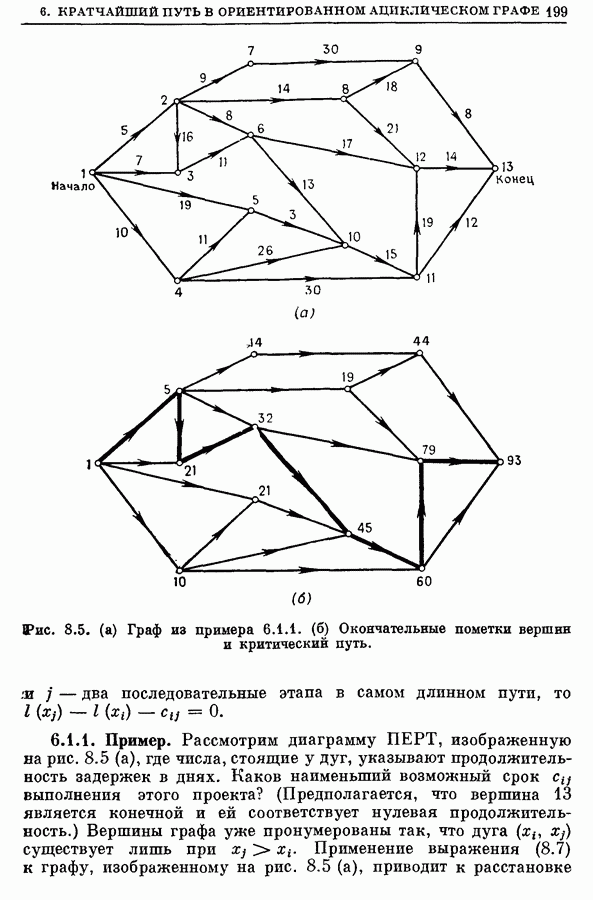
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
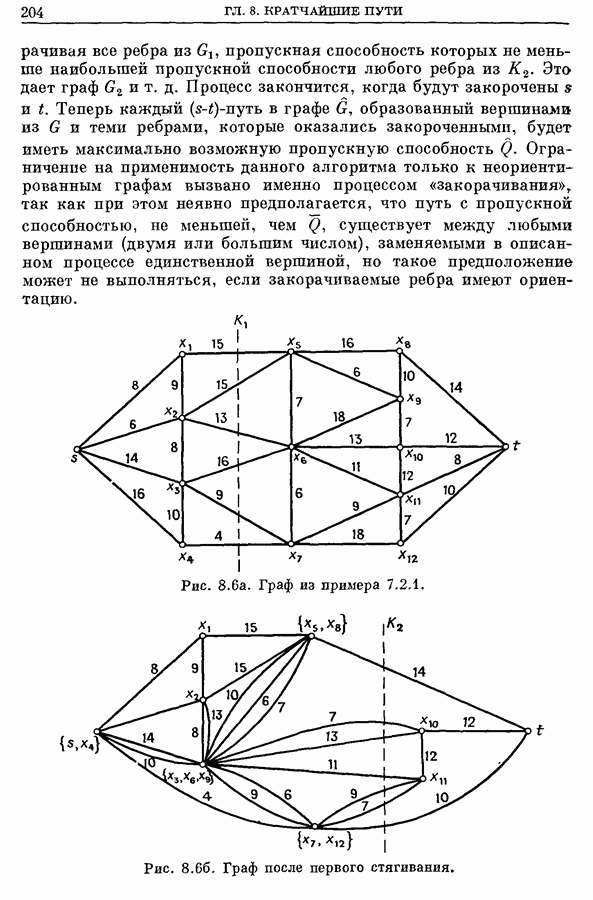
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
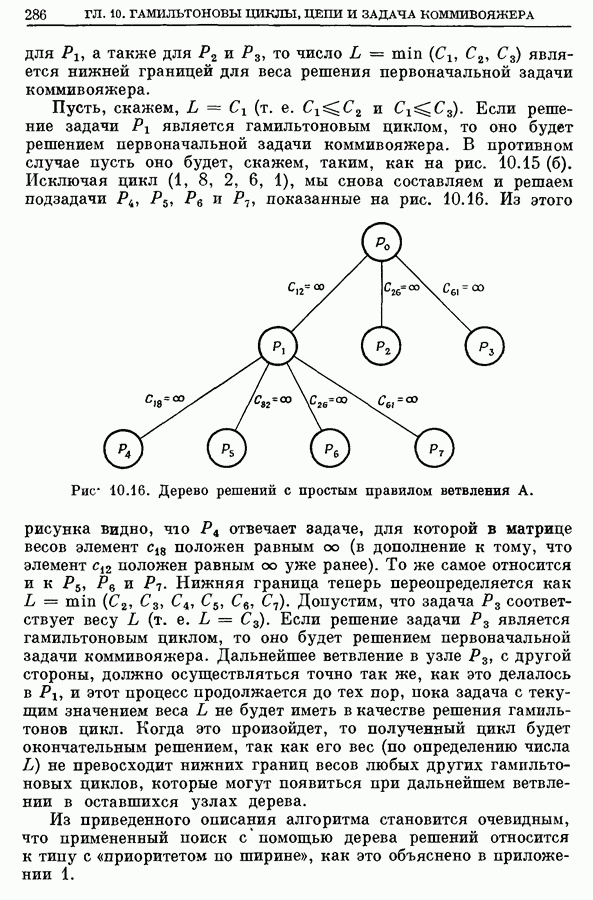
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
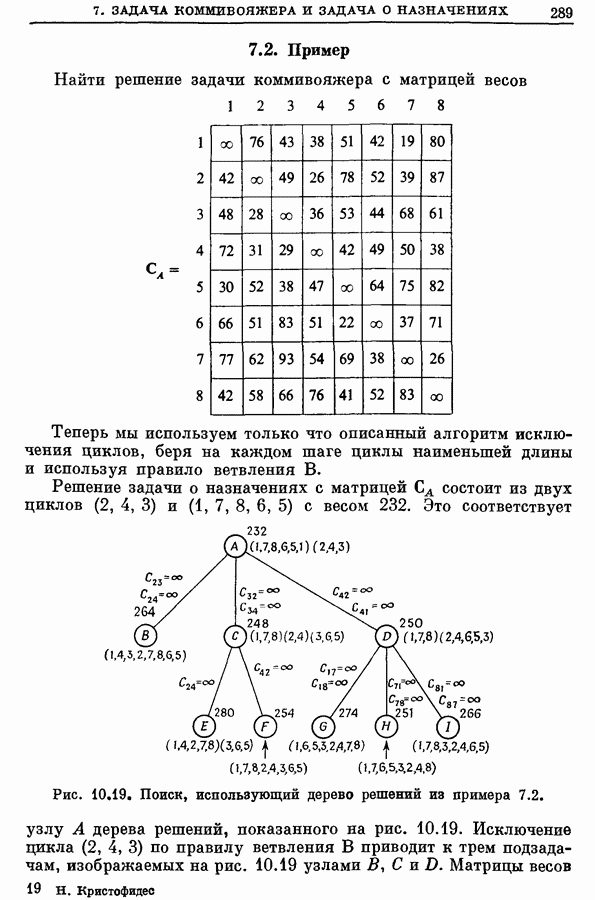
- 7. Задача коммивояжера и задача о назначениях
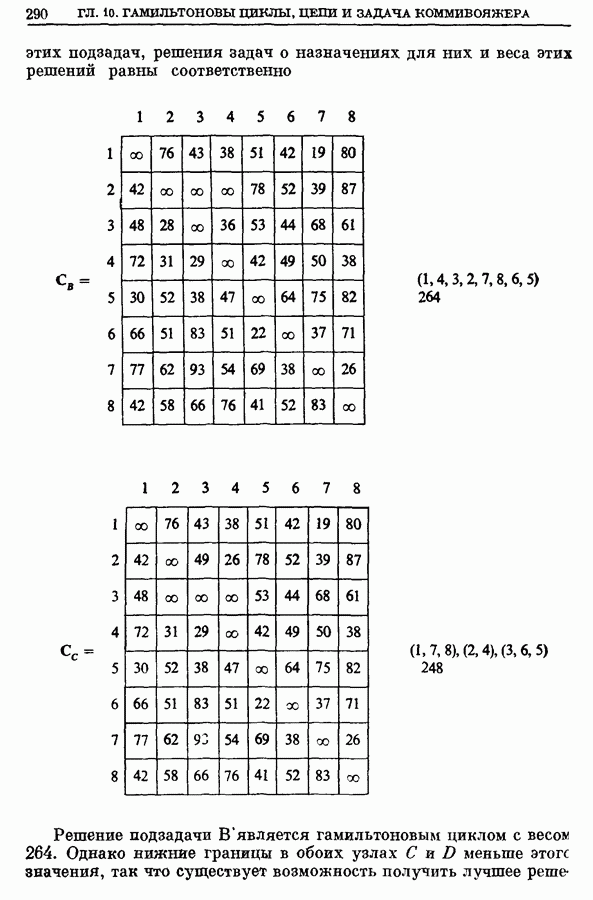
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
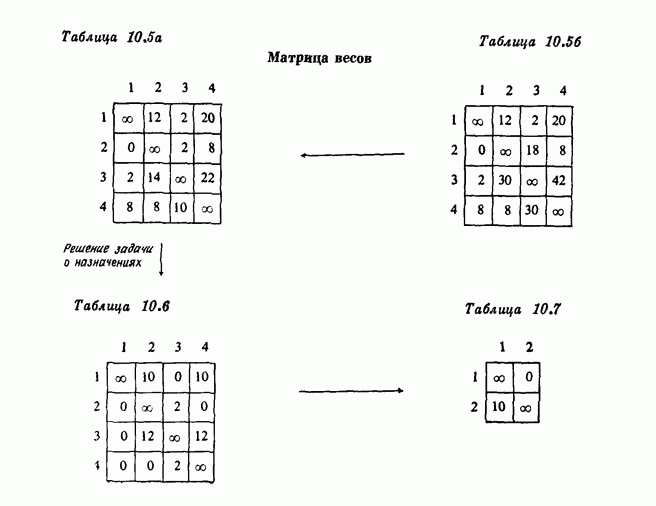
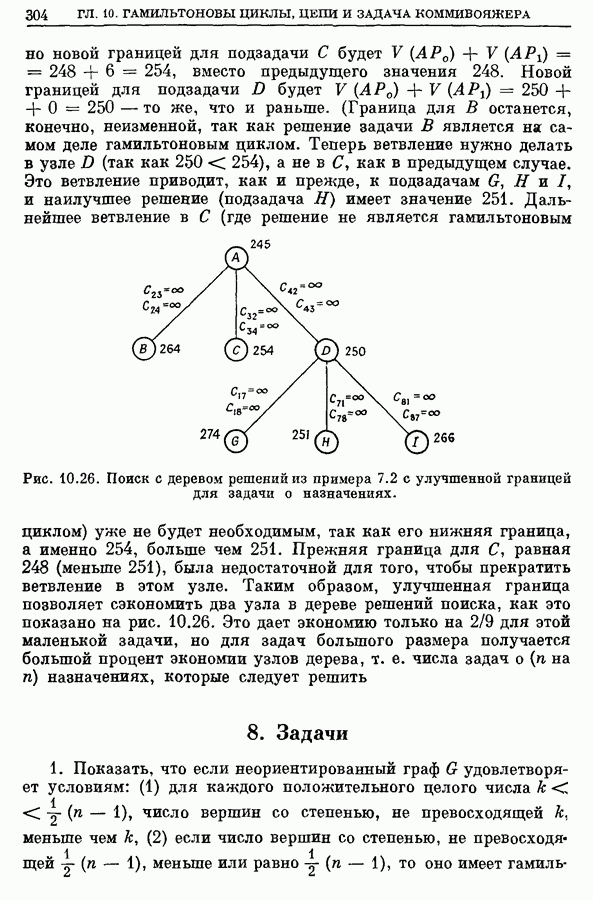
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
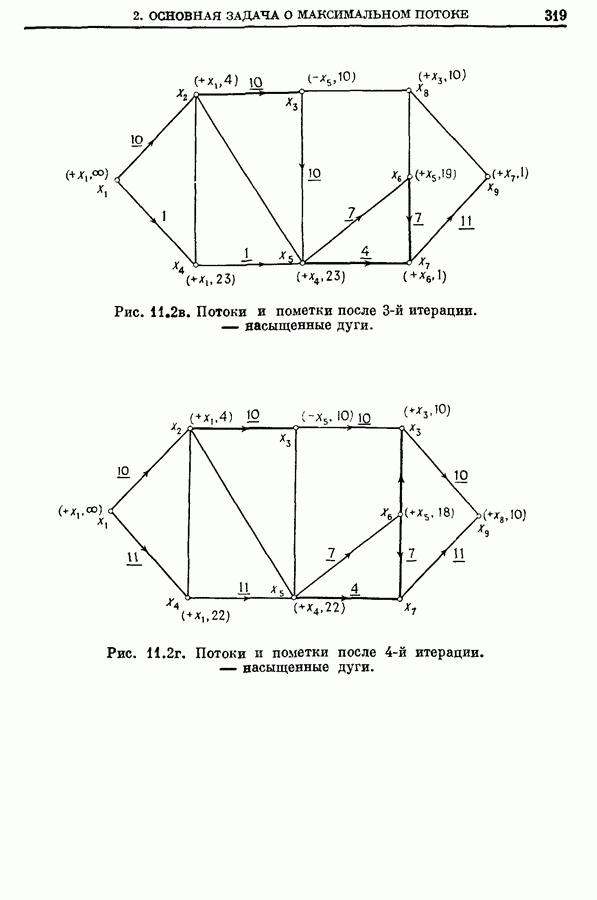
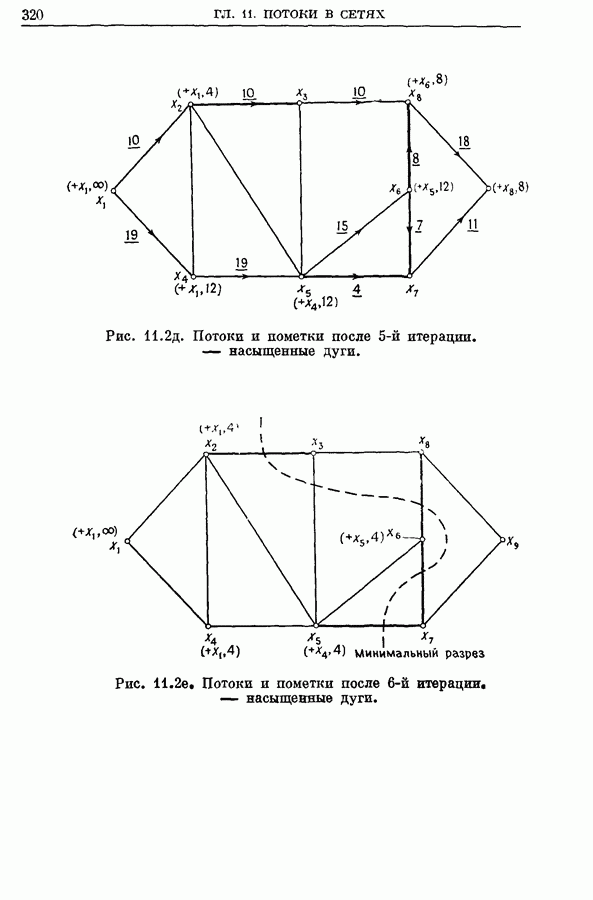
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
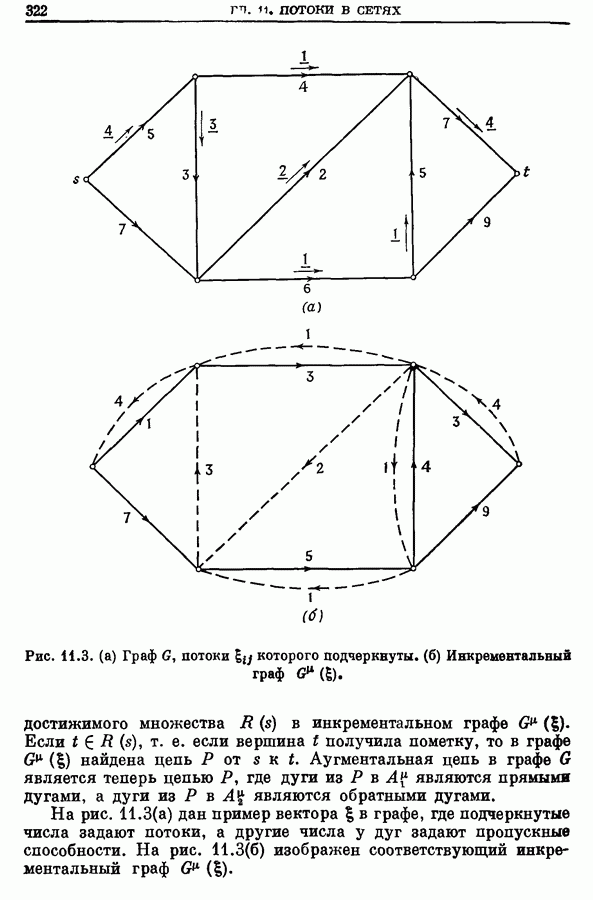
- 2.3. Инкрементальные графы
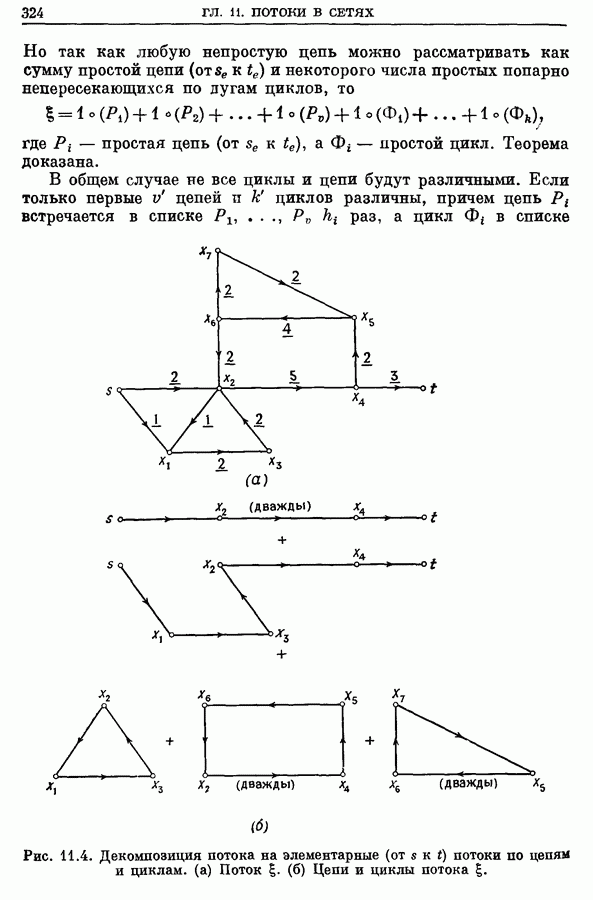
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
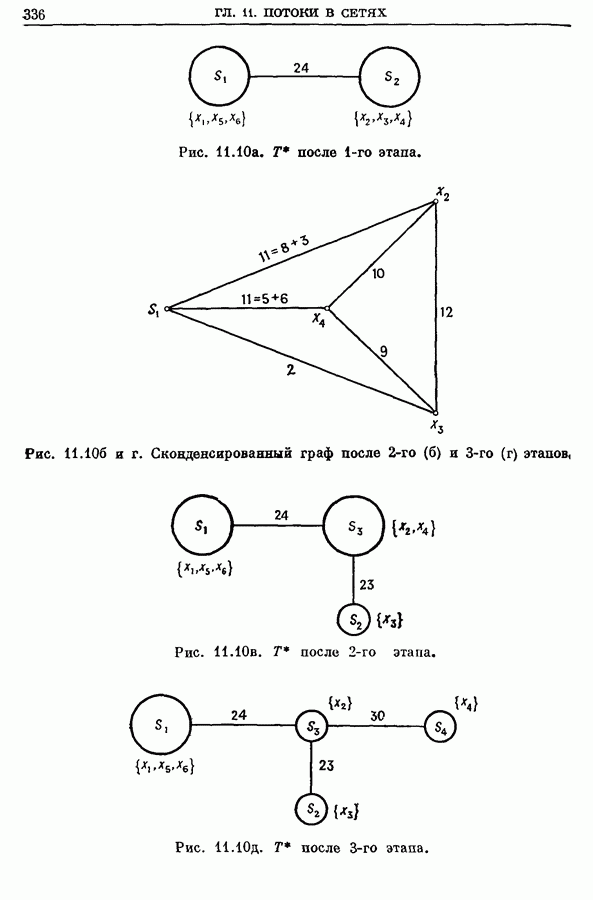
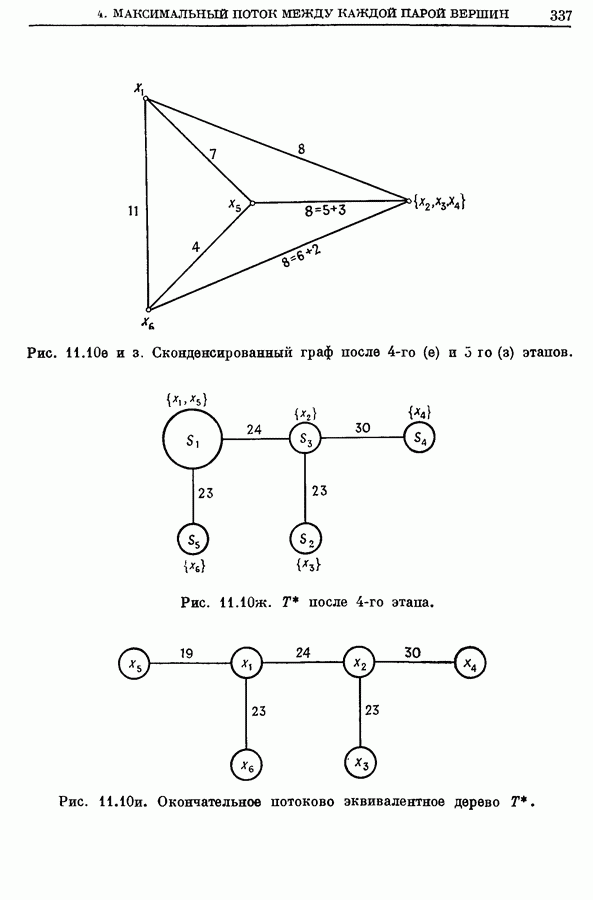
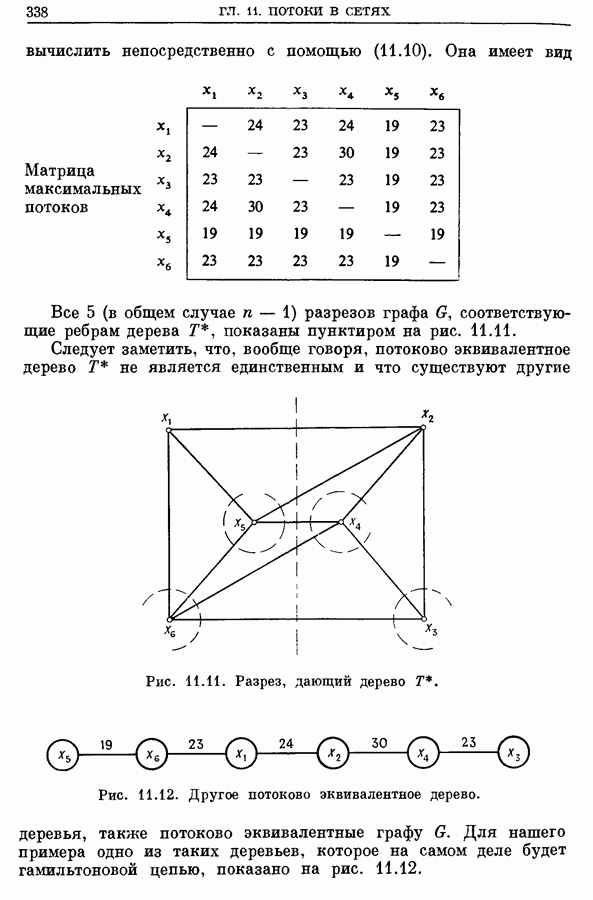
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
- 4.4. Пример
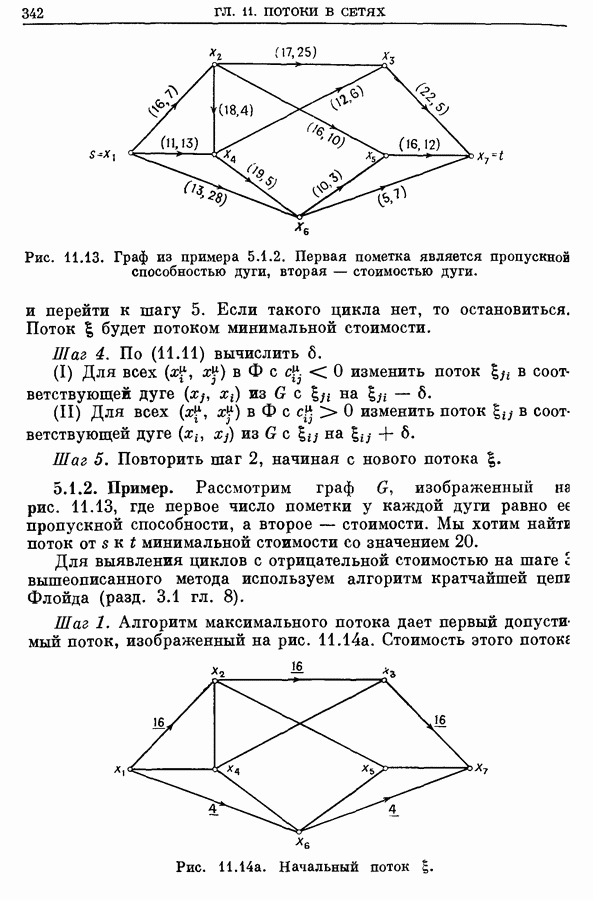
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
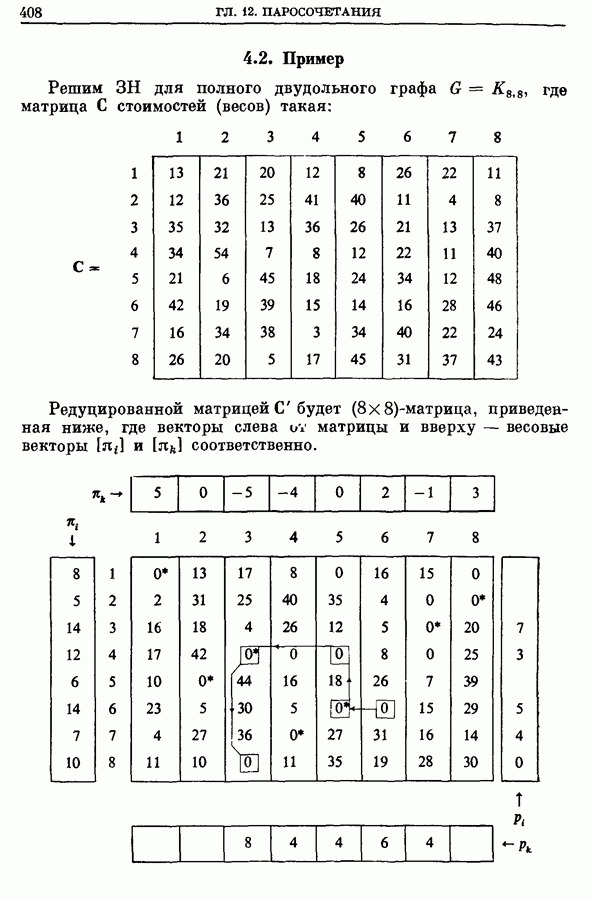
- 4.1. Алгоритм для ЗН (случай минимизации)
- 4.2. Пример
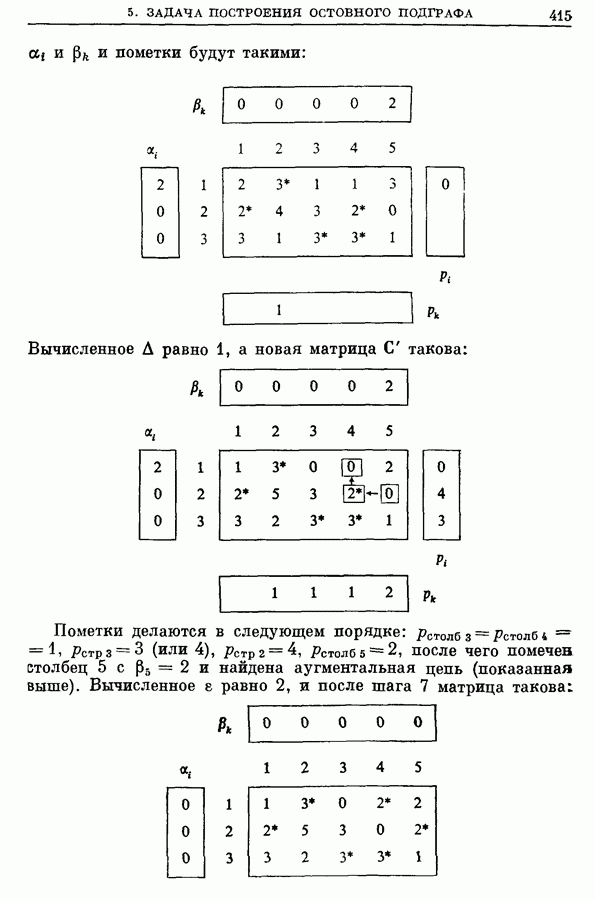
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
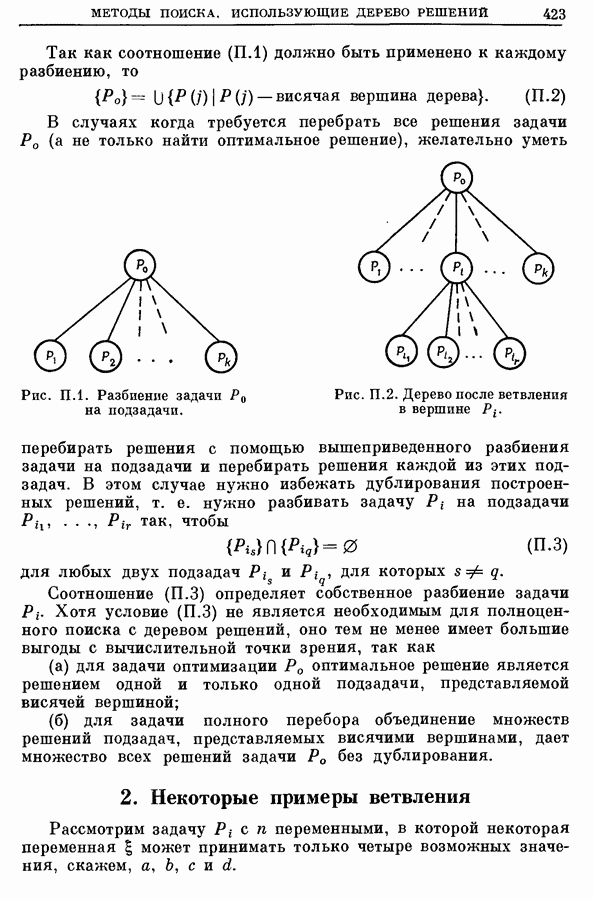
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
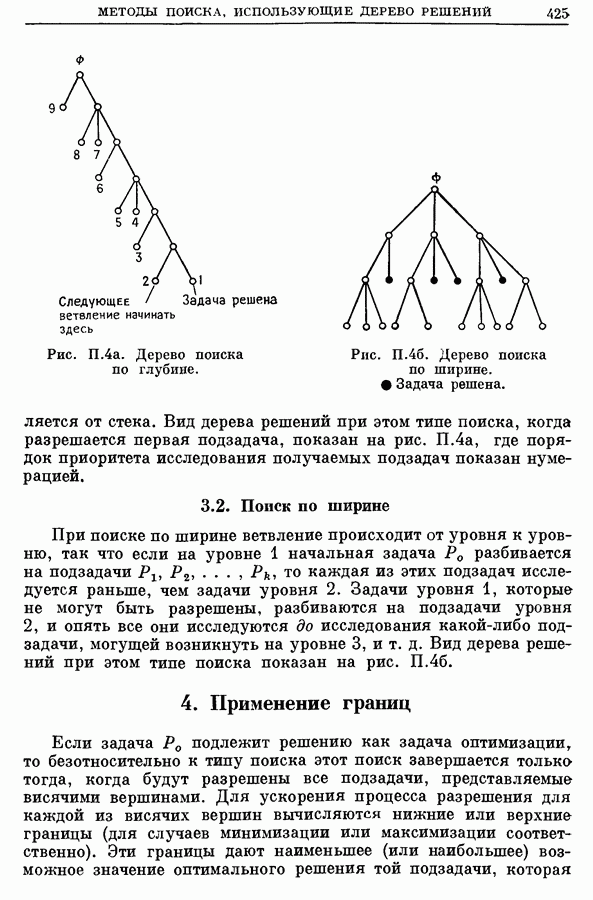
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
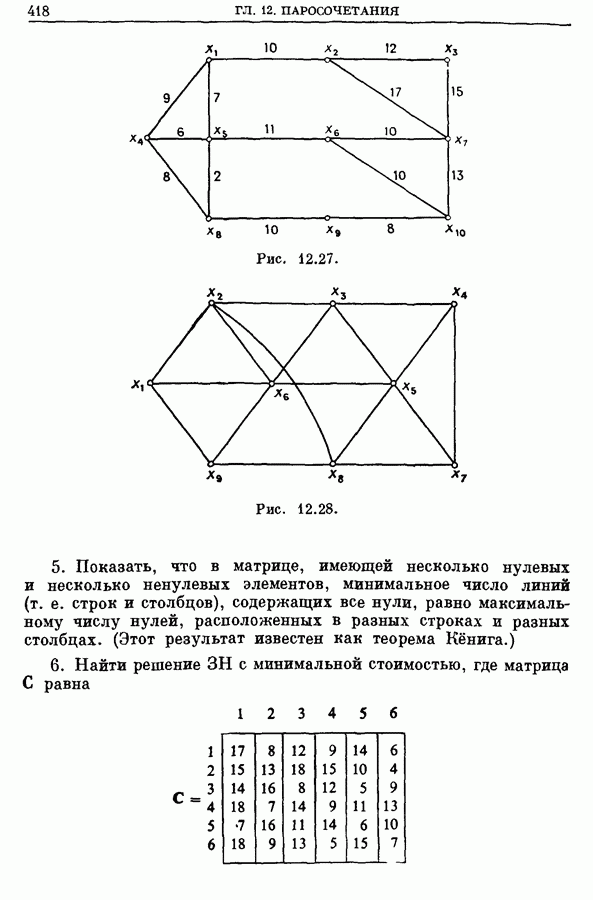
- 5. Функции ветвления