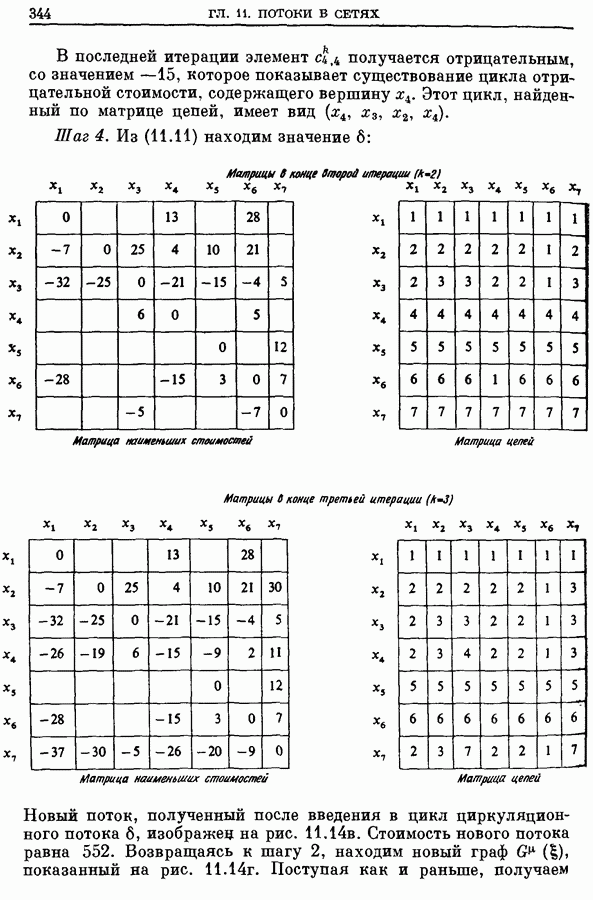
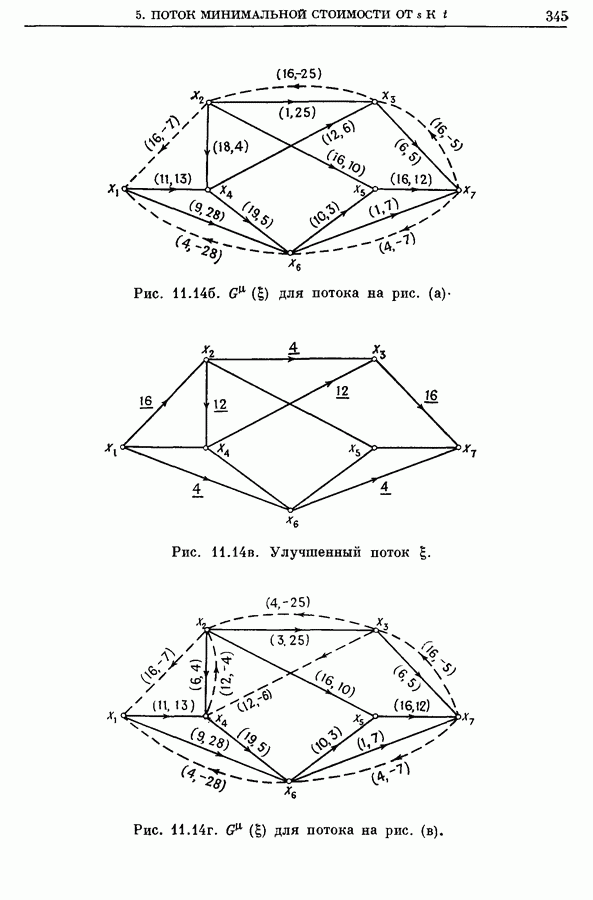
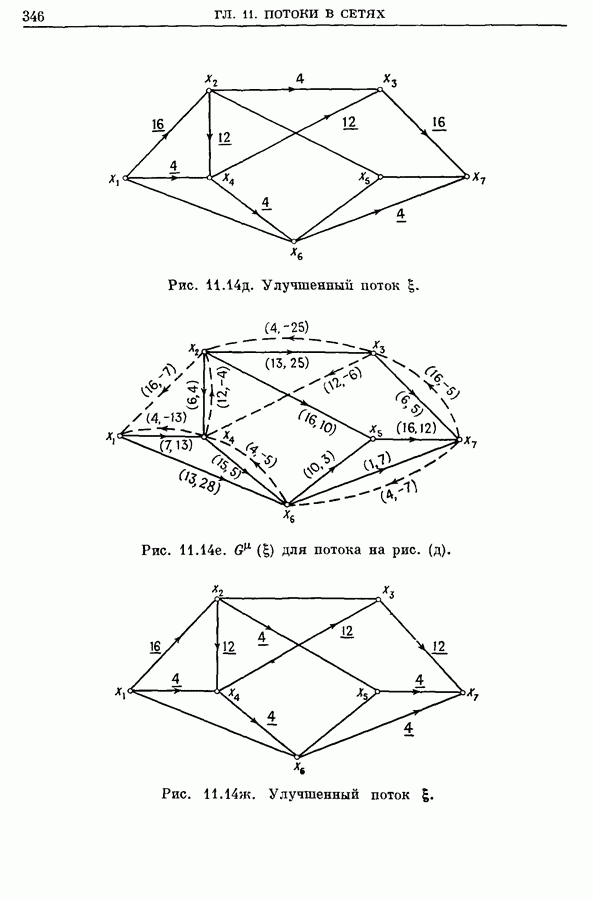
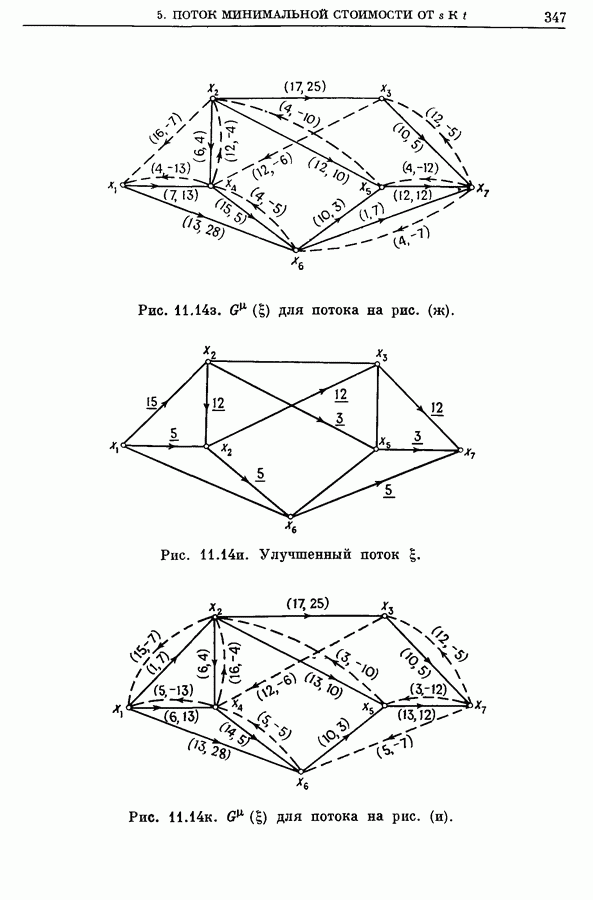
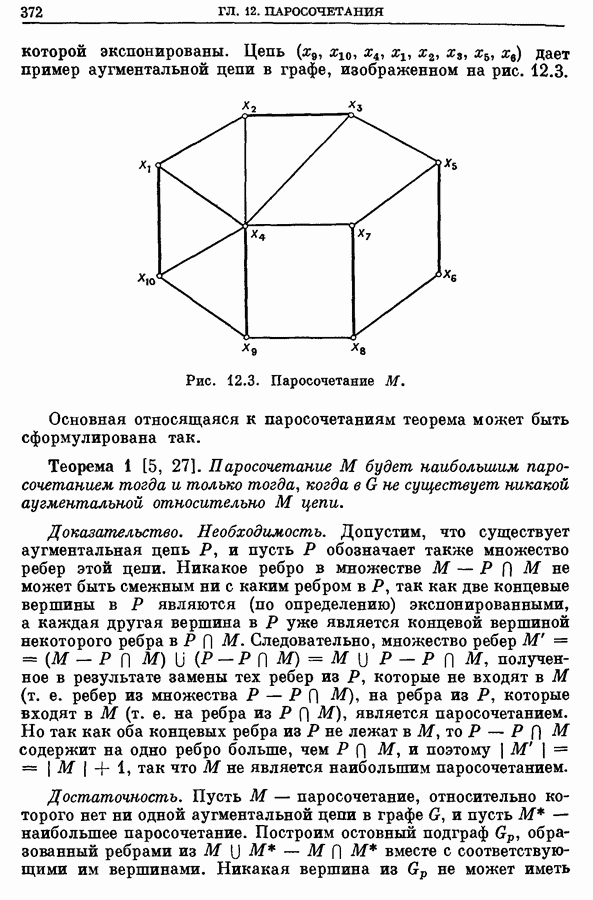
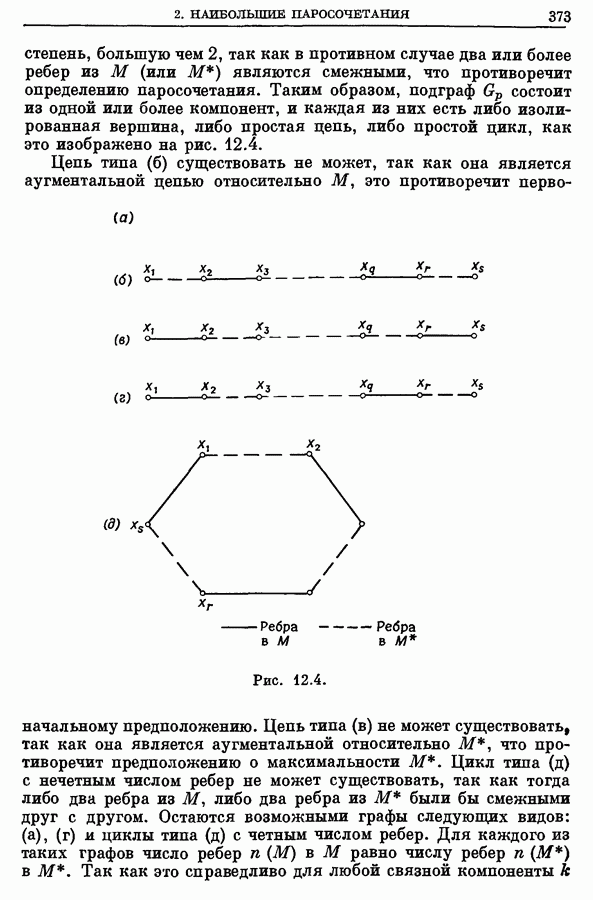
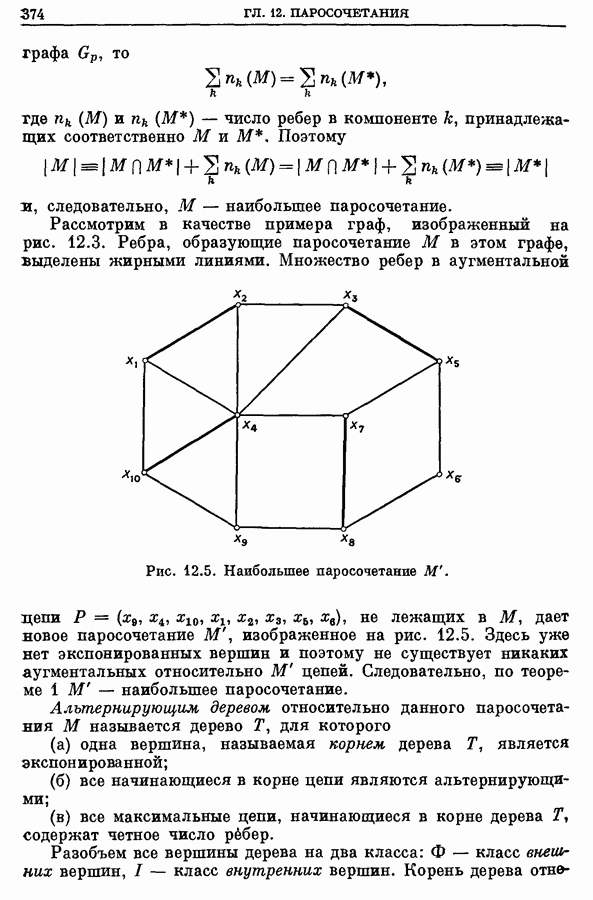
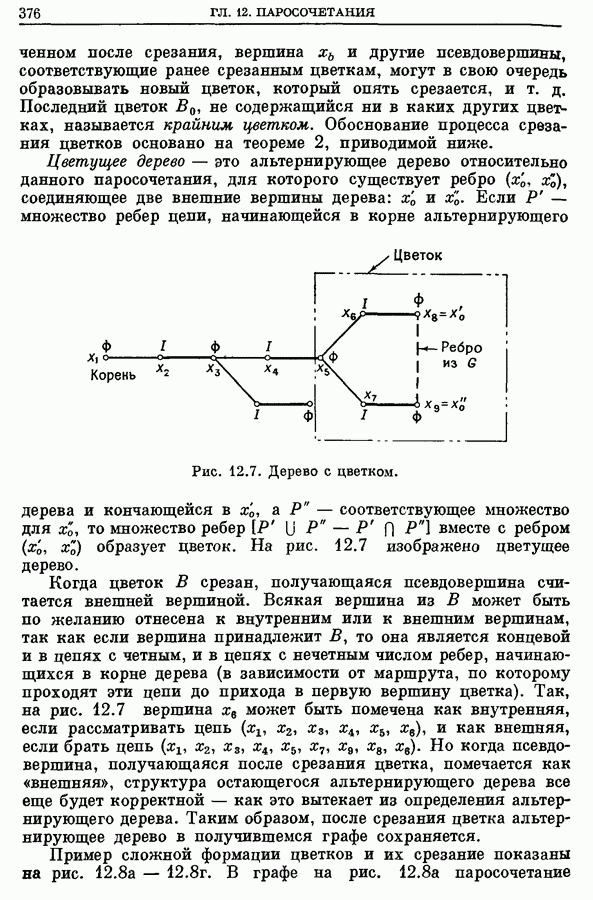
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
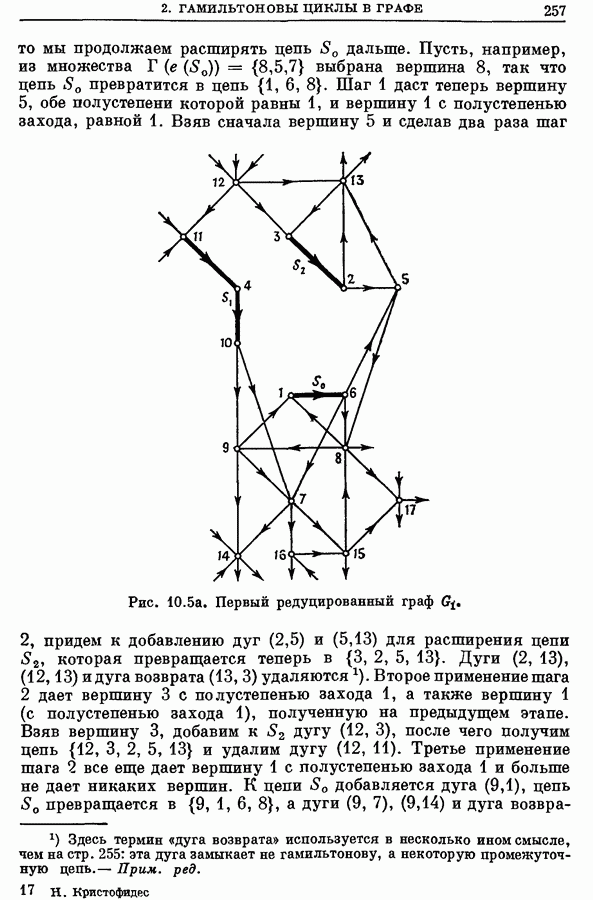
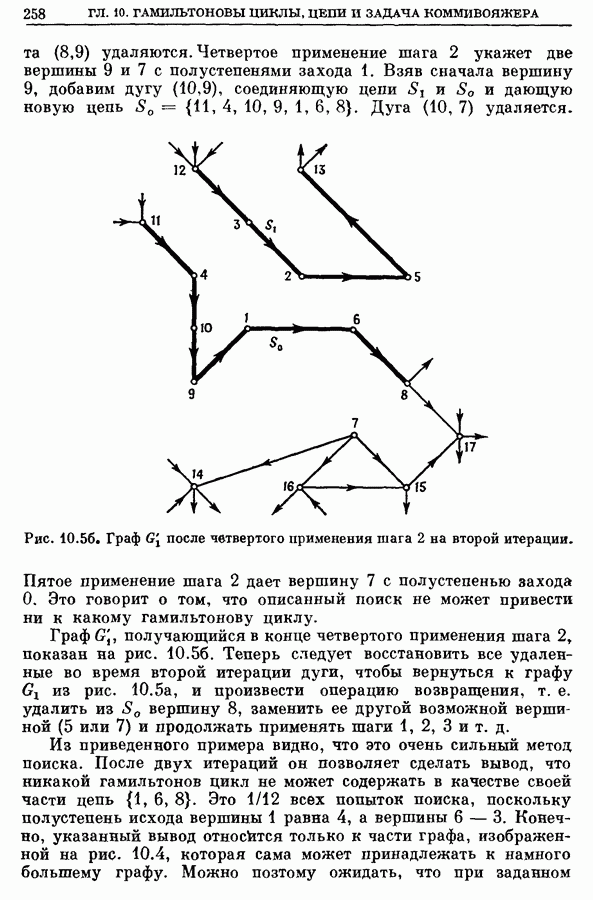
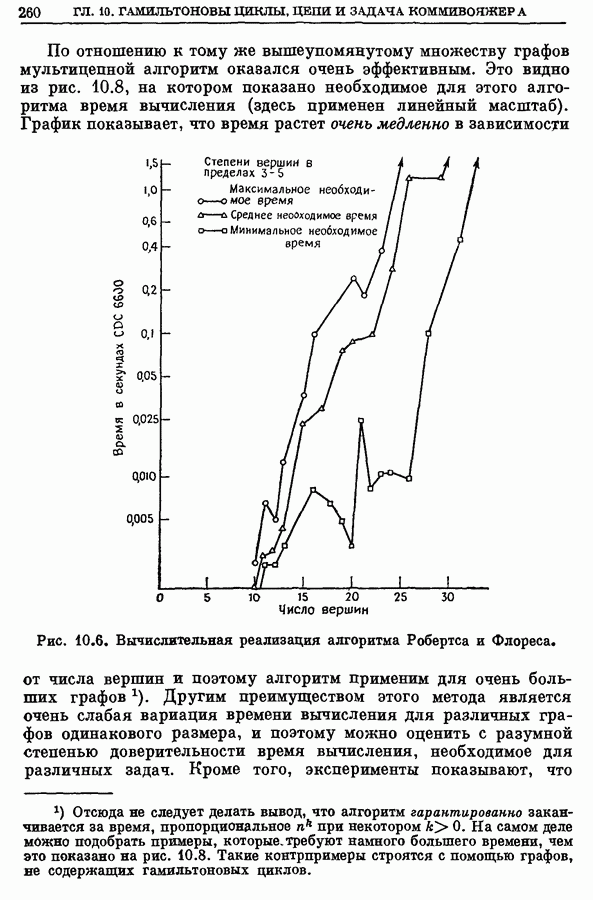
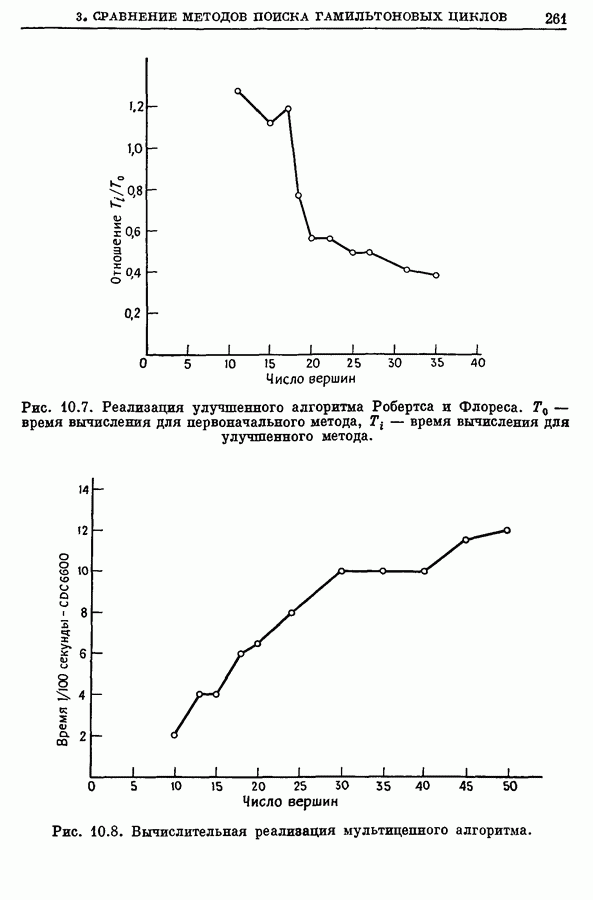
2. Медиана графа
Пусть дан граф  Для каждой вершины
Для каждой вершины  определим два числа, которые назовем передаточными числами:
определим два числа, которые назовем передаточными числами:

где  кратчайшее расстояние от вершины
кратчайшее расстояние от вершины  до вершины
до вершины  Числа
Числа  называются соответственно внешним и внутренним передаточными числами вершины
называются соответственно внешним и внутренним передаточными числами вершины  Число
Число  есть сумма элементов строки
есть сумма элементов строки  матрицы, полученной после умножения каждого столбца матрицы расстояний
матрицы, полученной после умножения каждого столбца матрицы расстояний  на вес соответствующей этому столбцу вершины,
на вес соответствующей этому столбцу вершины,  столбец умножается на
столбец умножается на  число
число  есть сумма элементов столбца
есть сумма элементов столбца  матрицы, полученной в результате умножения каждой строки матрицы расстояний
матрицы, полученной в результате умножения каждой строки матрицы расстояний  на соответствующий этой строке вес
на соответствующий этой строке вес  строка умножается на
строка умножается на 
Вершина  для которой
для которой

называется внешней медианой графа  а вершина
а вершина  для которой
для которой

называется внутренней медианой графа 
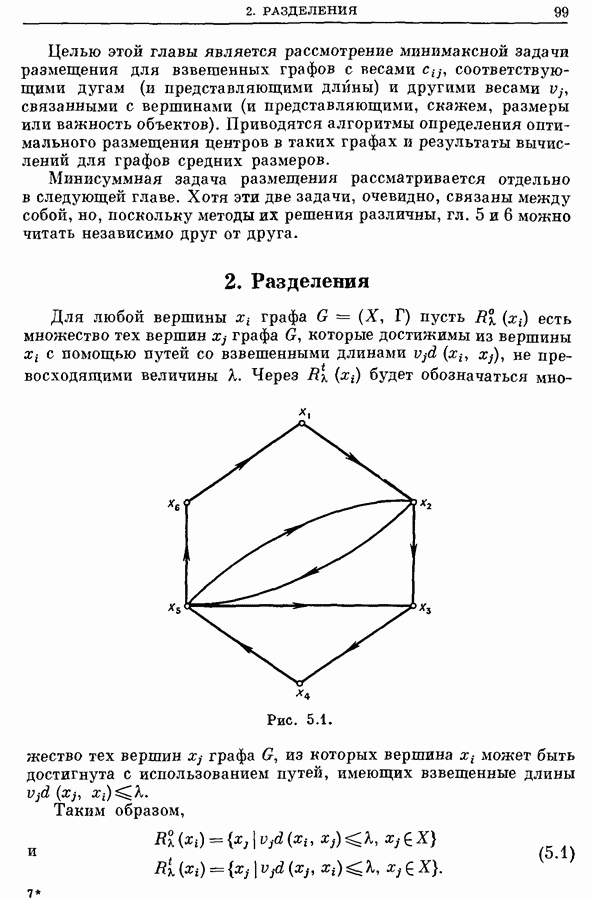
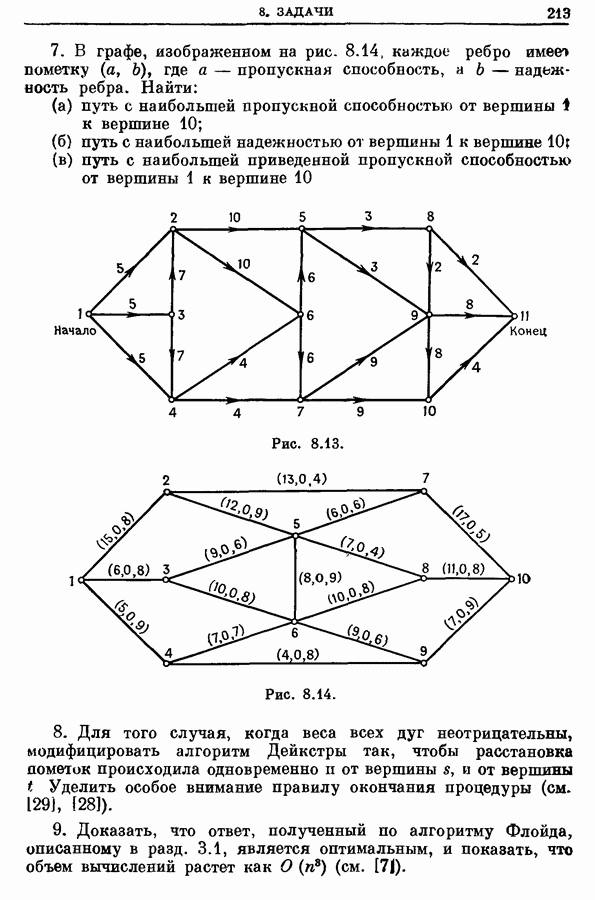
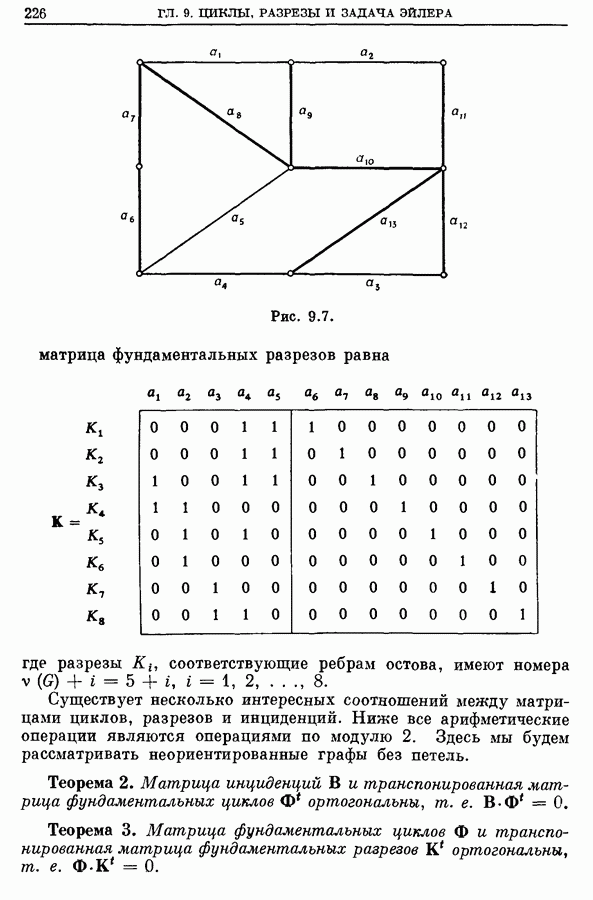
Рассмотрим еще раз граф, изображенный на рис. 5.1 (для которого все  приняты равными единице), и вычислим внешние и внутренние передаточные числа вершин. Эти числа приведены в присоединенных к матрице расстояний строке и столбце:
приняты равными единице), и вычислим внешние и внутренние передаточные числа вершин. Эти числа приведены в присоединенных к матрице расстояний строке и столбце:

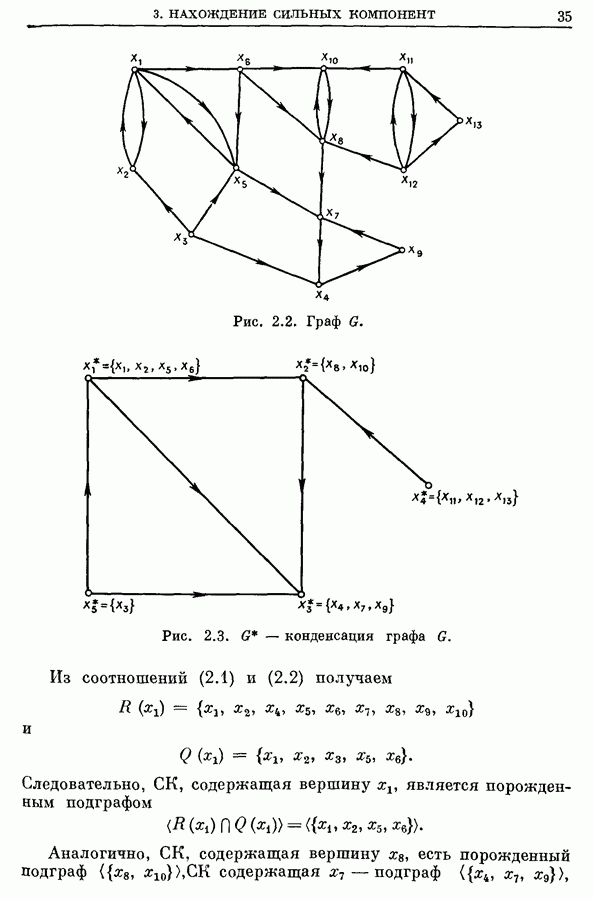
По полученным передаточным числам видно, что внешней медианой является  и что существуют три внутренние медианы
и что существуют три внутренние медианы  каждая с внутренним передаточным числом, равным 9.
каждая с внутренним передаточным числом, равным 9.
2.1. Выбор места для склада
Рассмотрим задачу снабжения ряда потребителей товарами поступающими с одного склада. Потребителей можно объединить в группы таким образом, чтобы каждую группу обслуживало целое число грузовиков. Машина выезжает со склада, обслуживает некоторую группу потребителей и возвращается на склад. Группы потребителей можно представить вершинами графа, а сеть дорог — его дугами. На практике каждой группе потребителей присваивается вес  представляющий ее «важность» (например,
представляющий ее «важность» (например,  может быть числом, пропорциональным годовому потреблению или частоте, с которой транспорт должен объезжать эту группу потребителей, чтобы удовлетворить их потребности).
может быть числом, пропорциональным годовому потреблению или частоте, с которой транспорт должен объезжать эту группу потребителей, чтобы удовлетворить их потребности).
В этом случае задача состоит в определении такого места для склада, чтобы общее расстояние, проходимое транспортом, было бы минимально возможным. Если матрица расстояний  задает действительные расстояния в километрах, то требуемым местом расположения склада будет такая вершина
задает действительные расстояния в километрах, то требуемым местом расположения склада будет такая вершина  для которой сумма внешних и внутренних передаточных чисел будет наименьшей. Вершина
для которой сумма внешних и внутренних передаточных чисел будет наименьшей. Вершина  может быть названа внешне-внутренней медианой и найдена из соотношения, аналогичного (6.1). В следующем разделе будет показано, что для любой точки (вершины или произвольной точки дороги), выбранной для размещения склада, общий километраж, покрываемый транспортом, не может быть меньше, чем для вершины
может быть названа внешне-внутренней медианой и найдена из соотношения, аналогичного (6.1). В следующем разделе будет показано, что для любой точки (вершины или произвольной точки дороги), выбранной для размещения склада, общий километраж, покрываемый транспортом, не может быть меньше, чем для вершины 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
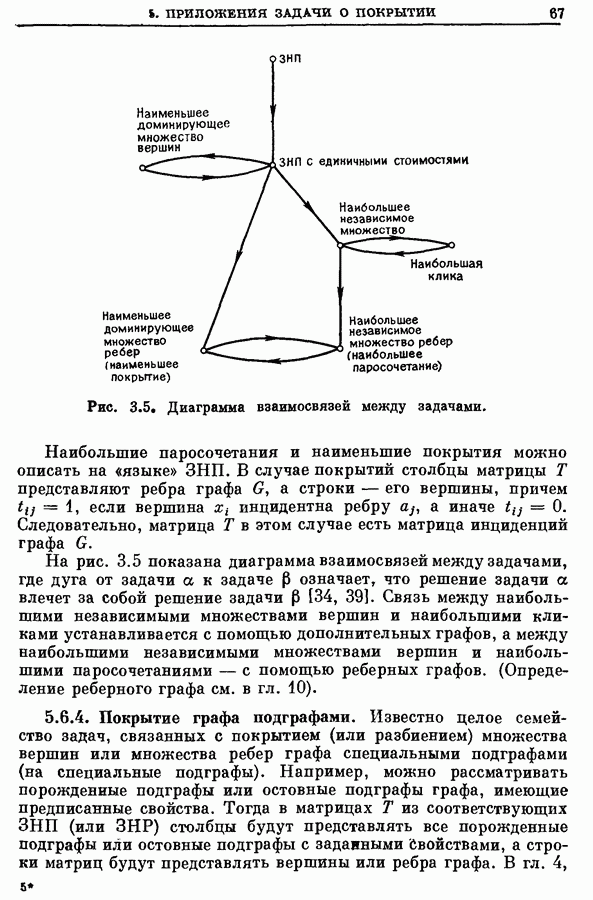
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
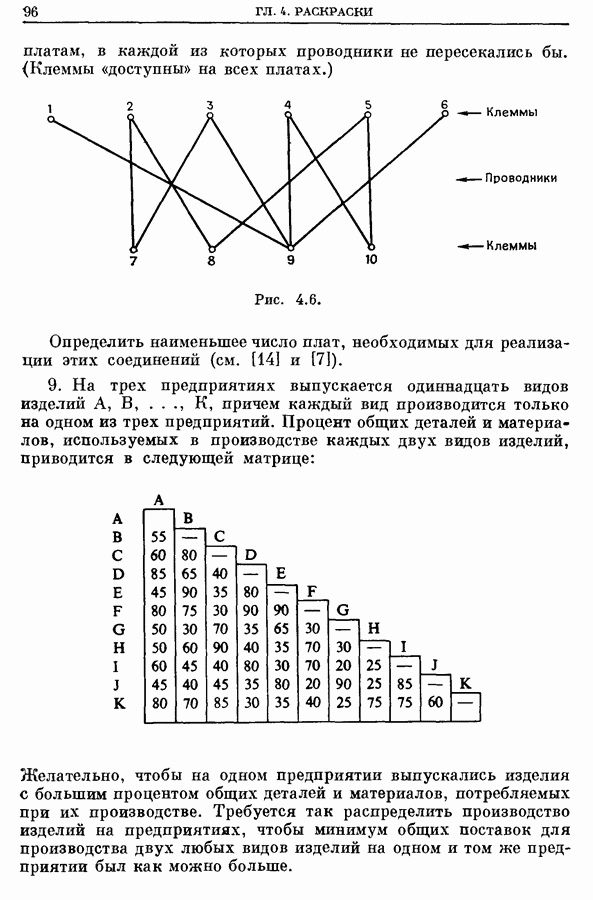
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
- 2.3. Инкрементальные графы
- 2.4. Декомпозиция потока
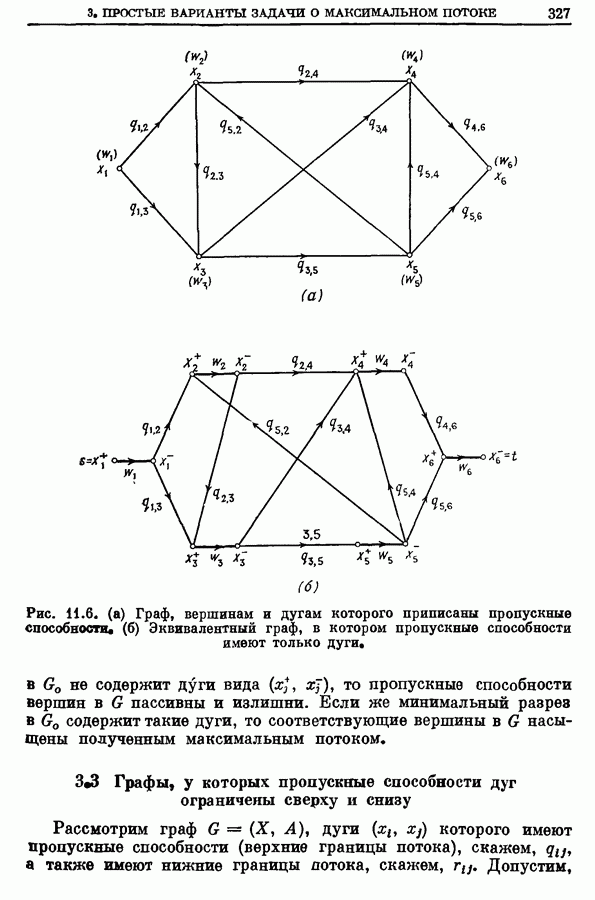
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
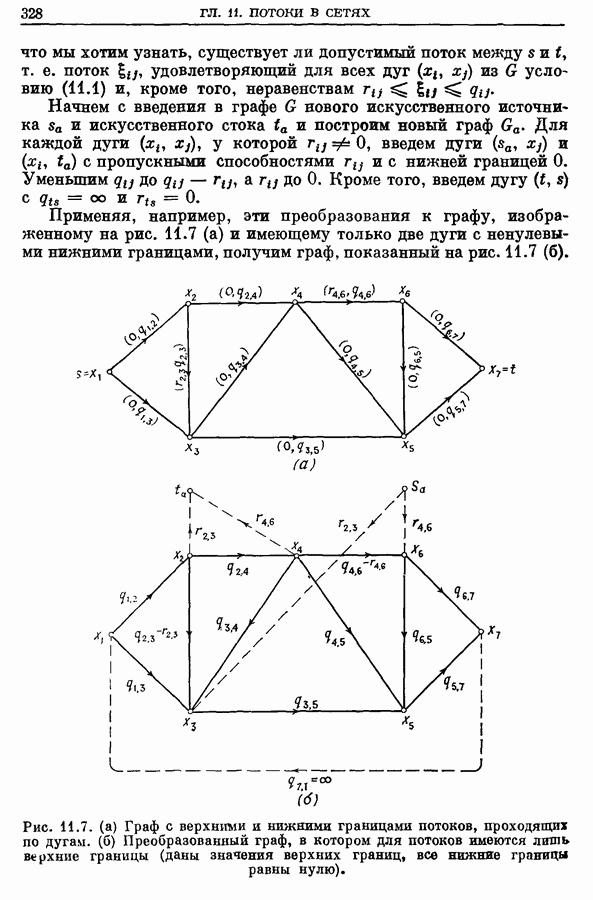
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
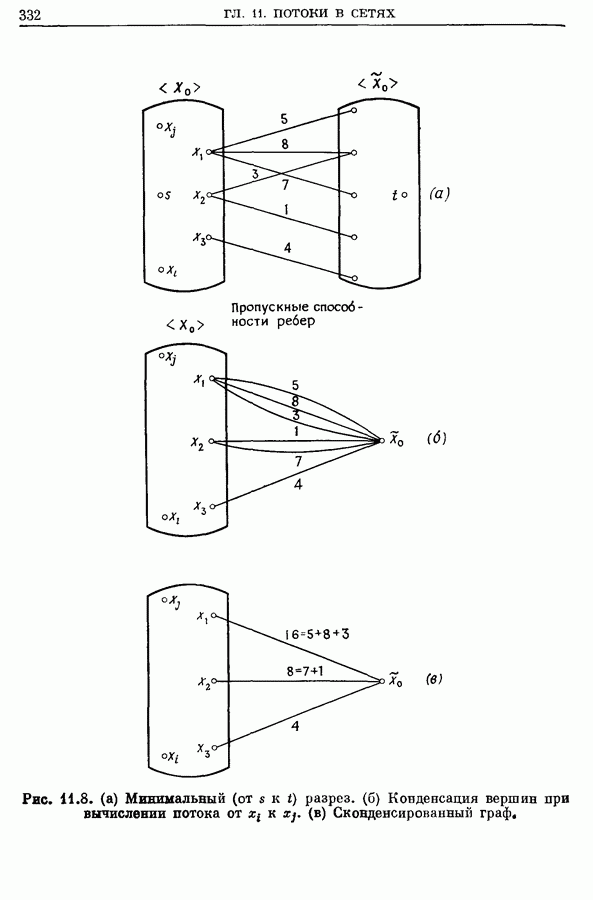
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
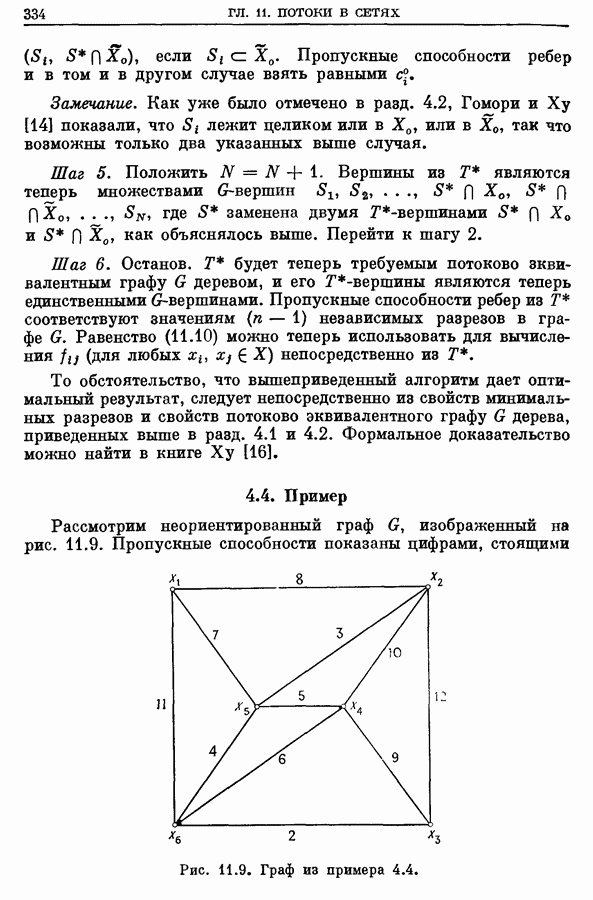
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
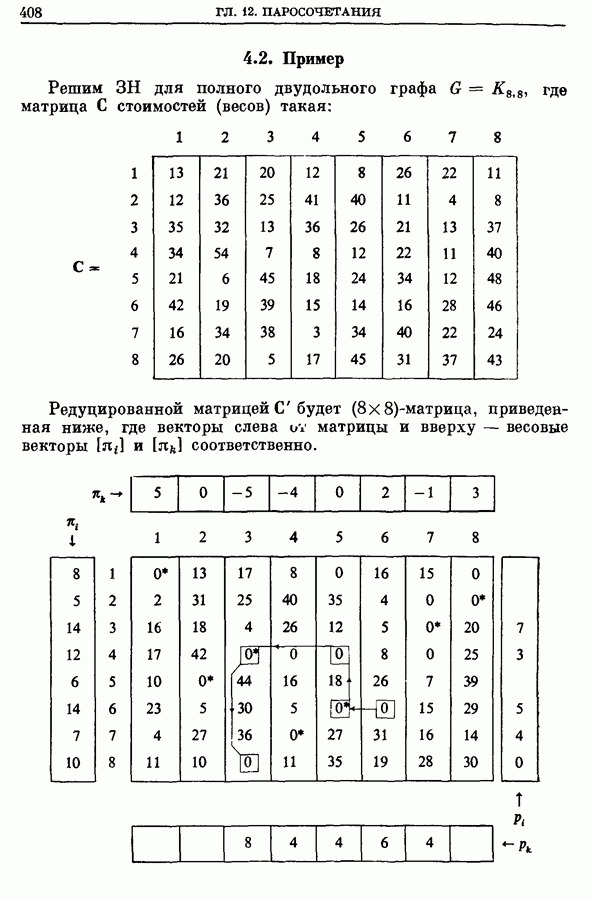
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
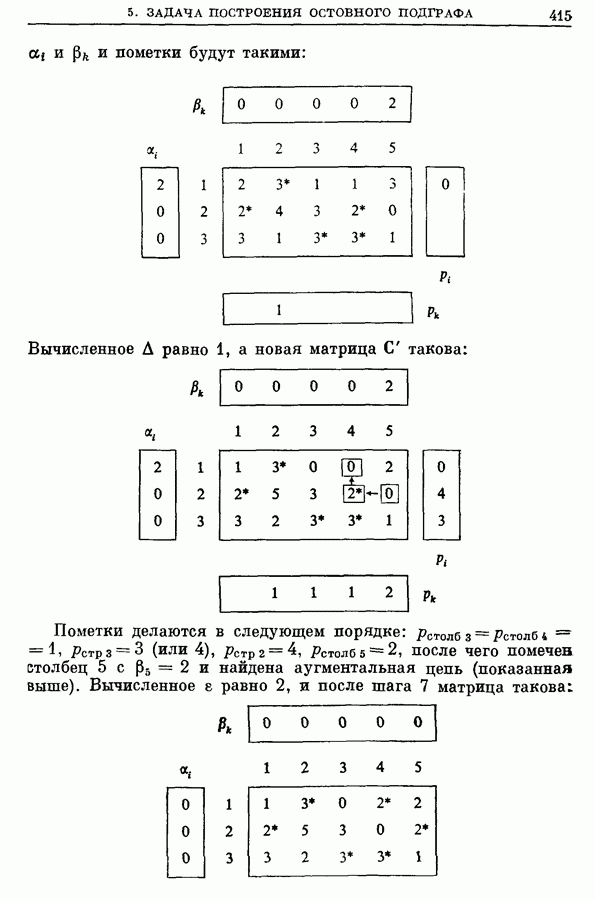
- 5.2. Пример
- 6. Задача о покрытии
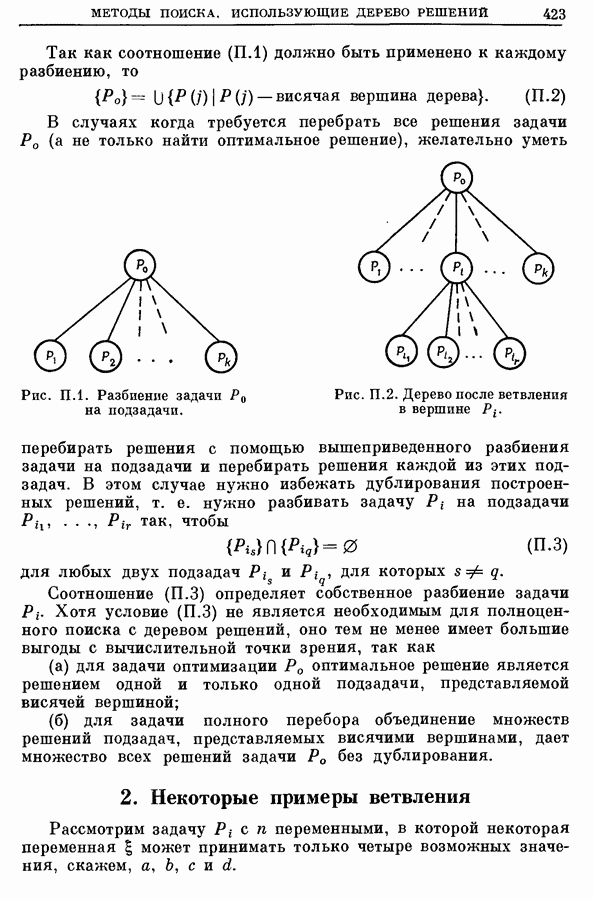
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
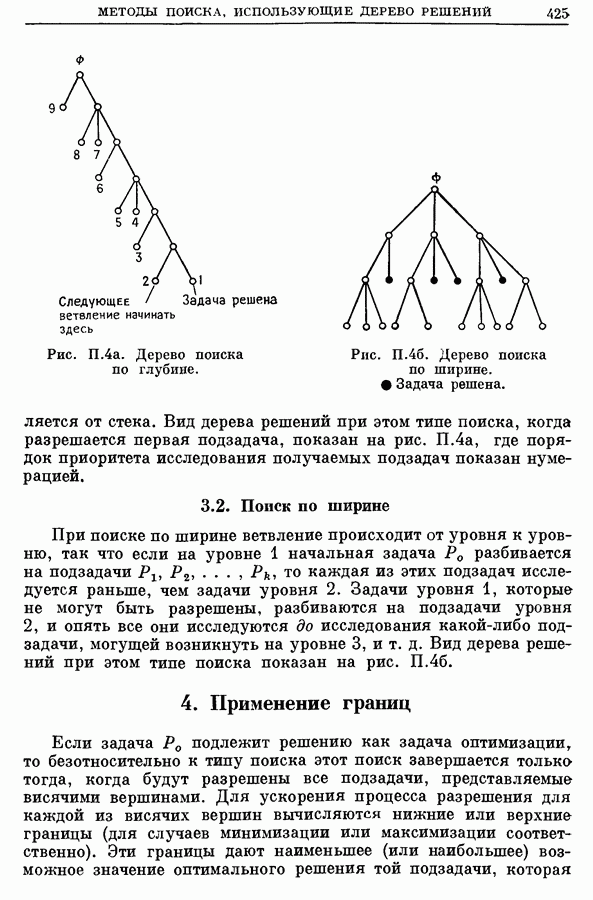
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления