| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Поток минимальной стоимости от s к t
В разделе 2 мы рассмотрели задачу максимизации потока от  безотносительно к какой-либо стоимости. Теперь мы рассмотрим задачу нахождения такого потока заданной величины
безотносительно к какой-либо стоимости. Теперь мы рассмотрим задачу нахождения такого потока заданной величины  от
от  стоимость которого минимальна. В этой задаче каждая дуга
стоимость которого минимальна. В этой задаче каждая дуга  имеет два связанных с ней числа — пропускную способность
имеет два связанных с ней числа — пропускную способность  и стоимость
и стоимость  единицы потока по этой дуге.
единицы потока по этой дуге.
Очевидно, что если  больше, чем значение максимального потока от
больше, чем значение максимального потока от  к
к  то не существует никакого решения. Если же
то не существует никакого решения. Если же  не превышает этого значения, то, вообще говоря, может существовать несколько различных потоков и требуется найти поток величины
не превышает этого значения, то, вообще говоря, может существовать несколько различных потоков и требуется найти поток величины  обеспечивающий минимальную стоимость. Наиболее известной процедурой решения задачи о потоке с минимальной стоимостью является так называемый алгоритм «беспорядка» Форда и Фалкерсона, и интересующийся читатель может найти описание этого эффективного алгоритма в [12], [4] и [7]. Алгоритмы, которые мы здесь опишем, принадлежат Клейну [20] и Басакеру и Гауэну [6]. Эти алгоритмы концептуально проще, чем метод беспорядка, и используют уже введенную технику. С вычислительной точки зрения эти методы сравнимы [2].
обеспечивающий минимальную стоимость. Наиболее известной процедурой решения задачи о потоке с минимальной стоимостью является так называемый алгоритм «беспорядка» Форда и Фалкерсона, и интересующийся читатель может найти описание этого эффективного алгоритма в [12], [4] и [7]. Алгоритмы, которые мы здесь опишем, принадлежат Клейну [20] и Басакеру и Гауэну [6]. Эти алгоритмы концептуально проще, чем метод беспорядка, и используют уже введенную технику. С вычислительной точки зрения эти методы сравнимы [2].
5.1. Алгоритм, основанный на выявлении отрицательных циклов
Предположим, что в графе существует допустимый поток  со значением
со значением  и что этот поток известен. Такой поток может быть получен с помощью алгоритма максимального потока (от s к t) из разд. 2 и добавления потока общей величины
и что этот поток известен. Такой поток может быть получен с помощью алгоритма максимального потока (от s к t) из разд. 2 и добавления потока общей величины  на всех аугментальных цепях (шаги с 4 по 6 алгоритма) до тех пор, пока поток
на всех аугментальных цепях (шаги с 4 по 6 алгоритма) до тех пор, пока поток  не достигнет значения
не достигнет значения  которое по условию меньше значения максимального потока.
которое по условию меньше значения максимального потока.
Для этого допустимого потока определим новый инкрементальный граф  в точности так, как это было объяснено в разд. 2.3, со следующими стоимостями дуг.
в точности так, как это было объяснено в разд. 2.3, со следующими стоимостями дуг.
Для каждой дуги  положим
положим 
Для каждой дуги  положим
положим 
Новый граф  дает теперь инкрементальные пропускные способности и стоимости (относительно начального потока
дает теперь инкрементальные пропускные способности и стоимости (относительно начального потока  любого дополнительного потока, введенного в
любого дополнительного потока, введенного в  Алгоритм основан на следующей теореме.
Алгоритм основан на следующей теореме.
Теорема 5. Поток  будет потоком минимальной стоимости со значением
будет потоком минимальной стоимости со значением  тогда и только тогда, когда в (|) не существует никакого цикла
тогда и только тогда, когда в (|) не существует никакого цикла  сумма стоимости дуг которого отрицательна.
сумма стоимости дуг которого отрицательна.
Доказательство. Пусть с  стоимость потока
стоимость потока  в графе
в графе  сумма стоимости
сумма стоимости  в цикле
в цикле  по отношению к графу
по отношению к графу 
Необходимость. Пусть с  для некоторого цикла
для некоторого цикла  из
из  Циркуляция дополнительной единицы потока по циклу
Циркуляция дополнительной единицы потока по циклу  дает новый поток
дает новый поток  оставляя значение
оставляя значение  потока от
потока от  неизменным. Стоимость потока
неизменным. Стоимость потока  равна с
равна с  а это противоречит допущению, что
а это противоречит допущению, что  поток минимальной стоимости со значением
поток минимальной стоимости со значением 
Достаточность. Допустим, что в графе  для каждого цикла
для каждого цикла  и что
и что  поток минимальной стоимости со значением
поток минимальной стоимости со значением  Обозначим теперь через
Обозначим теперь через  поток, значение которого на дуге
поток, значение которого на дуге  равно
равно 
Так как и  можно разложить в сумму потоков (от
можно разложить в сумму потоков (от  по цепям в
по цепям в  то построение унитарного графа
то построение унитарного графа  (см. разд. 2.4) для потока
(см. разд. 2.4) для потока  дает следующие полустепени вершин:
дает следующие полустепени вершин:

Так как в соответствии с разд.  состоит из наборов конформальных единичных потоков по циклам
состоит из наборов конформальных единичных потоков по циклам  (например), то мы можем написать
(например), то мы можем написать

Так как потоки  попарно конформальны и нам известно, что поток
попарно конформальны и нам известно, что поток  допустим, то любая сумма
допустим, то любая сумма  будет допустимой для любых
будет допустимой для любых  Таким образом, рассматривая поток
Таким образом, рассматривая поток  получаем
получаем

Рассмотрим теперь инкрементальный граф  Единственными дугами этого графа, стоимости которых уменьшились по сравнению с соответствующими стоимостями в графе
Единственными дугами этого графа, стоимости которых уменьшились по сравнению с соответствующими стоимостями в графе  являются те, которые будут «обращениями» дуг в
являются те, которые будут «обращениями» дуг в  Но, так как потоки
Но, так как потоки  конформальны, такие дуги не могут быть использованы ни одним из оставшихся циклов
конформальны, такие дуги не могут быть использованы ни одним из оставшихся циклов  следовательно, не влияют на последующие рассуждения.
следовательно, не влияют на последующие рассуждения.
Теперь мы имеем

для любого 
Стоимость потока  равна тогда С
равна тогда С 

Продолжая рассуждения аналогичным образом, мы получим окончательно с  а это противоречит предположению о том, что
а это противоречит предположению о том, что  поток минимальной стоимости со значением
поток минимальной стоимости со значением  Теорема доказана.
Теорема доказана.
Таким образом, в соответствии с теоремой 5, все, что требуется для нахождения потока минимальной стоимости со значением  это начать с допустимого потока
это начать с допустимого потока  со значением
со значением  построить граф (|) и проверить, нет ли в нем циклов с отрицательной стоимостью, используя любой из алгоритмов нахождения кратчайшей цепи, данных в разд. 3 и 4 гл. 9. Если не существует никакого цикла с отрицательной стоимостью, то поток будет потоком минимальной стоимости. Если цикл
построить граф (|) и проверить, нет ли в нем циклов с отрицательной стоимостью, используя любой из алгоритмов нахождения кратчайшей цепи, данных в разд. 3 и 4 гл. 9. Если не существует никакого цикла с отрицательной стоимостью, то поток будет потоком минимальной стоимости. Если цикл  с отрицательной стоимостью существует, то надо «пустить» по нему поток с максимально возможным значением 6. Суммарный поток от
с отрицательной стоимостью существует, то надо «пустить» по нему поток с максимально возможным значением 6. Суммарный поток от  не изменит своего значения у, а его стоимость уменьшится на
не изменит своего значения у, а его стоимость уменьшится на  где с
где с  величина стоимости отрицательного цикла. Очевидно,
величина стоимости отрицательного цикла. Очевидно,  должно быть выбрано так, чтобы пропускные способности дуг в
должно быть выбрано так, чтобы пропускные способности дуг в  не превышались, т. е.
не превышались, т. е.

Если этот поток  наложить на поток
наложить на поток  уже в графе
уже в графе  то, в силу первоначального выбора пропускных способностей дуг в
то, в силу первоначального выбора пропускных способностей дуг в  результирующий поток все еще будет допустимым. Процесс можно повторять, начиная его с полученного нового потока строя новый граф
результирующий поток все еще будет допустимым. Процесс можно повторять, начиная его с полученного нового потока строя новый граф  относительно нового потока и выявляя в этом графе циклы с отрицательной стоимостью. Описание алгоритма дано ниже.
относительно нового потока и выявляя в этом графе циклы с отрицательной стоимостью. Описание алгоритма дано ниже.
5.1.1. Описание алгоритма
Шаг 1. Использовать алгоритм максимального потока (от  из разд. 2 для нахождения в графе
из разд. 2 для нахождения в графе  допустимого потока
допустимого потока  со значением
со значением 
Шаг 2. Построить для этого потока граф  пользуясь цанными ранее правилами.
пользуясь цанными ранее правилами.
Шаг 3. Отправляясь от матрицы стоимостей графа  и используя алгоритм кратчайшей цепи (см. разд. 3.1 и 4 гл. 8), определить, существует ли в графе
и используя алгоритм кратчайшей цепи (см. разд. 3.1 и 4 гл. 8), определить, существует ли в графе  цикл с отрицательной стоимостью. Если такой цикл существует, то найти его (цикл
цикл с отрицательной стоимостью. Если такой цикл существует, то найти его (цикл  )
)

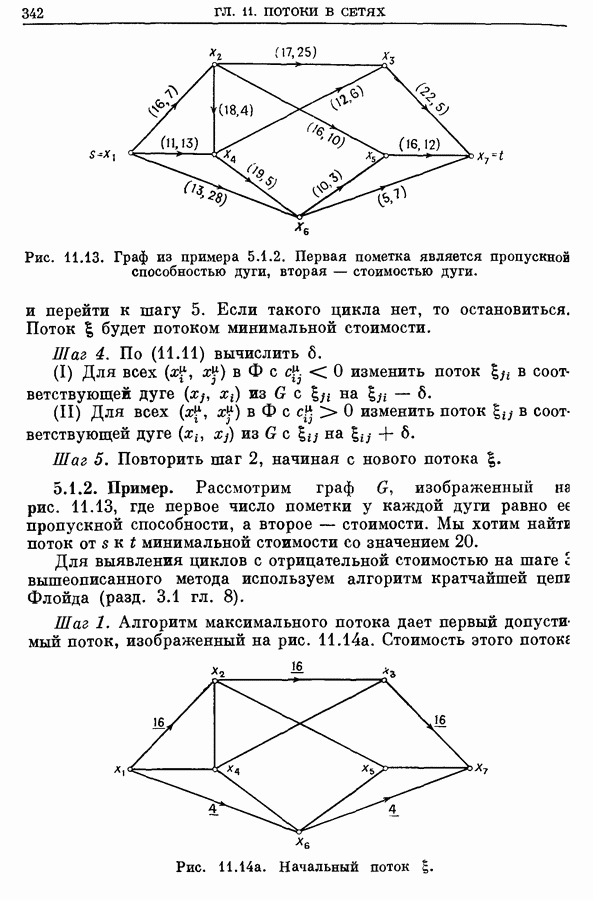
Рис. 11.13. Граф из примера 5.1.2. Первая пометка является пропускной способностью дуги, вторая — стоимостью дуги.
и перейти к шагу 5. Если такого цикла нет, то остановиться. Поток  будет потоком минимальной стоимости.
будет потоком минимальной стоимости.
Шаг 4. По (11.11) вычислить 
(I) Для всех  изменить поток
изменить поток  в соответствующей дуге
в соответствующей дуге  из
из  на
на 
(II) Для всех  изменить поток в соответствующей дуге
изменить поток в соответствующей дуге  из
из  на
на 
Шаг 5. Повторить шаг 2, начиная с нового потока
5.1.2. Пример.
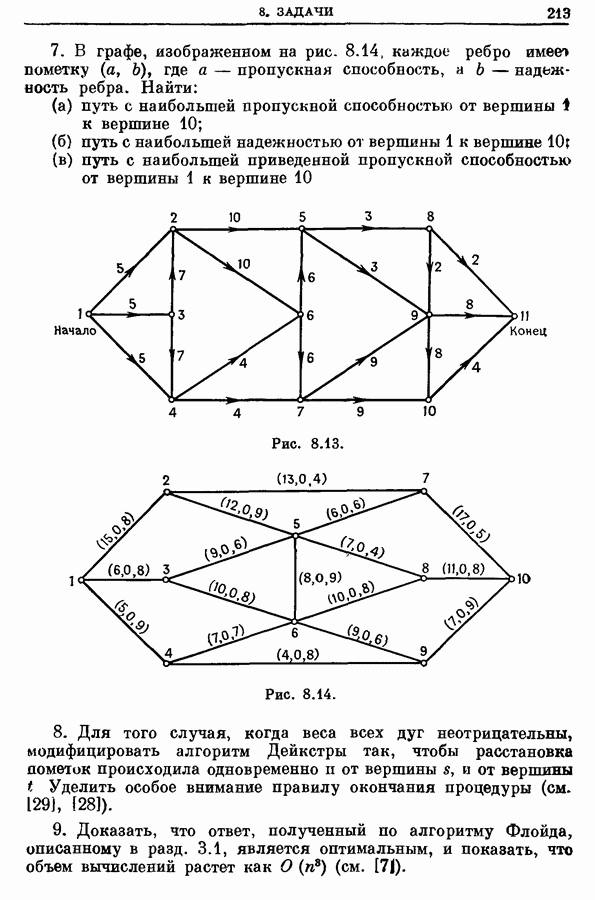
Рассмотрим граф  изображенный на рис. 11.13, где первое число пометки у каждой дуги равно ее пропускной способности, а второе — стоимости. Мы хотим найтв поток от
изображенный на рис. 11.13, где первое число пометки у каждой дуги равно ее пропускной способности, а второе — стоимости. Мы хотим найтв поток от  минимальной стоимости со значением 20.
минимальной стоимости со значением 20.
Для выявления циклов с отрицательной стоимостью на шаге с вышеописанного метода используем алгоритм кратчайшей  Флойда (разд. 3.1 гл. 8).
Флойда (разд. 3.1 гл. 8).
Шаг 1. Алгоритм максимального потока дает первый допустимый поток, изображенный на рис. 11.14а. Стоимость этого потокг

Рис. 11.14а. Начальный поток 
равна

Шаг 2. Исходя из этого потока, построим граф  как доказано на рис. 11.146, где цикл отрицательной стоимости изображен пунктиром.
как доказано на рис. 11.146, где цикл отрицательной стоимости изображен пунктиром.
Шаг 3. Начиная с матрицы стоимостей

(где на пустых местах должны стоять элементы  и применяя алгоритм Флойда, получаем следующие матрицы наименьших стоимостей вместе с соответствующими им матрицами цепей:
и применяя алгоритм Флойда, получаем следующие матрицы наименьших стоимостей вместе с соответствующими им матрицами цепей:

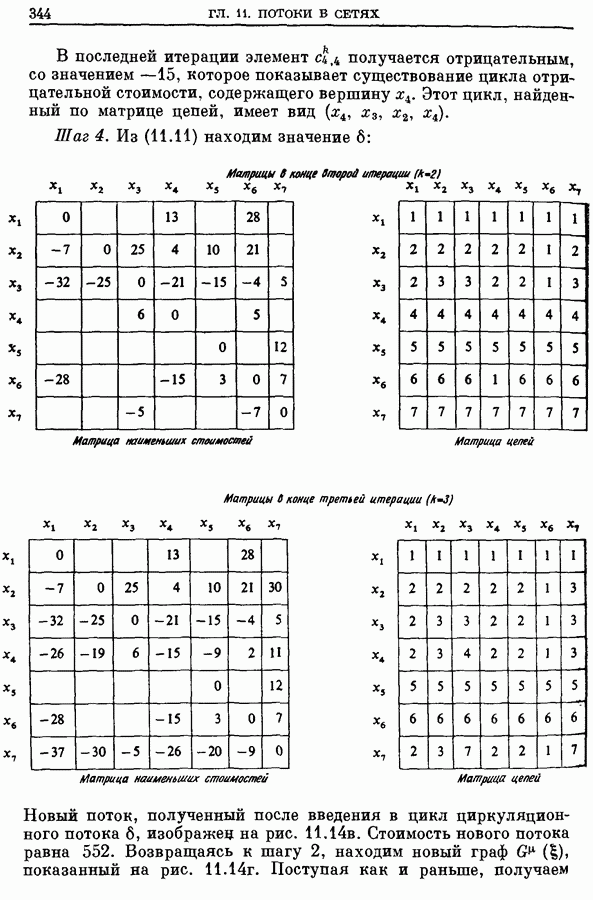
В последней итерации элемент получается отрицательным, со значением —15, которое показывает существование цикла отрицательной стоимости, содержащего вершину  Этот цикл, найденный по матрице цепей, имеет вид
Этот цикл, найденный по матрице цепей, имеет вид 
Шаг 4. Из (11.11) находим значение 6:
(см. скан)
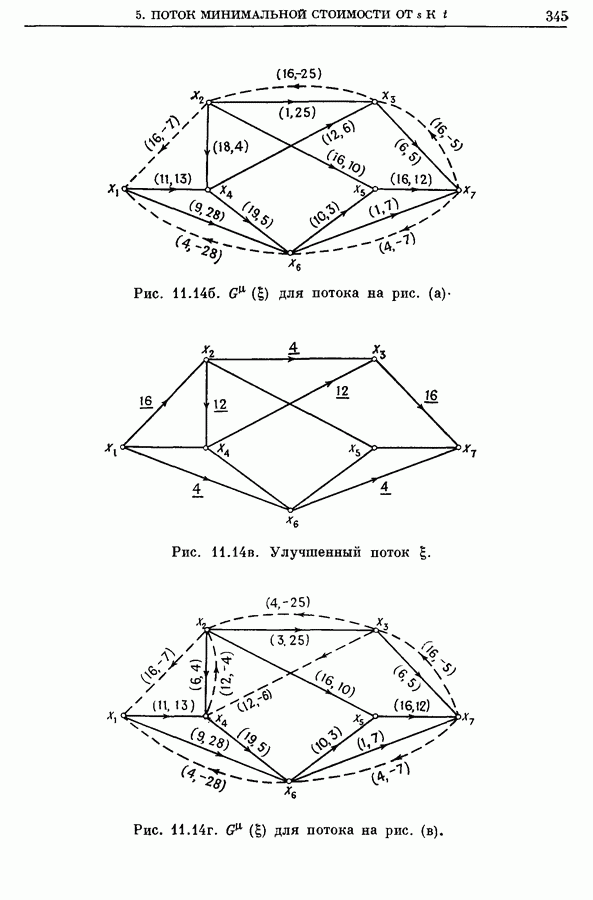
Новый поток, полученный после введения в цикл циркуляционного потока  изображен на рис. 11.14в. Стоимость нового потока равна 552. Возвращаясь к шагу 2, находим новый граф
изображен на рис. 11.14в. Стоимость нового потока равна 552. Возвращаясь к шагу 2, находим новый граф  показанный на рис. 11.14г. Поступая как и раньше, получаем
показанный на рис. 11.14г. Поступая как и раньше, получаем

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
Шаг 3. Обнаружен отрицательный цикл  со стоимостью —10.
со стоимостью —10.
Шаг 4. 
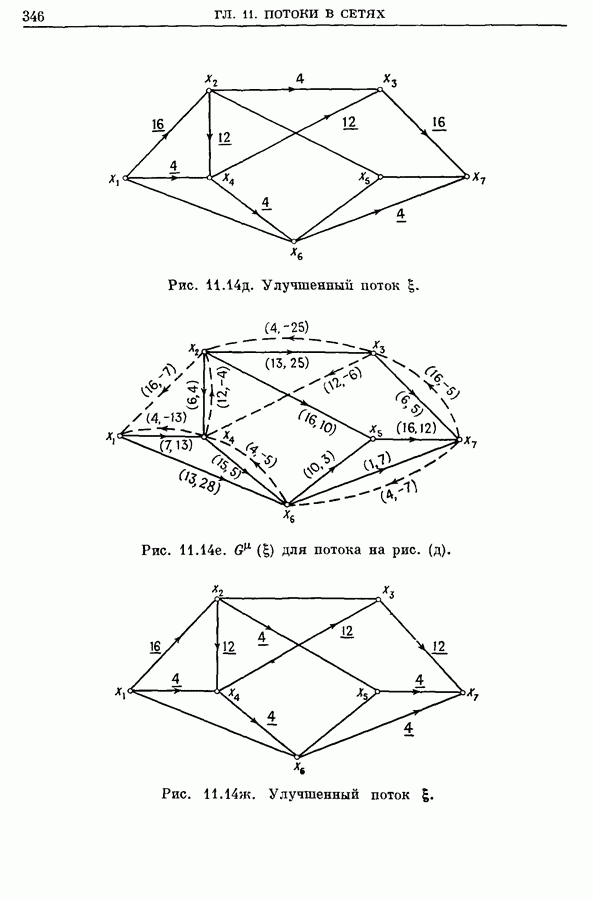
Новый поток со стоимостью 512 изображен на рис. 11.14д.
Шаг 2. Граф  соответствующий новому потоку, изображен на рис.
соответствующий новому потоку, изображен на рис. 
Шаг 3. Обнаружен отрицательный цикл  со стоимостью —8.
со стоимостью —8.
Шаг 4. 
Новый поток со стоимостью 480 изображен на рис. 11.14ж.
Шаг 2. Получившийся граф  показан на рис. 11.14з.
показан на рис. 11.14з.
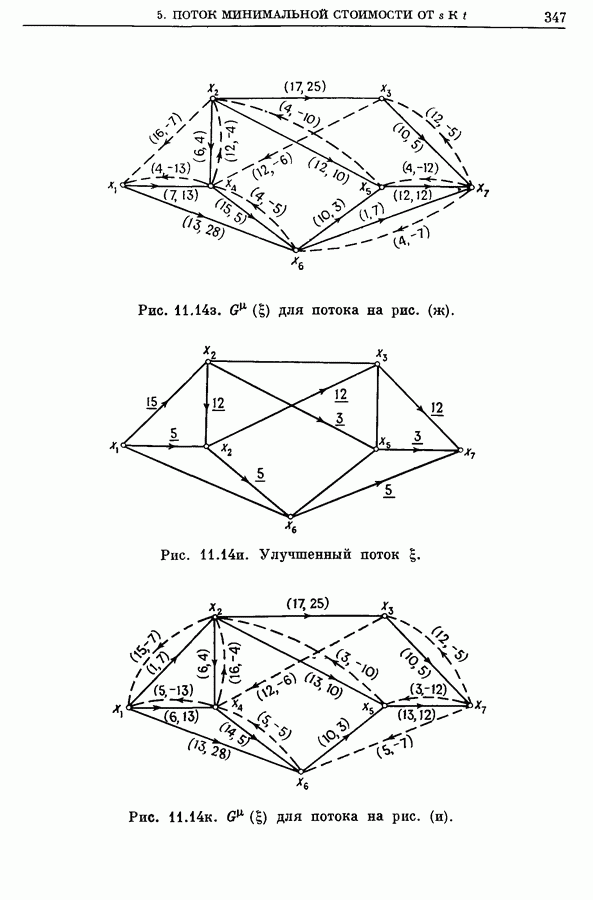
Шаг 3. Обнаружен отрицательный цикл  со стоимостью —4.
со стоимостью —4.
Шаг 4. 
Новый поток со стоимостью 476 изображен на рис. 11.14 и.
Шаг 2. Граф  изображен на рис.
изображен на рис. 
Шаг 3. Обнаружен отрицательный цикл  со стоимостью —2.
со стоимостью —2.
Шаг 4. 

Рис. 11.14л. Поток минимальной стоимости.
Новый поток со стоимостью 474 изображен на рис. 
В последнем инкрементальном графе нет никаких циклов с отрицательной стоимостью, и поэтому поток, изображенный на рис.  является потоком наименьшей стоимости со значением 20 и его стоимость равна 474.
является потоком наименьшей стоимости со значением 20 и его стоимость равна 474.
5.1.3. Шаг 3 из алгоритма 5.1.1.
В вышеприведенном примере был использован метод Флойда для нахождения циклов отрицательной стоимости в инкрементальном графе  на шаге 3 алгоритма определения потока минимальной стоимости, данного в разд. 5.1.1. Но, как уже отмечалось в разд. 4 гл. 8, это не лучший метод выявления циклов отрицательной стоимости для графа
на шаге 3 алгоритма определения потока минимальной стоимости, данного в разд. 5.1.1. Но, как уже отмечалось в разд. 4 гл. 8, это не лучший метод выявления циклов отрицательной стоимости для графа  в котором существует вершина
в котором существует вершина  достижимая из всех других вершин
достижимая из всех других вершин  Лучший способ состоит в использовании алгоритма, который находит кратчайшую цепь от
Лучший способ состоит в использовании алгоритма, который находит кратчайшую цепь от  ко всем другим вершинам, а не в применении алгоритма Флойда, находящего кратчайшие цепи между каждой парой вершин [2]. В этом отношении более успешно, как это объясняется в разд. 4 настоящей главы, может быть использован алгоритм кратчайшей цепи из разд. 2.2.1 главы 8.
ко всем другим вершинам, а не в применении алгоритма Флойда, находящего кратчайшие цепи между каждой парой вершин [2]. В этом отношении более успешно, как это объясняется в разд. 4 настоящей главы, может быть использован алгоритм кратчайшей цепи из разд. 2.2.1 главы 8.
Для инкрементального графа  очень просто показать, что в нем существует по крайней мере одна вершина, из которой можно достичь любую другую вершину графа
очень просто показать, что в нем существует по крайней мере одна вершина, из которой можно достичь любую другую вершину графа  и что на самом деле конечная вершина
и что на самом деле конечная вершина  обладает этим свойством. Это можно показать следующим образом.
обладает этим свойством. Это можно показать следующим образом.
Так как для любой дуги  из
из  для которой существует некоторый ненулевой поток, в инкрементальном графе
для которой существует некоторый ненулевой поток, в инкрементальном графе  существует дуга
существует дуга  то все вершины
то все вершины  из
из  соответствующие вершинам
соответствующие вершинам  из
из  лежащим на цепях потока от
лежащим на цепях потока от  могут быть достигнуты из
могут быть достигнуты из  с использованием «обратных» цепей, образованных дугами
с использованием «обратных» цепей, образованных дугами  Таким же способом может быть достигнут источник
Таким же способом может быть достигнут источник  Итак, каждая вершина
Итак, каждая вершина  из
из  может быть достигнута из
может быть достигнута из  (в противном случае
(в противном случае  может быть удалена из
может быть удалена из  и это не повлияет на поток). Следовательно, так как дуги
и это не повлияет на поток). Следовательно, так как дуги  не несущие никакого потока в
не несущие никакого потока в  появляются в
появляются в  в качестве дуг
в качестве дуг  вершины
вершины  из
из  соответствующие вершинам х из
соответствующие вершинам х из  не лежащим на цепях потока, могут быть достигнуты из
не лежащим на цепях потока, могут быть достигнуты из  через
через  Иными словами, сначала просто достигаем
Иными словами, сначала просто достигаем  как было сказано выше, а затем следуем по пути из
как было сказано выше, а затем следуем по пути из 
Поэтому в инкрементальном графе (|) все вершины могут быть достигнуты из  и если эта вершина используется в качестве источника при нахождении кратчайшей цепи от
и если эта вершина используется в качестве источника при нахождении кратчайшей цепи от  ко всем другим вершинам из
ко всем другим вершинам из  (например, с использованием алгоритма из 2.2.1 гл. 8), то все циклы отрицательной стоимости в
(например, с использованием алгоритма из 2.2.1 гл. 8), то все циклы отрицательной стоимости в  могут быть обнаружены.
могут быть обнаружены.
Используя такой подход при организации шага 3 основного алгоритма потока минимальной стоимости из разд. 5.1, Беннингтон [2] опубликовал вычислительные результаты, показывающие, что этот алгоритм не хуже алгоритма «беспорядка» [12, 4, 7]. Применение метода наименьших квадратов к оценке требуемого времени  вычисления по тестам, использующим случайно
вычисления по тестам, использующим случайно
порожденные графы с  вершинами и
вершинами и  дугами, дало такой результат:
дугами, дало такой результат:

Граф с 200 вершинами и 5000 дугами требует приблизительно 8 с машинного времени.
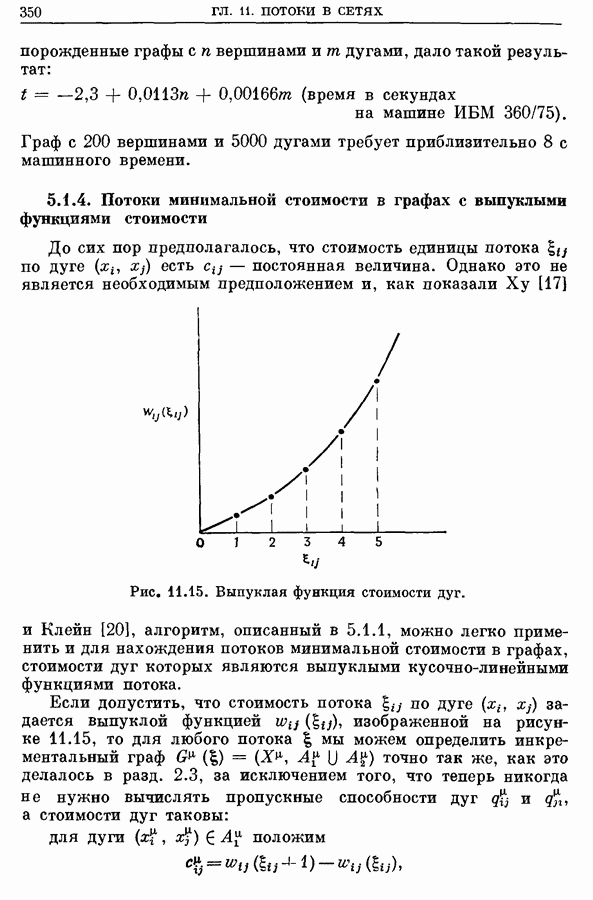
5.1.4. Потоки минимальной стоимости в графах с выпуклыми функциями стоимости
До сих пор предполагалось, что стоимость единицы потока по дуге  есть
есть  постоянная величина.
постоянная величина.

Рис. 11.15. Выпуклая функция стоимости дуг.
Однако это не является необходимым предположением и, как показали Ху [17] и Клейн [20], алгоритм, описанный в 5.1.1, можно легко применить и для нахождения потоков минимальной стоимости в графах, стоимости дуг которых являются выпуклыми кусочно-линейными функциями потока.
Если допустить, что стоимость потока  по дуге
по дуге  задается выпуклой функцией
задается выпуклой функцией  изображенной на рисунке 11.15, то для любого потока
изображенной на рисунке 11.15, то для любого потока  мы можем определить инкрементальный граф
мы можем определить инкрементальный граф  точно так же, как это делалось в разд. 2.3, за исключением того, что теперь никогда не нужно вычислять пропускные способности дуг
точно так же, как это делалось в разд. 2.3, за исключением того, что теперь никогда не нужно вычислять пропускные способности дуг  а стоимости дуг таковы:
а стоимости дуг таковы:
для дуги  положим
положим

для дуги  положим
положим

считая, что 
Теперь мы можем непосредственно использовать алгоритм из разд. 5.1.1, за исключением того, что  поток, посылаемый по любому циклу
поток, посылаемый по любому циклу  отрицательной стоимости, который можно найти в
отрицательной стоимости, который можно найти в  всегда берется равным 1. Заметим, что все инкрементальные стоимости были определены так, чтобы они приводили к увеличению или уменьшению значения потока на одну единицу. Заметим также, что при использовании только «единичных» преобразований потоков (т. е. при уменьшении или увеличении значения потока только на единицу) нет необходимости вычислять инкрементальные пропускные способности дуг в
всегда берется равным 1. Заметим, что все инкрементальные стоимости были определены так, чтобы они приводили к увеличению или уменьшению значения потока на одну единицу. Заметим также, что при использовании только «единичных» преобразований потоков (т. е. при уменьшении или увеличении значения потока только на единицу) нет необходимости вычислять инкрементальные пропускные способности дуг в  так как эти величины нужны лишь для вычисления
так как эти величины нужны лишь для вычисления 
Если при задании функции стоимости не требуется большой точности, то  можно аппроксимировать кусочно-линейной функцией. Тогда ограничение, что
можно аппроксимировать кусочно-линейной функцией. Тогда ограничение, что  выбирается равным единице потока, можно ослабить и достигнуть более быстрой сходимости к потоку минимальной стоимости. Инкрементальные стоимости каждой дуги могут быть теперь определены как угловые коэффициенты соответствующих линейных участков функций стоимости, а именно для данной дуги выбирается участок, отвечающий текущему значению потока на этой дуге. Затем можно вычислить пропускные способности, чтобы убедиться, что никакое увеличение или уменьшение потока
выбирается равным единице потока, можно ослабить и достигнуть более быстрой сходимости к потоку минимальной стоимости. Инкрементальные стоимости каждой дуги могут быть теперь определены как угловые коэффициенты соответствующих линейных участков функций стоимости, а именно для данной дуги выбирается участок, отвечающий текущему значению потока на этой дуге. Затем можно вычислить пропускные способности, чтобы убедиться, что никакое увеличение или уменьшение потока  не даст новый поток, выходящий за пределы применимости текущего линейного участка, аппроксимирующего функцию стоимости.
не даст новый поток, выходящий за пределы применимости текущего линейного участка, аппроксимирующего функцию стоимости.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
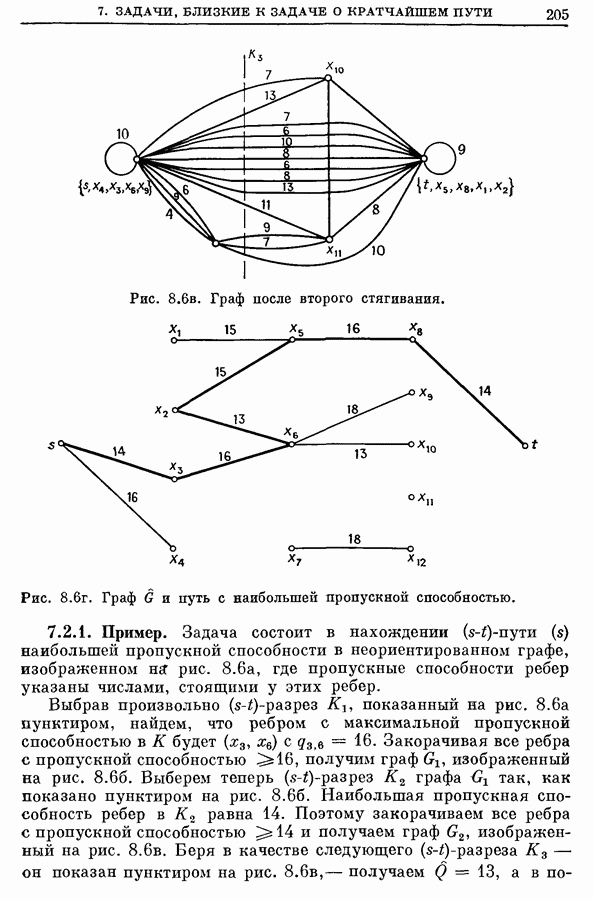
- 7.2. Путь с наибольшей пропускной способностью
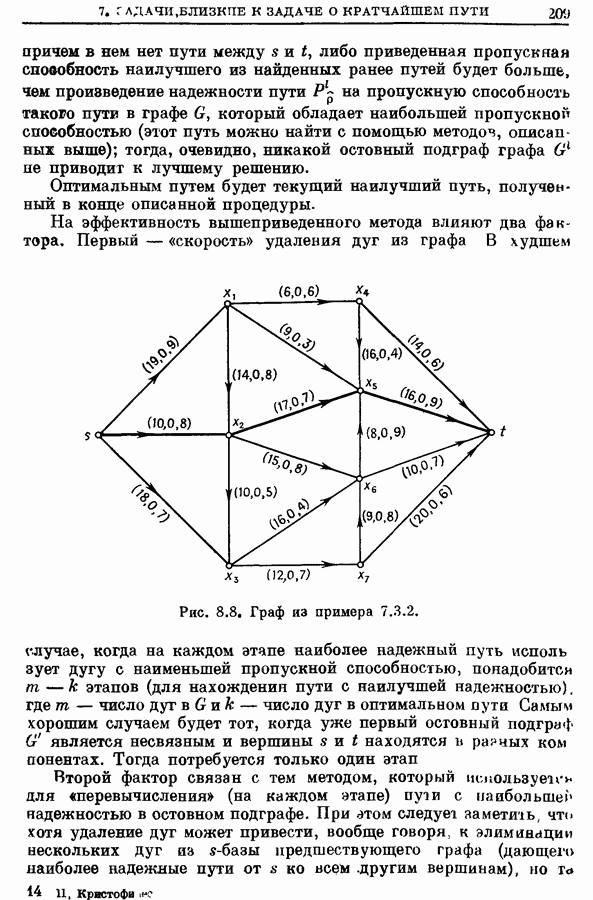
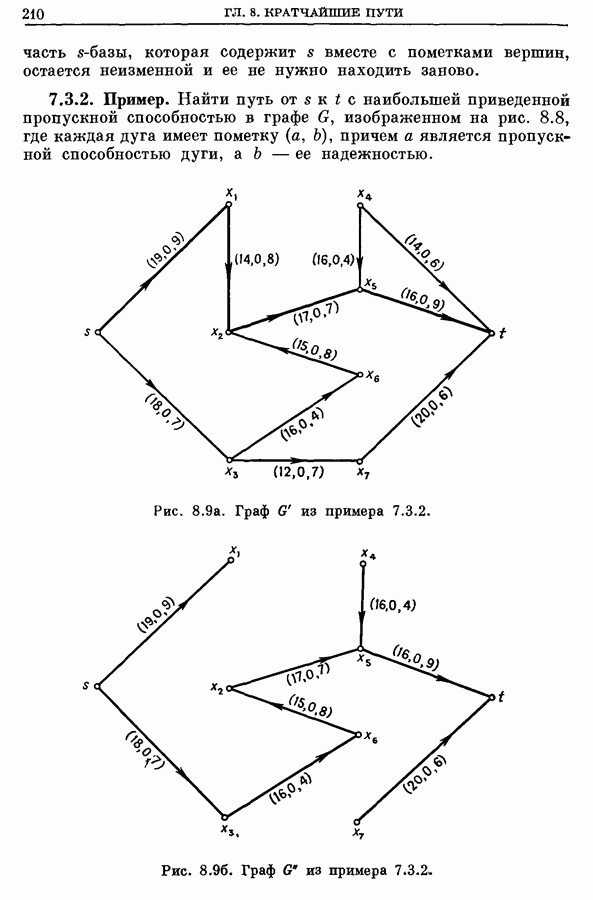
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
- 2.3. Инкрементальные графы
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
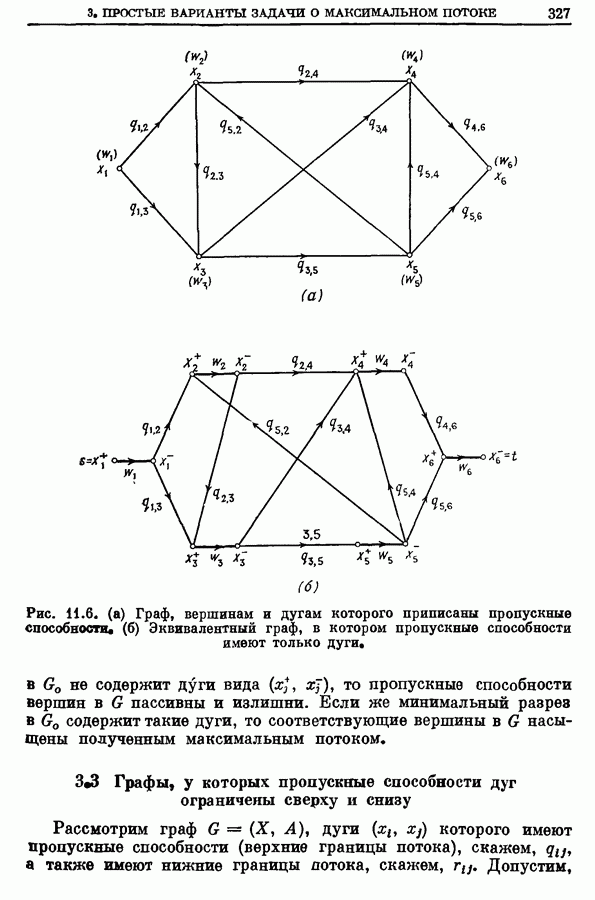
- 3.2. Графы с пропускными способностями дуг и вершин
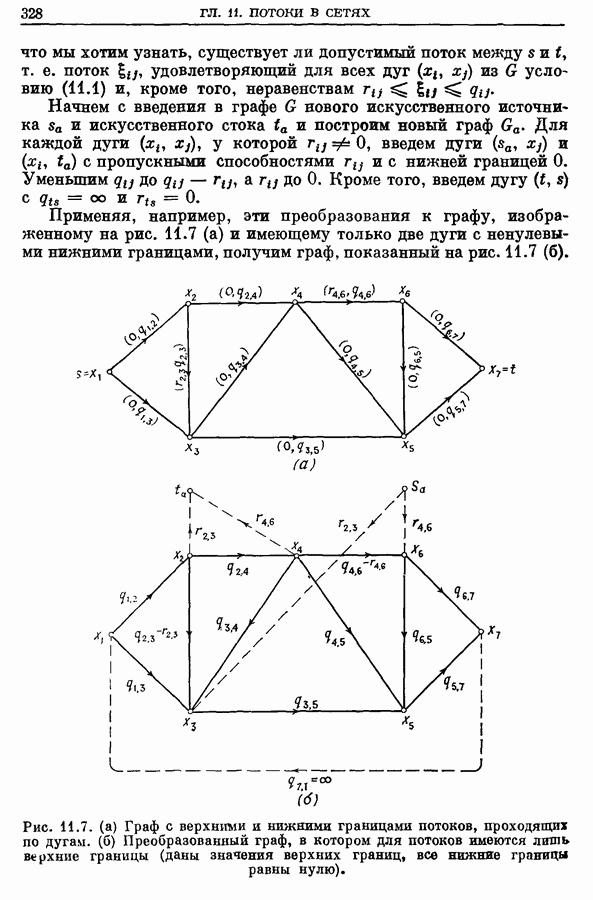
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
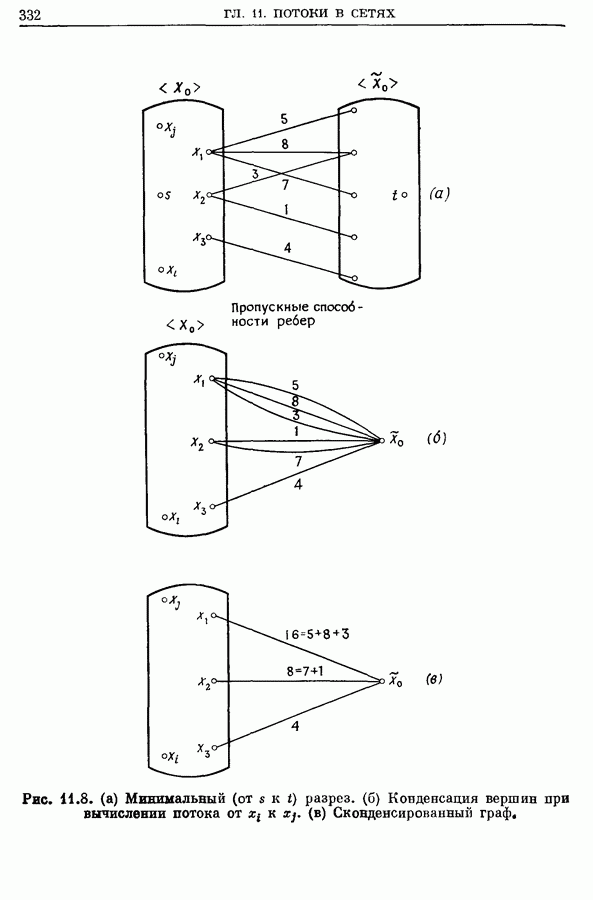
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
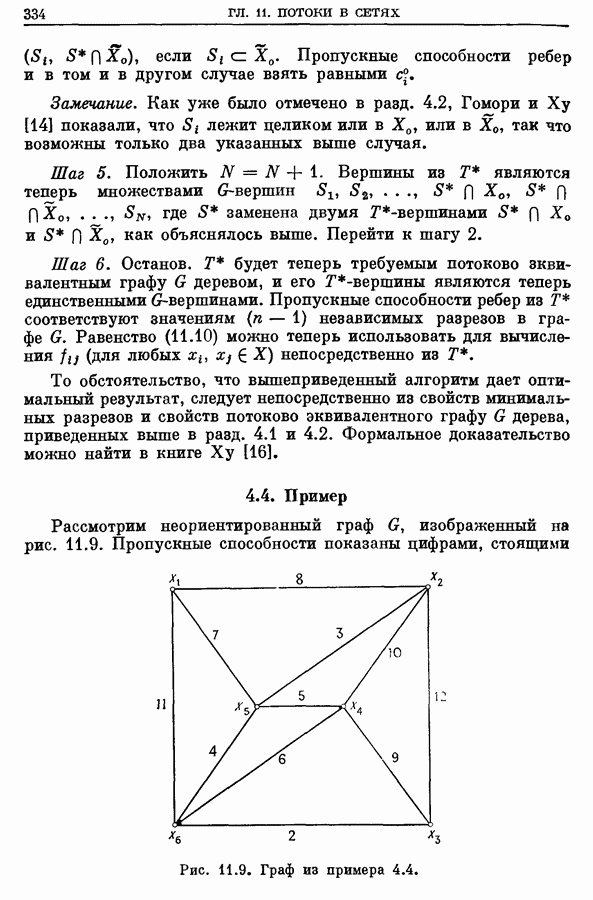
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
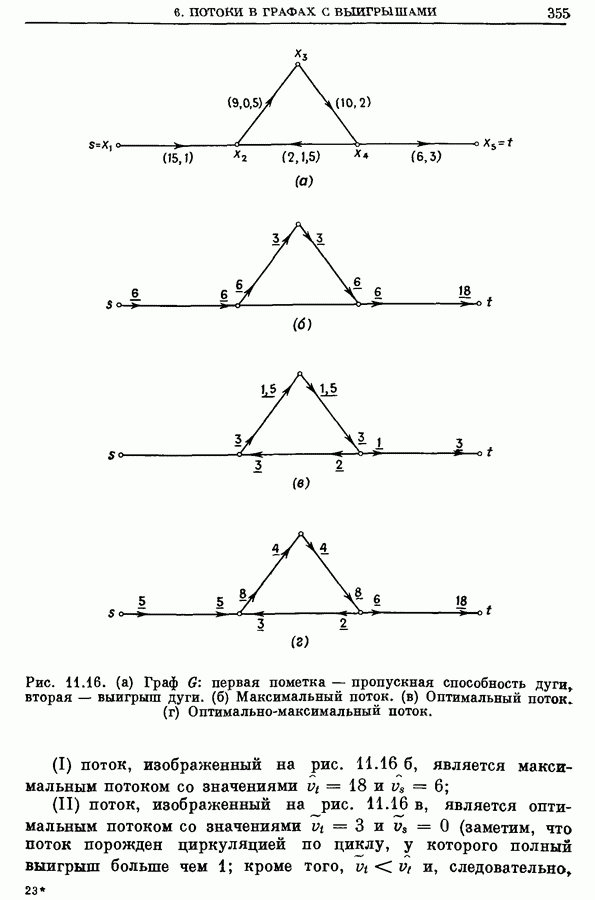
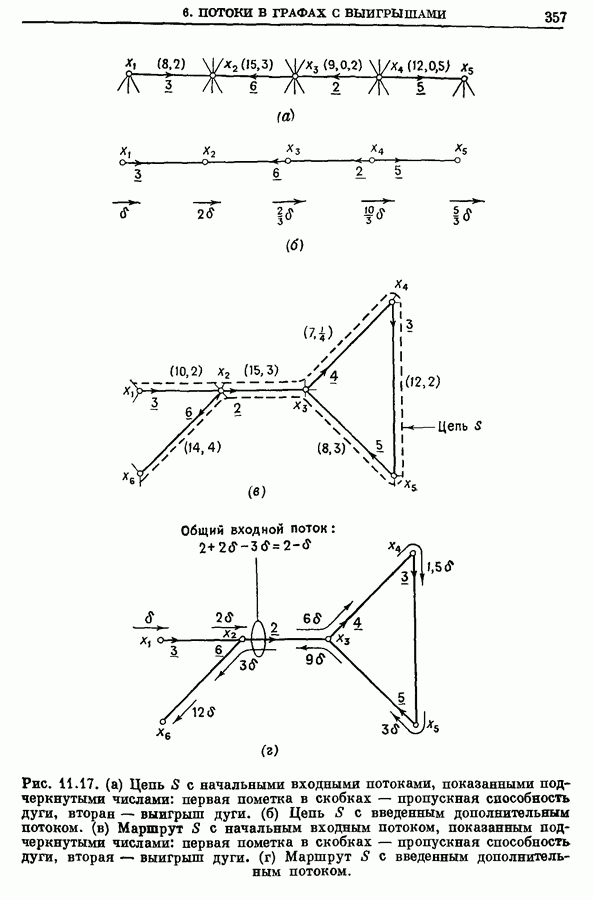
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
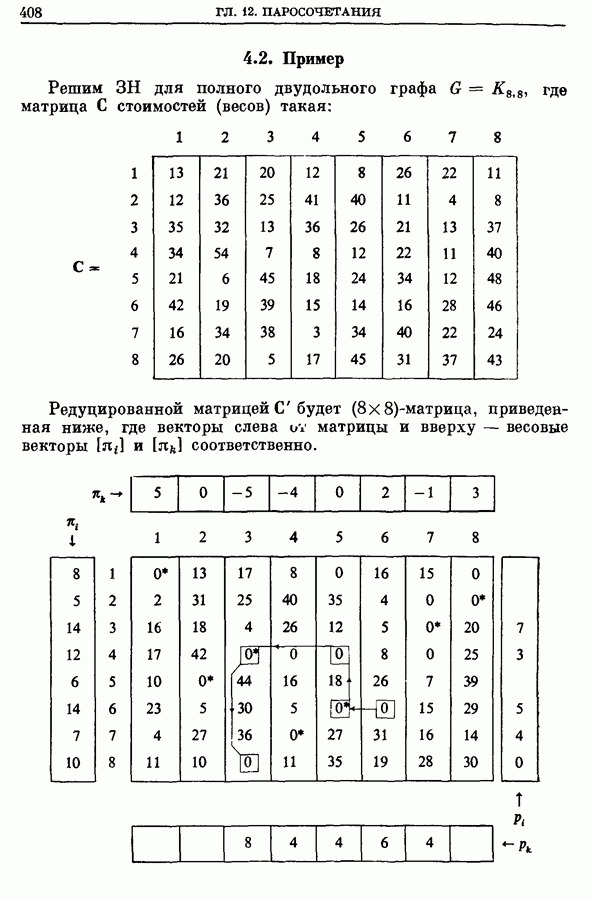
- 4.2. Пример
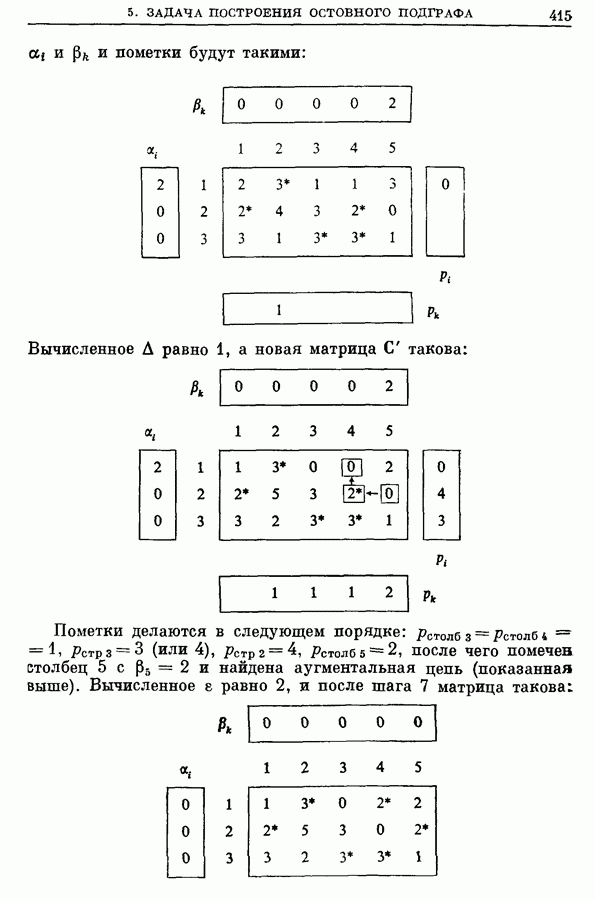
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
- 5.2. Пример
- 6. Задача о покрытии
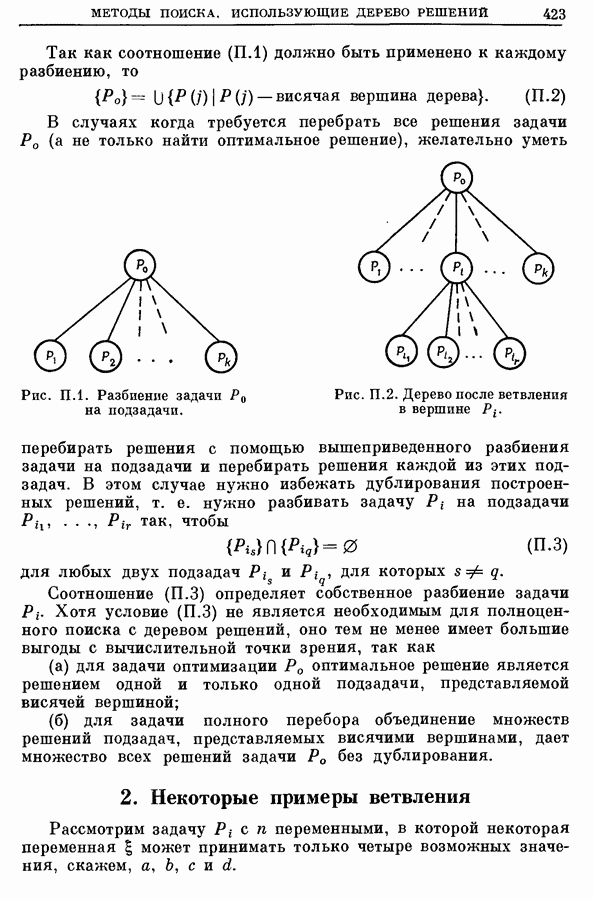
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
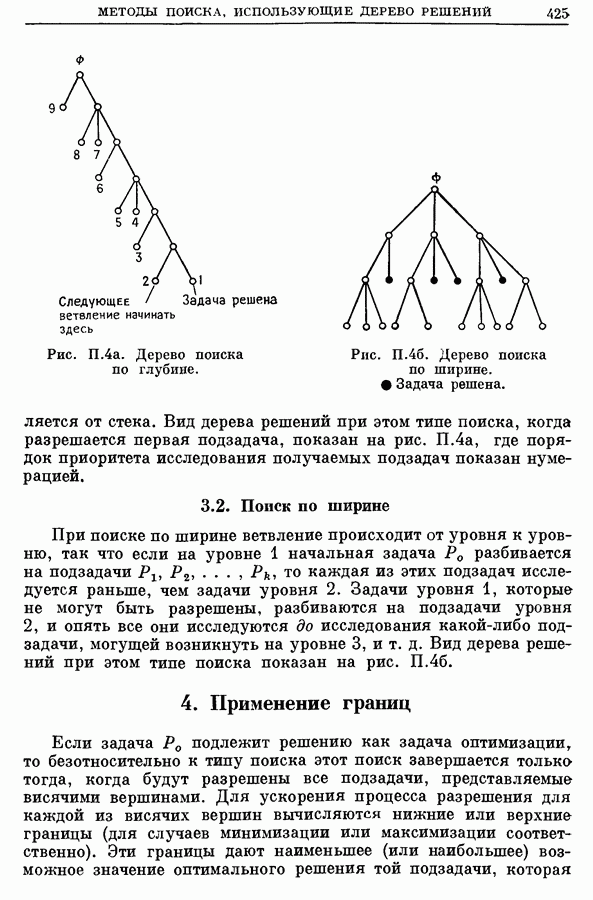
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления