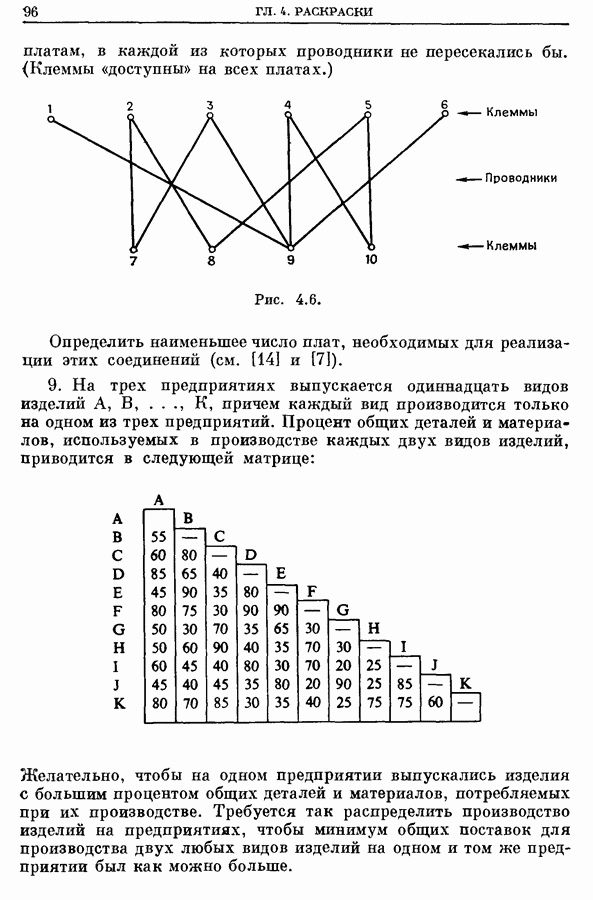
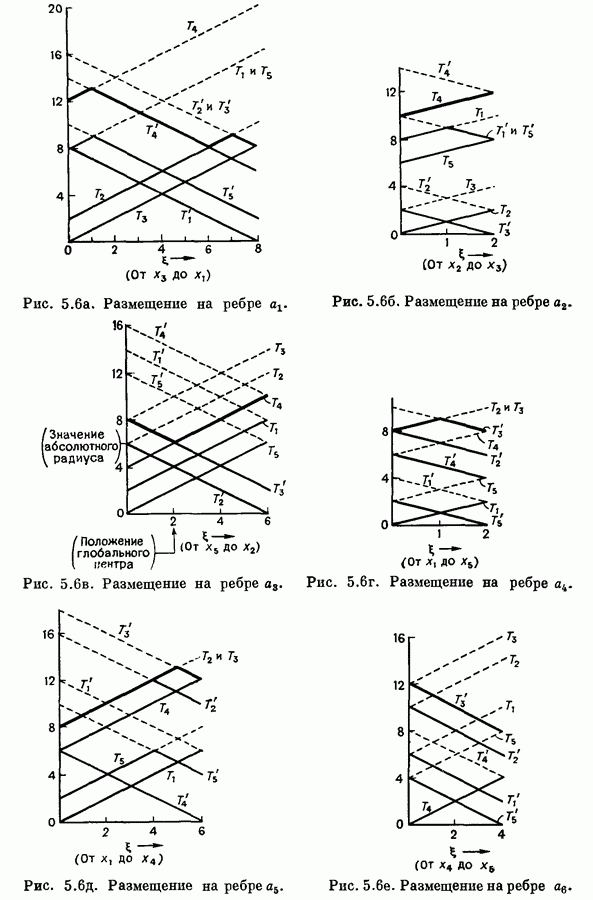
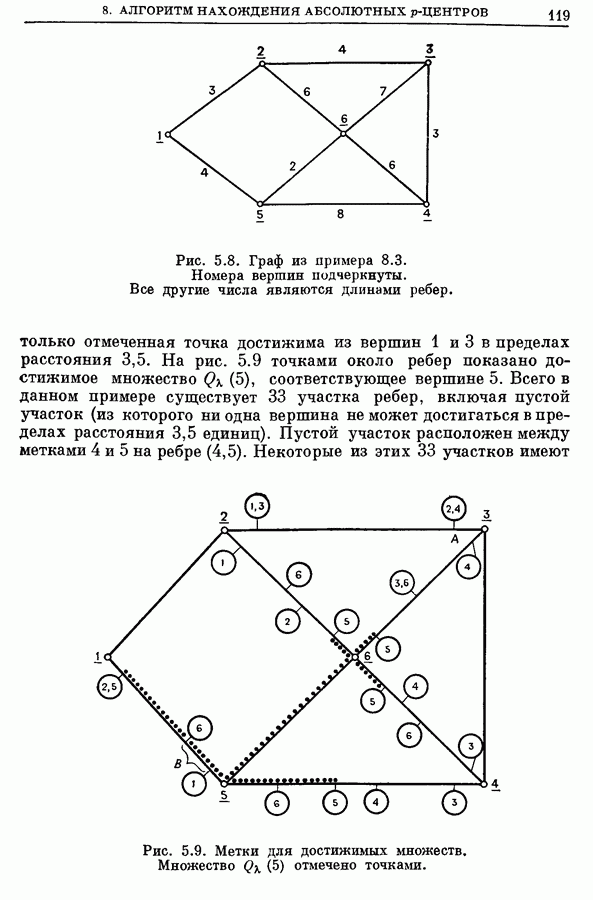
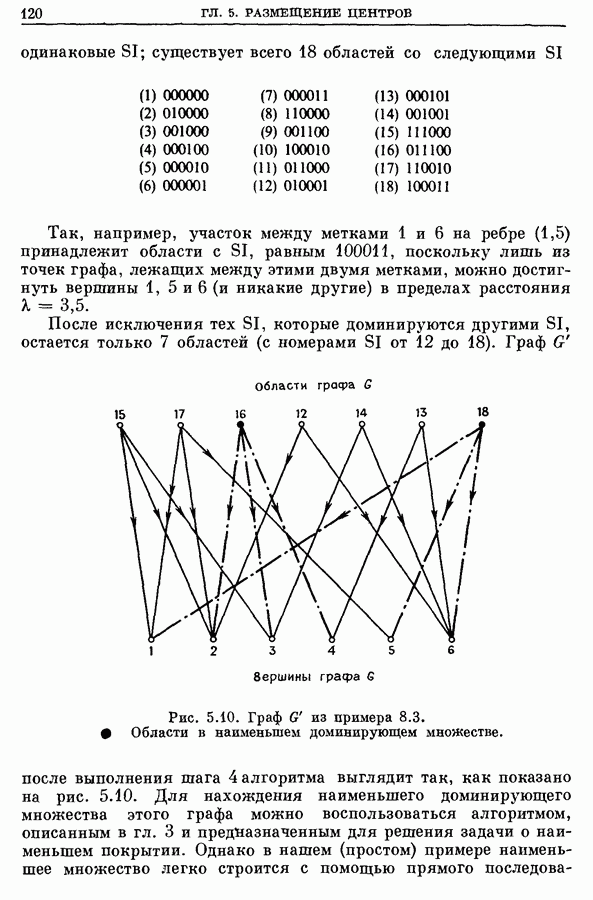
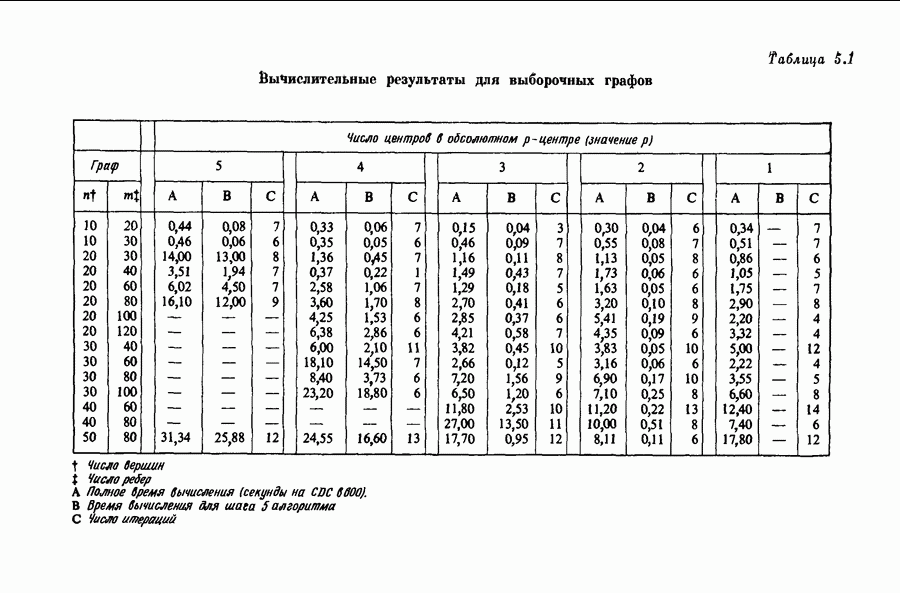
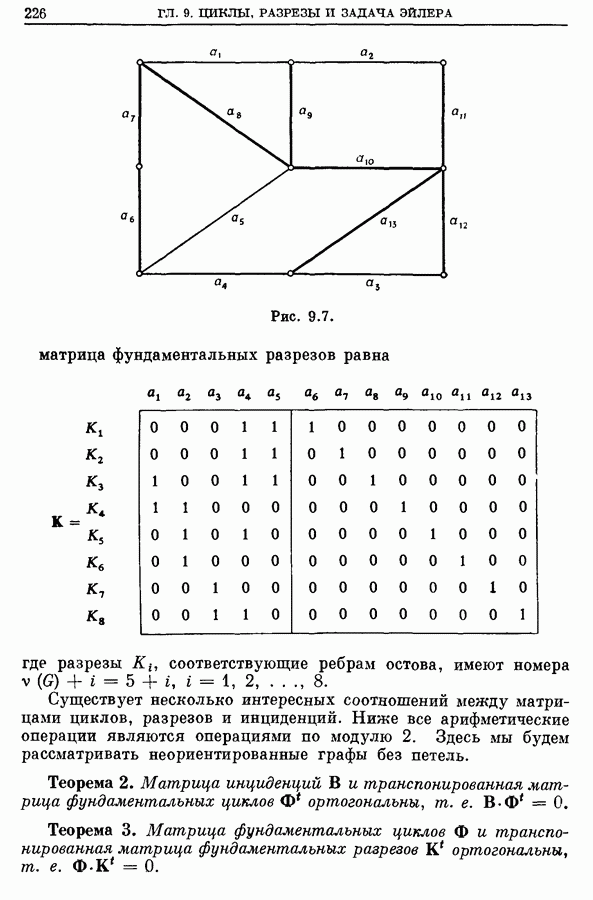
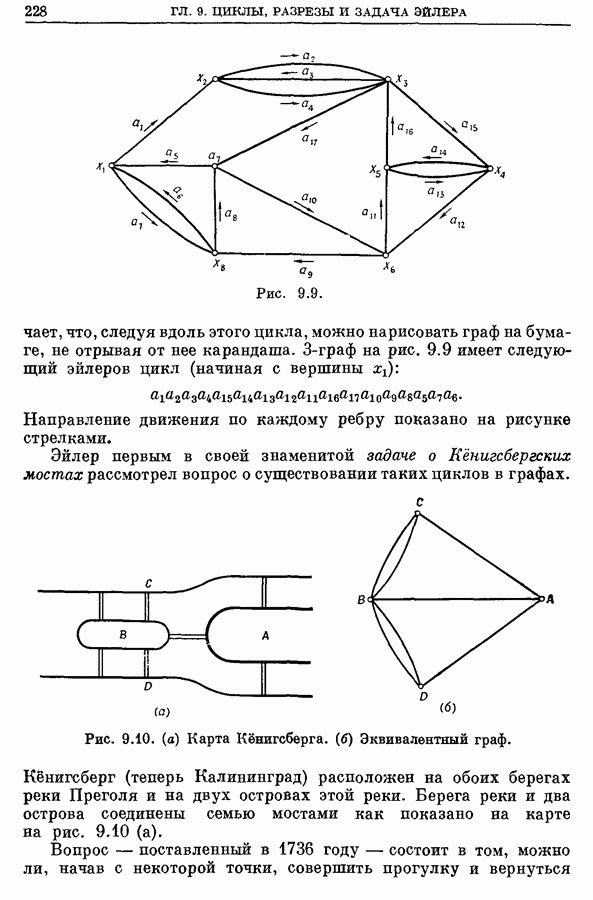
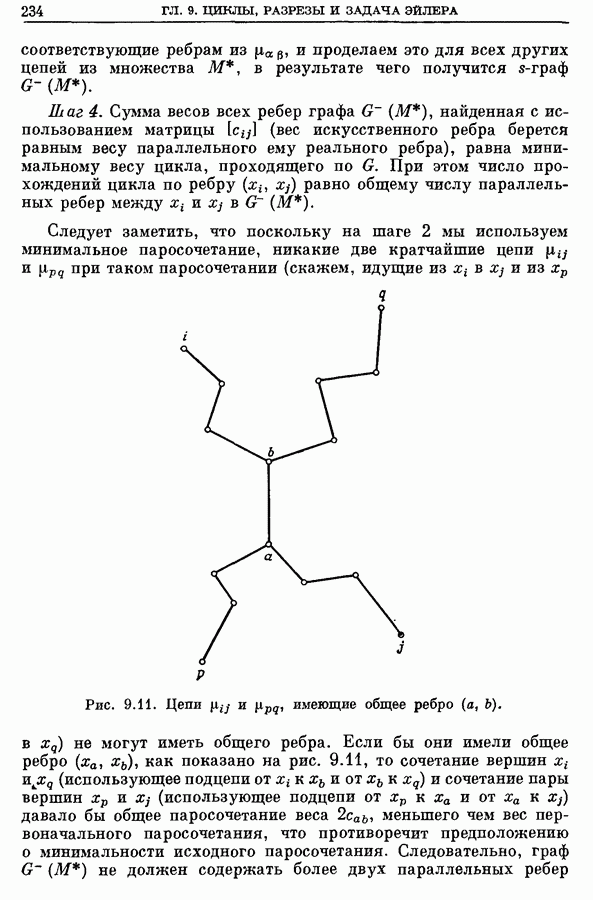
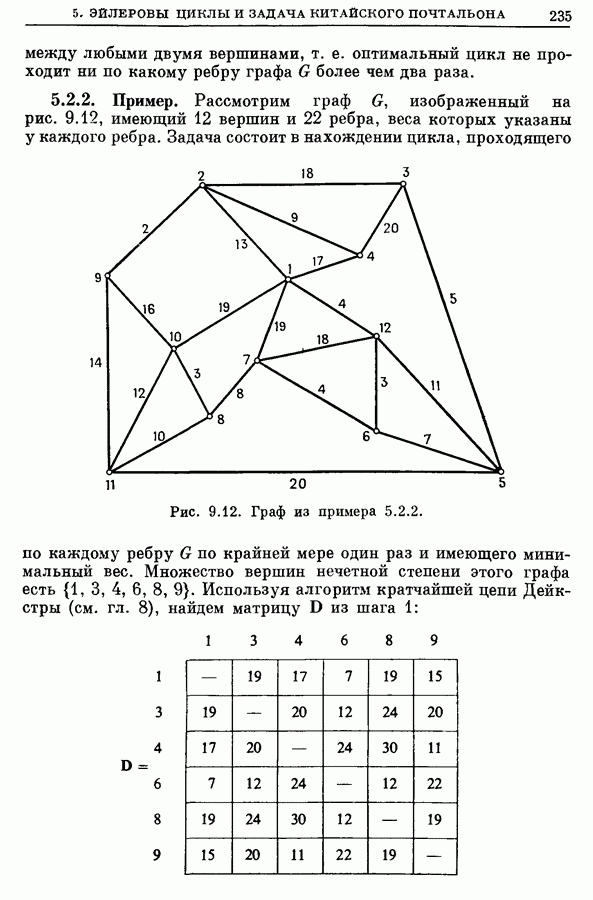
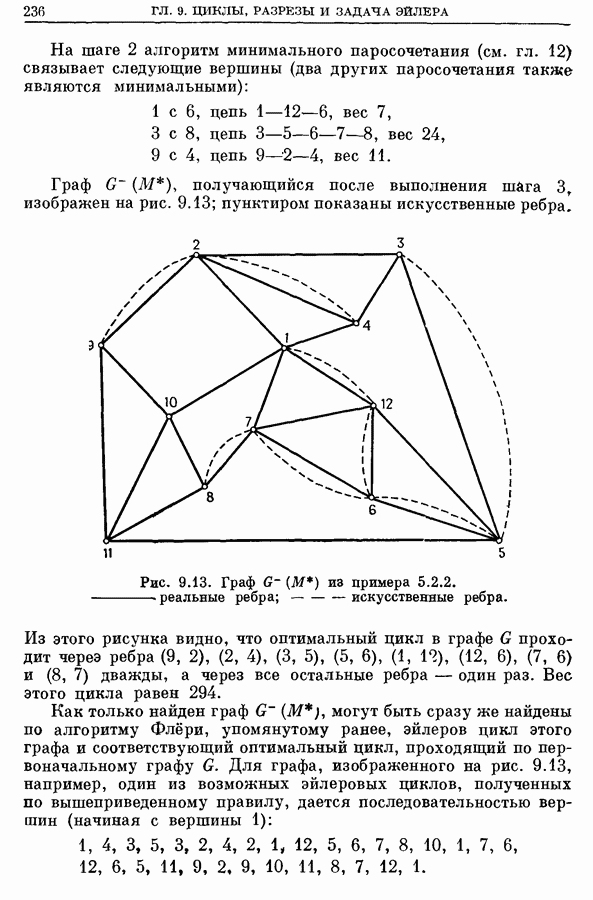
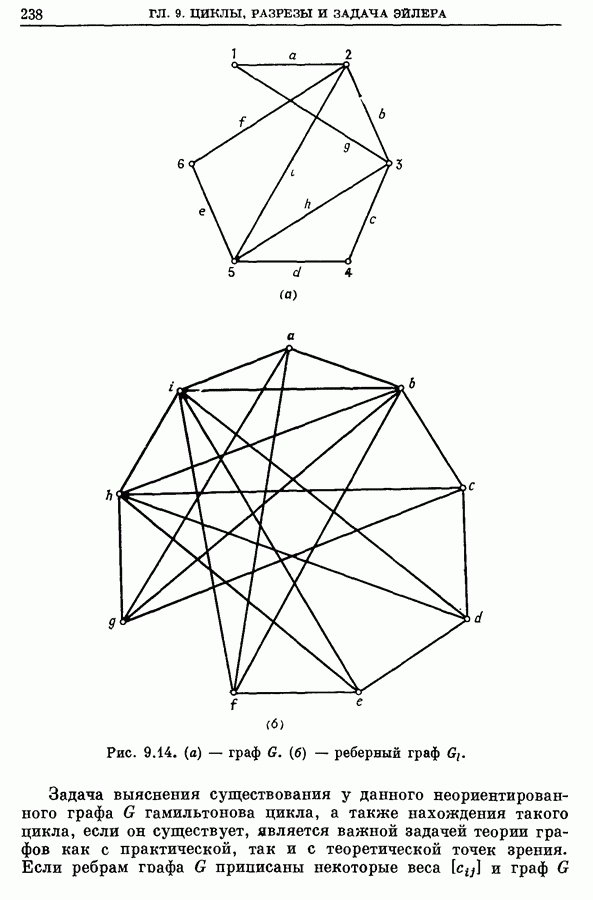
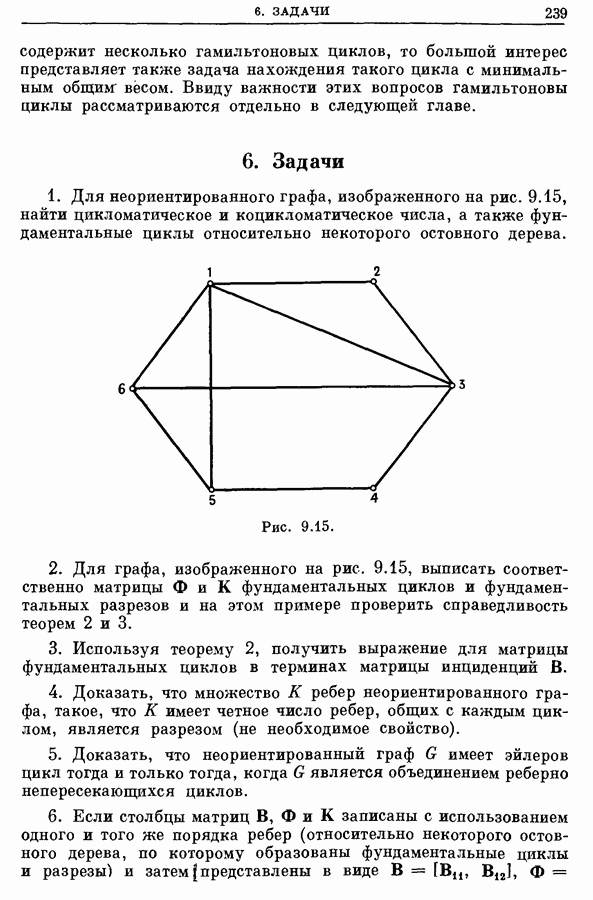
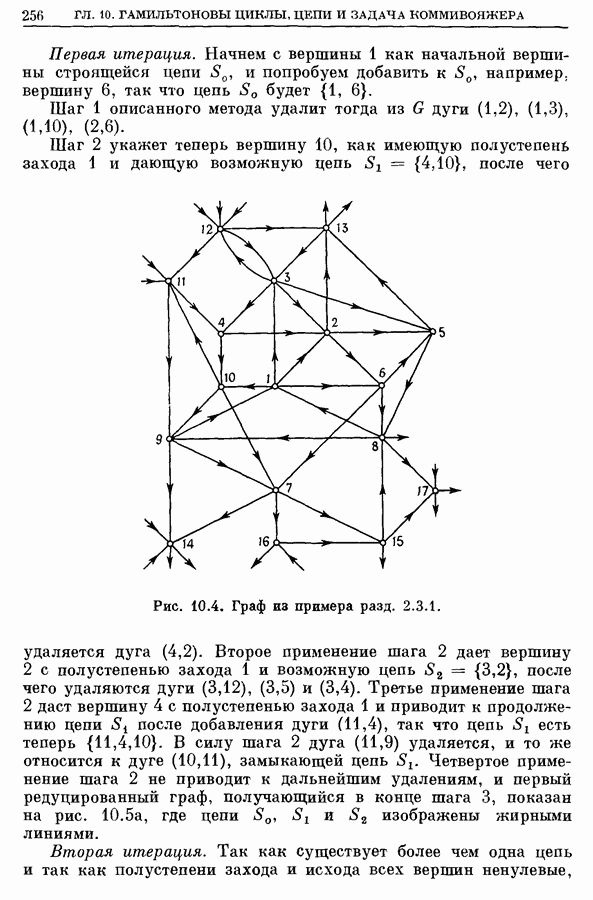
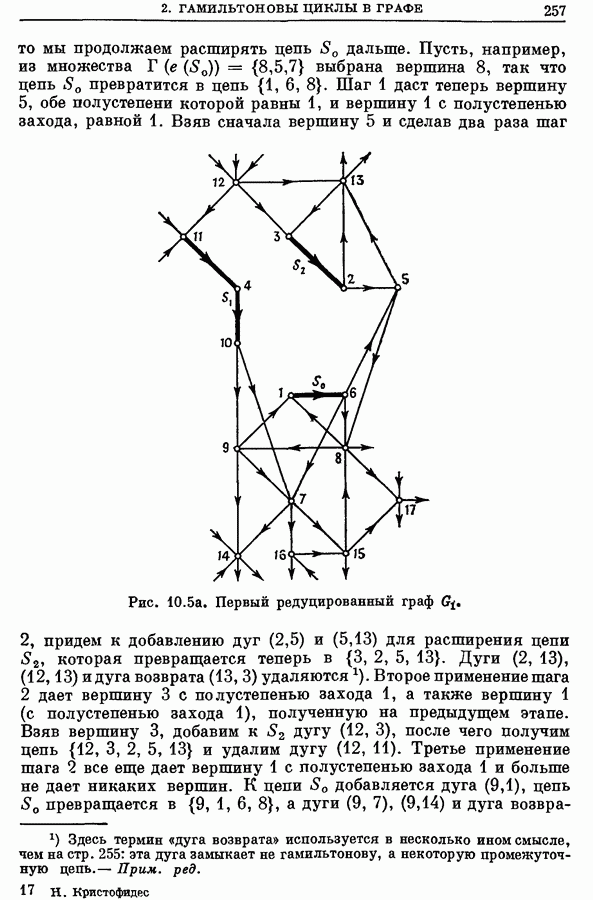
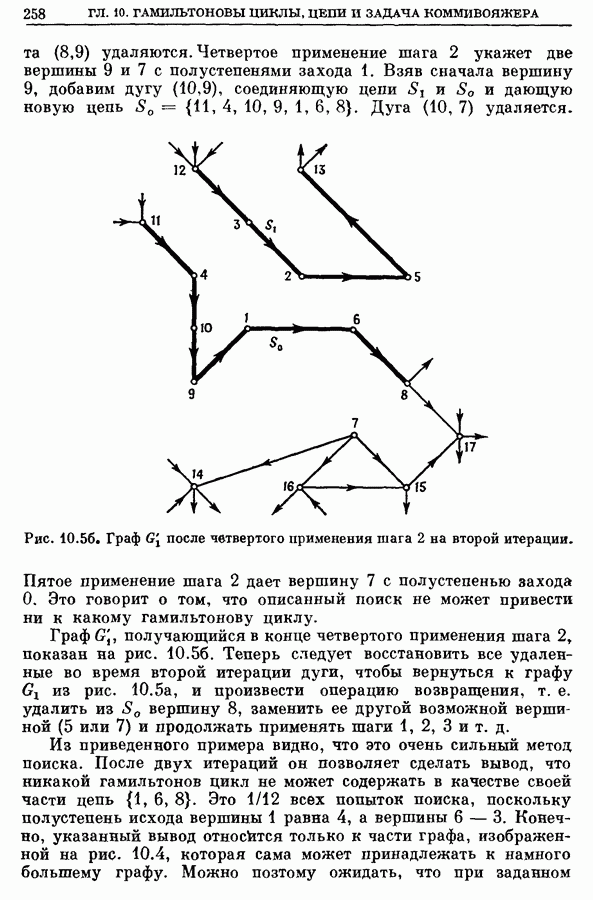
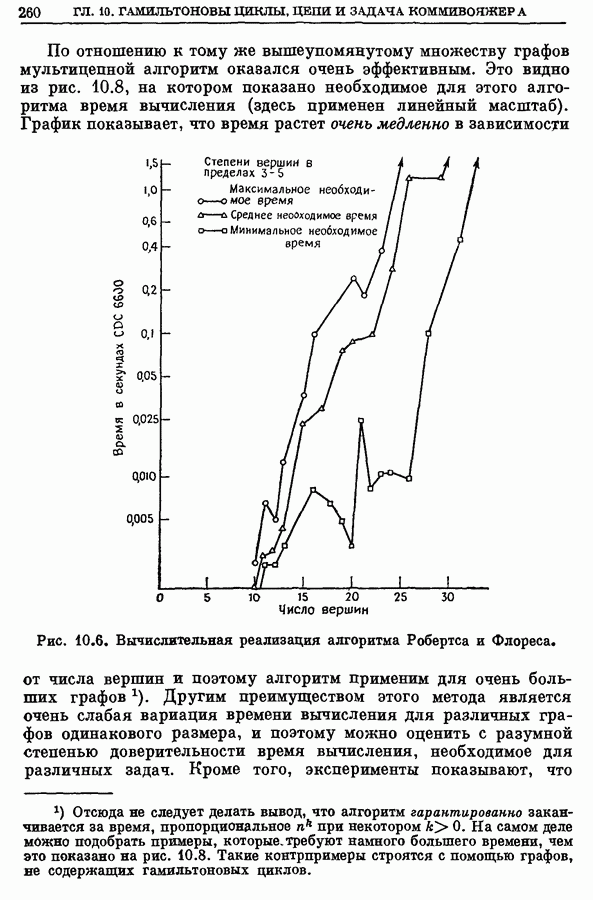
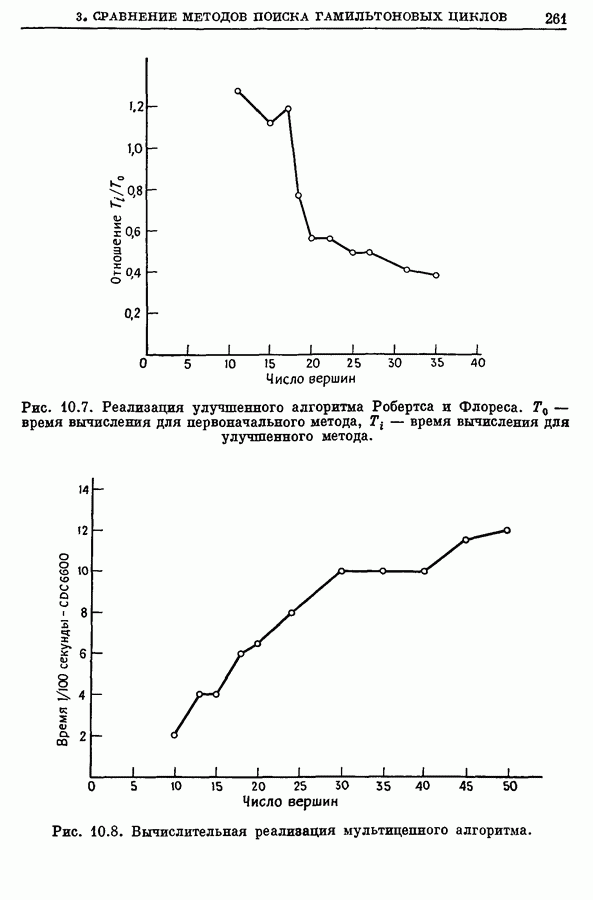
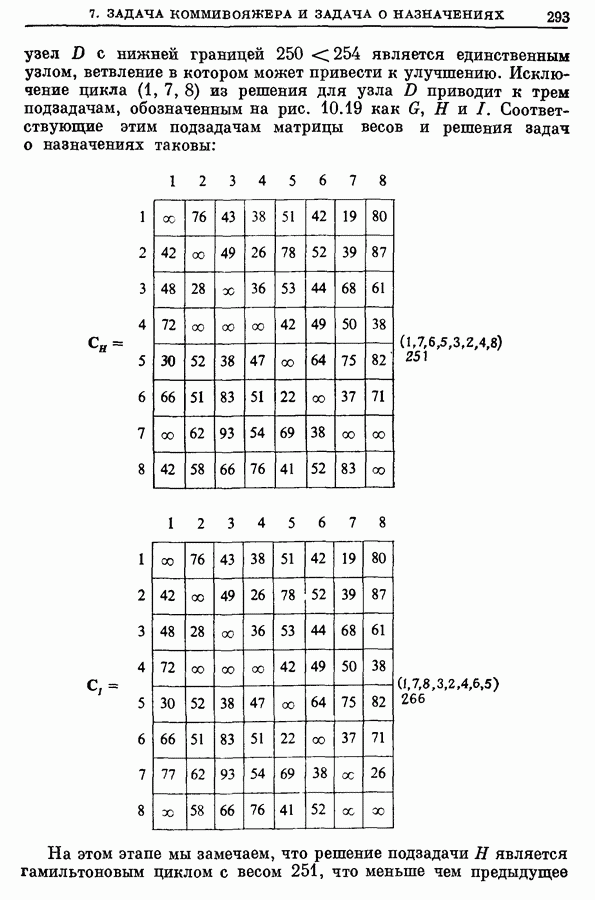
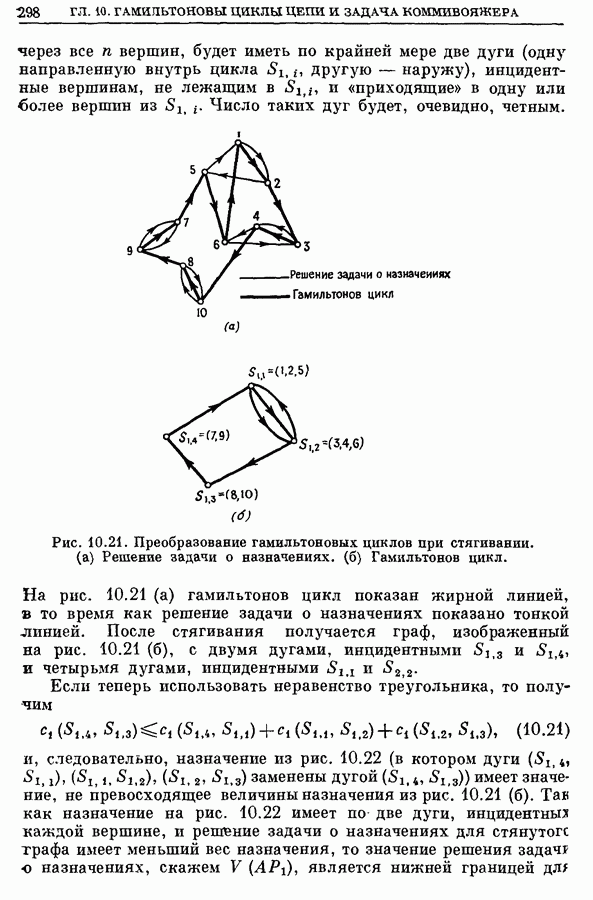
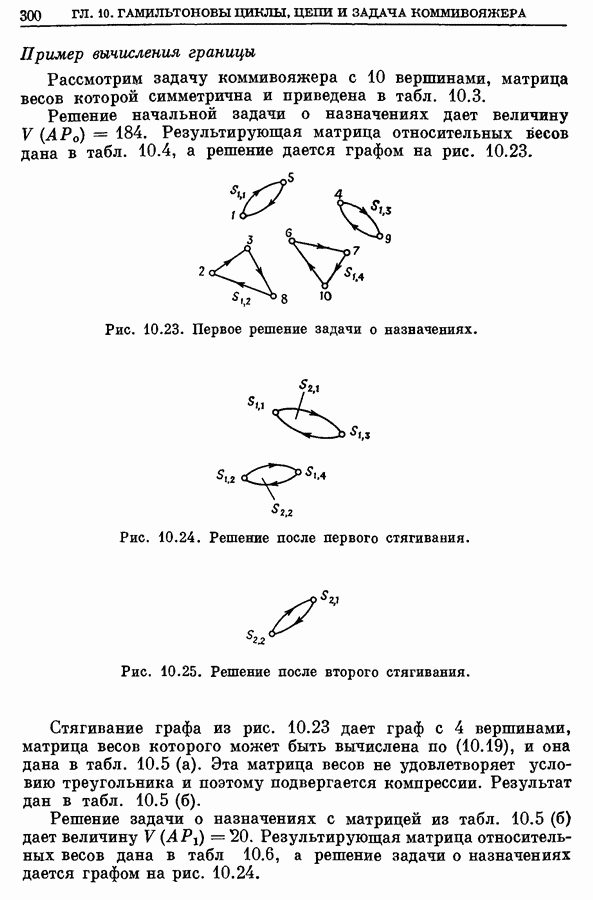
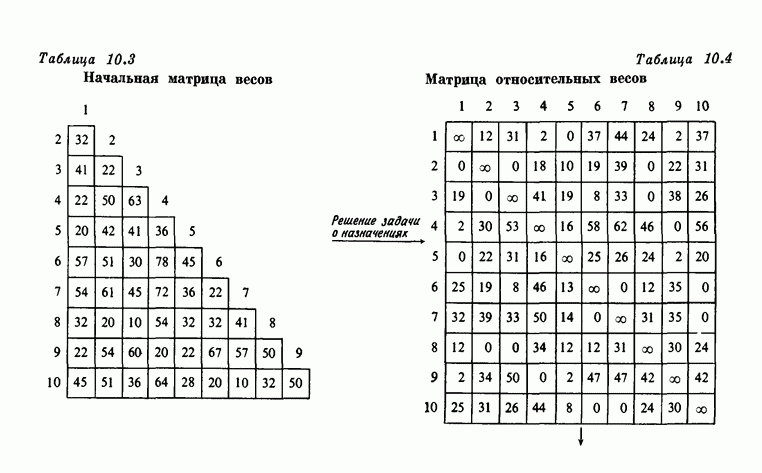
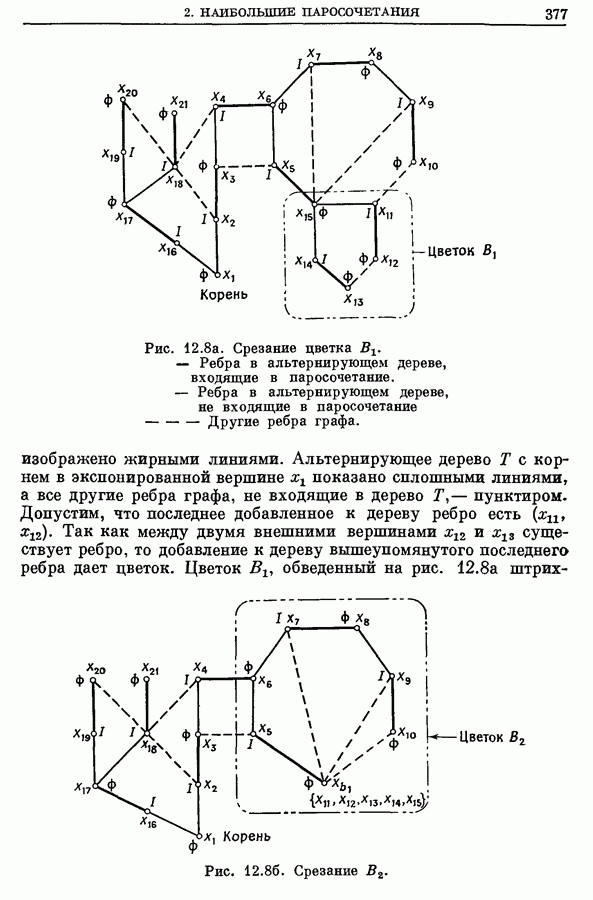
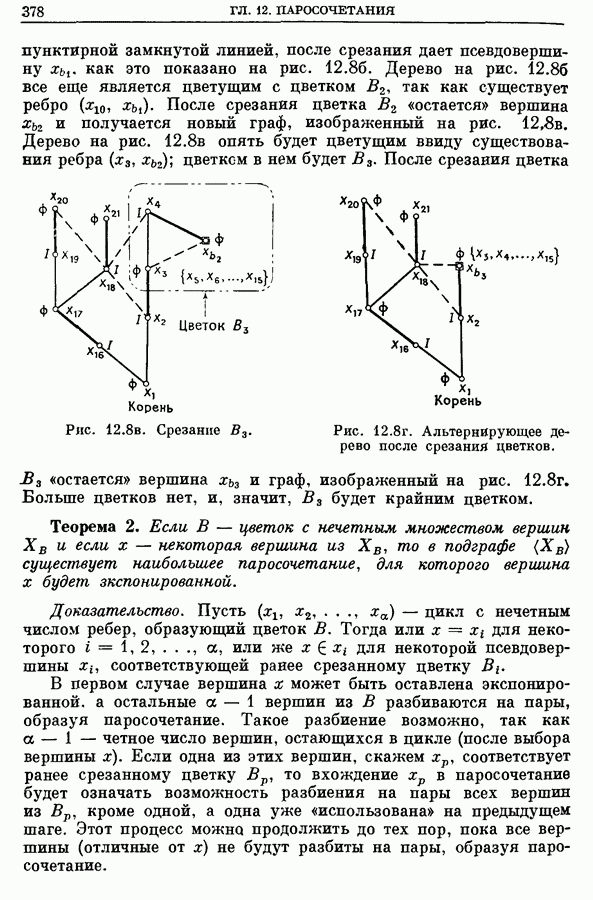
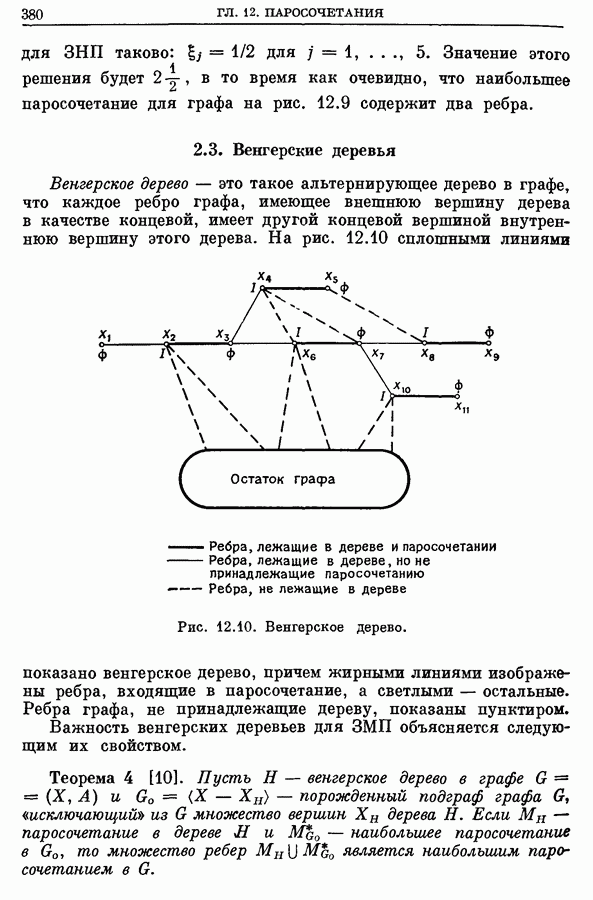
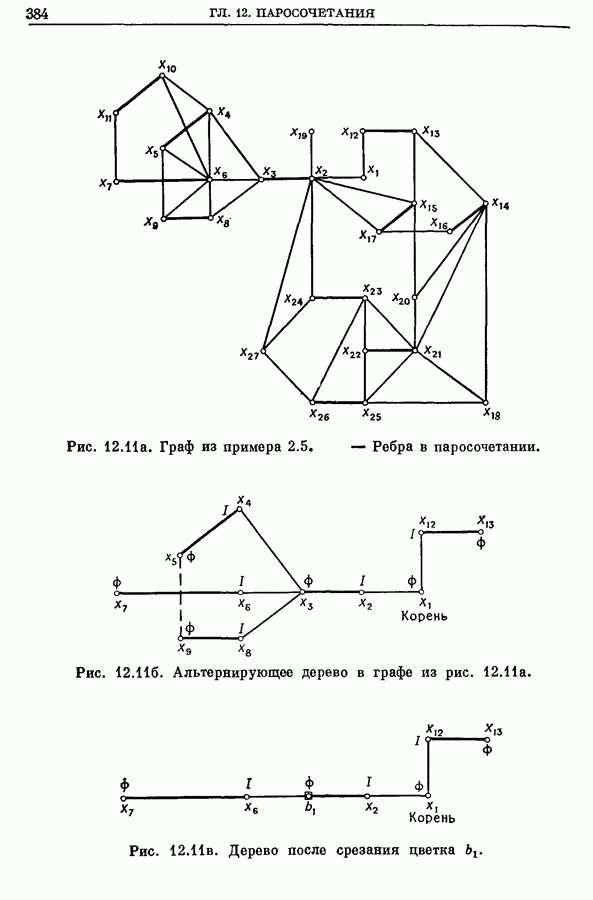
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Задача Штейнера
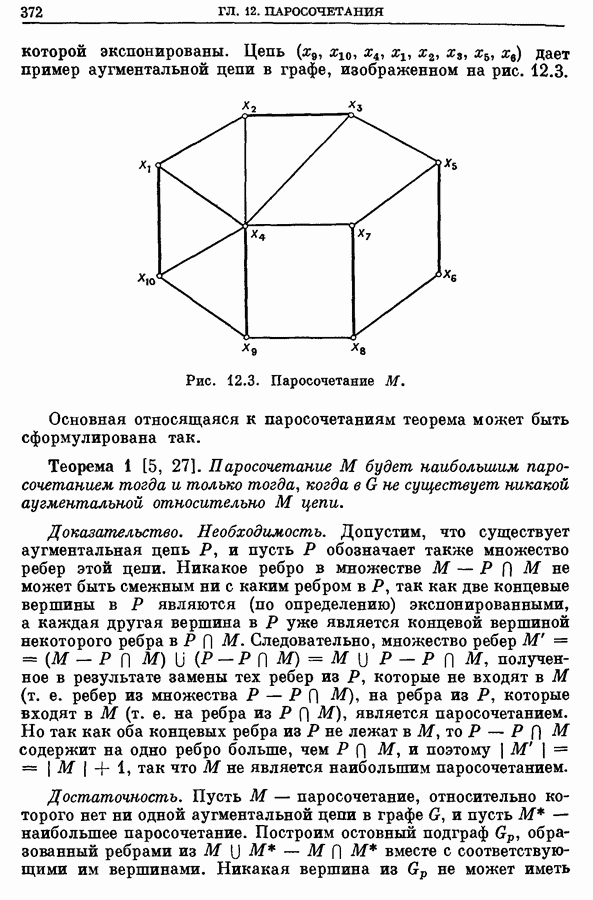
В предыдущем разделе в задаче определения SST, т. е. наикратчайшего дерева графа  ребрами «покрывались» все вершины множества
ребрами «покрывались» все вершины множества  С зтой задачей тесно связана задача, известная как «задача Штейнера на графах» [27, 18], но последняя значительно труднее.
С зтой задачей тесно связана задача, известная как «задача Штейнера на графах» [27, 18], но последняя значительно труднее.
В этой задаче требуется найти наикратчайшее дерево  которое «стягивает» («покрывает») заданное подмножество
которое «стягивает» («покрывает») заданное подмножество 
вершин графа  Другие вершины, принадлежащие
Другие вершины, принадлежащие  могут либо стягиваться деревом
могут либо стягиваться деревом  либо нет, в зависимости от требования минимизации длины дерева
либо нет, в зависимости от требования минимизации длины дерева  Таким образом, задача Штейнера на графе эквивалентна нахождению наикратчайшего остовного дерева произвольного подграфа
Таким образом, задача Штейнера на графе эквивалентна нахождению наикратчайшего остовного дерева произвольного подграфа  графа
графа  при условии
при условии 
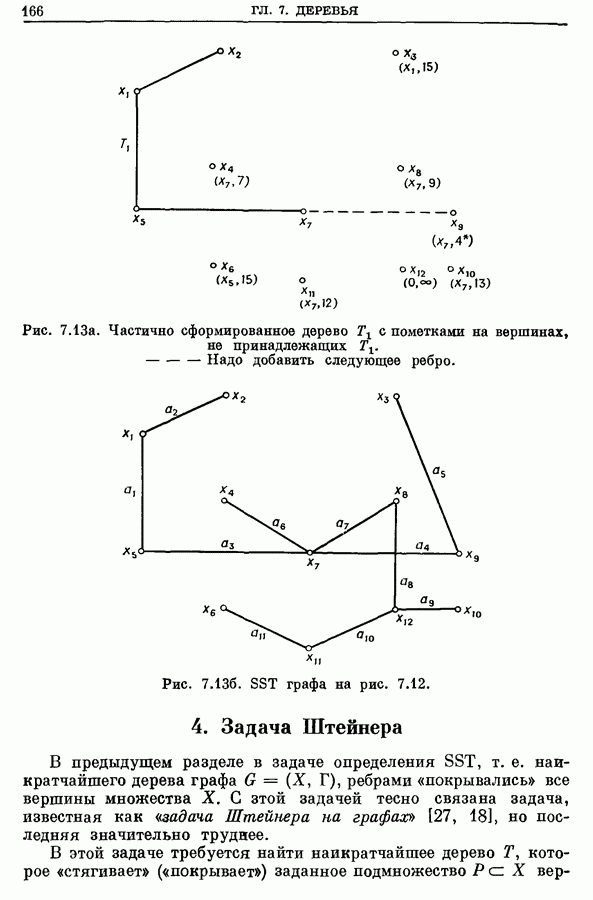
Евклидова задача Штейнера впервые была поставлена как геометрическая задача [13, 14, 44, 24], в которой нужно множество точек  на евклидовой плоскости соединить линиями так, чтобы сумма длин отрезков была минимальна.
на евклидовой плоскости соединить линиями так, чтобы сумма длин отрезков была минимальна.

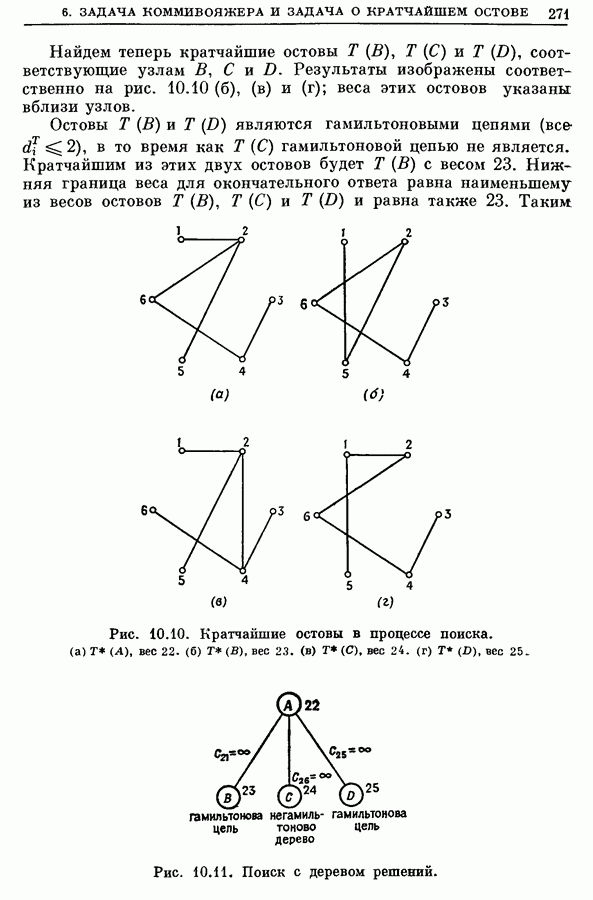
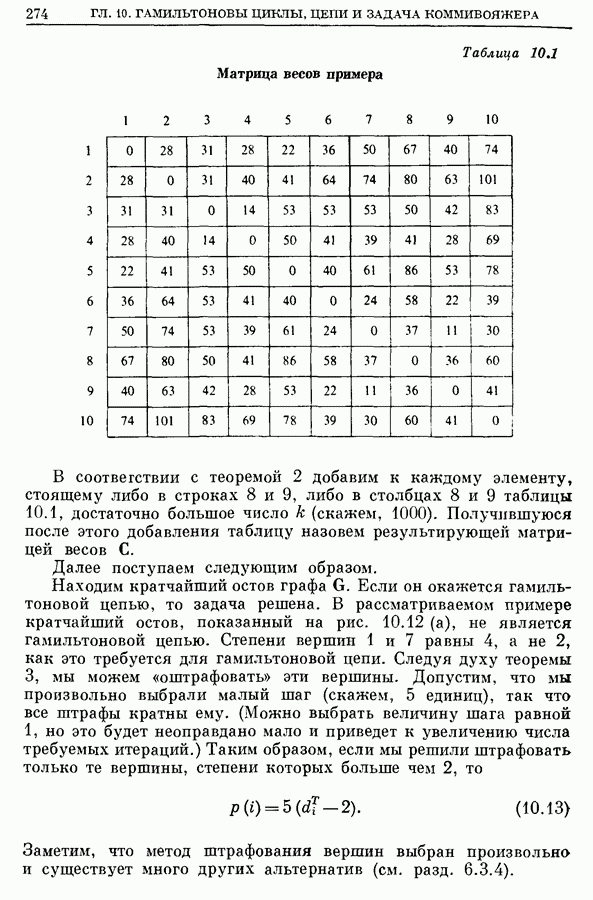
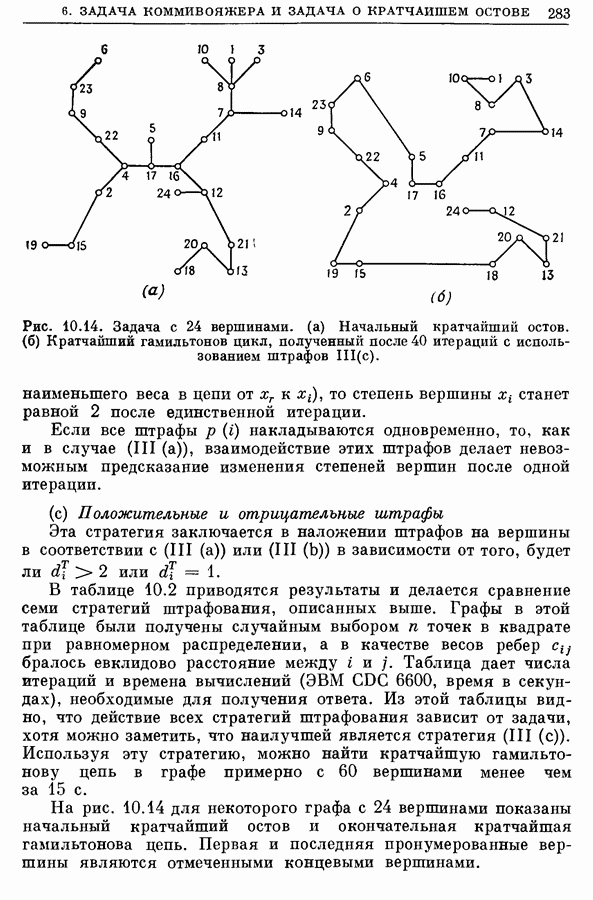
Рис. 7.14а. Кратчайшее остовное дерево. Длина 

Рис. 7.14б. Кратчайшее дерево Штейнера. Длина 9,196.
Если не допускаются пересечения любых двух линий в точках вне заданного множества  то задача сводится к одной из задач определения SST эквивалентного графа на
то задача сводится к одной из задач определения SST эквивалентного графа на  вершинах с матрицей весов, вычисленных как евклидово расстояние между точками множества
вершинах с матрицей весов, вычисленных как евклидово расстояние между точками множества  Если допускается на плоскости введение дополнительных «искусственных» вершин (называемых точками Штейнера), то длину SST на множестве точек
Если допускается на плоскости введение дополнительных «искусственных» вершин (называемых точками Штейнера), то длину SST на множестве точек  можно уменьшить соответствующим подбором точек. Например, для четырех точек, показанных на рис. 7.14а, SST имеет длину, большую, чем SST графа, получаемого после добавления двух новых точек
можно уменьшить соответствующим подбором точек. Например, для четырех точек, показанных на рис. 7.14а, SST имеет длину, большую, чем SST графа, получаемого после добавления двух новых точек  расположенных «между» исходными точками (см. рис. 7.146). Таким образом, для решения задачи Штейнера можно добавить в любых местах плоскости столько точек Штейнера, сколько необходимо для построения наикратчайшего дерева, стягивающего множество из
расположенных «между» исходными точками (см. рис. 7.146). Таким образом, для решения задачи Штейнера можно добавить в любых местах плоскости столько точек Штейнера, сколько необходимо для построения наикратчайшего дерева, стягивающего множество из  точек. Получающееся наикратчайшее дерево называют наикратчайшим деревом Штейнера.
точек. Получающееся наикратчайшее дерево называют наикратчайшим деревом Штейнера.
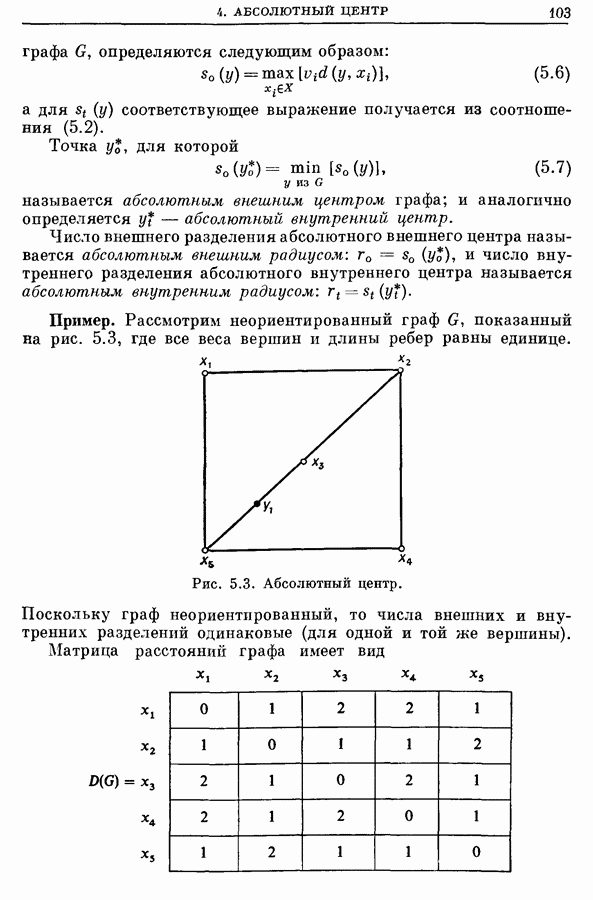
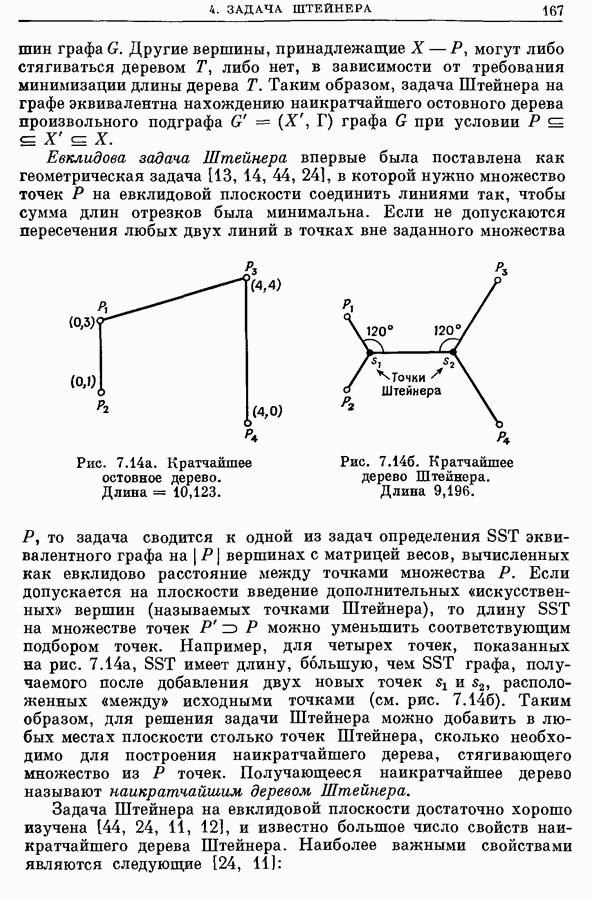
Задача Штейнера на евклидовой плоскости достаточно хорошо изучена [44, 24, 11, 12], и известно большое число свойств наикратчайшего дерева Штейнера. Наиболее важными свойствами являются следующие [24, 11]:
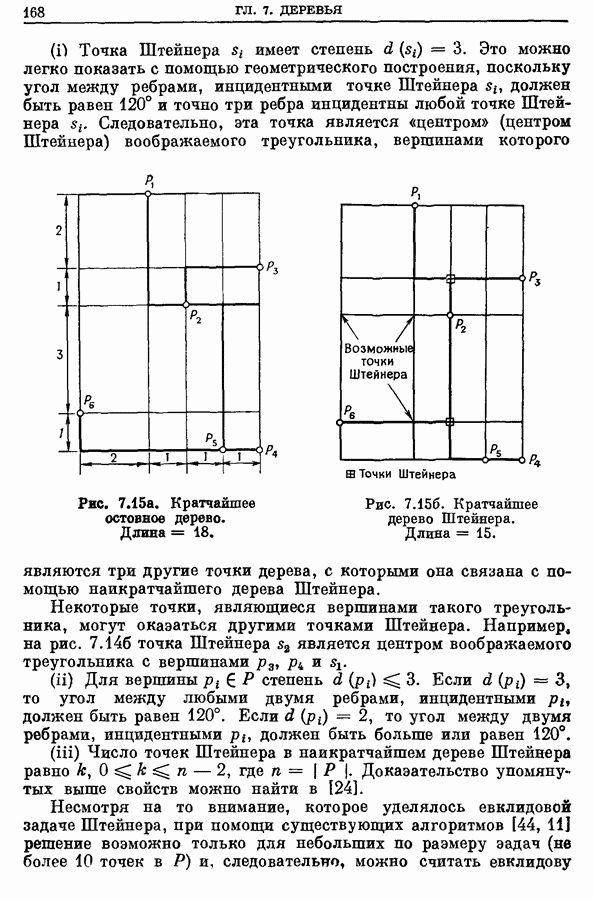
(i) Точка Штейнера  имеет степень
имеет степень  Это можно легко показать с помощью геометрического построения, поскольку угол между ребрами, инцидентными точке Штейнера
Это можно легко показать с помощью геометрического построения, поскольку угол между ребрами, инцидентными точке Штейнера  должен быть равен 120° и точно три ребра инцидентны любой точке Штейнера
должен быть равен 120° и точно три ребра инцидентны любой точке Штейнера  Следовательно, эта точка является «центром» (центром Штейнера) воображаемого треугольника, вершинами которого являются три другие точки дерева, с которыми она связана с помощью наикратчайшего дерева Штейнера.
Следовательно, эта точка является «центром» (центром Штейнера) воображаемого треугольника, вершинами которого являются три другие точки дерева, с которыми она связана с помощью наикратчайшего дерева Штейнера.

Рис. 7.15а. Кратчайшее остовное дерево. Длина 

Рис. 7.15б. Кратчайшее дерево Штейнера. Длина 
Некоторые точки, являющиеся вершинами такого треугольника, могут оказаться другими точками Штейнера. Например, на рис. 7.146 точка Штейнера  является центром воображаемого треугольника с вершинами
является центром воображаемого треугольника с вершинами  .
.
(ii) Для вершины  степень
степень  Если
Если  то угол между любыми двумя ребрами, инцидентными
то угол между любыми двумя ребрами, инцидентными  должен быть равен 120°. Если
должен быть равен 120°. Если  то угол между двумя ребрами, инцидентными
то угол между двумя ребрами, инцидентными  должен быть больше или равен 120°.
должен быть больше или равен 120°.
(iii) Число точек Штейнера в наикратчайшем дереве Штейнера равно  к
к  где
где  Доказательство упомянутых выше свойств можно найти в [24].
Доказательство упомянутых выше свойств можно найти в [24].
Несмотря на то внимание, которое уделялось евклидовой задаче Штейнера, при помощи существующих алгоритмов [44, 11] решение возможно только для небольших по размеру задач (не более 10 точек в  и, следовательно, можно считать евклидову
и, следовательно, можно считать евклидову
эадачу Штейнера нерешенной. Для задач большого размера можно обратиться к ряду эвристических методов [7, 50].
В более позднем варианте задачи Штейнера на плоскости используется обычно линейное (вместо евклидова) расстояние между точками. Такая постановка задач впервые была предложена Хэнном [28, 30] в связи с разработкой теории монтажа печатных схем электронных устройств. Расстояние между точками с координатами  в этом случае определяется следующим образом:
в этом случае определяется следующим образом:

При этих условиях можно легко показать [44], что если через каждую точку из множества  провести вертикальные и горизонтальные линии, то решение задачи Штейнера можно получить, рассматривая в качестве возможных точек Штейнера точки пересечения полученной сетки линий.
провести вертикальные и горизонтальные линии, то решение задачи Штейнера можно получить, рассматривая в качестве возможных точек Штейнера точки пересечения полученной сетки линий.
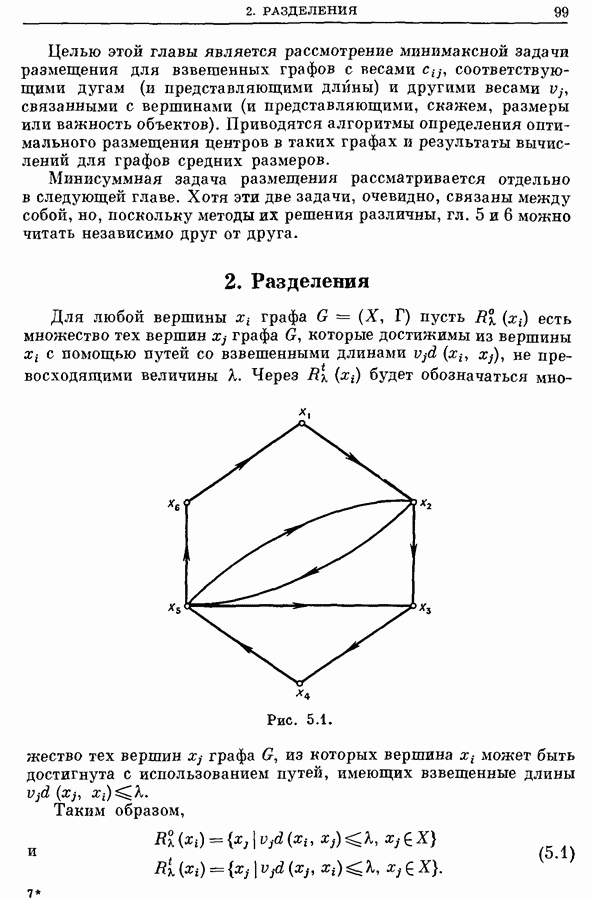
Пусть граф  построен так, что множество его вершин X является множеством точек пересечения некоторой сетки линий и ребра графа
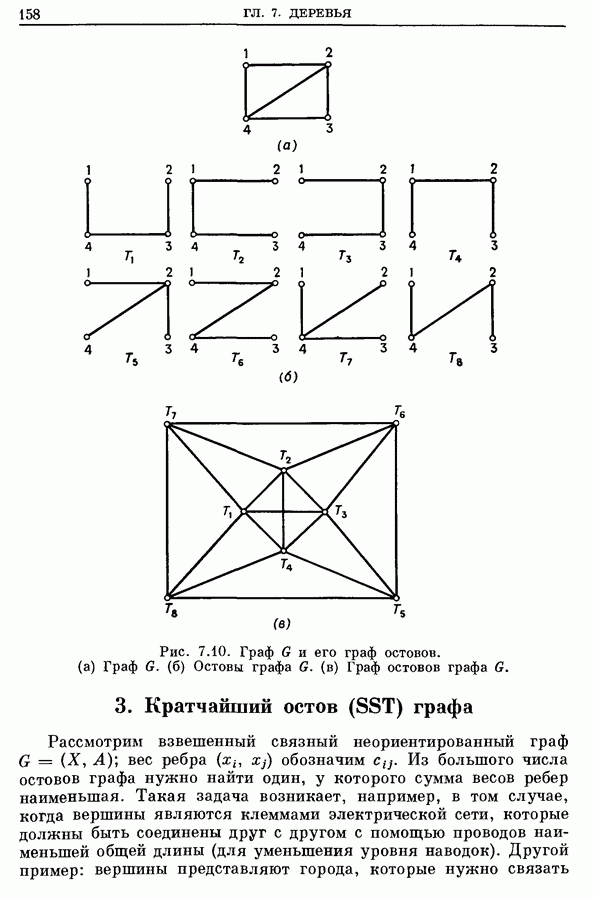
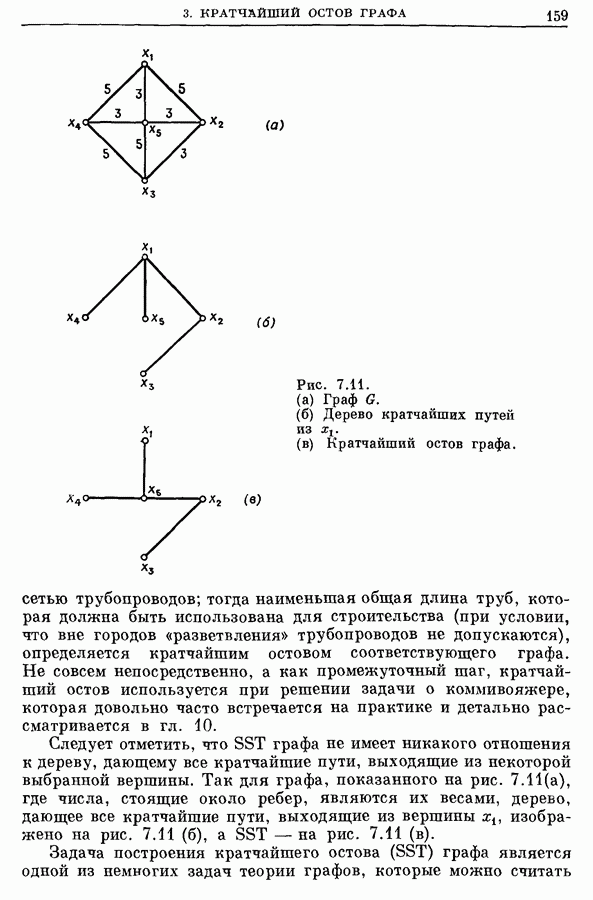
построен так, что множество его вершин X является множеством точек пересечения некоторой сетки линий и ребра графа  соответствуют линиям сетки, соединяющим две точки пересечения. Тогда задача Штейнера на плоскости с линейной метрикой переходит в задачу Штейнера для конечного графа, определенную в начале этого раздела [54]. На рис. 7.156 показан пример наикратчайшего дерева Штейнера для линейной задачи с шестью точками, а для сравнения на рис. 7.15а показан SST этой задачи.
соответствуют линиям сетки, соединяющим две точки пересечения. Тогда задача Штейнера на плоскости с линейной метрикой переходит в задачу Штейнера для конечного графа, определенную в начале этого раздела [54]. На рис. 7.156 показан пример наикратчайшего дерева Штейнера для линейной задачи с шестью точками, а для сравнения на рис. 7.15а показан SST этой задачи.
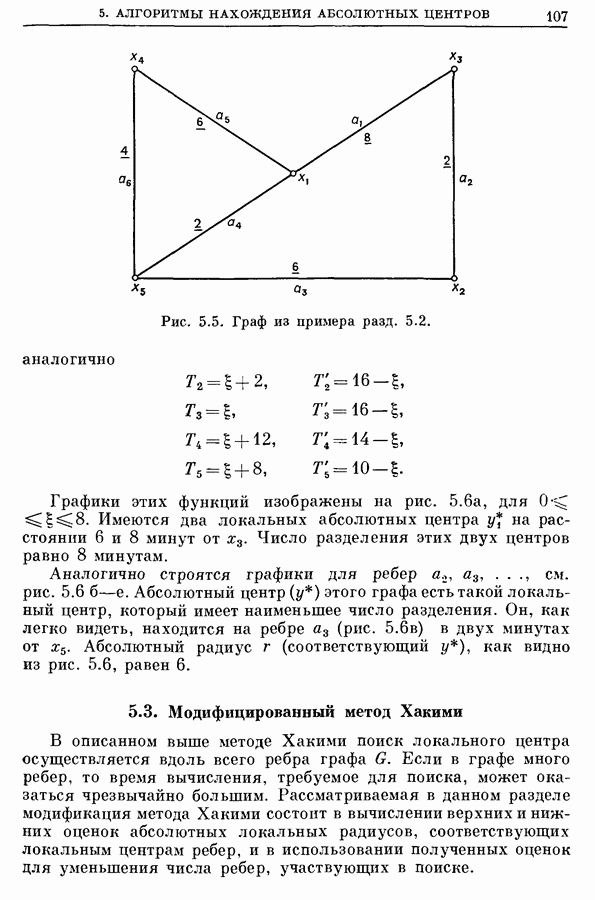
Задача Штейнера для обычных неориентированных графов рассматривалась Хакими [27] и Дрейфусом и Вагнером [18]. Они нашли точные алгоритмы решения таких задач. Однако эти алгоритмы с вычислительной точки зрения являются не эффективными процедурами, хотя они и значительно лучше, чем последовательный просмотр SST всех подграфов  графа
графа  В любом случае (как и в случае задач с евклидовым расстоянием) максимальный размер задач Штейнера, для решения которых требуется разумное вычислительное время, не превышает 10 вершин (в множестве
В любом случае (как и в случае задач с евклидовым расстоянием) максимальный размер задач Штейнера, для решения которых требуется разумное вычислительное время, не превышает 10 вершин (в множестве  С этой точки зрения задачу Штейнера на графе можно рассматривать как нерешенную проблему, и она в этой книге больше не будет обсуждаться.
С этой точки зрения задачу Штейнера на графе можно рассматривать как нерешенную проблему, и она в этой книге больше не будет обсуждаться.
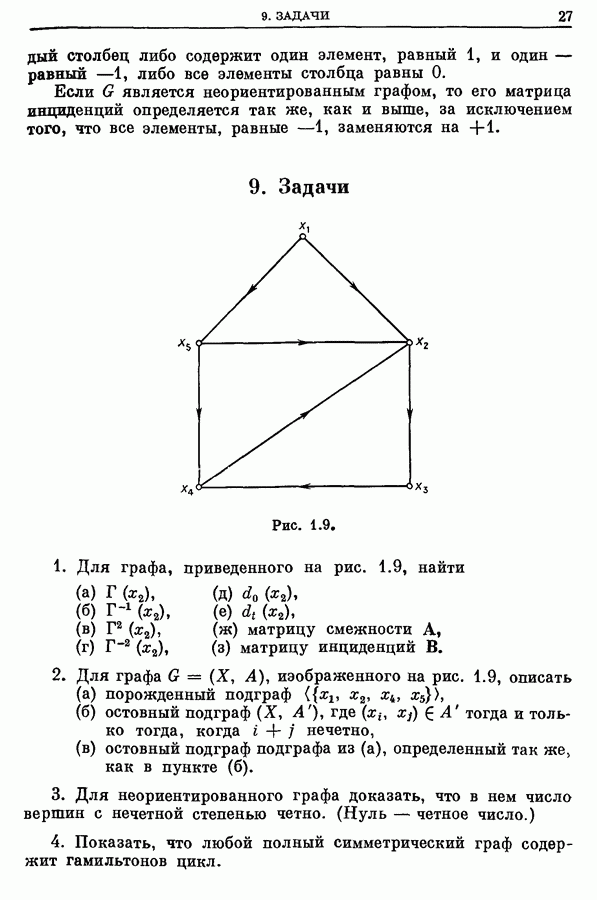
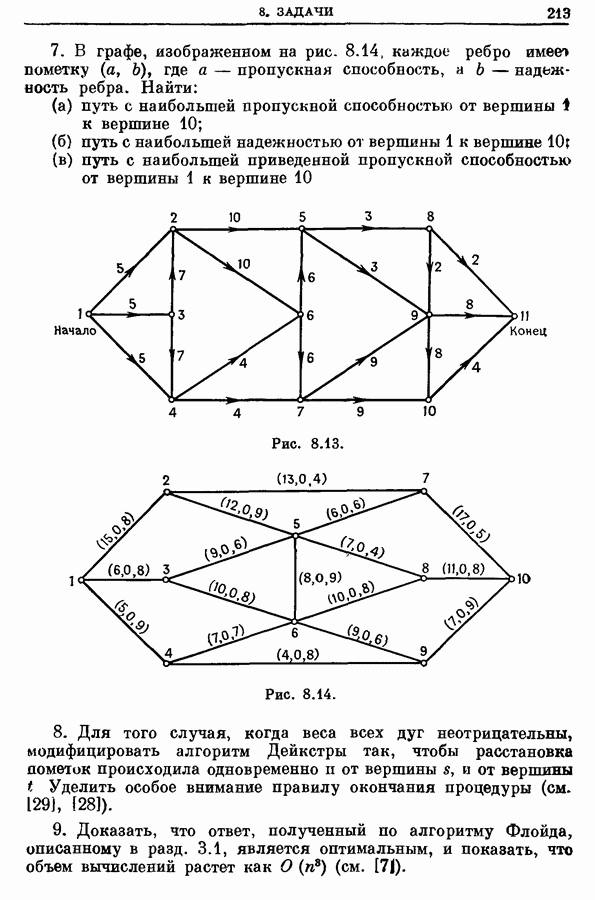
5. Задачи
(см. скан)
(см. скан)
(см. скан)
(см. скан)
6. Список литературы
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
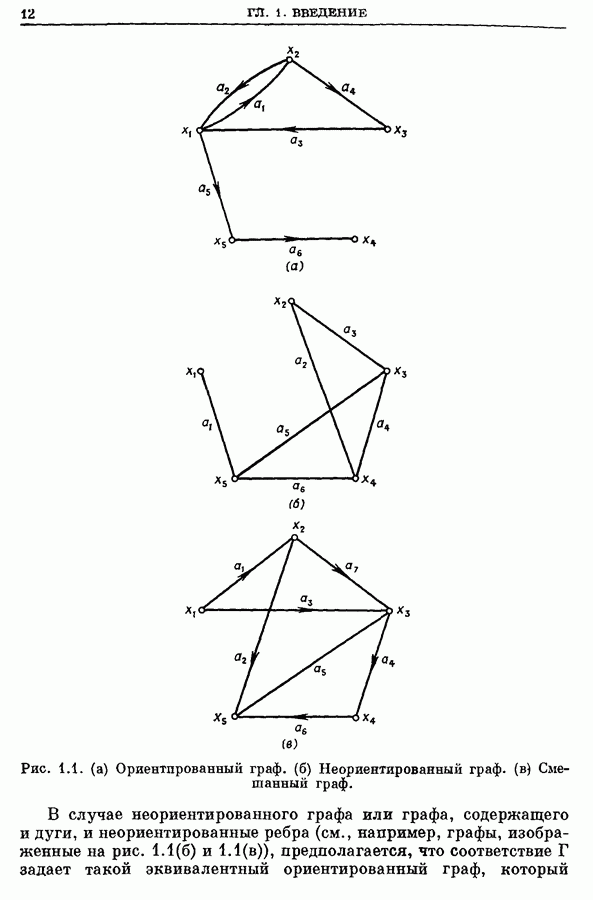
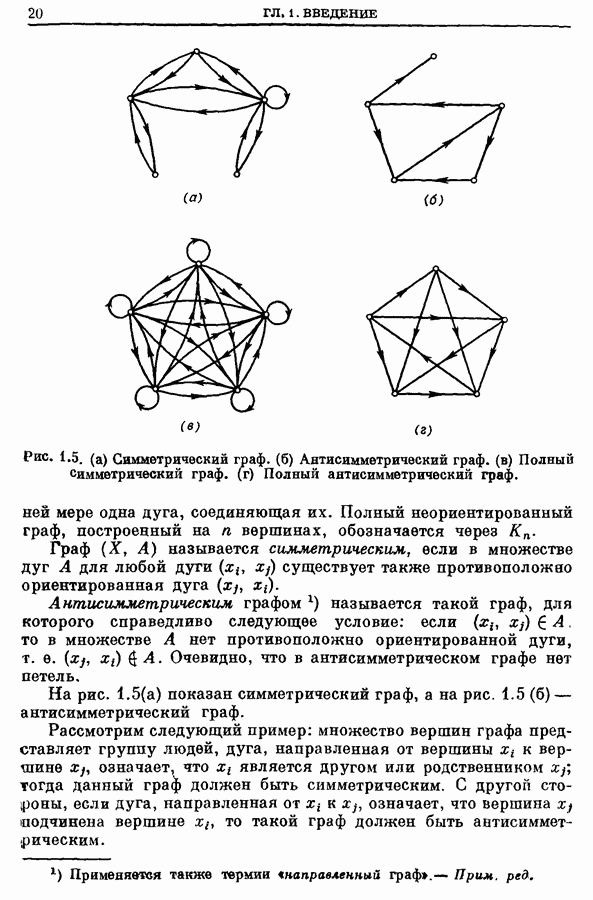
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
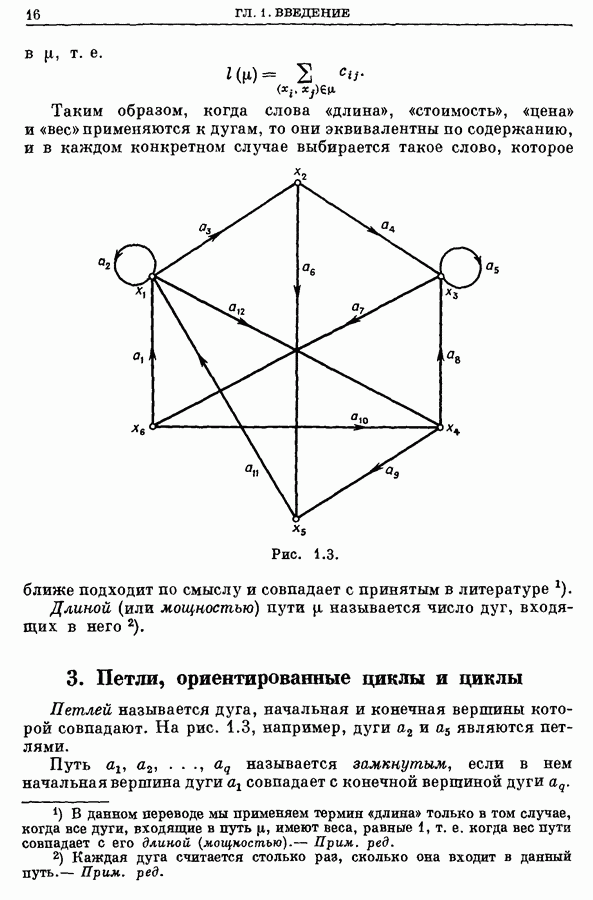
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
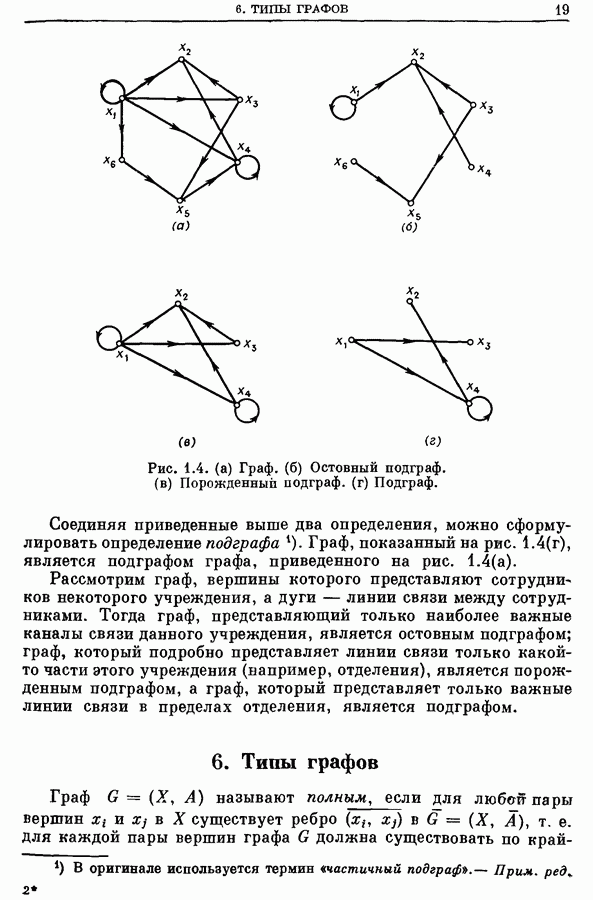
- 5. Подграфы
- 6. Типы графов
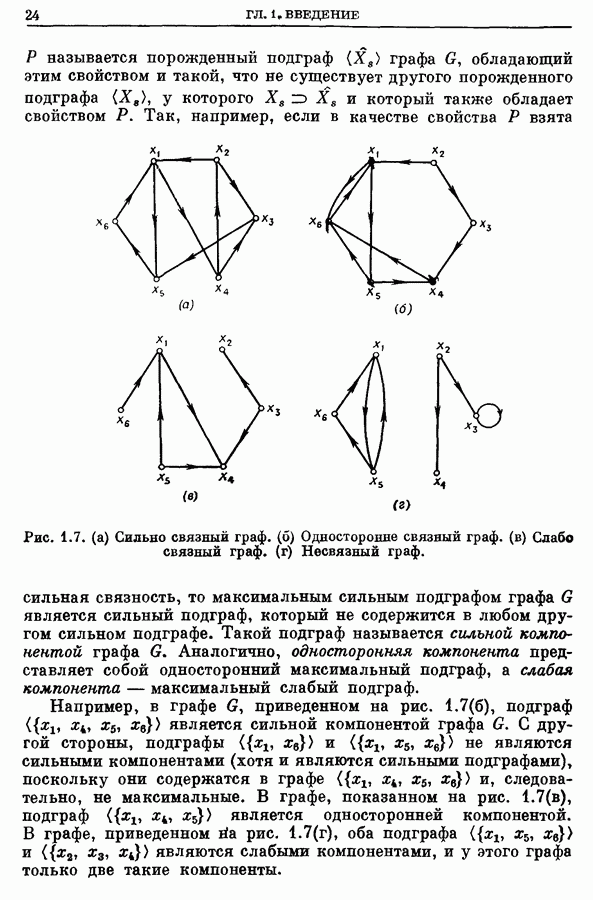
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
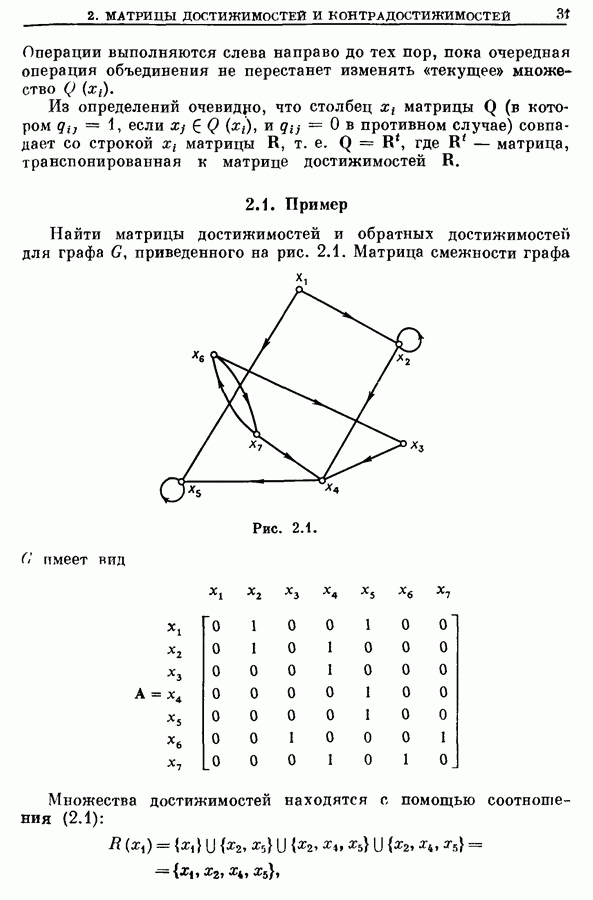
- 2. Матрицы достижимостеи и контрадостижимостей
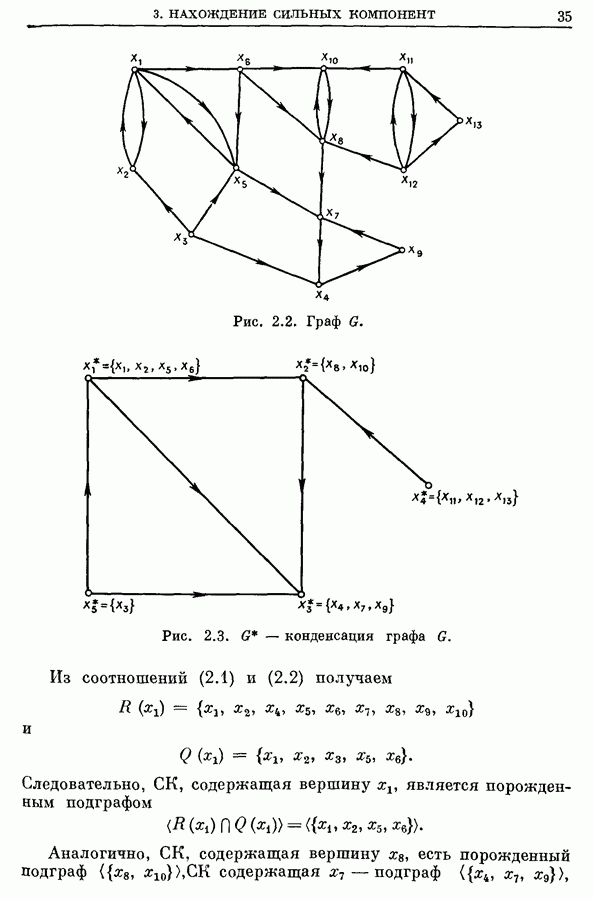
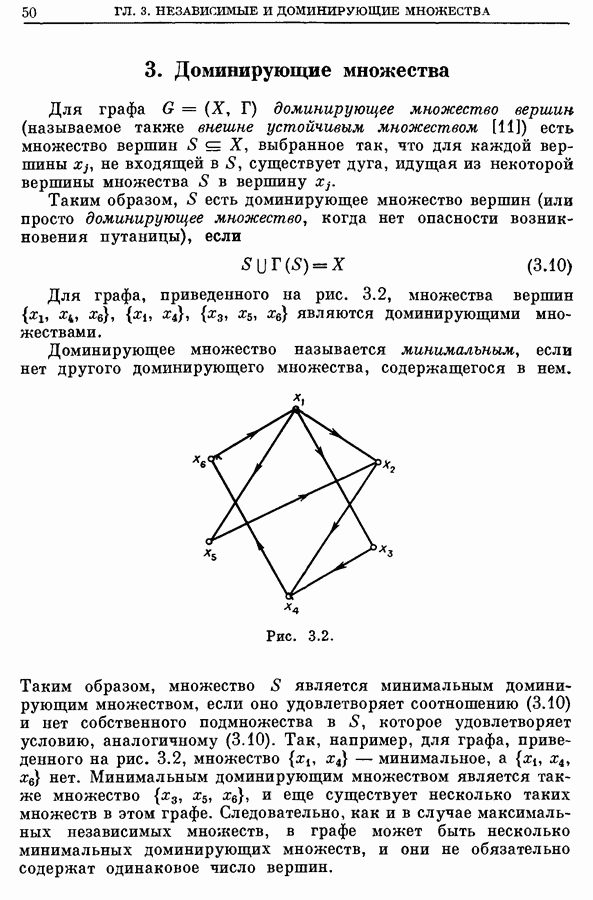
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
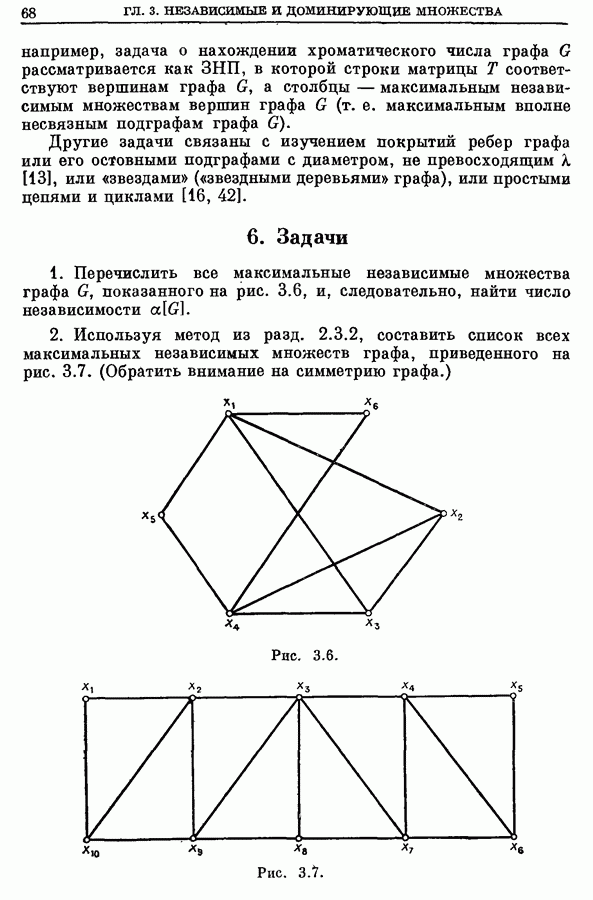
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
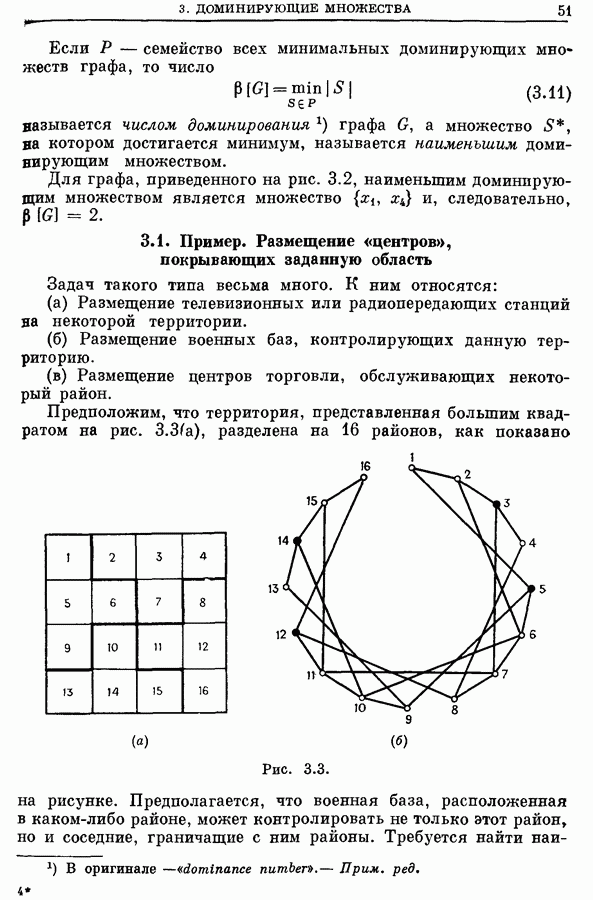
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
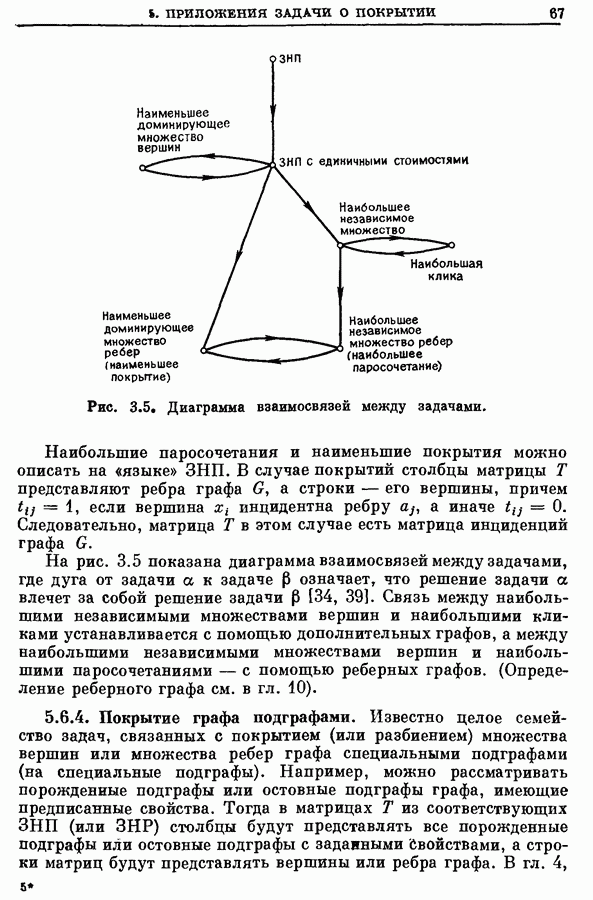
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
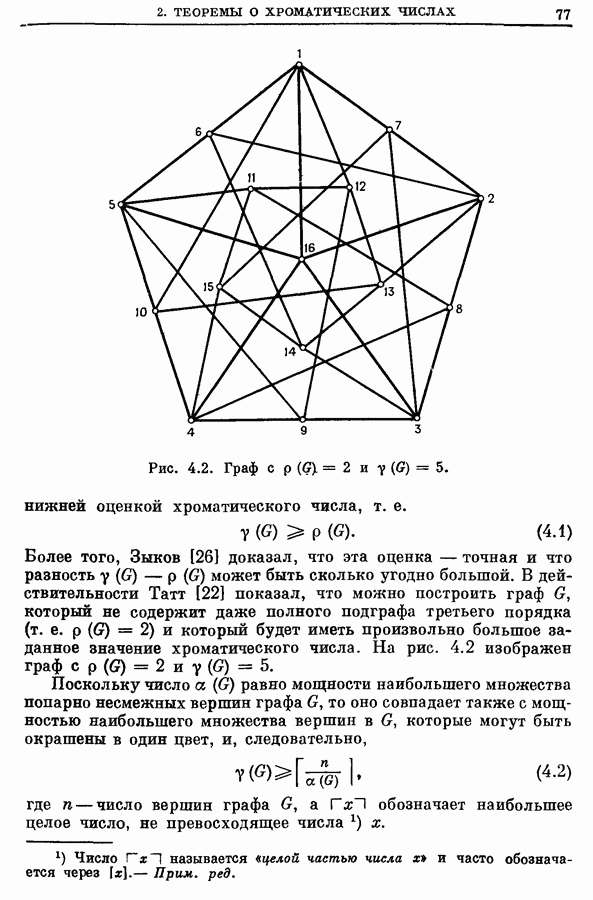
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
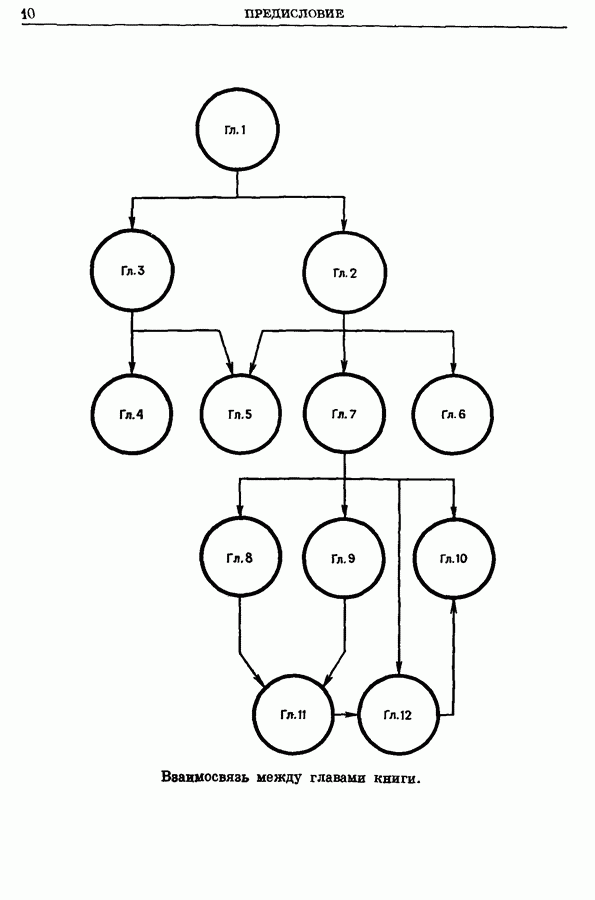
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
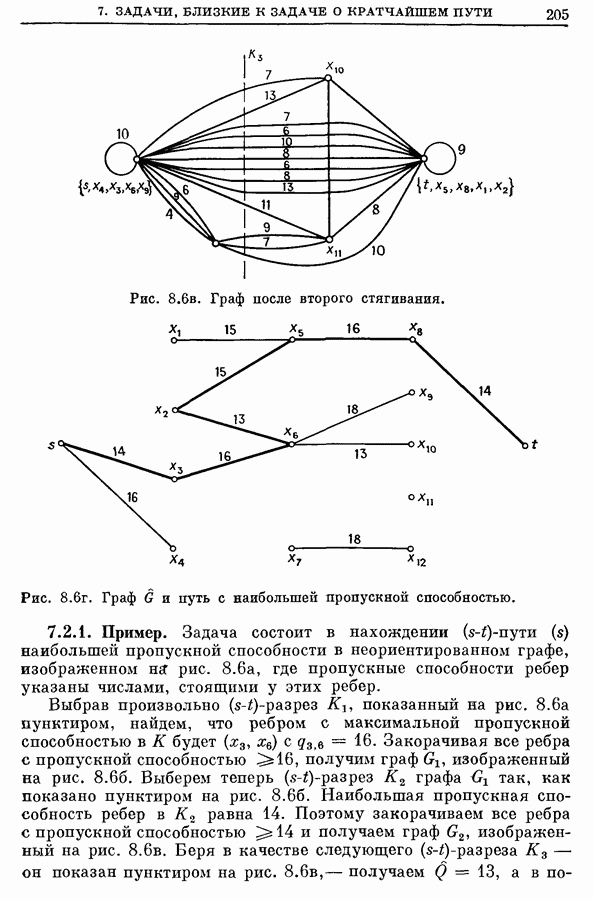
- 7.2. Путь с наибольшей пропускной способностью
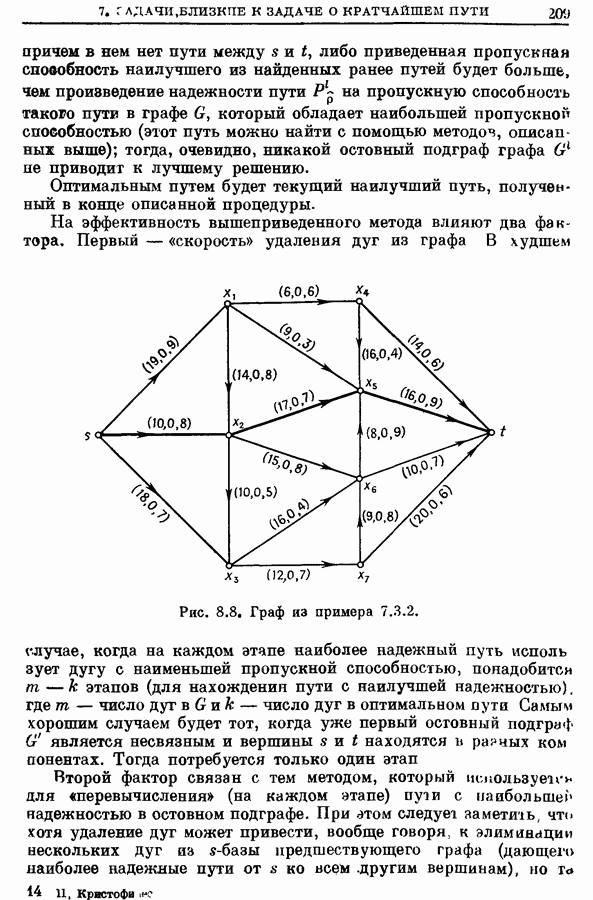
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
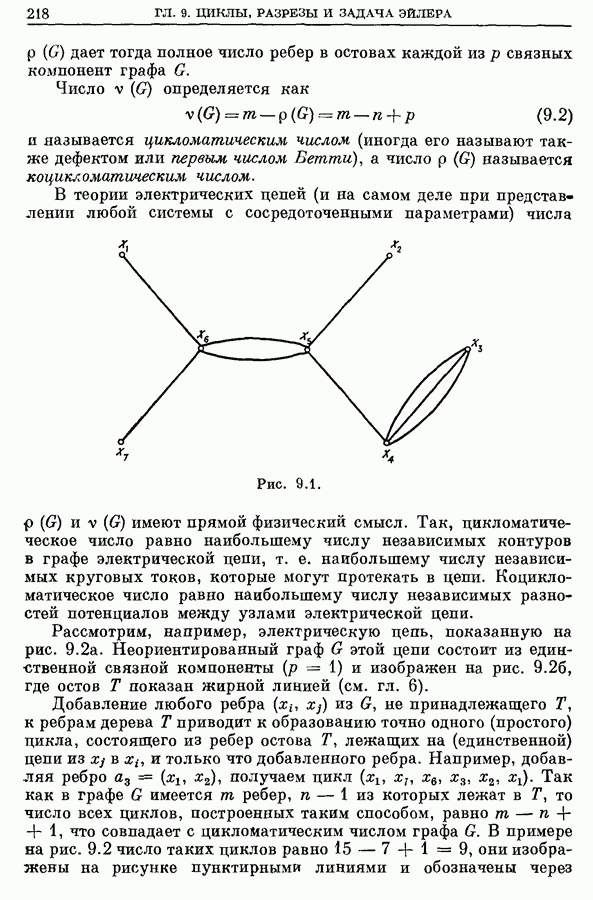
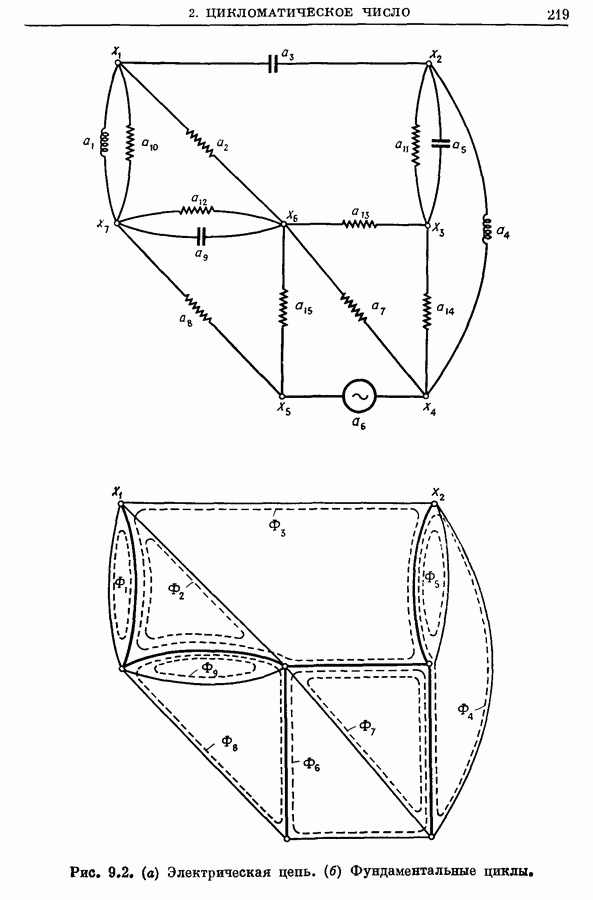
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
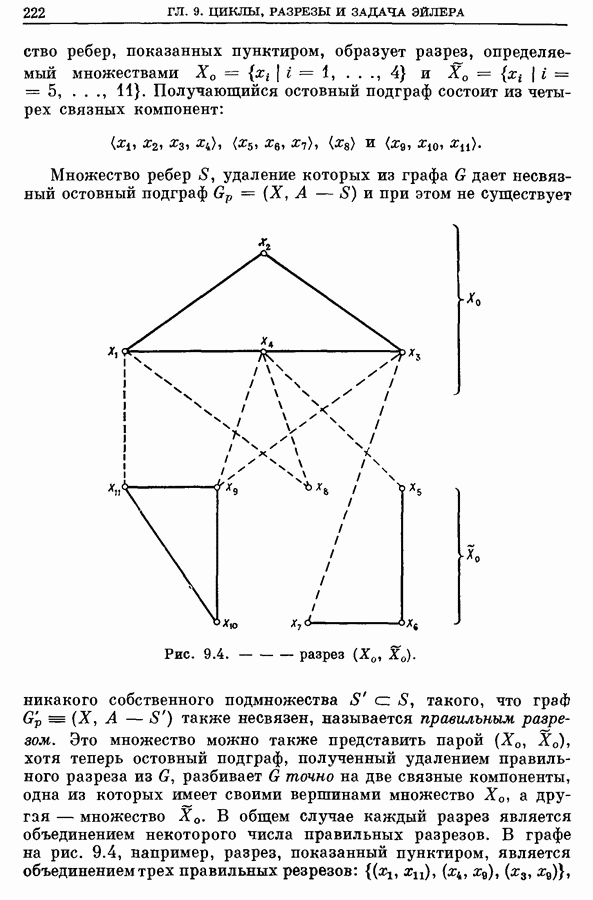
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
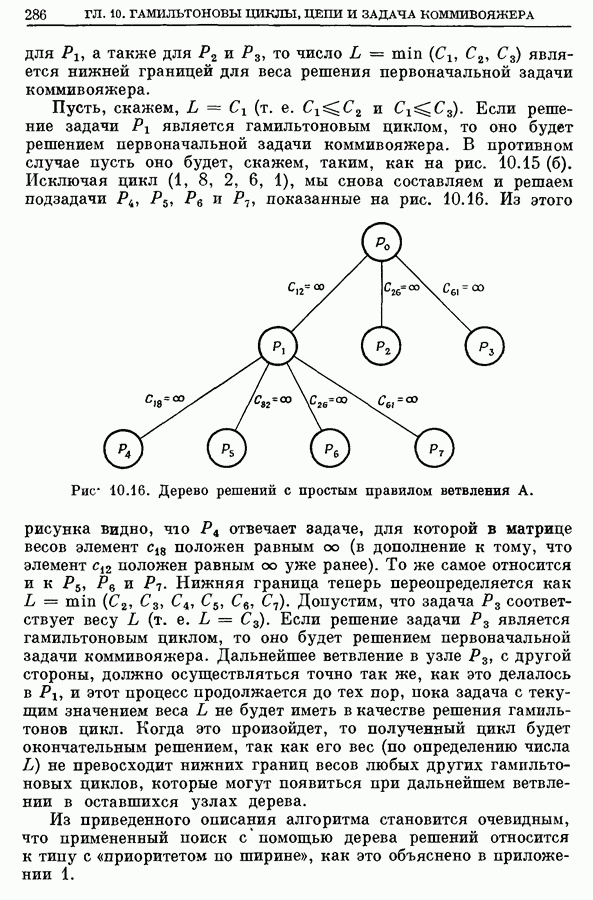
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
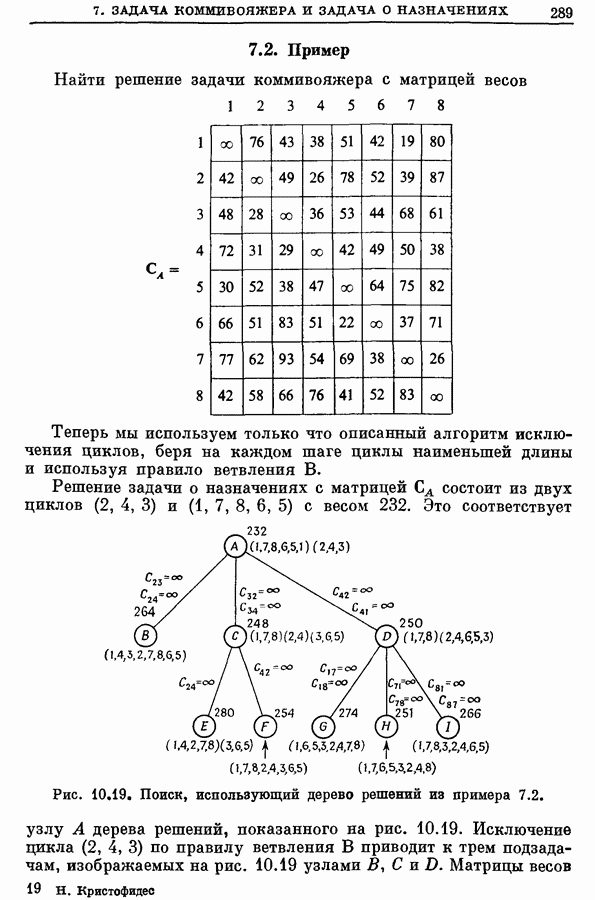
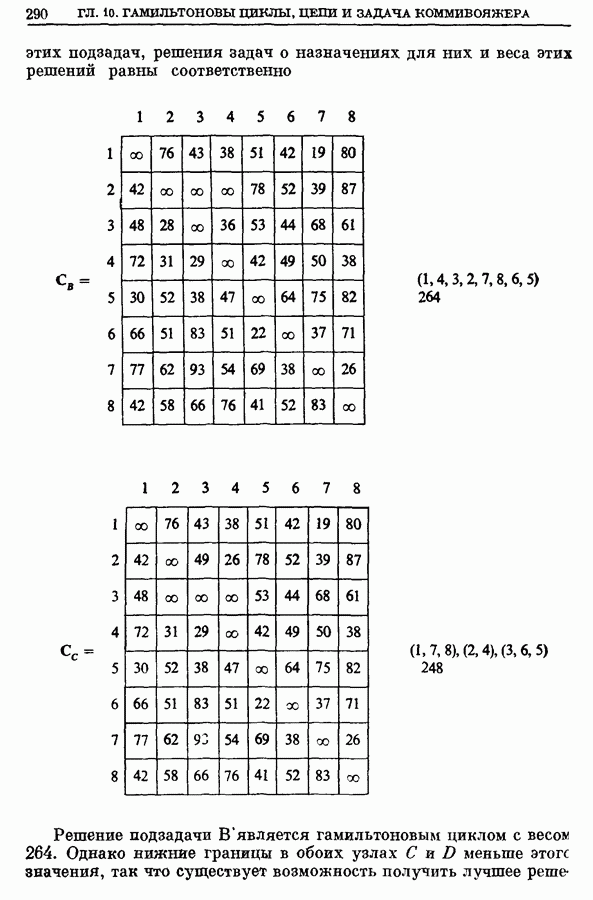
- 7. Задача коммивояжера и задача о назначениях
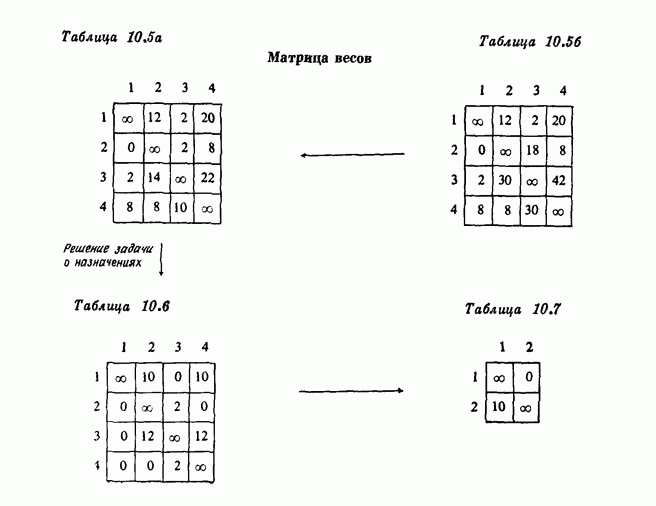
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
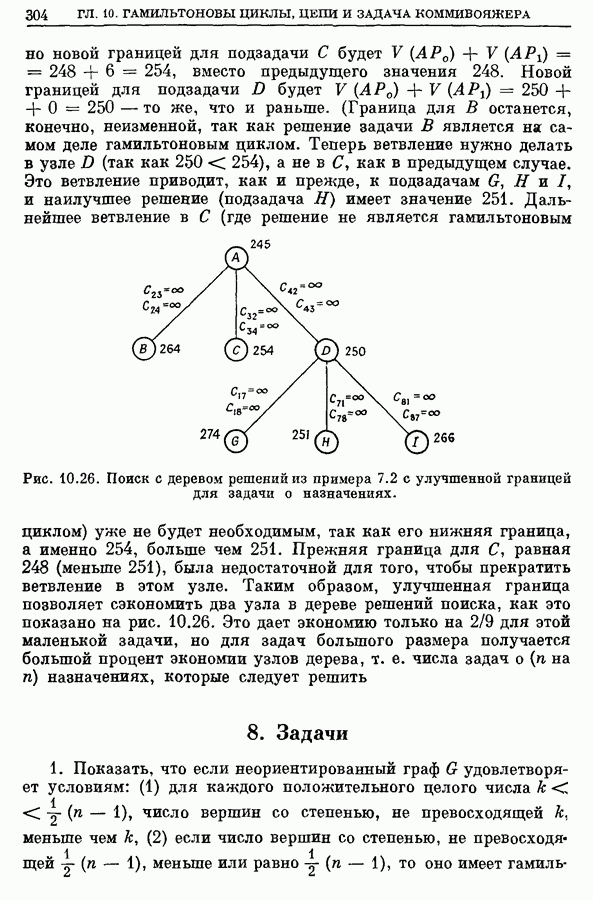
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
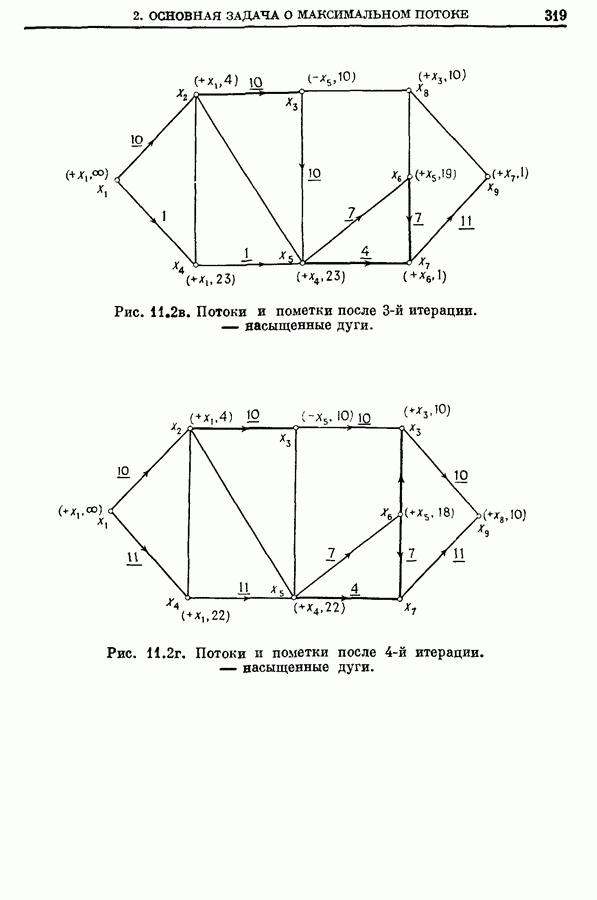
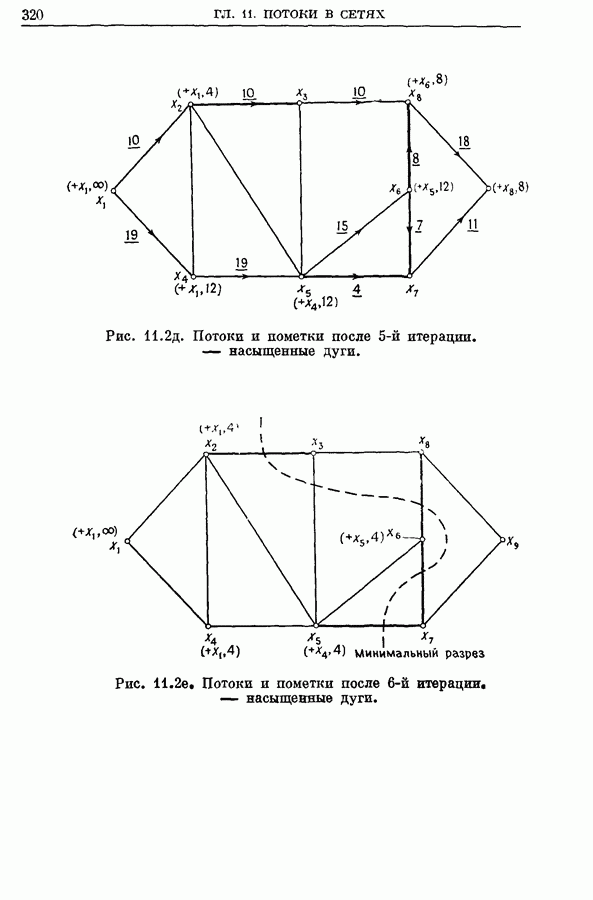
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
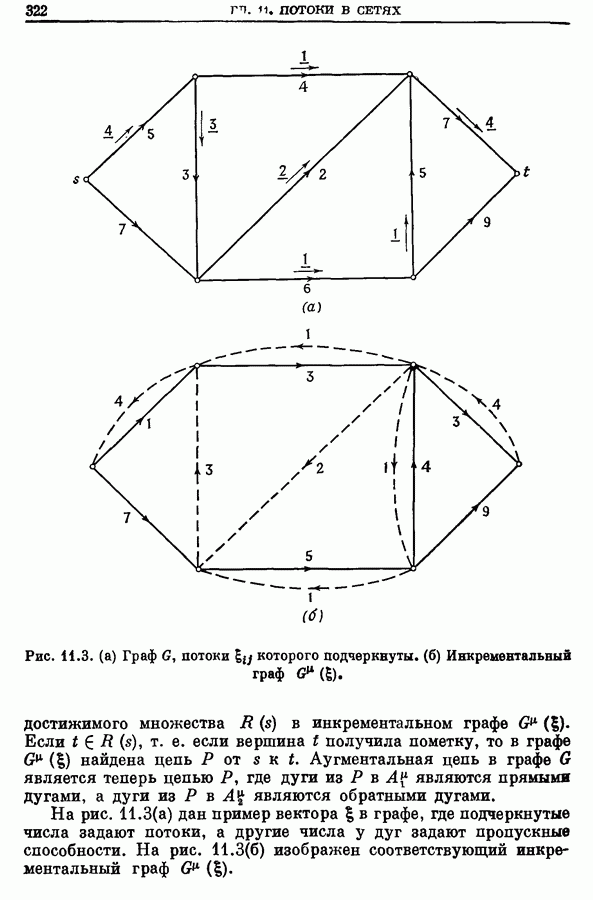
- 2.3. Инкрементальные графы
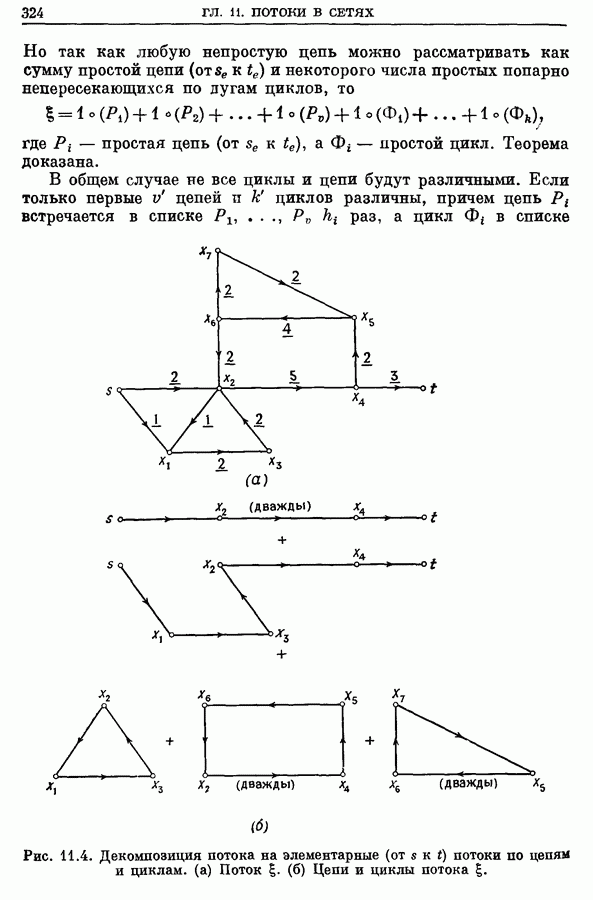
- 2.4. Декомпозиция потока
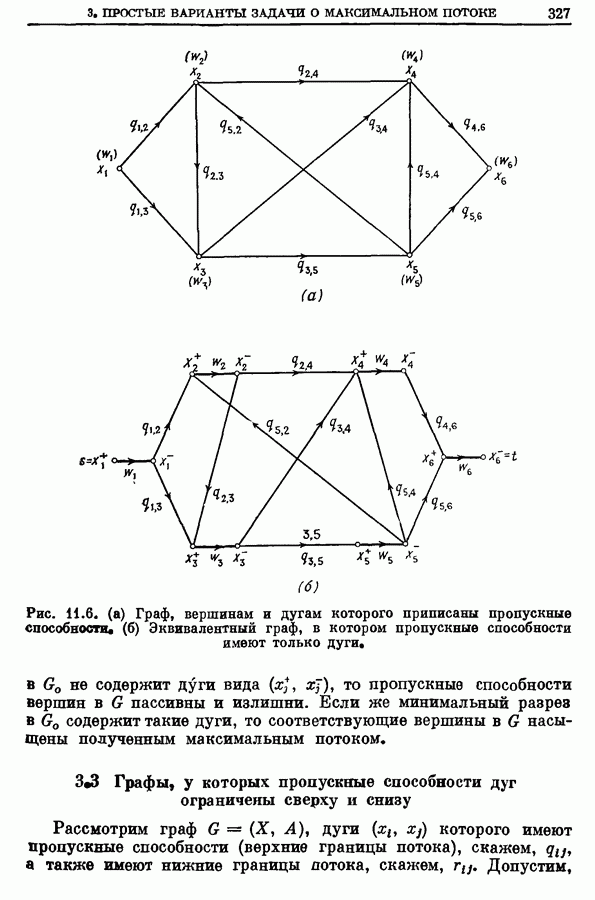
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
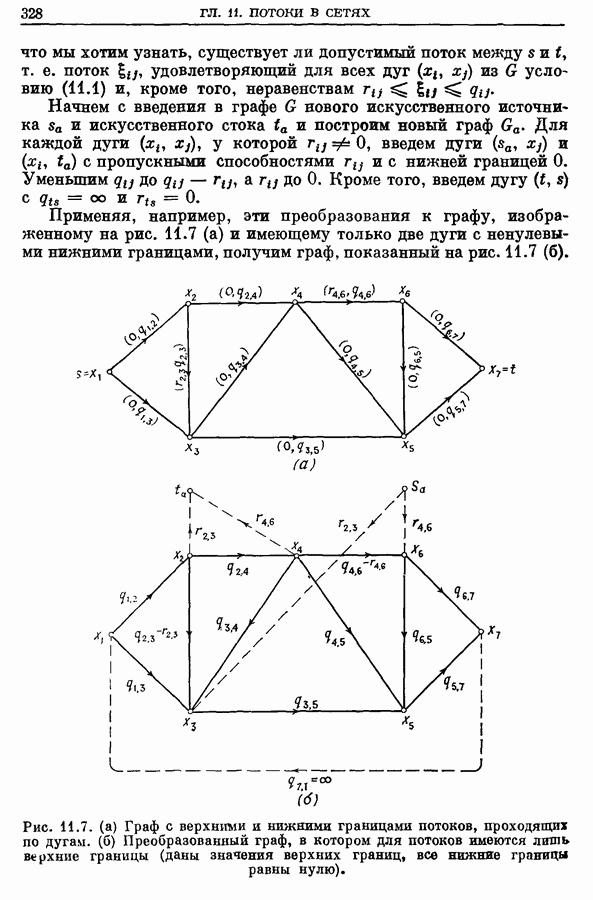
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
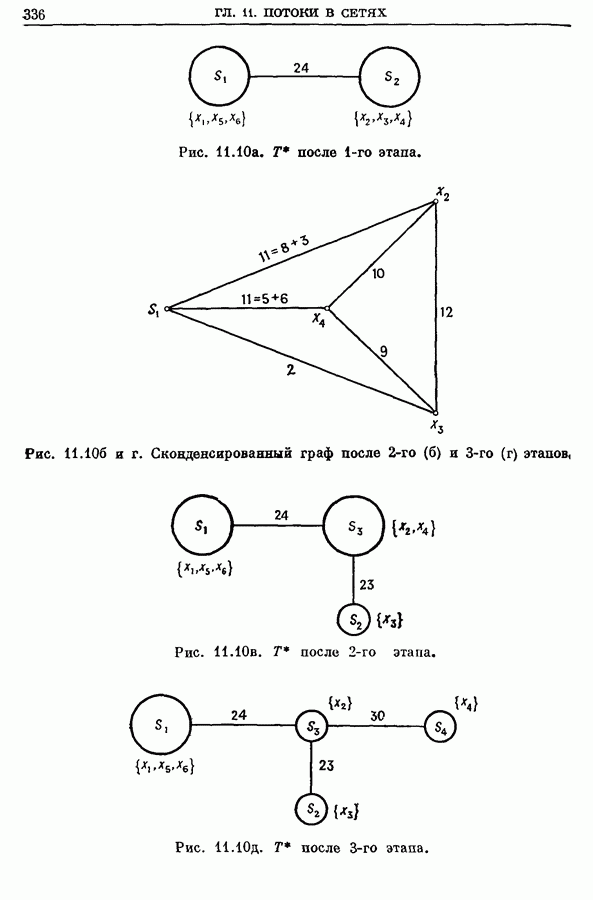
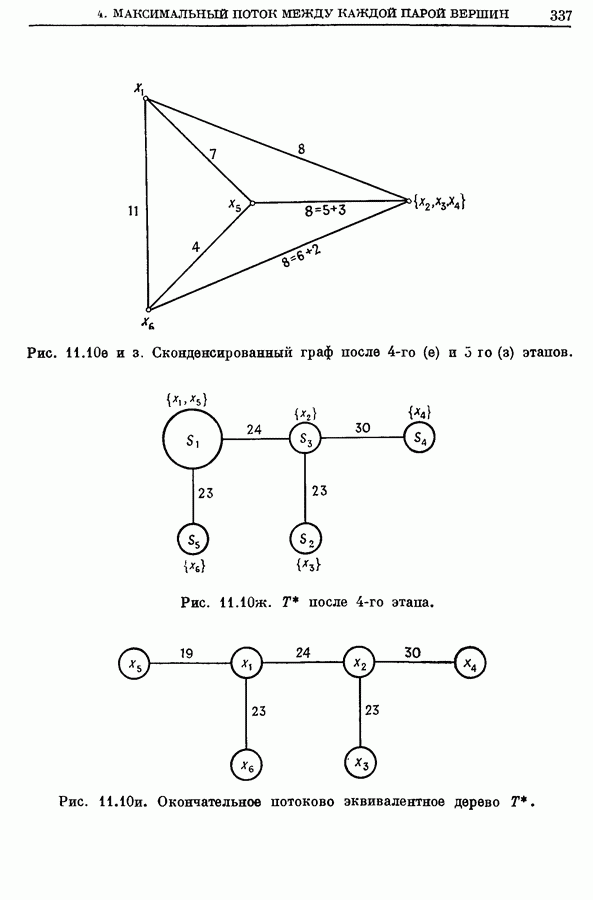
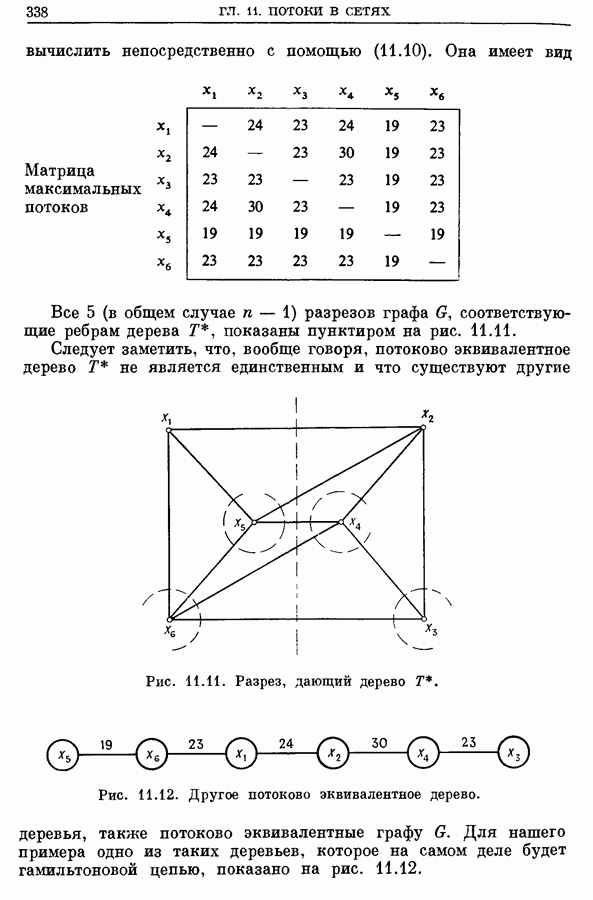
- 4. Максимальный поток между каждой паров вершин
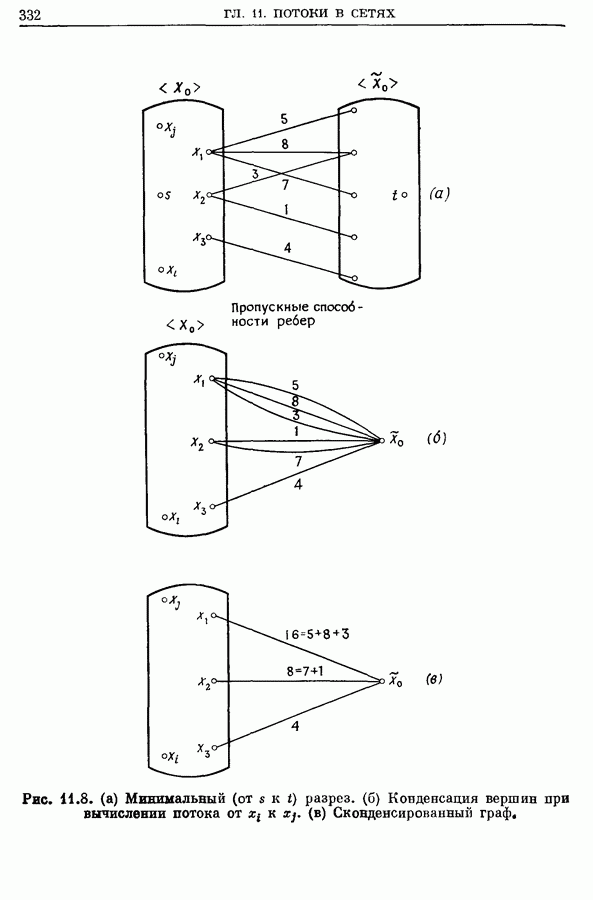
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
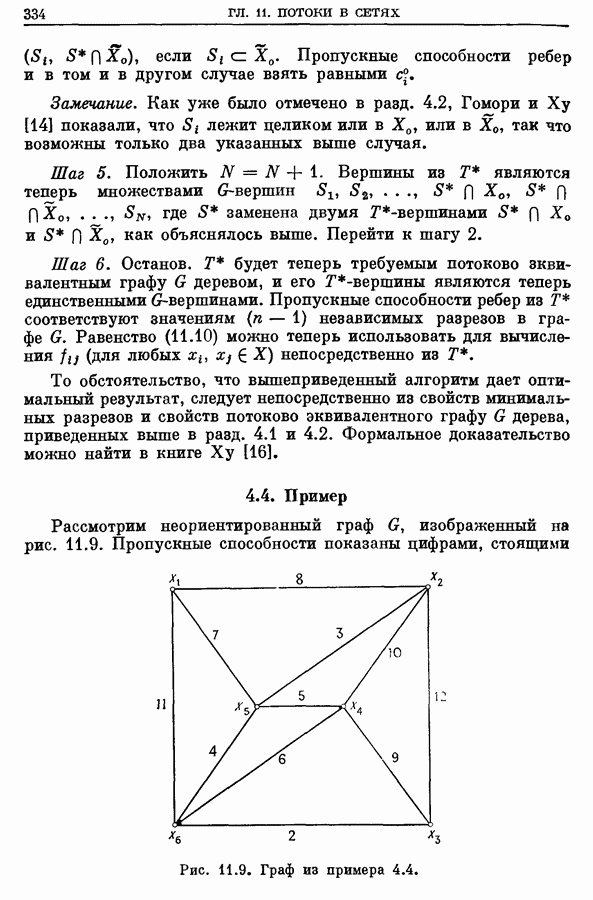
- 4.4. Пример
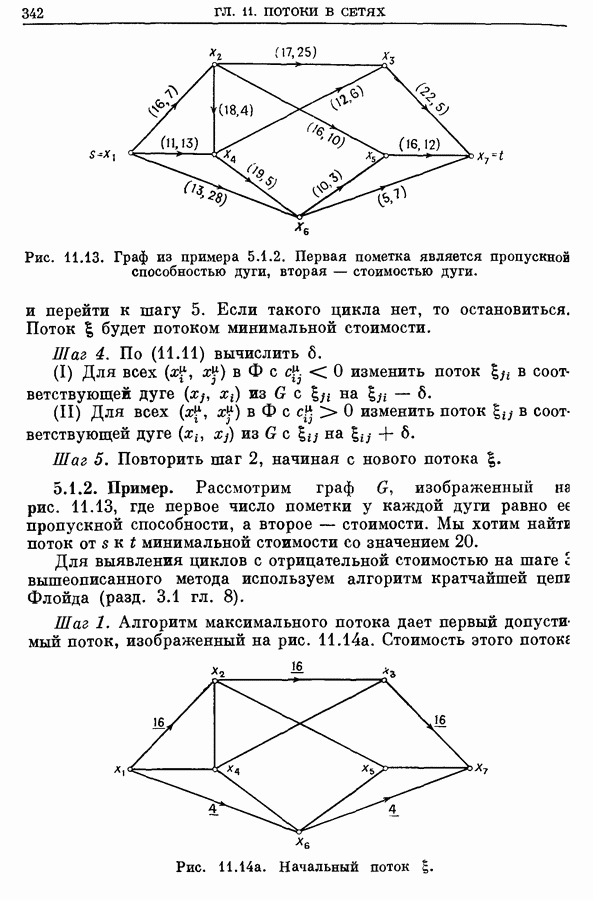
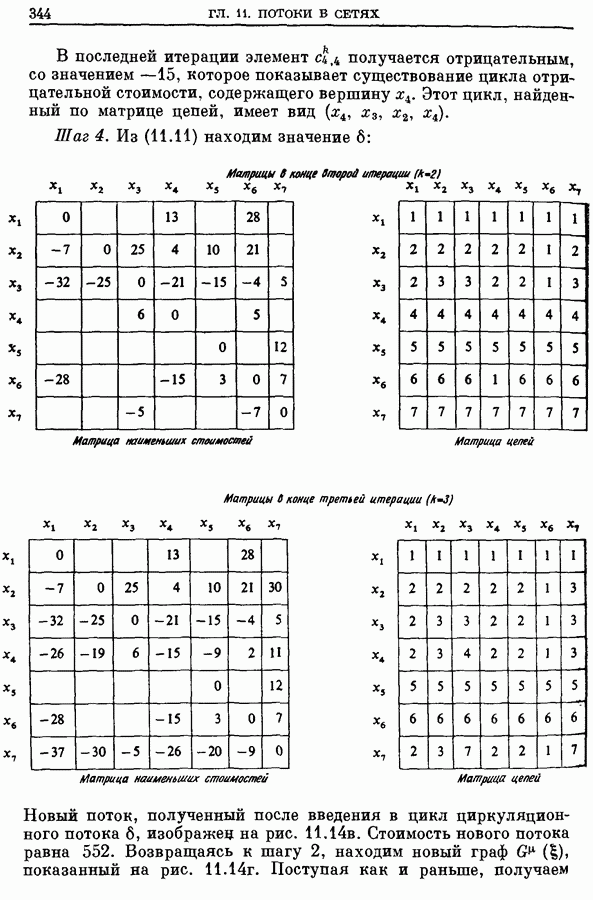
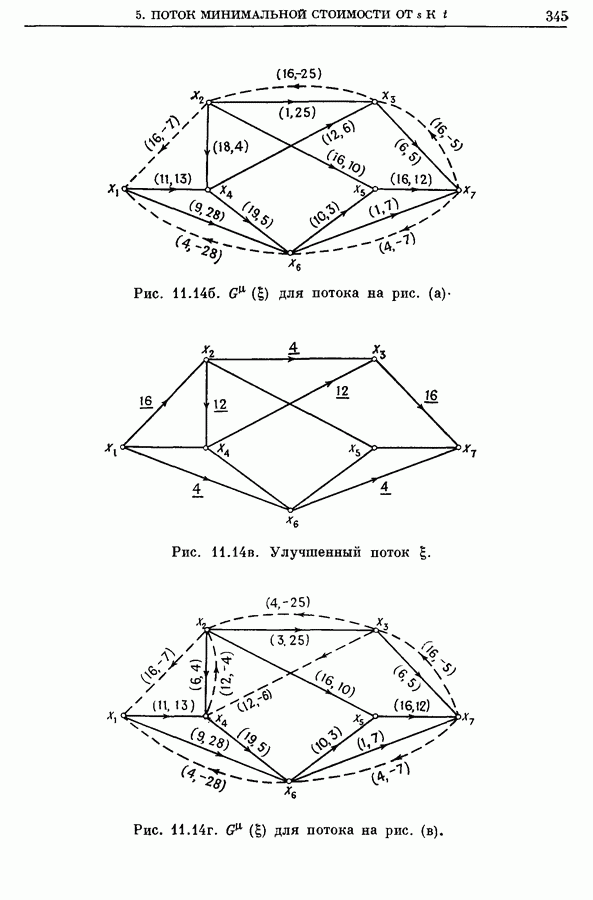
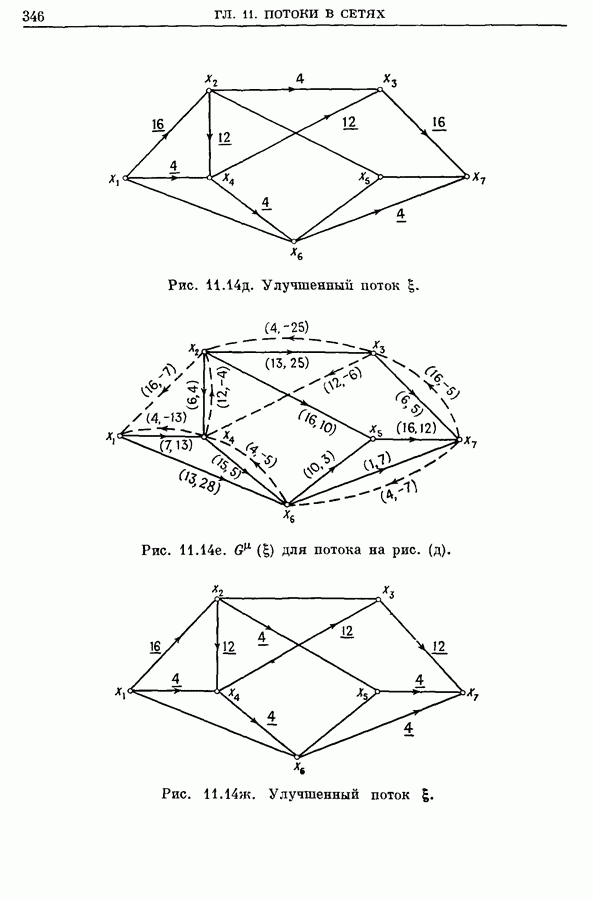
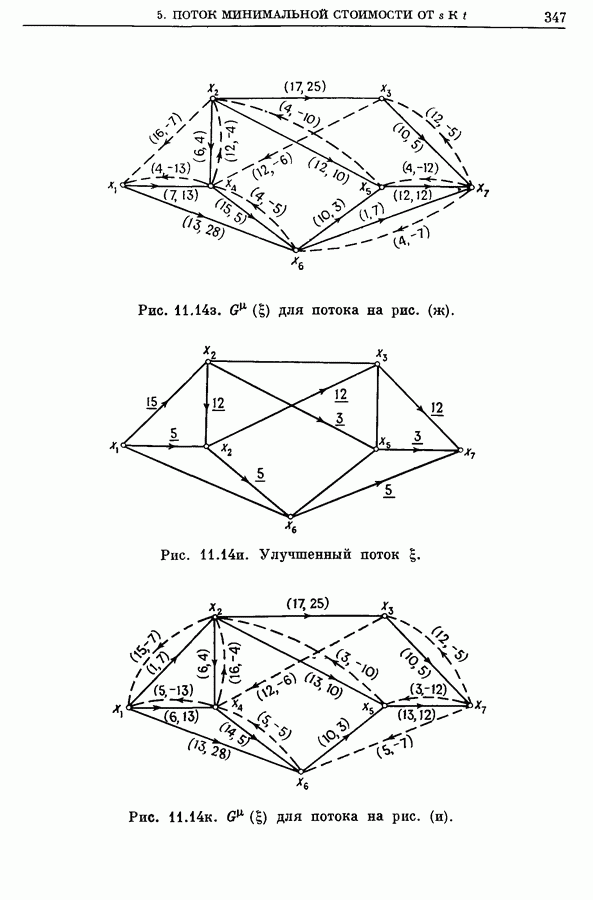
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
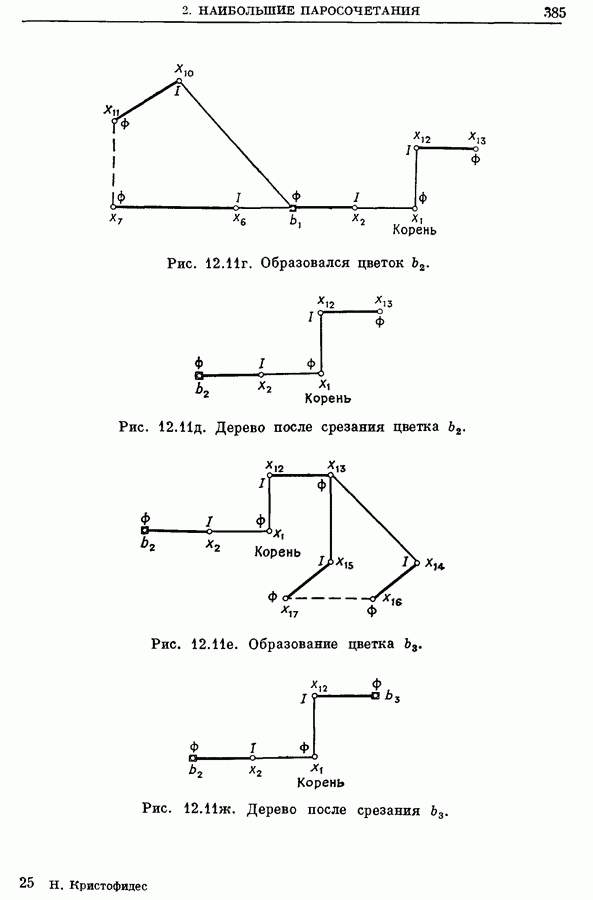
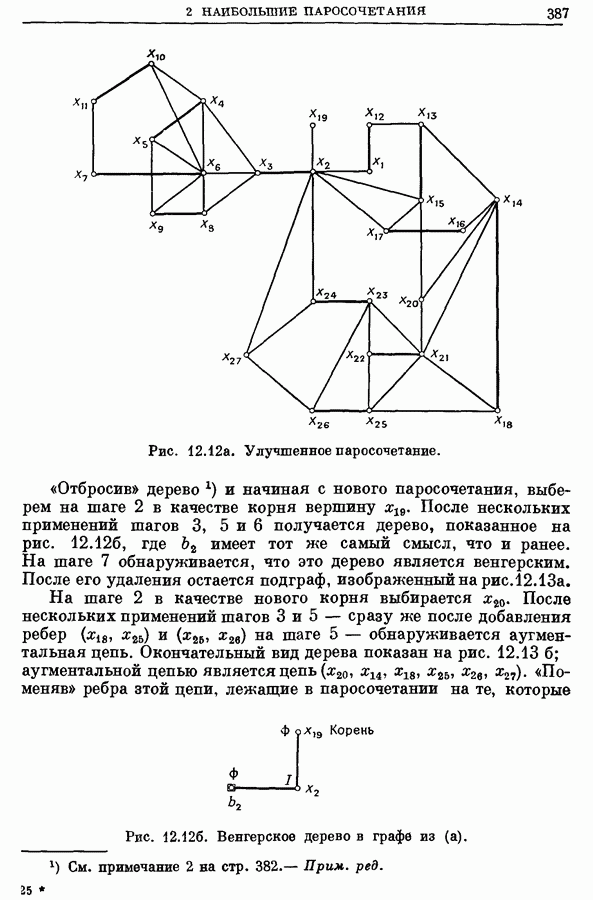
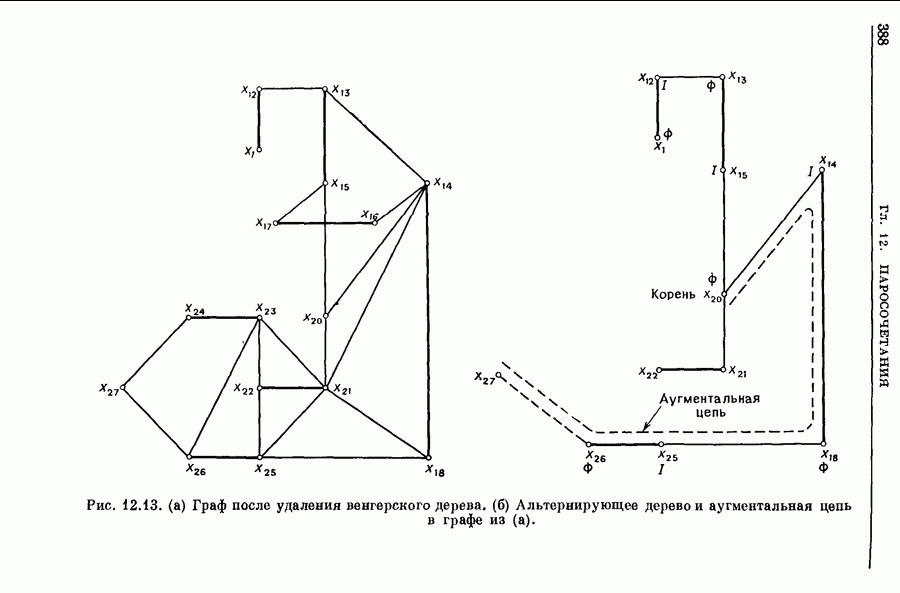
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
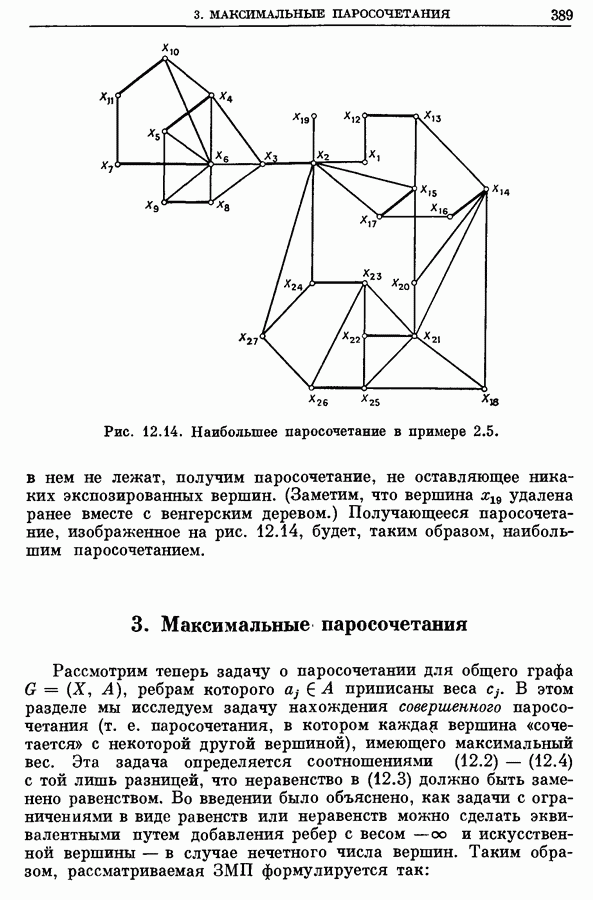
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
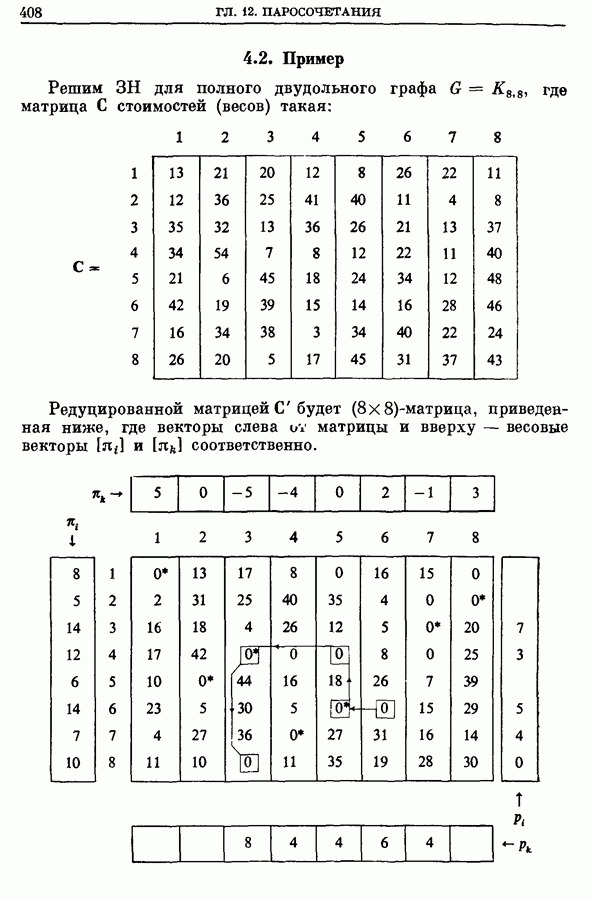
- 4.2. Пример
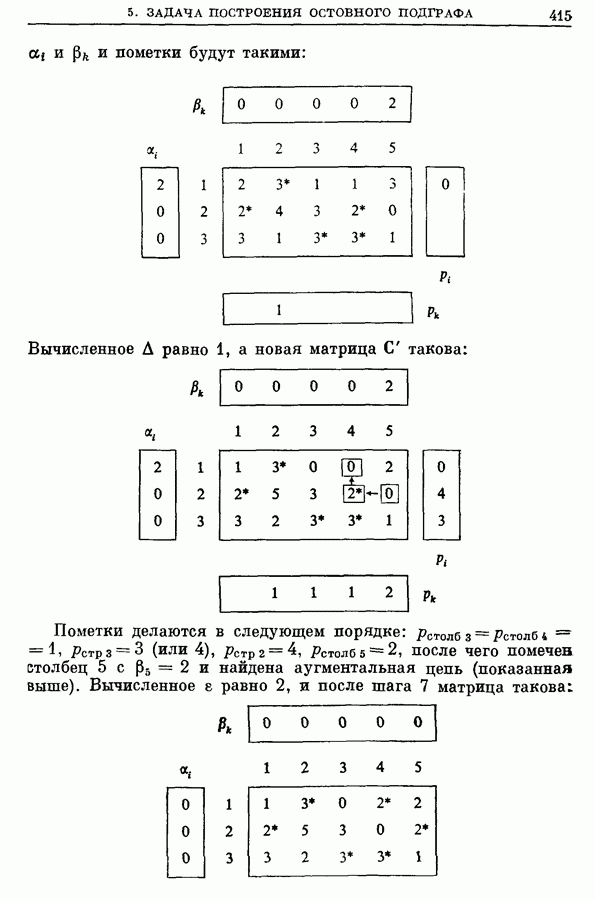
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
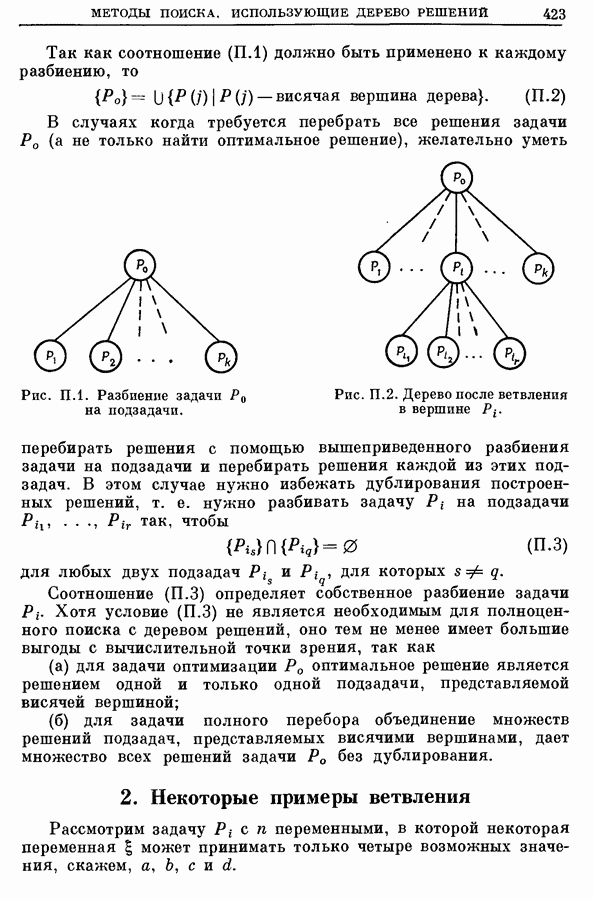
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
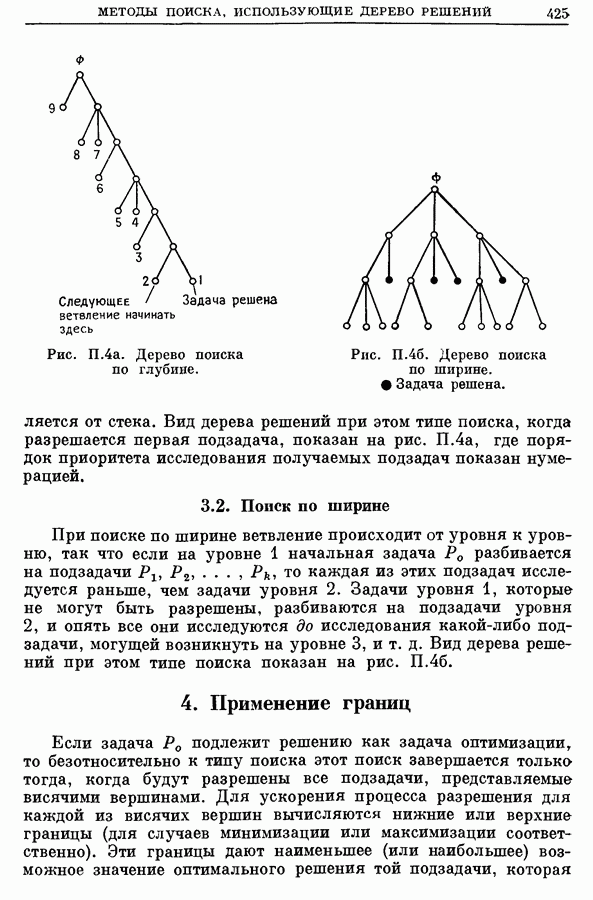
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления