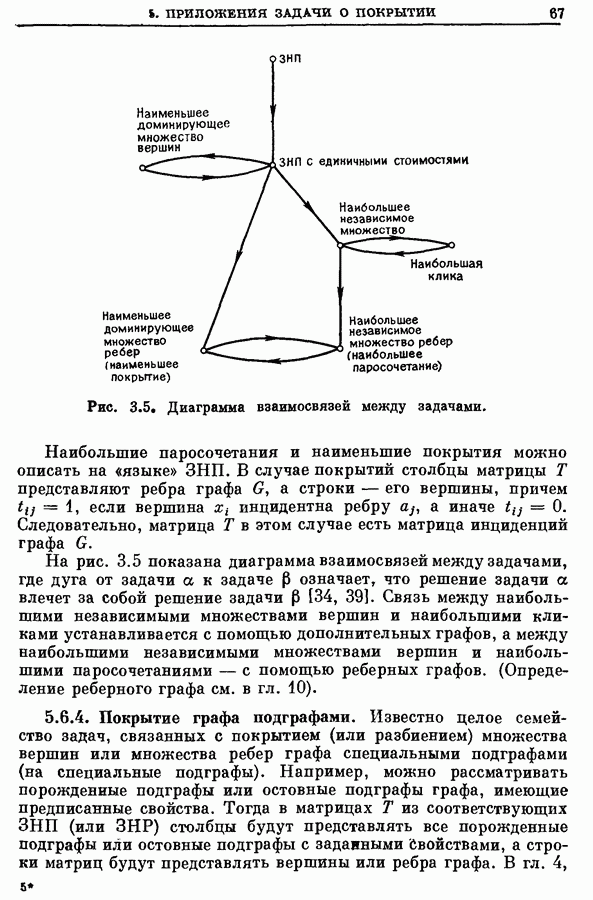
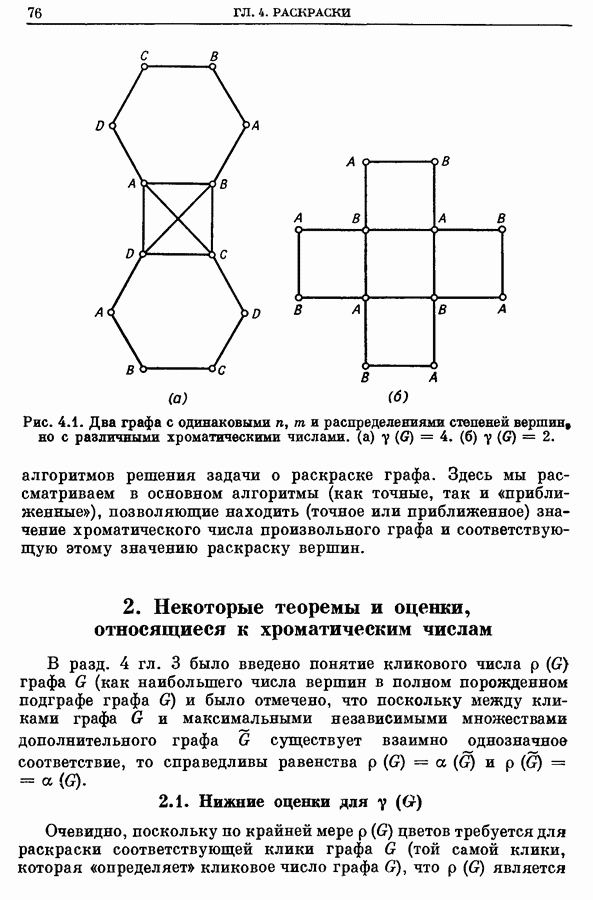
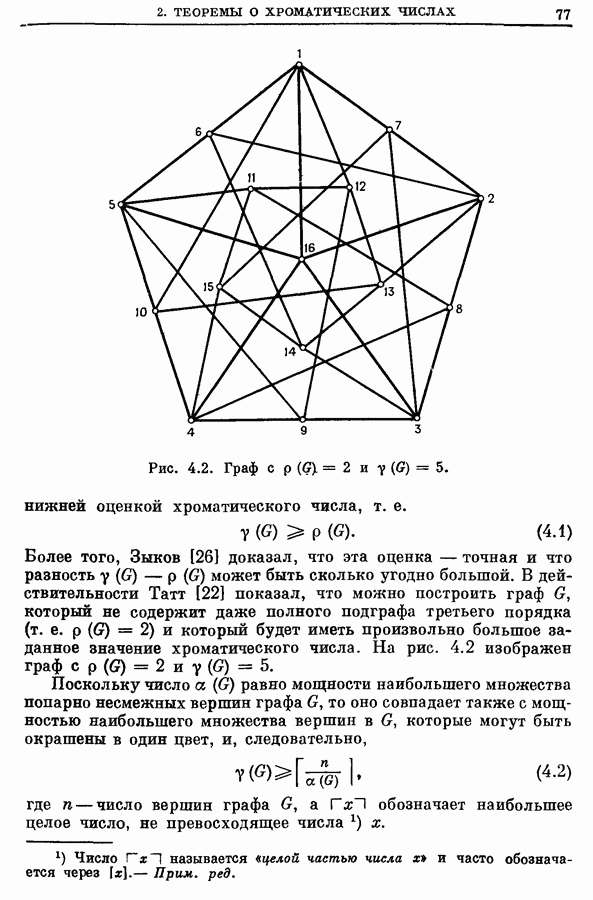
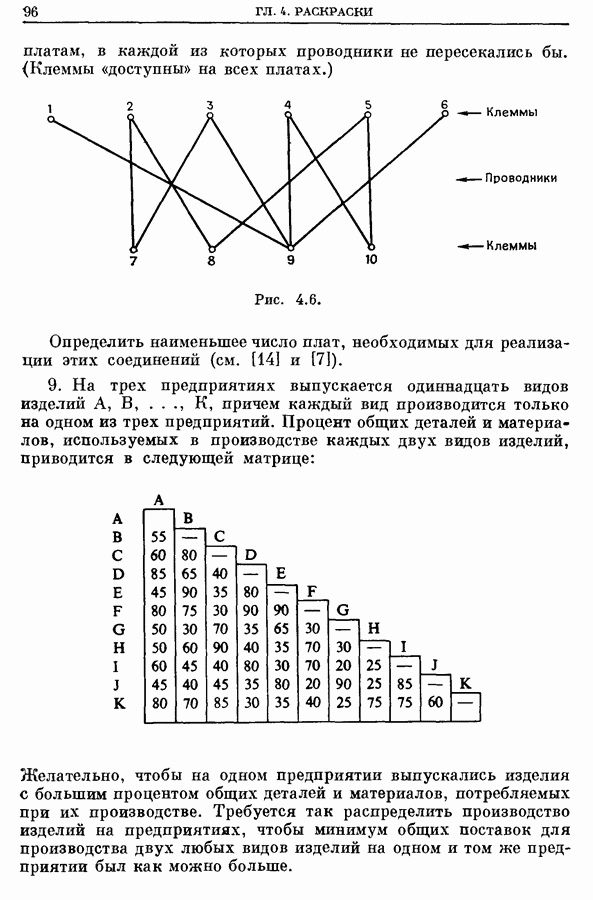
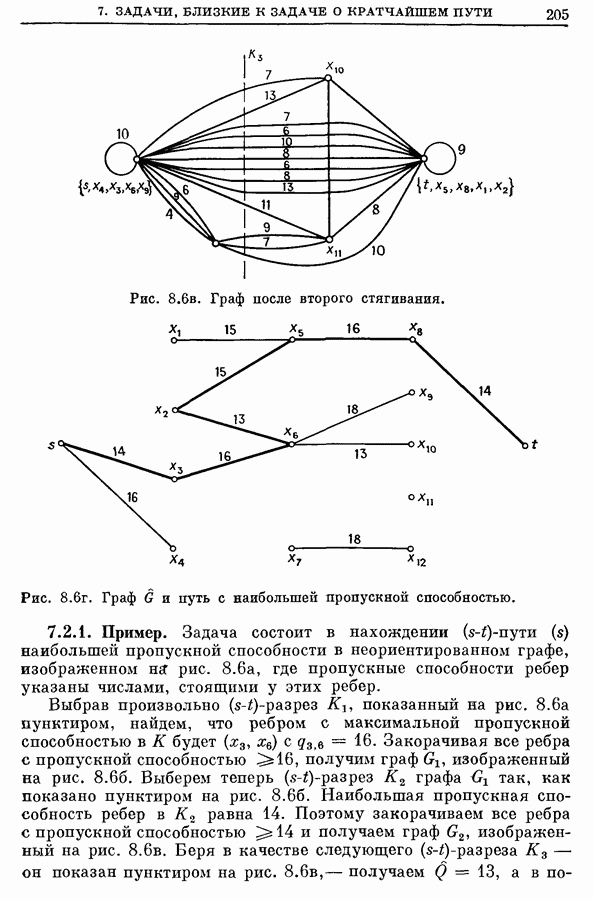
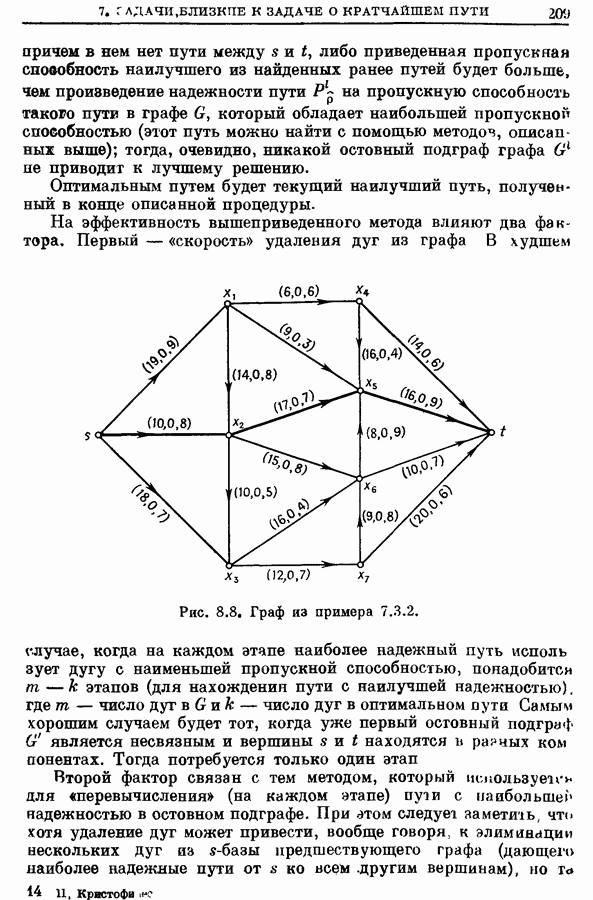
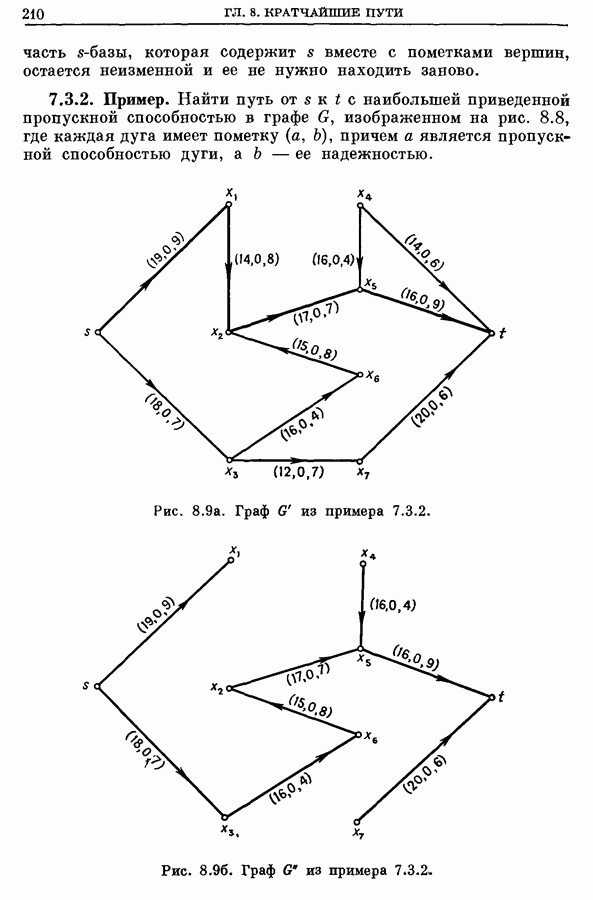
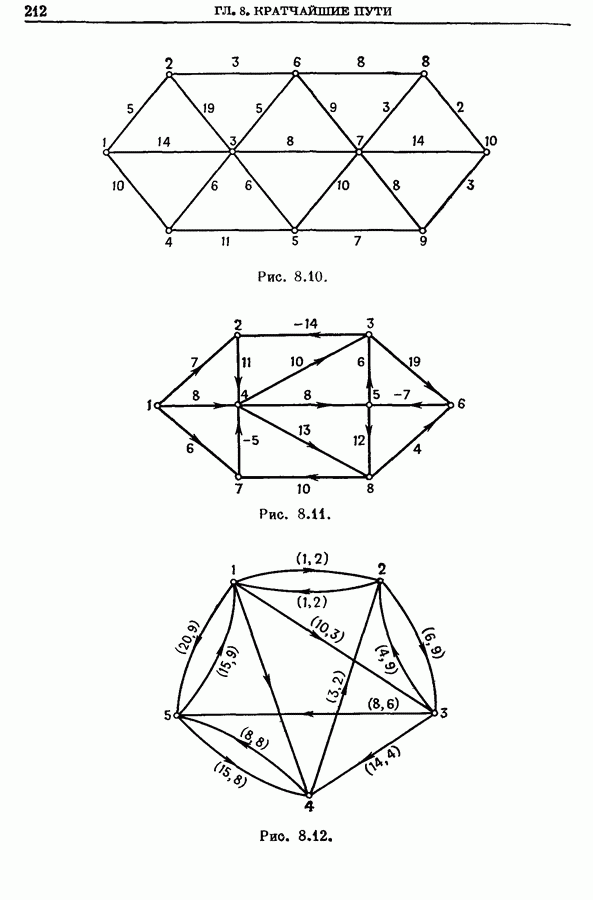
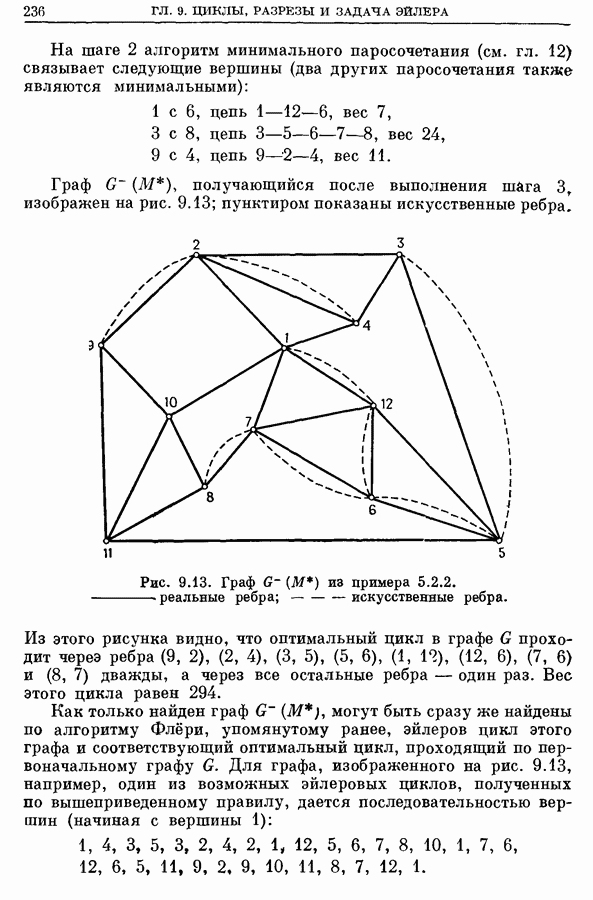
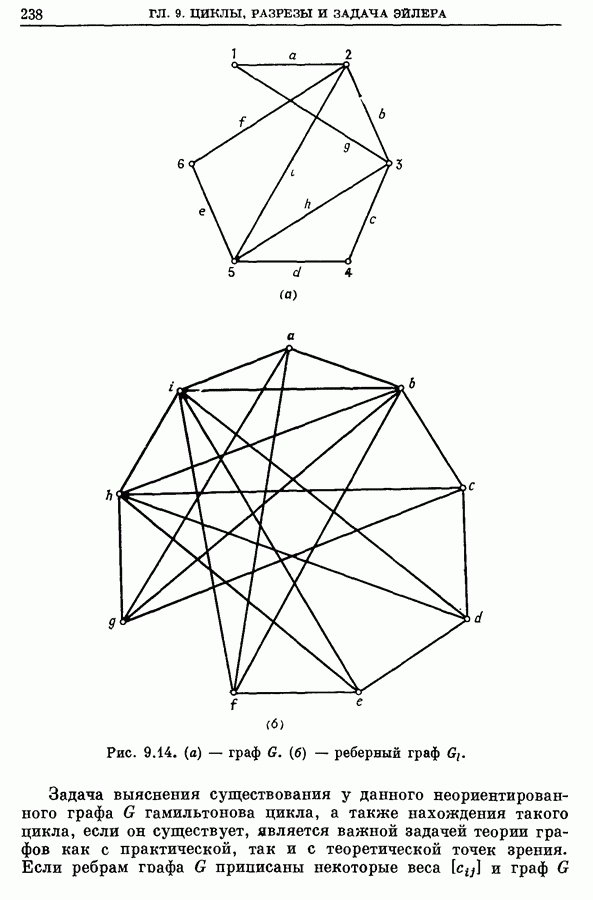
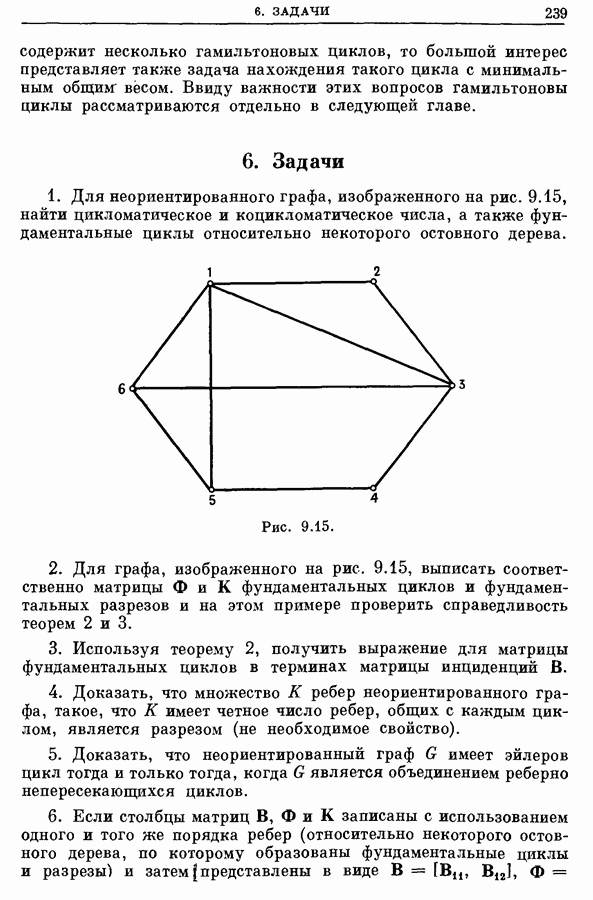
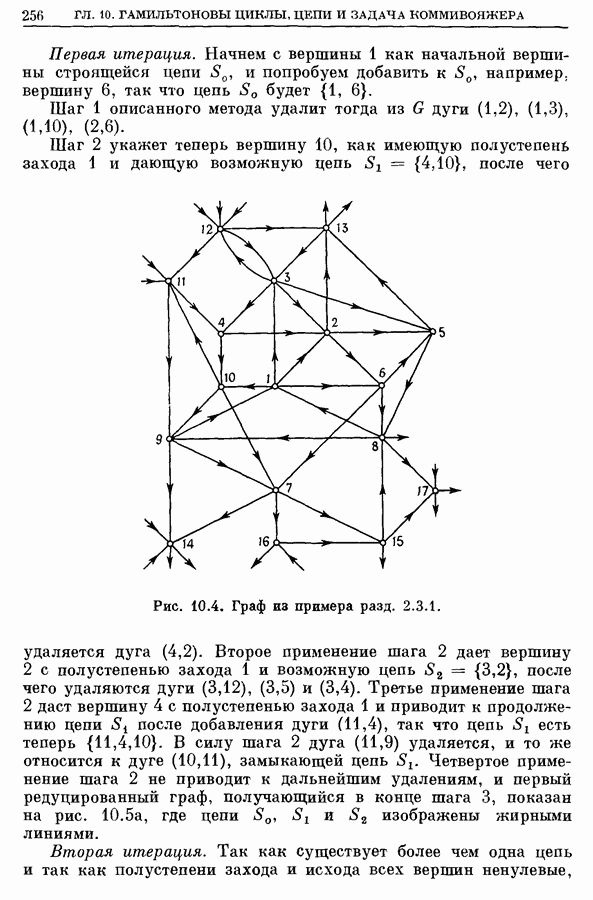
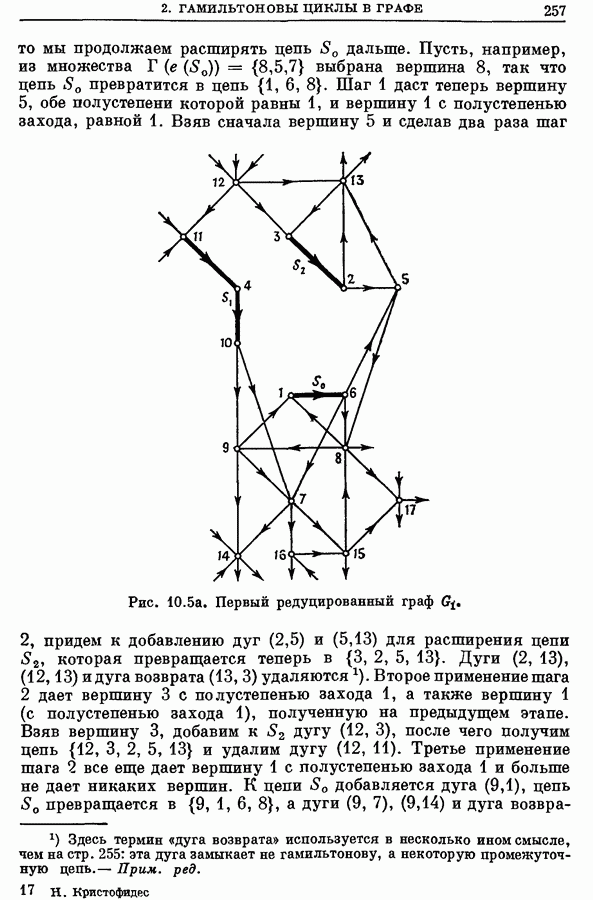
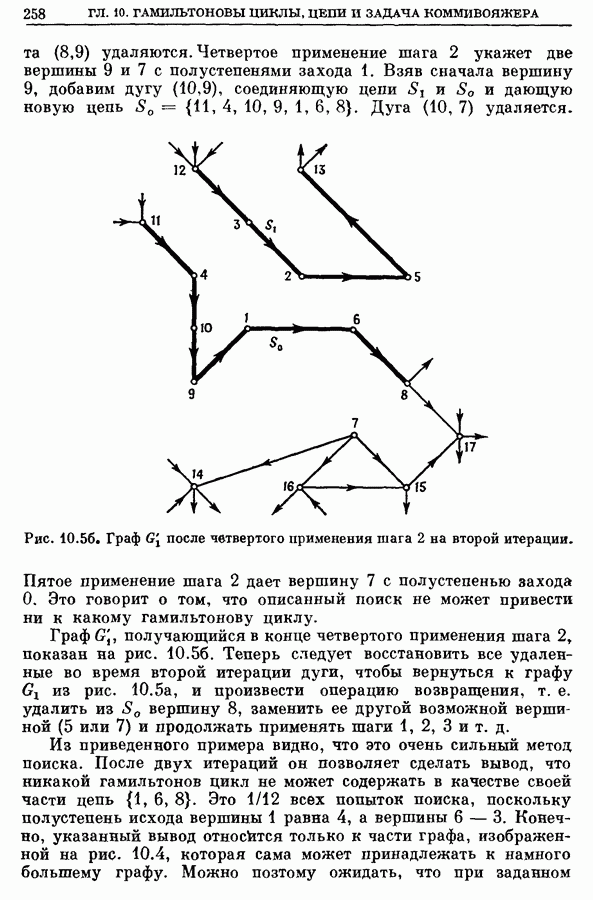
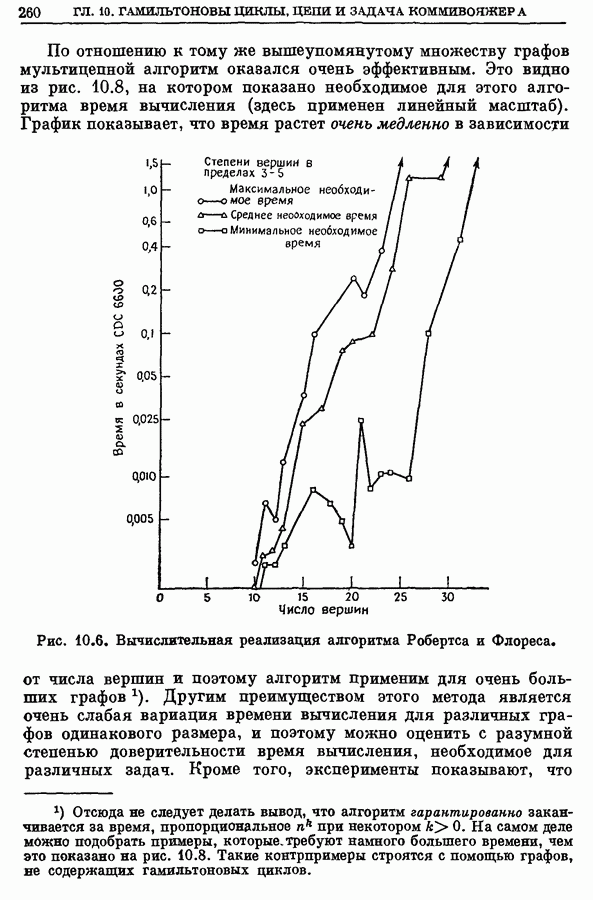
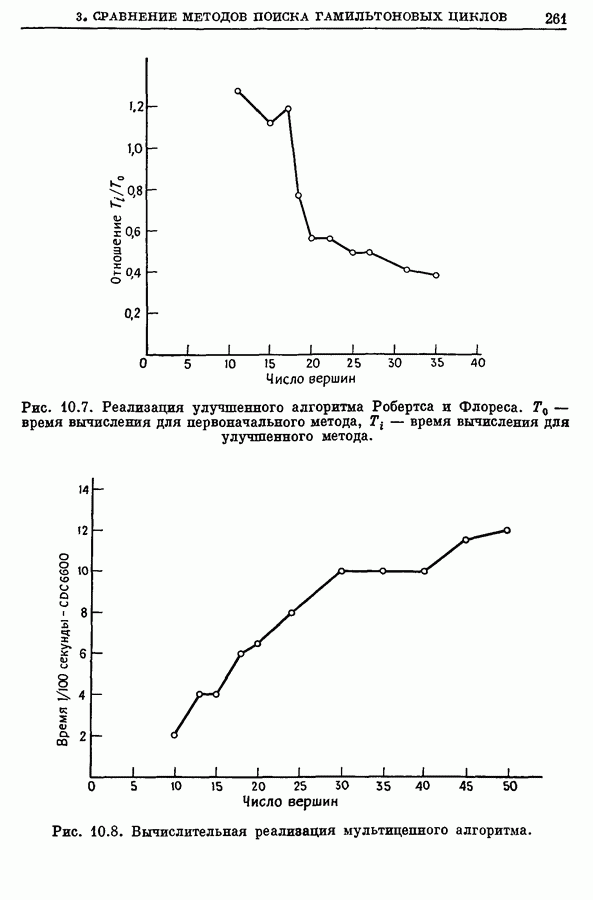
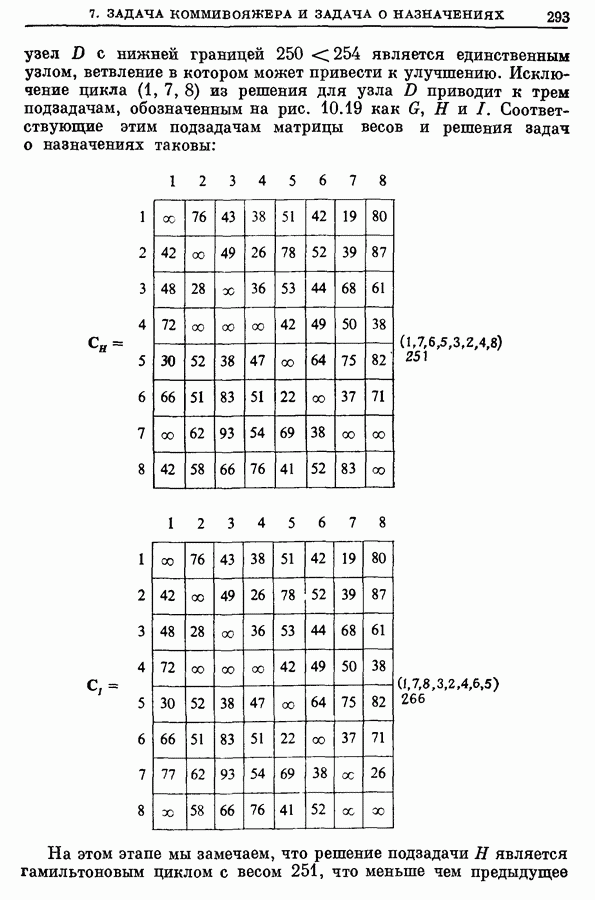
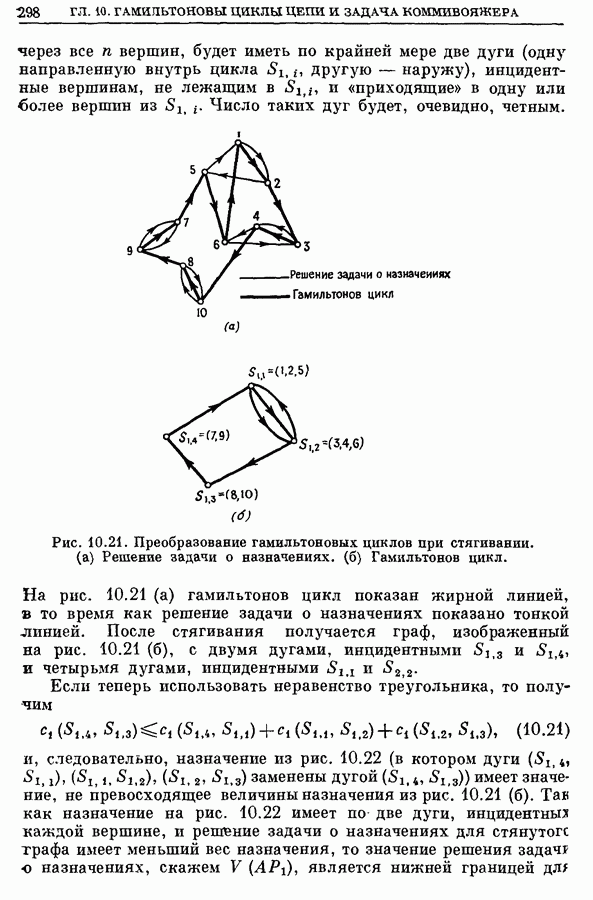
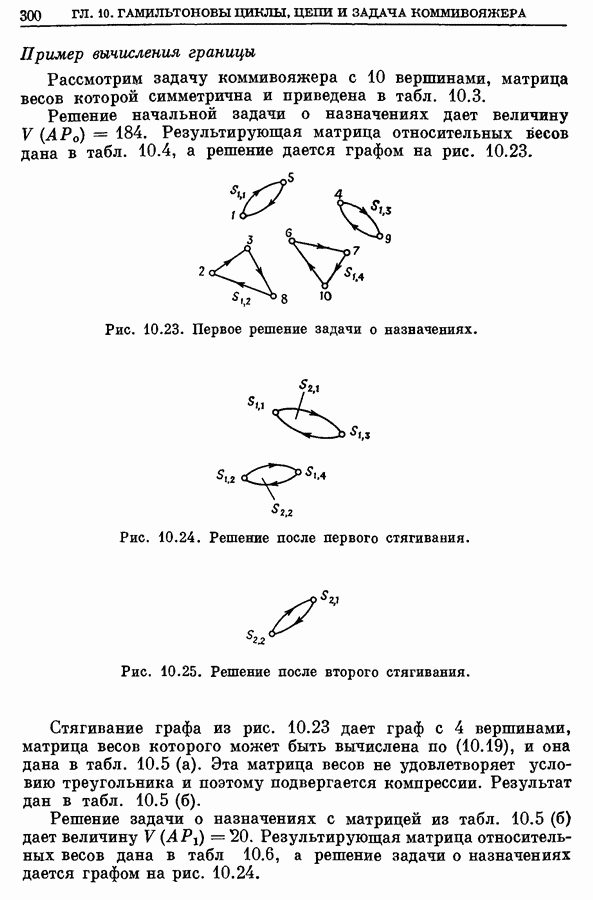
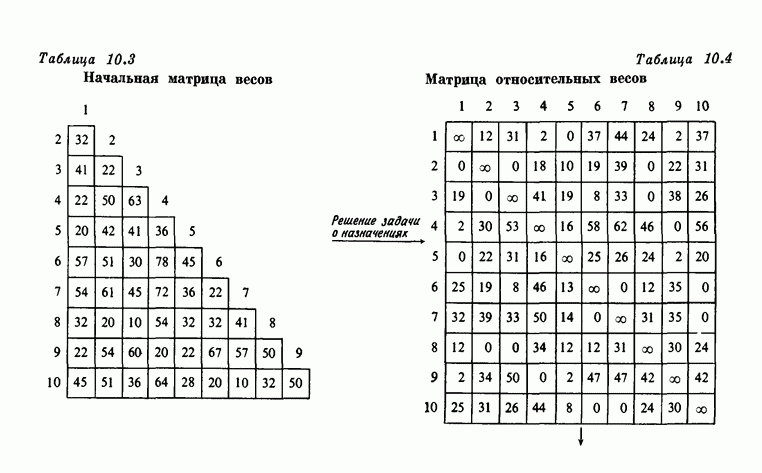
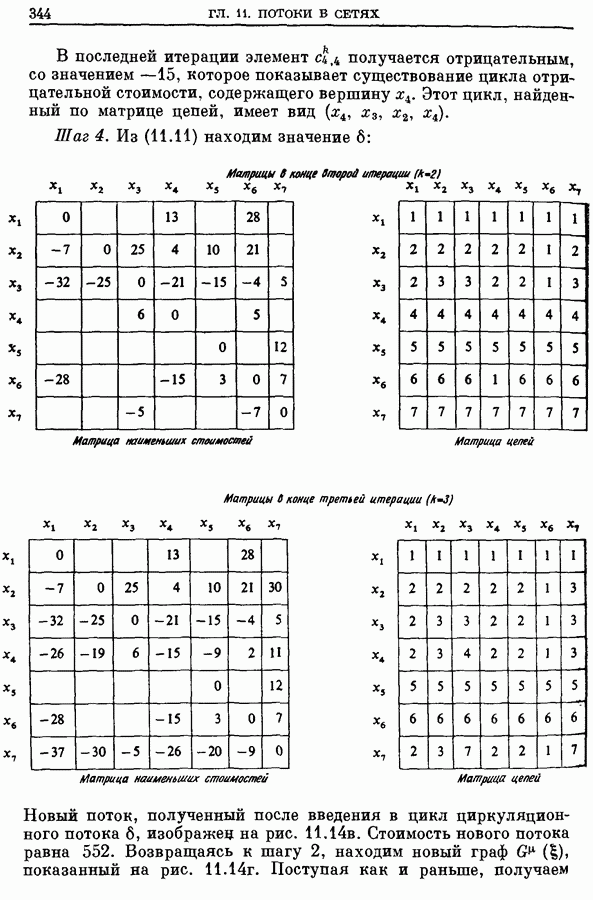
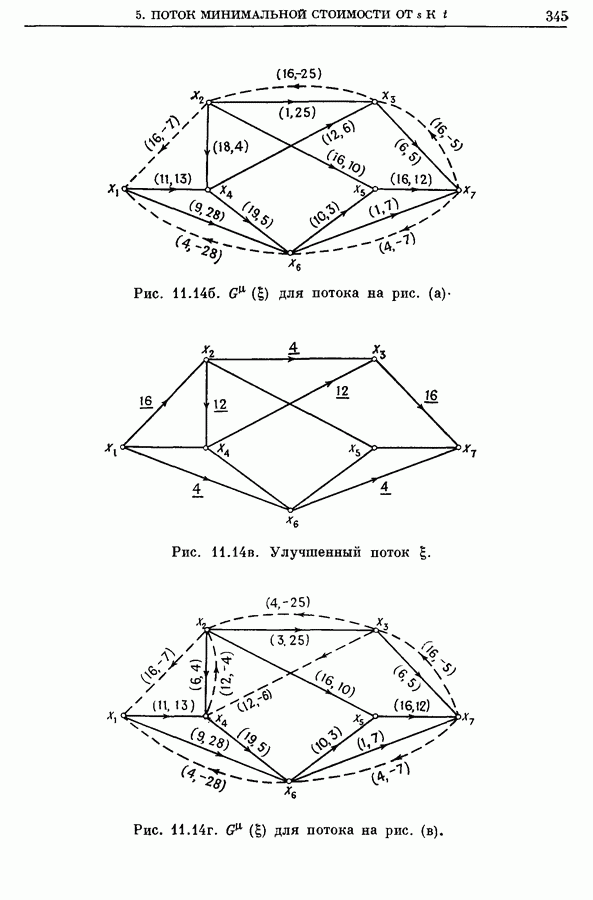
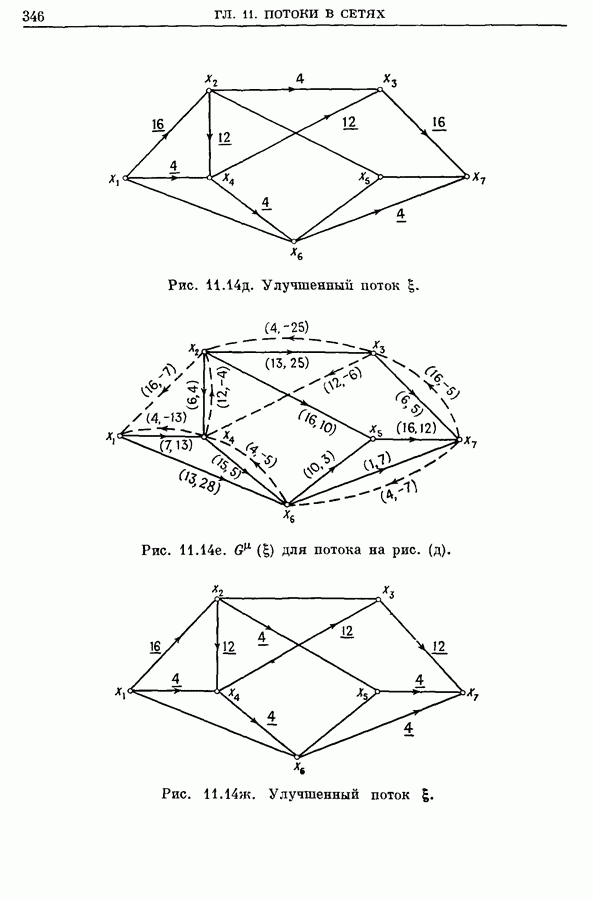
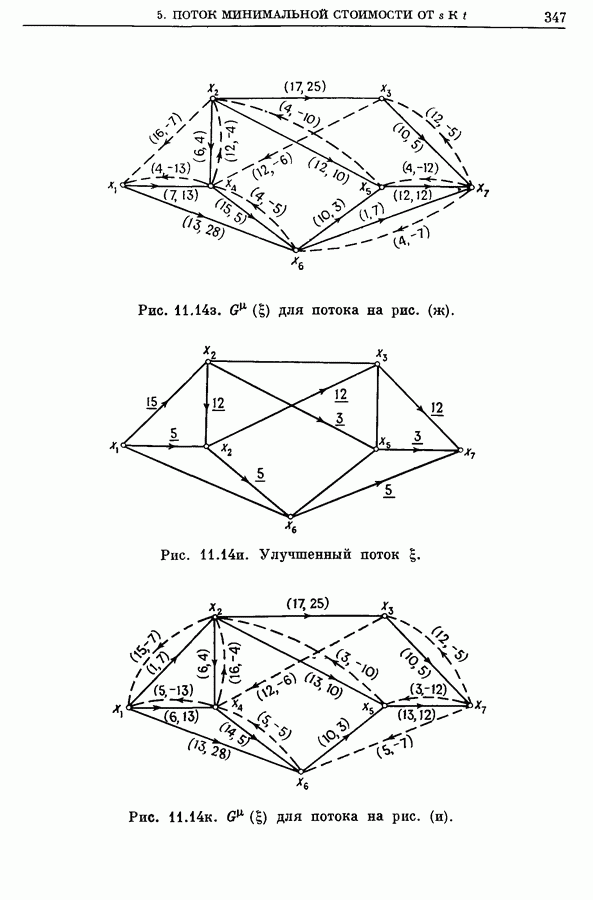
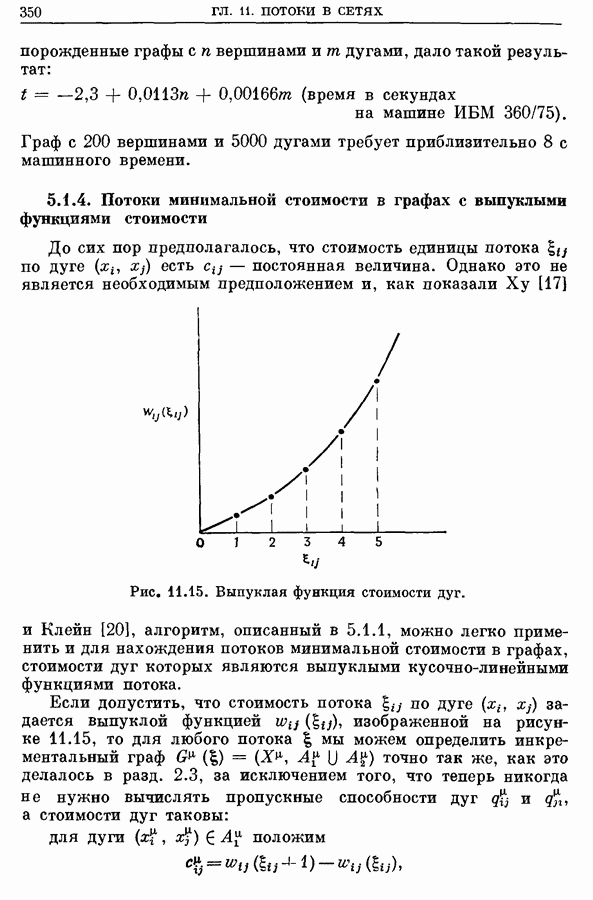
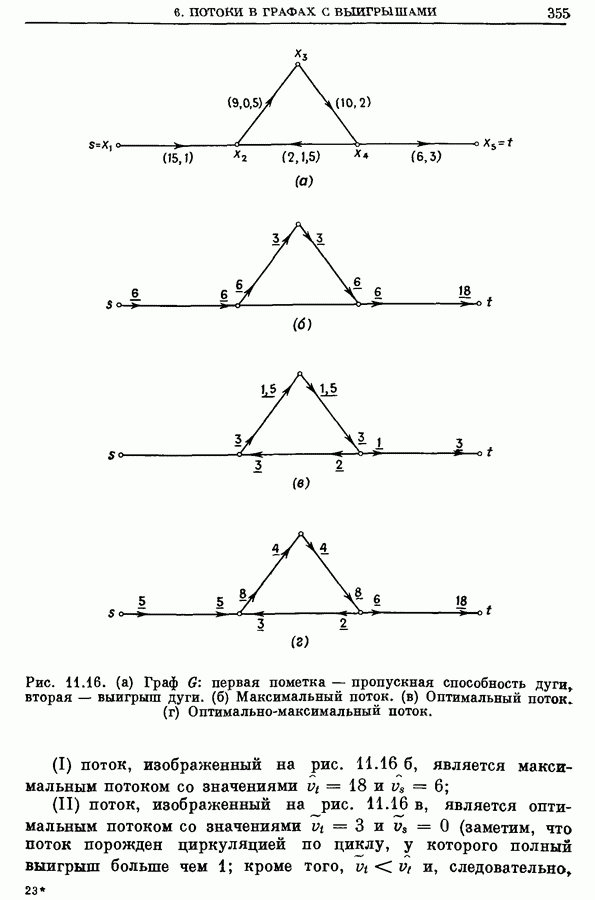
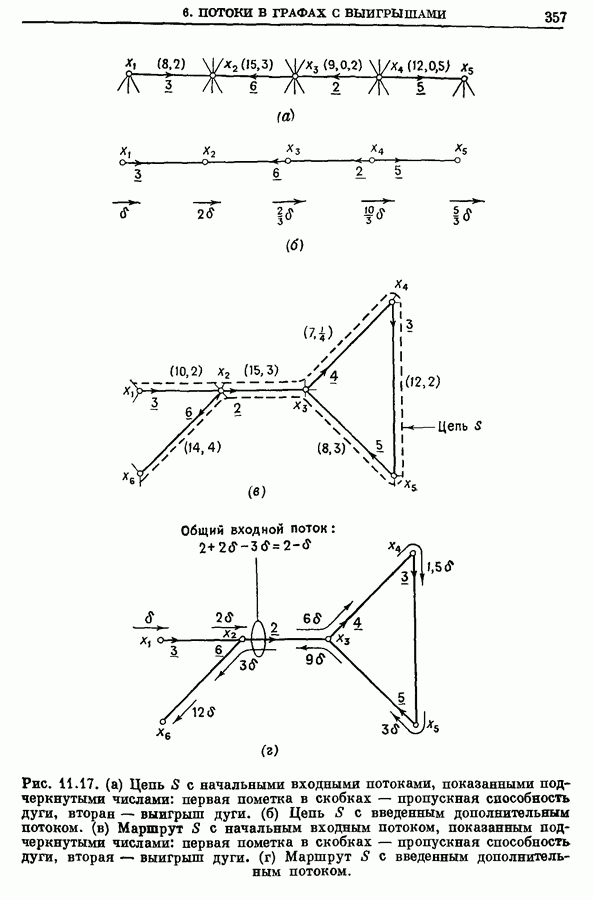
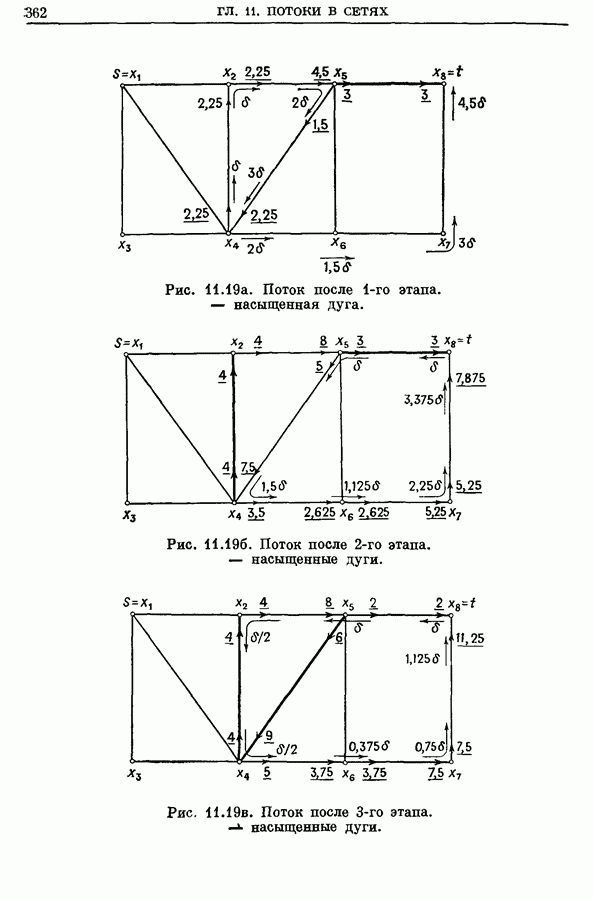
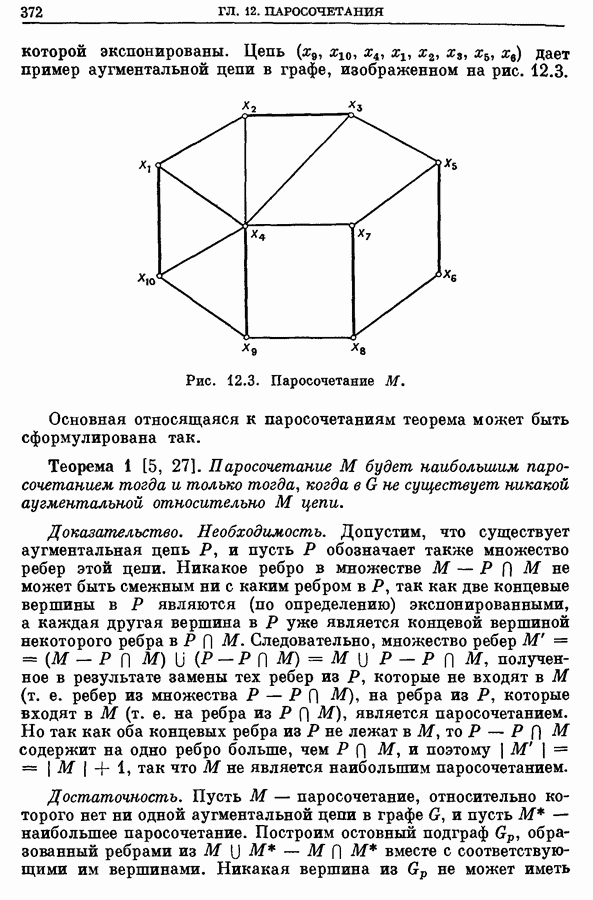
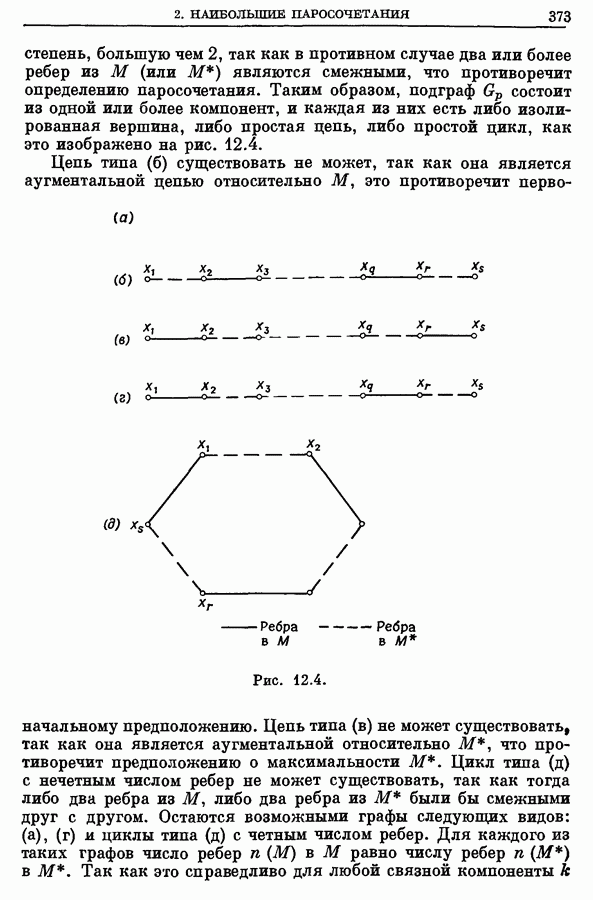
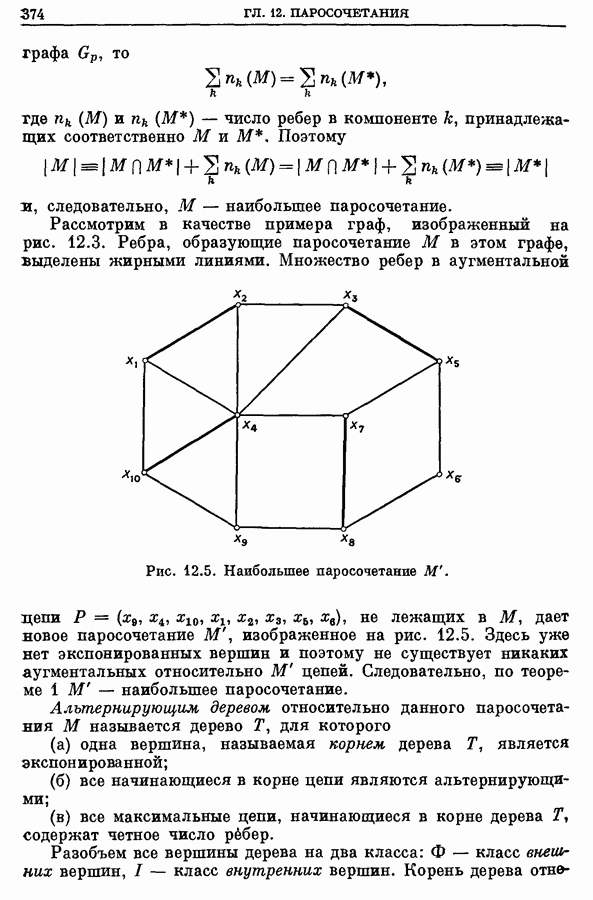
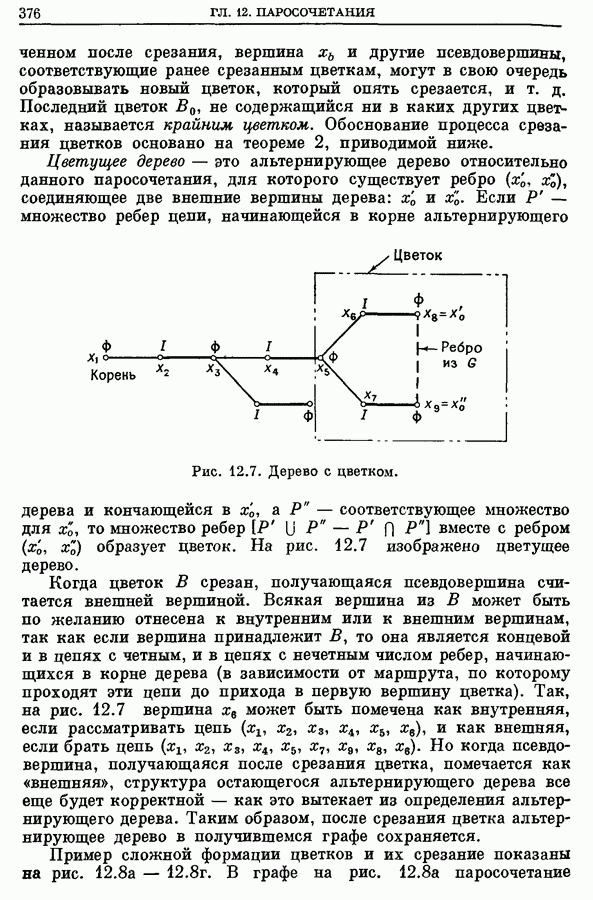
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
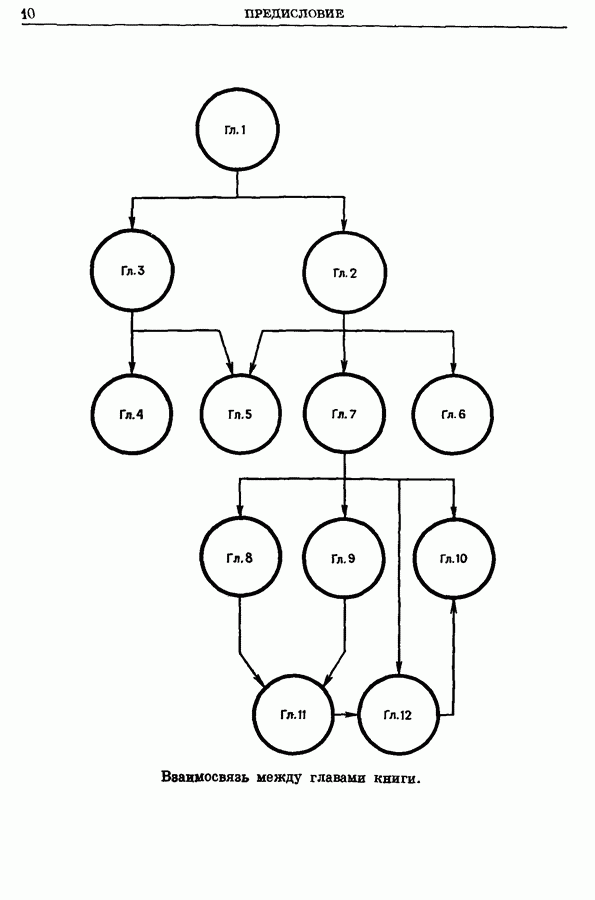
5.2. Алгоритм направленного древовидного поиска
Вместо того чтобы задачу нахождения  -медианы толковать как задачу целочисленного программирования, можно для ее решения использовать прямое дерево поиска. Этот подход лучше всего соответствует структуре рассматриваемой задачи. В настоящем разделе будет описан один из таких методов, в котором каждая подзадача, возникающая при ветвлении в каком-либо узле дерева, определяется тем, что (при заданной вершине
-медианы толковать как задачу целочисленного программирования, можно для ее решения использовать прямое дерево поиска. Этот подход лучше всего соответствует структуре рассматриваемой задачи. В настоящем разделе будет описан один из таких методов, в котором каждая подзадача, возникающая при ветвлении в каком-либо узле дерева, определяется тем, что (при заданной вершине  переменная
переменная  полагается равной 1 для некоторой вершины
полагается равной 1 для некоторой вершины  Равенство
Равенство  означает, что вершина
означает, что вершина  прикреплена к вершине
прикреплена к вершине  а также, очевидно, что
а также, очевидно, что  является медианной вершиной.
является медианной вершиной.
Этот поиск удобно выполнять следующим образом.
Построим матрицу  столбец которой содержит все вершины графа
столбец которой содержит все вершины графа  расположенные в порядке неубывания их расстояний от вершины
расположенные в порядке неубывания их расстояний от вершины  Таким образом, если
Таким образом, если  то вершина
то вершина  будет
будет  ближайшей к
ближайшей к  вершиной. Очевидно, что первой ближайшей к
вершиной. Очевидно, что первой ближайшей к  вершиной является она сама, т. е.
вершиной является она сама, т. е. 
Поиск начинается с последовательного просмотра всех вершин графа, с  по
по  Вершина
Вершина  вначале прикрепляется к вершине
вначале прикрепляется к вершине  затем к
затем к  пока не будут перебраны
пока не будут перебраны  возможности. Необходимо сделать несколько замечаний.
возможности. Необходимо сделать несколько замечаний.
1. Поскольку оптимальное решение состоит из  медианных вершин, то прикрепление вершины в этом решении к какой-либо медианной вершине должно быть наилучшим из
медианных вершин, то прикрепление вершины в этом решении к какой-либо медианной вершине должно быть наилучшим из  возможных прикреплений. Иными словами, для каждой вершины должно существовать по крайней мере еще
возможных прикреплений. Иными словами, для каждой вершины должно существовать по крайней мере еще  возможностей прикрепления с неменьшей стоимостью, чем у выбранной возможности. Следовательно, из матрицы
возможностей прикрепления с неменьшей стоимостью, чем у выбранной возможности. Следовательно, из матрицы  можно удалить
можно удалить  последних строк, и ото не отразится на оптимальном решении задачи
последних строк, и ото не отразится на оптимальном решении задачи  -медиане.
-медиане.
2. Предположим, что вершину  прикрепили к вершине
прикрепили к вершине  (которая является, например, вершиной
(которая является, например, вершиной  Пусть вершина
Пусть вершина  будет
будет  ближайшей вершиной к некоторой еще не прикрепленной вершине
ближайшей вершиной к некоторой еще не прикрепленной вершине  соответствующей
соответствующей  столбцу матрицы
столбцу матрицы  Тогда, очевидно, все элементы
Тогда, очевидно, все элементы  могут быть исключены из дальнейшего рассмотрения (отмечены), поскольку, прикрепив
могут быть исключены из дальнейшего рассмотрения (отмечены), поскольку, прикрепив  мы тем самым причисляем
мы тем самым причисляем  к медианным вершинам и поскольку вершина
к медианным вершинам и поскольку вершина  может быть прикреплена к
может быть прикреплена к  с меньшей стоимостью
с меньшей стоимостью  чем к любой другой вершине
чем к любой другой вершине  при
при  Ясно также, что если на некотором шаге возвращения процедуры поиска изменится распределение вершины Ху относительно
Ясно также, что если на некотором шаге возвращения процедуры поиска изменится распределение вершины Ху относительно  то элементы
то элементы  (неисключенные из рассмотрения, неотмеченные) должны быть рассмотрены заново.
(неисключенные из рассмотрения, неотмеченные) должны быть рассмотрены заново.
3. Пусть вершина Ху прикреплена к вершине  Тогда можно предположить, что все вершины ту»,
Тогда можно предположить, что все вершины ту»,  ту не являются медианными вершинами, поскольку в противном случае вершина
ту не являются медианными вершинами, поскольку в противном случае вершина  была бы расположена по крайней мере от одной из них не дальше, чем от
была бы расположена по крайней мере от одной из них не дальше, чем от  (с меньшей результирующей стоимостью). Эти вершины, следовательно, могут быть отмечены (исключены из рассмотрения) во всех столбцах с номерами
(с меньшей результирующей стоимостью). Эти вершины, следовательно, могут быть отмечены (исключены из рассмотрения) во всех столбцах с номерами  Нужно иметь в виду, что вершины эти исключаются временно и их надо «восстанавливать» всякий раз при изменении распределения вершины
Нужно иметь в виду, что вершины эти исключаются временно и их надо «восстанавливать» всякий раз при изменении распределения вершины  относительно тпуу.
относительно тпуу.
4. Если из рассмотрения исключены  верхних элементов
верхних элементов  столбца, соответствующего нераспределенной (неприкрепленной) вершине
столбца, соответствующего нераспределенной (неприкрепленной) вершине  элемент, т. е.
элемент, т. е.  является медианной вершиной, то
является медианной вершиной, то  должна быть прикреплена к вершине
должна быть прикреплена к вершине  В этом случае нет необходимости рассматривать какие-либо другие возможности до тех пор, пока некоторые из
В этом случае нет необходимости рассматривать какие-либо другие возможности до тех пор, пока некоторые из  верхних элементов не окажутся «восстановленными» (вследствие изменения в предыдущих распределениях вершин, что отразится на множестве «исключенных» вершин). Этот вывод является прямым следствием вышеприведенных замечаний 2 и 3.
верхних элементов не окажутся «восстановленными» (вследствие изменения в предыдущих распределениях вершин, что отразится на множестве «исключенных» вершин). Этот вывод является прямым следствием вышеприведенных замечаний 2 и 3.
5. Если на некотором этапе  проводимого поиска будет построено множество из
проводимого поиска будет построено множество из  медианных вершин (в результате применения «процедуры прикрепления» вершин), то каждую оставшуюся нераспределенную вершину можно прикрепить к ближайшей медианной вершине. Очевидно, что это является оптимальным завершением частного решения, соответствующего осуществленному прикреплению вершин. На следующем шаге процедуры — шаге возвращения — должно изменяться распределение вершин, полученное в конце
медианных вершин (в результате применения «процедуры прикрепления» вершин), то каждую оставшуюся нераспределенную вершину можно прикрепить к ближайшей медианной вершине. Очевидно, что это является оптимальным завершением частного решения, соответствующего осуществленному прикреплению вершин. На следующем шаге процедуры — шаге возвращения — должно изменяться распределение вершин, полученное в конце  этапа.
этапа.
5.2.1. Вычисление нижней границы. Замечания 1—5 можно использовать для ограничения размера дерева поиска путем уменьшения числа возможных прикреплений вершины  на любом этапе процедуры. Кроме того, на некоторых этапах, когда последней распределяемой вершиной является вершина
на любом этапе процедуры. Кроме того, на некоторых этапах, когда последней распределяемой вершиной является вершина  для ограничения дальнейшего поиска может быть использована нижняя граница величины полного оптимального решения (полученного для уже осуществленных прикреплений).
для ограничения дальнейшего поиска может быть использована нижняя граница величины полного оптимального решения (полученного для уже осуществленных прикреплений).
Предположим, что выполненные прикрепления (включая прикрепление вершины  дали
дали  медианных вершин. Тогда оставшиеся прикрепления должны привести к нахождению остальных
медианных вершин. Тогда оставшиеся прикрепления должны привести к нахождению остальных  медианных вершин. Пусть
медианных вершин. Пусть  множество индексов еще не распределенных вершин. В общем случае
множество индексов еще не распределенных вершин. В общем случае  есть множество индексов
есть множество индексов  для которых
для которых  за исключением индексов тех вершин, распределение которых индуцировано распределением первых
за исключением индексов тех вершин, распределение которых индуцировано распределением первых  вершин
вершин  (в соответствии с замечанием 4).
(в соответствии с замечанием 4).
Пусть  и
и  самый верхний и следующий за ним элементы
самый верхний и следующий за ним элементы  столбца, которые являются неотмеченными (не исключенными из рассмотрения). Тогда наилучшим распределением вершины
столбца, которые являются неотмеченными (не исключенными из рассмотрения). Тогда наилучшим распределением вершины  будет ее прикрепление к вершине
будет ее прикрепление к вершине  Если число различных вершин
Если число различных вершин  для
для  равно
равно  то все эти наилучшие распределения еще не прикрепленных вершин являются осуществимыми (т. е. получается множество, содержащее
то все эти наилучшие распределения еще не прикрепленных вершин являются осуществимыми (т. е. получается множество, содержащее  медианных вершин). Эти распределения образуют оптимальное пополнение частного решения, полученного при распределении вершин
медианных вершин). Эти распределения образуют оптимальное пополнение частного решения, полученного при распределении вершин  В таком случае записывается результат и шаг возвращения может быть предпринят с текущего частного решения.
В таком случае записывается результат и шаг возвращения может быть предпринят с текущего частного решения.
Если, однако,  то для получения всех
то для получения всех  медианных вершин надо заменить по крайней мере
медианных вершин надо заменить по крайней мере  лучших назначений на вторые лучшие или худшие. Тогда наименьшая дополнительная стоимость распределения является суммой
лучших назначений на вторые лучшие или худшие. Тогда наименьшая дополнительная стоимость распределения является суммой  наименьших разностей
наименьших разностей

по всем вершинам 
Нижняя граница стоимости оптимального решения, даваемая текущим частным решением, получается прибавлением к сумме стоимостей уже выполненных распределений

суммы  наименьших разностей, задаваемых выражением (6.20).
наименьших разностей, задаваемых выражением (6.20).
Может случиться, что  меньше
меньше  Тогда наилучшее пополнение текущего частного решения дает медианных вершин меньше
Тогда наилучшее пополнение текущего частного решения дает медианных вершин меньше
чем  Но поскольку очевидно, что передаточное число
Но поскольку очевидно, что передаточное число  оптимальной
оптимальной  -медианы
-медианы  монотонно убывает с увеличением
монотонно убывает с увеличением  то при
то при  текущее частное решение наверняка не является частью оптимального
текущее частное решение наверняка не является частью оптимального  -медианного решения и тогда можно выполнить шаг возвращения.
-медианного решения и тогда можно выполнить шаг возвращения.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
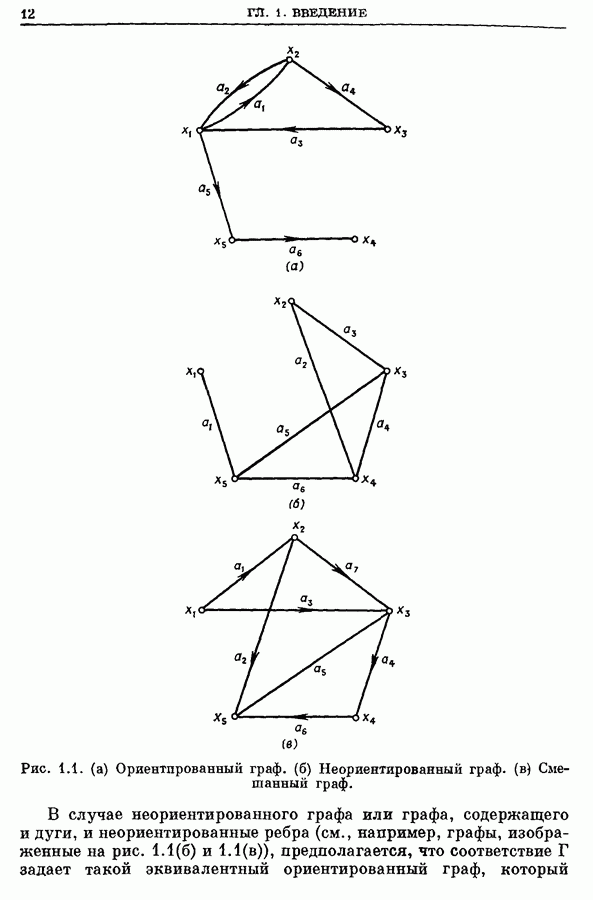
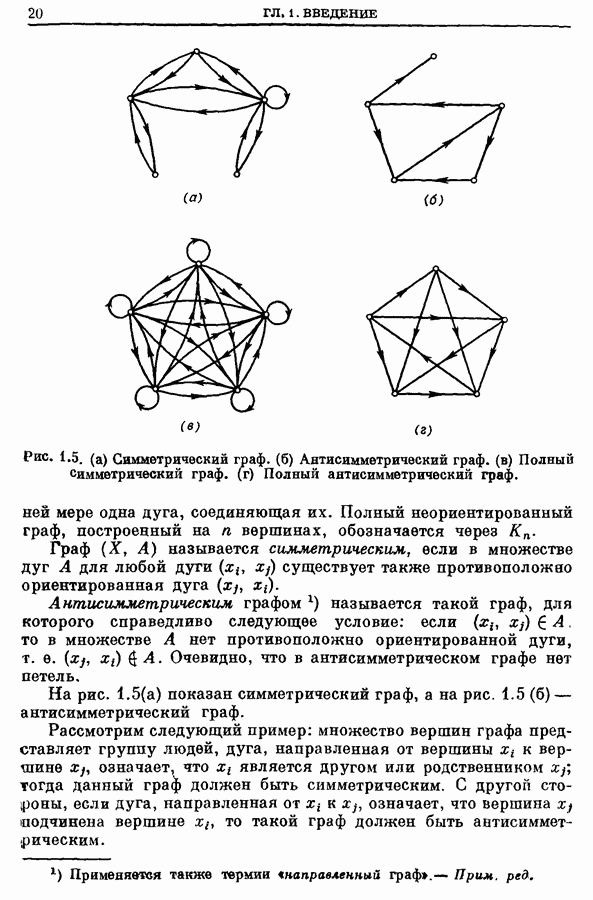
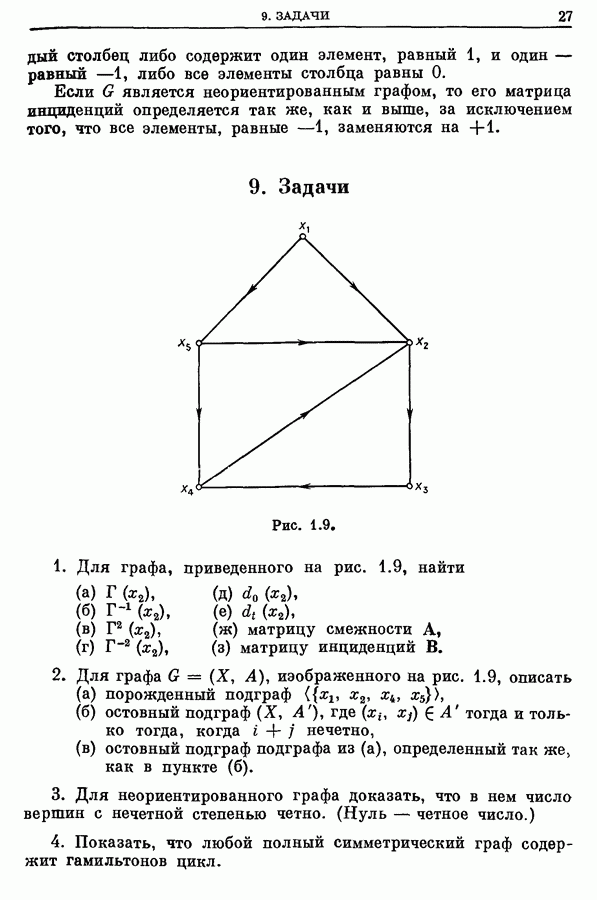
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
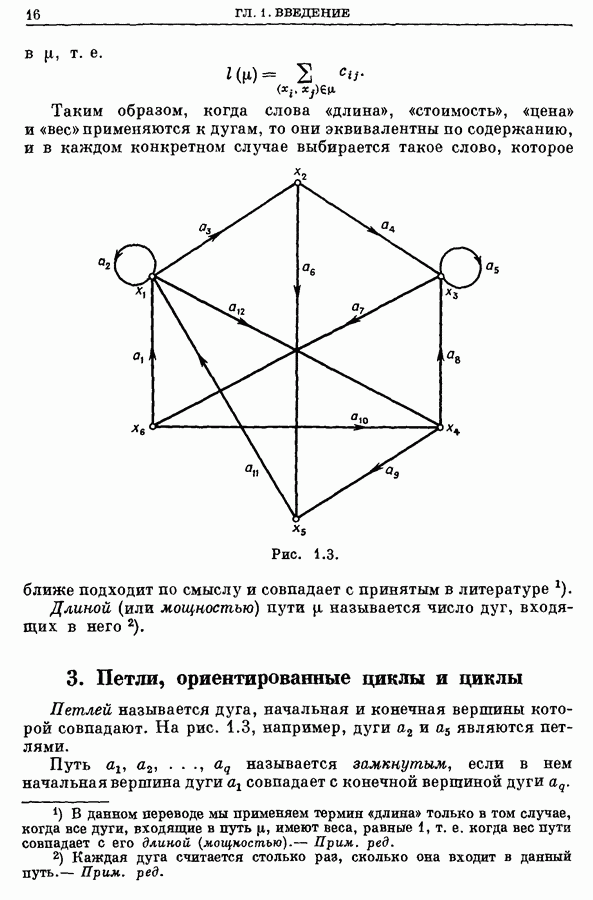
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
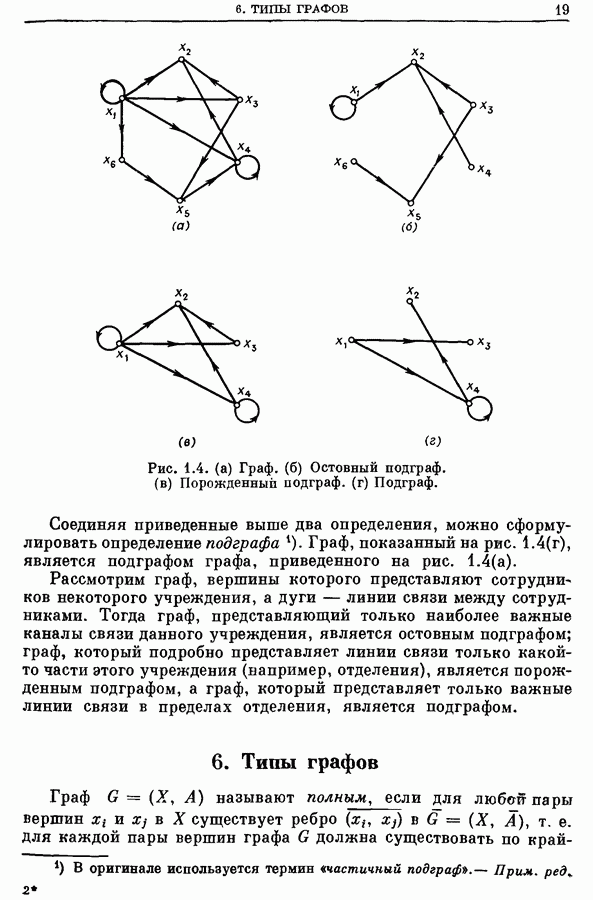
- 5. Подграфы
- 6. Типы графов
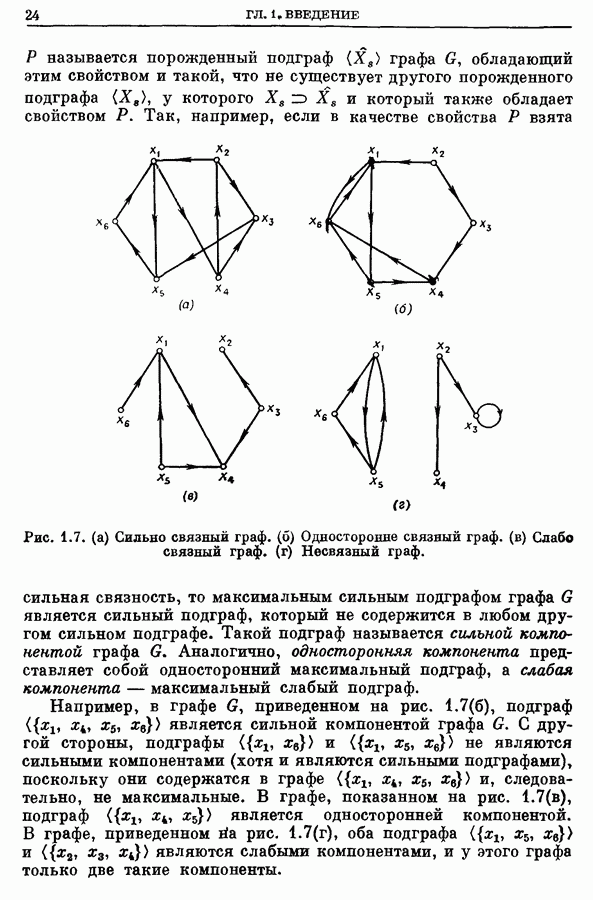
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
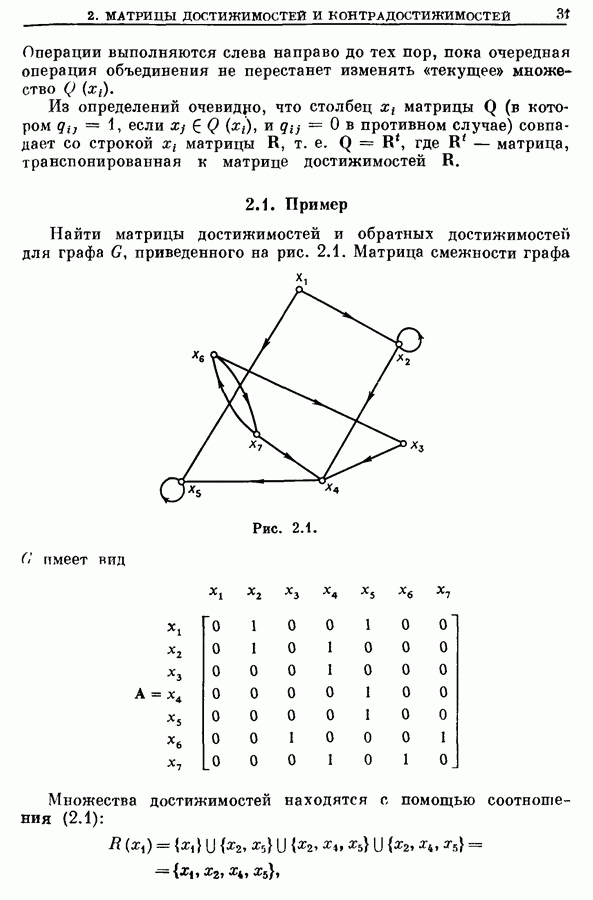
- 2. Матрицы достижимостеи и контрадостижимостей
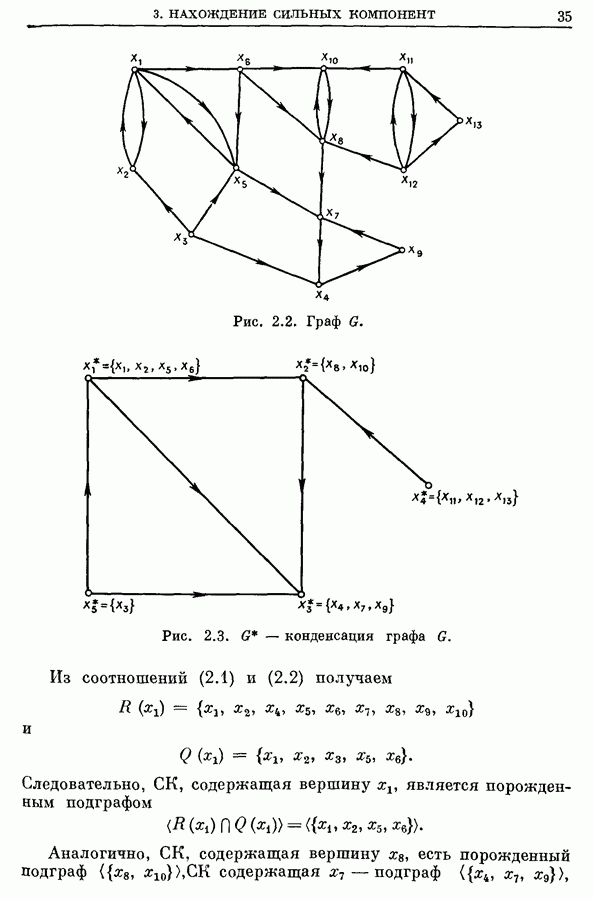
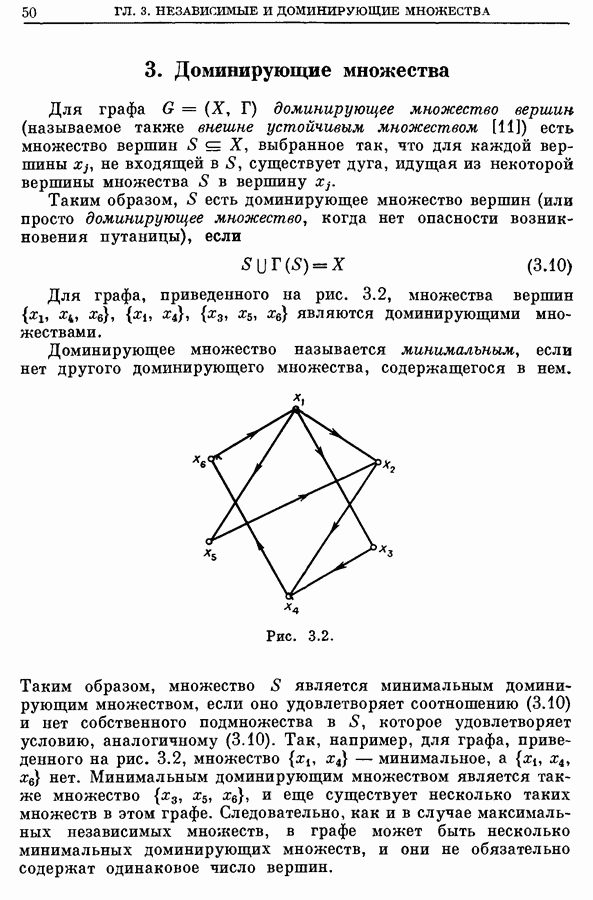
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
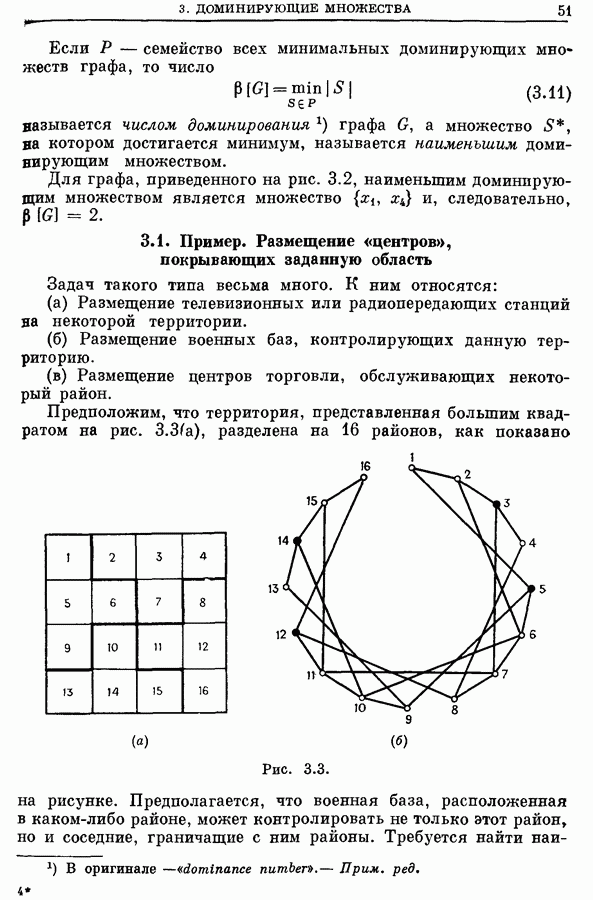
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
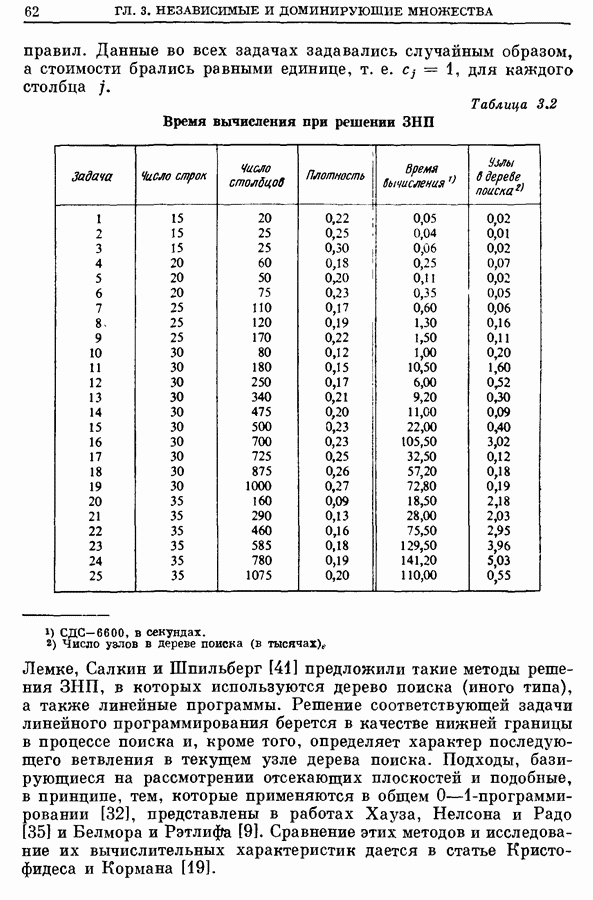
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
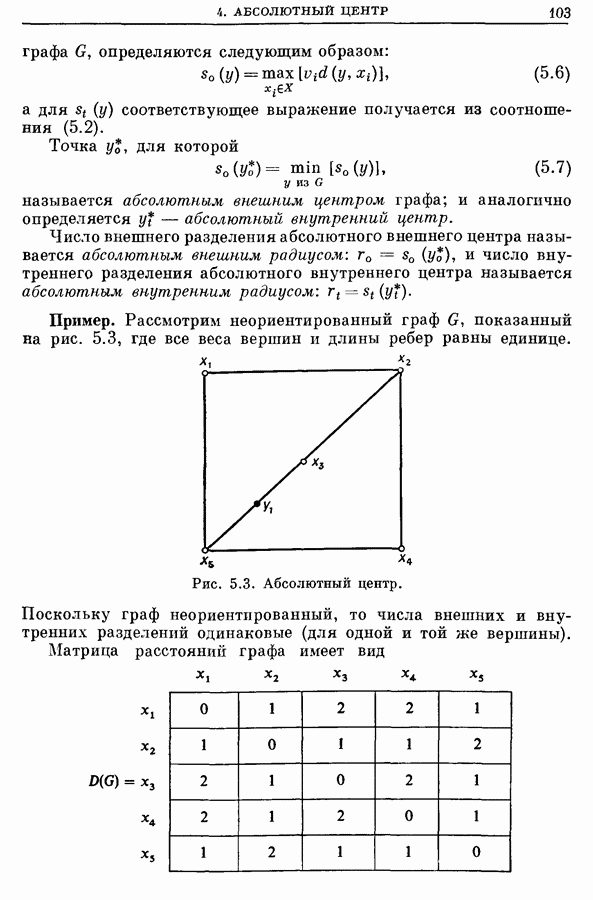
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
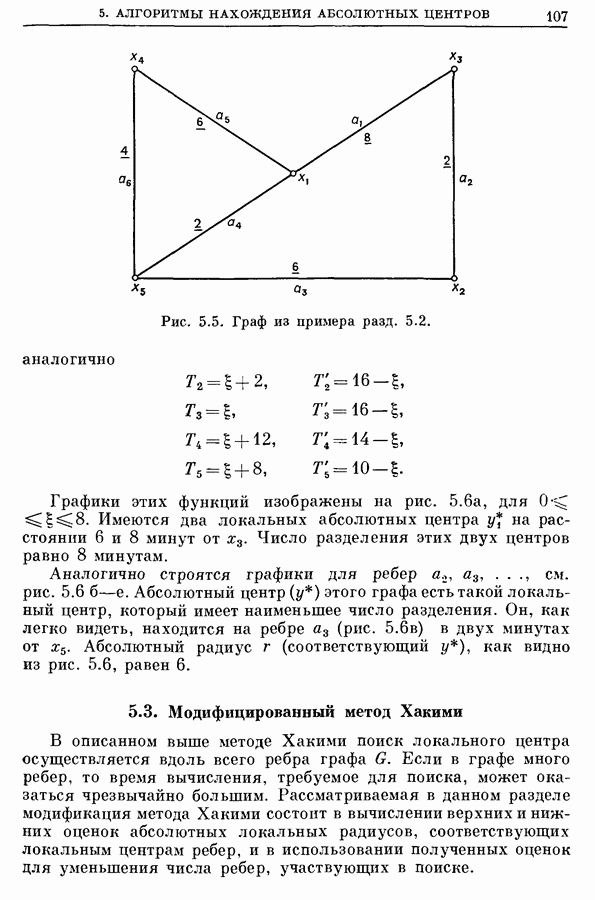
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
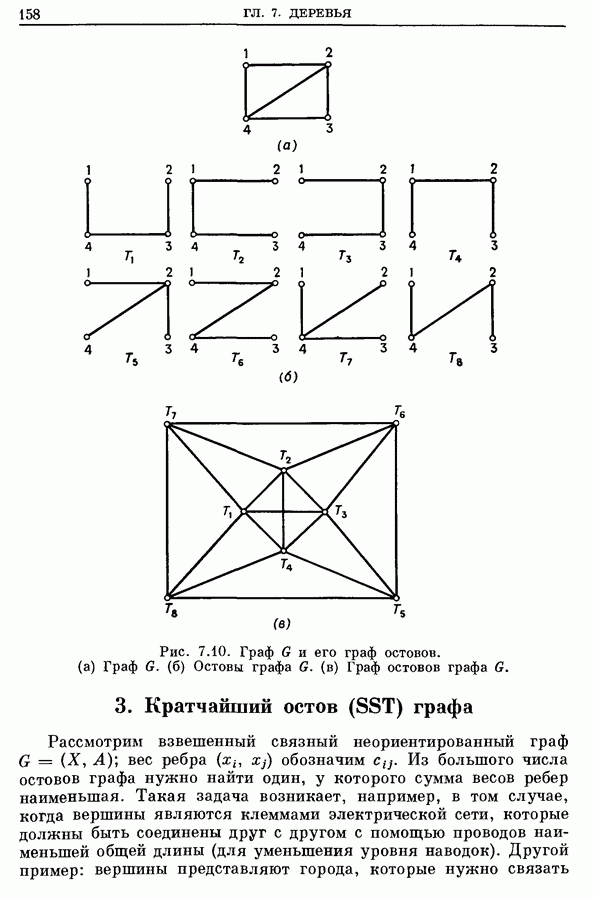
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
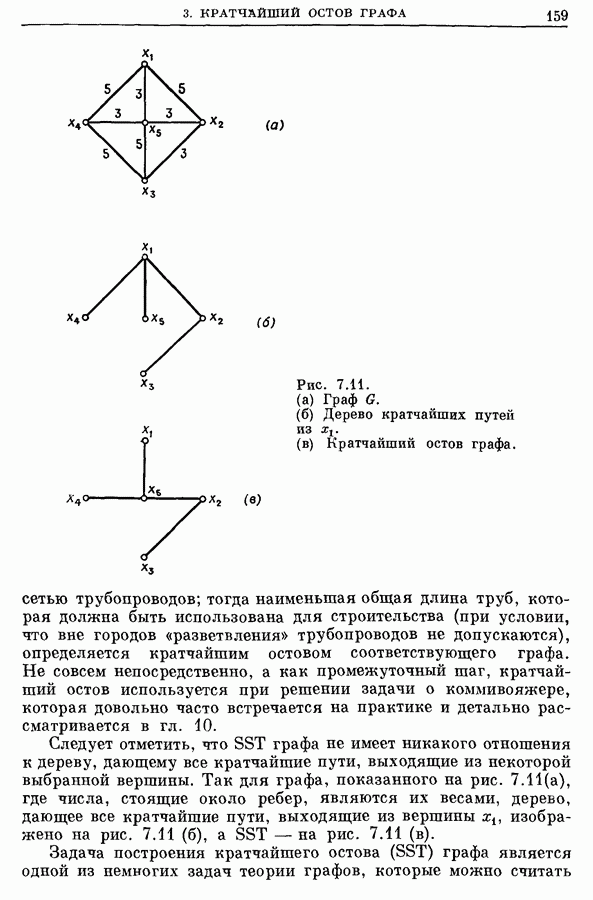
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
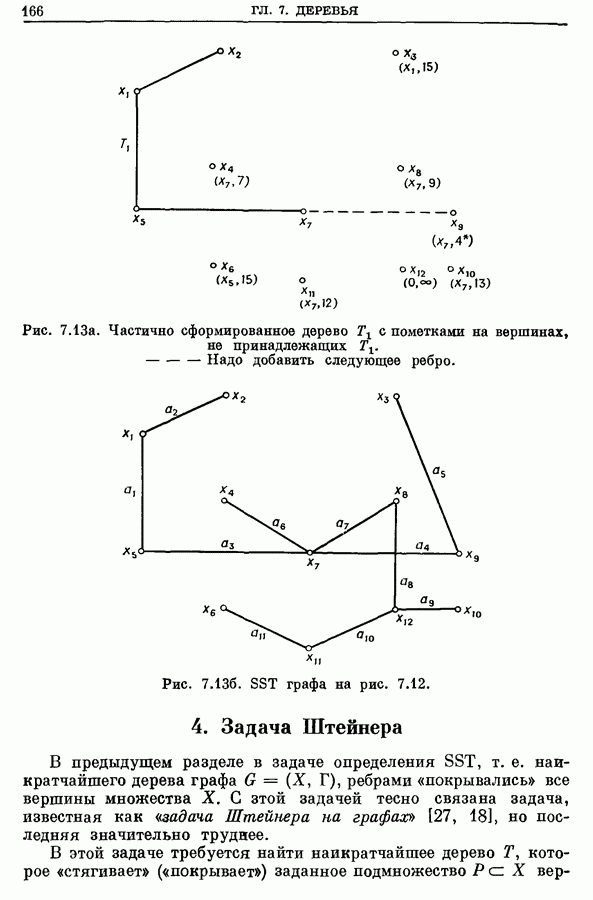
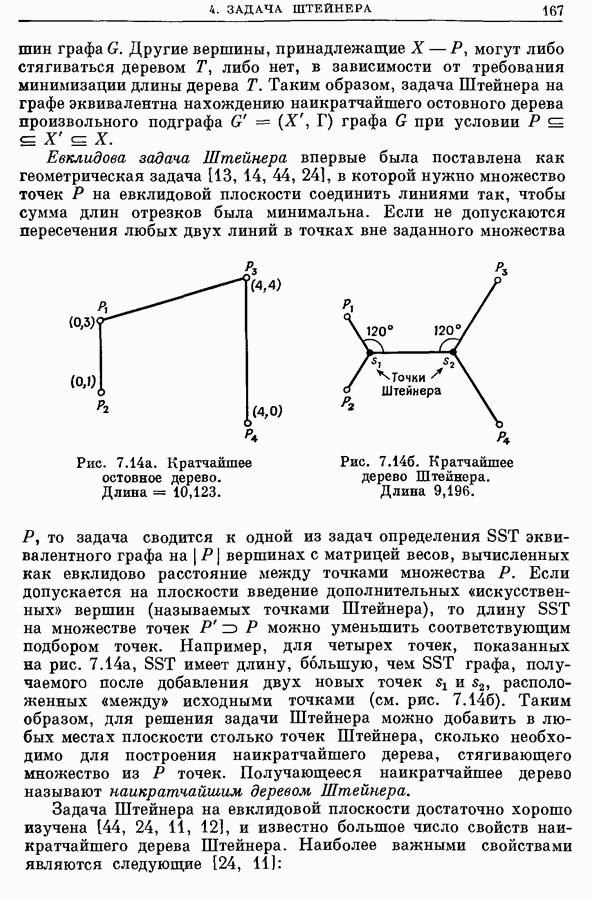
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
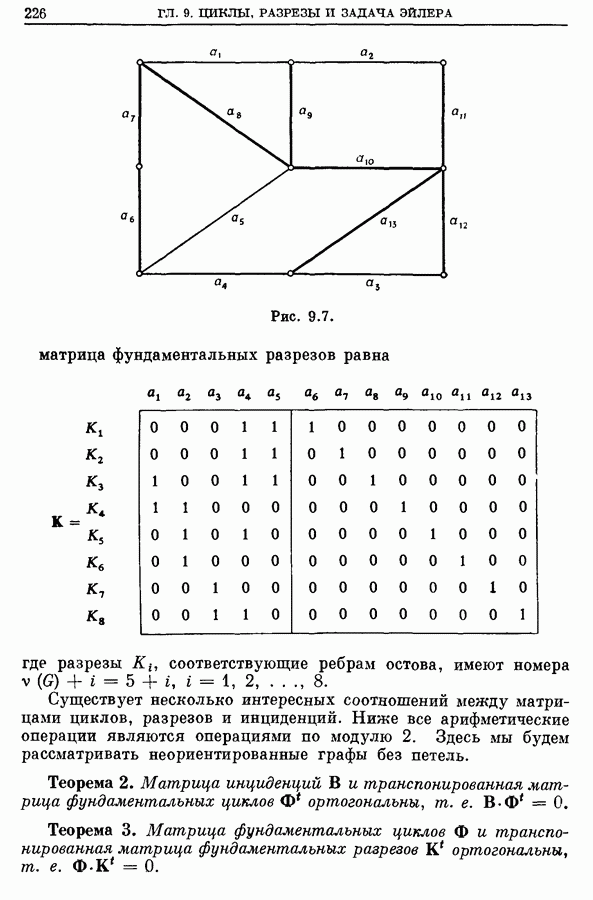
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
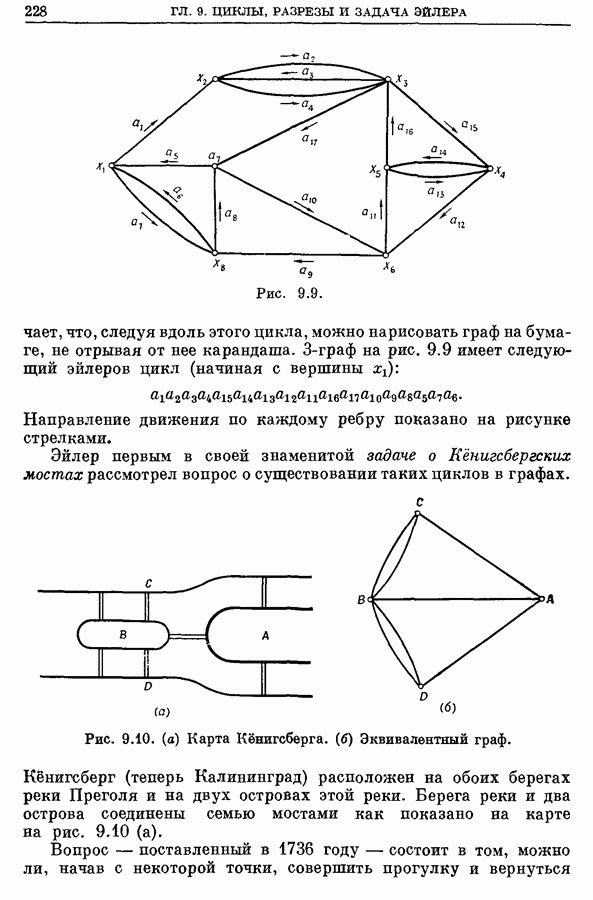
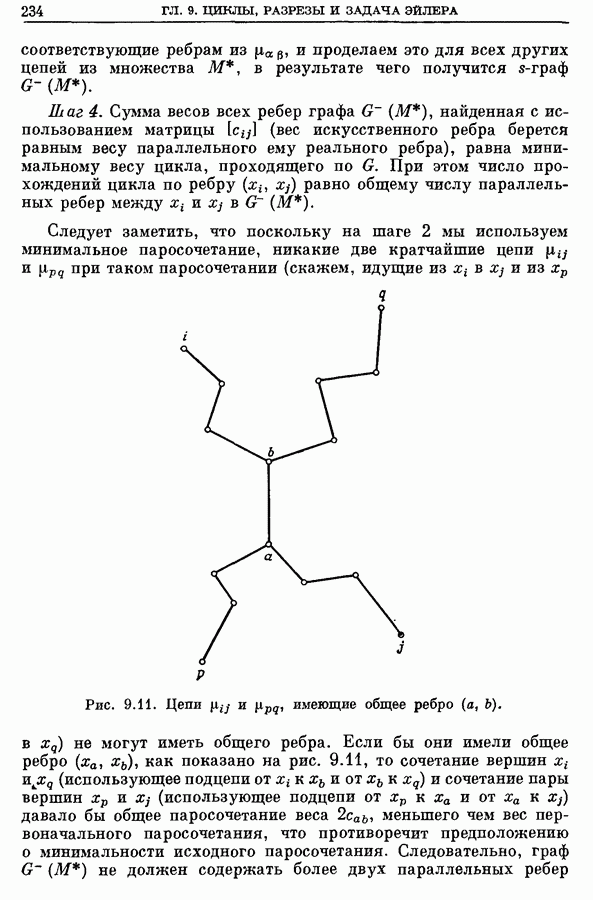
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
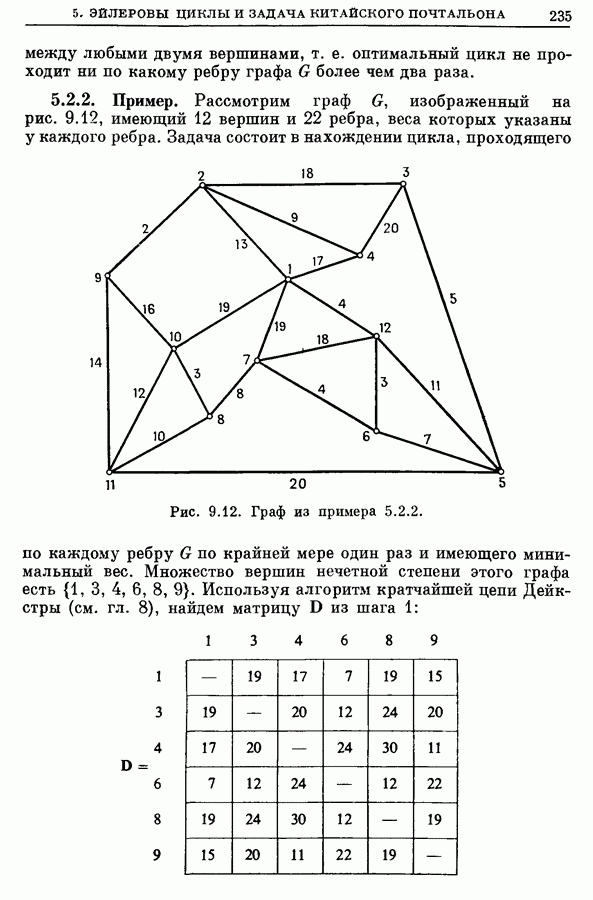
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
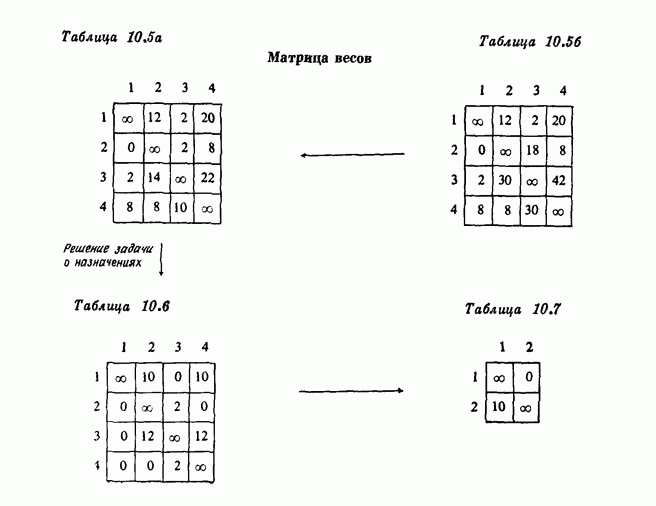
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
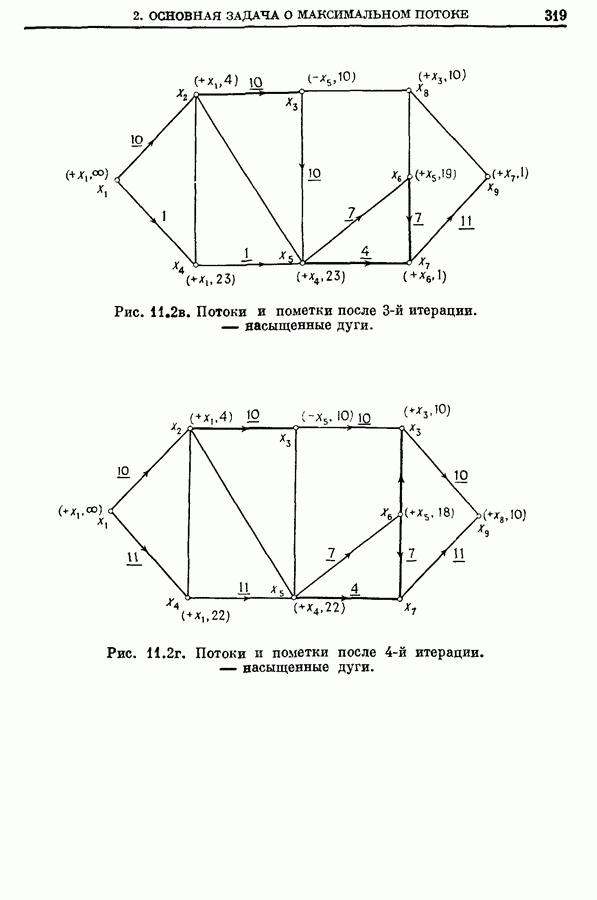
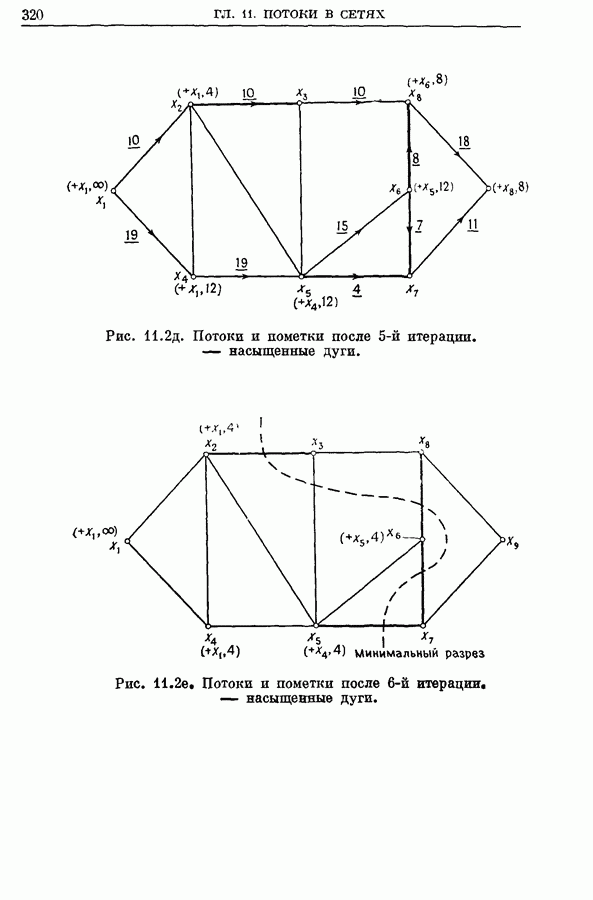
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
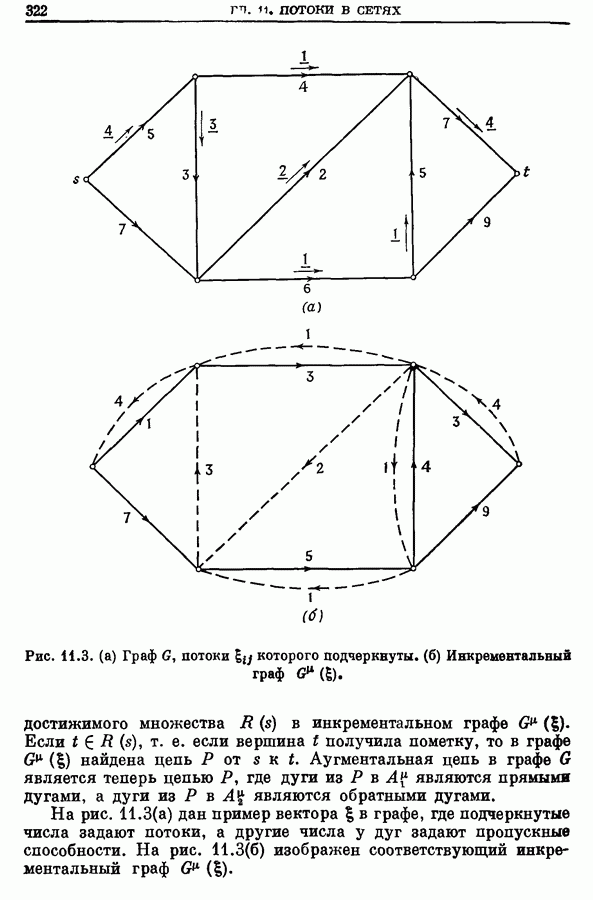
- 2.3. Инкрементальные графы
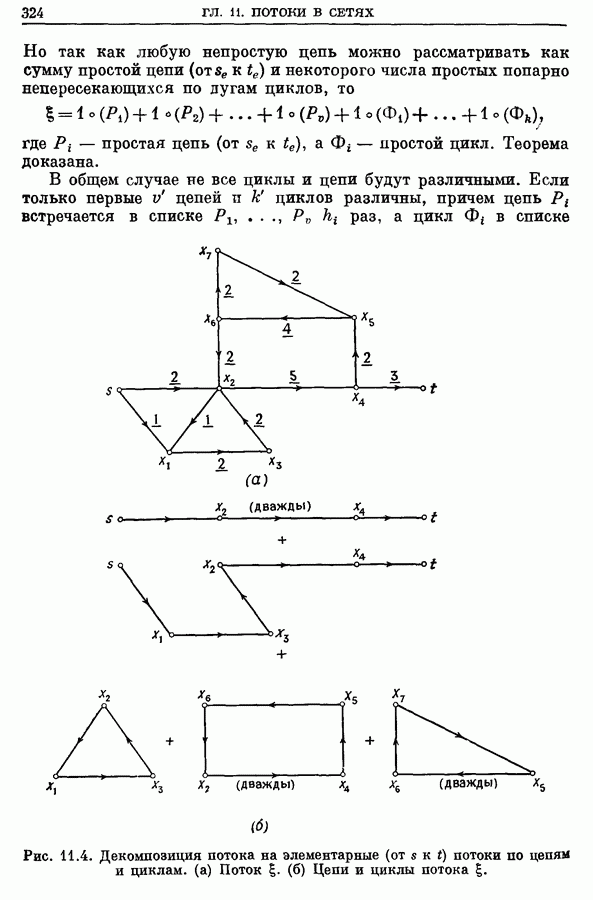
- 2.4. Декомпозиция потока
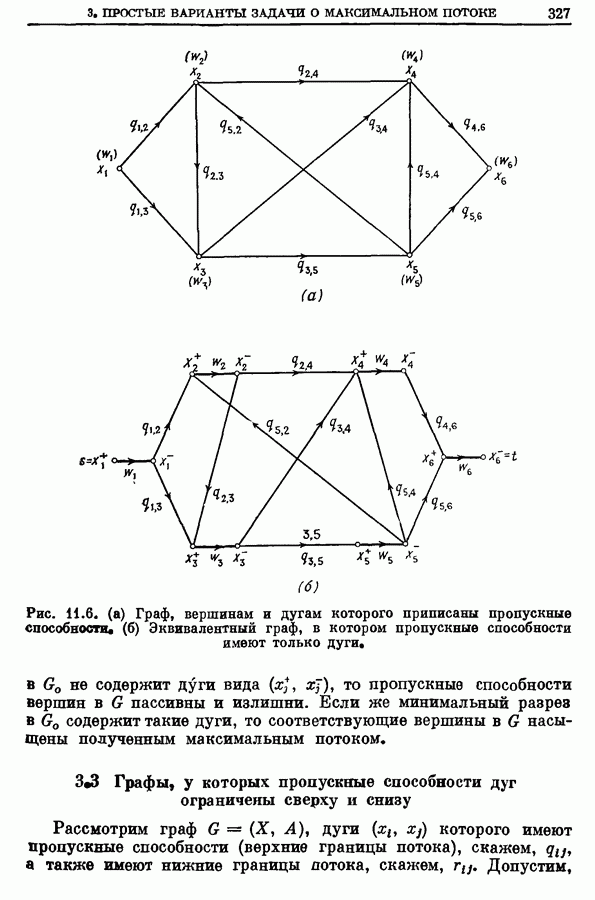
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
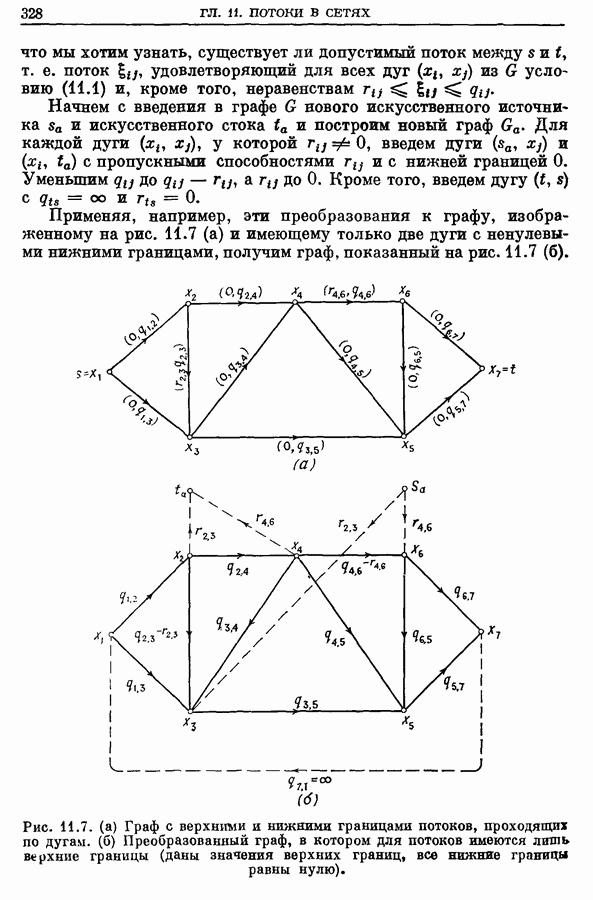
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
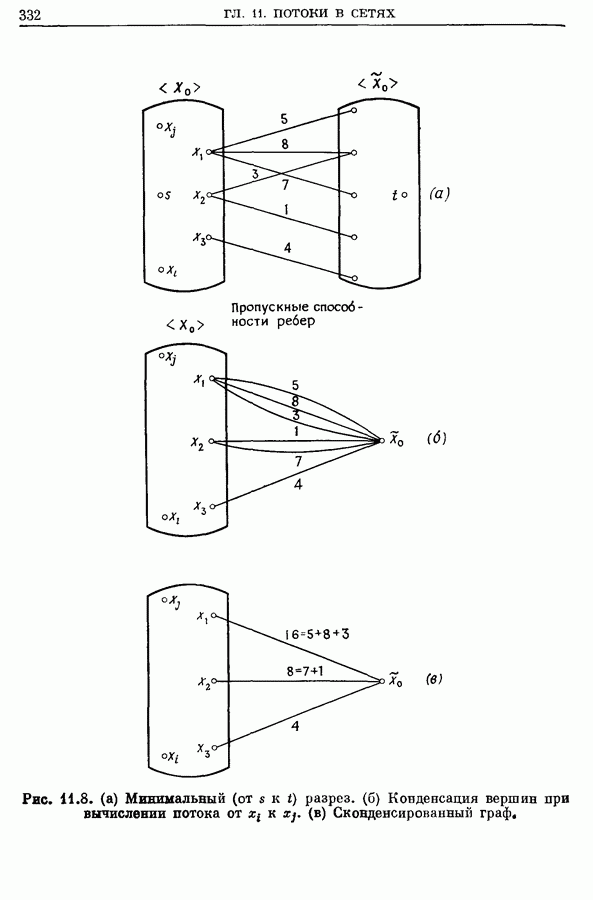
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
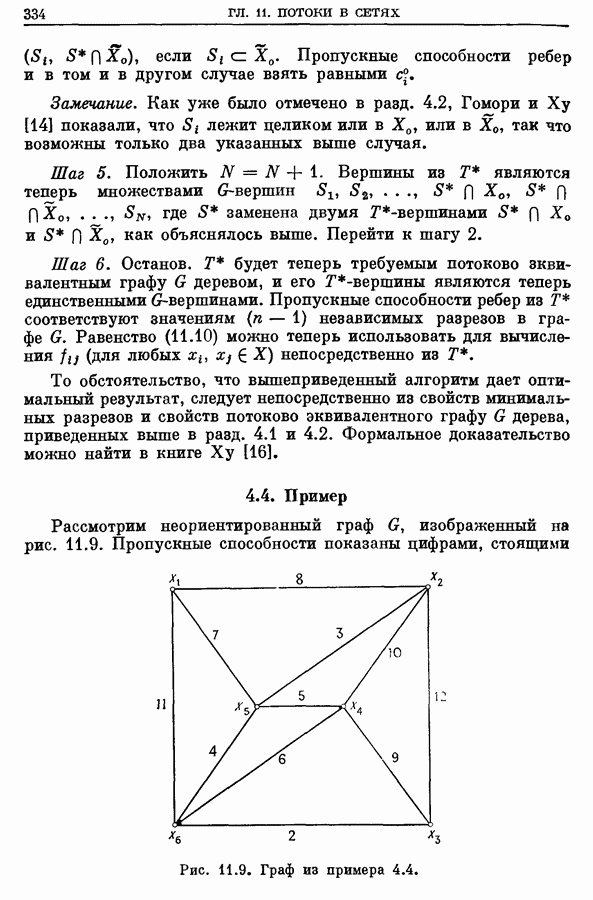
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
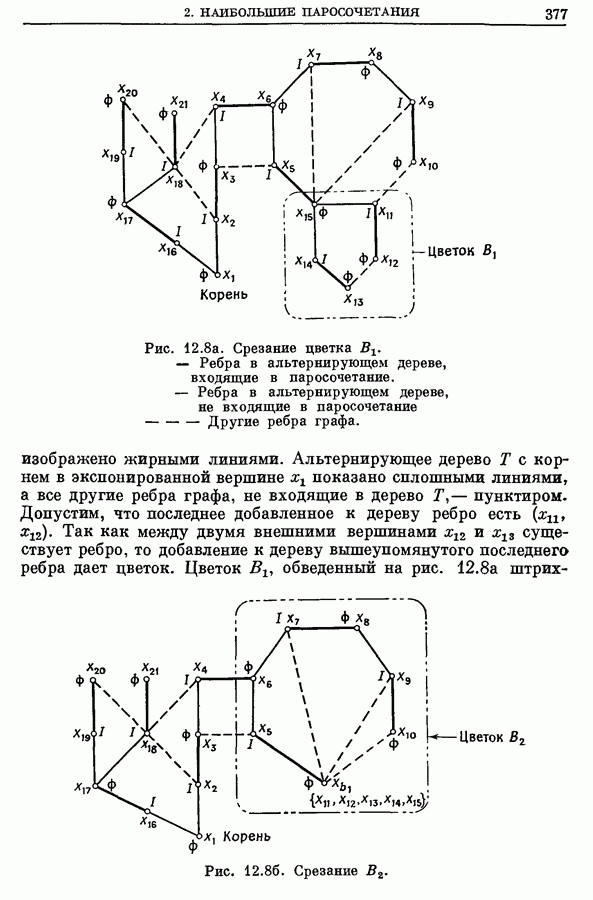
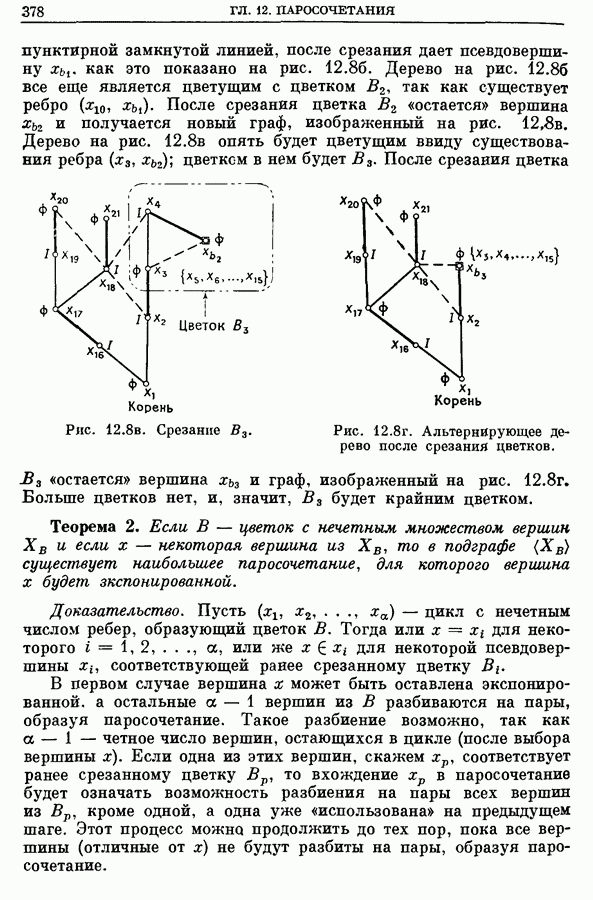
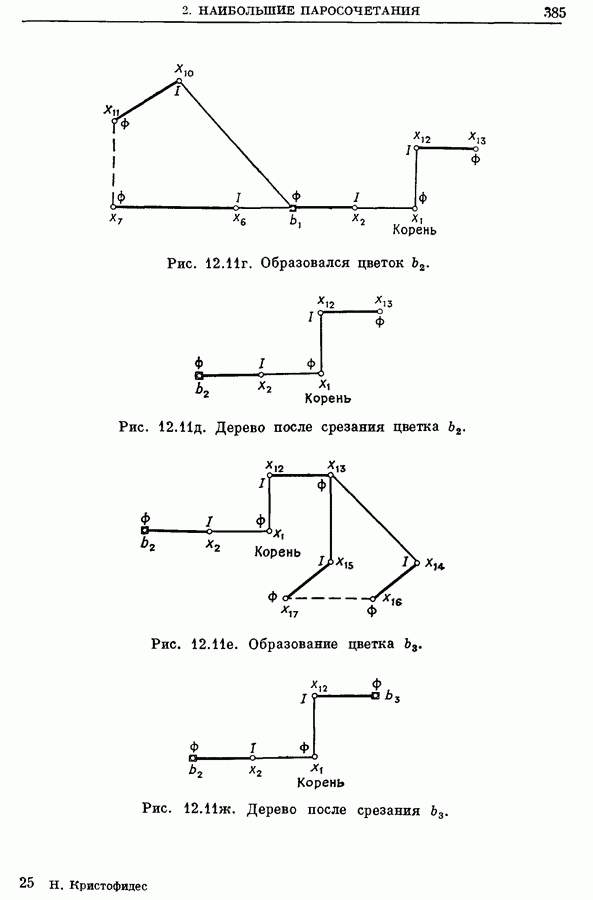
- 2.2. Цветки
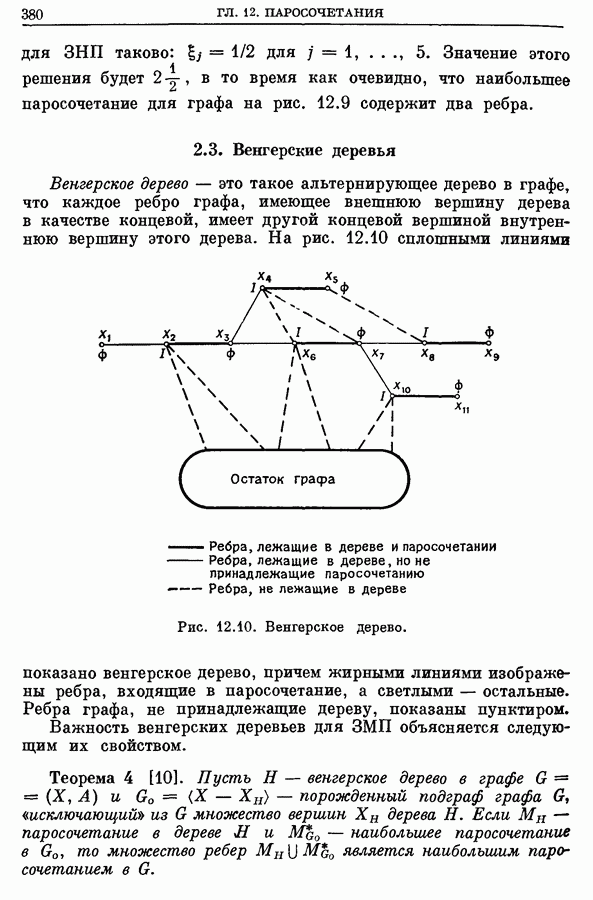
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
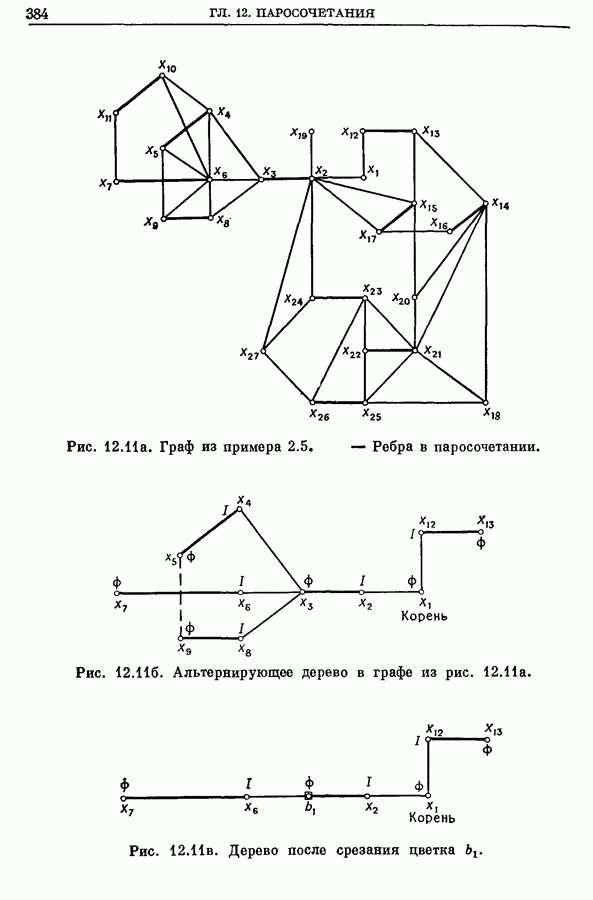
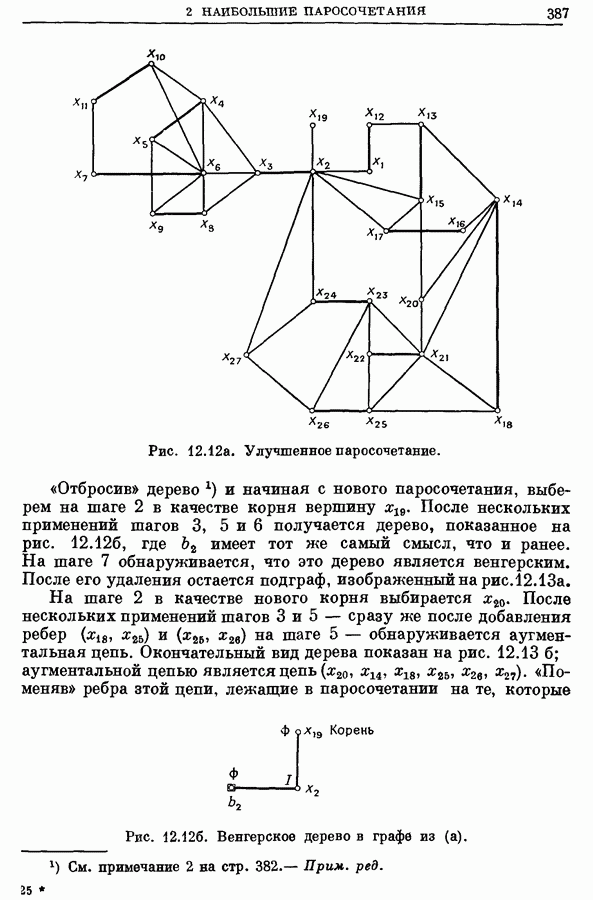
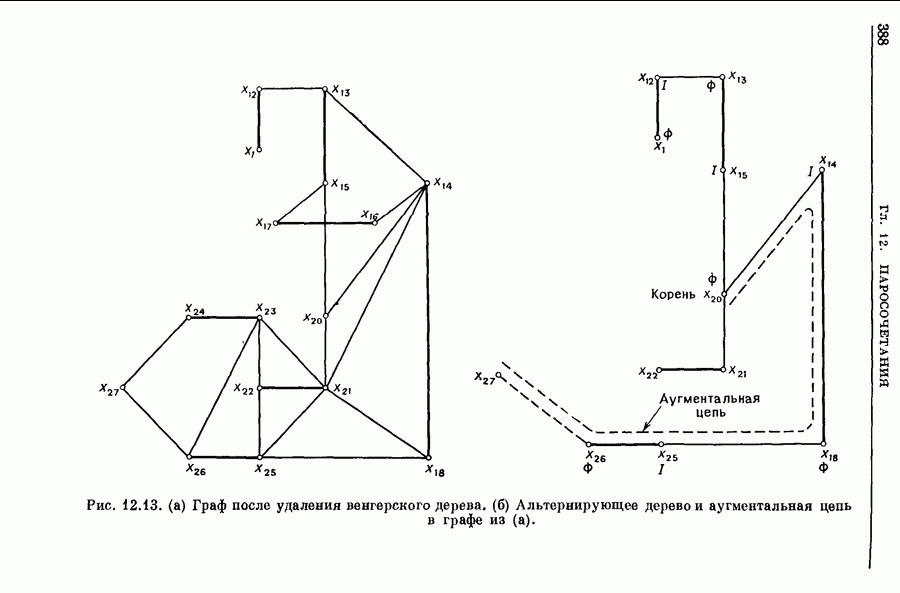
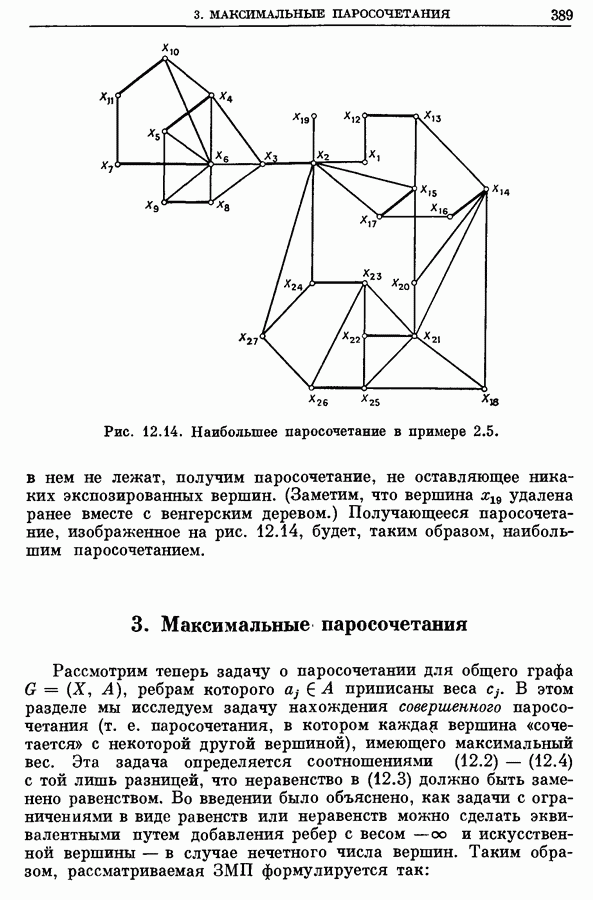
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
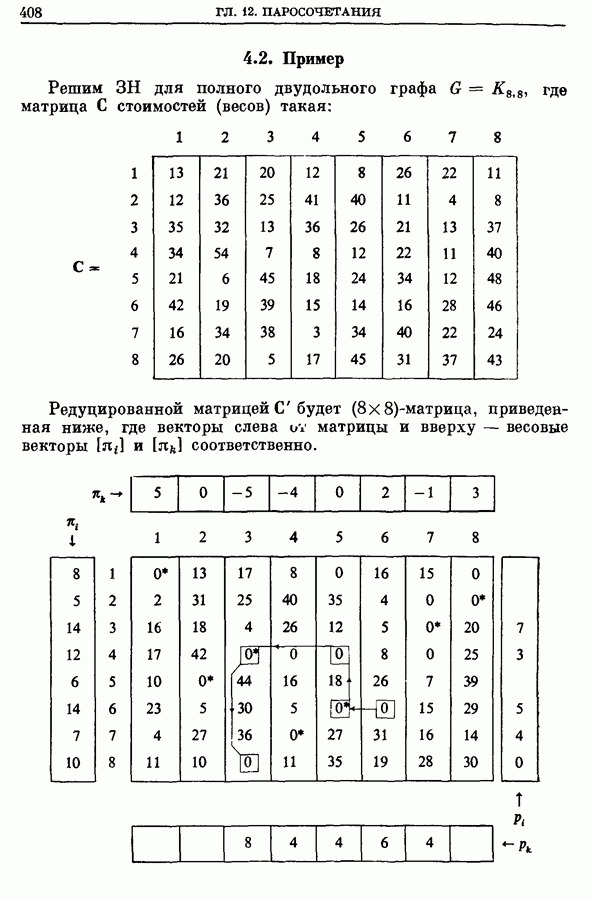
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
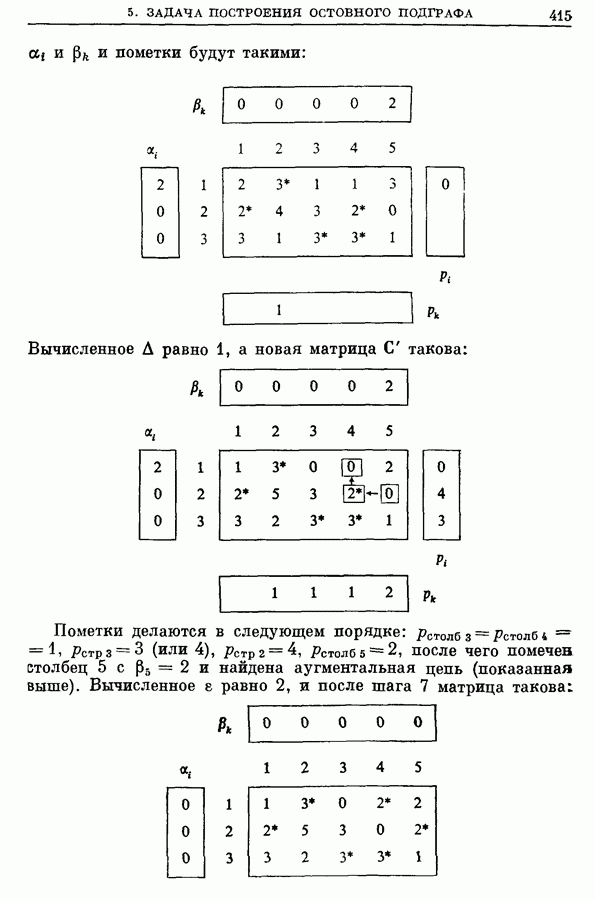
- 5.2. Пример
- 6. Задача о покрытии
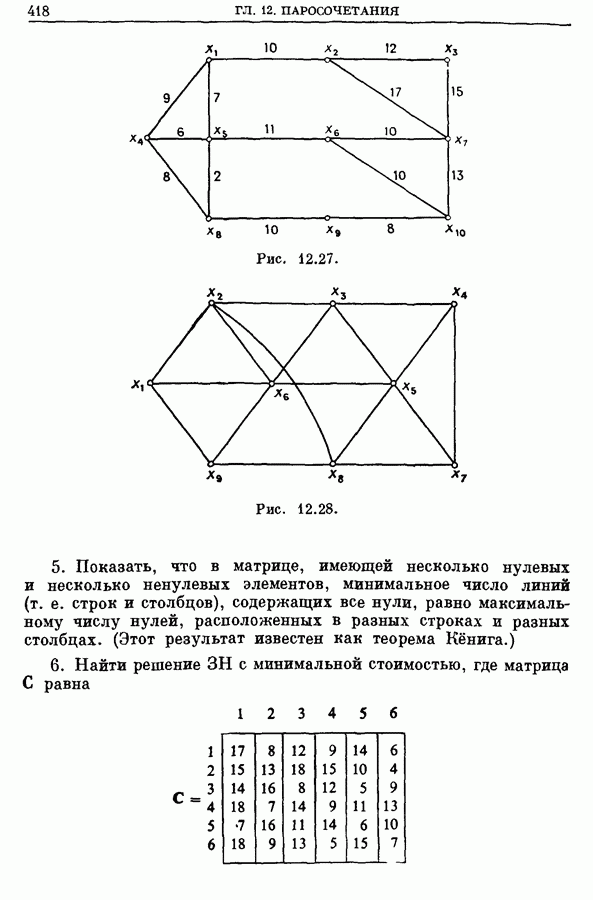
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
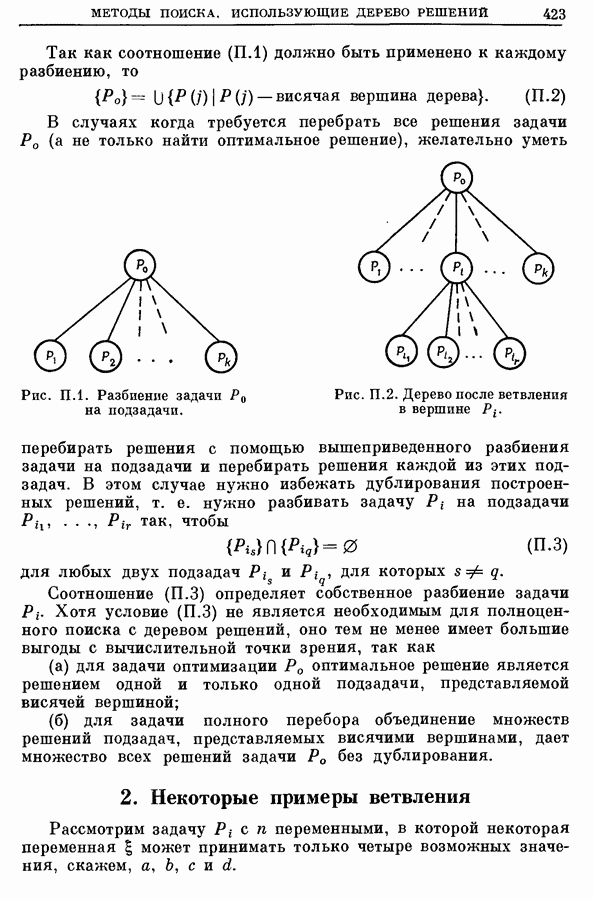
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
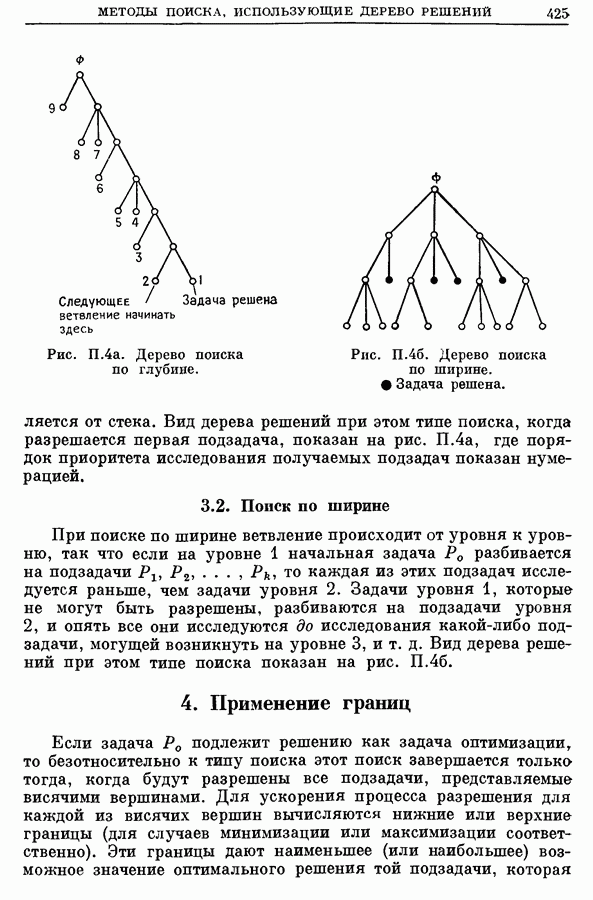
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления