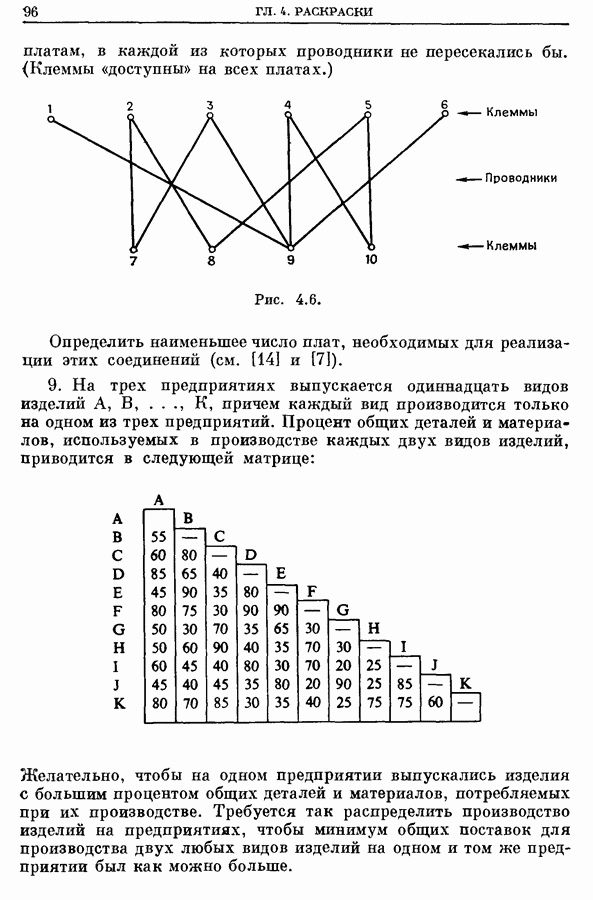
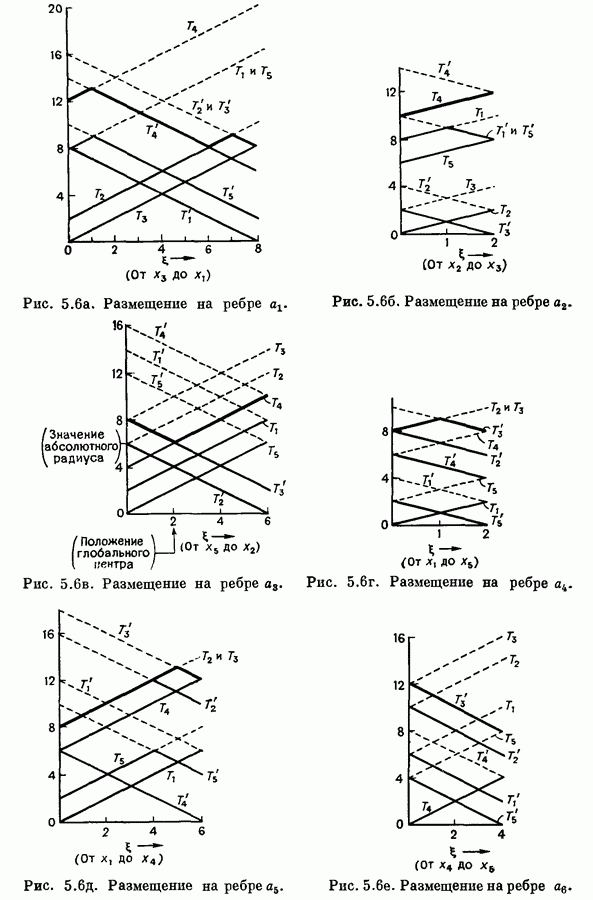
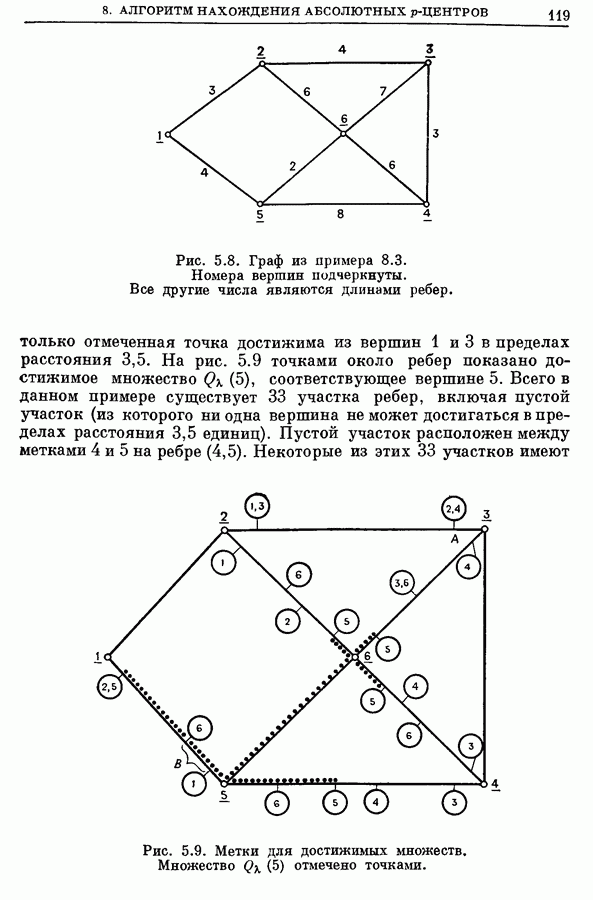
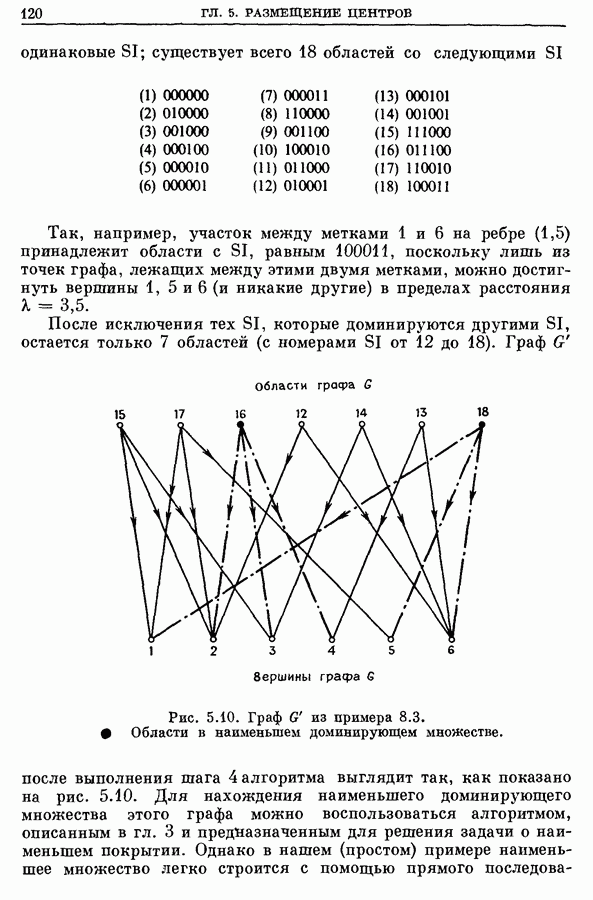
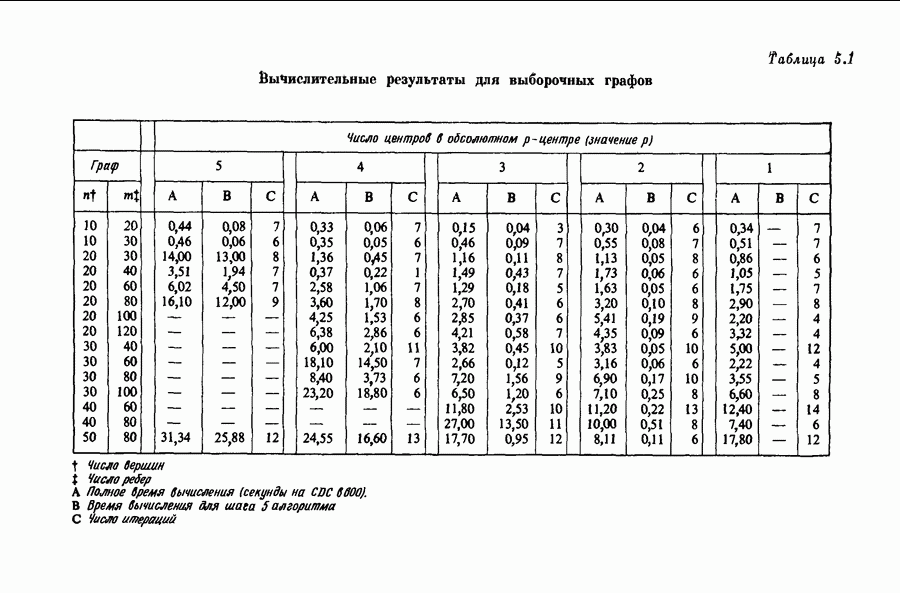
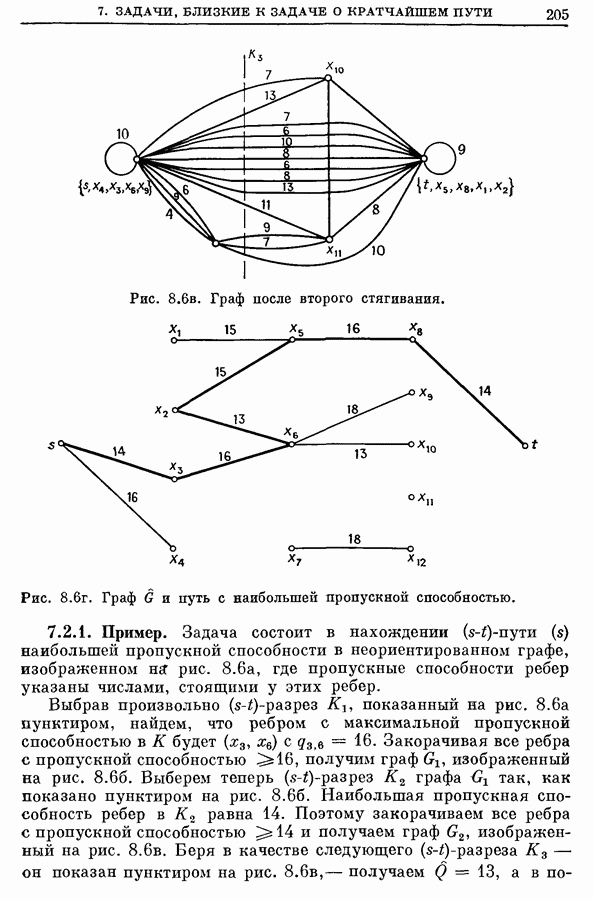
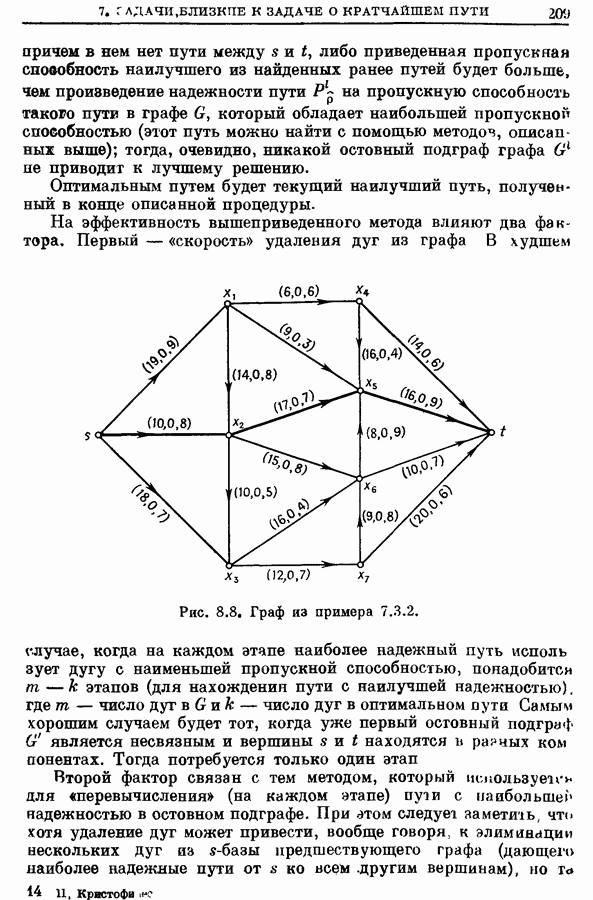
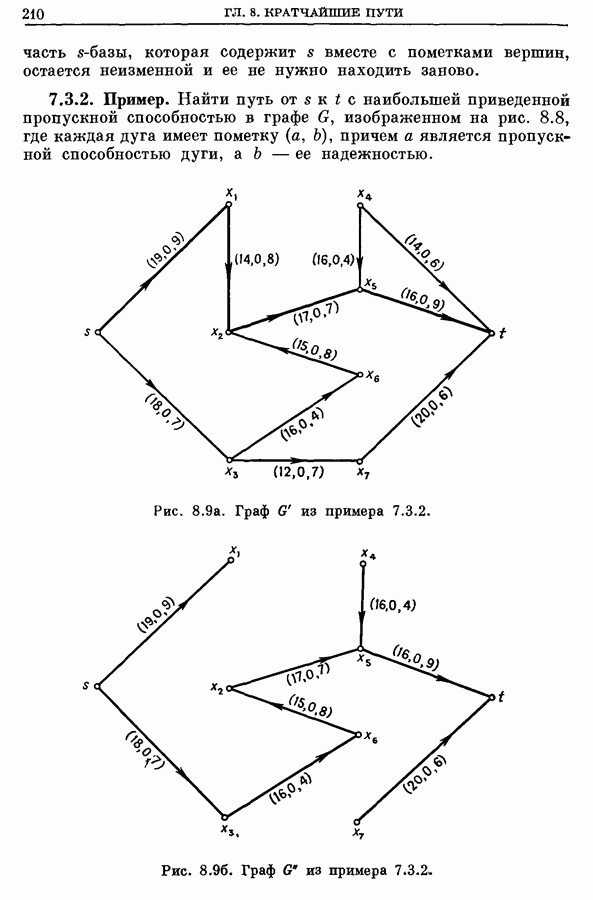
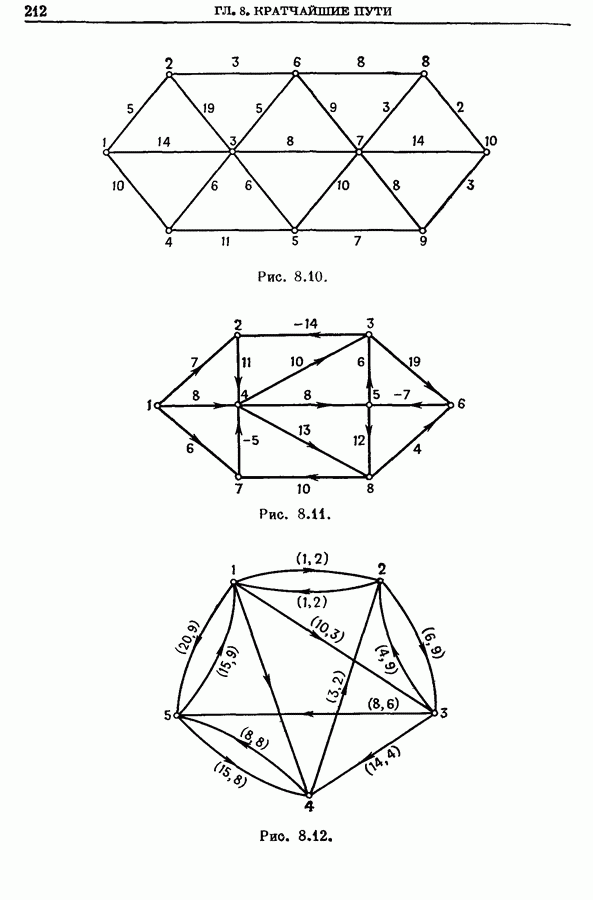
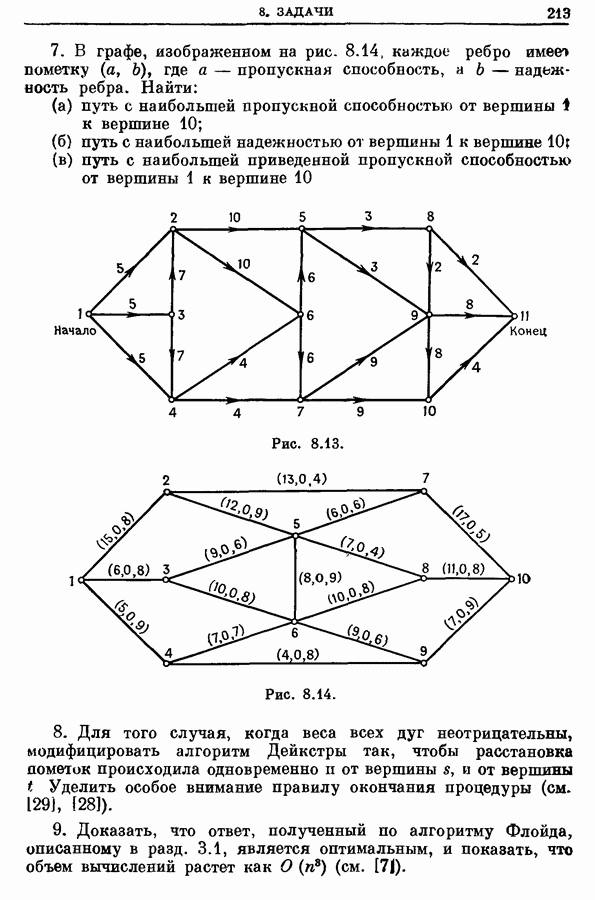
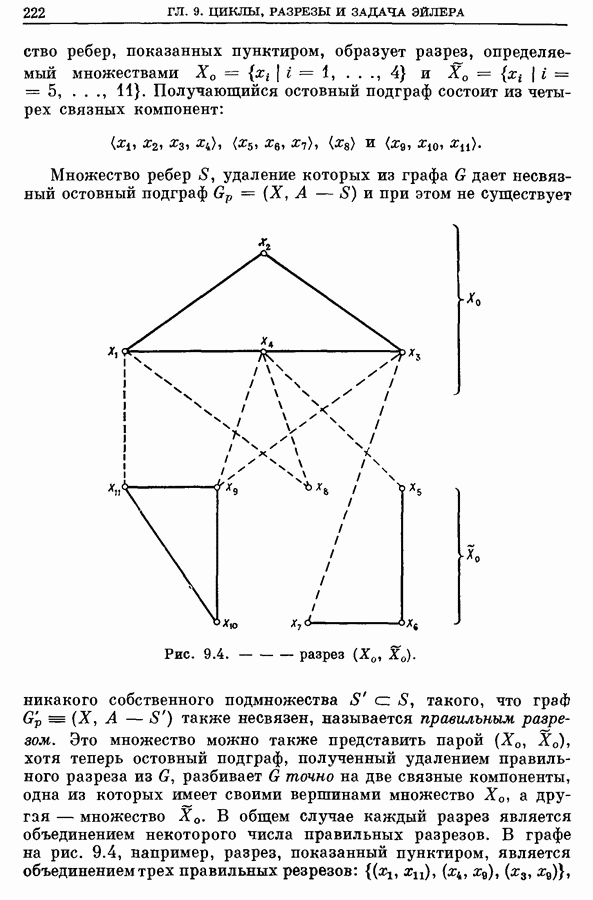
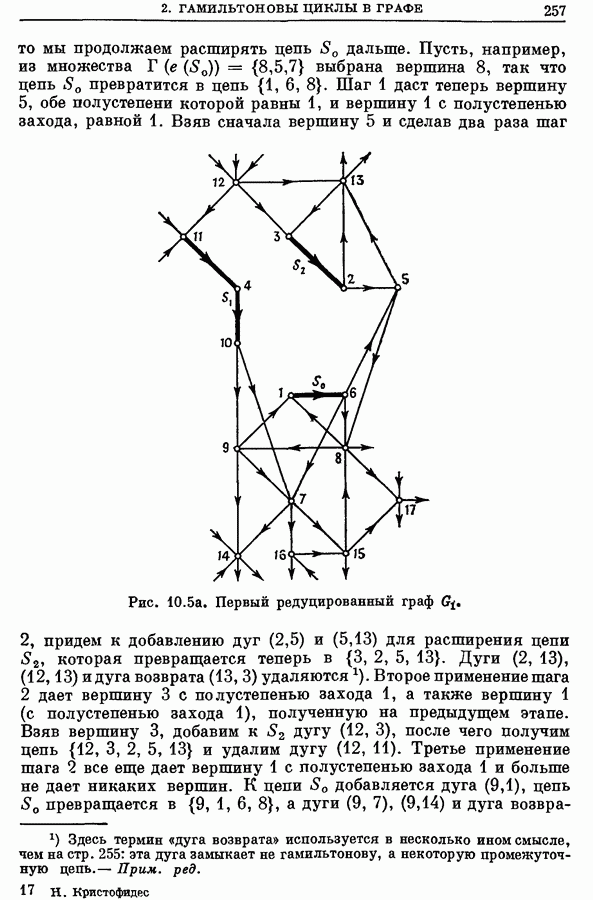
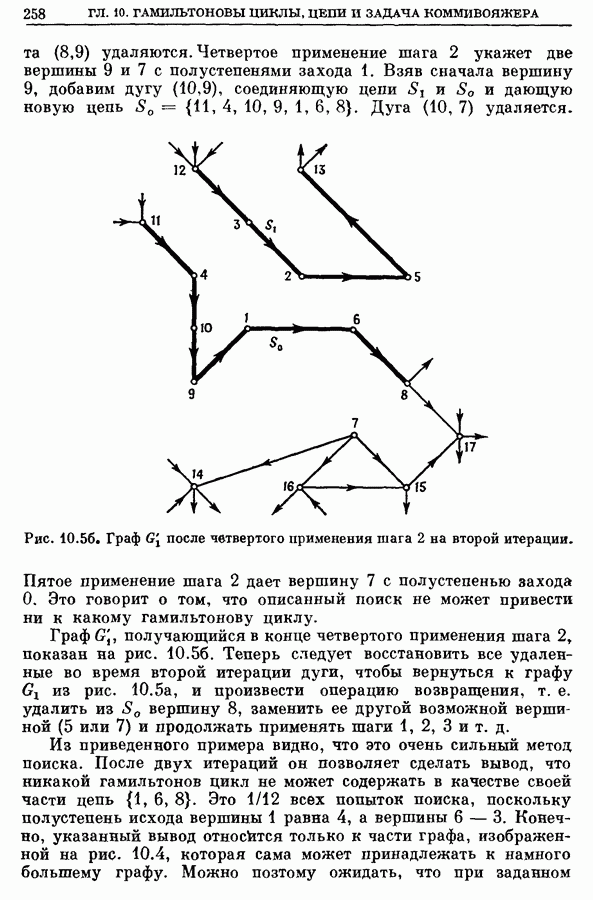
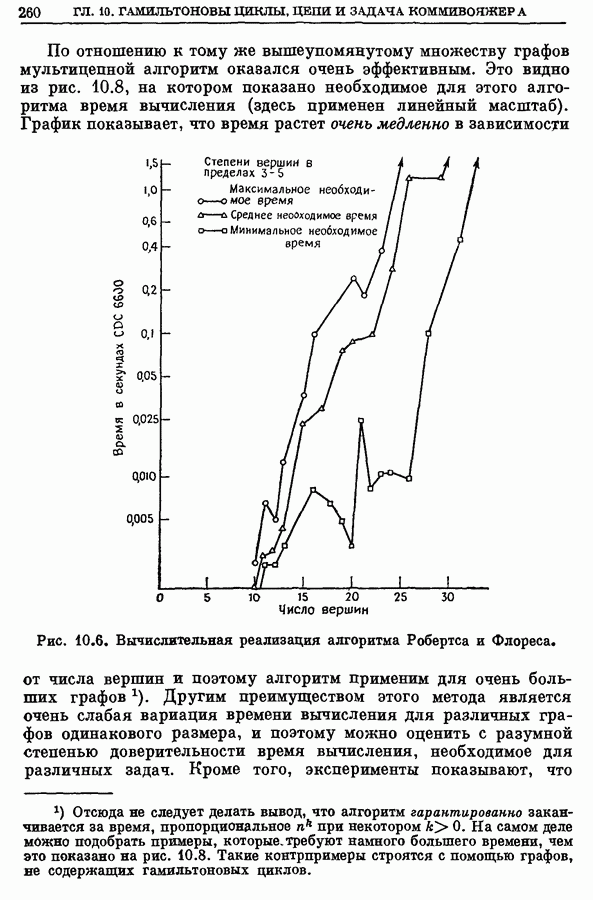
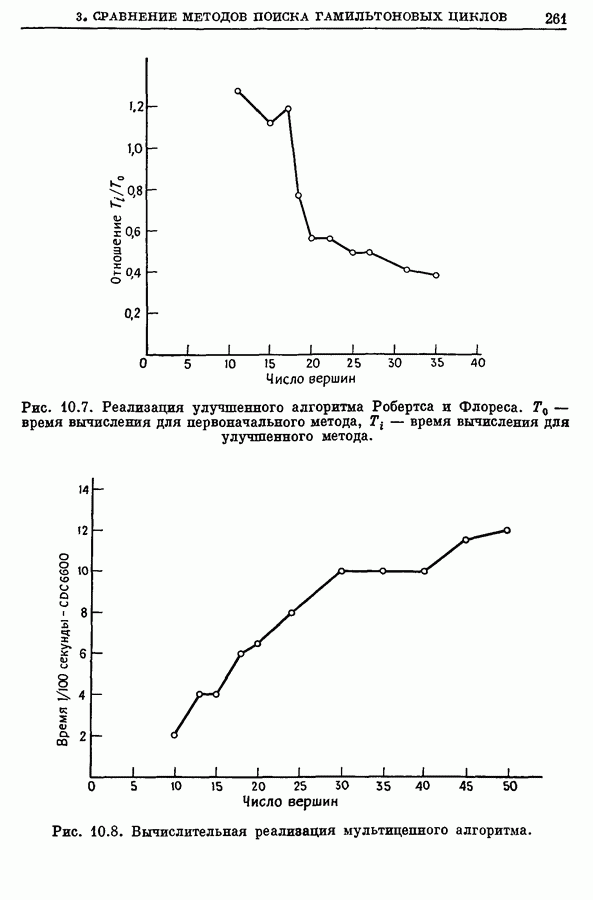
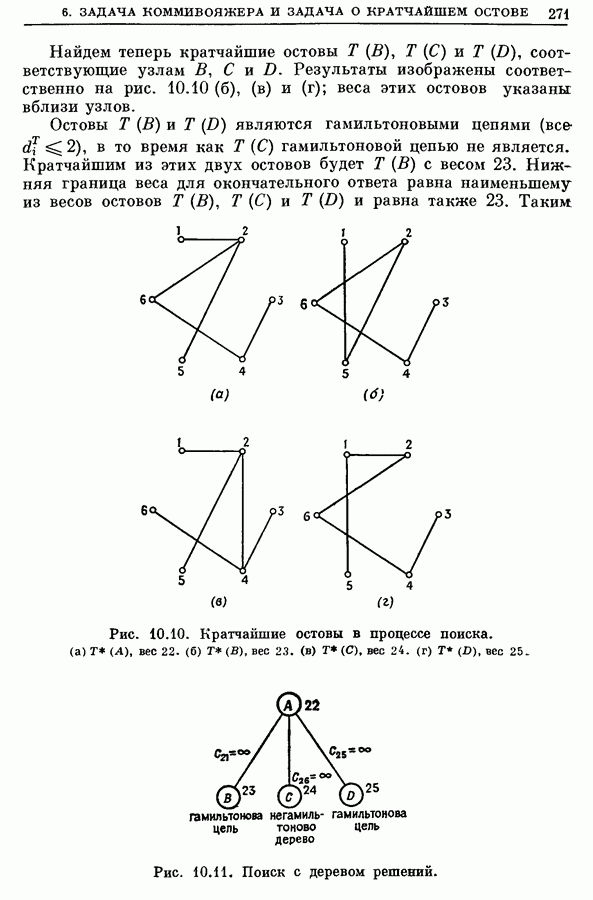
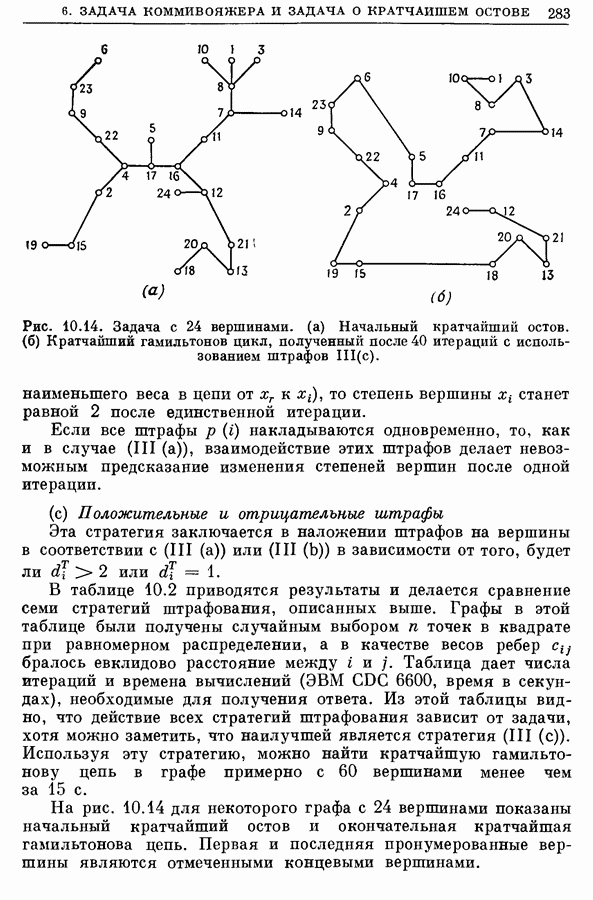
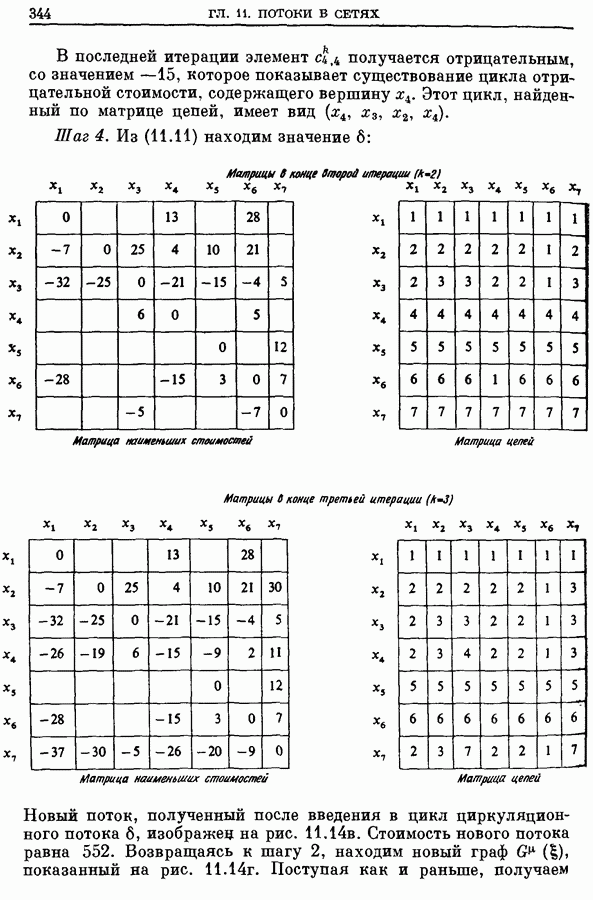
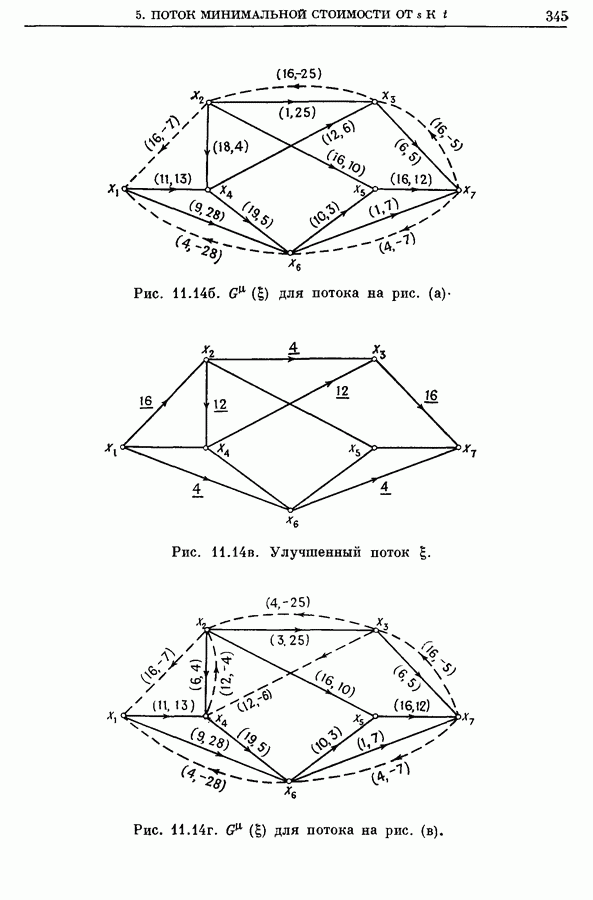
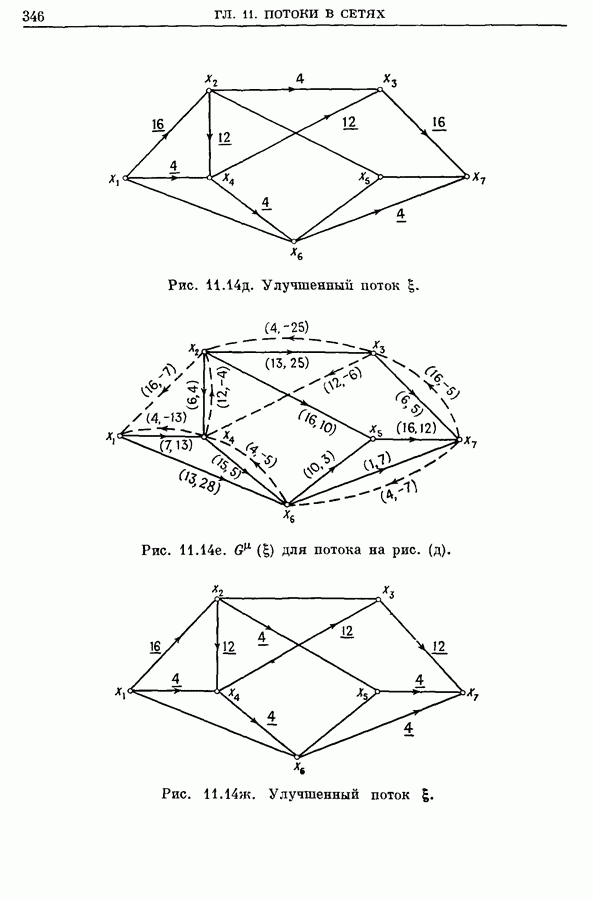
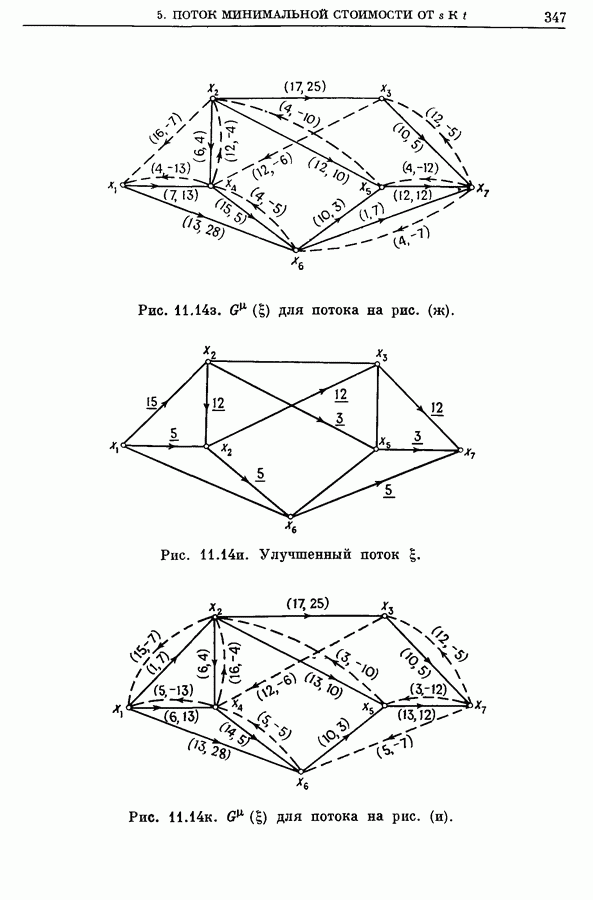
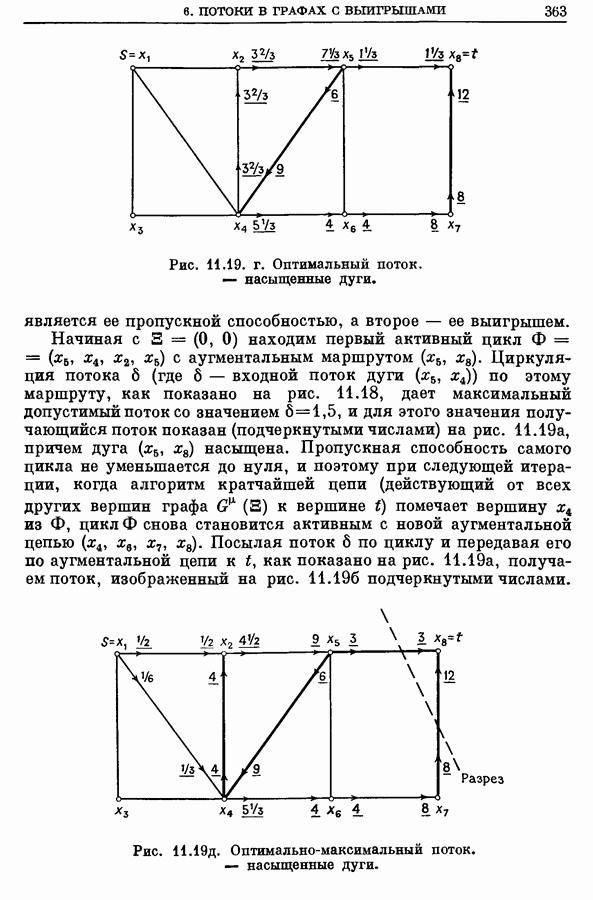
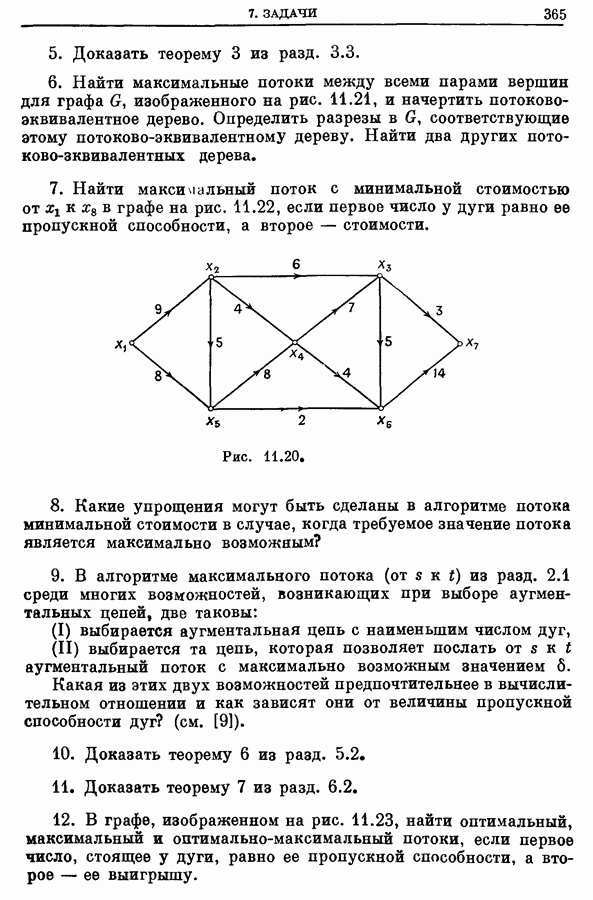
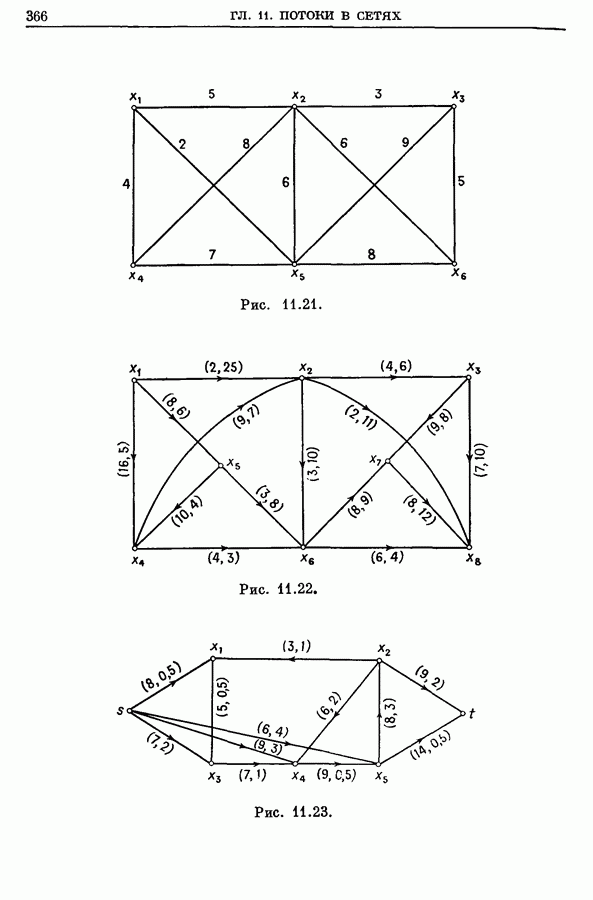
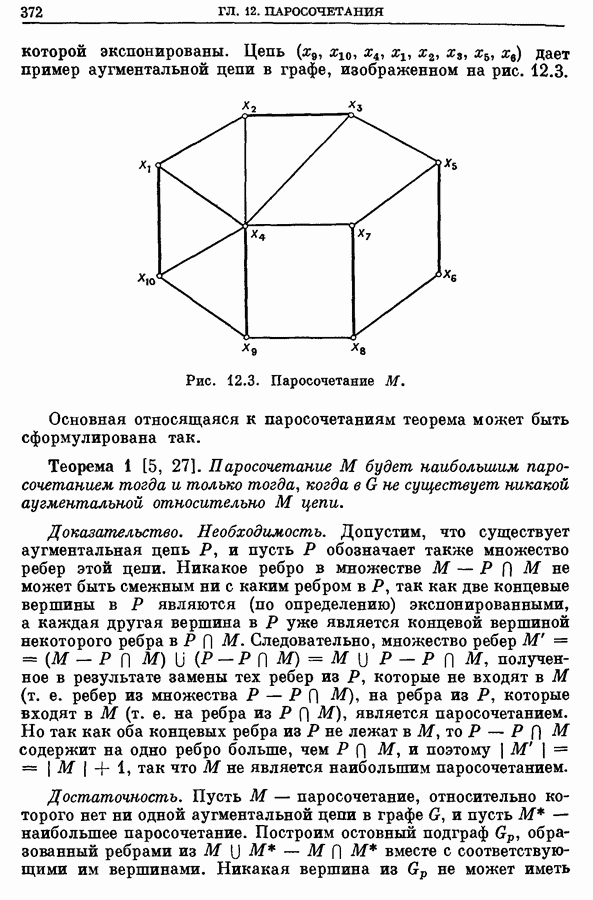
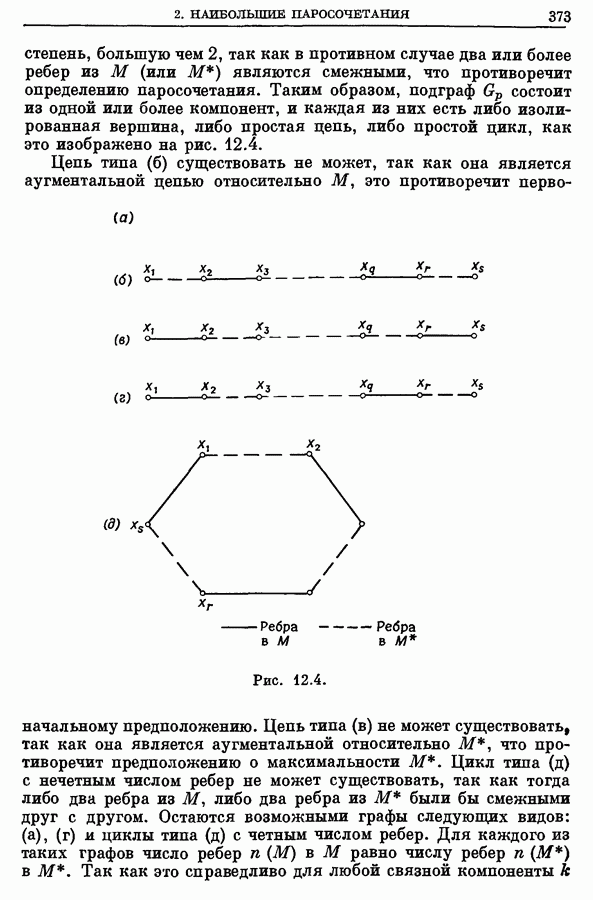
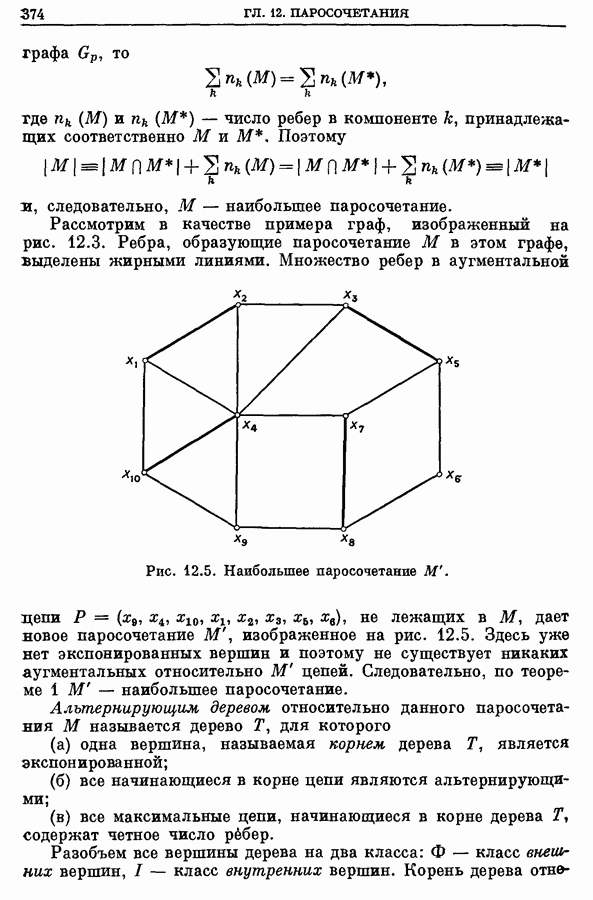
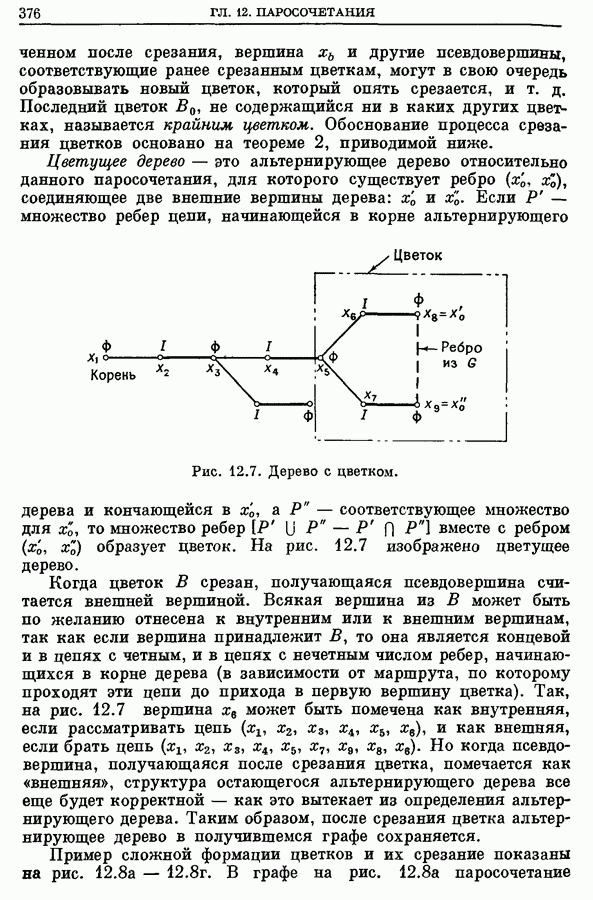
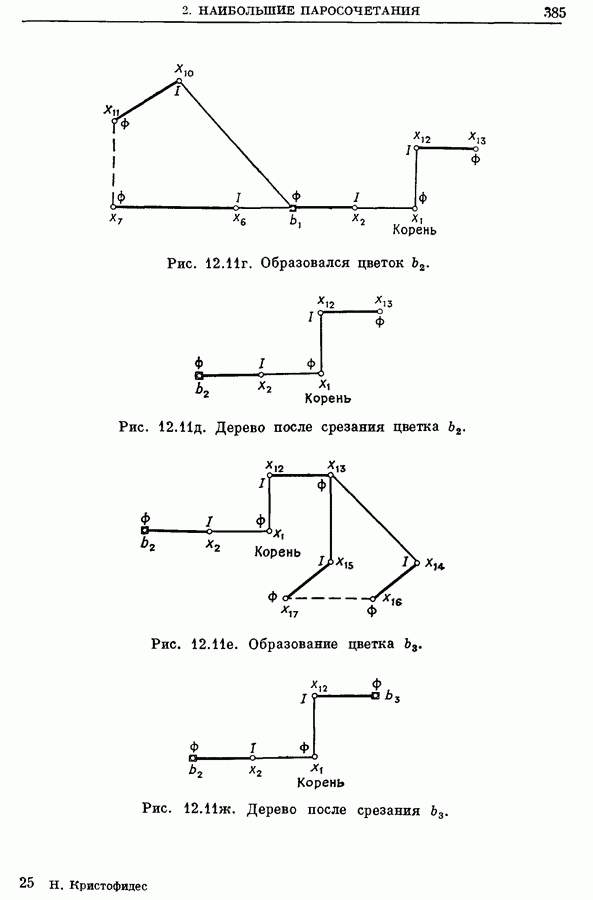
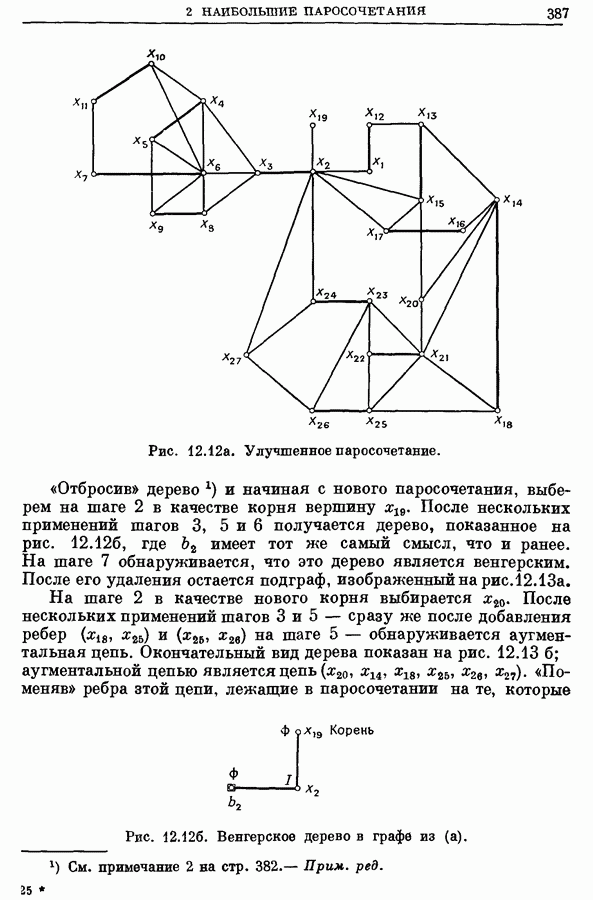
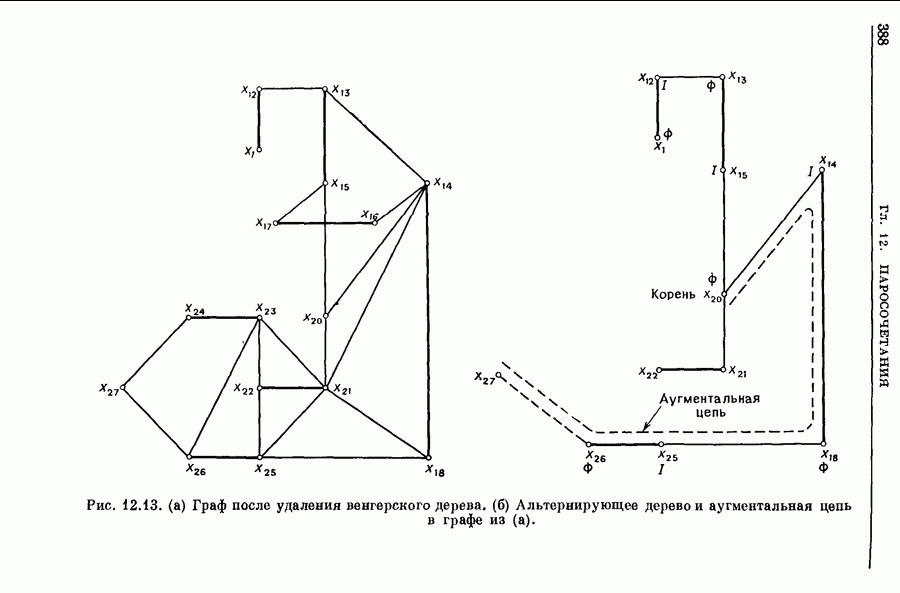
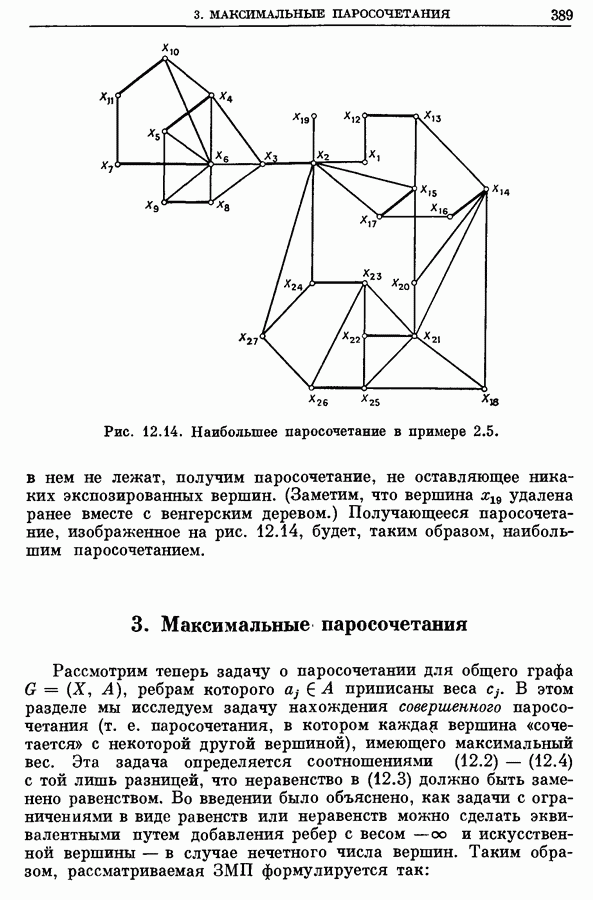
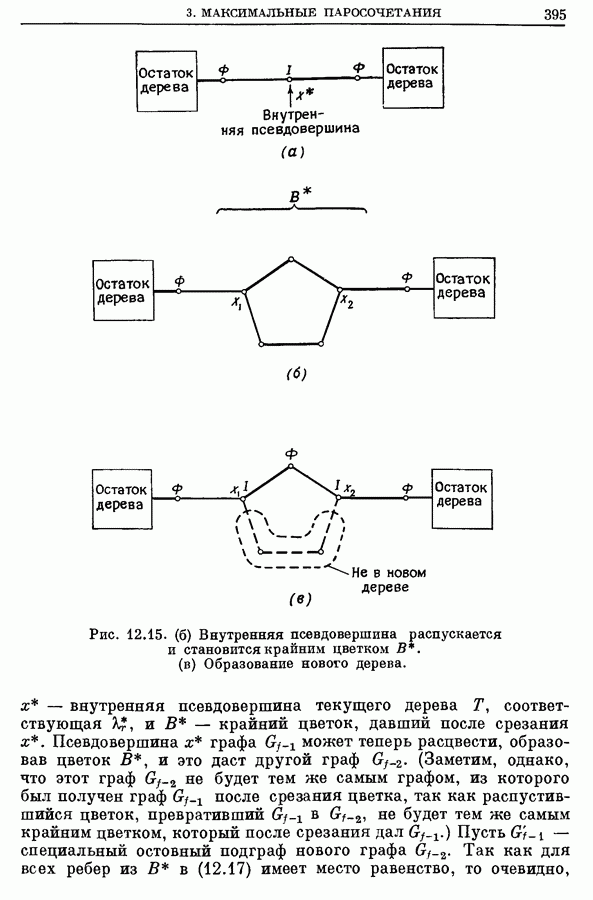
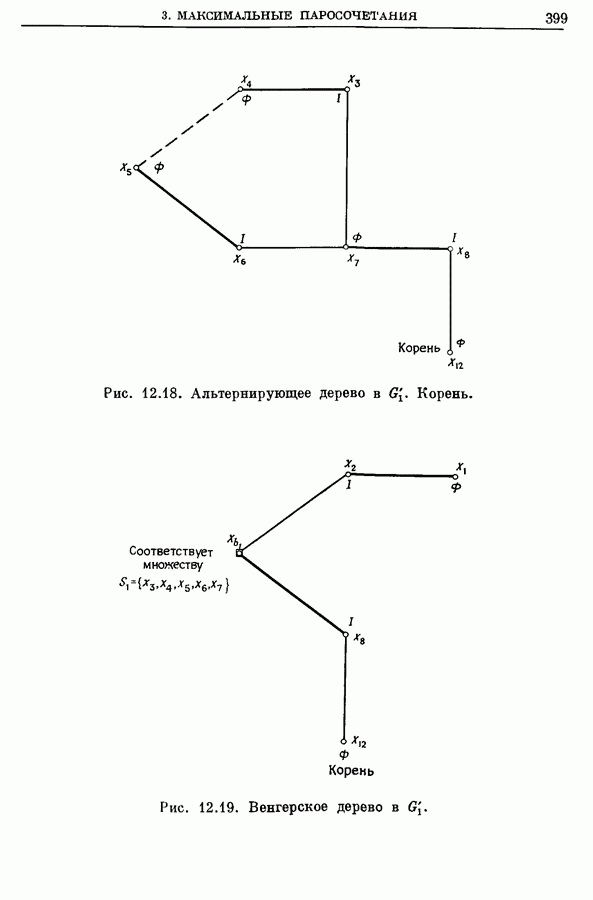
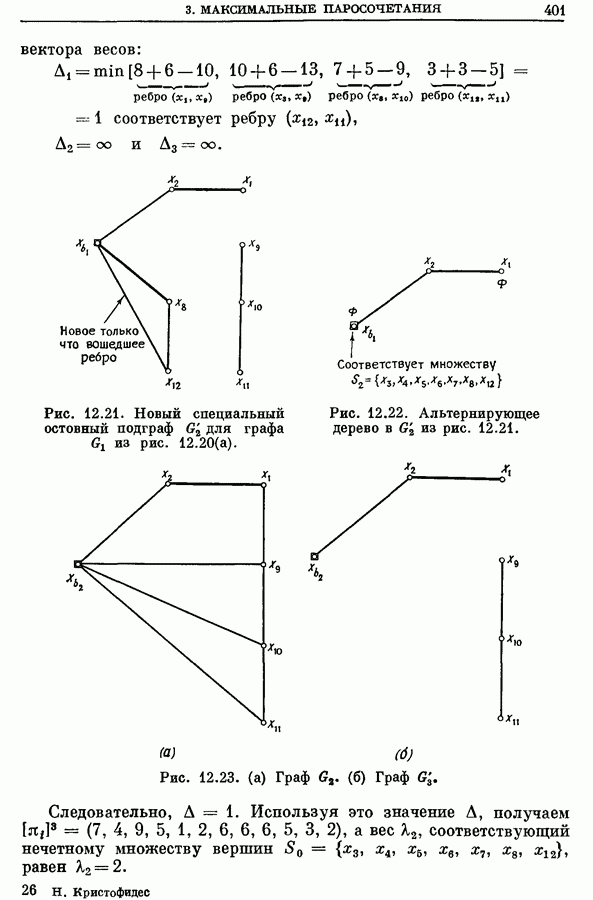
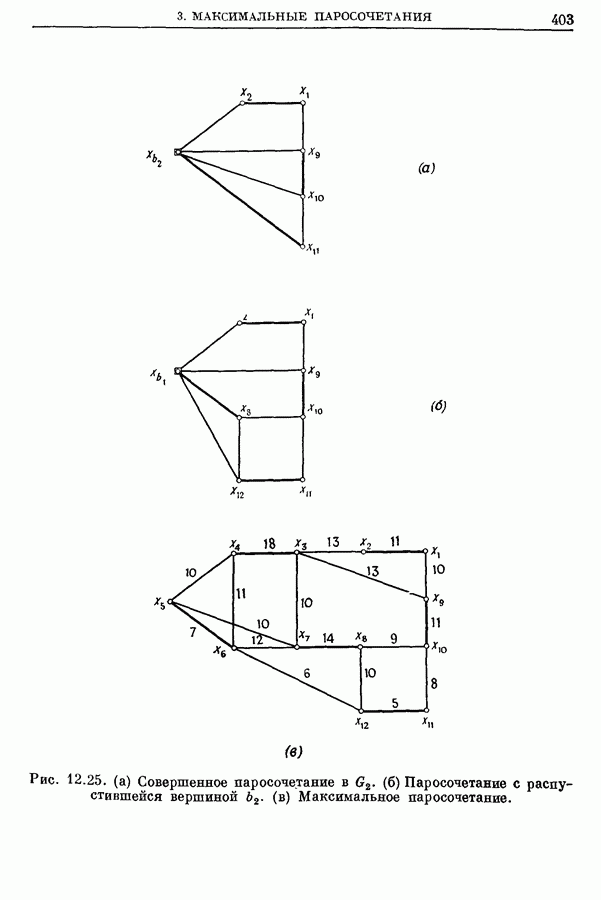
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
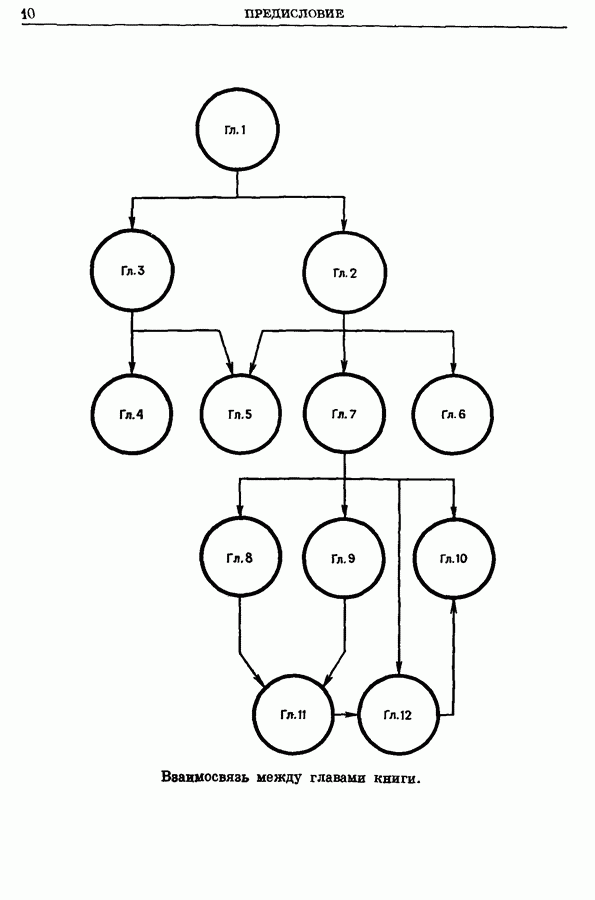
2.2. Процедура порождения всех деревьев графа
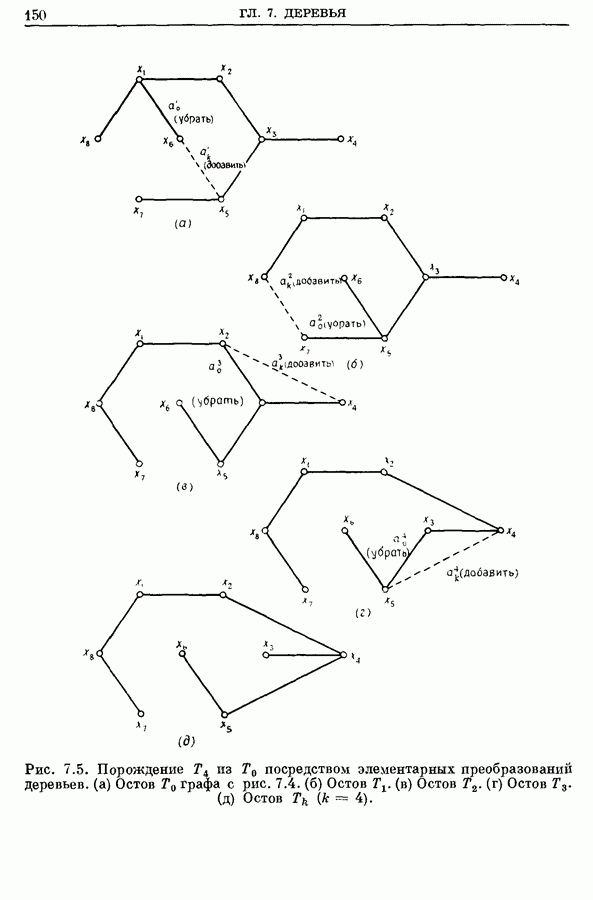
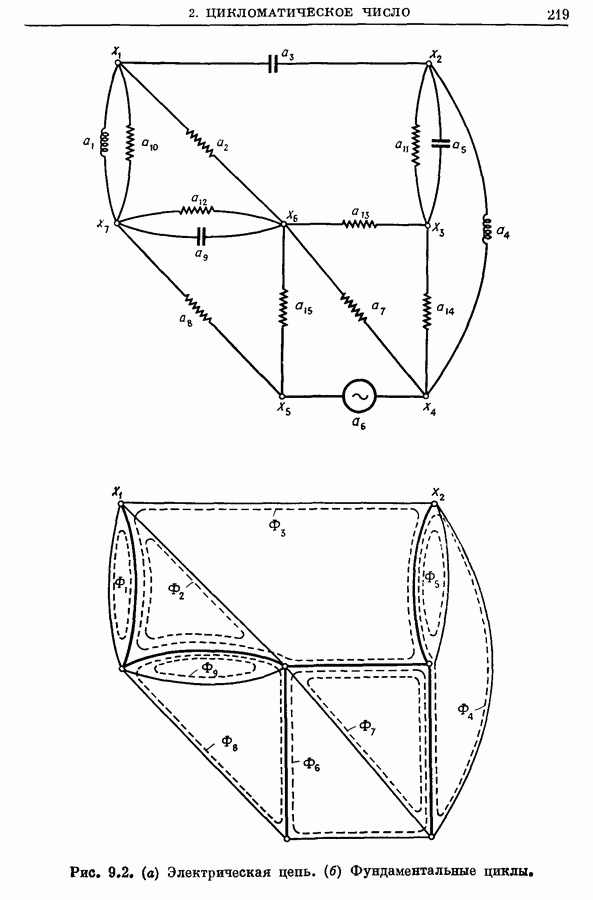
Поскольку, как уже упоминалось в начале этого раздела, число остовных деревьев графа очень быстро растет с ростом числа его дуг, то, очевидно, нужен эффективный метод порождения исчерпывающего, но без повторений, списка остовных деревьев. Один из таких способов состоит в использовании элементарных преобразований деревьев, описанных в предыдущем разделе, для последовательного порождения остовов, начиная с некоторого начального остова  Методы, основанные на этом принципе, даны в работах
Методы, основанные на этом принципе, даны в работах

(кликните для просмотра скана)
Маеды [42], Пауля [471, Чена [8] и других [20]. Однако процедурам, опирающимся на элементарные преобразования деревьев, присущ следующий недостаток: для порождения нового дерева необходимо привлекать все найденные ранее деревья. Число деревьев становится столь большим, что для хранения их необходимо (с вычислительной точки зрения) использовать вспомогательные устройства памяти, так как быстродействующая оперативная память для этой цели мала. Поскольку при обращении к вспомогательным устройствам памяти значительно возрастает время вычисления, то любой метод, базирующийся на элементарных преобразованиях деревьев, оказывается неэффективным, если не будут применяться такие преобразования, в которых используется только последнее из полученных остовных деревьев. (См. раздел 2.4.) Очевидно, что наилучшим будет такой алгоритм порождения всех остовов графа, когда список остовов строится без повторений и построенные остовы записываются во вспомогательную память, но в процессе работы алгоритма из этой памяти ничего не берется.
В следующем разделе будет описан один такой алгоритм, основанный на поиске, использующем дерево решений. В работах [10, 9, 43] даются другие алгоритмы, базирующиеся на порождении всех главных квадратных подматриц приведенной матрицы инциденций  о которой упоминалось в теореме 1.
о которой упоминалось в теореме 1.
2.2.1. Основной метод. Мы приводим описание алгоритма для случая неориентированного графа, но его распространение на ориентированные графы — для порождения всех остовных древовидностей ориентированного графа — совершенно очевидно.
Первый шаг метода состоит в приписывании номеров ребрам графа  (ребра нумеруются
(ребра нумеруются  число ребер в графе
число ребер в графе  На каждом этапе (т. е. при каждом ветвлении в дереве решений) выбирается ребро, которое вместе с остальными, выбранными уже на предыдущих этапах, будет образовывать часть конструируемого дерева. Таким образом, прежде чем отобрать такое ребро, выясняют, действительно ли добавление его к частично сформированному дереву (которое на этом шаге является набором поддеревьев) не приводит к появлению цикла. Если цикл появляется, то данное ребро отбрасывается и проверке подвергается следующее ребро, с большим номером. Если цикла нет, то ребро добавляется к другим, уже отобранным, и процесс продолжается до тех пор, пока не будет построено остовное дерево. Ребра перебираются в порядке возрастания их номеров; это приводит к исчерпывающему и без повторений решению задачи.
На каждом этапе (т. е. при каждом ветвлении в дереве решений) выбирается ребро, которое вместе с остальными, выбранными уже на предыдущих этапах, будет образовывать часть конструируемого дерева. Таким образом, прежде чем отобрать такое ребро, выясняют, действительно ли добавление его к частично сформированному дереву (которое на этом шаге является набором поддеревьев) не приводит к появлению цикла. Если цикл появляется, то данное ребро отбрасывается и проверке подвергается следующее ребро, с большим номером. Если цикла нет, то ребро добавляется к другим, уже отобранным, и процесс продолжается до тех пор, пока не будет построено остовное дерево. Ребра перебираются в порядке возрастания их номеров; это приводит к исчерпывающему и без повторений решению задачи.
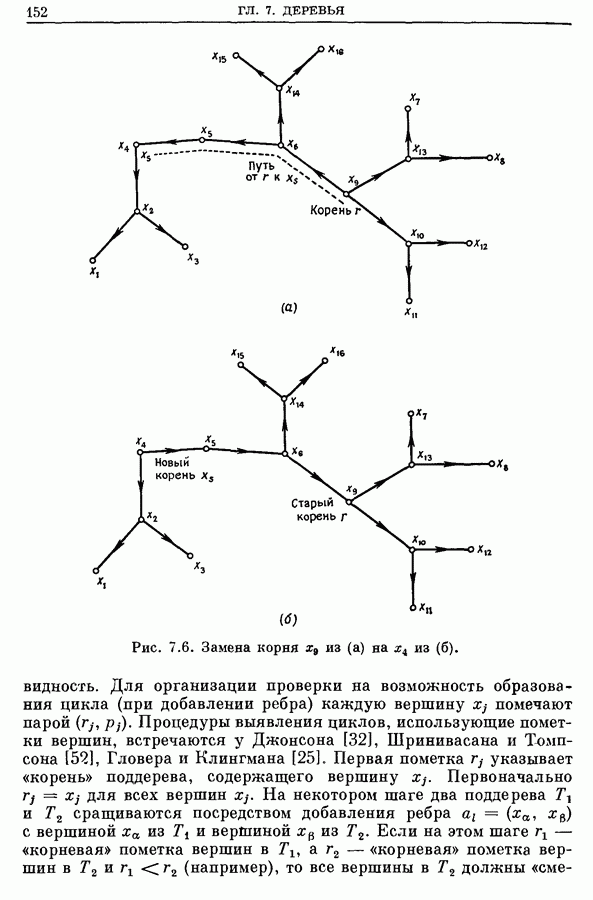
Для облегчения манипуляций с поддеревьями в каждом поддереве выделяют произвольным образом корень (некоторую вершину поддерева) и затем рассматривают поддерево уже как
Рис. 7.6. (см. скан) Замена корня  из (а) на
из (а) на  из (б).
из (б).
древовидность. Для организации проверки на возможность образования цикла (при добавлении ребра) каждую вершину  помечают парой
помечают парой  Процедуры выявления циклов, использующие пометки вершин, встречаются у Джонсона [32], Шринивасана и Томпсона [52], Гловера и Клингмана [25]. Первая пометка
Процедуры выявления циклов, использующие пометки вершин, встречаются у Джонсона [32], Шринивасана и Томпсона [52], Гловера и Клингмана [25]. Первая пометка  указывает «корень» поддерева, содержащего вершину
указывает «корень» поддерева, содержащего вершину  Первоначально
Первоначально  для всех вершин
для всех вершин  На некотором шаге два поддерева
На некотором шаге два поддерева  сращиваются посредством добавления ребра
сращиваются посредством добавления ребра  с вершиной
с вершиной  из
из  и вершиной
и вершиной  из
из  Если на этом шаге
Если на этом шаге  «корневая» пометка вершин в
«корневая» пометка вершин в  «корневая» пометка вершин в
«корневая» пометка вершин в  (например), то все вершины в
(например), то все вершины в  должны
должны
«сменить» свои корневые пометки на  и два поддерева
и два поддерева  «сольются» в единственное новое дерево
«сольются» в единственное новое дерево 
Вторая пометка  приписанная вершине
приписанная вершине  указывает вершину, предшествующую вершине
указывает вершину, предшествующую вершине  т. е. если
т. е. если  дуга рассматриваемого поддерева, то
дуга рассматриваемого поддерева, то  Для корневой вершины дерева такая пометка полагается равной нулю. Для дерева, изображенного на рис.
Для корневой вершины дерева такая пометка полагается равной нулю. Для дерева, изображенного на рис. 
A. Замена корня дерева
Если корнем дерева  является вершина
является вершина  и нужно в качестве корня выбрать новую вершину
и нужно в качестве корня выбрать новую вершину  то такую «замену»
то такую «замену»  на
на  можно осуществить простым обращением ориентации дуг, принадлежащих цепи, идущей от
можно осуществить простым обращением ориентации дуг, принадлежащих цепи, идущей от  не меняя при этом ориентацию других дуг (см. рис. 7.6). Соответствующие изменения пометок будут таковы.
не меняя при этом ориентацию других дуг (см. рис. 7.6). Соответствующие изменения пометок будут таковы.
Изменение пометок «предшествования»
1. Пусть 
2. Положить 
3. Шаг обновления: 
4. Если  то перейти к шагу 5, в противном случае положить
то перейти к шагу 5, в противном случае положить  и перейти к шагу 2.
и перейти к шагу 2.
5. Положить  стоп.
стоп.
Изменение корневых пометок
1. У всех вершин, имеющих корневую пометку  заменить ее на пометку
заменить ее на пометку 
Б. Сращивание двух поддеревьев
Если осуществлено сращивание двух поддеревьев  (путем добавления ребра
(путем добавления ребра  как было описано ранее), то в пометки необходимо внести следующие изменения:
как было описано ранее), то в пометки необходимо внести следующие изменения:
(i) У вершин с корневой пометкой  заменить эту пометку на
заменить эту пометку на 
(ii) Заменить в дереве  корень
корень  на (так, как было описано выше в пункте А), после чего изменить пометку «предшествования» у вершины
на (так, как было описано выше в пункте А), после чего изменить пометку «предшествования» у вершины 
Расщепление дерева на две части
Поскольку метод порождения деревьев, рассматриваемый ниже, является поиском, использующим дерево решений, то возникает необходимость удаления некоторых ребер (на шагах возвращения), чтобы испытать затем другие ребра. В такой ситуации удаление ребра приводит к расщеплению некоторого дерева на две части, например на  и в пометки одного из этих поддеревьев должны быть внесены изменения. Пусть удаляется ребро
и в пометки одного из этих поддеревьев должны быть внесены изменения. Пусть удаляется ребро  где
где  и
и  Тогда при
Тогда при  (т. е. если ребро
(т. е. если ребро
 в первоначальном дереве ориентировано от
в первоначальном дереве ориентировано от  пометки в дереве
пометки в дереве  можно оставить прежними, а пометки в дереве
можно оставить прежними, а пометки в дереве  должны быть изменены. Если же
должны быть изменены. Если же  ребро
ребро  ориентировано от
ориентировано от  то можно не менять пометки в дереве
то можно не менять пометки в дереве  но нужно изменить пометки в
но нужно изменить пометки в  Предполагая, что пометки меняются в дереве
Предполагая, что пометки меняются в дереве  покажем, как надо «восстанавливать» корень в этом дереве.
покажем, как надо «восстанавливать» корень в этом дереве.
1. Положить  будет корнем дерева
будет корнем дерева 
2. Найти все вершины  и изменить их корневые пометки на
и изменить их корневые пометки на  Если таких вершин нет, остановиться.
Если таких вершин нет, остановиться.
3. Шаг обновления:  вернуться к шагу 2.
вернуться к шагу 2.
Следует отметить, что ни у одной вершины, кроме нового корня  пометки предшествования менять не нужно. Заметим также, что число описанных выше шагов 2 и 3, которое необходимо для восстановления корня, равно длине самой длинной цепи в
пометки предшествования менять не нужно. Заметим также, что число описанных выше шагов 2 и 3, которое необходимо для восстановления корня, равно длине самой длинной цепи в  исходящей из вершины
исходящей из вершины 
2.2.2. Описание алгоритма. Возьмем произвольную вершину х графа  Пусть ее степень равна
Пусть ее степень равна  Перенумеруем ребра, инцидентные этой вершине:
Перенумеруем ребра, инцидентные этой вершине:  Затем перенумеруем остальные ребра графа
Затем перенумеруем остальные ребра графа  При порождении деревьев ребра будут перебираться в соответствии с введенной нумерацией.
При порождении деревьев ребра будут перебираться в соответствии с введенной нумерацией.
Шаг 1. Приписать вершинам пометки:  где
где  Положить
Положить 
Шаг 2. Выбрать для исследования некоторое ребро. Например,  Если к
Если к  где
где  число ребер графа, то перейти к
число ребер графа, то перейти к  При
При  т. е. если «неисследованных» ребер нет, перейти к шагу 5.
т. е. если «неисследованных» ребер нет, перейти к шагу 5.
(i) Если  то это означает, что вершины
то это означает, что вершины  принадлежат одному и тому же поддереву и добавление ребра
принадлежат одному и тому же поддереву и добавление ребра  приведет к появлению цикла. Отбросить ребро
приведет к появлению цикла. Отбросить ребро  т. е. положить
т. е. положить  и вернуться к шагу 2.
и вернуться к шагу 2.
(ii) Если  то ребро
то ребро  можно добавить к ребрам построенных поддеревьев. Перейти к шагу 3.
можно добавить к ребрам построенных поддеревьев. Перейти к шагу 3.
Шаг 3. Срастить два поддерева, у которых вершины имеют корневые пометки  применив для этого метод, описанный выше в пункте
применив для этого метод, описанный выше в пункте 
Шаг 4. Отобрав  ребер, мы получаем некоторое дерево. Запомнить это дерево и перейти к шагу 5. Если отобрано меньше чем
ребер, мы получаем некоторое дерево. Запомнить это дерево и перейти к шагу 5. Если отобрано меньше чем  ребер, то положить
ребер, то положить  и вернуться к шагу 2.
и вернуться к шагу 2.
Шаг 5. (Возвращение.) Удалить ребро, добавленное последним. Предположим, что таким ребром является  Если
Если 

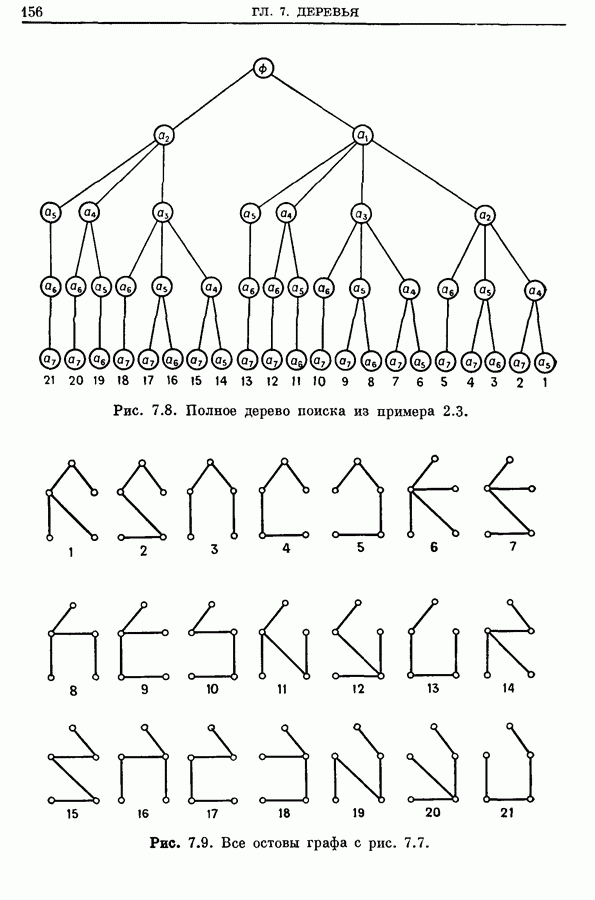
Рис. 7.7. Граф из примера 2.3.
единственное оставшееся для добавления ребро,  то остановиться. Все остовные деревья, таким образом, построены. (При любом дальнейшем ветвлении дерева решений вершина х останется изолированной.)
то остановиться. Все остовные деревья, таким образом, построены. (При любом дальнейшем ветвлении дерева решений вершина х останется изолированной.)
В противном случае надо обновить пометки, действуя так, как указано в пункте В, положить  и возвратиться к шагу 2.
и возвратиться к шагу 2.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
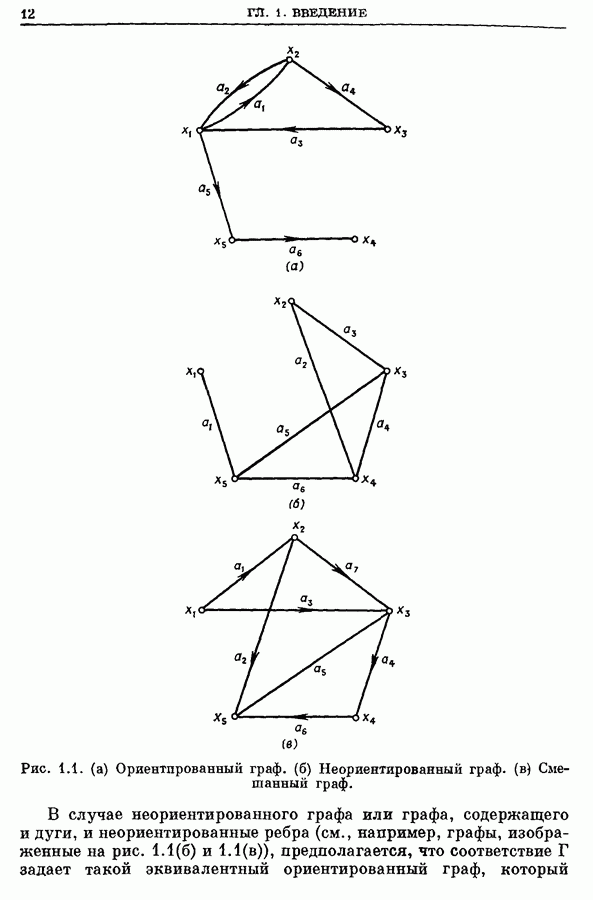
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
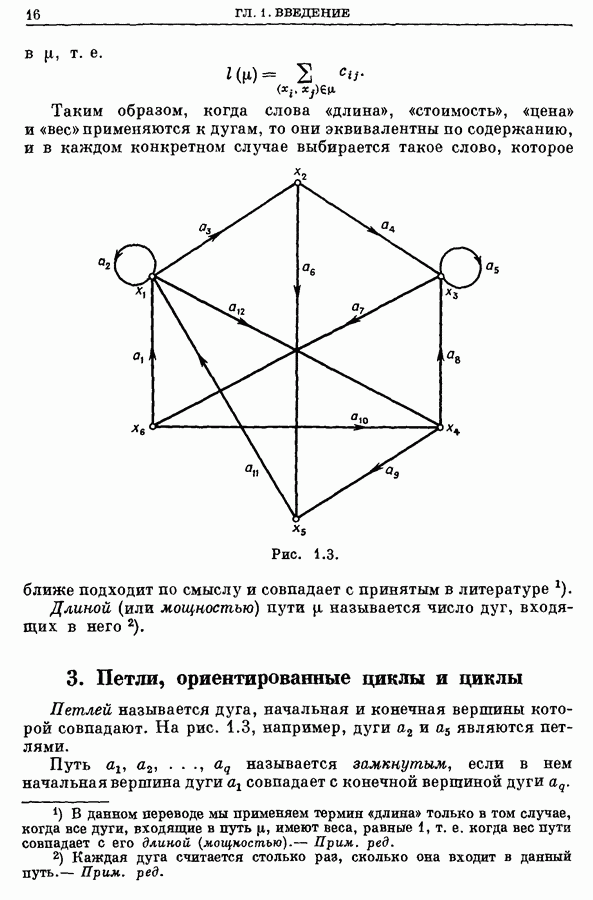
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
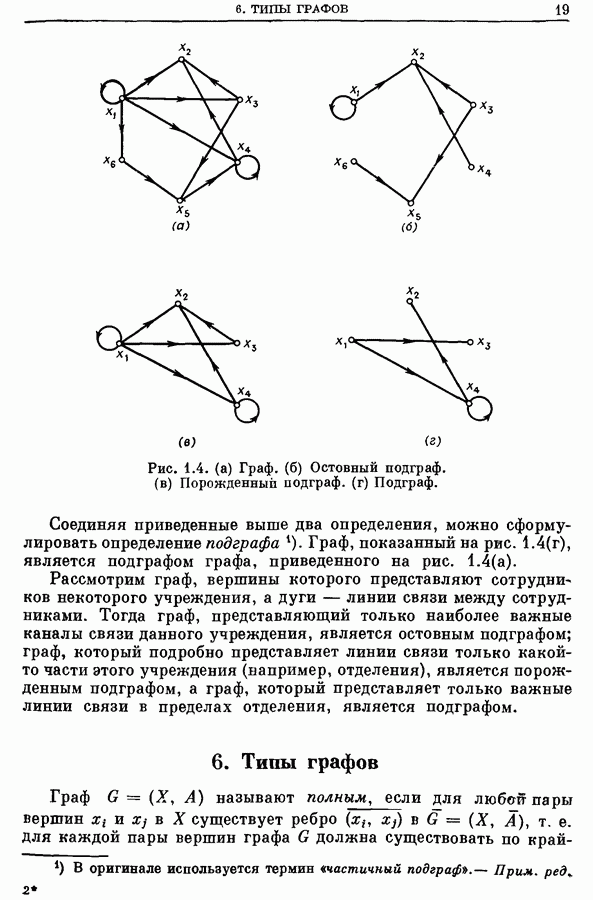
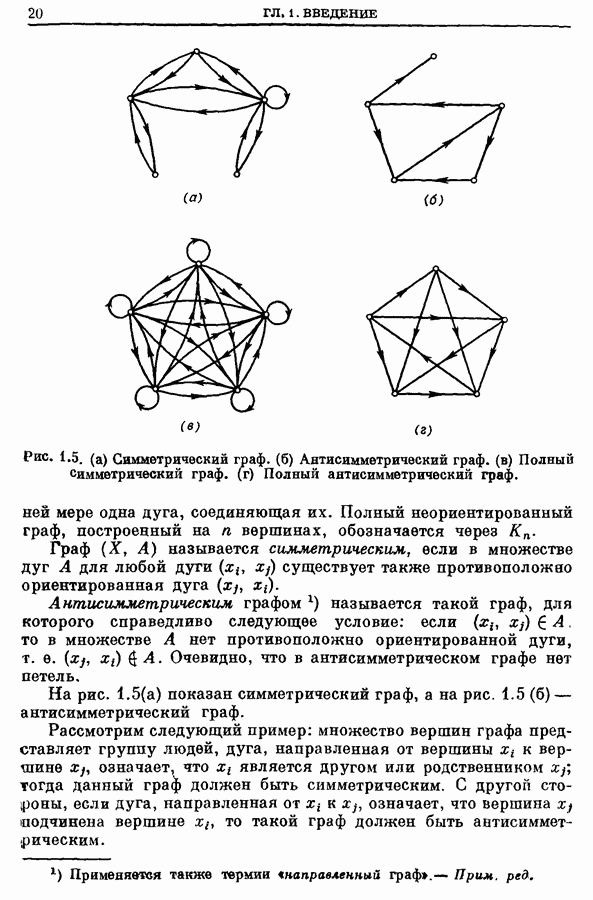
- 5. Подграфы
- 6. Типы графов
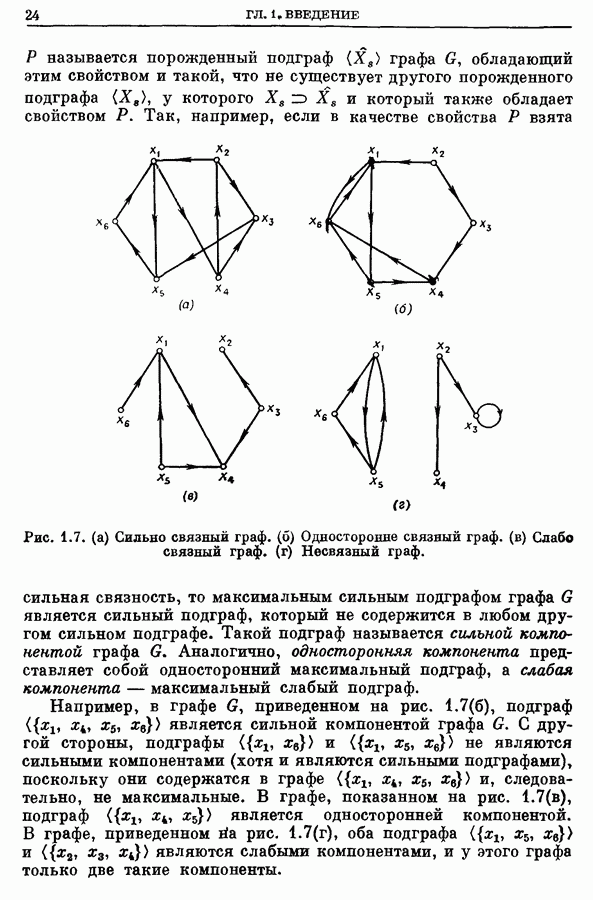
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
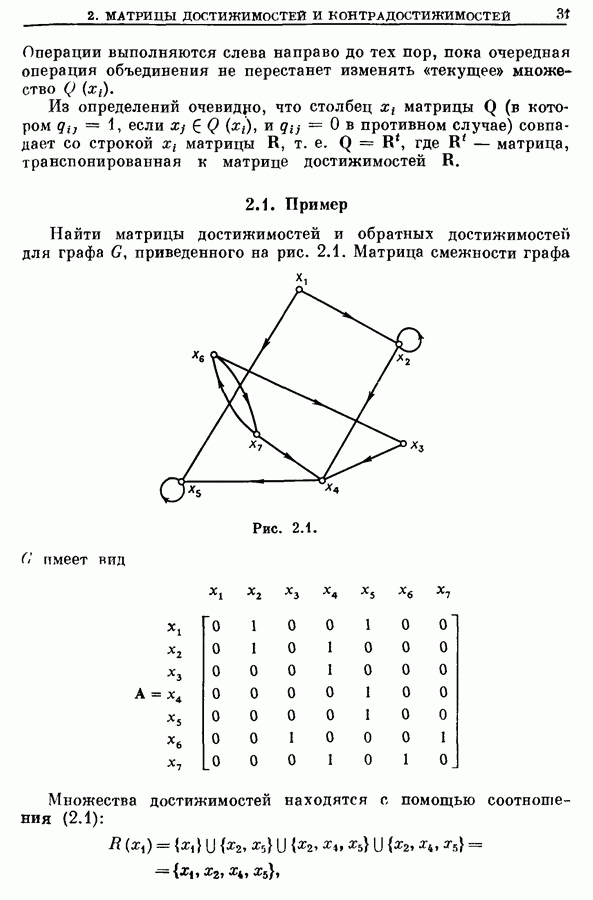
- 2. Матрицы достижимостеи и контрадостижимостей
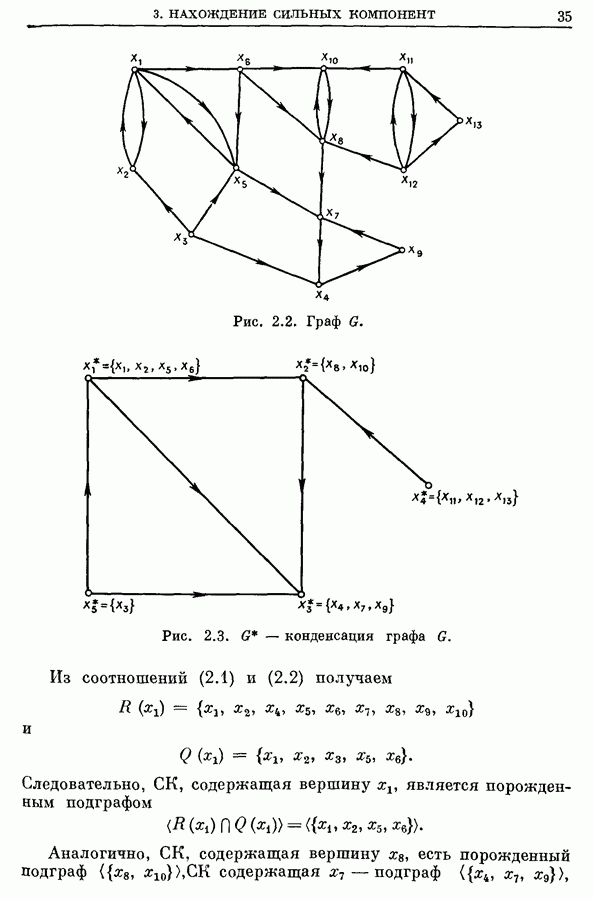
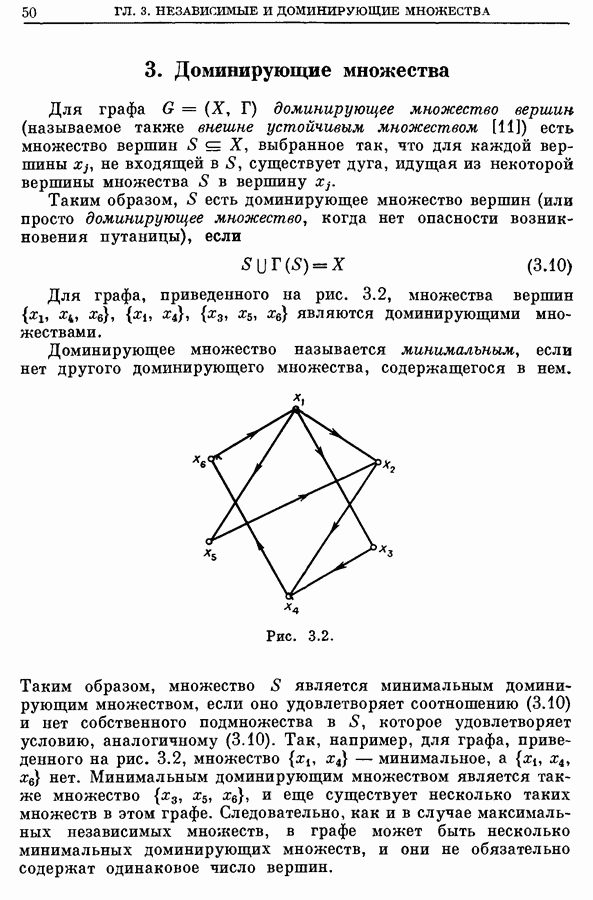
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
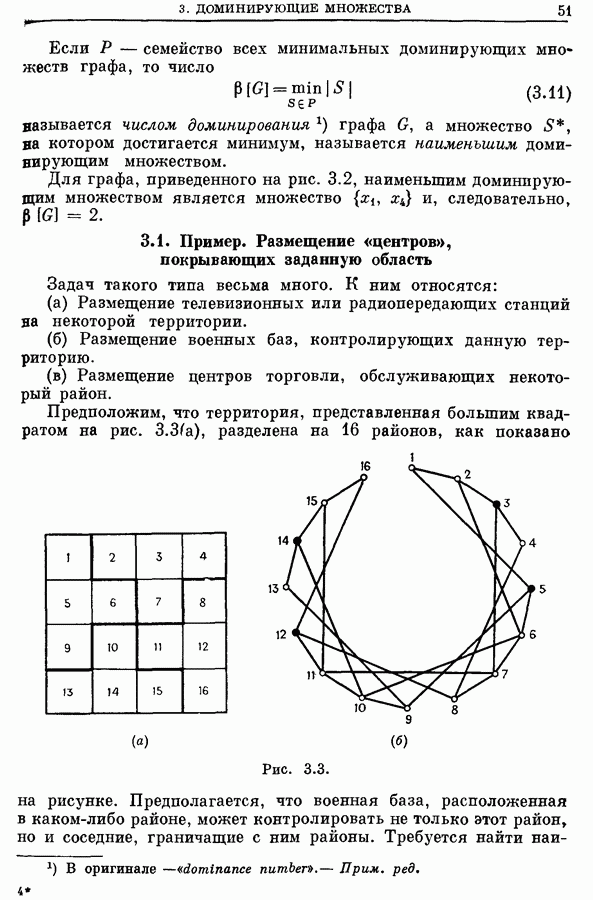
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
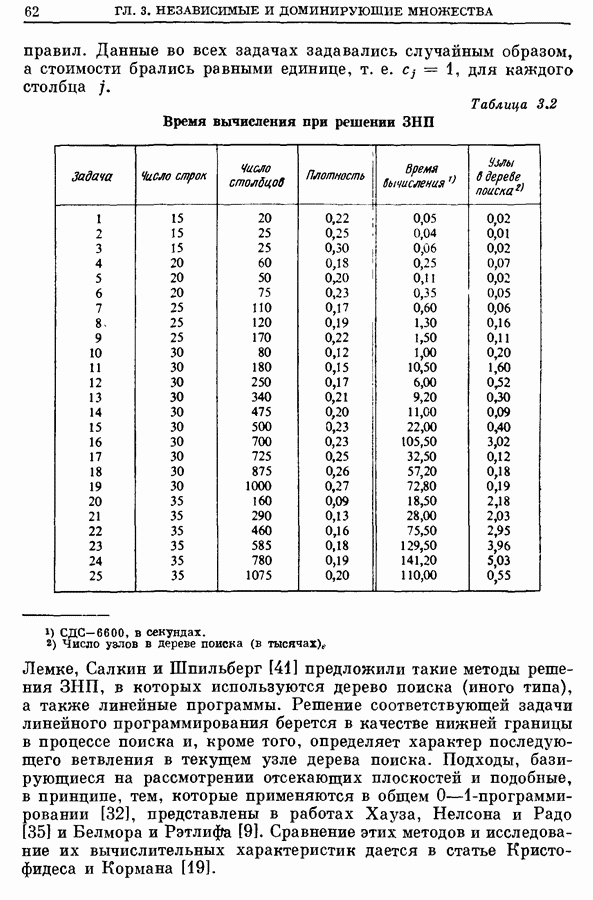
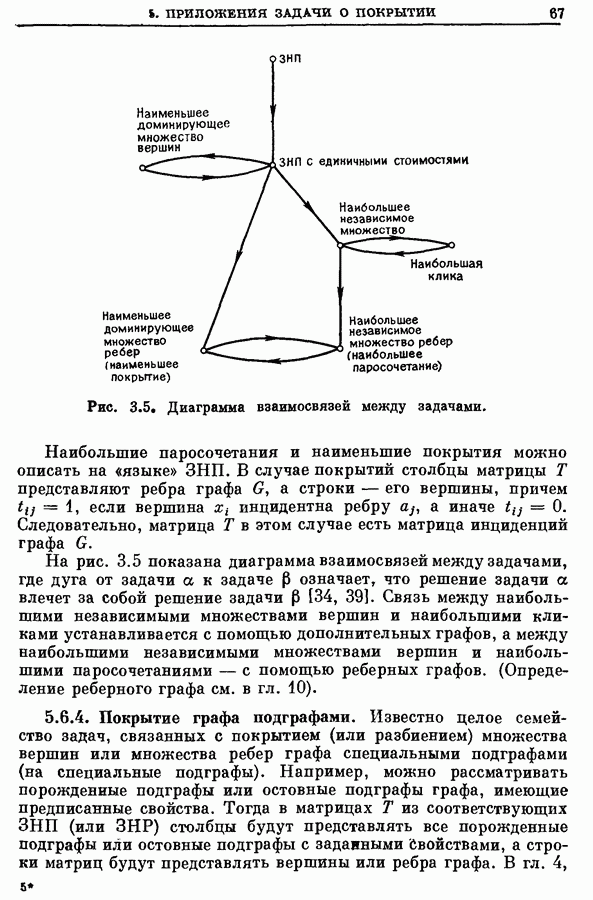
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
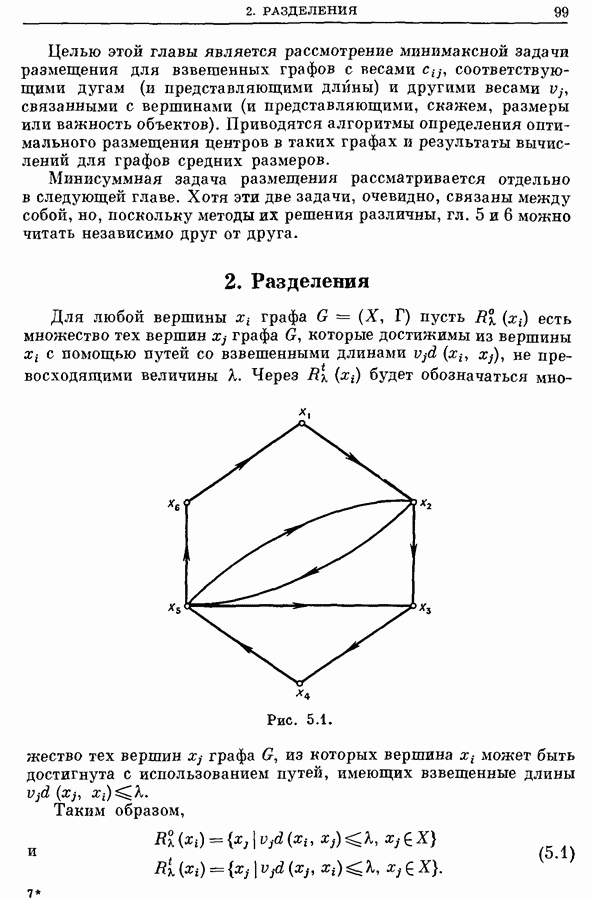
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
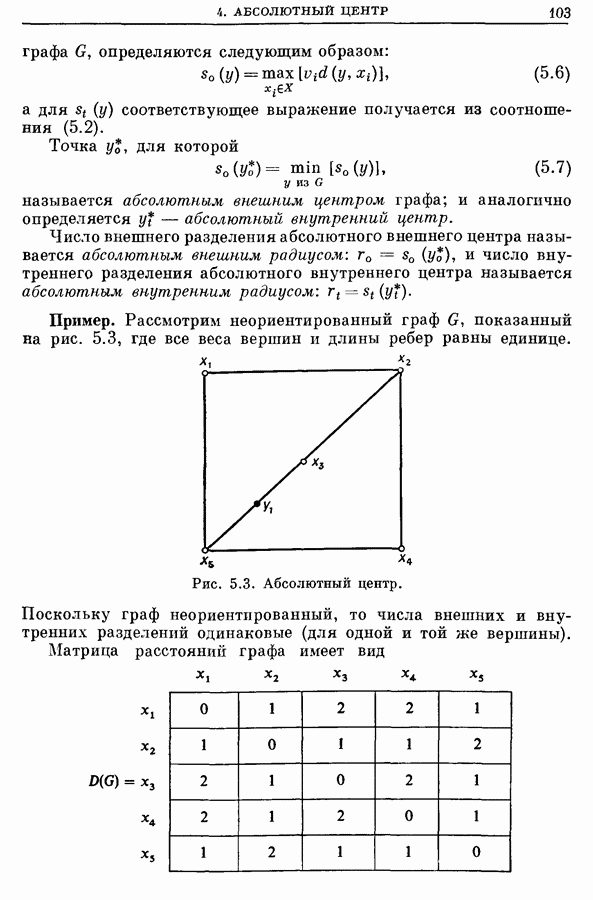
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
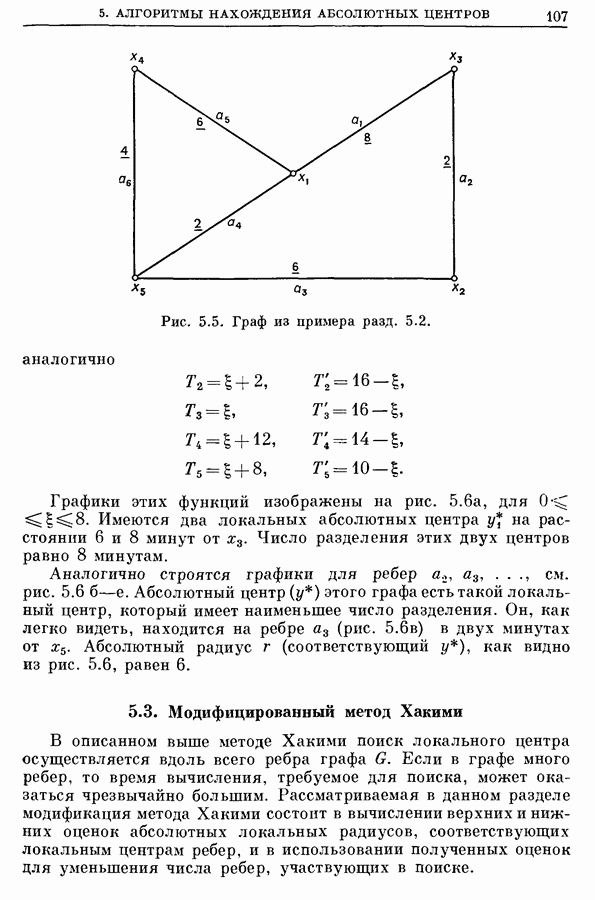
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
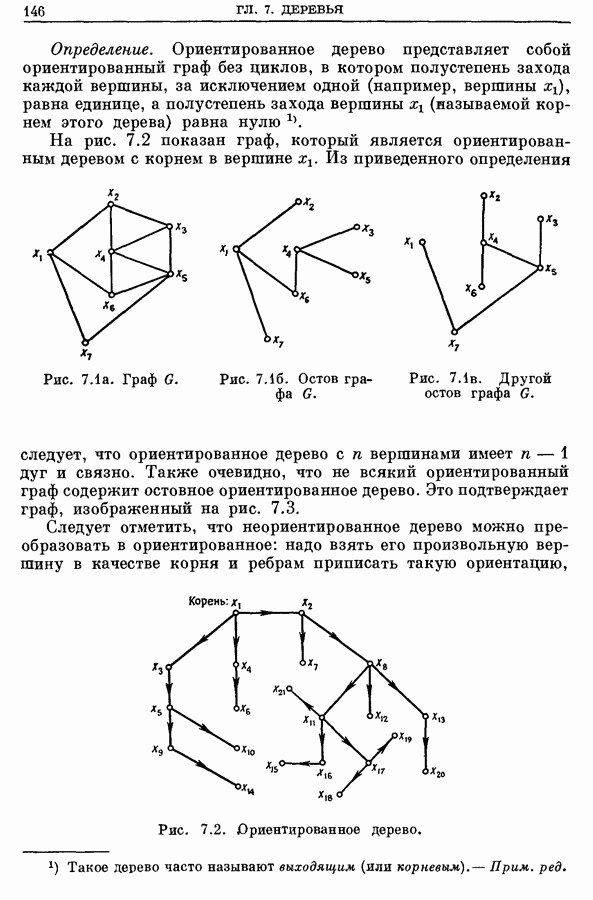
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
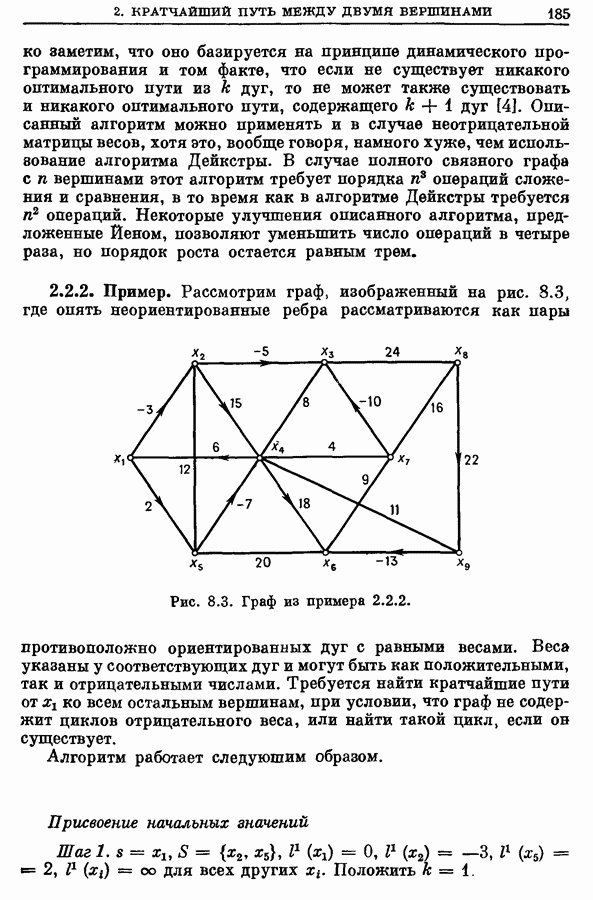
- 2.3. Пример
- 2.4. Граф остовов
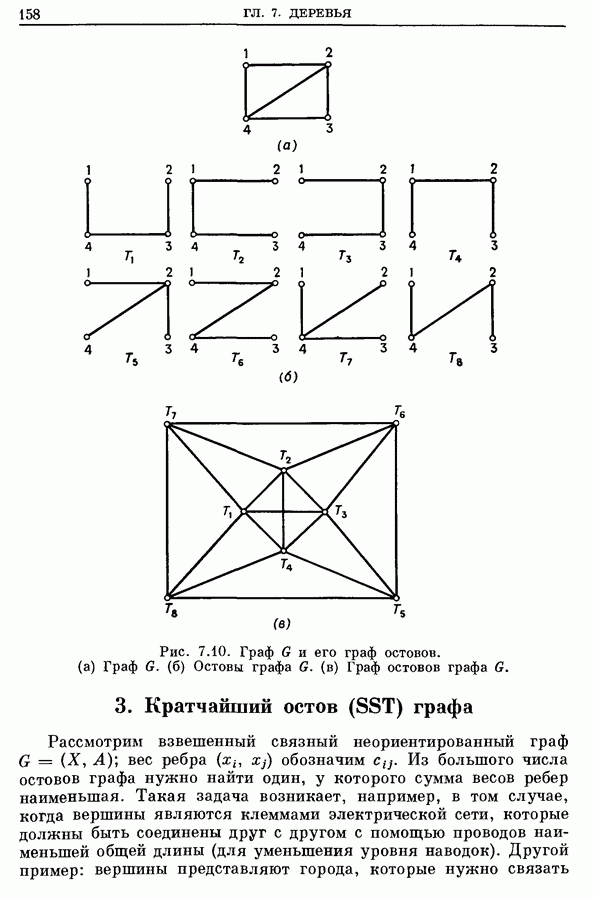
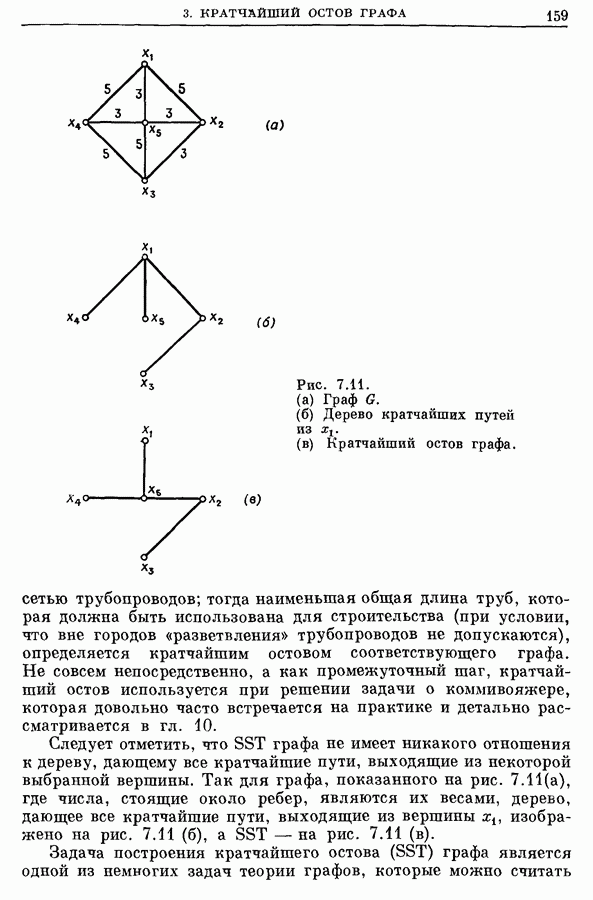
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
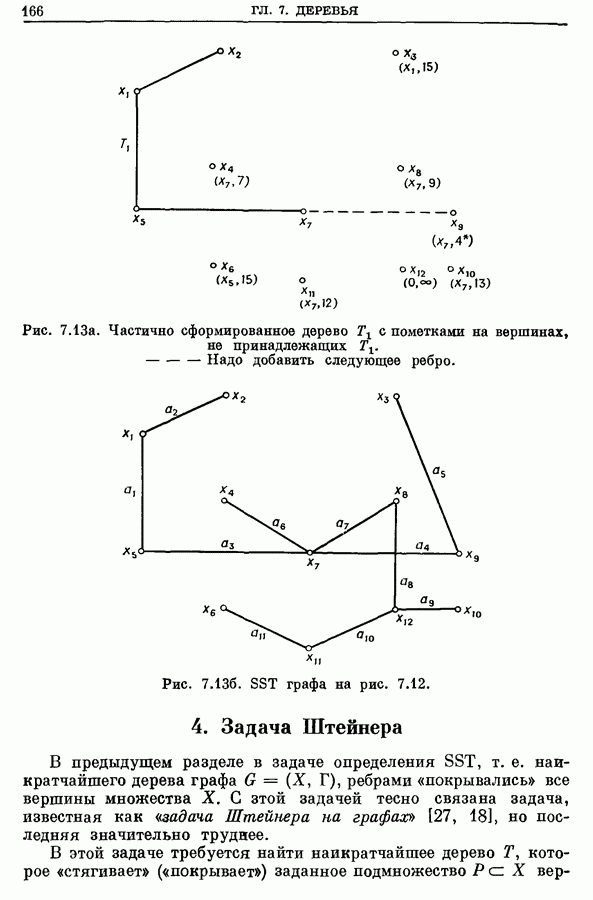
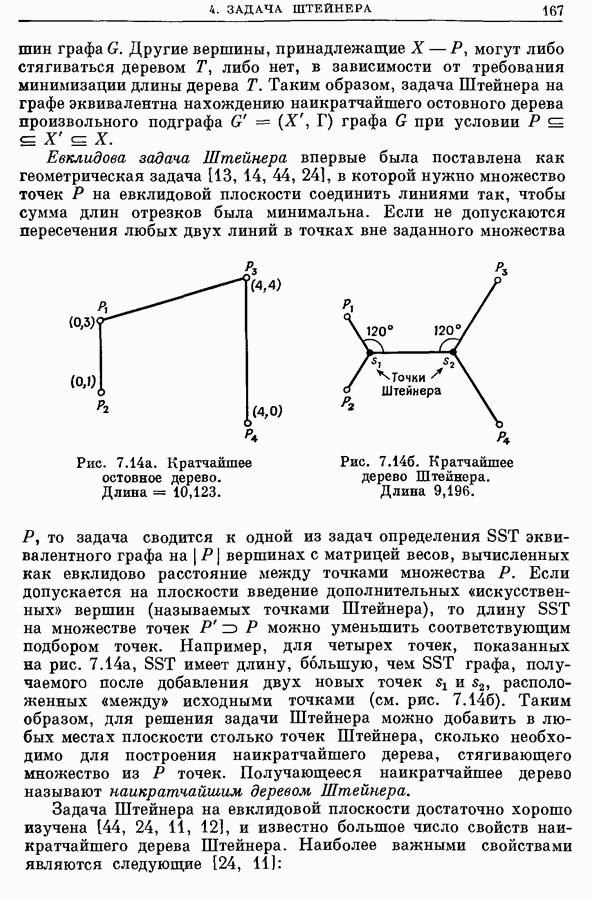
- 4. Задача Штейнера
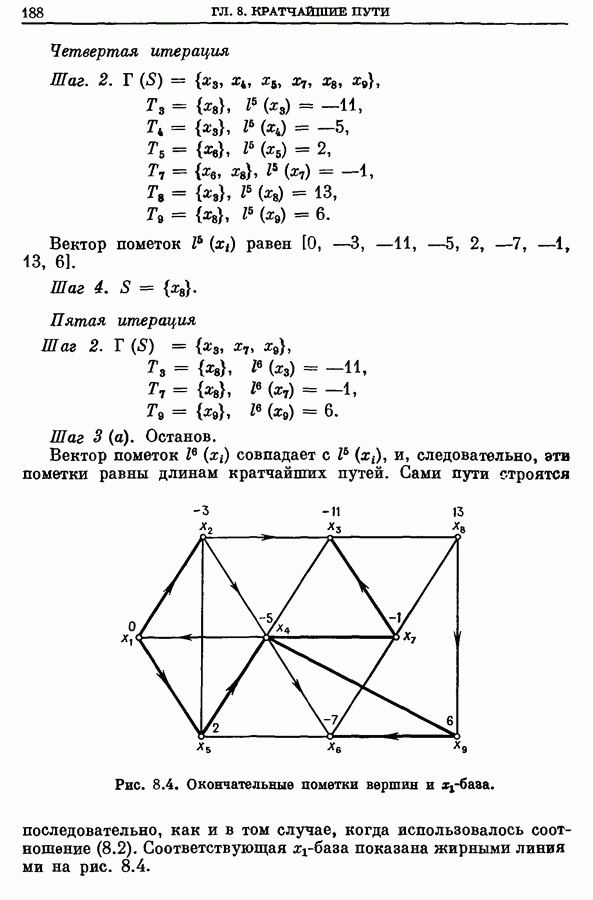
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
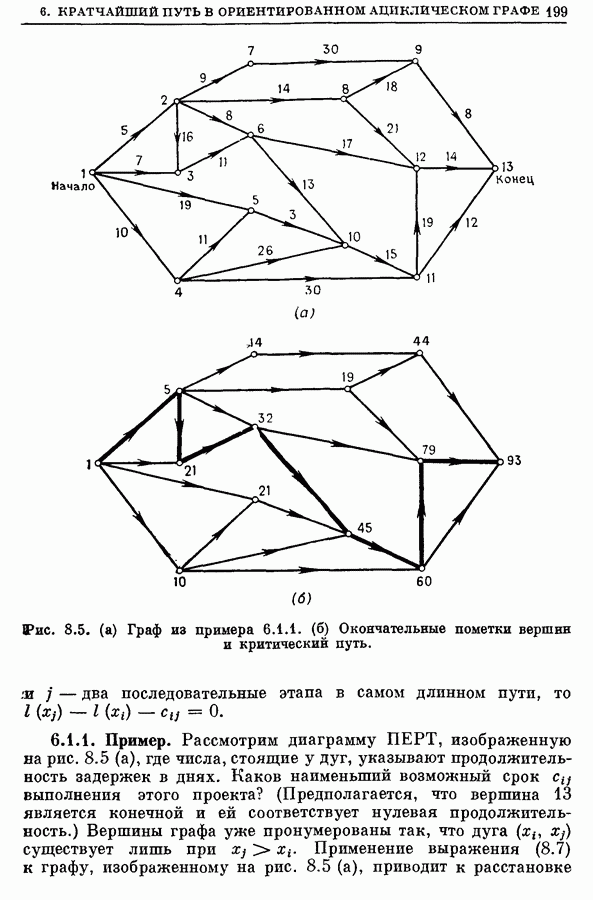
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
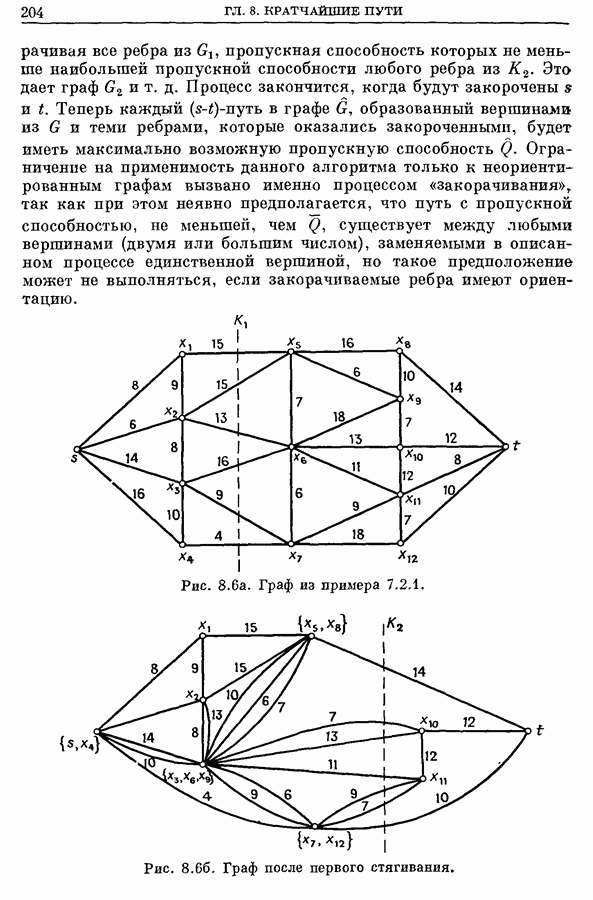
- 7. Задачи, близкие к задаче о кратчайшем пути
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
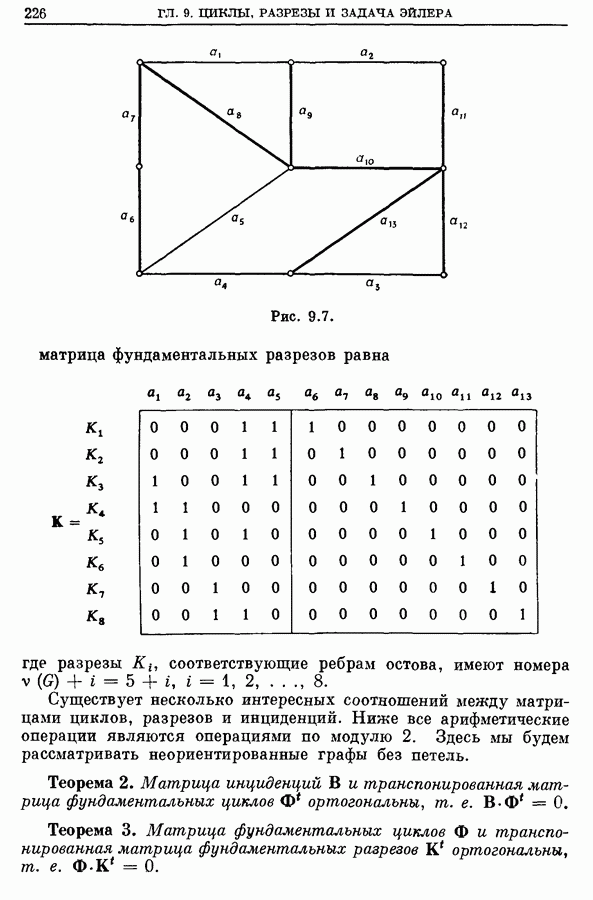
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
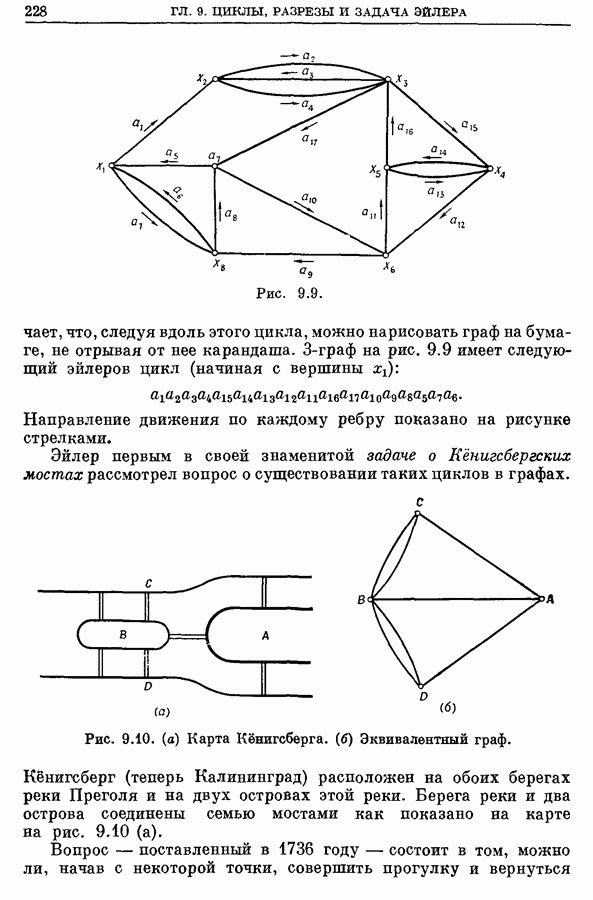
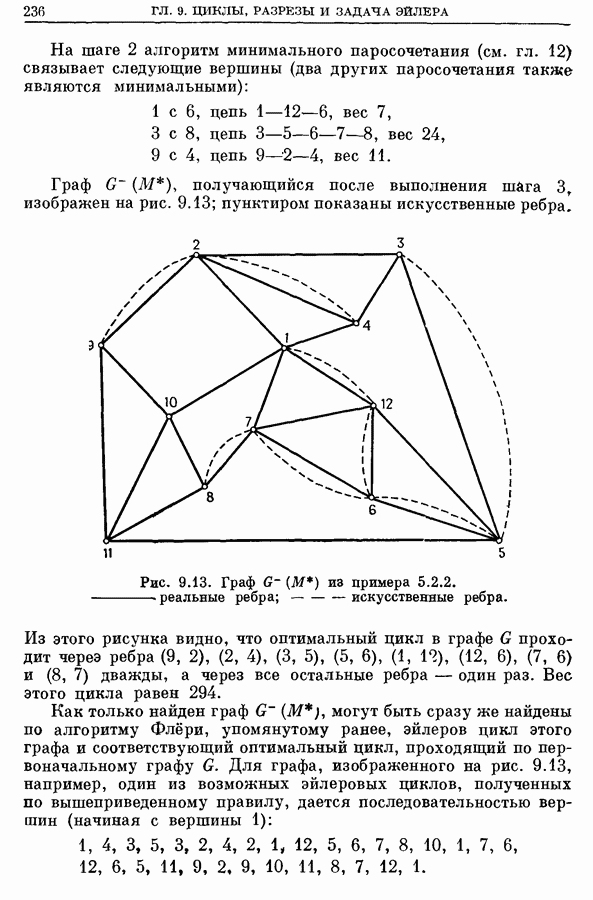
- 5. Эйлеровы циклы и задача китайского почтальона
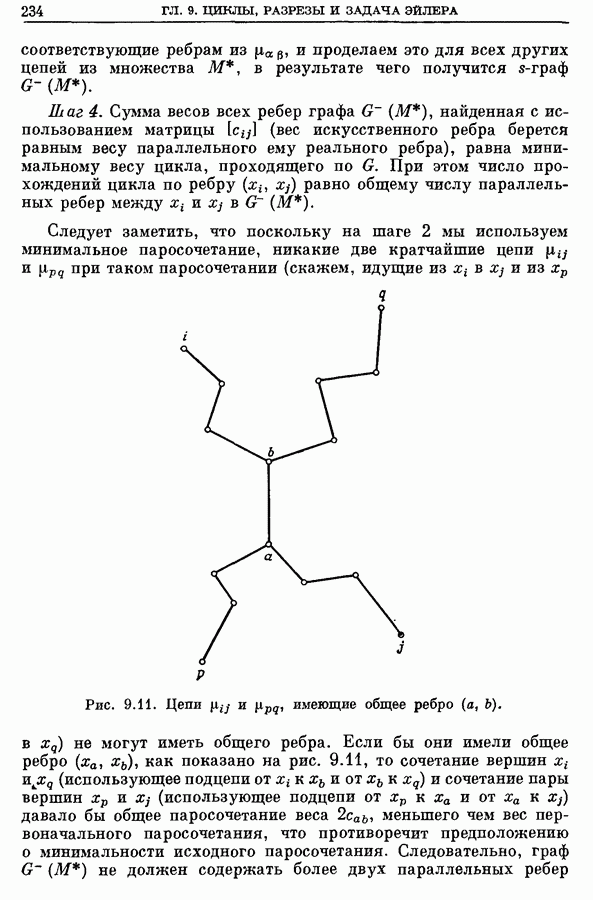
- 5.1. Некоторые родственные задачи
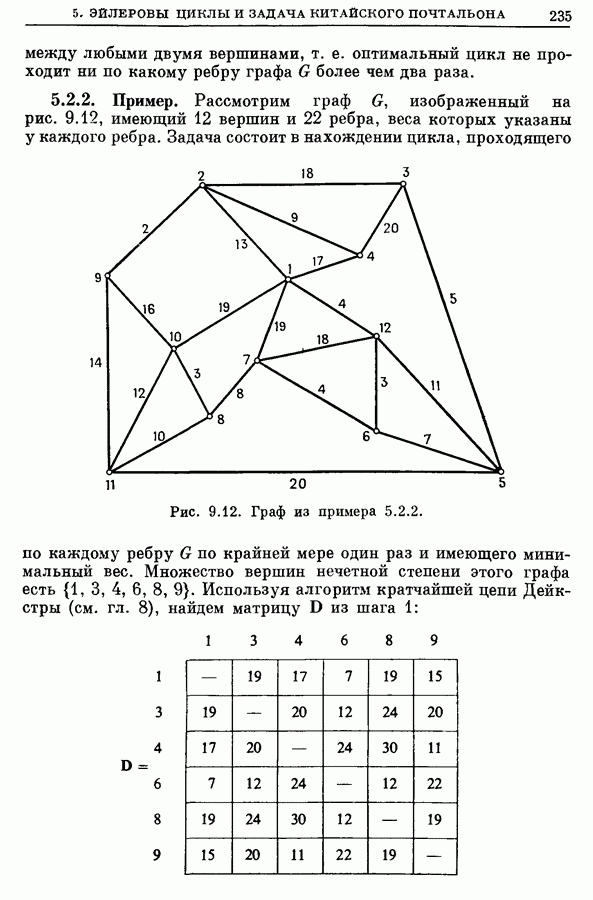
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
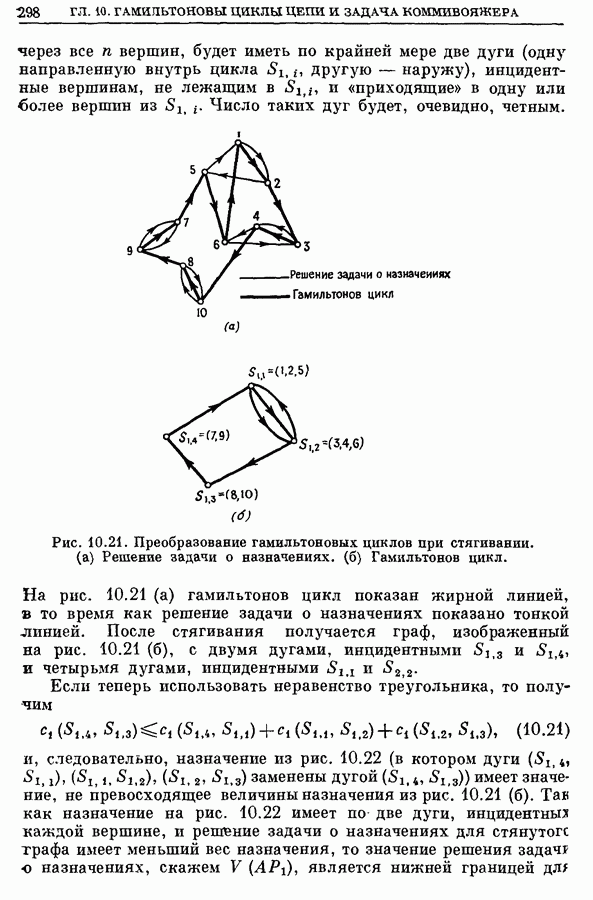
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
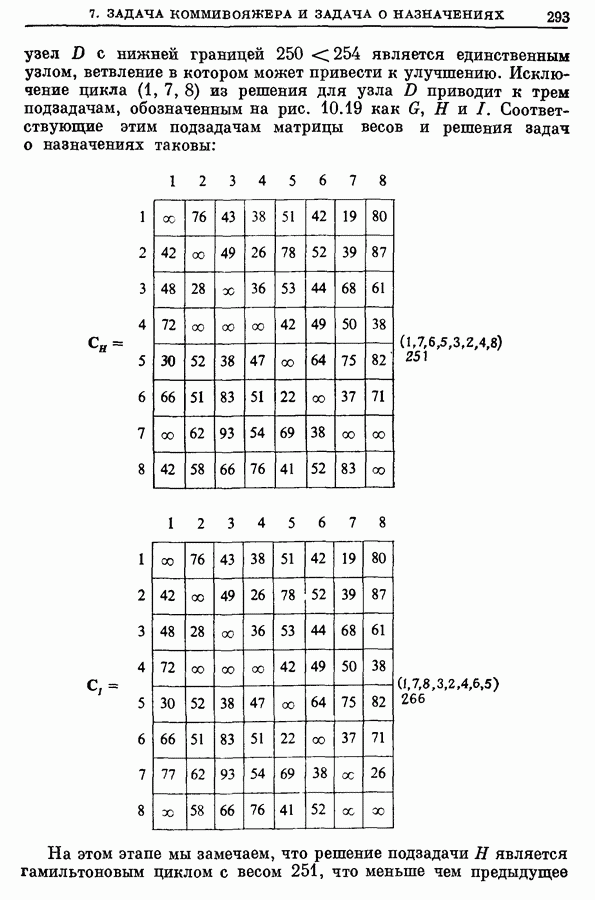
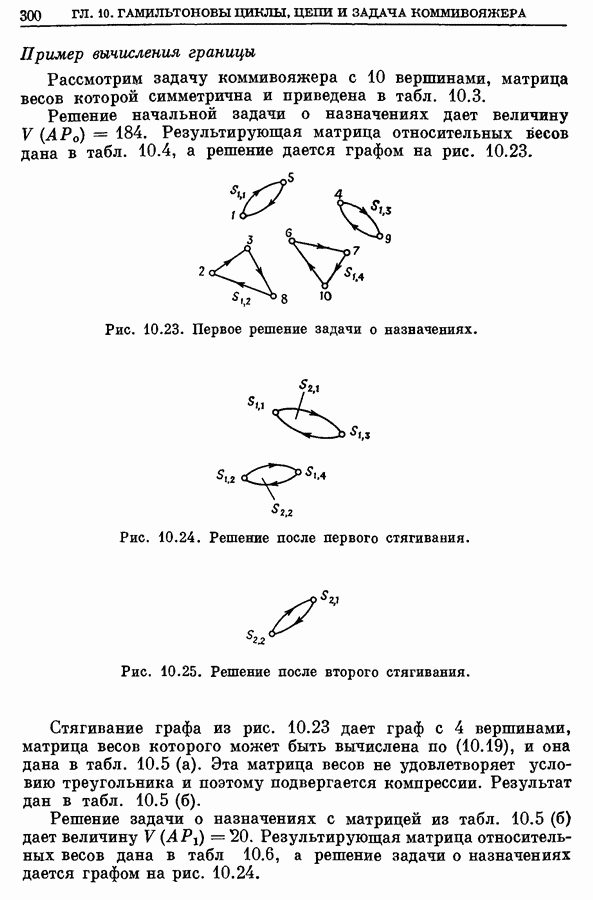
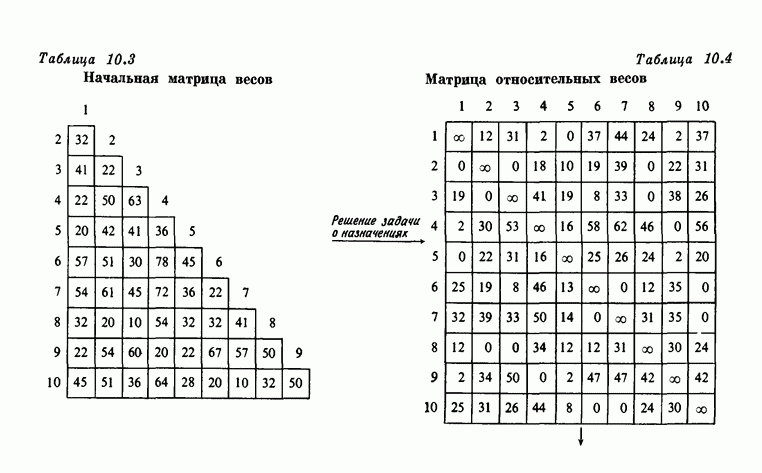
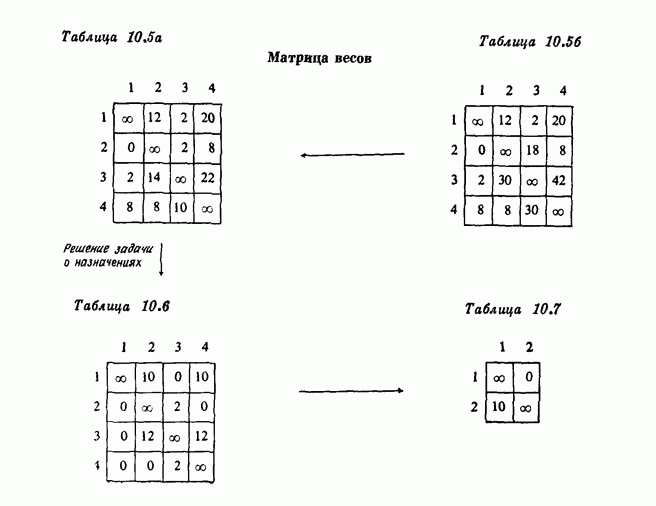
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
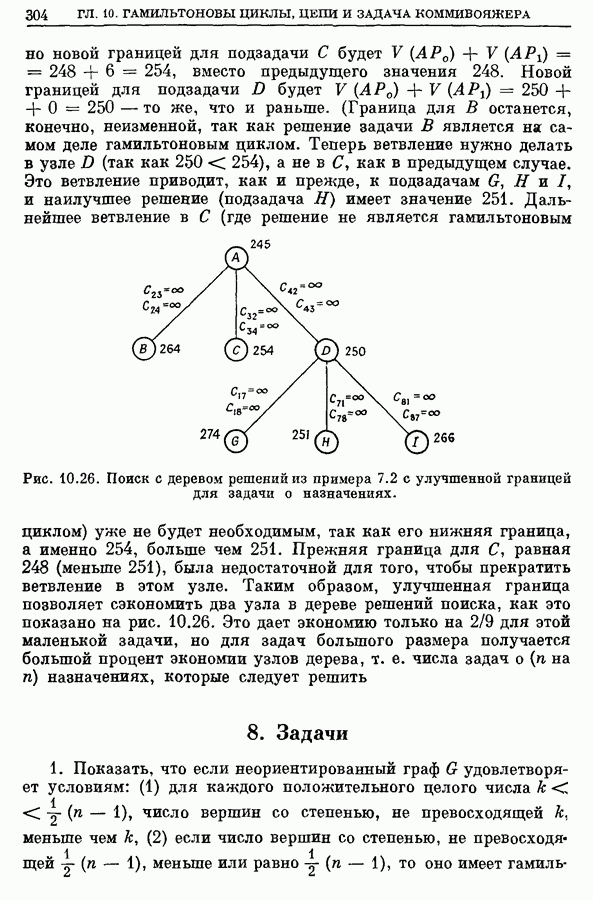
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
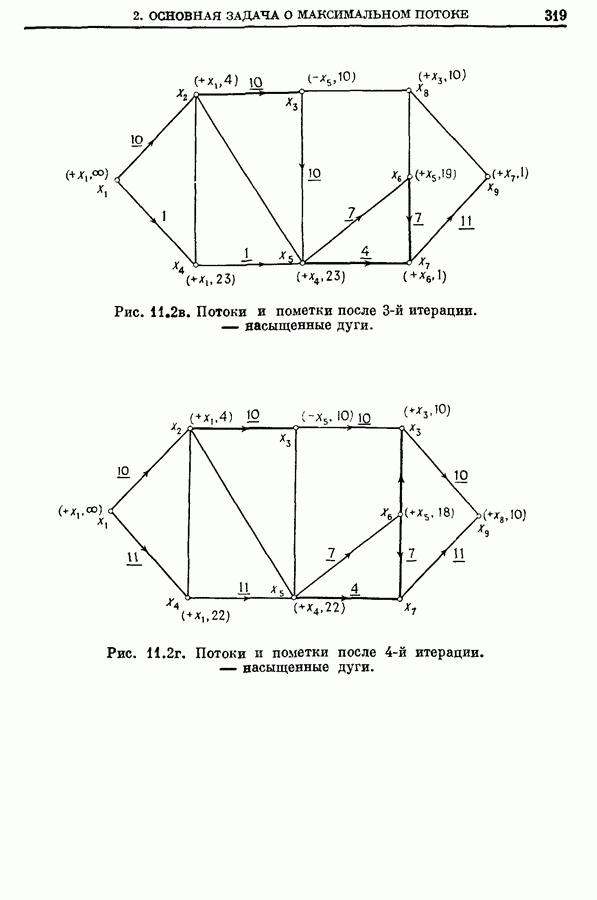
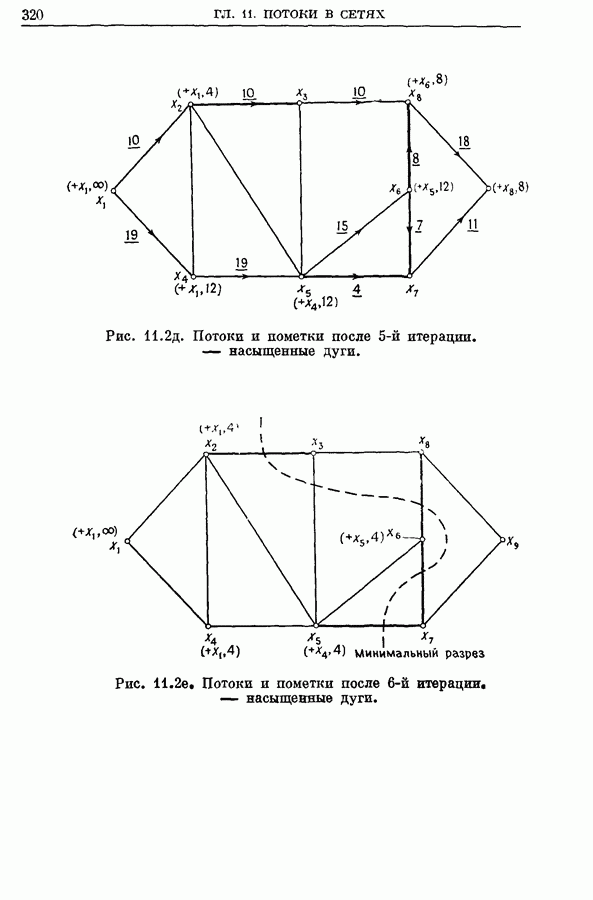
- 2. Основная задача о максимальном потоке (от s к t)
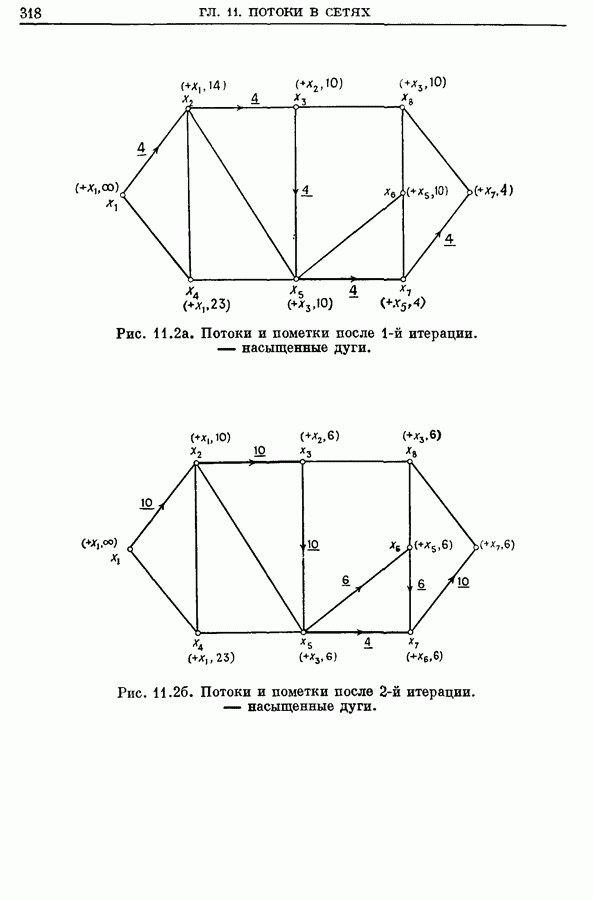
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
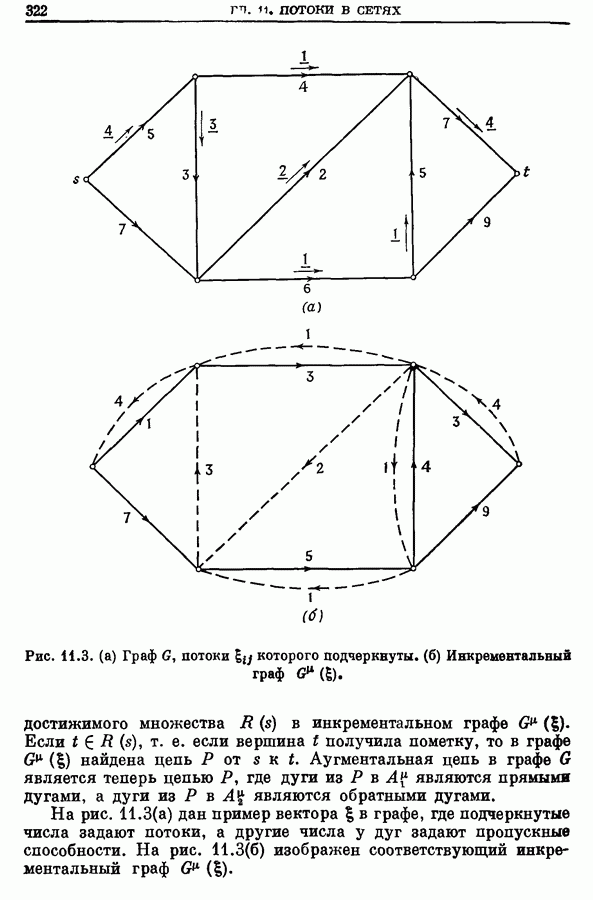
- 2.3. Инкрементальные графы
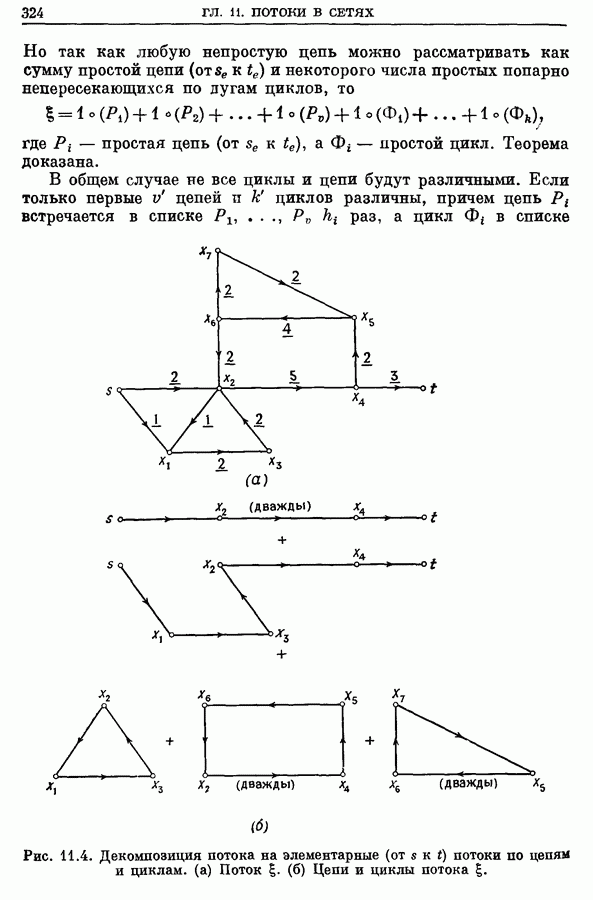
- 2.4. Декомпозиция потока
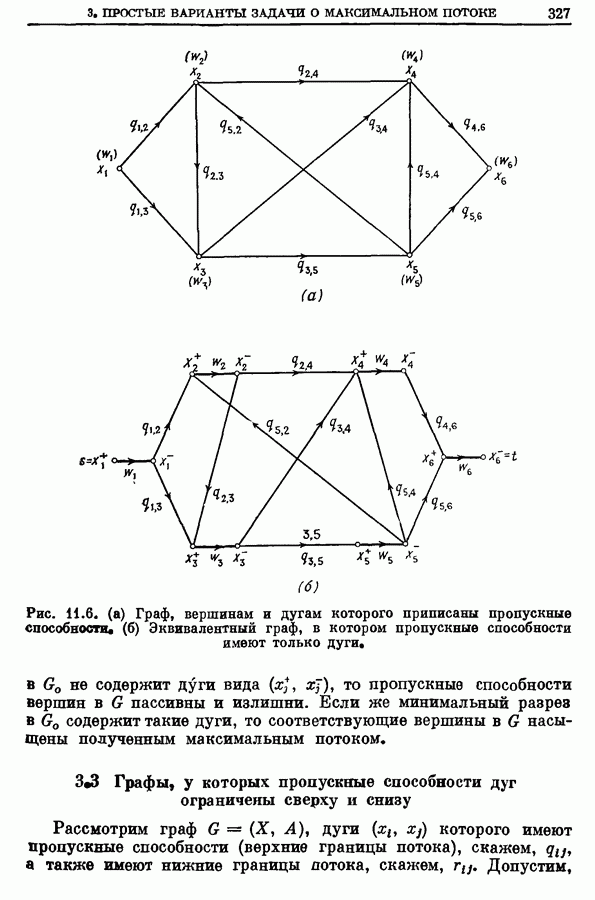
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
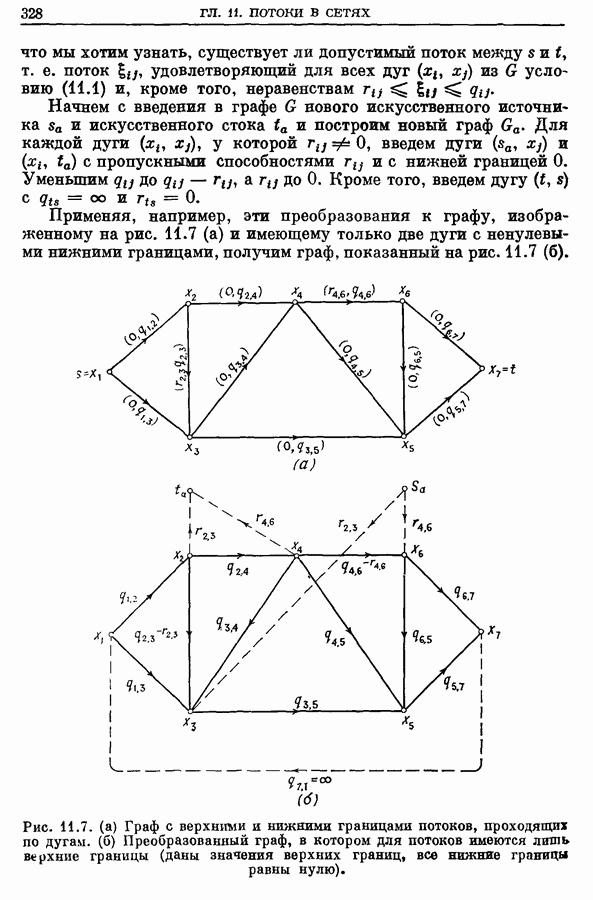
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
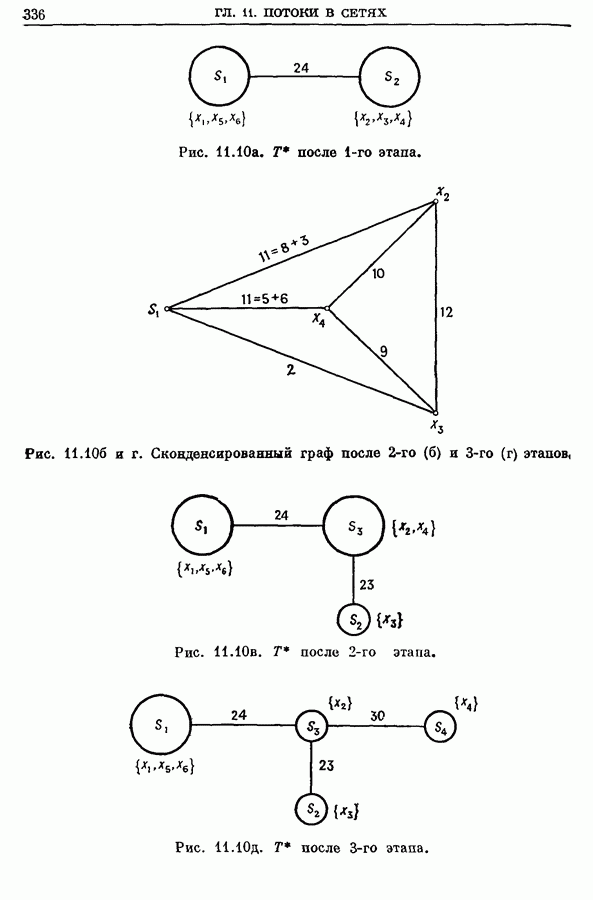
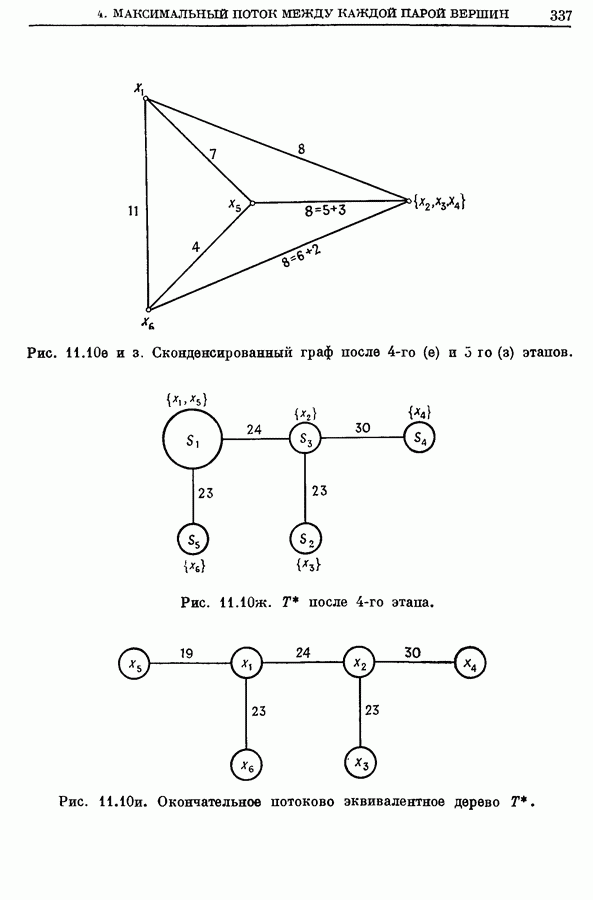
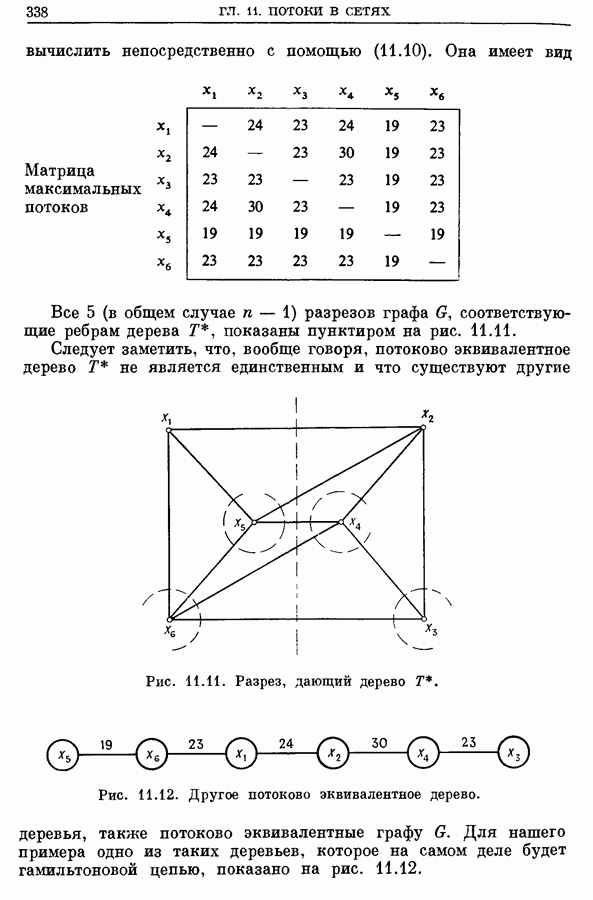
- 4. Максимальный поток между каждой паров вершин
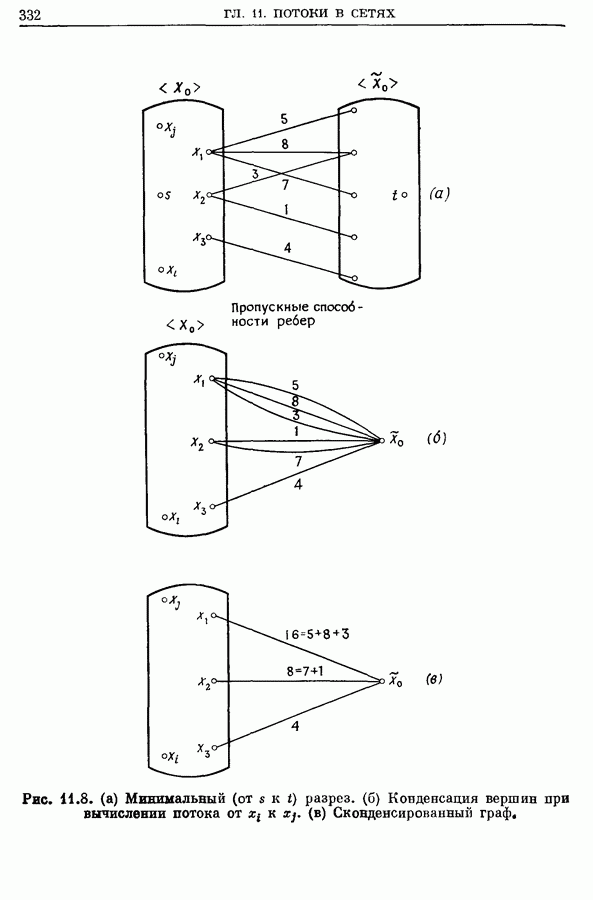
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
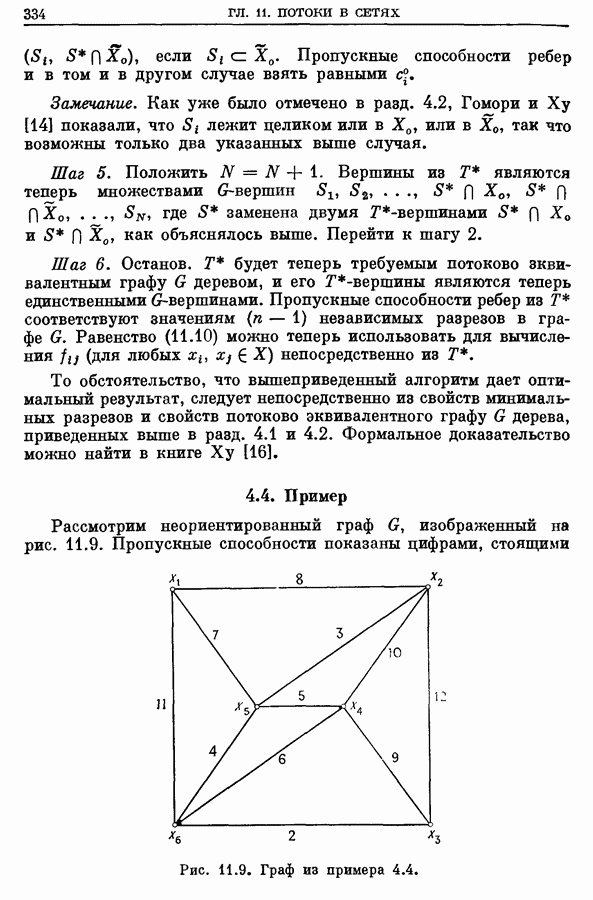
- 4.4. Пример
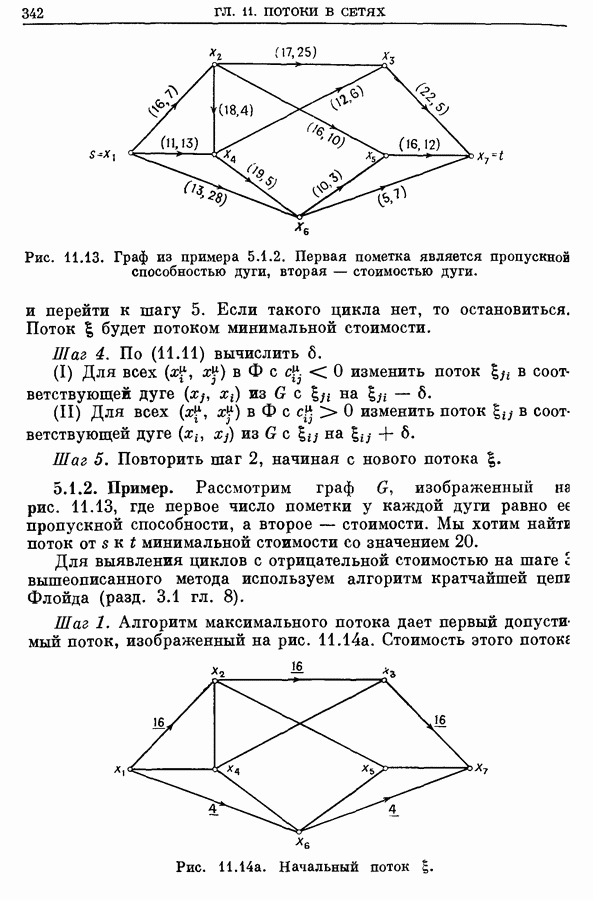
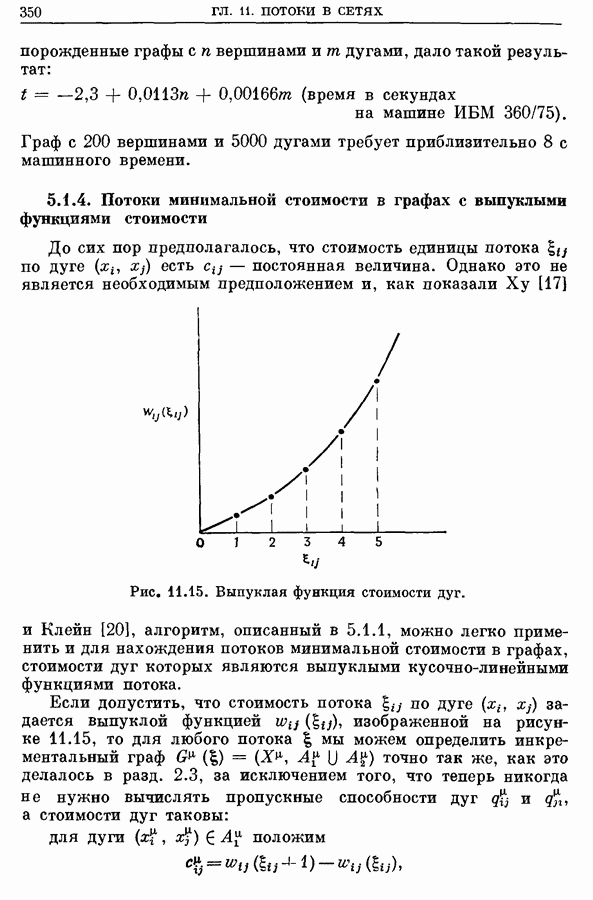
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
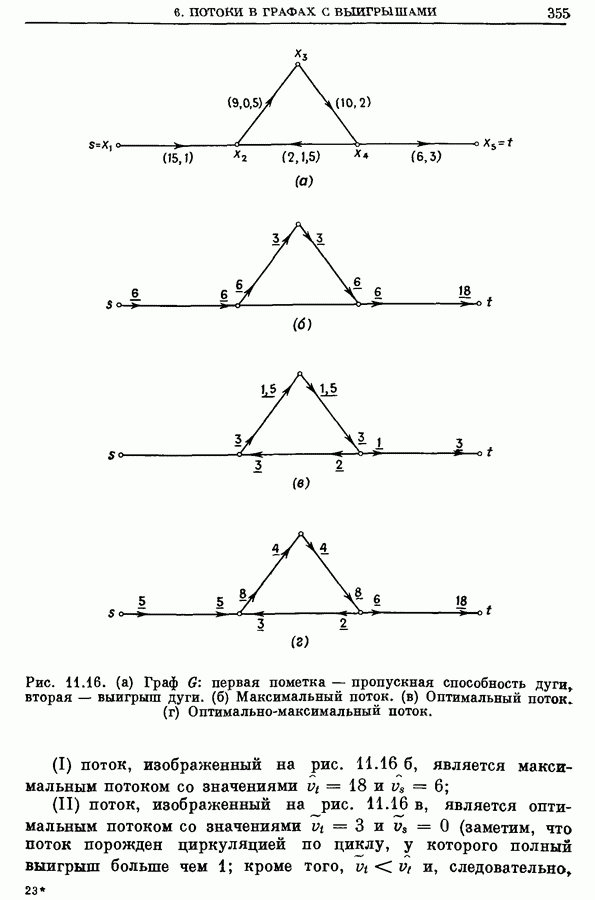
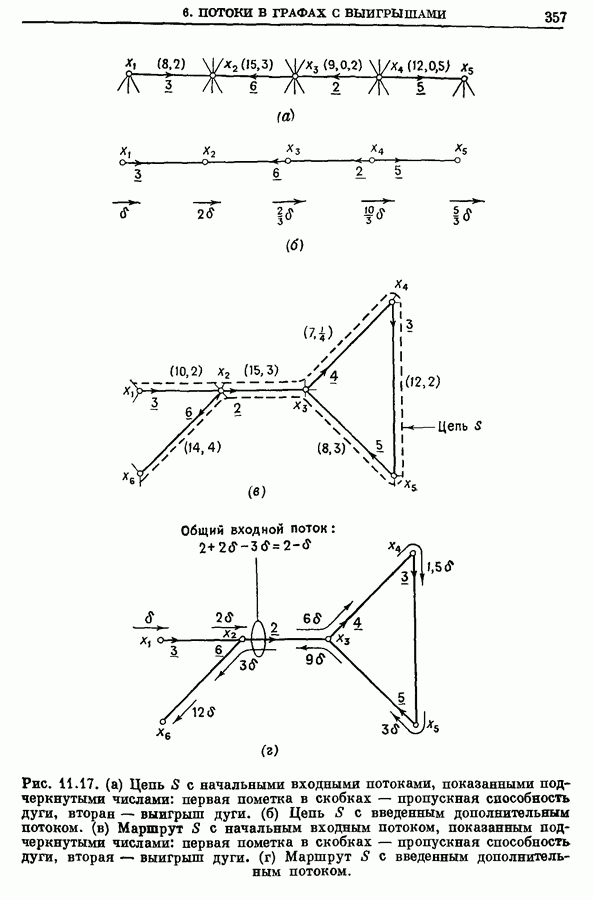
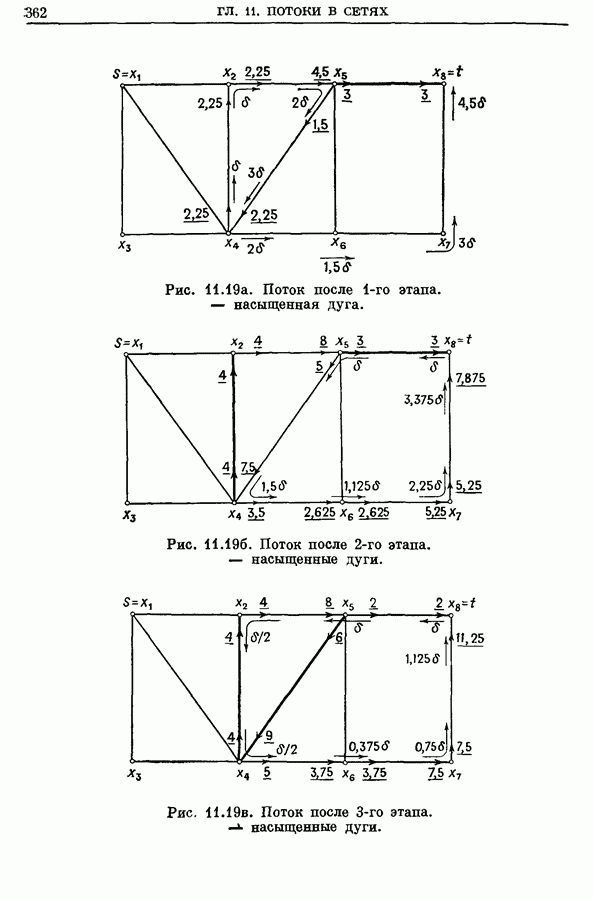
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
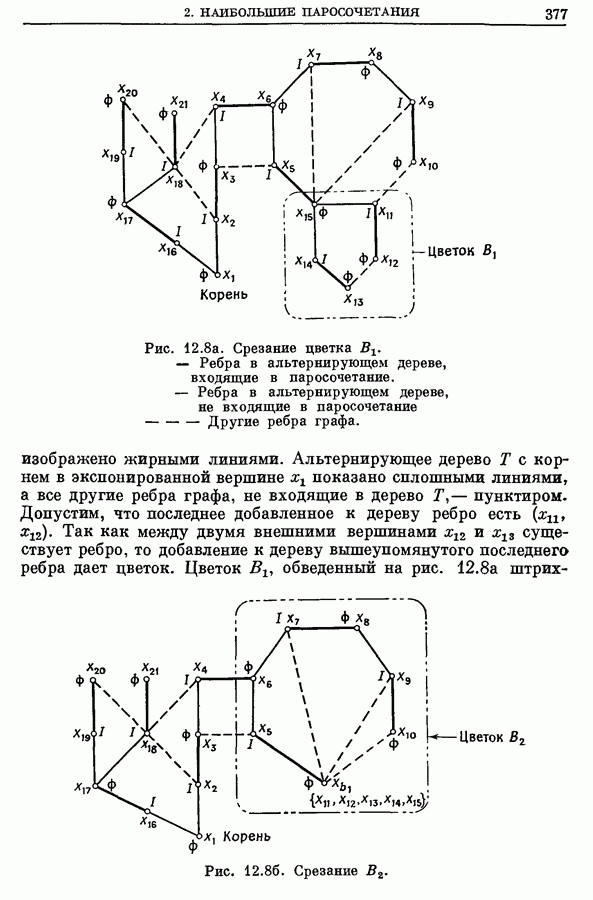
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
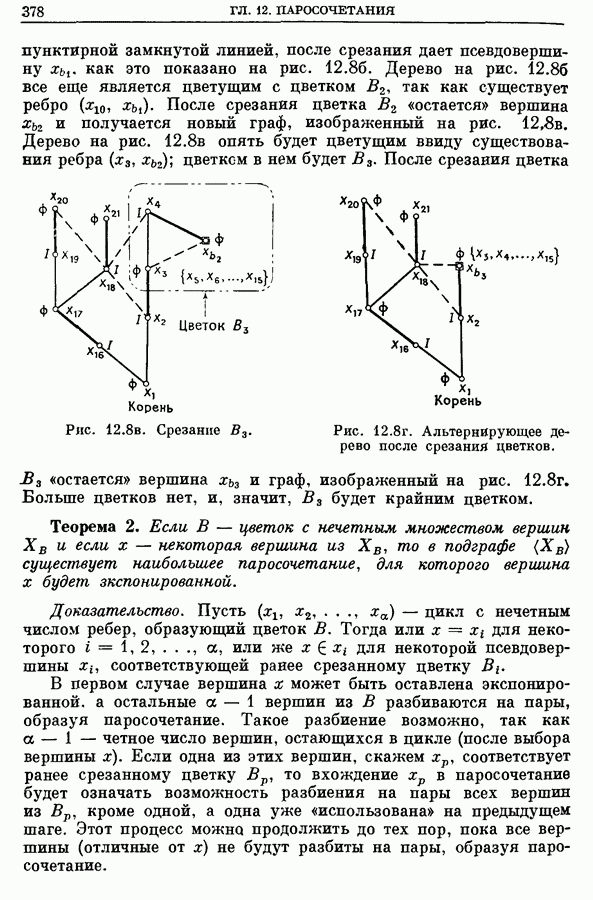
- 2.2. Цветки
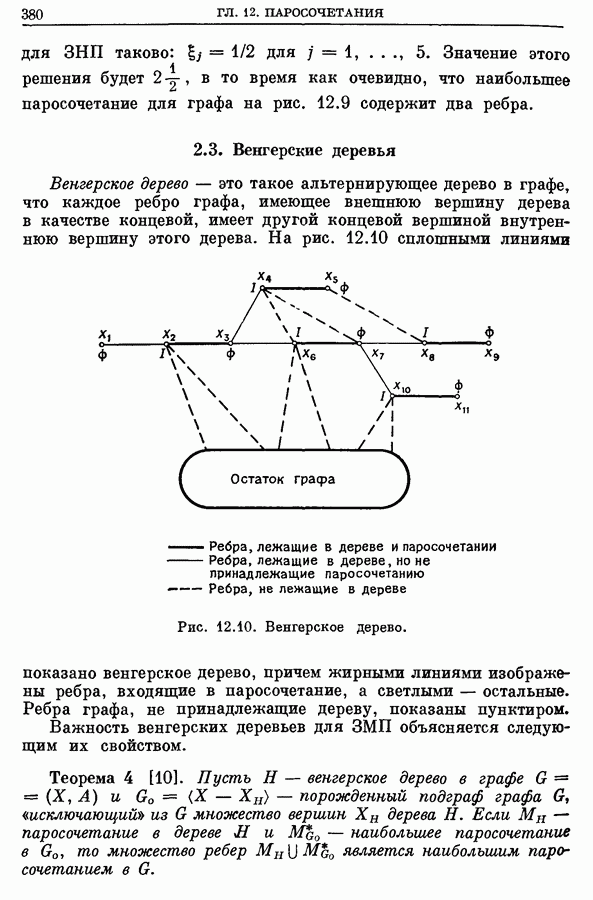
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
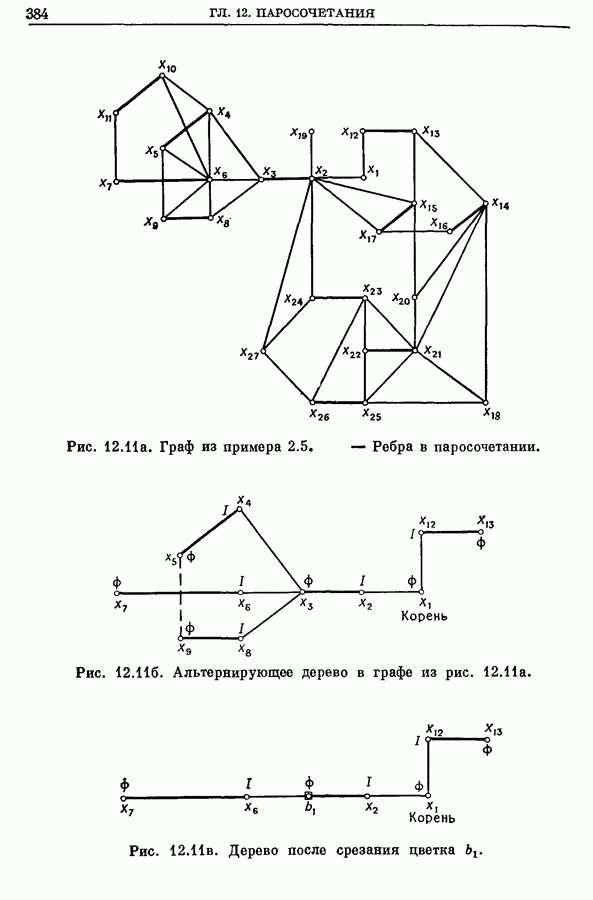
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
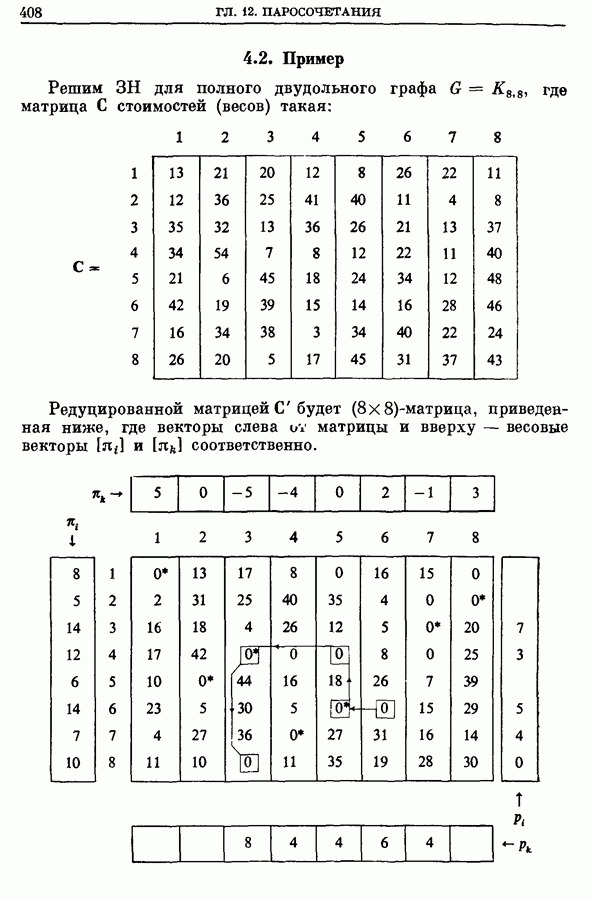
- 4.2. Пример
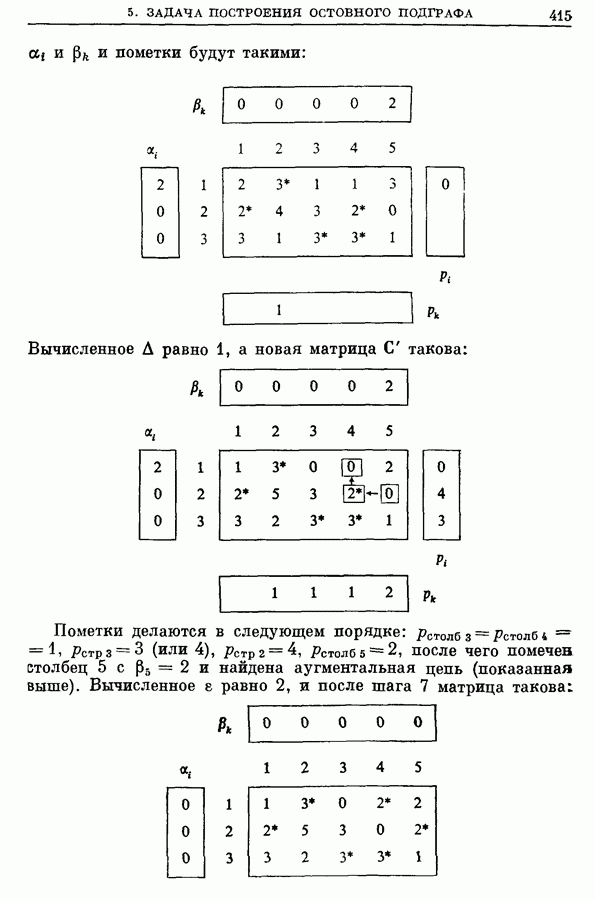
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
- 5.2. Пример
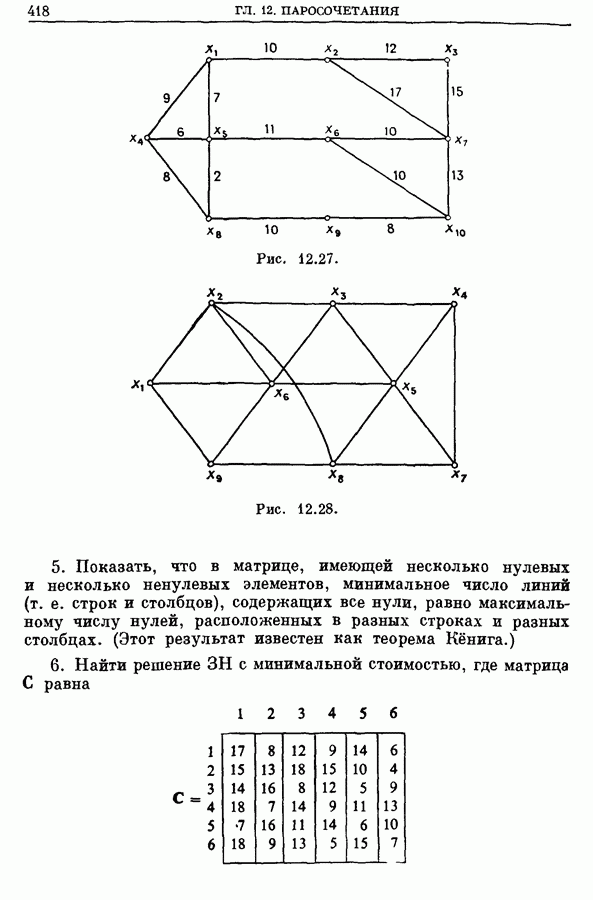
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
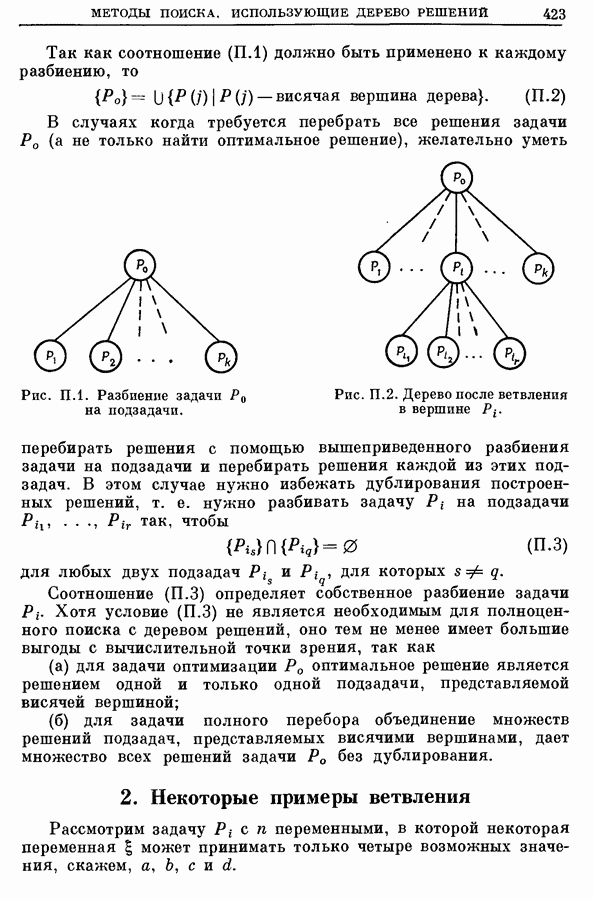
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
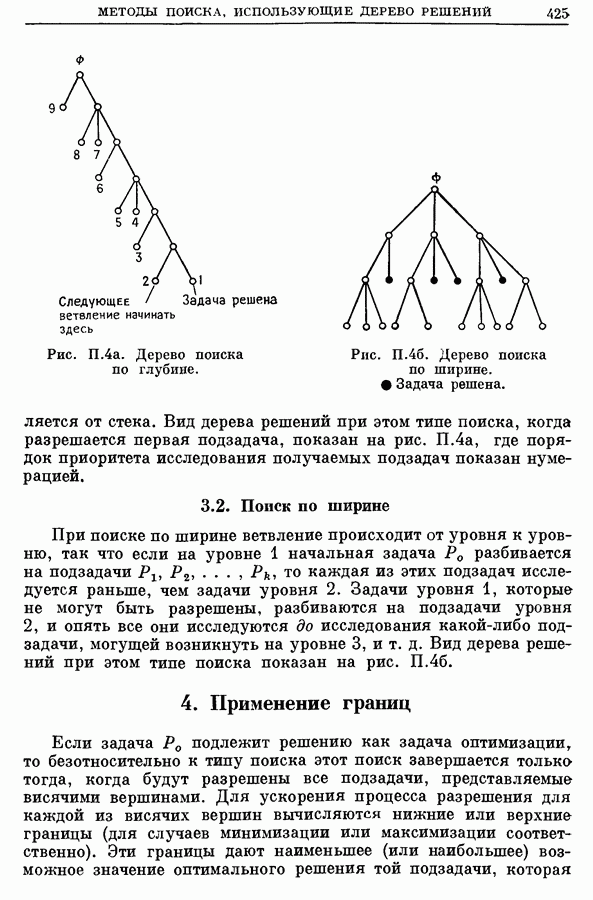
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления