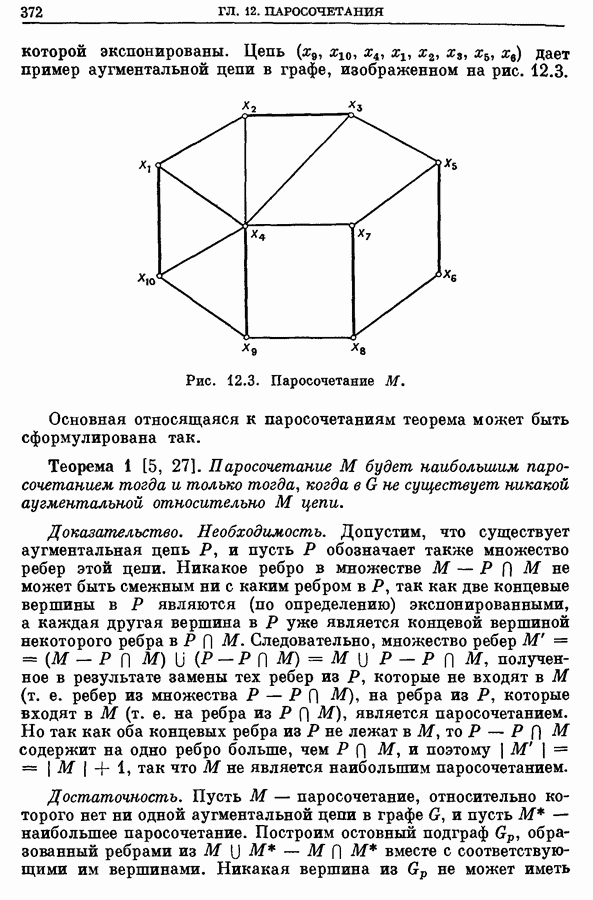
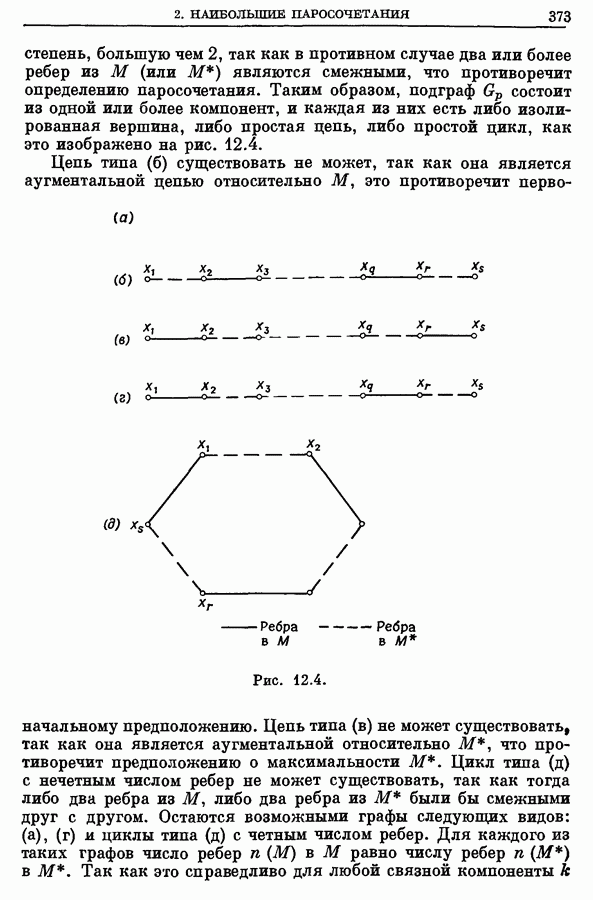
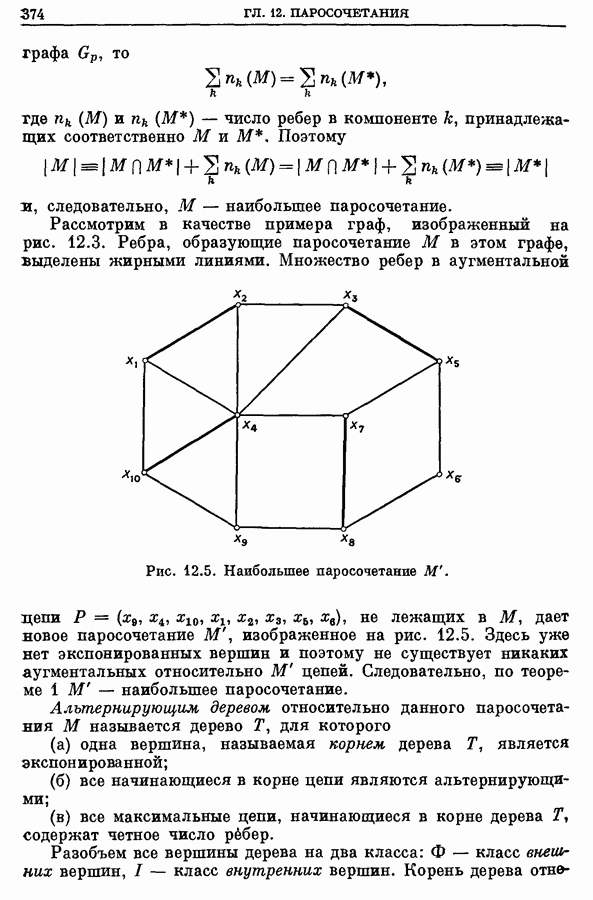
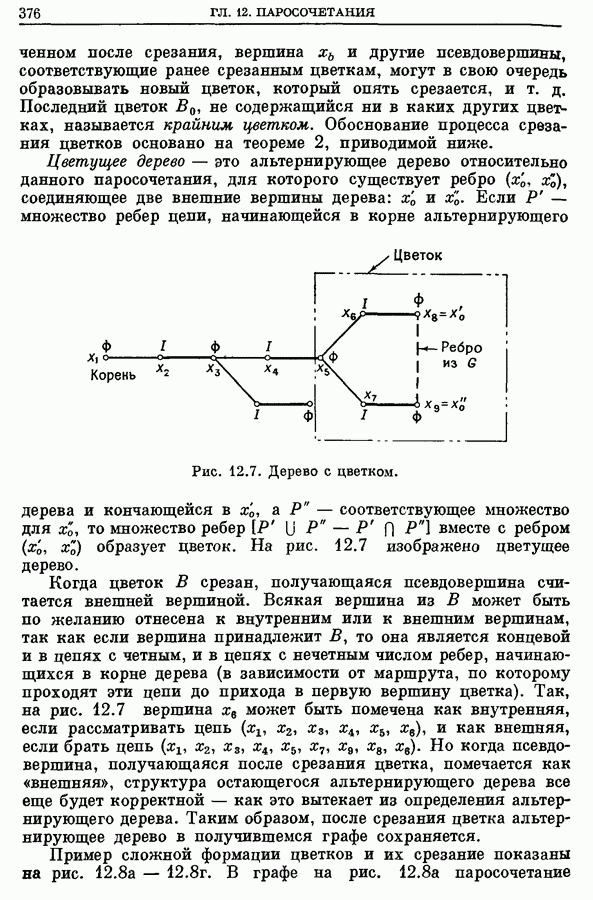
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
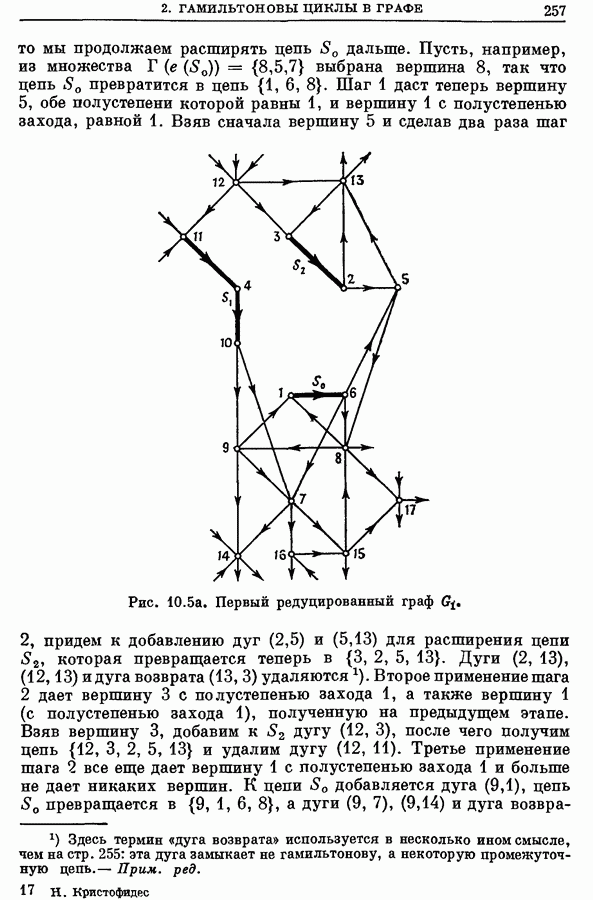
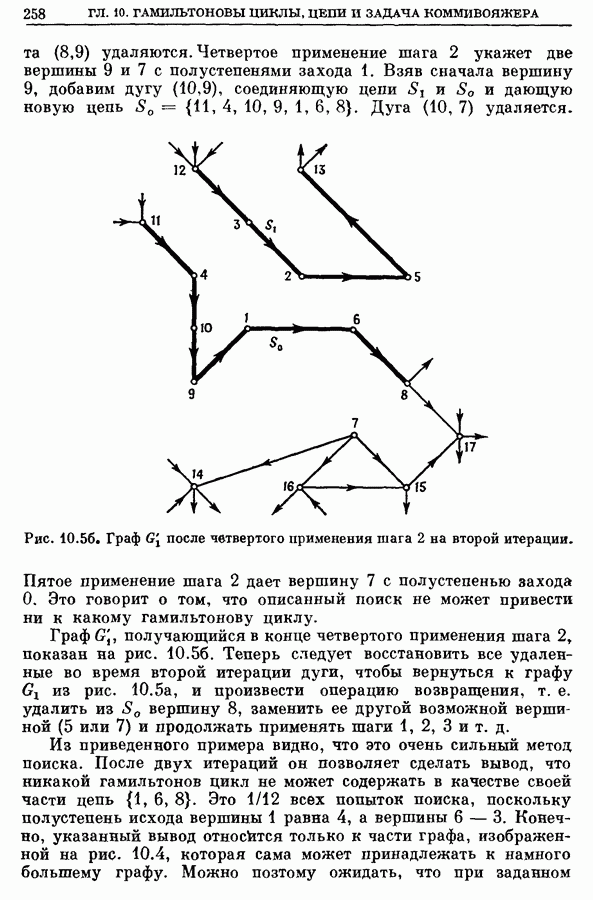
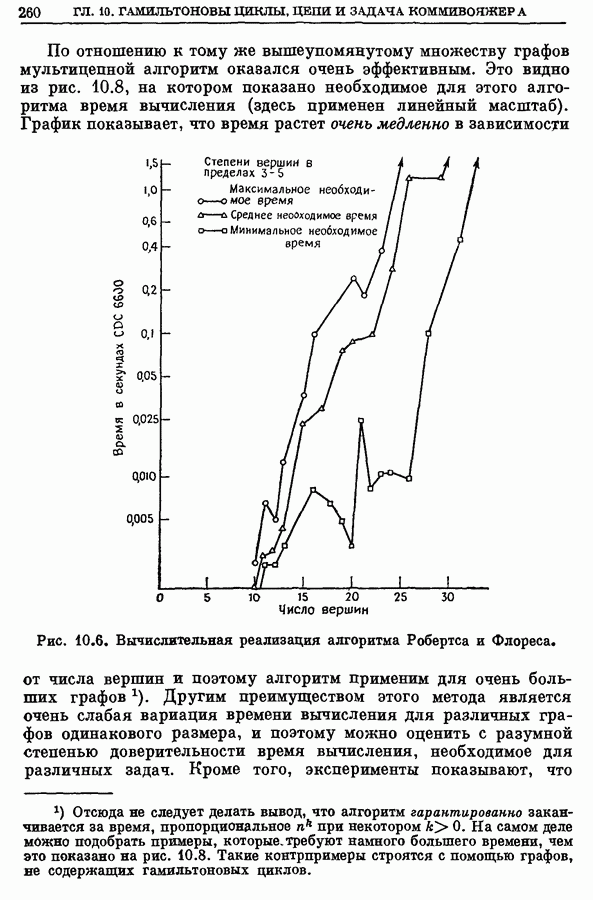
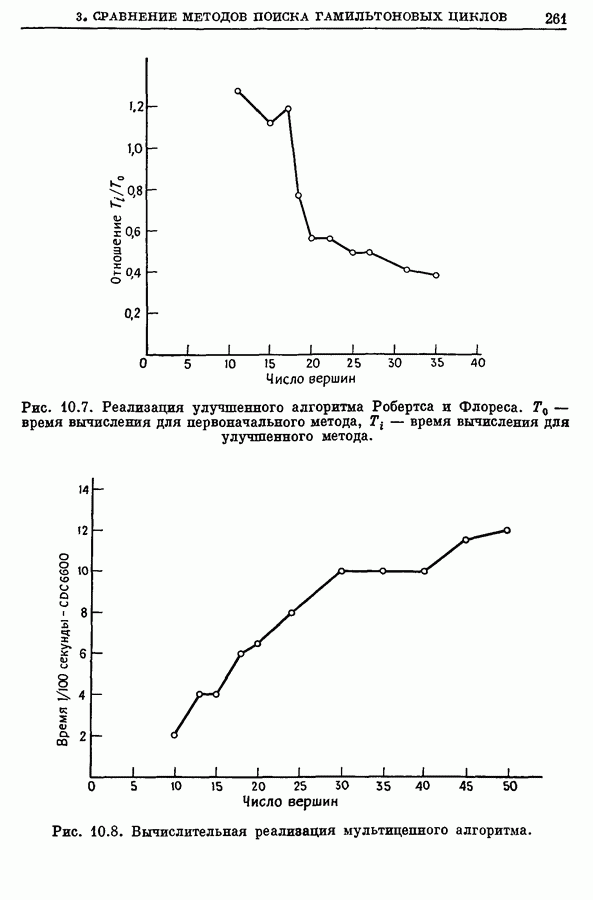
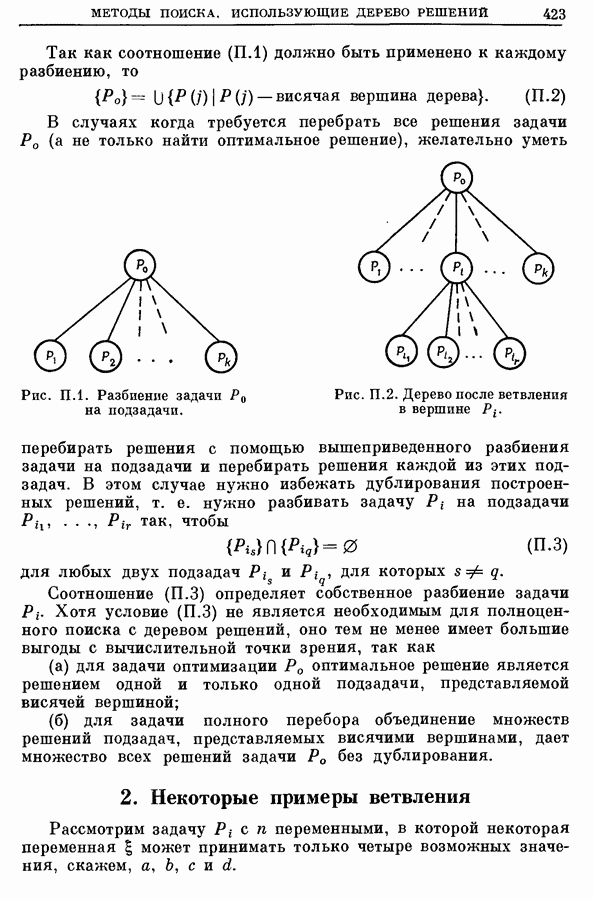
3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
Для определения хроматического числа графа может быть использован с поразительной эффективностью очень простой метод неявного перебора, не содержащий никаких хитростей [4, 9]. Метод состоит в следующем.
Предположим, что множество вершин как-то упорядочено и  вершина этого множества. Тогда первоначальная допустимая раскраска может быть получена так:
вершина этого множества. Тогда первоначальная допустимая раскраска может быть получена так:
(i) окрасить  в цвет 1.
в цвет 1.
(ii) каждую из оставшихся вершин окрашивать последовательно: вершина  окрашивается в цвет с наименьшим возможным «номером» (т. е. выбираемый цвет должен быть первым в данном упорядочении цветом, не использованным при окраске какой-либо вершины, смежной с
окрашивается в цвет с наименьшим возможным «номером» (т. е. выбираемый цвет должен быть первым в данном упорядочении цветом, не использованным при окраске какой-либо вершины, смежной с 
Пусть  число цветов, требуемое для вышеупомянутой раскраски. Если существует раскраска, использующая только
число цветов, требуемое для вышеупомянутой раскраски. Если существует раскраска, использующая только  цветов, то все вершины, окрашенные в цвет
цветов, то все вершины, окрашенные в цвет  должны быть перекрашены в цвет
должны быть перекрашены в цвет  Пусть
Пусть  первая вершина при заданном упорядочении, которая была окрашена в цвету. Поскольку (согласно (ii)) она была так окрашена потому, что не могла быть окрашена в цвет
первая вершина при заданном упорядочении, которая была окрашена в цвету. Поскольку (согласно (ii)) она была так окрашена потому, что не могла быть окрашена в цвет  то ее можно перекрасить в цвет
то ее можно перекрасить в цвет  лишь перекрасив предварительно хотя бы одну из смежных с ней вершин. Итак, шаг возвращения из вершины
лишь перекрасив предварительно хотя бы одну из смежных с ней вершин. Итак, шаг возвращения из вершины  можно осуществить следующим образом.
можно осуществить следующим образом.
Из смежных с  вершин в множестве
вершин в множестве  найти последнюю (при заданном упорядочении), т. е. вершину с наибольшим индексом. Пусть это будет вершина
найти последнюю (при заданном упорядочении), т. е. вершину с наибольшим индексом. Пусть это будет вершина  Если
Если  окрашена в цвет
окрашена в цвет  то
то  перекрашивается в другой допустимый цвет с наименьшим возможным «номером»
перекрашивается в другой допустимый цвет с наименьшим возможным «номером»  таким, что
таким, что 
Если  то надо продолжать последовательно перекрашивать все вершины с
то надо продолжать последовательно перекрашивать все вершины с  до
до  применяя указанное выше правило (ii) и помня о том, что цвет
применяя указанное выше правило (ii) и помня о том, что цвет  использовать нельзя. Если такая процедура осуществима, то будет найдена новая лучшая раскраска, использующая меньше, чем
использовать нельзя. Если такая процедура осуществима, то будет найдена новая лучшая раскраска, использующая меньше, чем  цветов. В противном случае, т. е. если встретится вершина, «требующая» цвет
цветов. В противном случае, т. е. если встретится вершина, «требующая» цвет  то можно снова сделать шаг возвращения
то можно снова сделать шаг возвращения  из такой вершины.
из такой вершины.
Если  или нет другого допустимого цвета
или нет другого допустимого цвета  (см. ниже замечание
(см. ниже замечание  то можно сразу же делать шаг возвращения из вершины
то можно сразу же делать шаг возвращения из вершины  Алгоритм заканчивает работу, когда на шаге возвращения достигается вершина
Алгоритм заканчивает работу, когда на шаге возвращения достигается вершина 
Следующие замечания могут помочь ускорить вышеприведенную процедуру прямого неявного перебора.
(а) При любом упорядочении вершин допустимые цвета  для вершины
для вершины  удовлетворяют условию
удовлетворяют условию  (если
(если  Это очевидно, так как вершине
Это очевидно, так как вершине  предшествуют (при данном упорядочении) только
предшествуют (при данном упорядочении) только  вершин и, следовательно, никакой цвет
вершин и, следовательно, никакой цвет  не использовался. Таким образом, для вершины
не использовался. Таким образом, для вершины  допустимым является только цвет 1, для
допустимым является только цвет 1, для  цвет 1 и цвет 2 (если
цвет 1 и цвет 2 (если  смежна с
смежна с  то для
то для  допустим только цвет 2) и
допустим только цвет 2) и 
(б) Из замечания (а) следует, что с вычислительной точки зрения выгодно располагать переменные в таком порядке, чтобы, например, первые  вершин образовывали наибольшую клику графа
вершин образовывали наибольшую клику графа  Это приведет к тому, что каждая вершина
Это приведет к тому, что каждая вершина  будет иметь только один допустимый цвет, т. е. цвет
будет иметь только один допустимый цвет, т. е. цвет  и алгоритм может закончить работу раньше, когда на шаге возвращения будет достигнута вершина
и алгоритм может закончить работу раньше, когда на шаге возвращения будет достигнута вершина 
Хотя процедура неявного перебора, описанная в этом разделе, является примитивным древовидным поиском (в котором не нужно вычислять никакие оценки для ограничения ветвлений), тем не менее она нисколько не хуже других известных методов раскраски графов. Так, например, для графа с 30 вершинами, содержащего приблизительно третью часть множества всех ребер полного  -вершинного графа, нахождение оптимальной раскраски с помощью алгоритма неявного перебора требует около 30 с машинного времени на вычислительной машине
-вершинного графа, нахождение оптимальной раскраски с помощью алгоритма неявного перебора требует около 30 с машинного времени на вычислительной машине 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
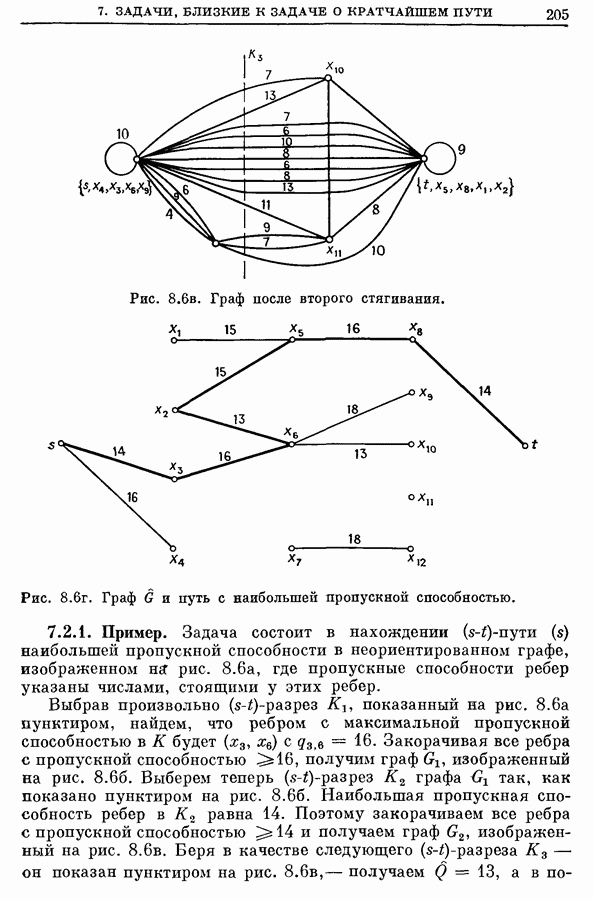
- 7. Задачи, близкие к задаче о кратчайшем пути
- 7.2. Путь с наибольшей пропускной способностью
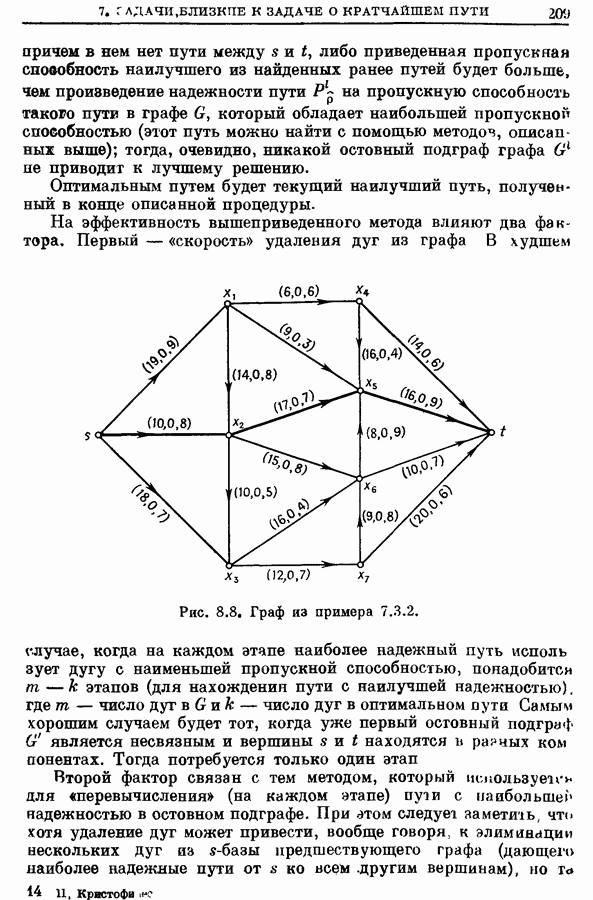
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
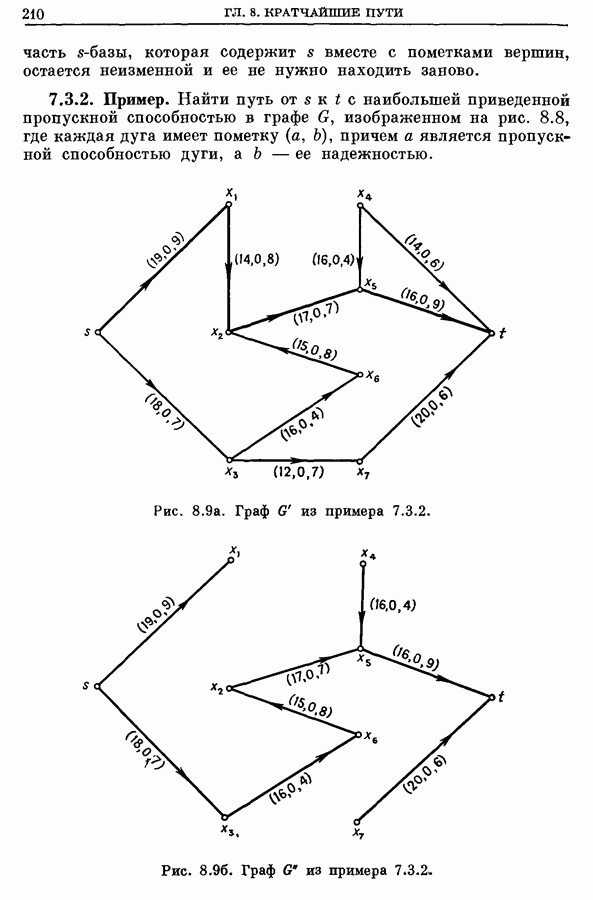
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
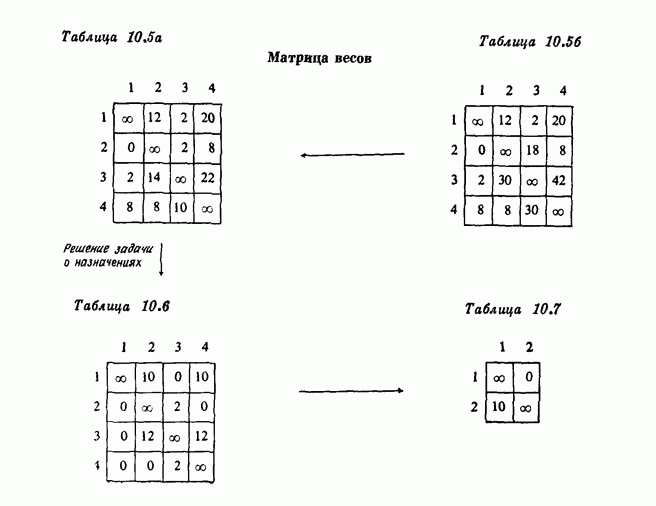
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
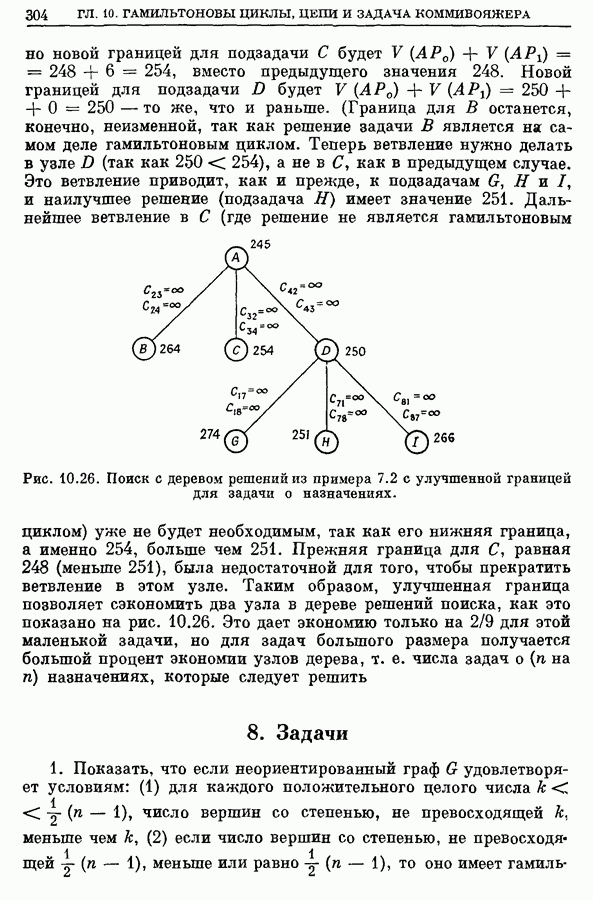
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
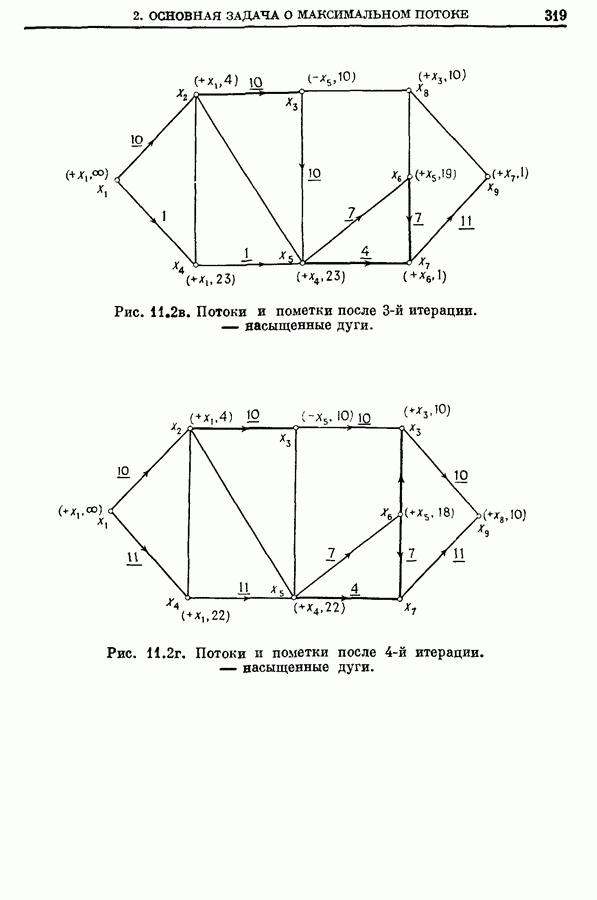
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
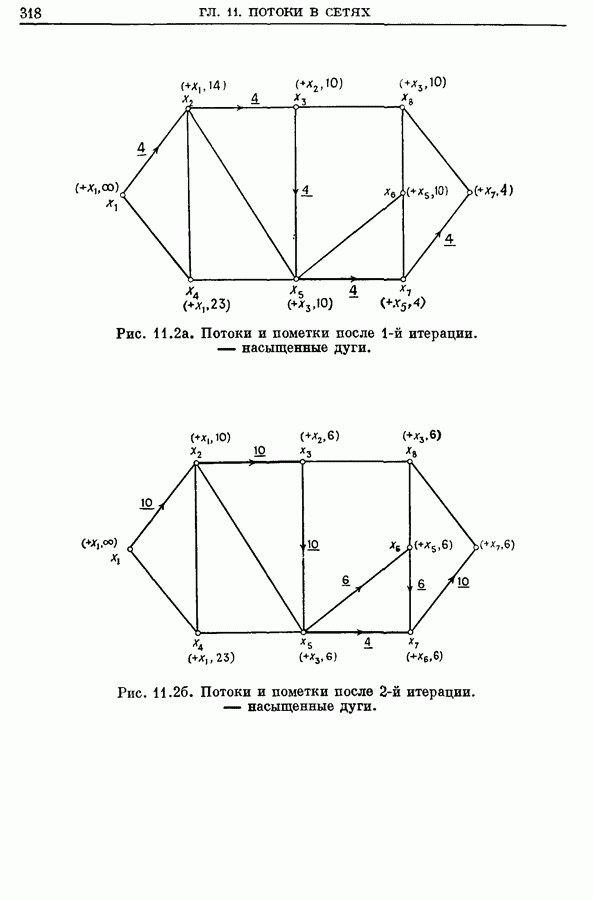
- 2.2. Пример
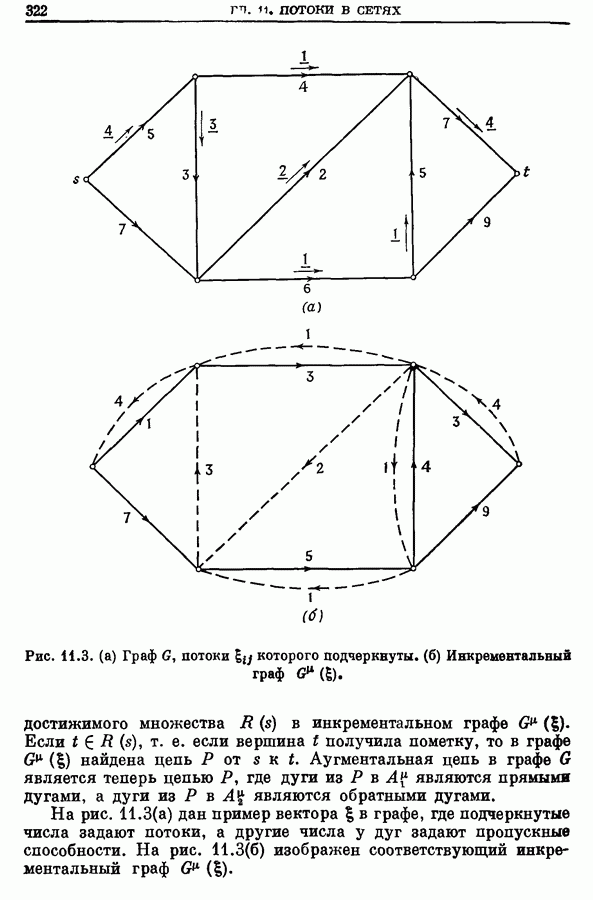
- 2.3. Инкрементальные графы
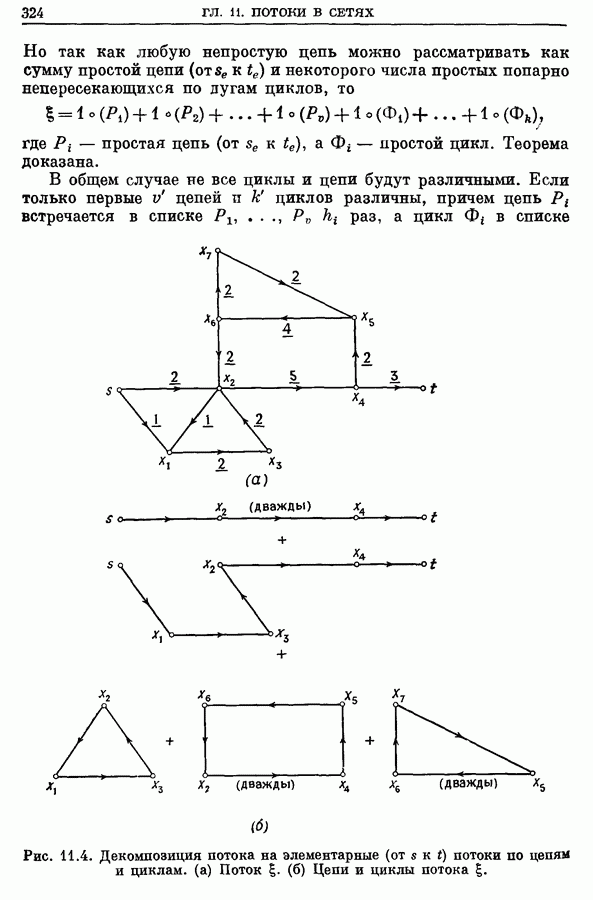
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
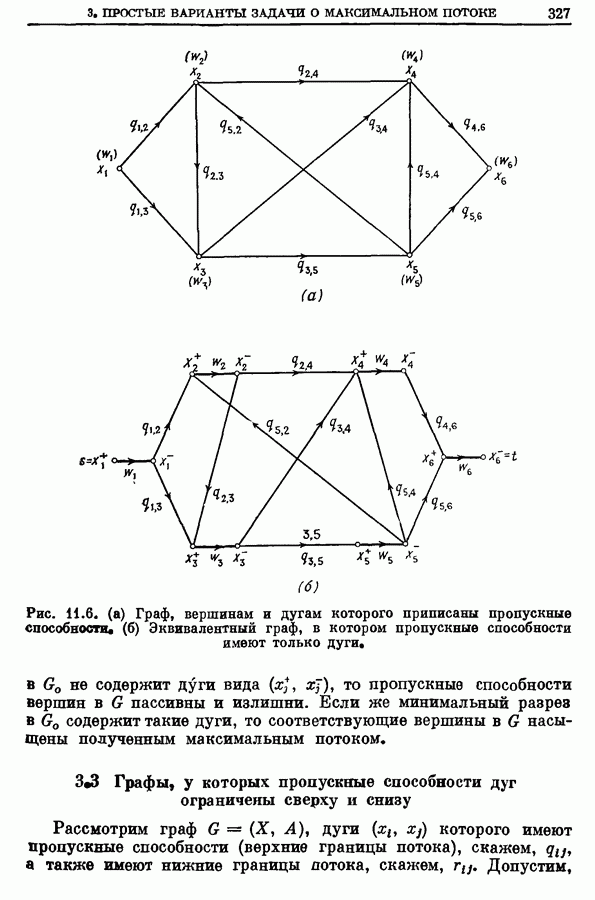
- 3.2. Графы с пропускными способностями дуг и вершин
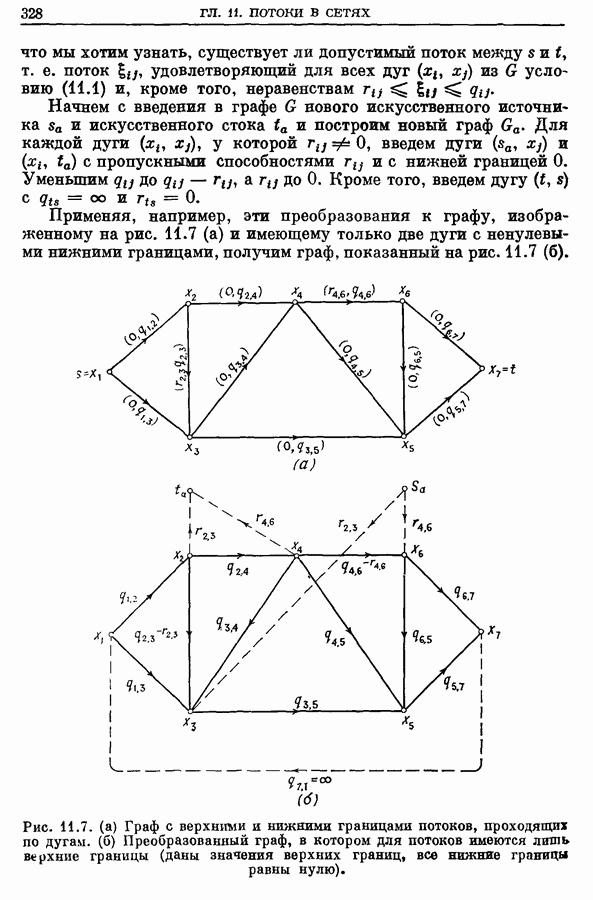
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
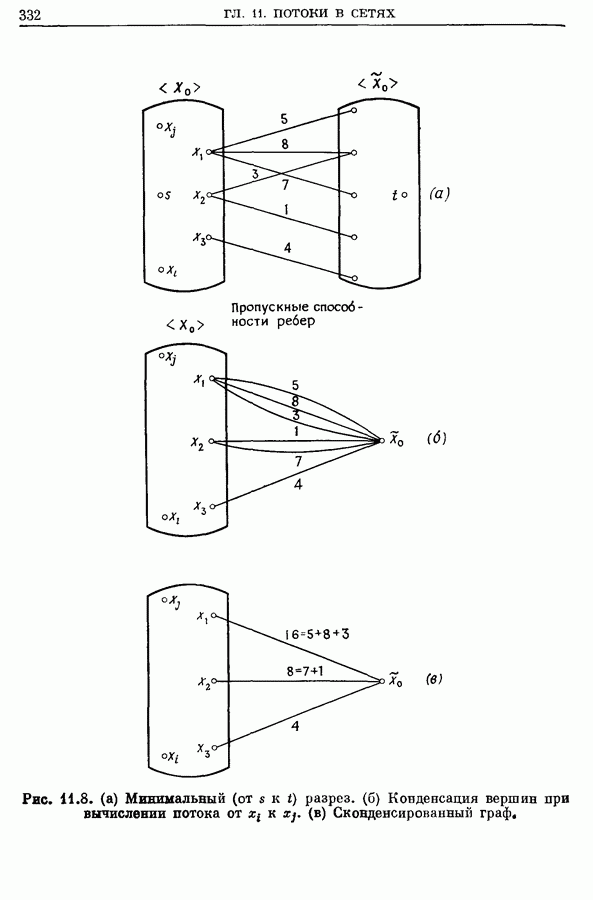
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
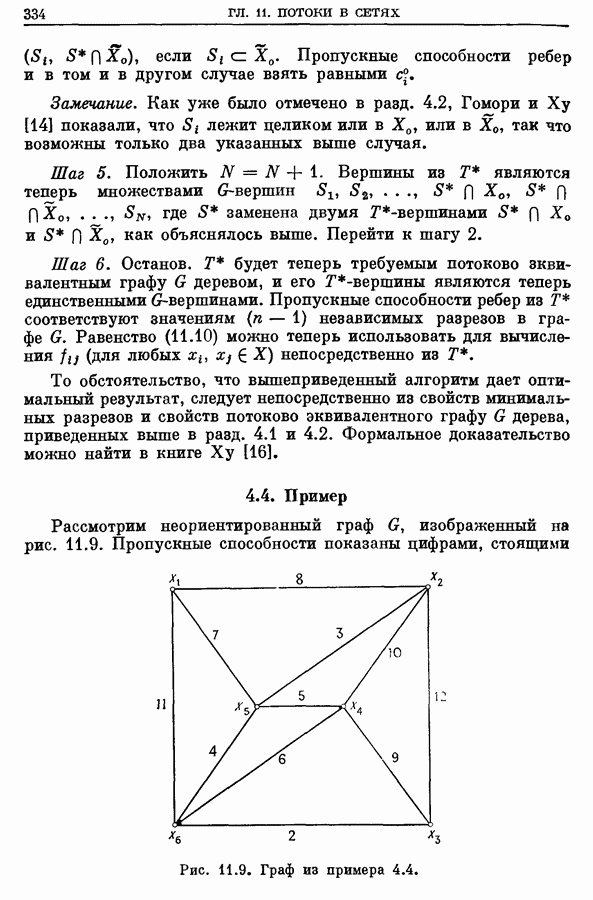
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
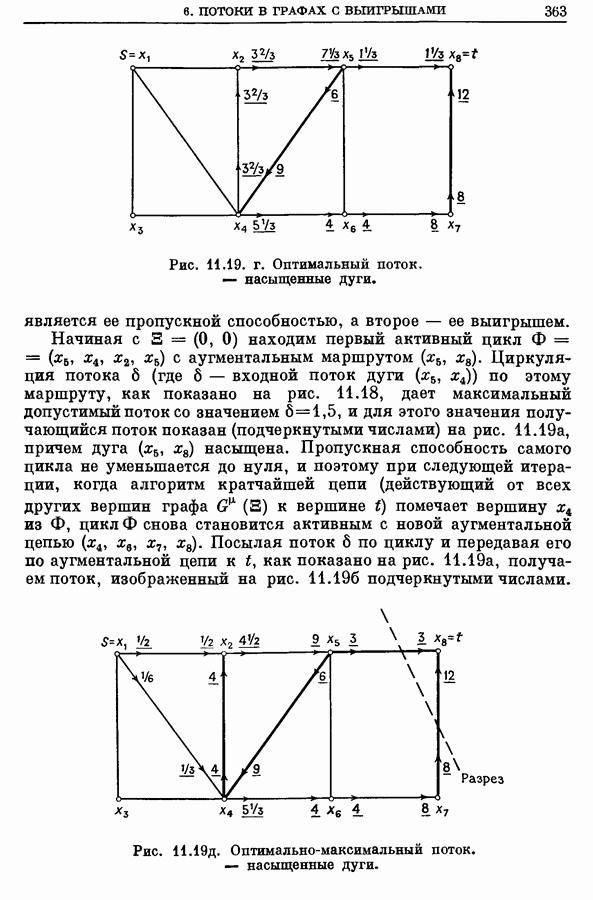
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
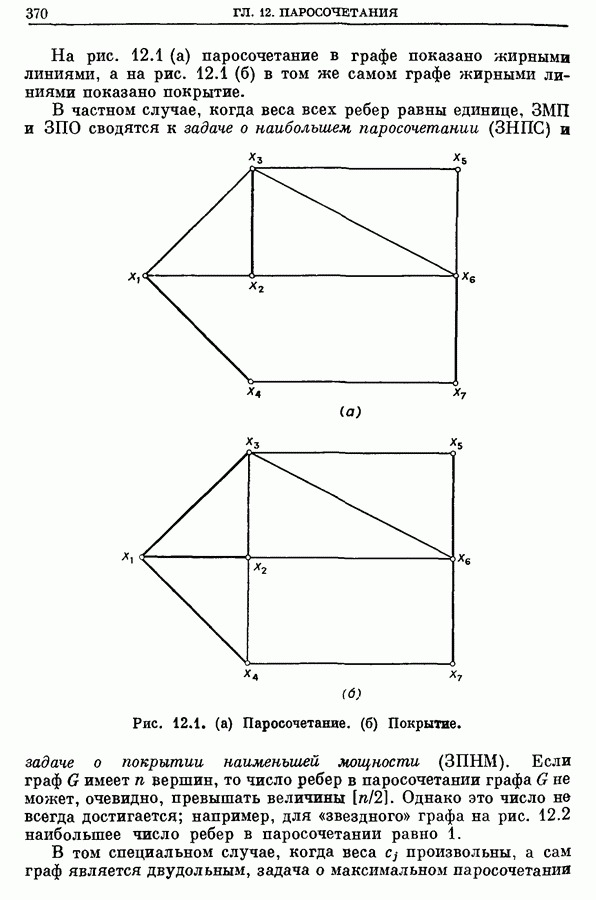
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
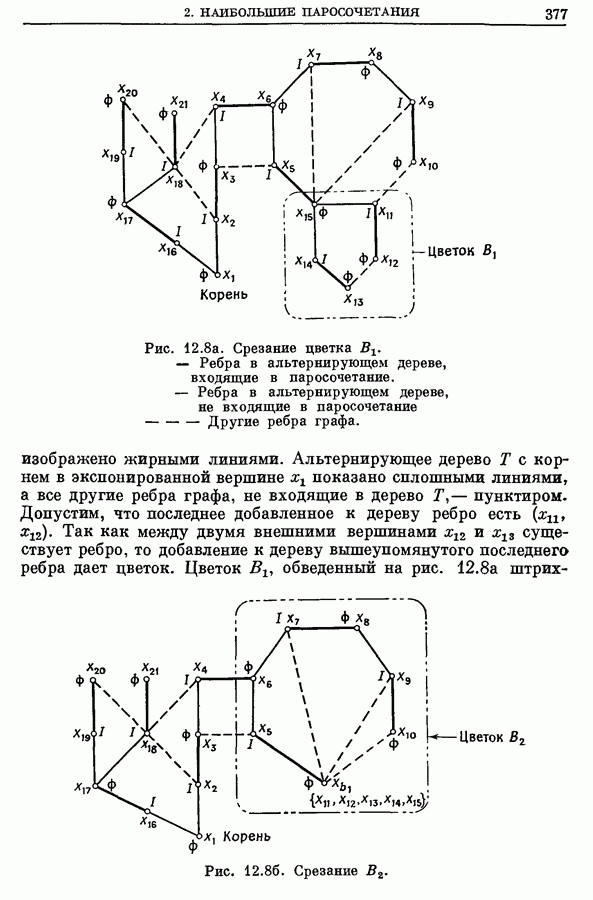
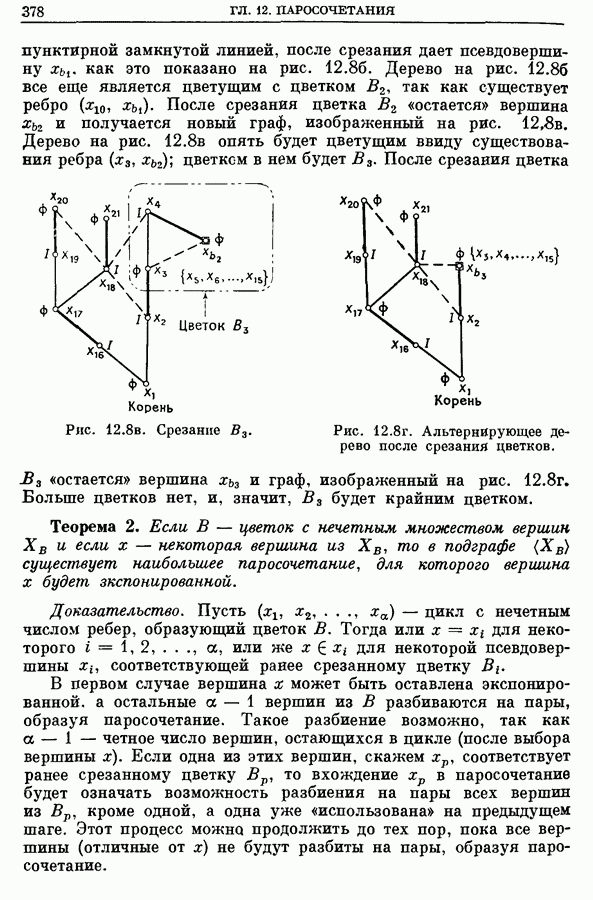
- 2.2. Цветки
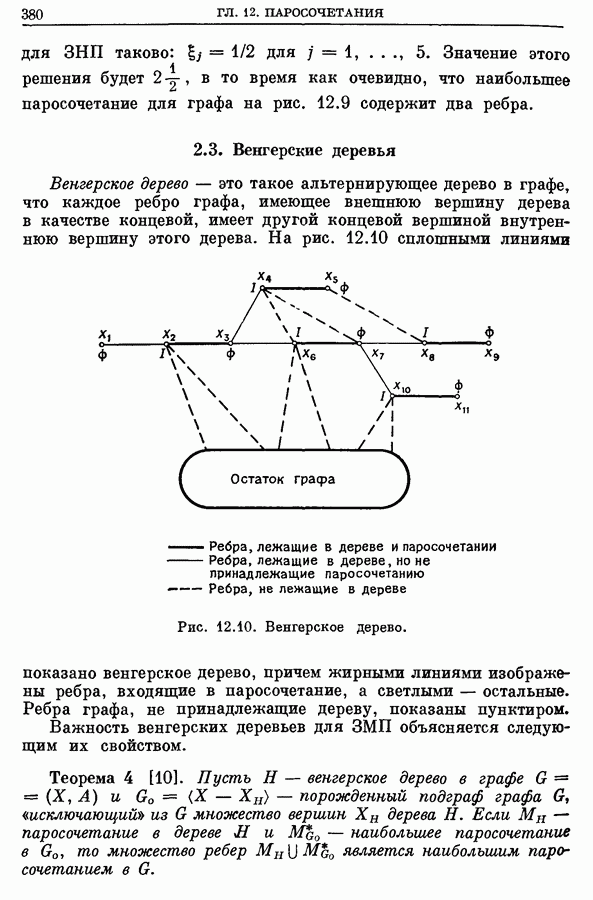
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
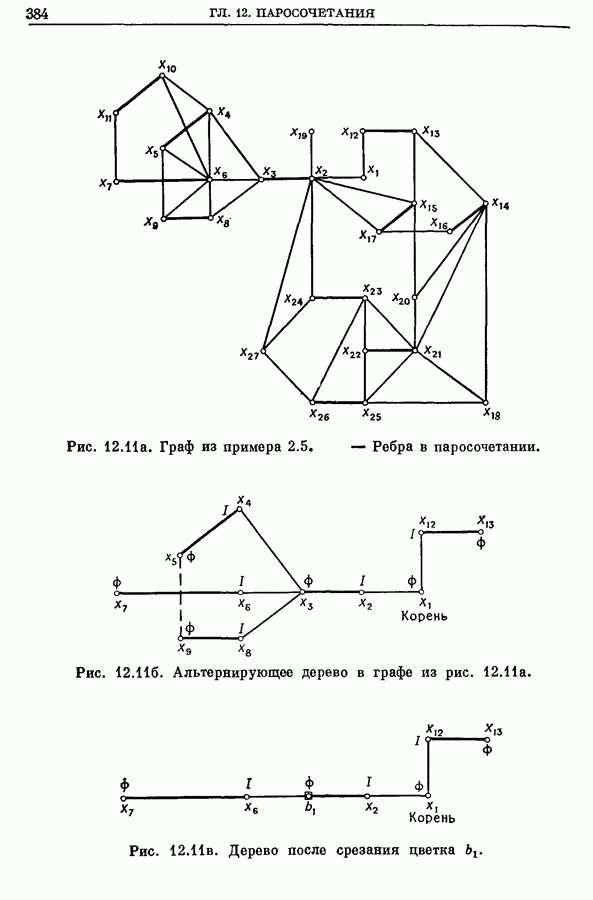
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
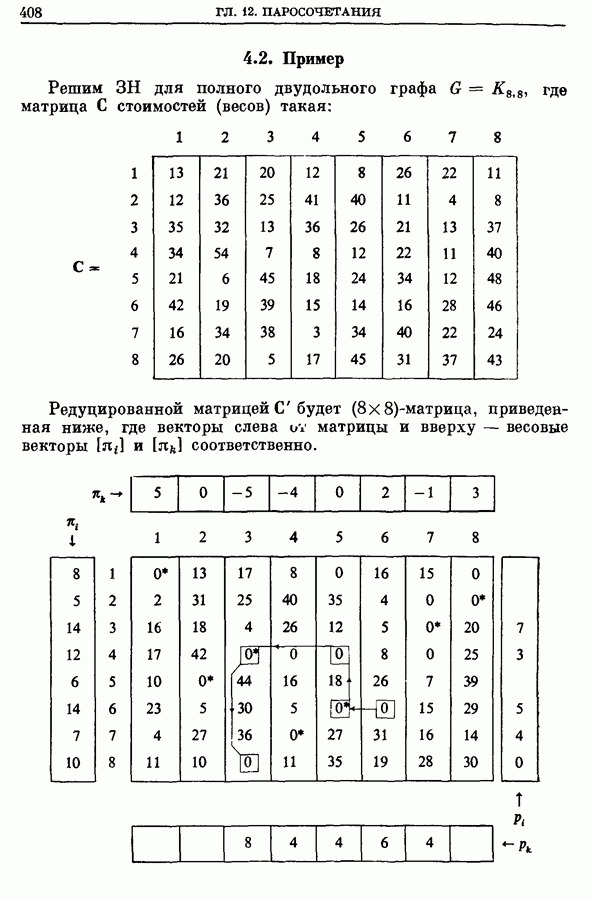
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
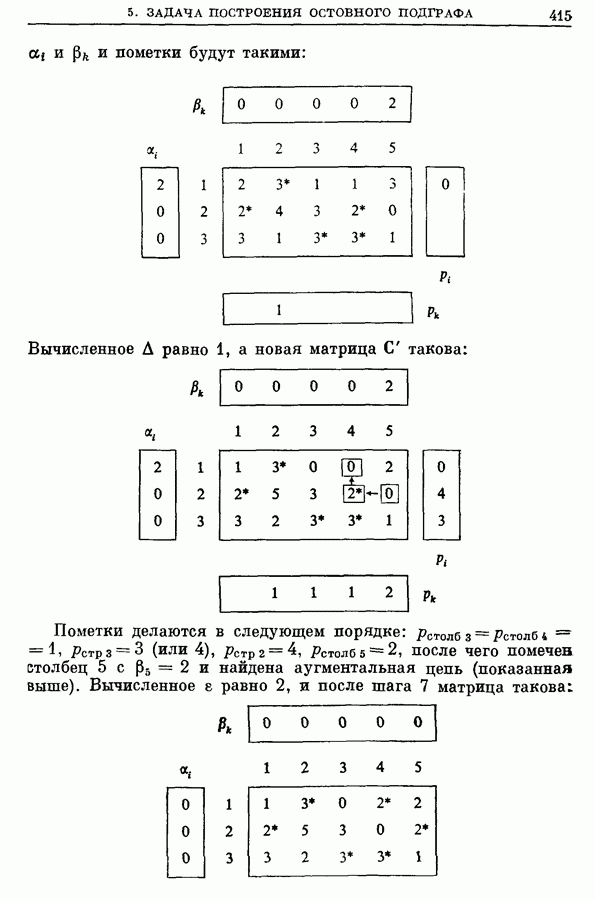
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления