| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
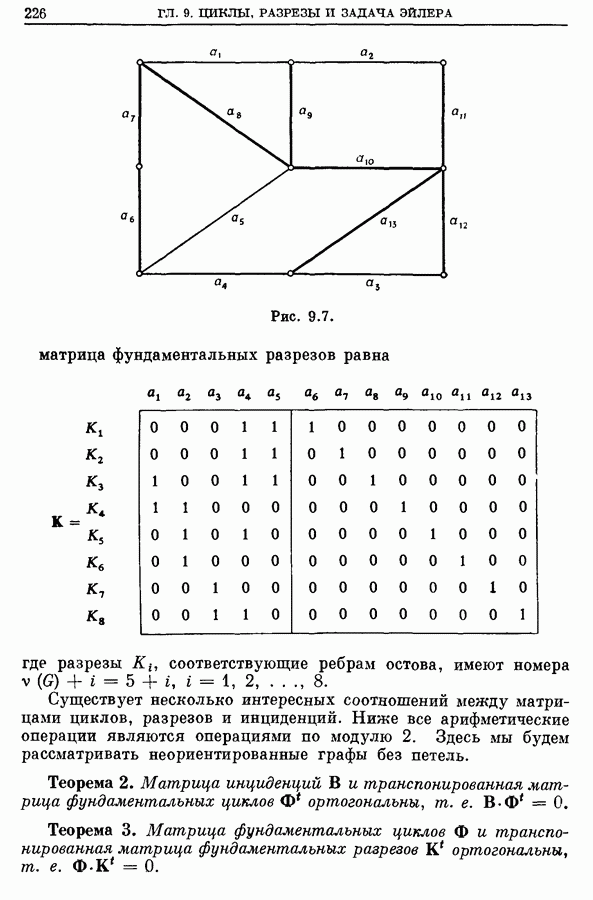
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
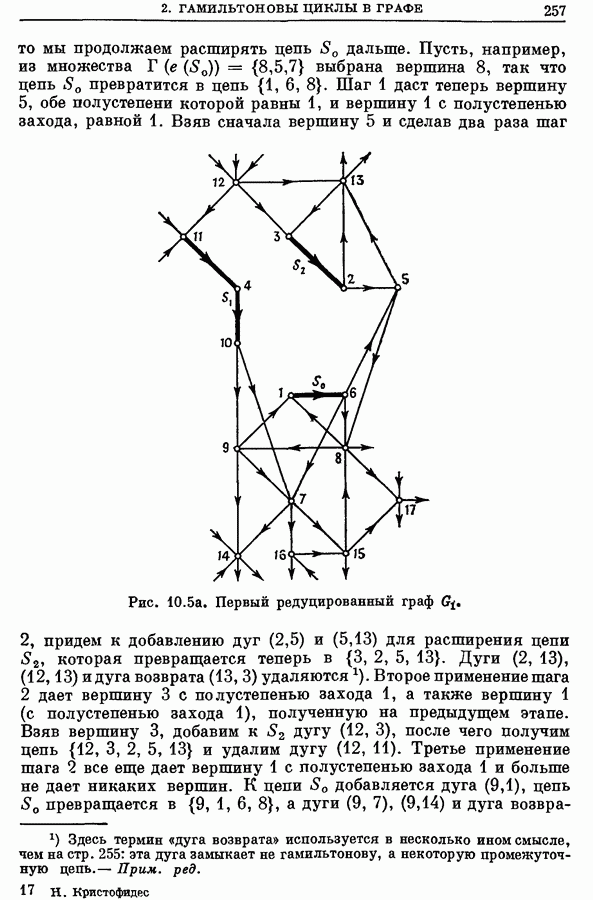
257
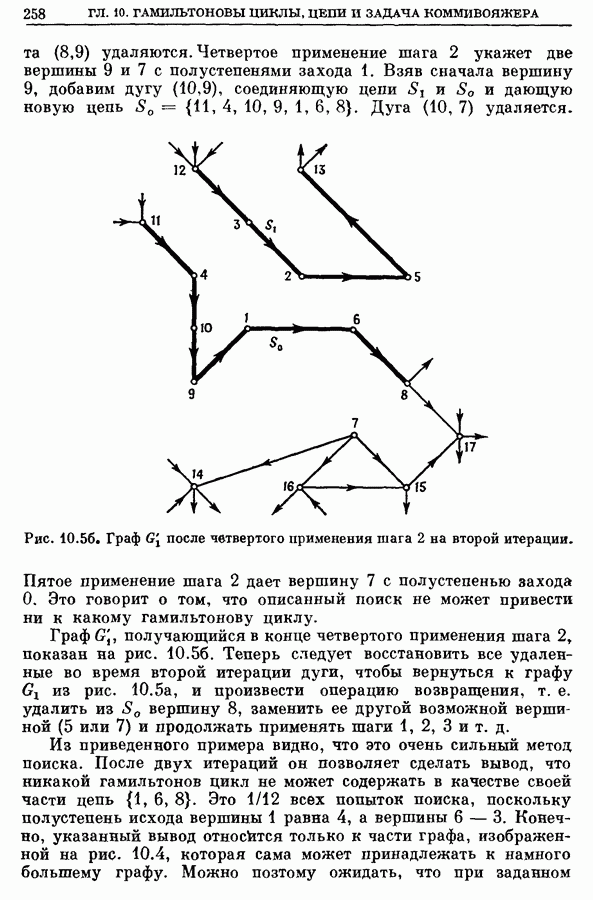
258
259
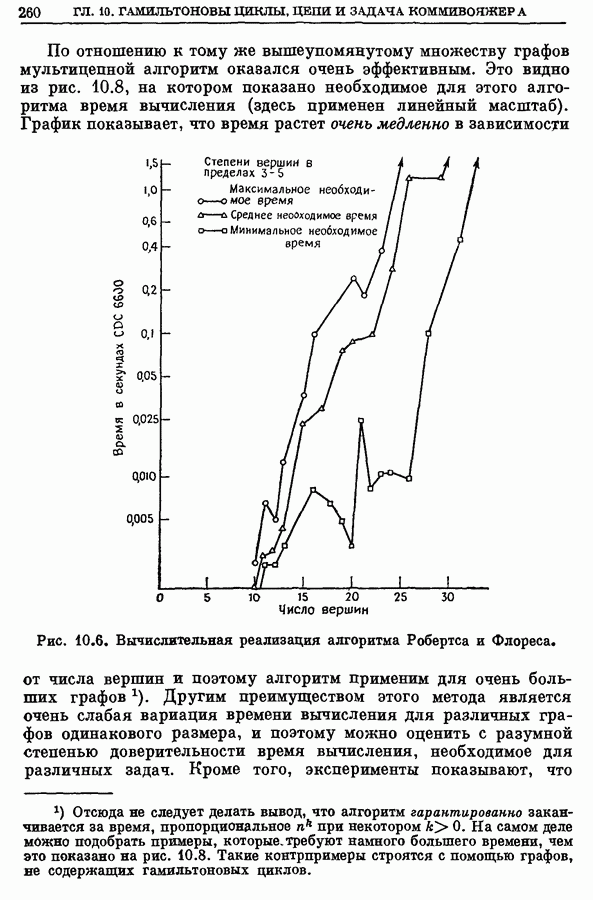
260
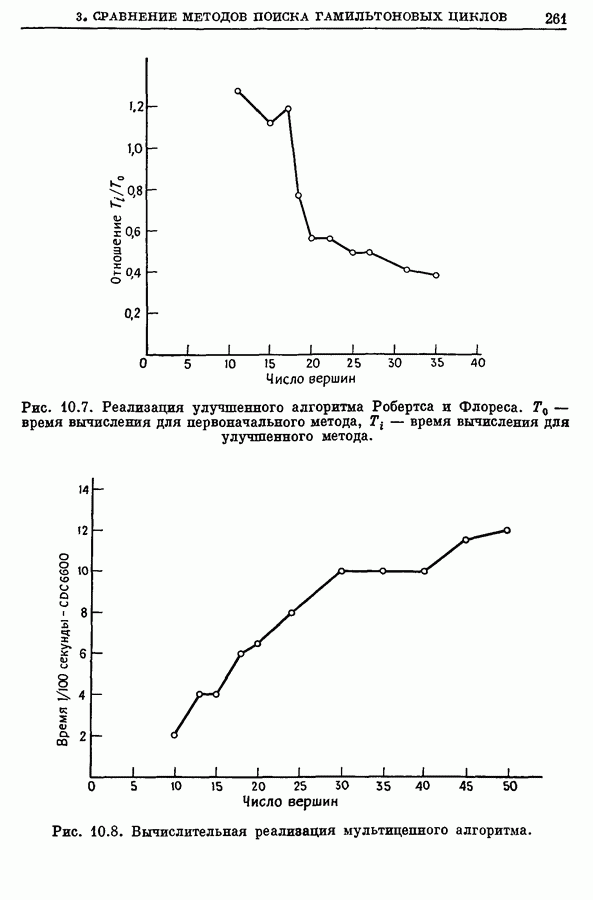
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
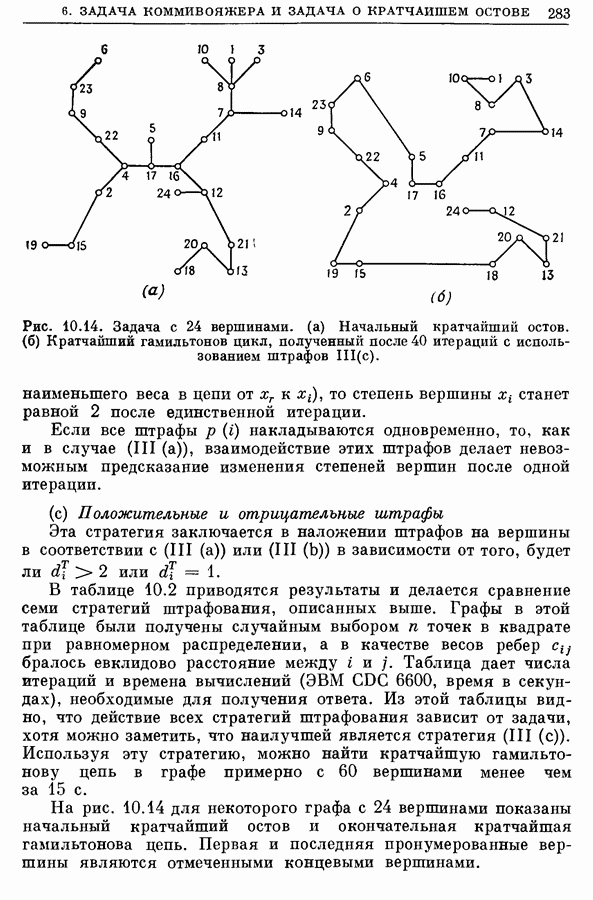
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
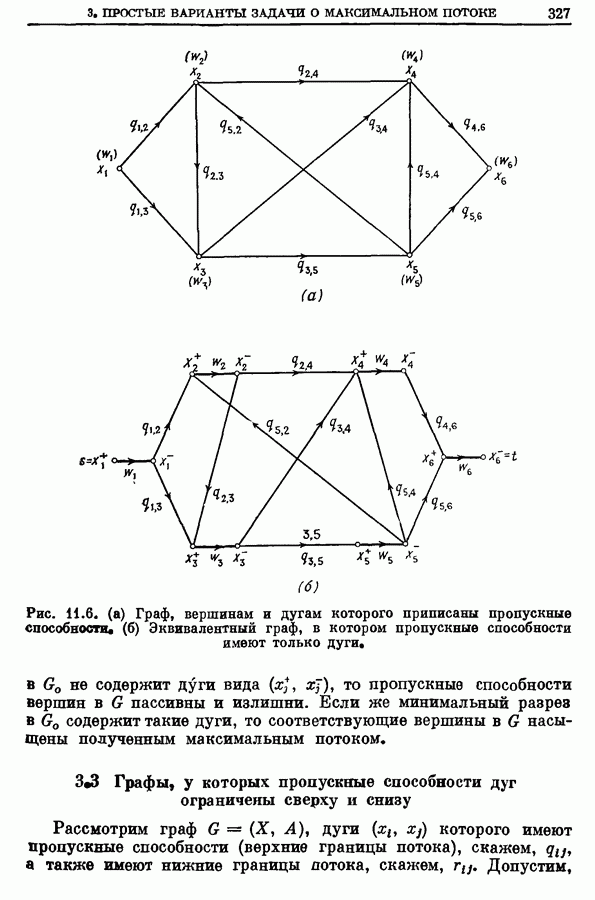
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
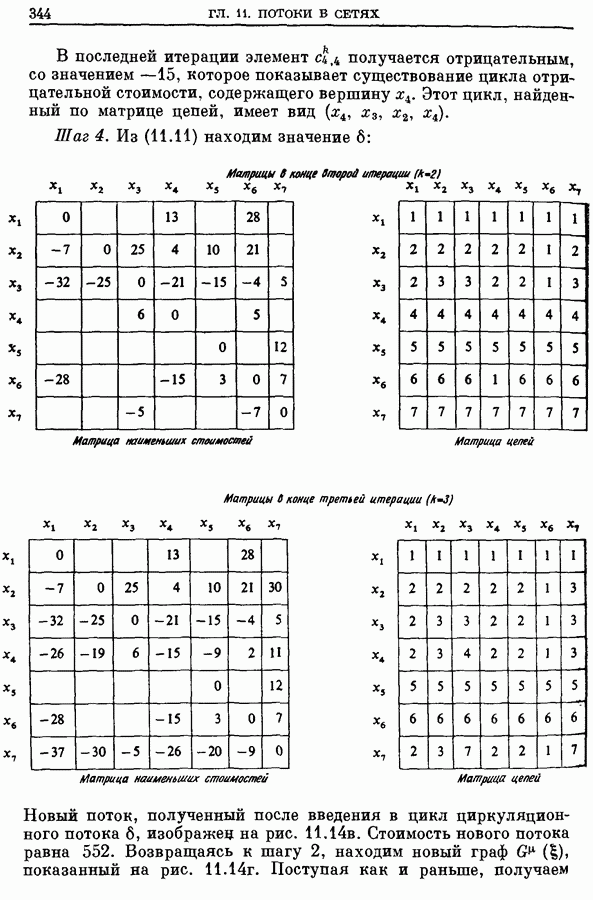
344
345
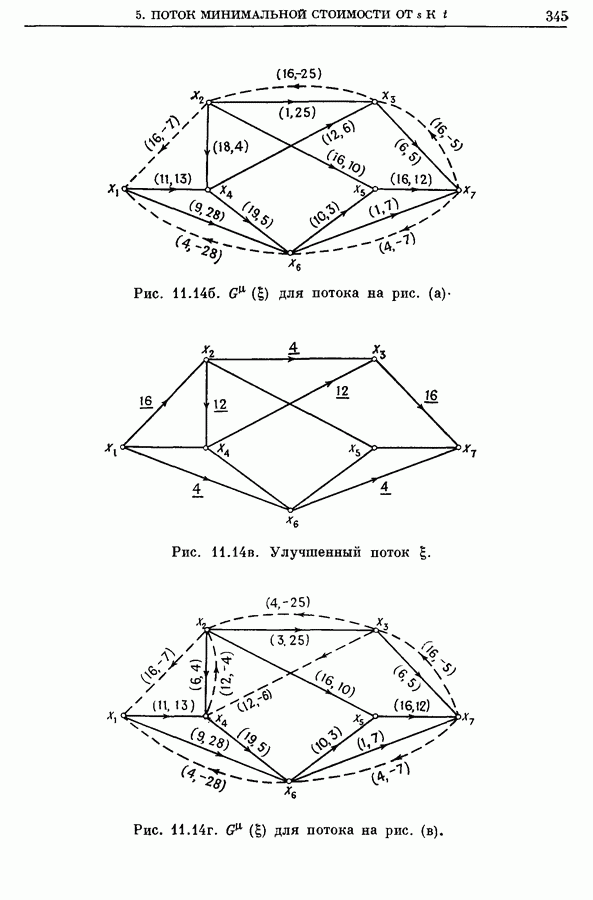
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
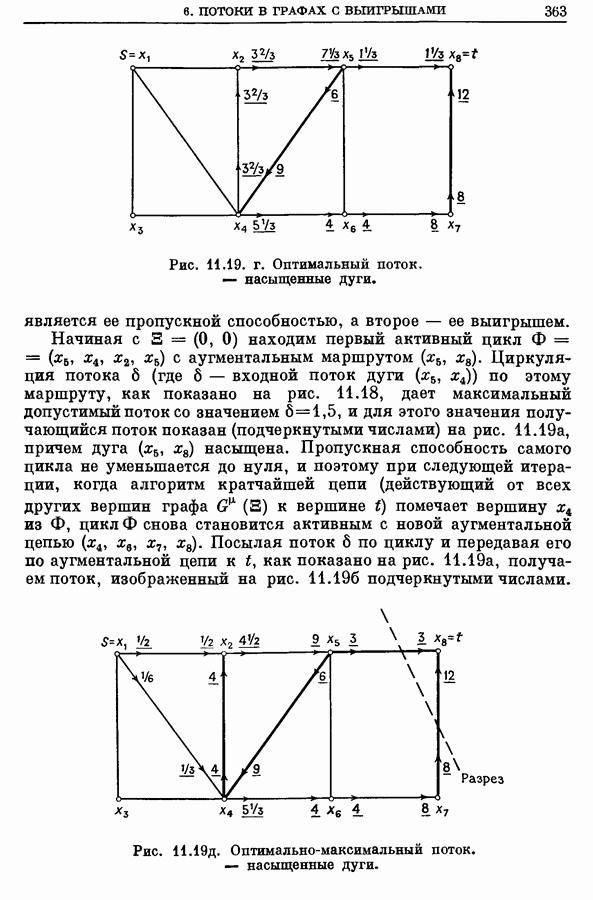
363
364
365
366
367
368
369
370
371
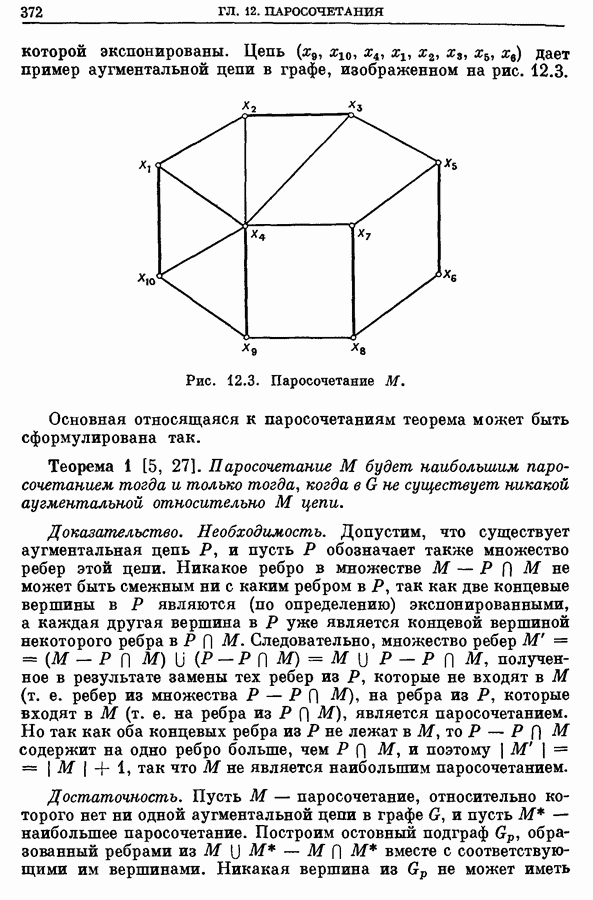
372
373
374
375
376
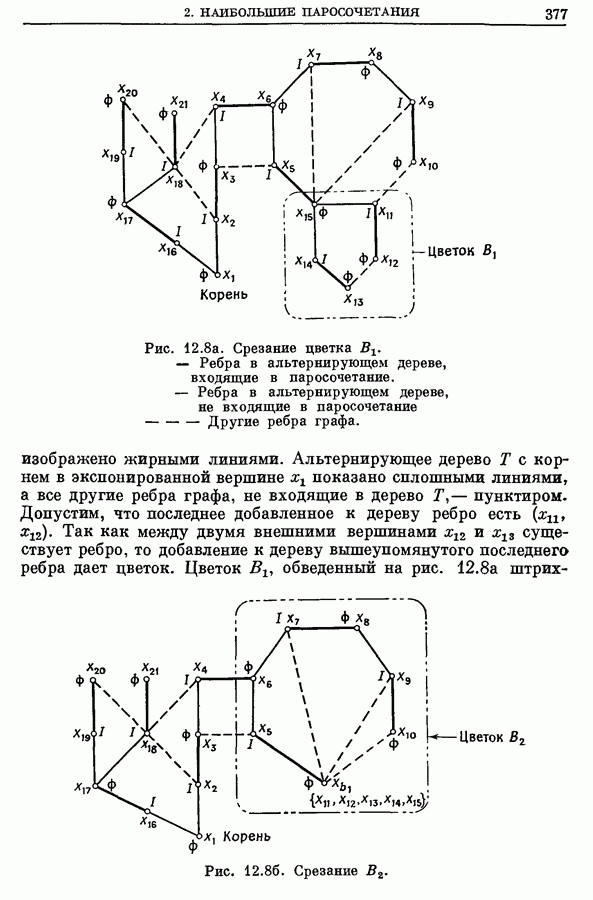
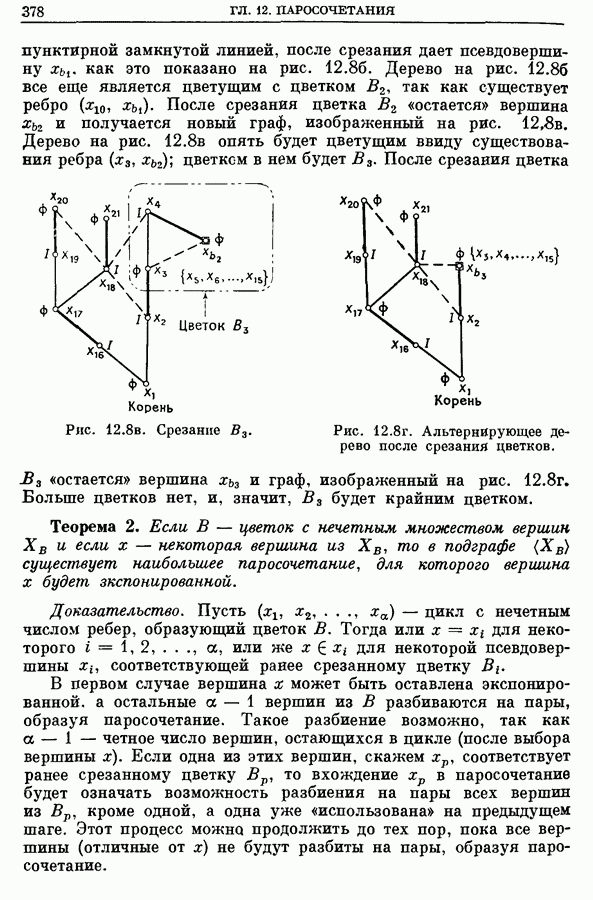
377
378
379
380
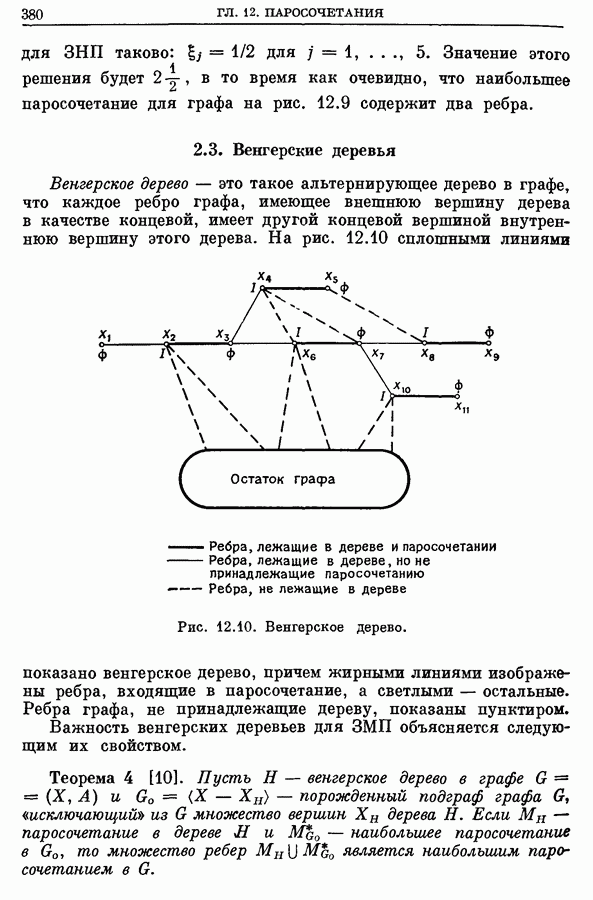
381
382
383
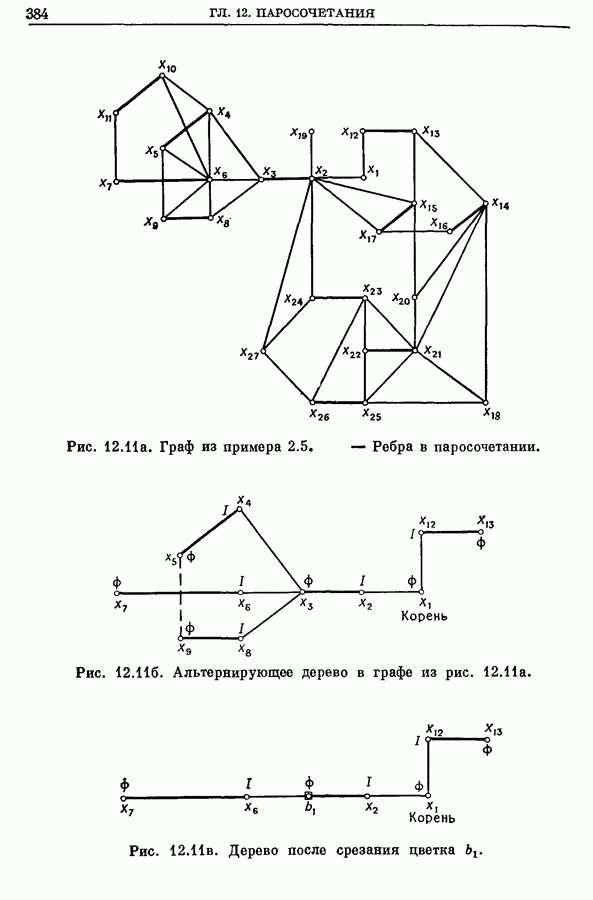
384
385
386
387
388
389
390
391
392
393
394
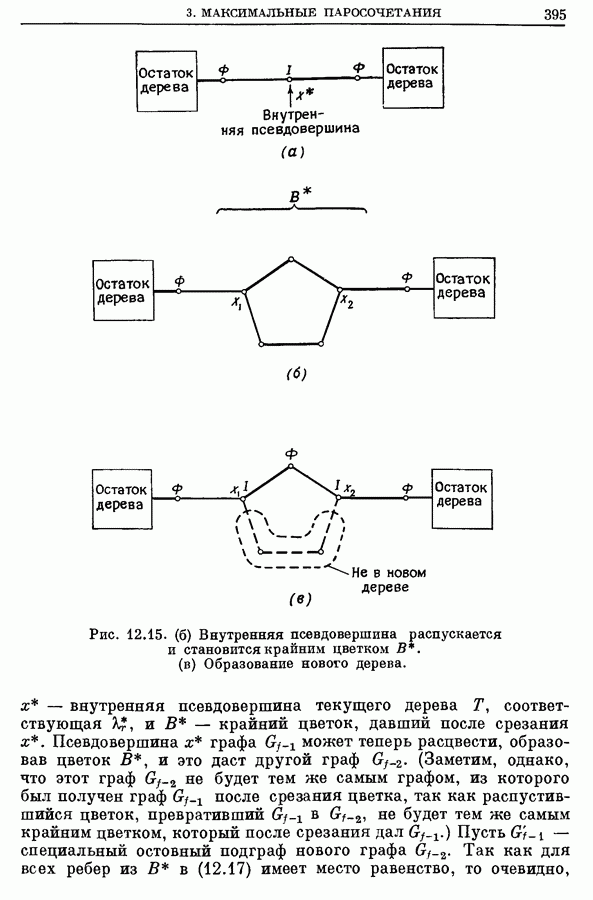
395
396
397
398
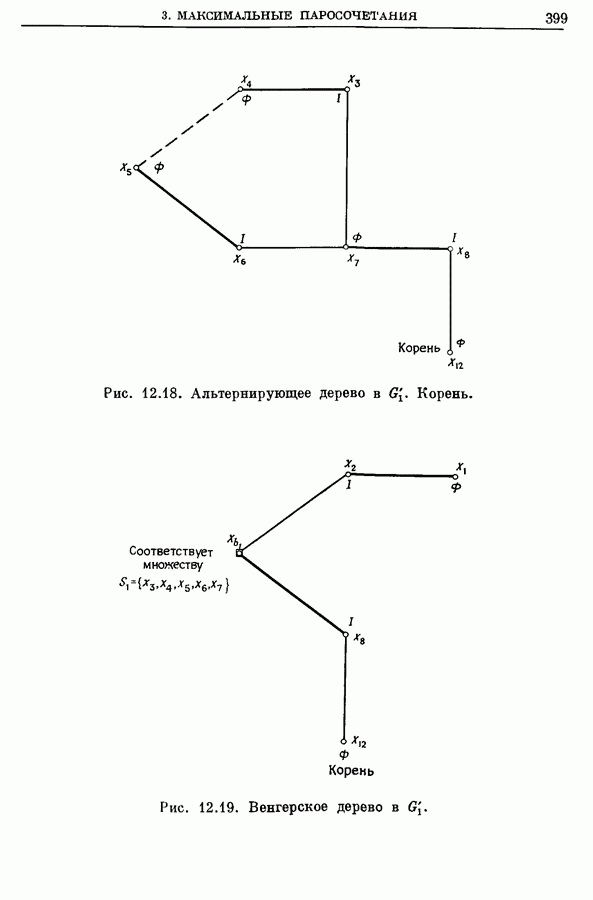
399
400
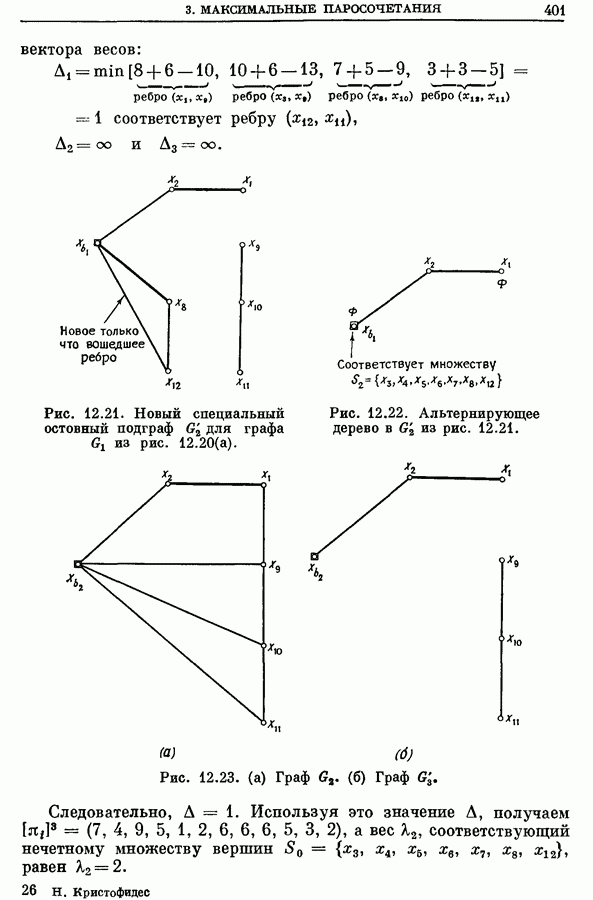
401
402
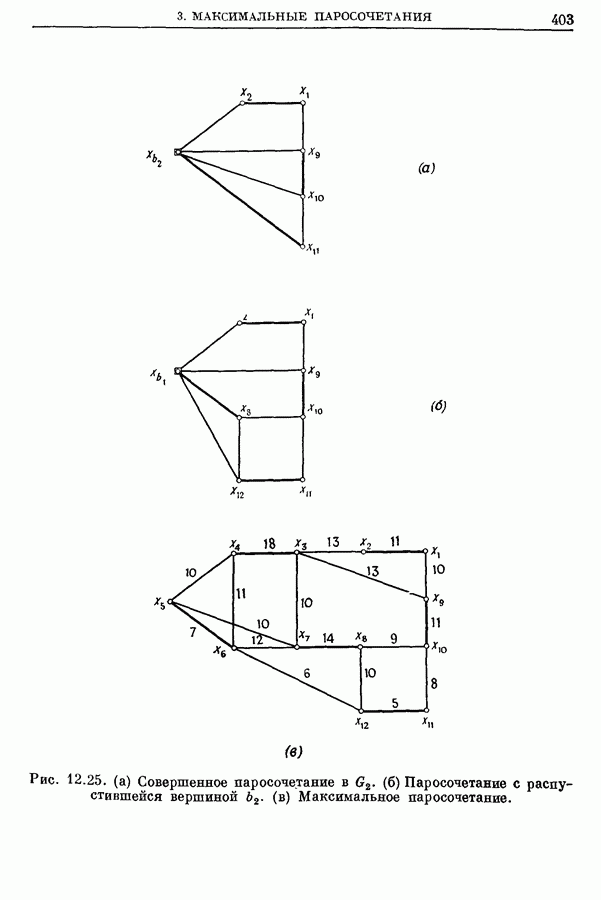
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5.3. Связь между эйлеровыми и гамильтоновыми циклами
Гамильтонов цикл в графе  был определен в главе 1 как простой цикл, проходящий (один, и только один раз) через каждую вершину графа
был определен в главе 1 как простой цикл, проходящий (один, и только один раз) через каждую вершину графа  Не удивительно, что двойственность между эйлеровыми и гамильтоновыми циклами (замена вершины на ребро и наоборот) приводит к тесной связи между этими двумя понятиями в применении к неориентированному графу
Не удивительно, что двойственность между эйлеровыми и гамильтоновыми циклами (замена вершины на ребро и наоборот) приводит к тесной связи между этими двумя понятиями в применении к неориентированному графу  и соответствующему ему реберному графу, определяемому ниже.
и соответствующему ему реберному графу, определяемому ниже.
Определение. Реберный граф  графа
графа  имеет столько же вершин, сколько ребер у графа
имеет столько же вершин, сколько ребер у графа  Ребро между двумя вершинами графа
Ребро между двумя вершинами графа  существует тогда и только тогда, когда ребра графа
существует тогда и только тогда, когда ребра графа  соответствующие этим двум вершинам, смежны (т. е. инцидентны одной и той же вершине графа
соответствующие этим двум вершинам, смежны (т. е. инцидентны одной и той же вершине графа 
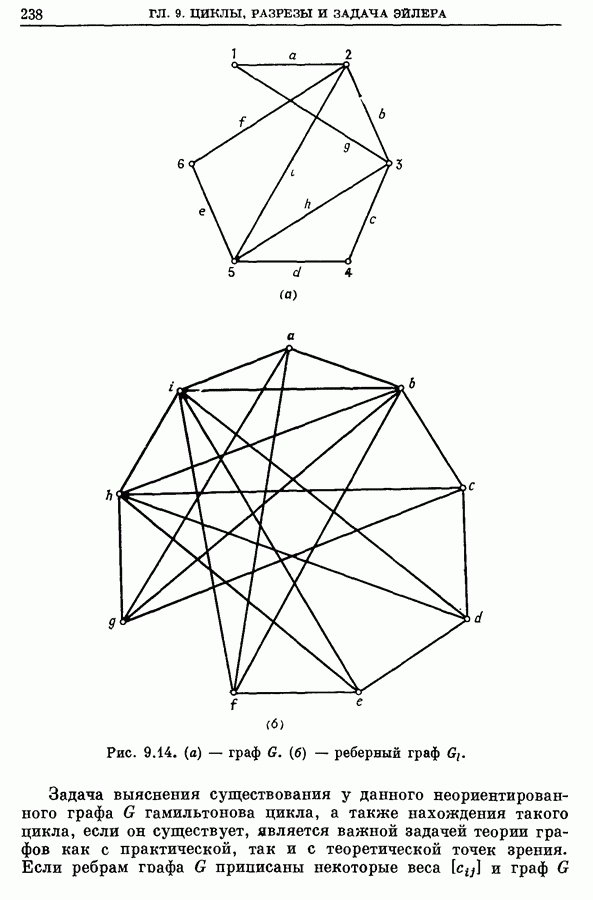
Например, для графа, показанного на рис.  граф
граф  изображен на рис.
изображен на рис. 
Легко можно показать [15], что верны два следующие утверждения о взаимоотношении между эйлеровыми и гамильтоновыми циклами.
(1) Если  имеет эйлеров цикл, то
имеет эйлеров цикл, то  имеет как эйлеров, так и гамильтонов циклы.
имеет как эйлеров, так и гамильтонов циклы.
(2) Если  имеет гамильтонов цикл, то
имеет гамильтонов цикл, то  также имеет гамильтонов цикл.
также имеет гамильтонов цикл.
Обращение этих утверждений, как нетрудно продемонстрировать, неверно. Для графа, изображенного на рис.  степени всех его вершин четны и поэтому существует эйлеров цикл. Таким образом, граф
степени всех его вершин четны и поэтому существует эйлеров цикл. Таким образом, граф  изображенный на рис. 9.14(6), также имеет эйлеров цикл (поскольку степени всех его вершин опять четны) и, кроме того, имеет гамильтонов цикл, задаваемый последовательностью вершин
изображенный на рис. 9.14(6), также имеет эйлеров цикл (поскольку степени всех его вершин опять четны) и, кроме того, имеет гамильтонов цикл, задаваемый последовательностью вершин  Если теперь из графа
Если теперь из графа  удалить ребро
удалить ребро  то новый граф
то новый граф  не имеет эйлерова цикла, но все еще имеет гамильтонов цикл 1, 2, 6, 5, 4, 3, 1. Реберный граф
не имеет эйлерова цикла, но все еще имеет гамильтонов цикл 1, 2, 6, 5, 4, 3, 1. Реберный граф  графа
графа  является тогда графом из рис.
является тогда графом из рис.  с удаленной вершиной
с удаленной вершиной  (и без ребер, инцидентных вершине
(и без ребер, инцидентных вершине  Этот граф все еще имеет гамильтонов цикл
Этот граф все еще имеет гамильтонов цикл 
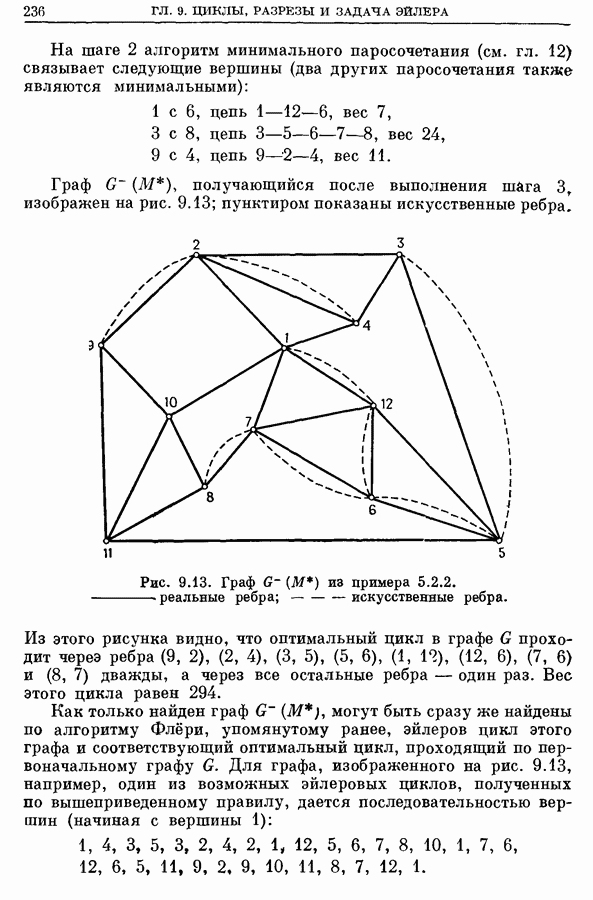
Рис. 9.14. (см. скан) (а) - граф G. (б) - реберный граф 
Задача выяснения существования у данного неориентированного графа  гамильтонова цикла, а также нахождения такого цикла, если он существует, является важной задачей теории графов как с практической, так и с теоретической точек зрения. Если ребрам гвафа
гамильтонова цикла, а также нахождения такого цикла, если он существует, является важной задачей теории графов как с практической, так и с теоретической точек зрения. Если ребрам гвафа  приписаны некоторые веса
приписаны некоторые веса  и граф
и граф 
содержит несколько гамильтоновых циклов, то большой интерес представляет также задача нахождения такого цикла с минимальным общим весом. Ввиду важности этих вопросов гамильтоновы циклы рассматриваются отдельно в следующей главе.
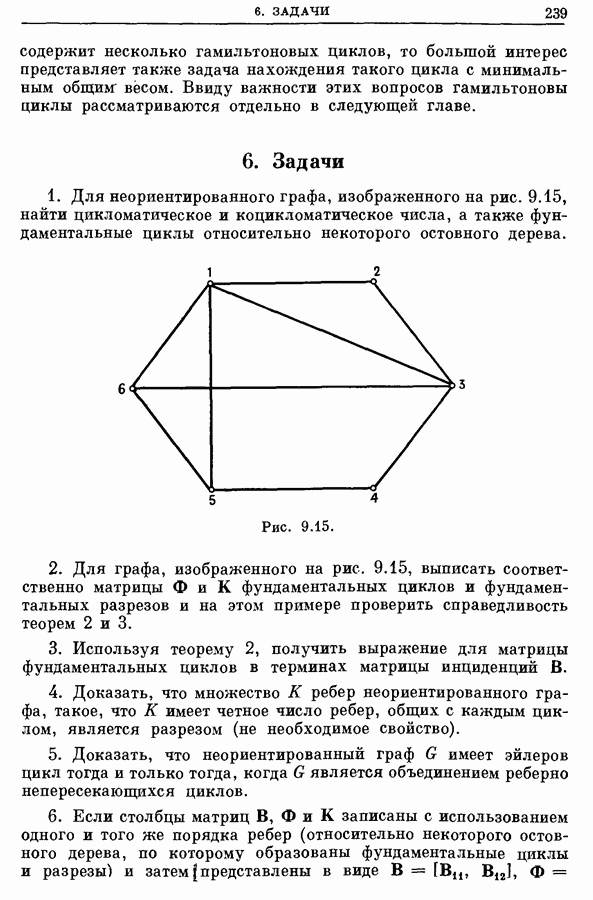
6. Задачи
(см. скан)
(см. скан)
7. Список литературы
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
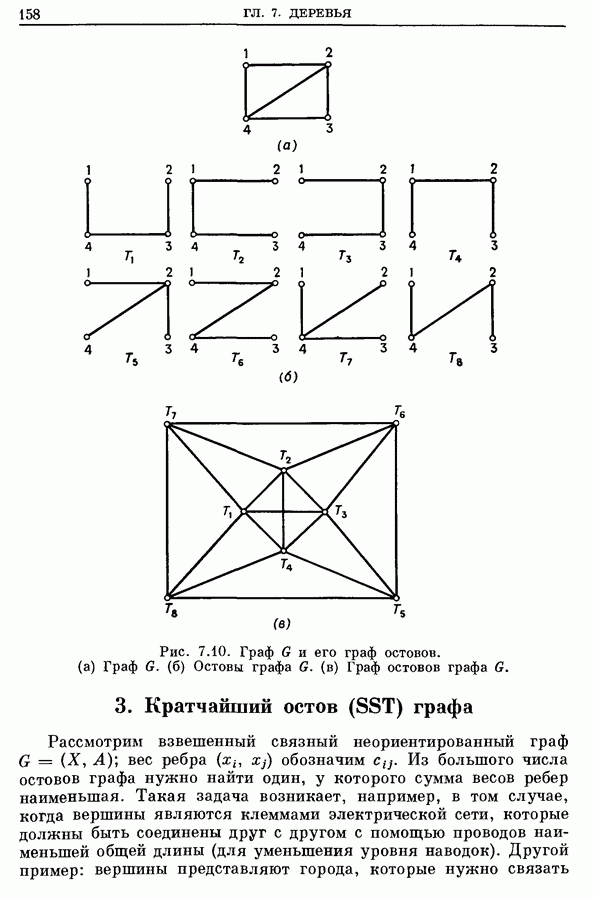
- 2.4. Граф остовов
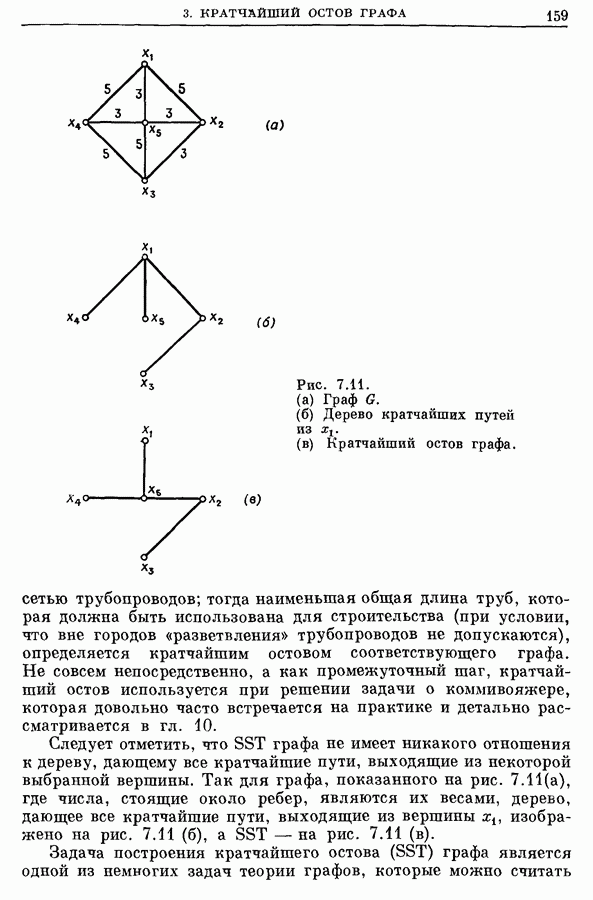
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
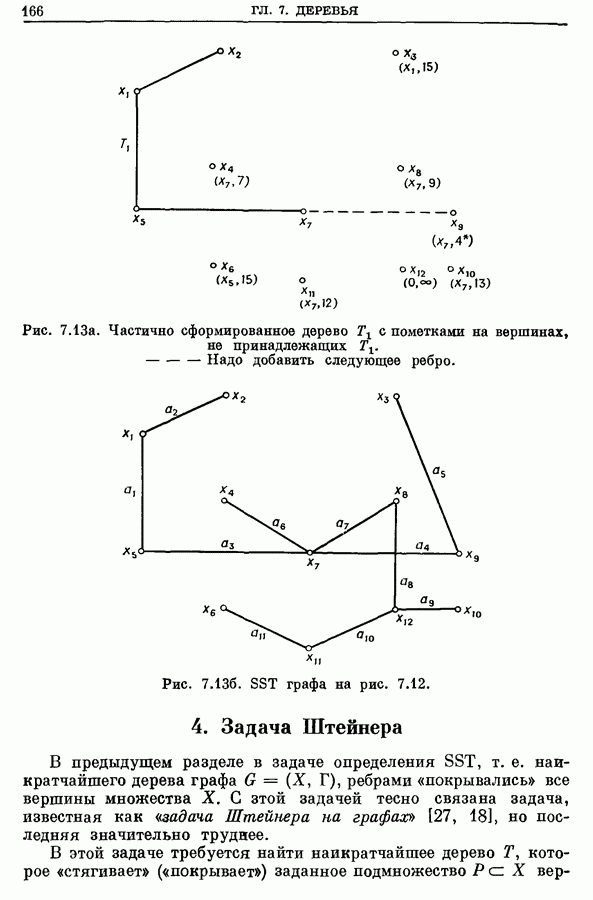
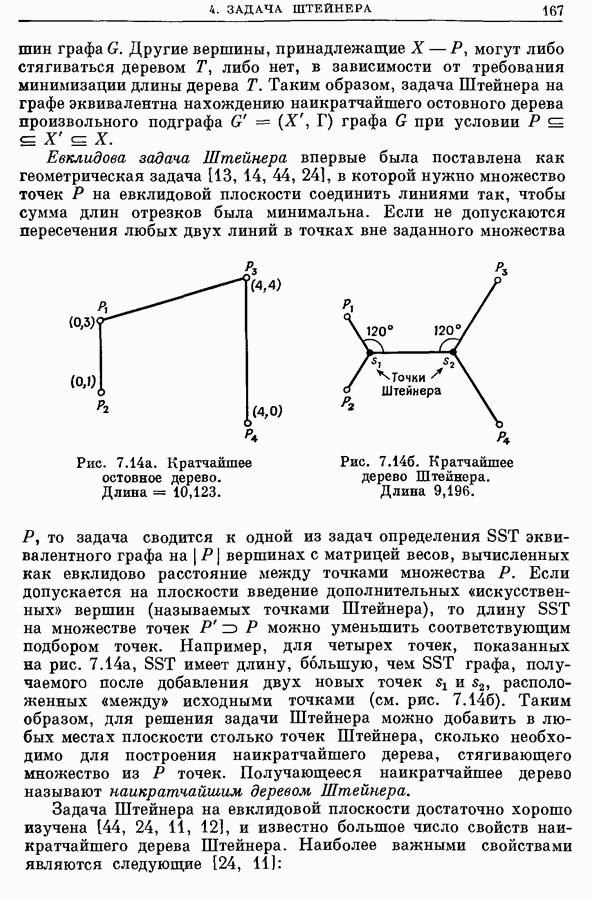
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
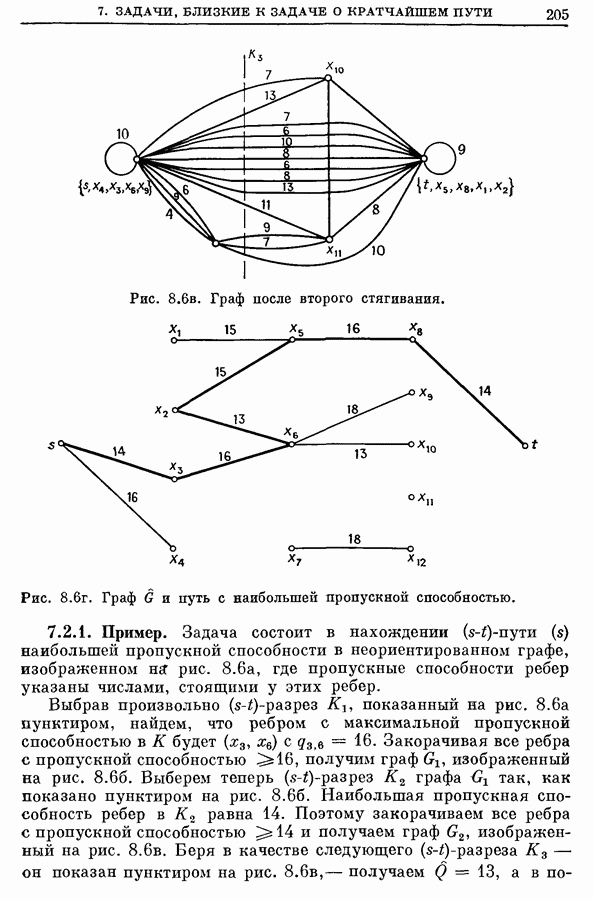
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
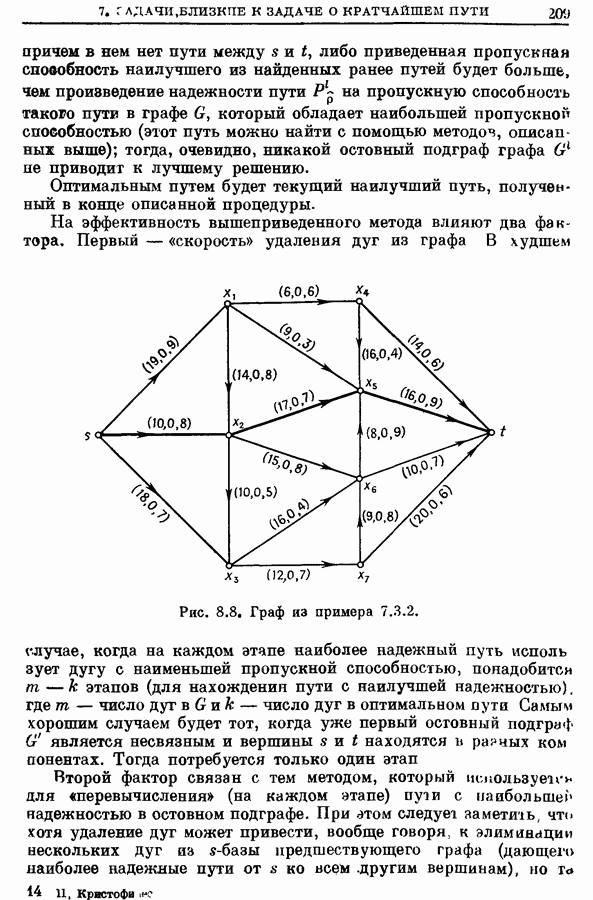
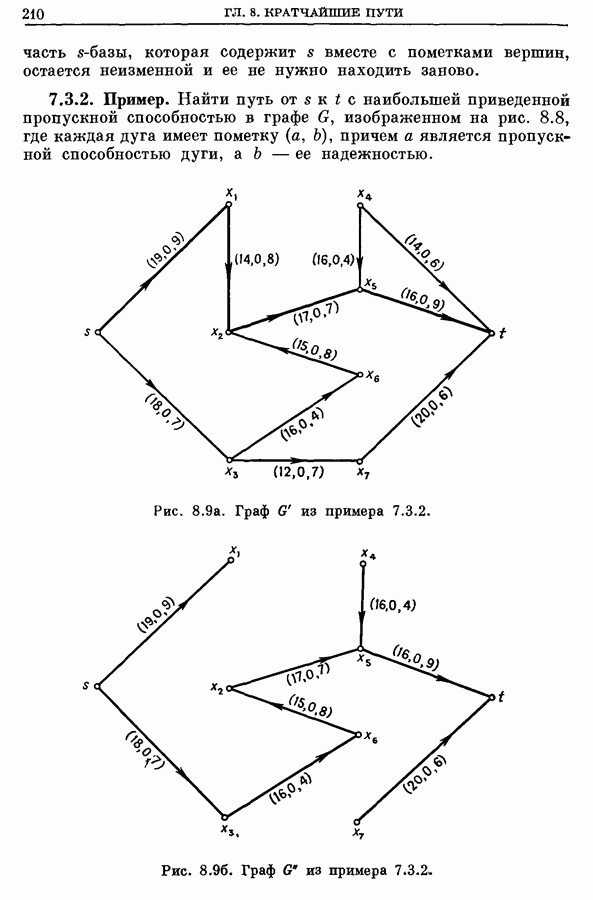
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
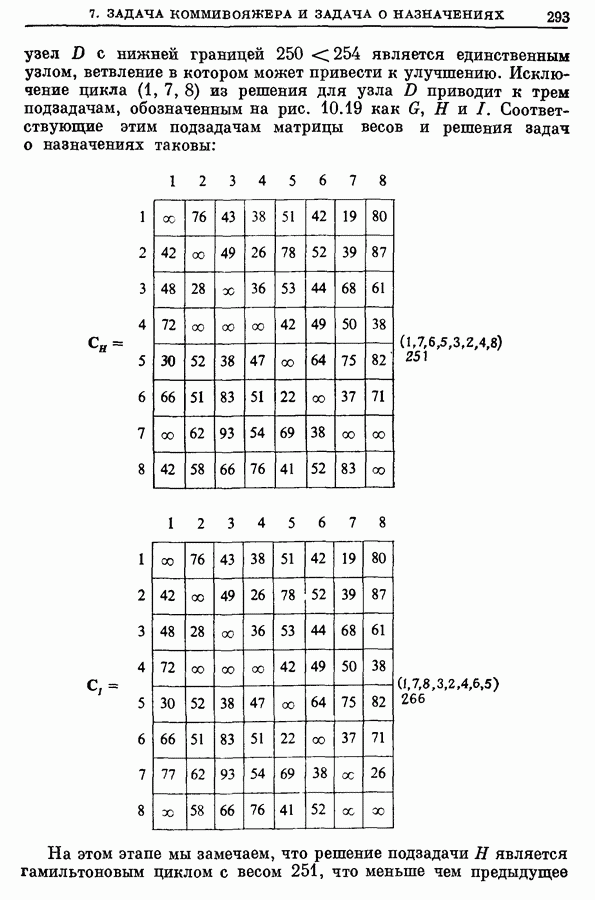
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
- 2.3. Инкрементальные графы
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
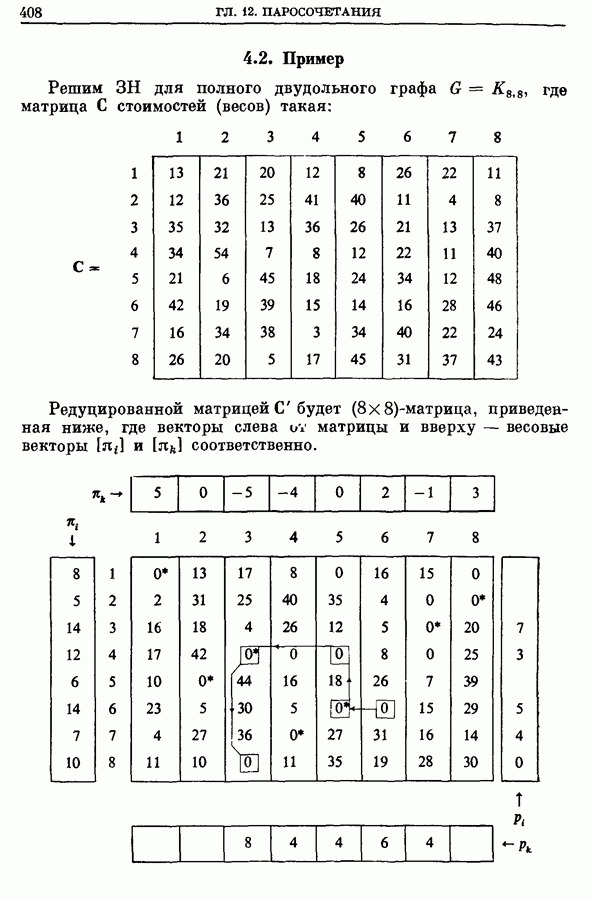
- 4.2. Пример
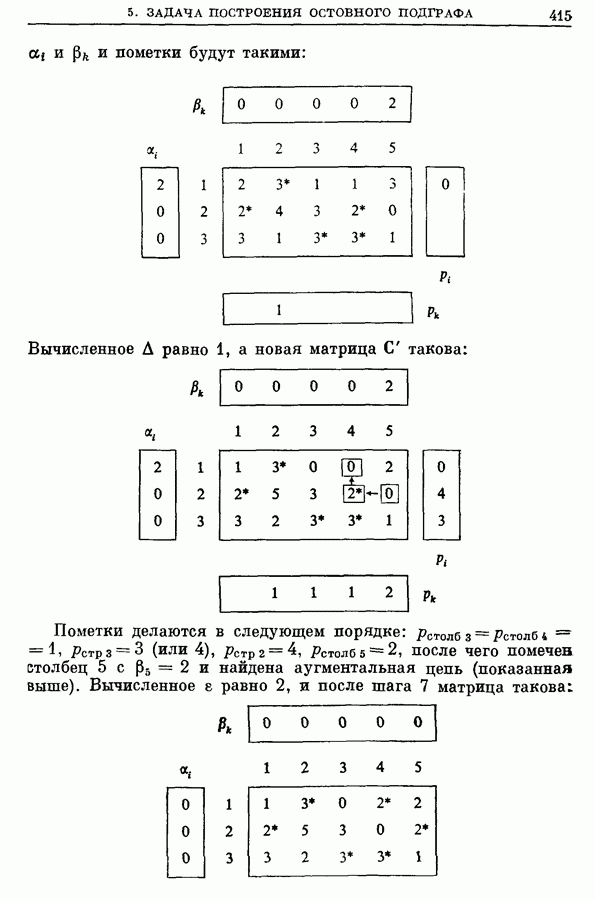
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления