| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. Метод перебора Робертса и Флореса
В противоположность алгебраическим методам, с помощью которых пытаются найти сразу все гамильтоновы циклы и при реализации которых приходится хранить поэтому все цепи, которые могут оказаться частями таких циклов, метод перебора имеет дело с одной цепью, непрерывно продлеваемой вплоть до момента, когда либо получается гамильтонов цикл, либо становится ясно, что эта цепь не может привести к гамильтонову циклу. Тогда цепь модифицируется некоторым систематическим способом (который гарантирует, что в конце концов будут исчерпаны все возможности), после чего продолжается поиск гамильтонова цикла. В этом способе для поиска требуется очень небольшой объем памяти и за один раз находится один гамильтонов цикл.
Следующая схема перебора, использующая обычную технику возвращения, была первоначально предложена Робертсом и Флоресом [30, 31]. Начинают с построения  -матрицы
-матрицы  где элемент есть
где элемент есть  вершина (скажем
вершина (скажем  для которой в графе
для которой в графе  существует дуга
существует дуга  Вершины
Вершины  в множестве
в множестве  можно упорядочить произвольно, образовав элементы
можно упорядочить произвольно, образовав элементы  столбца матрицы
столбца матрицы  Число строк к матрицы
Число строк к матрицы  будет равно наибольшей полустепени исхода вершины.
будет равно наибольшей полустепени исхода вершины.
Метод состоит в следующем. Некоторая начальная вершина (скажем,  выбирается в качестве отправной и образует первый
выбирается в качестве отправной и образует первый
элемент множества  которое каждый раз будет хранить уже найденные вершины строящейся цепи. К S добавляется первая вершина (например, вершина а) в столбце
которое каждый раз будет хранить уже найденные вершины строящейся цепи. К S добавляется первая вершина (например, вершина а) в столбце  Затем к множеству
Затем к множеству  добавляется первая возможная вершина (например, вершина
добавляется первая возможная вершина (например, вершина  в столбце а, потом добавляется к
в столбце а, потом добавляется к  первая возможная вершина (например, вершина с) в столбце
первая возможная вершина (например, вершина с) в столбце  Под «возможной» вершиной мы понимаем вершину, еще не принадлежащую
Под «возможной» вершиной мы понимаем вершину, еще не принадлежащую  Существуют две причины, препятствующие включению некоторой вершины на шаге
Существуют две причины, препятствующие включению некоторой вершины на шаге  в множестве
в множестве  Или (1) в столбце
Или (1) в столбце  нет возможной вершины, или (2) цепь, определяемая последовательностью вершин в
нет возможной вершины, или (2) цепь, определяемая последовательностью вершин в  имеет длину
имеет длину  является гамильтоновой цепью.
является гамильтоновой цепью.
В случае (2)
(а) в графе  существует дуга
существует дуга  и поэтому найден гамильтонов цикл, или
и поэтому найден гамильтонов цикл, или
(б) дуга  не существует и не может быть получен никакой гамильтонов цикл.
не существует и не может быть получен никакой гамильтонов цикл.
В случаях (1) и (26) следует прибегнуть к возвращению, в то время как в случае (2а) можно прекратить поиск и напечатать результат (если требуется найти только один гамильтонов цикл), или (если нужны все такие циклы) произвести печать и прибегнуть к возвращению. Возвращение состоит в удалении последней включенной вершины  из
из  после чего остается множество
после чего остается множество  и добавлении к
и добавлении к  первой возможной вершины, следующей за
первой возможной вершины, следующей за  в столбце хтматрицы
в столбце хтматрицы  Если не существует никакой возможной вершины, делается следующий шаг возвращения и т. д.
Если не существует никакой возможной вершины, делается следующий шаг возвращения и т. д.
Поиск заканчивается в том случае, когда множество  состоит только из вершины
состоит только из вершины  и не существует никакой возможной вершины, которую можно добавить к
и не существует никакой возможной вершины, которую можно добавить к  так что шаг возвращения делает множество
так что шаг возвращения делает множество  пустым. Гамильтоновы циклы, найденные к зтому моменту, являются тогда всеми гамильтоновыми циклами, существующими в графе.
пустым. Гамильтоновы циклы, найденные к зтому моменту, являются тогда всеми гамильтоновыми циклами, существующими в графе.
2.2.1. Пример.
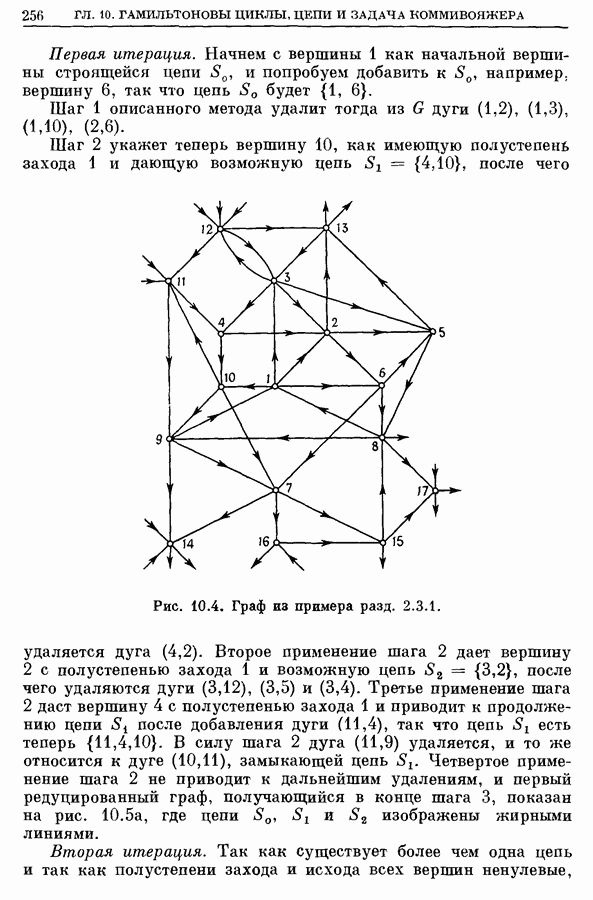
Рассмотрим граф, изображенный на рис. 10.2. Матрица  приводится ниже, вершины в каждом столбце расположены в алфавитном порядке:
приводится ниже, вершины в каждом столбце расположены в алфавитном порядке:


Рис. 10.2. Граф из примера 2.2.1.
Поиск всех гамильтоновых циклов производится так (вершина а берется в качестве отправной вершины):
(см. скан)
(см. скан)
2.2.2. Улучшение основного метода.
Допустим, что на некотором этапе поиска построенная цепь задается множеством  и что следующей вершиной, которую предполагается добавить к
и что следующей вершиной, которую предполагается добавить к  является
является 

Рис. 10.3а.  Следующей дугой должна быть
Следующей дугой должна быть 

Рис. 10.36.  Следующей дугой не должна быть
Следующей дугой не должна быть 
Рассмотрим теперь две следующие ситуации, в которых вершина является изолированной в подграфе, остающемся после удаления из  всех вершин, образующих построенную до этого цепь.
всех вершин, образующих построенную до этого цепь.
(а) Если существует такая вершина  что
что  (см. рис. 10.3а), то, добавляя к
(см. рис. 10.3а), то, добавляя к  любую вершину
любую вершину  отличную от
отличную от  мы не сможем в последующем достигнуть вершины х ни из какой конечной вершины построенной цепи, и, значит, эта цепь не сможет привести нас к построению гамильтонова цикла. Таким образом, в этом случае х является единственной вершиной, которую можно добавить к
мы не сможем в последующем достигнуть вершины х ни из какой конечной вершины построенной цепи, и, значит, эта цепь не сможет привести нас к построению гамильтонова цикла. Таким образом, в этом случае х является единственной вершиной, которую можно добавить к  для продолжения цепи.
для продолжения цепи.
(б) Если существует такая вершина  что
что  и
и  для некоторой другой вершины
для некоторой другой вершины  то х не может быть добавлена к
то х не может быть добавлена к  так как тогда в остающемся подграфе не может существовать никакой цепи между
так как тогда в остающемся подграфе не может существовать никакой цепи между  Цепь, определяемая множеством
Цепь, определяемая множеством  не может поэтому привести к гамильтонову циклу, а в качестве кандидата на добавление к множеству
не может поэтому привести к гамильтонову циклу, а в качестве кандидата на добавление к множеству  следует рассмотреть другую вершину, отличную от х (см. рис. 10.36).
следует рассмотреть другую вершину, отличную от х (см. рис. 10.36).
В только что приведенном примере ситуация (а) возникает на шаге 2, когда множество  есть
есть  Если заметить теперь, что для вершины
Если заметить теперь, что для вершины  справедливо соотношение
справедливо соотношение  то становится ясным, что
то становится ясным, что  следует добавить в качестве очередной вершины к множеству
следует добавить в качестве очередной вершины к множеству  Поэтому в приведенном примере можно опустить шаги 3—8 и сразу от шага 2 перейти, как показано стрелкой, к шагу 9.
Поэтому в приведенном примере можно опустить шаги 3—8 и сразу от шага 2 перейти, как показано стрелкой, к шагу 9.
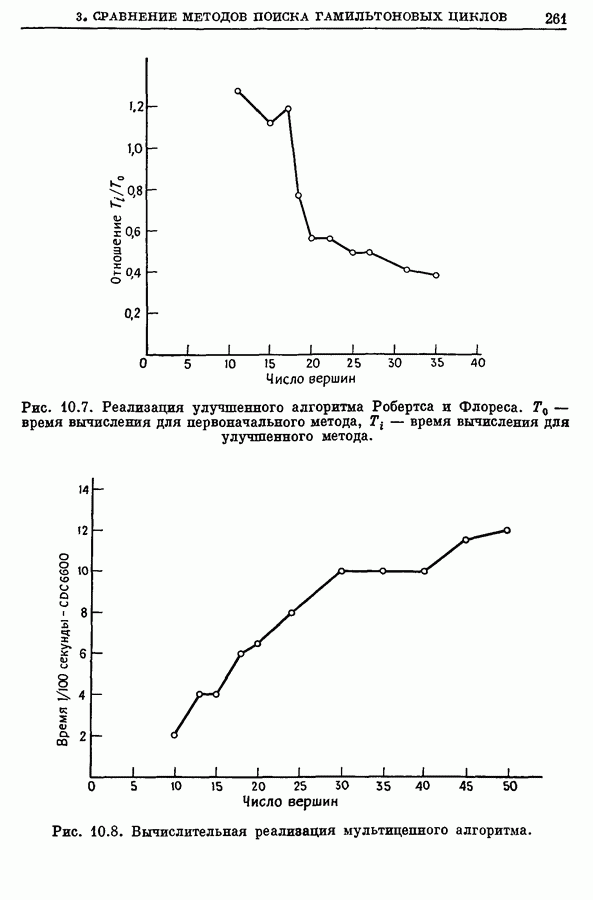
Проверка условий (а) и (б) будет, конечно, замедлять итеративную процедуру, и для небольших графов (менее чем с 20 вершинами) не получается никакого улучшения первоначального алгоритма Робертса и Флореса. Но для больших графов эта проверка приводит к заметному сокращению необходимого времени вычислений, уменьшая его обычно в 2 или более раз. Подробные результаты вычислений для различных методов приводятся на рис. 10.7 в разд. 3.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
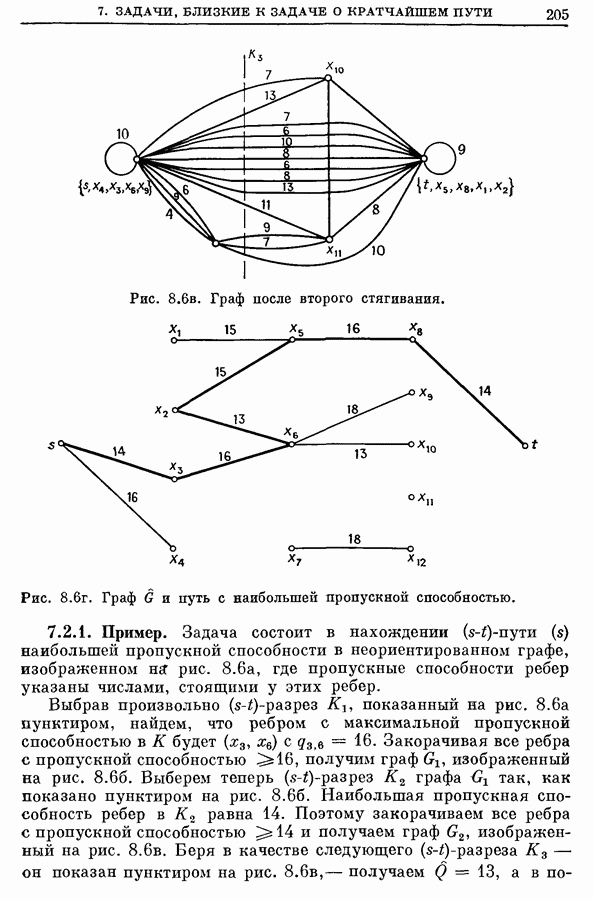
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
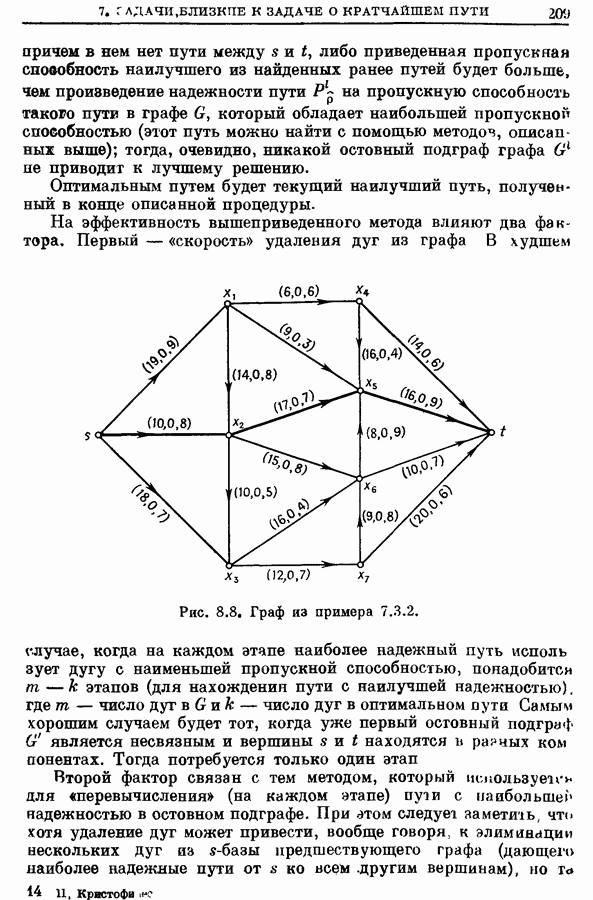
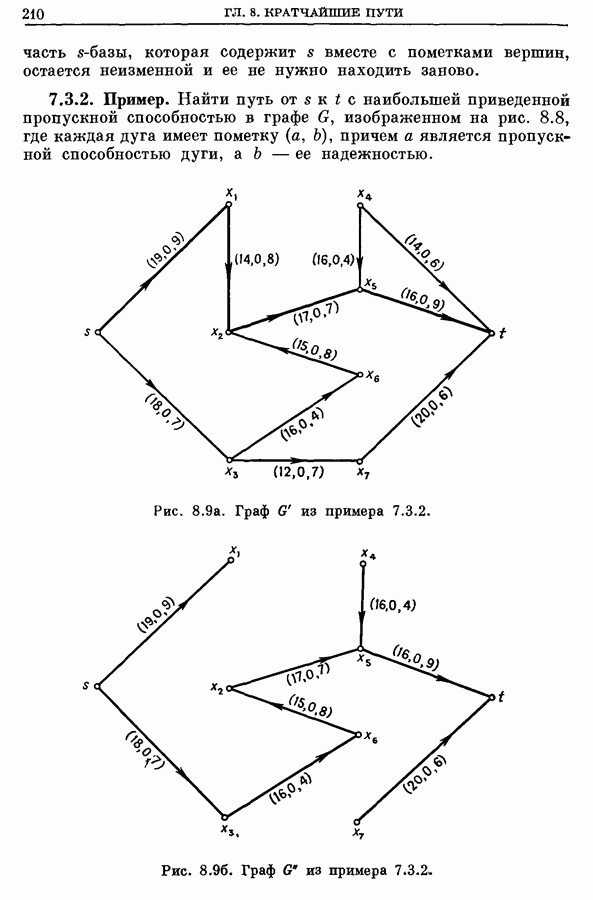
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
- 2.3. Инкрементальные графы
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
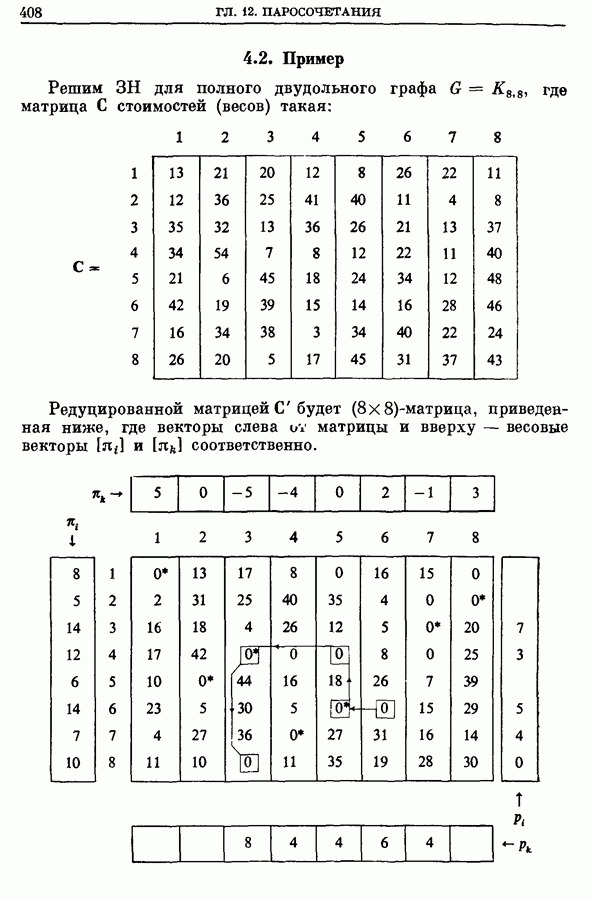
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
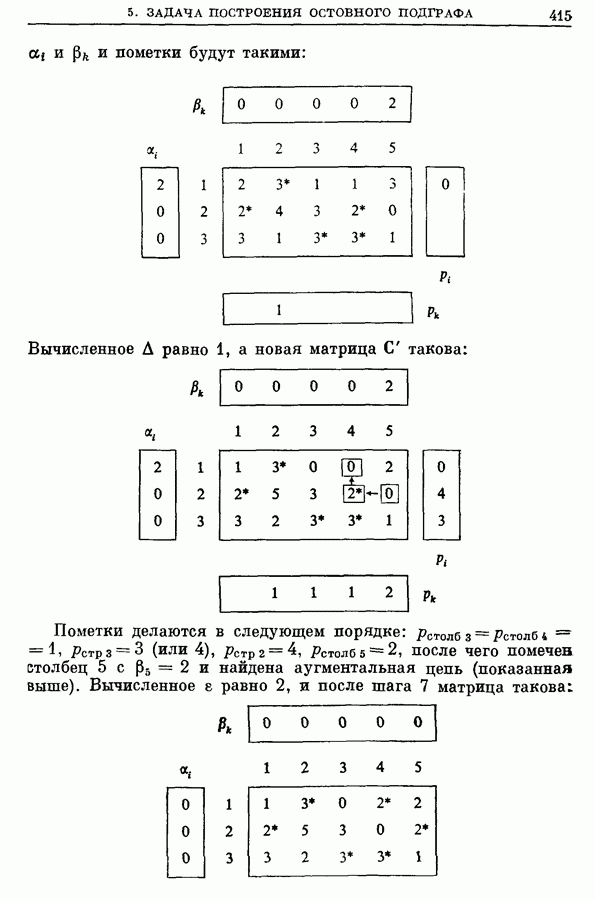
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
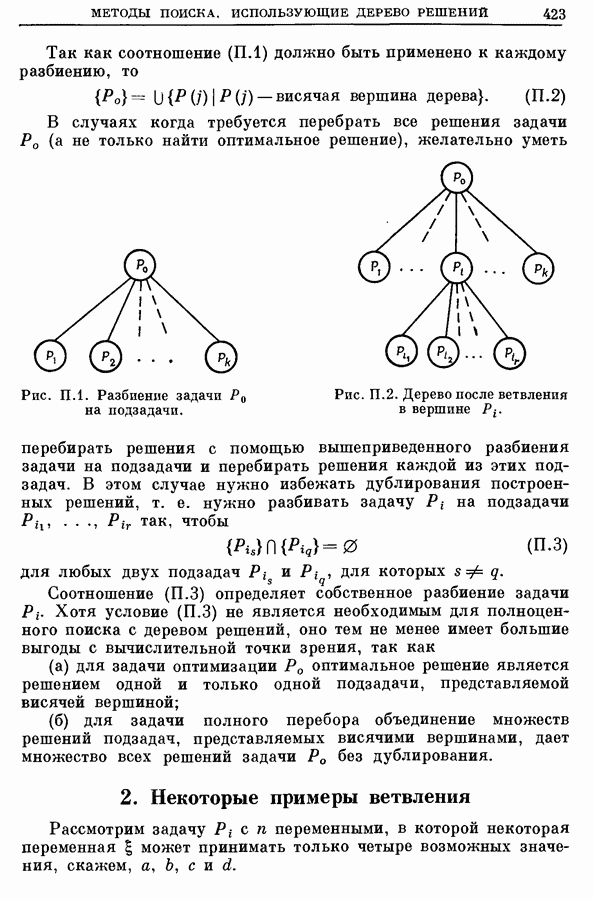
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
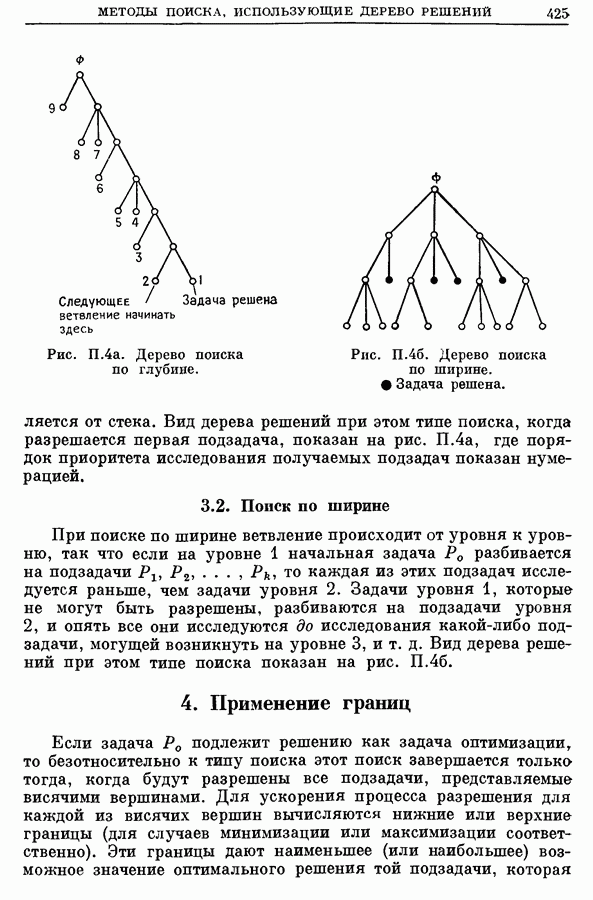
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления