| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1.2. Несимметричная полосковая линия
1. Определение. Конструкция. Поле основной волны.
Несимметричная полосковая линия (НПЛ) (иногда ее называют микрополосковой линией) выполняется нанесением слоя металла бесконечной ширины с одной стороны подложки и проводника конечной ширины — с другой стороны (рис. 1.4, а).
Рис. 1.4. (см. скан) Несимметричная полосковая линия: а), б) поперечный и продольный вид; б) распределение продольных токов; г) структура токов; д, е) структура полей поверхностных волн в НПЛ
Основным (низшим) типом волны, распространяющейся в НПЛ, является квази-Т-волна, структура полей которой схематически показана на рис. 1.4, а, б.
Продольное распределение тока в узком проводнике описывается экспоненциальной либо логарифмической функцией, в слое металла — колоколообразной функцией вида  (рис. 1.4, в).
(рис. 1.4, в).
Общее распределение тока в проводниках НПЛ приведено на рис. 1.4, г.
Структура полей поверхностных воли дана на рис. 1 
Несмотря на внешнюю простоту конструкции, НПЛ по своим электродинамическим характеристикам существенно отличается от СПЛ. Основное отличие состоит в том, что НПЛ представляет собой открытую электродинамическую структуру, и построение ее теории оказалось связанным с целым рядом сложнейших проблем математической теории дифракции и вычислительной электродинамики. Здесь мы приведем только основные данные этой теории, отсылая читателя за подробностями к материалам книг [1, 24]. Вместе с тем для целого ряда приложений и использования НПЛ в ОИС достаточно длинноволновых диапазонов оказываются весьма полезными различные приближенные результаты. Поэтому вначале мы приведем сводку результатов по квазистатической теории НПЛ, а потом уже перейдем к электродинамическому приближению, в котором отметим основные принципиальные моменты теории.
2. Квазистатическое приближение.
В этом случае  и волновое сопротивление рассчитывается с довольно низкой погрешностью (порядка ±1%) для параметров подложки:
и волновое сопротивление рассчитывается с довольно низкой погрешностью (порядка ±1%) для параметров подложки:  и геометрических размеров в области
и геометрических размеров в области  [25]. Волновое сопротивление НПЛ для широких проводников
[25]. Волновое сопротивление НПЛ для широких проводников  равно
равно

для узких проводников 

Формулы (1), (2) справедливы для бесконечно топкого проводника, а эффективная диэлектрическая проницаемость, входящая в них, определяется так:

где

Для проектирования ИС и ОИС СВЧ схем желательно иметь зависимости геометрических размеров от волнового сопротивления  и диэлектрической проницаемости
и диэлектрической проницаемости  подложки. Это нетрудно сделать, пользуясь формулами (1) — (3) и записав их в виде
подложки. Это нетрудно сделать, пользуясь формулами (1) — (3) и записав их в виде

где значение  аппроксимируется выражением
аппроксимируется выражением

Формулы (4) — (6) дают максимальную погрешность 4% при значениях 5; 250) Ом и  Для значений
Для значений  Ом погрешность не превышает 2%. Если же проведенную процедуру повторить еще раз, произведя при этом замену
Ом погрешность не превышает 2%. Если же проведенную процедуру повторить еще раз, произведя при этом замену  на
на  то погрешность уменьшается до 0,5%.
то погрешность уменьшается до 0,5%.
3. Учет реальных особенностей конструкции и материала проводника.
При конструировании ИС на НПЛ часто оказывается, что характеристики физической цепи значительно отличаются от теоретических даппых. Это объясняется наличием таких факторов, как конечная толщина проводников, потери на нагревание проводников и диэлектрика, излучение и пр. Поэтому при проектировании ИС следует учитывать влияние перечисленных факторов.Краевые поля в НПЛ, образованные за счет конечной толщины  проводников, влияют на эффективную ширину проводников
проводников, влияют на эффективную ширину проводников  следующим образом [26]:
следующим образом [26]:
для гомогенных (однородных) подложек

для гетерогенных (многослойных) подложек

Без учета свойств материала подложки [27] выражения (7) и (8) будут иметь более простой вид:

Формулы  получены для подложек с диэлектрической проницаемостью 8 128 и размеров проводника НПЛ
получены для подложек с диэлектрической проницаемостью 8 128 и размеров проводника НПЛ  .
.
Затухание в НПЛ определяется формулой [26]

где с — скорость света,  собственная добротность НПЛ, включающая в себя потери в металлическом слое (обусловленные тепловым действием тока), в диэлектрических слоях и на излучение. Величина, обратная общей добротности, является аддитивной по отношению к обратным значениям частных добротностей ее составляющих:
собственная добротность НПЛ, включающая в себя потери в металлическом слое (обусловленные тепловым действием тока), в диэлектрических слоях и на излучение. Величина, обратная общей добротности, является аддитивной по отношению к обратным значениям частных добротностей ее составляющих: 
Рассмотрим собственную добротность для каждого случая.
Добротность НПЛ, «подвешенной» в воздухе (диэлектрическая проницаемость подложки  согласно [28], равна
согласно [28], равна

где  поверхностное сопротивление скин-слоя
поверхностное сопротивление скин-слоя  (
( — удельная проводимость металла),
— удельная проводимость металла),  коэффициент, учитывающий распределение тока в НПЛ [26]:
коэффициент, учитывающий распределение тока в НПЛ [26]:

При необходимости можно учесть зависимость поверхностного сопротивления от величины шероховатости проводников:

где  среднеквадратичная шероховатость поверхности.
среднеквадратичная шероховатость поверхности.
Добротность диэлектрического слоя НПЛ  определяется добротностью подложки
определяется добротностью подложки  и воздушного пространства над полоской
и воздушного пространства над полоской  которая практически весьма велика
которая практически весьма велика 

Коэффициент заполнения НПЛ диэлектриком [28] равен

Потери на излучение практически не учитываются, поскольку они проявляются при большой толщине проводника (превышающей толщину шести скин-слоев) и, кроме того, от них можно избавиться путем экранирования НПЛ. Добротность излучения  при этом стремится к бесконечности.
при этом стремится к бесконечности.
Более простые выражения для расчета затухания в НПЛ, в которых не учитываются распределение тока в проводнике, неоднородность материалов подложки и коэффициент заполнения диэлектрика, можно найти в [27].
4. Электродинамическое приближение.
Основное отличие НПЛ от СПЛ состоит в том, что основная волна  -волна) обладает «вол но водным характером», т. е. имеет достаточно заметную дисперсию. Это обстоятельство особенно сказывается при проектировании и реализации разнообразных резонансных структур типа, например, полосовых фильтров
-волна) обладает «вол но водным характером», т. е. имеет достаточно заметную дисперсию. Это обстоятельство особенно сказывается при проектировании и реализации разнообразных резонансных структур типа, например, полосовых фильтров 
Продольное волновое число  обладает спектром собственных значений, состоящим из двух множеств:
обладает спектром собственных значений, состоящим из двух множеств:
а) конечное множество дискретных собственных значений, соответствующих конечному числу волн различных типов, включающее основной тип волны («дискретный» спектр);
б) последовательность собственных значений, соответствующих полю излучения («непрерывный» спектр).
Дискретные волны не являются чисто волнами  или
или  -типов, а представляют собой гибридные волны. Поэтому для их определения необходимо решать уравнение Гельмгольца для продольных составляющих поля:
-типов, а представляют собой гибридные волны. Поэтому для их определения необходимо решать уравнение Гельмгольца для продольных составляющих поля:

где

В плоскости  продольные составляющие поля должны удовлетворять следующим граничным условиям:
продольные составляющие поля должны удовлетворять следующим граничным условиям:

На границе подложка — пространство тангенциальные составляющие поля должны быть непрерывны:

где индекс 1 относится к области  а индекс 2 — к области подложки, т. е.
а индекс 2 — к области подложки, т. е.  Полосковый проводник заменяется неизвестным эквивалентным распределением тока, равным
Полосковый проводник заменяется неизвестным эквивалентным распределением тока, равным

После применения комплексного преобразования Фурье к (16) и перехода от действительной переменной х к комплексной переменной  , необходимо удовлетворить условиям (17), (18).
, необходимо удовлетворить условиям (17), (18).
Для полоскового проводника граничные условия можно записать следующим образом 

Эти условия, применимые только для действительных значений переменной х, приводят к интегральному уравнению, связывающему функции распределения токов  для каждого собственного значения продольного волнового числа
для каждого собственного значения продольного волнового числа 

где функции  есть комплексные преобразования Фурье неизвестных составляющих тока
есть комплексные преобразования Фурье неизвестных составляющих тока  Полное решение (21) дает бесконечное число возможных дискретных типов волн, но на каждой данной частоте существует только конечное число волн различных типов.
Полное решение (21) дает бесконечное число возможных дискретных типов волн, но на каждой данной частоте существует только конечное число волн различных типов.
Для решения (21) существует несколько методов, выбор которых определяется необходимой точностью расчета. Так, если необходимо рассмотреть только основной тип гибридной волны, то можно использовать метод спектрального разложения [29]. Расчет,
проведепный в [30] для четырех высших типов воли, основывается на предположениях, что поперечная составляющая тока  пренебрежимо мала и заряд в полосковом проводнике распределен согласно функции Максвелла. Тогда примеиение комплексного преобразования Фурье приводит к тому, что функции распределения тока
пренебрежимо мала и заряд в полосковом проводнике распределен согласно функции Максвелла. Тогда примеиение комплексного преобразования Фурье приводит к тому, что функции распределения тока  соответствующие высшим типам волн, описываются функциями Бесселя первого рода. Еще более точное решение (21) получают там, где составляющие тока после применения комплексного преобразования Фурье представляются полиномами либо Лежандра [31], либо Чебышева [32].
соответствующие высшим типам волн, описываются функциями Бесселя первого рода. Еще более точное решение (21) получают там, где составляющие тока после применения комплексного преобразования Фурье представляются полиномами либо Лежандра [31], либо Чебышева [32].
Таким образом, поскольку в НПЛ распространяется не чистая  -волна, то волновое сопротивление линии и эффективная диэлектрическая проницаемость подложки изменяются с изменением частоты. Существует несколько возможных путей учета дисперсии в НПЛ. Так, в результате решения интегральных уравнепий (21) получено, что дисперсия приводит к изменению значения постоянной распространения основного типа волны по следующему закону [33]:
-волна, то волновое сопротивление линии и эффективная диэлектрическая проницаемость подложки изменяются с изменением частоты. Существует несколько возможных путей учета дисперсии в НПЛ. Так, в результате решения интегральных уравнепий (21) получено, что дисперсия приводит к изменению значения постоянной распространения основного типа волны по следующему закону [33]:

где

 постоянная распространения, полученная в
постоянная распространения, полученная в  -приближенпи. Дисперсия при этом учитывается путем изменения эффективной диэлектрической проницаемости подложки [34, 35] (ср. [18]):
-приближенпи. Дисперсия при этом учитывается путем изменения эффективной диэлектрической проницаемости подложки [34, 35] (ср. [18]):

Здесь 

Волновое сопротивление  зависит от частоты и может быть записано так:
зависит от частоты и может быть записано так:

Расчет по формулам  дает хорошее совпадение с экспериментальными данными для подложек с диэлектрической проницаемостью 20]. Другие параметры имеют следующие значения: [0,1; 100],
дает хорошее совпадение с экспериментальными данными для подложек с диэлектрической проницаемостью 20]. Другие параметры имеют следующие значения: [0,1; 100],  . Формулы
. Формулы  дают
дают
удовлетворительные результаты до частот миллиметрового диапазона (порядка 60 ГГц) [35].
5. Дисперсия в НПЛ с широким проводником.
Расчет дисперсионных характеристик НПЛ с широким проводником  и экраном, расположенным над плоскостью проводника на расстоянии
и экраном, расположенным над плоскостью проводника на расстоянии  проведен в работе [36]. НПЛ выполнена на подложке
проведен в работе [36]. НПЛ выполнена на подложке  толщины
толщины  На рис. 1.5 представлены дисперсионные кривые для различного типа гибридных волн и проведена область собственных значений, соответствующих полю излучения.
На рис. 1.5 представлены дисперсионные кривые для различного типа гибридных волн и проведена область собственных значений, соответствующих полю излучения.

Рис. 1.5. Дисперсионные характеристики экранирований НПЛ
На основании результатов, полученных в [1, 29—32, 36], можно сделать следующие выводы, Для основного типа волны  собственное значение продольного волнового числа существует, начиная с нулевой частоты. Для каждой волны высшего типа есть своя нижняя частота среза, отличная от нуля, которая возрастает с увеличением порядка волны. На частотах, лежащих ниже частоты среза для данного типа волны, последняя в НПЛ не распространяется, поскольку возбуждающаяся в линии энергия, соответствующая данному типу волны, не распространяется вдоль линии, а излучается в пространство [30]. На частотах, больших частоты среза, волны высших типов распространяются в НПЛ с фазовыми скоростями большими, чем фазовые скорости всех волн более низкого типа на данной частоте. С ростом частоты фазовая скорость имеет нижний предел, численная величина которого равна фазовой скорости в диэлектрике подложки.
собственное значение продольного волнового числа существует, начиная с нулевой частоты. Для каждой волны высшего типа есть своя нижняя частота среза, отличная от нуля, которая возрастает с увеличением порядка волны. На частотах, лежащих ниже частоты среза для данного типа волны, последняя в НПЛ не распространяется, поскольку возбуждающаяся в линии энергия, соответствующая данному типу волны, не распространяется вдоль линии, а излучается в пространство [30]. На частотах, больших частоты среза, волны высших типов распространяются в НПЛ с фазовыми скоростями большими, чем фазовые скорости всех волн более низкого типа на данной частоте. С ростом частоты фазовая скорость имеет нижний предел, численная величина которого равна фазовой скорости в диэлектрике подложки.
На рис. 1.6 представлено распределение продольной составляющей тока гибридных волн  по ширине проводника. Сравнение кривых рис. 1.5 и 1.6 показывает, что гибридные волны имеют распределение поперечной составляющей тока в виде стоячей волны.
по ширине проводника. Сравнение кривых рис. 1.5 и 1.6 показывает, что гибридные волны имеют распределение поперечной составляющей тока в виде стоячей волны.
6. Сравнение НПЛ и прямоугольного волновода.
Электромагнитное поле НПЛ сосредоточено в основном в области под токонесущим проводником (см., например, рис. 1.4, а). С ростом частоты поле все более концентрируется в этой области. Указанное обстоятельство дает повод сравнить свойства НПЛ и прямоугольного волновода  [37]. Строго говоря, продольное волновое число
[37]. Строго говоря, продольное волновое число  в НПЛ с идеально проводящими проводниками и идеальным диэлектрическим заполнением есть комплексная величина:
в НПЛ с идеально проводящими проводниками и идеальным диэлектрическим заполнением есть комплексная величина:  Наличие мнимой части
Наличие мнимой части  связапо с дифракционным излучением волны из линии. На графиках, представленных на рис. 1.7, показано поведение нормированного продольного волнового числа
связапо с дифракционным излучением волны из линии. На графиках, представленных на рис. 1.7, показано поведение нормированного продольного волнового числа  волновое число в воздухе) в зависимости
волновое число в воздухе) в зависимости
от  для основной волны НПЛ [37]. Здесь же нанесены значения продольного волнового числа прямоугольного волновода с поперечным сечением
для основной волны НПЛ [37]. Здесь же нанесены значения продольного волнового числа прямоугольного волновода с поперечным сечением 

Рис. 1.6. Распределение продольных токов в проводнике НПЛ для  -воли (а) и
-воли (а) и  -волн (б)
-волн (б)
Наличие дифракциопных потерь в НПЛ приводит к существованию волны в закритической области (в прямоугольном волноводе с идеальными стенками распространение в этой области отсутствует:  На рис. 1.8 показана зависимость волнового сопротивления НПЛ от
На рис. 1.8 показана зависимость волнового сопротивления НПЛ от  Здесь же представлены соответствующие кривые для прямоугольного волновода.
Здесь же представлены соответствующие кривые для прямоугольного волновода.

Рис. 1.7. Сравнение затухания одинаковых по высоте НПЛ и ПВ. Левые части кривых относятся к затухаиию мнимой части продольного волнового числа
7. Учет анизотропных свойств подложки.
Нужно отметить, что учет анизотропных свойств тел, вводимых в направляющие или резонансные структуры, делает возможным реализацию устройств с весьма интересными характеристиками (невзаимность, направленность и пр.). Вместе с тем анализ свойств структур с анизотропными
включениями весьма сложен (см., например, [38, 39]). Во всех приведенных выше формулах предполагалось, что материал подложки изотропеп. На самом же деле практически все применяемые современные материалы подложек ИС СВЧ обладают ярко выраженной анизотропией свойств. Так, например, для сапфировых подложек 
Метод анализа НПЛ (в статическом приближении) с анизотропной подложкой состоит в том, что вся исследуемая структура в поперечном сечении разбивается на треугольные элементы, причем по мере удаления от полоски НПЛ площадь треугольных элементов возрастает по логарифмическому закону [41].

Рис. 1.8. Сравнение волновых сопротивлений разных по высоте НПЛ и ПВ
После определения всех элементов и узлов потенциальная функция внутри каждого элемента интерполируется функционалом вида

Потенциальная функция  должна удовлетворять уравнению Лапласа
должна удовлетворять уравнению Лапласа

На следующем шаге в результате минимизации функционала получается система линейных уравнений

где  — симметричиая матрица, элементы которой зависят от узловых координат, а
— симметричиая матрица, элементы которой зависят от узловых координат, а  матрица узловых потепциалов. Затем система уравнений (28) модифицируется так, чтобы выполнялись граничные условия на границах металл — свободное пространство
матрица узловых потепциалов. Затем система уравнений (28) модифицируется так, чтобы выполнялись граничные условия на границах металл — свободное пространство  где
где  электрическое смещение), что приводит к виду
электрическое смещение), что приводит к виду

Решая систему уравнений (29), получаем узловые потенциалы  которые определяют потенциальную функцию
которые определяют потенциальную функцию  Зная потенциальную
Зная потенциальную
функцию, определяем электрическое поле около проводников и распределение зарядов в проводнике, по которым можпо найти основные параметры НПЛ. Данный метод позволяет анализировать не только НПЛ, расположенную на анизотропной подложке, по и линию, расположенную на многослойной (гетерогенной) подложке.
Более простой квазистатический метод учета анизотропии подложек, но имеющий и более узкую область применимости, основан на отображении некоторой области  плоскости
плоскости  в область
в область  плоскости
плоскости  при котором функция отображения и задастся в виде [41]
при котором функция отображения и задастся в виде [41]

При таком отображении потенциал точки  принадлежащей области
принадлежащей области  равен потенциалу точки
равен потенциалу точки  области
области  кроме того, электростатическая энергия системы остается постоянной. Если функцию отображения выбрать так, чтобы матрица
кроме того, электростатическая энергия системы остается постоянной. Если функцию отображения выбрать так, чтобы матрица

удовлетворяла условию

то тензор диэлектрической проницаемости  диэлектрика, находящегося в области
диэлектрика, находящегося в области  трансформируется в тензор
трансформируется в тензор

Согласно  расположенная на анизотропной подложке с тензором диэлектрической проницаемости
расположенная на анизотропной подложке с тензором диэлектрической проницаемости

эквивалентна НПЛ, расположенной на изотропной подложке с относительной диэлектрической проницаемостью

и эффективной толщиной

При этом ширина проводника эквивалентной НПЛ остается неизменной:  Формулы (35) и (36) можно широко использовать при расчете волнового сопротивления и эффективной диэлектрической проницаемости. Данный метод дает погрешность, не превышающую 3% при
Формулы (35) и (36) можно широко использовать при расчете волнового сопротивления и эффективной диэлектрической проницаемости. Данный метод дает погрешность, не превышающую 3% при  и погрешность менее 1% при
и погрешность менее 1% при  т. е. он позволяет поучить достаточно высокую точность при относительно простых расчетных формулах.
т. е. он позволяет поучить достаточно высокую точность при относительно простых расчетных формулах.
При использовании НПЛ в ОИС СВЧ необходимо учитывать все типы воли, возникающих как в поперечном, так и продольном направлениях. Особенно это важно при сборке модуля СВЧ, где могут возбуждаться паразитные типы колебаний (объемные и поверхностные) на границах раздела: воздух — диэлектрик — металл. Наиболее опасной из паразитных колебаний является поверхностная волна, методике расчета которой посвящен следующий пункт.
8. Поверхностные волны в НПЛ.
Волны поверхностного типа возникают на границе поверхности диэлектрических слоев НПЛ. Существование поверхностных волн электрического  (рис. 1.4, д) и магнитного
(рис. 1.4, д) и магнитного  (рис. 1.4, е) типов обусловлено их связью с поперечной волной
(рис. 1.4, е) типов обусловлено их связью с поперечной волной  -типа в НПЛ. Действительно, фазовая скорость
-типа в НПЛ. Действительно, фазовая скорость  -волны лежит в области
-волны лежит в области  а фазовая скорость поверхностной волны с увеличением частоты уменьшается, причем оба типа волны не имеют отсечки.
а фазовая скорость поверхностной волны с увеличением частоты уменьшается, причем оба типа волны не имеют отсечки.
При больших частотах между волнами возникает синхронная связь, условием которой является равенство фазовых скоростей  -волны и поверхностных волн. В данном случае в НПЛ на верхних граничных частотах эти условия выполняются, что приводит к возбуждению паразитных поверхностных волн и, как следствие, к нежелательным связям между элементами схемы или к паразитным резонансным явлениям, возникающим за счет отражении от корпуса СВЧ модуля, краев подложки и пр.
-волны и поверхностных волн. В данном случае в НПЛ на верхних граничных частотах эти условия выполняются, что приводит к возбуждению паразитных поверхностных волн и, как следствие, к нежелательным связям между элементами схемы или к паразитным резонансным явлениям, возникающим за счет отражении от корпуса СВЧ модуля, краев подложки и пр.
Дисперсионное уравнение поверхностной волны, распространяющейся в диэлектрическом слое, нанесенном на бесконечно широкой идеально проводящей поверхности, имеет вид:

для  -типа
-типа

Максимальная синхронная связь волн  и
и  достигается при равенстве эффективных диэлектрических проницаемостей среды для этих волн (равенство фазовых скоростей):
достигается при равенстве эффективных диэлектрических проницаемостей среды для этих волн (равенство фазовых скоростей):

где  эффективная проницаемость НПЛ, определяемая из выражения (3),
эффективная проницаемость НПЛ, определяемая из выражения (3),
Подставляя условия (39) в (37) и (38), получим значения граничной длины волны, при которых возникают электрические поверхностные волны:

и магнитные поверхностные волны:

Из выражений (40) и (41) видно, что с увеличением ширины проводника НПЛ граничная длина волны возрастает. На практике НПЛ обычно выполняется на подложках с высоким значением диэлектрической проницаемости, поэтому знаменатель в выражениях для  стремится к
стремится к  Использовав данное условие, получим с достаточно высокой «инженерной» точностью простые выражения: для НПЛ с широким проводником граничная длина волны равна
Использовав данное условие, получим с достаточно высокой «инженерной» точностью простые выражения: для НПЛ с широким проводником граничная длина волны равна

и узким проводником —

Формулы (42) и (43) справедливы для квази-Т-волны. Вместе с тем известно, что в НПЛ существуют гибридные волны  поэтому необходимо учитывать их дисперсионные характеристики в сочетании с уравнениями (40) и (41). Расчет излучающих волн проведен в работе [36], где показано (рис. 1.5), что они не имеют нижней частоты отсечки. При низких частотах поверхностная волна слабо связана с подложкой и по мере увеличения частоты энергия волны все более концентрируется в подложке, что приводит к уменьшению фазовой скорости (увеличению излучаемой энергии с НПЛ).
поэтому необходимо учитывать их дисперсионные характеристики в сочетании с уравнениями (40) и (41). Расчет излучающих волн проведен в работе [36], где показано (рис. 1.5), что они не имеют нижней частоты отсечки. При низких частотах поверхностная волна слабо связана с подложкой и по мере увеличения частоты энергия волны все более концентрируется в подложке, что приводит к уменьшению фазовой скорости (увеличению излучаемой энергии с НПЛ).
Зависимость излучаемой мощности от волнового сопротивления НПЛ получена в [42]:

где

Экспериментальные исследования показали, что излучение поверхностных волн возникает при толщине подложки  для
для  для
для  [43]. Результаты этих экспериментальных исследований с погрешностью до 2% совпадают с расчетными данными по формуле (44).
[43]. Результаты этих экспериментальных исследований с погрешностью до 2% совпадают с расчетными данными по формуле (44).
9. Варианты НПЛ для ОИС СВЧ.
Для формирования элементной базы ОИС СВЧ необходимо иметь набор НПЛ с проводниками, расположенными в комбинации между различными слоями диэлектриков. Некоторые варианты наиболее удачных конструкций ЛП, имеющие практическое значение в проектировании ИС и ОИС, рассмотрены в обзоре [44] (рис. 1.9).
Результаты расчетов и экспериментальные данные мы не приводим из-за ограниченного объема книги; дадим только некоторые литературные сноски, которые позволят читателю при необходимости найти нужные данные. НПЛ с внешним слоем диэлектрика
(рис. 1.9, а, г), выполняющего функции защиты схемы от климатических и радиационных воздействий, достаточно подробно рассмотрена в [45—48]. «Подвешенная» НПЛ (рис. 1.9,6), отличающаяся высоким значением собственной добротности (малые потери), — [33]. Проводники НПЛ, связапиые по электромагнитному полю (лицевая связь рис. 1.9, в и боковая связь рис. 1.9, - [49, 50].

Рис. 1.9. Наиболее распространенные варианты НПЛ
Модифицированные НПЛ (рис. 1.9, е, ж, з), позволяющие строить БЭ и СВЧ модули РЭА,- [51—53]. В дальнейшем мы неоднократно обратимся к вопросам использования разных типов ЛП в ОИС СВЧ (в духе принципа конструкционного соответствия).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- 1. Основные тенденции развития современной радиоэлектроники.
- 2. Общие соображения о переходе к ОИС СВЧ.
- 3. Некоторые предварительные общие результаты.
- § В.2. Принципиальные основы подхода к автоматизированному проектированию ОИС СВЧ
- 2. Принцип декомпозиции.
- 3. Матрица рассеяния функционально-конструктивного узла РЭА.
- 4. Структура системы АП и режимы ее функционирования.
- ГЛАВА 1. Линии передачи для ОИС СВЧ
- 2. Учет реальных размеров СПЛ.
- 3. Потери в СПЛ.
- 4. Максимальная рабочая частота СПЛ
- § 1.2. Несимметричная полосковая линия
- § 1.3. Симметричная щелевая линия
- 2. Многослойная подвешенная СЩЛ.
- 3. СЩЛ типа «сэндвич».
- § 1.4. Несимметричная щелевая линия
- 2. Интегральные уравнения для НЩЛ. Собственные волны.
- 3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
- 4. Структура поля в НЩЛ.
- 5. Экспериментальные исследования НЩЛ.
- 6. Модификации НЩЛ.
- § 1.5. Копланарная линия передачи
- 2. Электродинамическое приближение в теории КЛ. Метод Галеркина. Численные результаты.
- 3. Экранированные КЛ.
- 4. Модификации экранированных КЛ.
- § 1.6. Линии передачи магнитостатических волн
- ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
- § 2.1. Метод Олинера и модели некоторых линий
- 2. Модели некоторых полосковых линий передачи.
- § 2.2. Неоднородности в ОИС СВЧ
- 2. Неоднородности в H-плоскости.
- 3. Неоднородности в Е-плоскости.
- 4. Неоднородности в копланарной линии.
- 5. Т-соединения различных типов линий в ОИС СВЧ.
- 6. Некоторые примеры тройников для ОИС СВЧ.
- ГЛАВА 3. Переходы между различными типами направляющих структур ОИС СВЧ
- § 3.1. Сверхширокополосные переходы — переходы с непосредственным гальваническим контактом
- § 3.2. Широкополосные шлейфные переходы
- § 3.3. Узкополосные резонансные переходы щелевого типа
- 2. Расчет щелевого перехода [226].
- 3. Согласование перехода.
- 4. Синтез перехода [224].
- 5. Частотные характеристики переходов.
- § 3.4. БЭ согласования ОИС СВЧ
- 2. Несинхронный трансформатор.
- 3. Шлейфный трансформатор.
- 4. Подстройка шлейфов согласующих трансформаторов.
- ГЛАВА 4. Гибридные мостовые устройства ОИС СВЧ
- § 4.1. Балансные делители (сумматоры) мощности
- § 4.2. Кольцевые мосты
- 2. Гибридный кольцевой мост с обращением фазы.
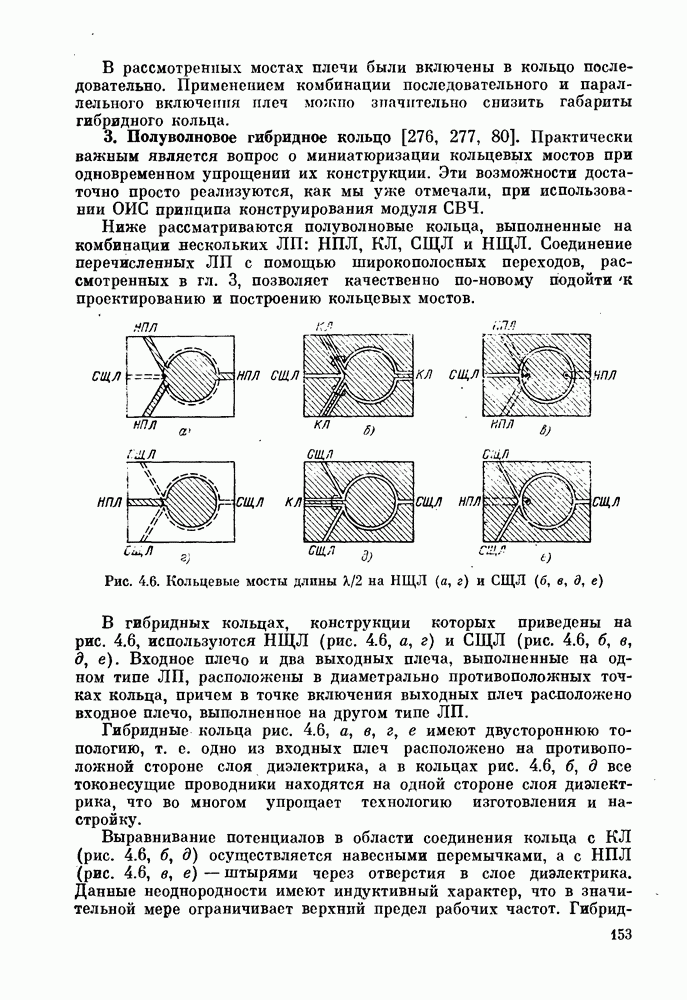
- 3. Полуволновое гибридное кольцо [276, 277, 80].
- 4. Гибридное кольцо периметра 3l/2
- 5. «Магические» Т-соединения.
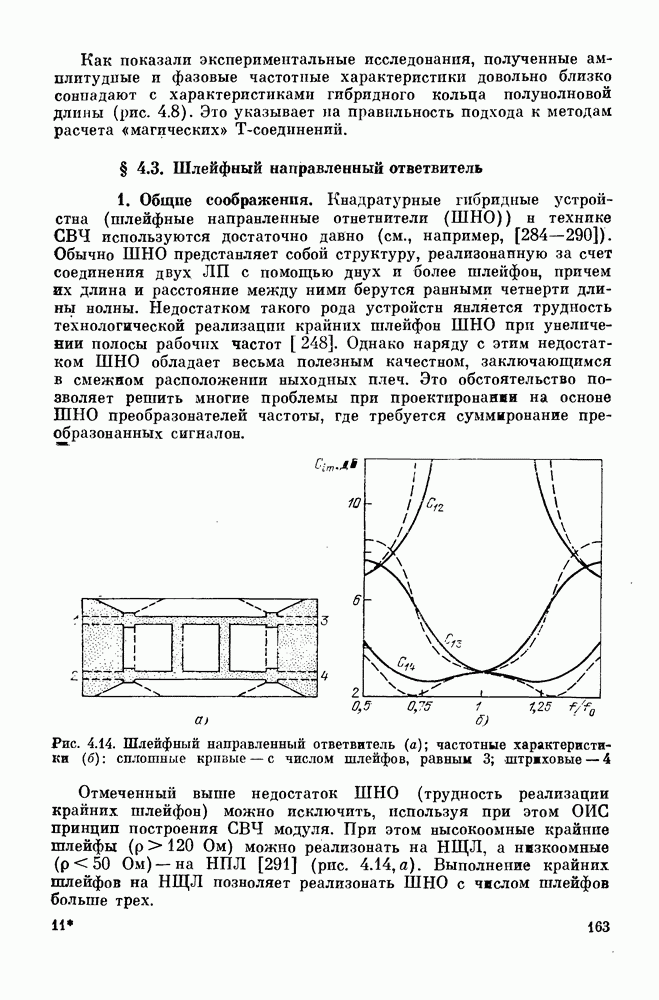
- § 4.3. Шлейфный направленный ответвитель
- § 4.4. Квадратурные направленные ответвители
- § 4.5. Связь двух полосковых линий с переменными параметрами и критическим сечением
- ГЛАВА 5. Объемные многослойные фильтры СВЧ
- § 5.2. Диэлектрические резонаторы
- § 5.3. Полосковые резонаторы
- § 5.4. Фильтры на ОИС СВЧ
- ГЛАВА 6. СВЧ устройства на ОИС
- § 6.1. Многоканальные делители мощности
- § 6.2. Фазовые манипуляторы
- § 6.3. Широкополосные модуляторы
- § 6.4. Приемно-передающие модули
- ГЛАВА 7. Применение ОИС СВЧ в измерительной технике
- § 7.1. Многозондовый датчик для измерения комплексных сопротивлений
- § 7.2. Экспресс-метод контроля диэлектрических проницаемостей подложек ОИС СВЧ
- § 7.3. Устройство дискретизации частотного масштаба
- Заключение