| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
Полученная система интегральных уравнений (1) является достаточно общей. Из нее непосредственно следует система интегральных уравнений четвертого порядка для НЩЛ. В этом случае матрицей проводимости будет служить одна клетка  при подстановке в нее размеров диэлектрических слоев и их проницаемостей. Для алгебраизации системы интегральных уравнений воспользуемся методом Галеркииа. Существенным моментом этого подхода является проблема выбора системы базисных функций. Как уже отмечалось выше, поверхностные токи в НЩЛ из-за дифракционных эффектов должны иметь весьма слолшый вид, далекий от классического степенного распределения
при подстановке в нее размеров диэлектрических слоев и их проницаемостей. Для алгебраизации системы интегральных уравнений воспользуемся методом Галеркииа. Существенным моментом этого подхода является проблема выбора системы базисных функций. Как уже отмечалось выше, поверхностные токи в НЩЛ из-за дифракционных эффектов должны иметь весьма слолшый вид, далекий от классического степенного распределения  типичного, например, для узкой СЩЛ [1]. По этой причине крайне трудно подобрать удачный базис. Однако из теории приближения функций известно, что в подобной ситуации хорошие результаты дают кусочно-определенные полиномы, которыми легче аппроксимировать сплыю осциллирующие зависимости [85].
типичного, например, для узкой СЩЛ [1]. По этой причине крайне трудно подобрать удачный базис. Однако из теории приближения функций известно, что в подобной ситуации хорошие результаты дают кусочно-определенные полиномы, которыми легче аппроксимировать сплыю осциллирующие зависимости [85].
Вопросам применения кусочно-определенных функций для исследования интегральных уравнений электродинамики посвящено сравнительно ограниченное число работ (в отличие от метода конечных элементов для дифференциальных уравнений) [86]. Поэтому многие важные вопросы (сходимость метода, обусловленность систем линейных алгебраических уравнений (СЛАУ) в зависимости от вида базисных функций и способа разбиения) остаются плохо изученными и представляют значительный самостоятельный интерес. Ниже мы коспемся некоторых этих моментов.
Итак, разобьем поверхность диэлектрика от края металлического слоя до экрана на  отрезков-элементов. В качестве базисной функции для поперечного магнитного тока (продольное электрическое поле) возьмем, например, линейный интерполирующий многочлен [85]
отрезков-элементов. В качестве базисной функции для поперечного магнитного тока (продольное электрическое поле) возьмем, например, линейный интерполирующий многочлен [85]

где  неизвестные коэффициенты, равные значению
неизвестные коэффициенты, равные значению
магнитного тока в  узле,
узле,  разбиения.
разбиения.  учтено, что в двух крайних узлах (на экране и ребре) ток удовлетворяет нулевым граничным условиям.
учтено, что в двух крайних узлах (на экране и ребре) ток удовлетворяет нулевым граничным условиям.
В пределах малого отрезка между продольным и поперечным магнитными токами в квазистатическом приближении  имеется связь, вытекающая из уравнений Максвелла:
имеется связь, вытекающая из уравнений Максвелла:

Удовлетворение базисными функциями условия (7) улучшвет сходимость и повышает устойчивость алгоритма [67]. Поэтому базис для продольного магнитного тока в данном случае выберем в классе кусочно-постоянных функций:

где  неизвестные коэффициенты, равные значению магнитного тока в центре
неизвестные коэффициенты, равные значению магнитного тока в центре  отрезка,
отрезка,

Далее, используя стандартную процедуру Галеркина для интегральных уравнений, получим однородную СЛАУ относительно неизвестных коэффициентов 6:

Здесь  матрица, полученная в результате применения к (1) метода Галеркина. Условие совместности для СЛАУ (10) позволяет получить дисперсионное соотношение для НЩЛ:
матрица, полученная в результате применения к (1) метода Галеркина. Условие совместности для СЛАУ (10) позволяет получить дисперсионное соотношение для НЩЛ:

На рис. 1.20 изображены некоторые результаты исследования полученного дисперсионного уравнения (11): зависимость замедления  от параметра
от параметра  отражающего изменение расстояния от экрана до металлического ребра. Параметр
отражающего изменение расстояния от экрана до металлического ребра. Параметр  имеет отрицательный знак в случае разнесенных ребер металла и положительный — для НЩЛ с перекрытыми слоями металла.
имеет отрицательный знак в случае разнесенных ребер металла и положительный — для НЩЛ с перекрытыми слоями металла.
Кривая 1 описывает зависимость замедления основной волны от 5. При разнесении ребер металла  замедление
замедление  стремится к замедлению основной волны
стремится к замедлению основной волны  трехслойного волновода (штриховая горизонтальная линия). С другой стороны, увеличение степени перекрытия
трехслойного волновода (штриховая горизонтальная линия). С другой стороны, увеличение степени перекрытия  приводит к тому, что волна в НЩЛ приобретает все больше свойств волны распространяющейся в прямоугольном волноводе, высота которого равна толщине диэлектрической подложки. В исследуемой модели существуют и
приводит к тому, что волна в НЩЛ приобретает все больше свойств волны распространяющейся в прямоугольном волноводе, высота которого равна толщине диэлектрической подложки. В исследуемой модели существуют и
пространяющиеся высшие типы иолн (кривые 2—6), параметры и структура которых стремятся в пределе 1) к соответствующим параметрам волн  прямоугольного волновода с размерами поперечного сечения а
прямоугольного волновода с размерами поперечного сечения а  Это означает, что, например, вторая волна в области перекрытия имеет на металле две вариации электрического тока, третья — три и т. д.
Это означает, что, например, вторая волна в области перекрытия имеет на металле две вариации электрического тока, третья — три и т. д.

Рис. 1.20. Зависимость дисперсии основной и высших типов волн от перехлеста слоев металла в НЩЛ: сплошные кривые — расчет, точки — эксперимент; 
Таким образом, классификацию волн в НЩЛ можно проводить аналогично классификации волн в несимметричной полосковой линии [1]. Разнесение ребер металла сопровождается переходом в режим отсечки большинства высших волн полоскового типа, а замедление второй волны близко к замедлению распространяющейся волны 2 трехслойного волновода (четное возбуждение). Дальнейшее увеличение  сопровождается выходом из режима отсечки волны, природа которой аналогична природе высшей волны СЩЛ (кривая 7) [87].
сопровождается выходом из режима отсечки волны, природа которой аналогична природе высшей волны СЩЛ (кривая 7) [87].
На этом же рисунке приведены и: экспериментальные данные (точки), полученные резонансным методом для НЩЛ, свернутой в кольцо и возбуждаемой с помощью несимметричной полосковой линии [200].
Исследование алгоритма показало ухудшение его сходимости в области значений параметра  что объясняется сильным дифракционным взаимодействием ребер металла. Используя неравномерное разбиение поверхности слоя диэлектрика от ребра до экрана, удалось существенно улучшить сходимость алгоритма (табл. 1.1).
что объясняется сильным дифракционным взаимодействием ребер металла. Используя неравномерное разбиение поверхности слоя диэлектрика от ребра до экрана, удалось существенно улучшить сходимость алгоритма (табл. 1.1).
Значительное влияние на затраты машинного времени оказывает число учтенных гармоник  в элементах матрицы СЛАУ (10). В нашем случае вследствие выбранного базиса эти элементы имеют асимптотику
в элементах матрицы СЛАУ (10). В нашем случае вследствие выбранного базиса эти элементы имеют асимптотику 
Таблица 1.1 (см. скан)
Поэтому изменение основной волны слабо зависит от  начиная с
начиная с  (табл. 1.2).
(табл. 1.2).
Таблица 1.2 (см. скан)
Дальнейшее улучшение сходимости алгоритма связано с учетом особенности на ребре, использованием полиномов старших степеней и т. д.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- 1. Основные тенденции развития современной радиоэлектроники.
- 2. Общие соображения о переходе к ОИС СВЧ.
- 3. Некоторые предварительные общие результаты.
- § В.2. Принципиальные основы подхода к автоматизированному проектированию ОИС СВЧ
- 2. Принцип декомпозиции.
- 3. Матрица рассеяния функционально-конструктивного узла РЭА.
- 4. Структура системы АП и режимы ее функционирования.
- ГЛАВА 1. Линии передачи для ОИС СВЧ
- 2. Учет реальных размеров СПЛ.
- 3. Потери в СПЛ.
- 4. Максимальная рабочая частота СПЛ
- § 1.2. Несимметричная полосковая линия
- § 1.3. Симметричная щелевая линия
- 2. Многослойная подвешенная СЩЛ.
- 3. СЩЛ типа «сэндвич».
- § 1.4. Несимметричная щелевая линия
- 2. Интегральные уравнения для НЩЛ. Собственные волны.
- 3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
- 4. Структура поля в НЩЛ.
- 5. Экспериментальные исследования НЩЛ.
- 6. Модификации НЩЛ.
- § 1.5. Копланарная линия передачи
- 2. Электродинамическое приближение в теории КЛ. Метод Галеркина. Численные результаты.
- 3. Экранированные КЛ.
- 4. Модификации экранированных КЛ.
- § 1.6. Линии передачи магнитостатических волн
- ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
- § 2.1. Метод Олинера и модели некоторых линий
- 2. Модели некоторых полосковых линий передачи.
- § 2.2. Неоднородности в ОИС СВЧ
- 2. Неоднородности в H-плоскости.
- 3. Неоднородности в Е-плоскости.
- 4. Неоднородности в копланарной линии.
- 5. Т-соединения различных типов линий в ОИС СВЧ.
- 6. Некоторые примеры тройников для ОИС СВЧ.
- ГЛАВА 3. Переходы между различными типами направляющих структур ОИС СВЧ
- § 3.1. Сверхширокополосные переходы — переходы с непосредственным гальваническим контактом
- § 3.2. Широкополосные шлейфные переходы
- § 3.3. Узкополосные резонансные переходы щелевого типа
- 2. Расчет щелевого перехода [226].
- 3. Согласование перехода.
- 4. Синтез перехода [224].
- 5. Частотные характеристики переходов.
- § 3.4. БЭ согласования ОИС СВЧ
- 2. Несинхронный трансформатор.
- 3. Шлейфный трансформатор.
- 4. Подстройка шлейфов согласующих трансформаторов.
- ГЛАВА 4. Гибридные мостовые устройства ОИС СВЧ
- § 4.1. Балансные делители (сумматоры) мощности
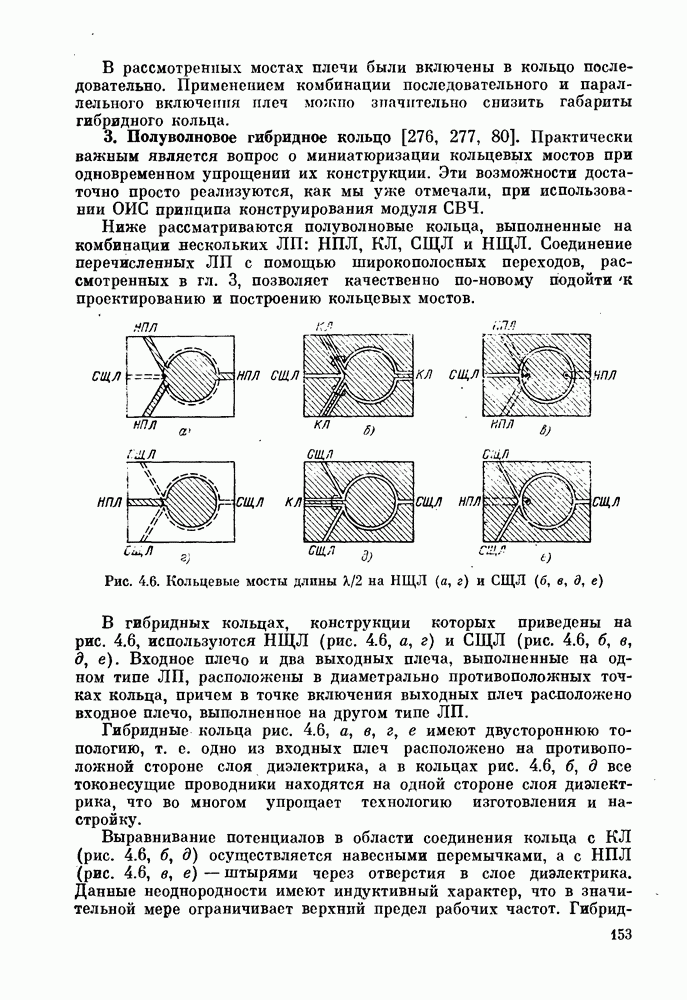
- § 4.2. Кольцевые мосты
- 2. Гибридный кольцевой мост с обращением фазы.
- 3. Полуволновое гибридное кольцо [276, 277, 80].
- 4. Гибридное кольцо периметра 3l/2
- 5. «Магические» Т-соединения.
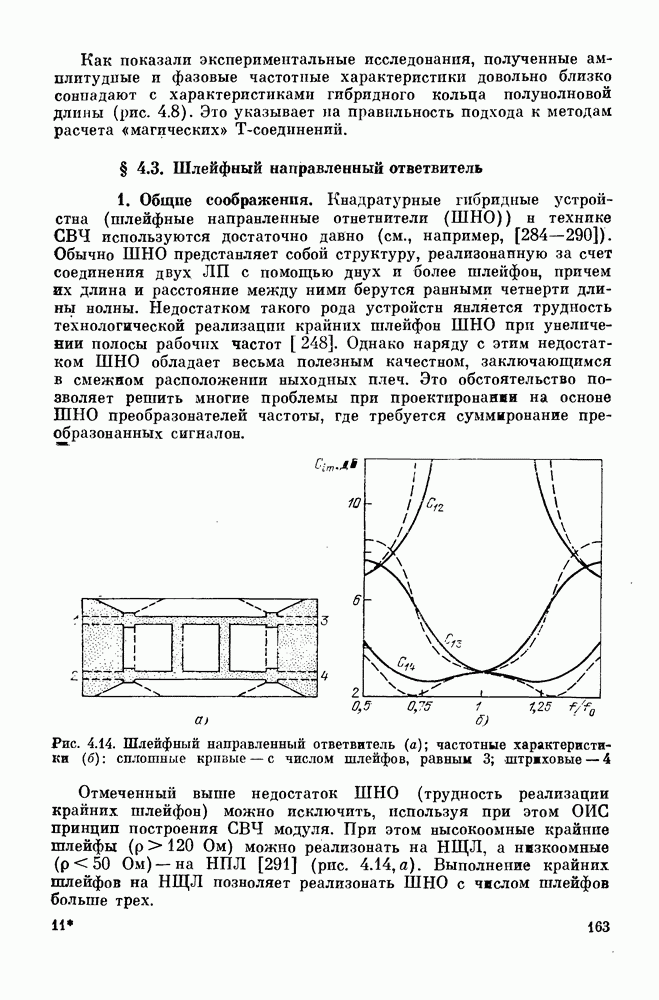
- § 4.3. Шлейфный направленный ответвитель
- § 4.4. Квадратурные направленные ответвители
- § 4.5. Связь двух полосковых линий с переменными параметрами и критическим сечением
- ГЛАВА 5. Объемные многослойные фильтры СВЧ
- § 5.2. Диэлектрические резонаторы
- § 5.3. Полосковые резонаторы
- § 5.4. Фильтры на ОИС СВЧ
- ГЛАВА 6. СВЧ устройства на ОИС
- § 6.1. Многоканальные делители мощности
- § 6.2. Фазовые манипуляторы
- § 6.3. Широкополосные модуляторы
- § 6.4. Приемно-передающие модули
- ГЛАВА 7. Применение ОИС СВЧ в измерительной технике
- § 7.1. Многозондовый датчик для измерения комплексных сопротивлений
- § 7.2. Экспресс-метод контроля диэлектрических проницаемостей подложек ОИС СВЧ
- § 7.3. Устройство дискретизации частотного масштаба
- Заключение