| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Расчет щелевого перехода [226].
Щелевой переход с элементами согласования и  в соединяемых линиях I и II и его эквивалентная схема представлены на рис. 3.6. В данной схеме переход разбивается «а простейшие участки волновые матрицы передачи и рассеяния которых известны [227].
в соединяемых линиях I и II и его эквивалентная схема представлены на рис. 3.6. В данной схеме переход разбивается «а простейшие участки волновые матрицы передачи и рассеяния которых известны [227].

Рис. 3.6. Щелевой переход между двумя линиями передачи (а); эквивалентная схема (б)
Матрица рассеяния согласованных линий, связанных щелевым резонатором, имеет вид

Здесь  коэффициент связи щелевого резонатора с согласованной линией передачи (влияние второй линии передачи не учитывается);
коэффициент связи щелевого резонатора с согласованной линией передачи (влияние второй линии передачи не учитывается);  параметр связи,
параметр связи,  собственная и внешняя добротности щелевого резонатора,
собственная и внешняя добротности щелевого резонатора,  нормированная расстройка частоты.
нормированная расстройка частоты.
Вычисляя общую матрицу щелевого перехода с согласующей проводимостью  в одной из линий передачи, как произведение «частичных» матриц передачи
в одной из линий передачи, как произведение «частичных» матриц передачи  отдельных участков перехода (рис. 3.6, б), и переходя к общей матрице рассеяния, пайдем коэффициенты передачи
отдельных участков перехода (рис. 3.6, б), и переходя к общей матрице рассеяния, пайдем коэффициенты передачи  и отражения со стороны плеча, в котором расположена согласующая проводимость:
и отражения со стороны плеча, в котором расположена согласующая проводимость:

Здесь  электрическая длина отрезка линии между плоскостью щелевого резонатора и проводимостью
электрическая длина отрезка линии между плоскостью щелевого резонатора и проводимостью  электрические длины короткозамкнутых шлейфов, которыми заканчиваются линии за резонатором.
электрические длины короткозамкнутых шлейфов, которыми заканчиваются линии за резонатором.
Параметр связи щелевого резонатора (имеющего косинусоидальное распределение поля) с волной низшего типа линии определяется следующим образом. С помощью леммы Лоренца находим амплитуды волн, возбуждаемые щелевым резонатором в линии передачи [39, 228]. Подставляя полученные результаты в уравнение энергетического баланса, найдем параметры связи щелевого резонатора с 

Здесь  собственная добротность,
собственная добротность,  длина щелевого резонатора, определенная без учета дисперсии СЩЛ и потерь в короткозамыкающих перемычках на концах щели.
длина щелевого резонатора, определенная без учета дисперсии СЩЛ и потерь в короткозамыкающих перемычках на концах щели.
Выражения  найдены в предположении, что ширина щели много меньше длины волны и проводники линий передачи не влияют на параметры щелевого резонатора. Распределение тангенциальной составляющей магнитного поля на границе экранирующего слоя НПЛ аппроксимировано колоколообразной функцией
найдены в предположении, что ширина щели много меньше длины волны и проводники линий передачи не влияют на параметры щелевого резонатора. Распределение тангенциальной составляющей магнитного поля на границе экранирующего слоя НПЛ аппроксимировано колоколообразной функцией 
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- 1. Основные тенденции развития современной радиоэлектроники.
- 2. Общие соображения о переходе к ОИС СВЧ.
- 3. Некоторые предварительные общие результаты.
- § В.2. Принципиальные основы подхода к автоматизированному проектированию ОИС СВЧ
- 2. Принцип декомпозиции.
- 3. Матрица рассеяния функционально-конструктивного узла РЭА.
- 4. Структура системы АП и режимы ее функционирования.
- ГЛАВА 1. Линии передачи для ОИС СВЧ
- 2. Учет реальных размеров СПЛ.
- 3. Потери в СПЛ.
- 4. Максимальная рабочая частота СПЛ
- § 1.2. Несимметричная полосковая линия
- § 1.3. Симметричная щелевая линия
- 2. Многослойная подвешенная СЩЛ.
- 3. СЩЛ типа «сэндвич».
- § 1.4. Несимметричная щелевая линия
- 2. Интегральные уравнения для НЩЛ. Собственные волны.
- 3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
- 4. Структура поля в НЩЛ.
- 5. Экспериментальные исследования НЩЛ.
- 6. Модификации НЩЛ.
- § 1.5. Копланарная линия передачи
- 2. Электродинамическое приближение в теории КЛ. Метод Галеркина. Численные результаты.
- 3. Экранированные КЛ.
- 4. Модификации экранированных КЛ.
- § 1.6. Линии передачи магнитостатических волн
- ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
- § 2.1. Метод Олинера и модели некоторых линий
- 2. Модели некоторых полосковых линий передачи.
- § 2.2. Неоднородности в ОИС СВЧ
- 2. Неоднородности в H-плоскости.
- 3. Неоднородности в Е-плоскости.
- 4. Неоднородности в копланарной линии.
- 5. Т-соединения различных типов линий в ОИС СВЧ.
- 6. Некоторые примеры тройников для ОИС СВЧ.
- ГЛАВА 3. Переходы между различными типами направляющих структур ОИС СВЧ
- § 3.1. Сверхширокополосные переходы — переходы с непосредственным гальваническим контактом
- § 3.2. Широкополосные шлейфные переходы
- § 3.3. Узкополосные резонансные переходы щелевого типа
- 2. Расчет щелевого перехода [226].
- 3. Согласование перехода.
- 4. Синтез перехода [224].
- 5. Частотные характеристики переходов.
- § 3.4. БЭ согласования ОИС СВЧ
- 2. Несинхронный трансформатор.
- 3. Шлейфный трансформатор.
- 4. Подстройка шлейфов согласующих трансформаторов.
- ГЛАВА 4. Гибридные мостовые устройства ОИС СВЧ
- § 4.1. Балансные делители (сумматоры) мощности
- § 4.2. Кольцевые мосты
- 2. Гибридный кольцевой мост с обращением фазы.
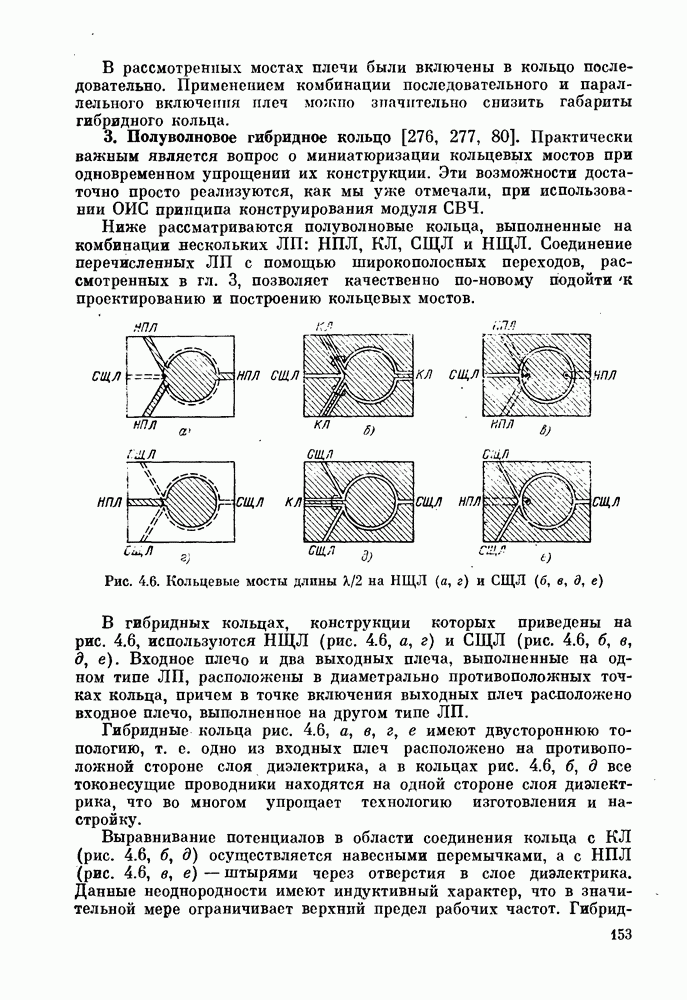
- 3. Полуволновое гибридное кольцо [276, 277, 80].
- 4. Гибридное кольцо периметра 3l/2
- 5. «Магические» Т-соединения.
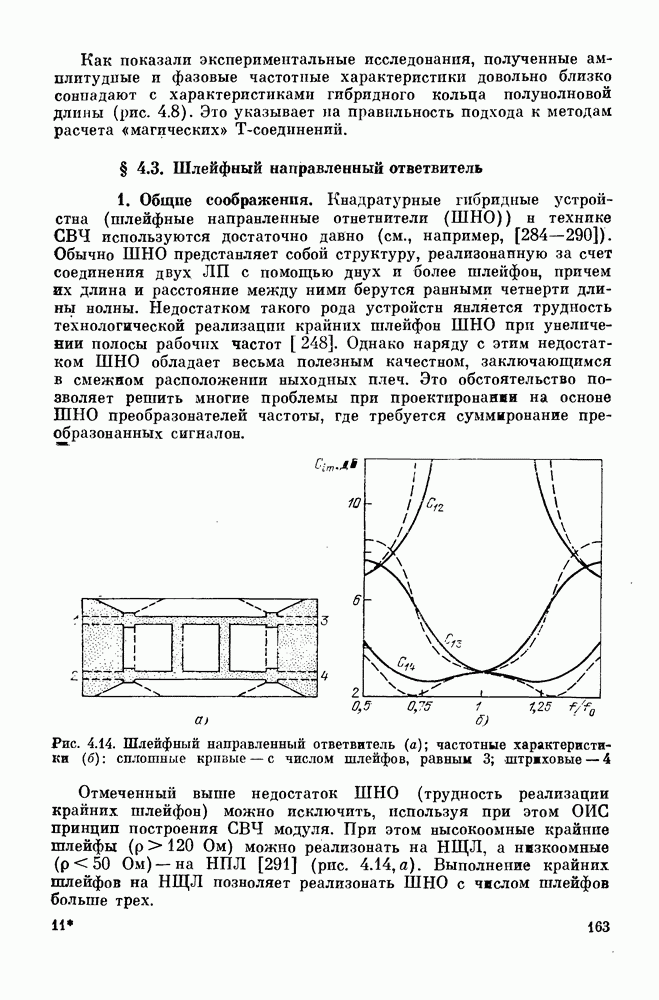
- § 4.3. Шлейфный направленный ответвитель
- § 4.4. Квадратурные направленные ответвители
- § 4.5. Связь двух полосковых линий с переменными параметрами и критическим сечением
- ГЛАВА 5. Объемные многослойные фильтры СВЧ
- § 5.2. Диэлектрические резонаторы
- § 5.3. Полосковые резонаторы
- § 5.4. Фильтры на ОИС СВЧ
- ГЛАВА 6. СВЧ устройства на ОИС
- § 6.1. Многоканальные делители мощности
- § 6.2. Фазовые манипуляторы
- § 6.3. Широкополосные модуляторы
- § 6.4. Приемно-передающие модули
- ГЛАВА 7. Применение ОИС СВЧ в измерительной технике
- § 7.1. Многозондовый датчик для измерения комплексных сопротивлений
- § 7.2. Экспресс-метод контроля диэлектрических проницаемостей подложек ОИС СВЧ
- § 7.3. Устройство дискретизации частотного масштаба
- Заключение