| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
В этой главе будут рассмотрены основные типы неоднородностей (базовых элементов), встречающихся в полосковых линиях передачи и составляющих, по существу, элементную базу ОИС СВЧ. На материале предыдущей главы читатель мог убедиться, что только строгий подход позволяет понять физическое содержание задачи и построить адекватную модель, например, регулярной линии передачи. Там же было показано, что, получив на основе строгой постановки задачи ясную физическую картину явлении, для практических потребностей можно удовлетвориться некоторыми приближенными результатами, особенно, если при этом удается получить оценку степени приближения. Гораздо более сложный объект исследования представляют неоднородности в полосковых ДП и тем более в базовых элементах ОИС СВЧ, в которых электродинамические структуры представляют собой принципиально трехмерные образовании. Разумеется, и НПЛ есть трехмерная структура, однако после приведения ее к эквивалентным парметрам (на основании строгого анализа  ) с нею можно обращаться как с двумерной структурой. В еще большей степени это относится к СПЛ и другим волноведущим структурам ОИС СВЧ (рис. В.1). Однако и при наличии верхнего экрана ЛП ОИС оказываются открытыми в поперечных направлениях и любая неоднородность вызывает излучение в этих поперечных направлениях. Таким образом, возможно более правильно отнести ЛП в ОИС к классу квазизакрытых ЛП. В этой главе мы остановимся на общем эвристическом методе моделирования как регулярных, так и нерегулярных полосковых структур — методе Олинера. Он позволяет на основе физических рассуждений свести открытую или квазиоткрытую структуру к закрытой и воспользоваться для последней развитым мощным аппаратом и результатами анализа закрытых структур.
) с нею можно обращаться как с двумерной структурой. В еще большей степени это относится к СПЛ и другим волноведущим структурам ОИС СВЧ (рис. В.1). Однако и при наличии верхнего экрана ЛП ОИС оказываются открытыми в поперечных направлениях и любая неоднородность вызывает излучение в этих поперечных направлениях. Таким образом, возможно более правильно отнести ЛП в ОИС к классу квазизакрытых ЛП. В этой главе мы остановимся на общем эвристическом методе моделирования как регулярных, так и нерегулярных полосковых структур — методе Олинера. Он позволяет на основе физических рассуждений свести открытую или квазиоткрытую структуру к закрытой и воспользоваться для последней развитым мощным аппаратом и результатами анализа закрытых структур.
§ 2.1. Метод Олинера и модели некоторых линий
1. Метод Олинера.
Долгое время развитый в 50-х годах А. Олвнером [170] подход к анализу полосковых структур оставался практически единственным методом, с помощью которого удавалось
получить приемлемые физические результаты. Строгий подход потребовал бы решения трехмерных векторных задач для областей со сложными границами и при отсутствии в общем случае каких-либо явно выделяемых малых параметров. Поэтому такая строгая постановка задачи даже для наиболее мощных современных ЦЭВМ представляется нецелесообразной. Вместе с тем метод Олипера позволяет при наличии ряда ограничений (одноволновый режим линии или неоднородности, наличие решения модельной задачи и др.) и определенной осторожности при его использовании получать приемлемые для практики результаты. С его помощью в [1] был рассмотрен широкий класс неоднородностей в симметричных и несимметричных полосковых структурах. Мы здесь не будем, разумеется, воспроизводить результаты [1], а лишь коротко остановимся на существе метода Олинера и его обобщении на открытые линии, так как и при анализе БЭ ОИС СВЧ он может оказаться полезным.
Физическую основу эвристического подхода Олинера составляет предположение о том, что энергия рабочей волны ПЛП (например, квази-Т-волна) сконцентрирована в небольшой окрестности токонесущего проводника (для регулярной линии) или вблизи неоднородности (для нерегулярной ГШ). Пусть распределение энергии в поперечном сеченнп линии известно. Предположим, что распределение полей в поперечном сечении линии мало изменится, если на некотором расстоянии слева и справа от токонесущего проводника поместить идеальные электрические или магнитные стенки. Рассмотрим, для примера, СПЛ, представленную на рис. В.1, где магнитные стенки вводятся в вертикальные плоскости: расстояние между стенками составляет величину  Теперь, если увеличить ширину токонесущей полоски до пересечения ее с магнитными стенками, мы получим взамен СПЛ два прямоугольных волновода (с поперечными сечениями
Теперь, если увеличить ширину токонесущей полоски до пересечения ее с магнитными стенками, мы получим взамен СПЛ два прямоугольных волновода (с поперечными сечениями  которых горизонтальные стенки являются идеально электрическими, а вертикальные — идеально магнитными. В каждом из этих прямоугольных волноводов возможно распространение квази-Т-волны, так как к горизонтальным стенкам перпендикулярпо электрическое поле этой волны, а к вертикальным — магнитное поле, и, таким образом, граничные условия удовлетворяются.
которых горизонтальные стенки являются идеально электрическими, а вертикальные — идеально магнитными. В каждом из этих прямоугольных волноводов возможно распространение квази-Т-волны, так как к горизонтальным стенкам перпендикулярпо электрическое поле этой волны, а к вертикальным — магнитное поле, и, таким образом, граничные условия удовлетворяются.
Итак, в эквивалентном СПЛ прямоугольном волноводе может распространяться квази-Т-волна. Для установления эквивалентности линии и волновода необходимо также, чтобы длина волны, волновое сопротивление и фазовые скорости были однаковы в СПЛ (это же в равной степени относится и к линиям других
типов, между которыми устанавливается соответствие в указанном смысле) и ее прототипе.
Волновое сопротивление СПЛ имеет вид

Общее волновое сопротпвление двух параллельно соединенных прямоугольных волноводов есть

Здесь под волновым сопротивлением понимается отношение напряжения в линии к току. Сравнивая (1) и (2), получаем искомую ширину волновода  в впде
в впде

где  полные эллиптические иитегралы.
полные эллиптические иитегралы.
Применение метода Олинера к БЭ, выполненным на основе НПЛ, требует некоторой его модификации, а именно перехода к двумерной модели с установкой виртуальных магнитных стенок в местах, определяемых строгой теорией ключевой структуры  и заменой реальной диэлектрической проницаемости
и заменой реальной диэлектрической проницаемости  подложки на ее эффективное значенне
подложки на ее эффективное значенне

где с — скорость света в вакууме,  фазовая скорость квазн-Т-волны в НПЛ. Магнитные стенки размещаются на расстоянии
фазовая скорость квазн-Т-волны в НПЛ. Магнитные стенки размещаются на расстоянии  друг от друга, определяемом (3), однако модуль к для НПЛ определяется не из (1), а является корнем трансцендентного уравнения
друг от друга, определяемом (3), однако модуль к для НПЛ определяется не из (1), а является корнем трансцендентного уравнения

в котором  — ширина токонесущей полоски.
— ширина токонесущей полоски.
Равенство (4) означает одинаковость фазовых скоростей в модели и прототипе,  равенство волновых сопротивлений. Обычно элементы матрицы рассеяния БЭ сильно зависят от скорости волны возбуждения, и поэтому условие (4) должно непременно выполняться во избежание неадекватности описания БЭ его моделью.
равенство волновых сопротивлений. Обычно элементы матрицы рассеяния БЭ сильно зависят от скорости волны возбуждения, и поэтому условие (4) должно непременно выполняться во избежание неадекватности описания БЭ его моделью.
Более подробные сведения по обобщенному методу Олинера и данные конкретных расчетов читатель найдет в книге [1, гл. 3, 4].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- 1. Основные тенденции развития современной радиоэлектроники.
- 2. Общие соображения о переходе к ОИС СВЧ.
- 3. Некоторые предварительные общие результаты.
- § В.2. Принципиальные основы подхода к автоматизированному проектированию ОИС СВЧ
- 2. Принцип декомпозиции.
- 3. Матрица рассеяния функционально-конструктивного узла РЭА.
- 4. Структура системы АП и режимы ее функционирования.
- ГЛАВА 1. Линии передачи для ОИС СВЧ
- 2. Учет реальных размеров СПЛ.
- 3. Потери в СПЛ.
- 4. Максимальная рабочая частота СПЛ
- § 1.2. Несимметричная полосковая линия
- § 1.3. Симметричная щелевая линия
- 2. Многослойная подвешенная СЩЛ.
- 3. СЩЛ типа «сэндвич».
- § 1.4. Несимметричная щелевая линия
- 2. Интегральные уравнения для НЩЛ. Собственные волны.
- 3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
- 4. Структура поля в НЩЛ.
- 5. Экспериментальные исследования НЩЛ.
- 6. Модификации НЩЛ.
- § 1.5. Копланарная линия передачи
- 2. Электродинамическое приближение в теории КЛ. Метод Галеркина. Численные результаты.
- 3. Экранированные КЛ.
- 4. Модификации экранированных КЛ.
- § 1.6. Линии передачи магнитостатических волн
- ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
- § 2.1. Метод Олинера и модели некоторых линий
- 2. Модели некоторых полосковых линий передачи.
- § 2.2. Неоднородности в ОИС СВЧ
- 2. Неоднородности в H-плоскости.
- 3. Неоднородности в Е-плоскости.
- 4. Неоднородности в копланарной линии.
- 5. Т-соединения различных типов линий в ОИС СВЧ.
- 6. Некоторые примеры тройников для ОИС СВЧ.
- ГЛАВА 3. Переходы между различными типами направляющих структур ОИС СВЧ
- § 3.1. Сверхширокополосные переходы — переходы с непосредственным гальваническим контактом
- § 3.2. Широкополосные шлейфные переходы
- § 3.3. Узкополосные резонансные переходы щелевого типа
- 2. Расчет щелевого перехода [226].
- 3. Согласование перехода.
- 4. Синтез перехода [224].
- 5. Частотные характеристики переходов.
- § 3.4. БЭ согласования ОИС СВЧ
- 2. Несинхронный трансформатор.
- 3. Шлейфный трансформатор.
- 4. Подстройка шлейфов согласующих трансформаторов.
- ГЛАВА 4. Гибридные мостовые устройства ОИС СВЧ
- § 4.1. Балансные делители (сумматоры) мощности
- § 4.2. Кольцевые мосты
- 2. Гибридный кольцевой мост с обращением фазы.
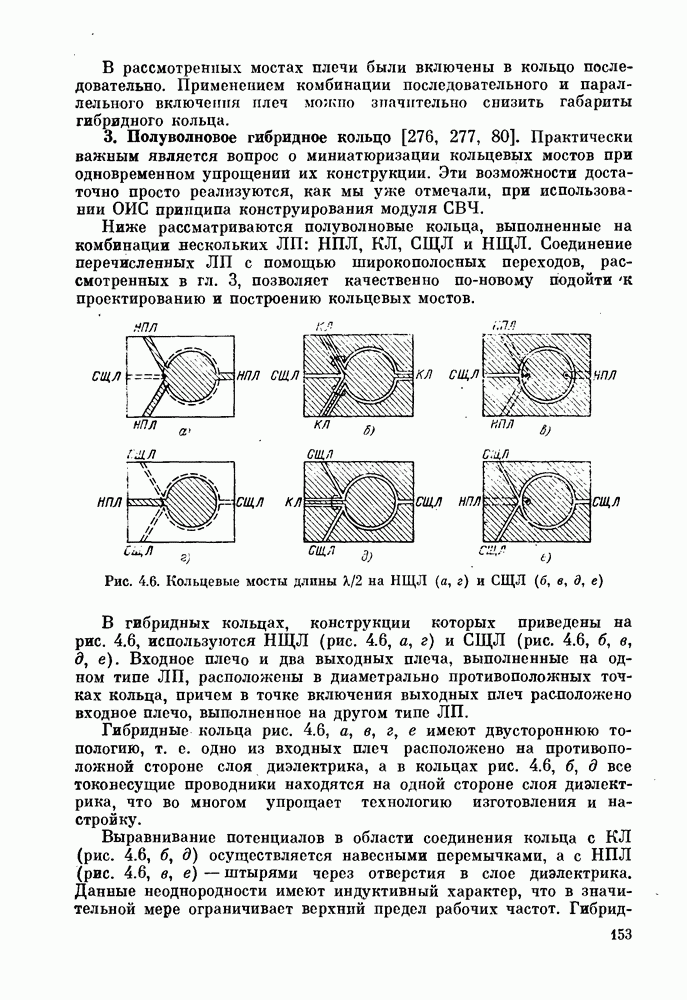
- 3. Полуволновое гибридное кольцо [276, 277, 80].
- 4. Гибридное кольцо периметра 3l/2
- 5. «Магические» Т-соединения.
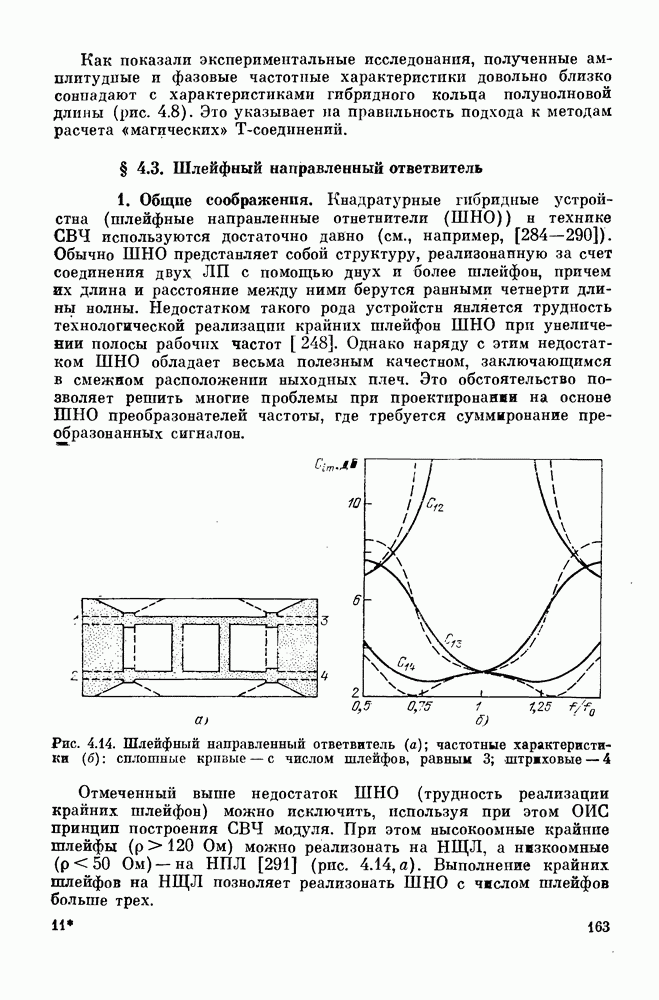
- § 4.3. Шлейфный направленный ответвитель
- § 4.4. Квадратурные направленные ответвители
- § 4.5. Связь двух полосковых линий с переменными параметрами и критическим сечением
- ГЛАВА 5. Объемные многослойные фильтры СВЧ
- § 5.2. Диэлектрические резонаторы
- § 5.3. Полосковые резонаторы
- § 5.4. Фильтры на ОИС СВЧ
- ГЛАВА 6. СВЧ устройства на ОИС
- § 6.1. Многоканальные делители мощности
- § 6.2. Фазовые манипуляторы
- § 6.3. Широкополосные модуляторы
- § 6.4. Приемно-передающие модули
- ГЛАВА 7. Применение ОИС СВЧ в измерительной технике
- § 7.1. Многозондовый датчик для измерения комплексных сопротивлений
- § 7.2. Экспресс-метод контроля диэлектрических проницаемостей подложек ОИС СВЧ
- § 7.3. Устройство дискретизации частотного масштаба
- Заключение