| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Неоднородности в H-плоскости.
Под БЭ этого класса понимаются полосковые структуры, токонесущие проводники которых располагаются в плоскости, перпендикулярной вектору  Наиболее тпппчными представителями этого класса БЭ являются устройства на основе СПЛ и
Наиболее тпппчными представителями этого класса БЭ являются устройства на основе СПЛ и  открытый конец ЛП, разрыв токонесущего проводника, отверстие, изгиб (излом), скачок ширины проводника и др.
открытый конец ЛП, разрыв токонесущего проводника, отверстие, изгиб (излом), скачок ширины проводника и др.

Рис. 2.1. Топология открытого конца полосковой линии (а); эквивалентные схемы 
Приведем данные по некоторым из них.
Открытый конец  Этот тип неоднородности (рис. 2.1, а) встречается практически во всех БЭ, используемых в ИС и
Этот тип неоднородности (рис. 2.1, а) встречается практически во всех БЭ, используемых в ИС и  разомкнутый или частично разомкнутый конец токонесущего проводника.
разомкнутый или частично разомкнутый конец токонесущего проводника.  квазистатическом приближении открытый конец представляет собой некоторую эквивалентную емкость
квазистатическом приближении открытый конец представляет собой некоторую эквивалентную емкость  вызывающую так называемое «удлинение»
вызывающую так называемое «удлинение»  проводника (рис. 2.1, в), которое определяется как
проводника (рис. 2.1, в), которое определяется как

где  В высокочастотном (квазпоптнческом) приближении реакция открытого конца может быть не емкостной, а индуктивной,
В высокочастотном (квазпоптнческом) приближении реакция открытого конца может быть не емкостной, а индуктивной,  тогда «удлинение» меняет знак и превращается в эквивалентное «укорочение»
тогда «удлинение» меняет знак и превращается в эквивалентное «укорочение» 
Использование открытого края структуры позволяет реализовать два класса БЭ: резонаторы (излучение мало) и излучающие элементы (см., например, [179]). Природа этого явления
(«вытекающие» волны), разумеется, едина, однако с вытеканием энергии из открытого конца всегда следует считаться. Так, папример, эффективное несанкционированное возбуждение поверхностной волны (в структуре металлическое основание — диэлектрическая подложка) может быть причиной заметных паразитных связей между отдельными БЭ, паразитным излучением в ненужную сторону (в излучающих структурах) и т. п. Это приводит к необходимости разнесения БЭ на «безопасное» расстояние, что ведет к увеличению габаритов СВЧ модуля; не всегда положение спасает введение дополнительных поглощающих экранов, металлических стенок, штырей и пр.

Рис. 2.2. Вид сбоку разомкнутого конца НПЛ (а); частотная зависимость проводимости излучения (б) и проводимости поверхностной волны (в) открытого конца линии
При проектировании необходимо учитывать долю излучаемой и преобразуемой в поверхностные волны энергии. На эквивалентной схеме рис. 2.1, б отмеченное вытекание энергии учитывается введением входной проводимости  для приближенного учета которой можно воспользоваться результатами [1].
для приближенного учета которой можно воспользоваться результатами [1].
Коэффициент отражения от открытого конца НПЛ имеет вид

или

Согласно (3) входная проводимость  определяется так:
определяется так:

Приведенные аналитические результатах можно использовать при первоначальных прикидочных оценках. Более строгие результаты получены, например, в [180] (см. также [2, 181]; в этих работах дап обзор литературы и результатов по другим многочисленным источникам). На рис. 2.2 приведены данные по входной проводимости  [180]; из них видно, что энергия излучения
[180]; из них видно, что энергия излучения  открытым концом увеличивается по мере роста частоты и уменьшения диэлектрической проницаемости подложки. На низких частотах превалирует поле излучения, а на высоких — энергия излучения
открытым концом увеличивается по мере роста частоты и уменьшения диэлектрической проницаемости подложки. На низких частотах превалирует поле излучения, а на высоких — энергия излучения  оказывается сравнимой; с энергией поверхностной волны
оказывается сравнимой; с энергией поверхностной волны  (см. также [179]).
(см. также [179]).

Рис. 2.3. Разрыв в полосковой линии (а); эквивалентная схема (б)
Вытекающие волны не имеют нижней частоты отсечки, что необходимо учитывать при проектировании высокодобротных резонансных и излучающих БЭ ОИС.
Разрыв в токонесущем проводнике ПЛ. В том же квазистатическом приближении плоскопараллельиый разрыв (рис. 2.3, а) можно представить в виде «аддитивного» положения независимых друг от друга емкостей  открытых концов, емкости собственно разрыва
открытых концов, емкости собственно разрыва  и параллельно последней — проводимости
и параллельно последней — проводимости  излучения
излучения  Для величин
Для величин  в этом приближении имеют место оценки [23]:
в этом приближении имеют место оценки [23]:

где

В формулах (5), (6) и в дальнейших выражениях проводимости нормированы на волновое сопротивление входной линии. Излучение здесь не учтено.
Круглое отверстие в середине токонесущего проводника. Отверстия (и в том числе круглые) в проводнике ПЛП (рис. 2.4, а) широко используются в практике ИС для параллельного включения сосредоточенных активных элементов, для задач согласования БЭ и др.

Рис. 2.4. Круглое отверстие в проводнике (а); эквивалентная схема (б)
Значения реакгивностсй эквивалентной схемы (рис. 2.4, б) в зависимости от размера отверстия определяются следующим образом [23]:

Здесь  эффективная ширина проводника. Излучение из отверстия во внешнее пространство в (7), (8) не учтено.
эффективная ширина проводника. Излучение из отверстия во внешнее пространство в (7), (8) не учтено.
Симметричный скачок ширины проводника. Такие элементы в ИС СВЧ находят самое разнообразное применение в согласующих трансформаторах, фильтрах, соединительных элементах и т. п. (рис. 2.5, а). В квазистатическом приближении эквивалентная схема имеет вид, представленный на рис. 2.5, б. При составлении ее учитывалось, что выступ перехода от широкой части проводника к узкой имеет индуктивный характер  [23]:
[23]:

где  обозначают эффективную ширину соответствующего проводника (рис. 2.5, а). Неоднородность частично открытого конца проводника имеет емкостную проводимость
обозначают эффективную ширину соответствующего проводника (рис. 2.5, а). Неоднородность частично открытого конца проводника имеет емкостную проводимость  Эффективное
Эффективное
удлинение  выступов проводника и входная проводимость излучения
выступов проводника и входная проводимость излучения  его концов определяются с помощью (1), (4).
его концов определяются с помощью (1), (4).
Прямоугольный изгиб (излом) проводника. На практике широко используются изломы под разными углами [1]. Однако наиболее частый случай — излом под прямым углом (рис. 2.6, а).

Рис. 2.5. Скачок ширины проводника (а); эквивалентная схема (б)
При составлении эквивалентной схемы прямоугольного излома (рис. 2.6, б) учитывалось, что внешние стороны проводника в области изгиба представляют индуктивную проводимость  а площадь изгиба — емкостную
а площадь изгиба — емкостную  Их значения суть [23]
Их значения суть [23]

В случае больших зпачений коэффициента отражения от рассмотренной неоднородности в области изгиба будет сильное излучение; при этом входная проводимость  и коэффициент отражения
и коэффициент отражения  определяются соотношениями (2), (4).
определяются соотношениями (2), (4).

Рис. 2,б. Прямоугольный изгиб проводника (а); эквивалентная схема (б)
Минимальное отражение  в прямоугольном изгибе проводника достигается при выборе топологии со срезом по диагонали внешней стороны изгиба проводника (на рис. 2.6, а срез показан пунктирной линией; см. [1]).
в прямоугольном изгибе проводника достигается при выборе топологии со срезом по диагонали внешней стороны изгиба проводника (на рис. 2.6, а срез показан пунктирной линией; см. [1]).
Т-образное разветвление проводника. Этот тип неоднородности является ключевым для целого ряда БЭ ОИС (делителя мощности, мостовые устройства, элементы полосовых фильтров и др.) (рис. 2.7, а). Эквивалентная схема представлена на рис. 2.7,6. В ней учтено: излучение во внешнее пространство (входная проводимость  идеальная трансформация сопротивлений
идеальная трансформация сопротивлений  и реактивный (емкостная
и реактивный (емкостная  и индуктивная
и индуктивная  проводимости)
проводимости)
характер (рис. 2.7,6). Анализ эквивалентной схемы (рис. 2.7,6) проведен в [176]. Входная проводимость излучения рассчитывается по (4), а остальные параметры эквивалентной схемы суть

Здесь

Соотношения (12), (13) дают возможность рассчитывать частотные характеристики коэффициентов волповой матрицы рассеяппя [1, 174].
Следует отметить, что исследованию  -образпых соединений посвящено большое количество работ [182—186], в которых показано, что при наилучших согласованиях
-образпых соединений посвящено большое количество работ [182—186], в которых показано, что при наилучших согласованиях  -соединение имеет выраженный емкостный характер.
-соединение имеет выраженный емкостный характер.

Рис. 2.7. Т-соединение проводников (а); эквивалентная схема (б); прямоугольный (в) и треугольный (г) согласующие профили
Для получения минимальных коэффициентов отражения ( ) необходимо изменить профиль
) необходимо изменить профиль  -соединения, например, путем удаления в области соединения
-соединения, например, путем удаления в области соединения
проводников металла прямоугольной или треугольной формы (рис. 2.7, в, г).
При формировании профиля  -соедипепия необходимо учитывать условия согласования (см., например, [187])
-соедипепия необходимо учитывать условия согласования (см., например, [187])

Использование условия (14) дозволяет в принципе подобрать такие профили  -образных соединений, в которых удается практически полностью скомпенсировать емкостную проводимость в определенном диапазоне частот. На рис. 2.8 для сравнения приведены частотные характеристики шлейфа на
-образных соединений, в которых удается практически полностью скомпенсировать емкостную проводимость в определенном диапазоне частот. На рис. 2.8 для сравнения приведены частотные характеристики шлейфа на  -соединении с учетом емкостной компенсации в виде прямоугольного выреза (кривая
-соединении с учетом емкостной компенсации в виде прямоугольного выреза (кривая  и без него (кривая 2) [188].
и без него (кривая 2) [188].

Рис. 2.8. Частотные характеристики коэффициентов волновой матрицы рассеяния  -соединения шлейфа без согласования (штриховые кривые) и с прямоугольным согласующим профилем (сплошные): крестики — результаты эксперимента
-соединения шлейфа без согласования (штриховые кривые) и с прямоугольным согласующим профилем (сплошные): крестики — результаты эксперимента
Видно, что использование вырезов позволяет резко увеличить полосу рабочих частот. Подробные численные результаты содержатся в [1].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- 1. Основные тенденции развития современной радиоэлектроники.
- 2. Общие соображения о переходе к ОИС СВЧ.
- 3. Некоторые предварительные общие результаты.
- § В.2. Принципиальные основы подхода к автоматизированному проектированию ОИС СВЧ
- 2. Принцип декомпозиции.
- 3. Матрица рассеяния функционально-конструктивного узла РЭА.
- 4. Структура системы АП и режимы ее функционирования.
- ГЛАВА 1. Линии передачи для ОИС СВЧ
- 2. Учет реальных размеров СПЛ.
- 3. Потери в СПЛ.
- 4. Максимальная рабочая частота СПЛ
- § 1.2. Несимметричная полосковая линия
- § 1.3. Симметричная щелевая линия
- 2. Многослойная подвешенная СЩЛ.
- 3. СЩЛ типа «сэндвич».
- § 1.4. Несимметричная щелевая линия
- 2. Интегральные уравнения для НЩЛ. Собственные волны.
- 3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
- 4. Структура поля в НЩЛ.
- 5. Экспериментальные исследования НЩЛ.
- 6. Модификации НЩЛ.
- § 1.5. Копланарная линия передачи
- 2. Электродинамическое приближение в теории КЛ. Метод Галеркина. Численные результаты.
- 3. Экранированные КЛ.
- 4. Модификации экранированных КЛ.
- § 1.6. Линии передачи магнитостатических волн
- ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
- § 2.1. Метод Олинера и модели некоторых линий
- 2. Модели некоторых полосковых линий передачи.
- § 2.2. Неоднородности в ОИС СВЧ
- 2. Неоднородности в H-плоскости.
- 3. Неоднородности в Е-плоскости.
- 4. Неоднородности в копланарной линии.
- 5. Т-соединения различных типов линий в ОИС СВЧ.
- 6. Некоторые примеры тройников для ОИС СВЧ.
- ГЛАВА 3. Переходы между различными типами направляющих структур ОИС СВЧ
- § 3.1. Сверхширокополосные переходы — переходы с непосредственным гальваническим контактом
- § 3.2. Широкополосные шлейфные переходы
- § 3.3. Узкополосные резонансные переходы щелевого типа
- 2. Расчет щелевого перехода [226].
- 3. Согласование перехода.
- 4. Синтез перехода [224].
- 5. Частотные характеристики переходов.
- § 3.4. БЭ согласования ОИС СВЧ
- 2. Несинхронный трансформатор.
- 3. Шлейфный трансформатор.
- 4. Подстройка шлейфов согласующих трансформаторов.
- ГЛАВА 4. Гибридные мостовые устройства ОИС СВЧ
- § 4.1. Балансные делители (сумматоры) мощности
- § 4.2. Кольцевые мосты
- 2. Гибридный кольцевой мост с обращением фазы.
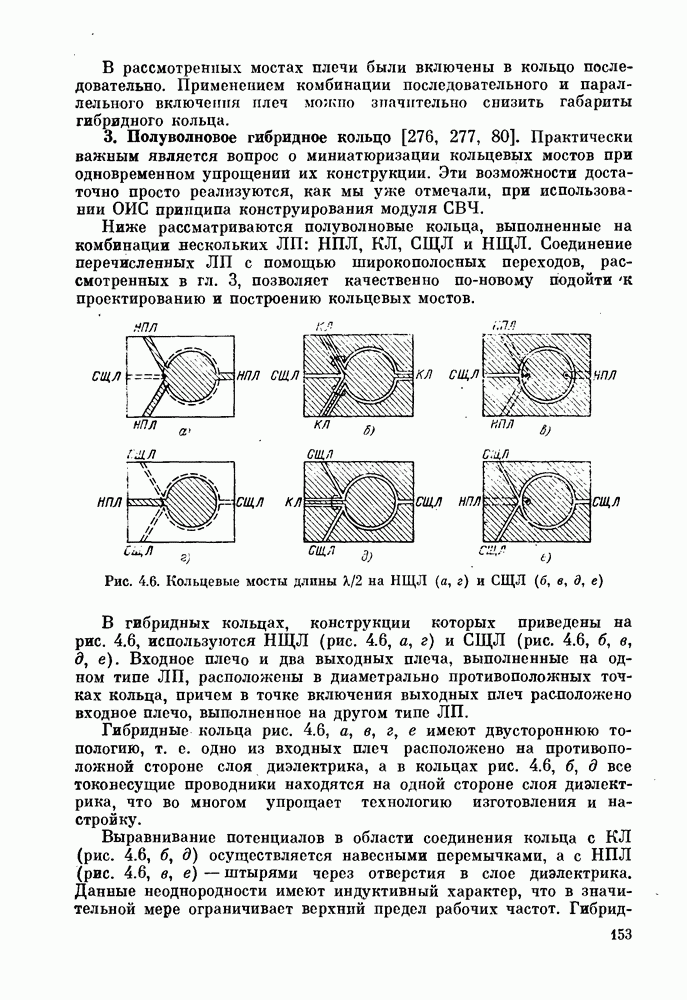
- 3. Полуволновое гибридное кольцо [276, 277, 80].
- 4. Гибридное кольцо периметра 3l/2
- 5. «Магические» Т-соединения.
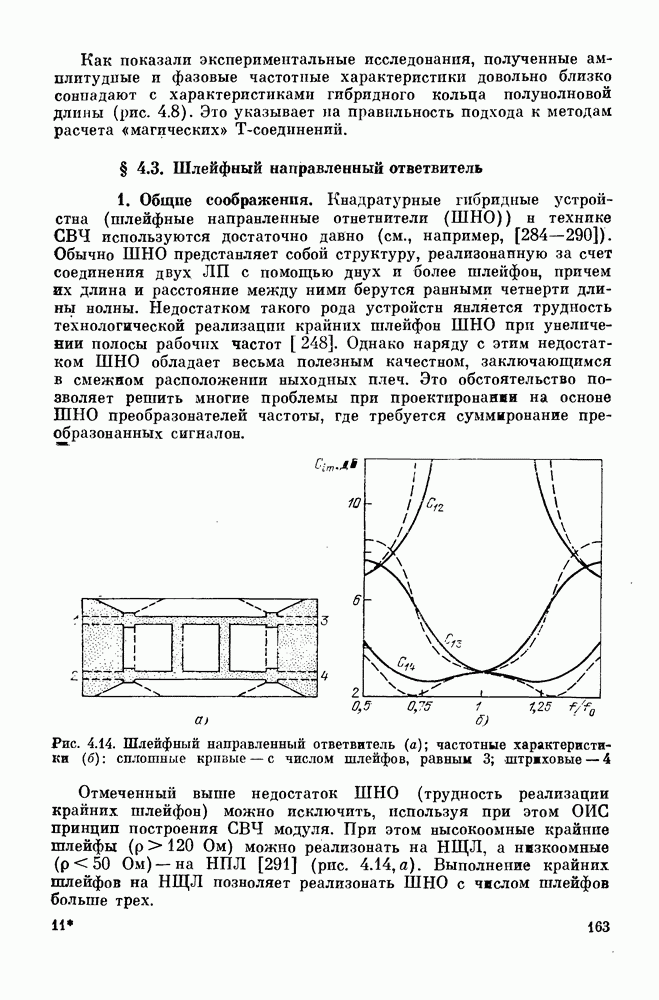
- § 4.3. Шлейфный направленный ответвитель
- § 4.4. Квадратурные направленные ответвители
- § 4.5. Связь двух полосковых линий с переменными параметрами и критическим сечением
- ГЛАВА 5. Объемные многослойные фильтры СВЧ
- § 5.2. Диэлектрические резонаторы
- § 5.3. Полосковые резонаторы
- § 5.4. Фильтры на ОИС СВЧ
- ГЛАВА 6. СВЧ устройства на ОИС
- § 6.1. Многоканальные делители мощности
- § 6.2. Фазовые манипуляторы
- § 6.3. Широкополосные модуляторы
- § 6.4. Приемно-передающие модули
- ГЛАВА 7. Применение ОИС СВЧ в измерительной технике
- § 7.1. Многозондовый датчик для измерения комплексных сопротивлений
- § 7.2. Экспресс-метод контроля диэлектрических проницаемостей подложек ОИС СВЧ
- § 7.3. Устройство дискретизации частотного масштаба
- Заключение