| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1.5. Копланарная линия передачи
1. Определение. Картины полей. Квазистатическое приближение.
Копланарная линия (КЛ) передачи относится к линиям квазиоткрытого типа, в которой распространяются волны квази-Т и Н типа. Токонесущие проводники КЛ образованы узким проводником и двумя полубесконечными слоями металла, расположенными на одной стороне диэлектрической подложки.

Рис. 1.25. Копланарная линия. Структура электромагнитного поля а) четной и б) нечетной волны; распределение в), г) продольных и д), е) полных токов
Структуры электромагнитных полей в КЛ для четного типа волн приведены на рис. 1.25, а, для нечетного — на рис. 1.25,б. Распределение поля в зазоре между узким проводником и полубесконечпыми с слоями металла папомннает распределение поля в СЩЛ. Распределение продольных токов в поперечном сечении КЛ представлено на
рис. 1.25, в, г, а распределение токов на проводящих слоях — на рис. 1.25, д, е.
Анализ КЛ, выполненной на пзотроппой подложке, проведен в работах [44, 95—97]. Рассмотрим более общий случай КЛ на анизотропной подложке, реализованной на одноосном кристалле, тензор диэлектрической проницаемости которого имеет вид диагональной матрицы [98, 99]:

Наиболее часто применяется симметричная относительно плоскости  конструкция КЛ. Поле в КЛ можно представить в виде суммы четного и нечетного решений, соответствующих размещению в плоскости симметрии
конструкция КЛ. Поле в КЛ можно представить в виде суммы четного и нечетного решений, соответствующих размещению в плоскости симметрии  магнитной или электрической стенок, и рассматривать только область
магнитной или электрической стенок, и рассматривать только область 
Поперечные поля в областях без диэлектрика  с диэлектриком
с диэлектриком  представим следующими интегралами Фурье [98]:
представим следующими интегралами Фурье [98]:

где  постоянная распространения в направлении
постоянная распространения в направлении  единичные векторы, индексы
единичные векторы, индексы  представляют
представляют  волны
волны  и
и  волны
волны  соответственно.
соответственно.
Напряжения и токи волн в каждой области можно связать с напряжением и током в плоскости щели  путем «сшивания» полей на границе
путем «сшивания» полей на границе 

Функции Грина и  определяются следующими выражениями:
определяются следующими выражениями:

где

В свою очередь напряжение в плоскости щели можно выразить через поперечное электрическое поле:

Для каждой области электромагнитные поля определяются путем подстановки выражения (3) в (2).
В квазистатическом приближении достаточно определить емкость КЛ на единицу длины. Распределение зарядов на проводниках в плоскости  можно получить с помощью уравнения непрерывности:
можно получить с помощью уравнения непрерывности:

Здесь ток в проводнике определяется из выражения

Подставляя (2) и (7) в (6), получим для случая  и
и  выражение, определяющее распределение зарядов
выражение, определяющее распределение зарядов

в котором функция  может быть представлена так:
может быть представлена так:

Полный погонный заряд  в КЛ определяется так:
в КЛ определяется так:

где функция Грина имеет вид

Выражение (10) является базовым для определения величины погонной емкости КЛ. Домножив (10) на  и проведя интегрирование по области щели
и проведя интегрирование по области щели  получим разность
получим разность
потенциалов между узким проводником и металлической полуплоскостью; 

Таким образом, емкость КЛ определяется из (10) и (12) так:

Расчет емкости осуществляется вариационным методом с помощью метода Ритца. При этом поле в щели полагается равным

где  полиномы Чебышева первого рода,
полиномы Чебышева первого рода,  варьируемые параметры. Отметим, что первый член в (14) соответствует распределению поля в КЛ без диэлектрика, а остальные члены введены специально для расчета КЛ на диэлектрической подложке. Более точпая аппроксимация получается при подстановке (14) в (13) при выполнении условия
варьируемые параметры. Отметим, что первый член в (14) соответствует распределению поля в КЛ без диэлектрика, а остальные члены введены специально для расчета КЛ на диэлектрической подложке. Более точпая аппроксимация получается при подстановке (14) в (13) при выполнении условия

Для изотропной подложки  выражение (13) сводится к известной формуле, полученной методом конформных отображений [100]:
выражение (13) сводится к известной формуле, полученной методом конформных отображений [100]:

где 
Таблица 1.3 (см. скан)
Результаты расчета емкости  на единицу длины в отсутствие диэлектрической подложки представлены в табл. 1.3, из которой видно, что для больших значений отношения
на единицу длины в отсутствие диэлектрической подложки представлены в табл. 1.3, из которой видно, что для больших значений отношения  достаточно учитывать только один член
достаточно учитывать только один член  в (14), а члены более высокого порядка необходимо учитывать при меньших значениях
в (14), а члены более высокого порядка необходимо учитывать при меньших значениях  ковда возрастает степень взаимодействия между узкими щелевыми зазорами в
ковда возрастает степень взаимодействия между узкими щелевыми зазорами в 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- 1. Основные тенденции развития современной радиоэлектроники.
- 2. Общие соображения о переходе к ОИС СВЧ.
- 3. Некоторые предварительные общие результаты.
- § В.2. Принципиальные основы подхода к автоматизированному проектированию ОИС СВЧ
- 2. Принцип декомпозиции.
- 3. Матрица рассеяния функционально-конструктивного узла РЭА.
- 4. Структура системы АП и режимы ее функционирования.
- ГЛАВА 1. Линии передачи для ОИС СВЧ
- 2. Учет реальных размеров СПЛ.
- 3. Потери в СПЛ.
- 4. Максимальная рабочая частота СПЛ
- § 1.2. Несимметричная полосковая линия
- § 1.3. Симметричная щелевая линия
- 2. Многослойная подвешенная СЩЛ.
- 3. СЩЛ типа «сэндвич».
- § 1.4. Несимметричная щелевая линия
- 2. Интегральные уравнения для НЩЛ. Собственные волны.
- 3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
- 4. Структура поля в НЩЛ.
- 5. Экспериментальные исследования НЩЛ.
- 6. Модификации НЩЛ.
- § 1.5. Копланарная линия передачи
- 2. Электродинамическое приближение в теории КЛ. Метод Галеркина. Численные результаты.
- 3. Экранированные КЛ.
- 4. Модификации экранированных КЛ.
- § 1.6. Линии передачи магнитостатических волн
- ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
- § 2.1. Метод Олинера и модели некоторых линий
- 2. Модели некоторых полосковых линий передачи.
- § 2.2. Неоднородности в ОИС СВЧ
- 2. Неоднородности в H-плоскости.
- 3. Неоднородности в Е-плоскости.
- 4. Неоднородности в копланарной линии.
- 5. Т-соединения различных типов линий в ОИС СВЧ.
- 6. Некоторые примеры тройников для ОИС СВЧ.
- ГЛАВА 3. Переходы между различными типами направляющих структур ОИС СВЧ
- § 3.1. Сверхширокополосные переходы — переходы с непосредственным гальваническим контактом
- § 3.2. Широкополосные шлейфные переходы
- § 3.3. Узкополосные резонансные переходы щелевого типа
- 2. Расчет щелевого перехода [226].
- 3. Согласование перехода.
- 4. Синтез перехода [224].
- 5. Частотные характеристики переходов.
- § 3.4. БЭ согласования ОИС СВЧ
- 2. Несинхронный трансформатор.
- 3. Шлейфный трансформатор.
- 4. Подстройка шлейфов согласующих трансформаторов.
- ГЛАВА 4. Гибридные мостовые устройства ОИС СВЧ
- § 4.1. Балансные делители (сумматоры) мощности
- § 4.2. Кольцевые мосты
- 2. Гибридный кольцевой мост с обращением фазы.
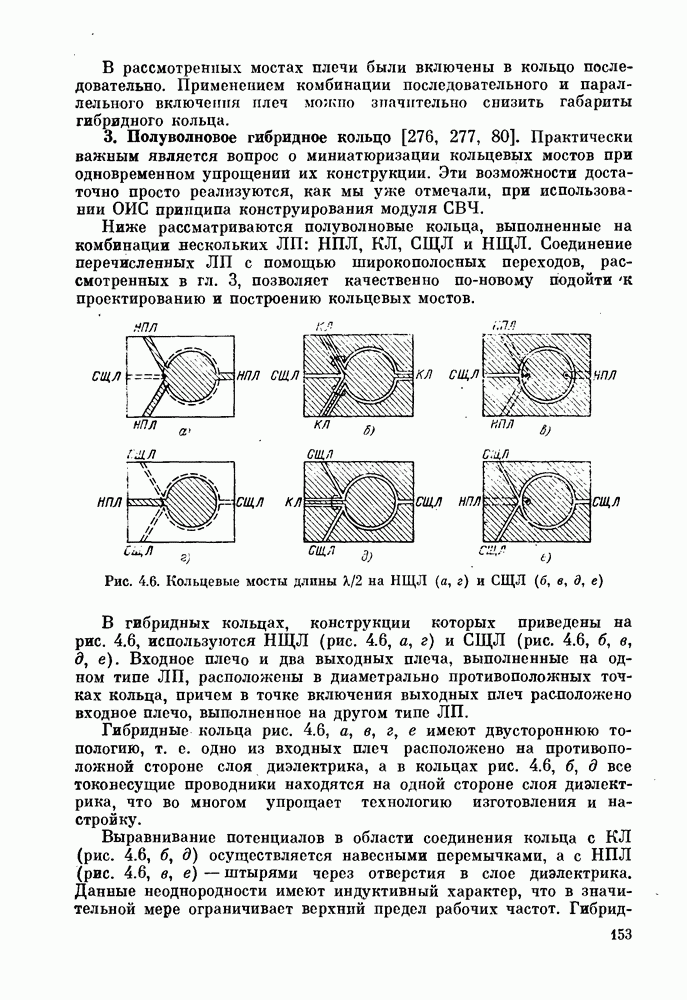
- 3. Полуволновое гибридное кольцо [276, 277, 80].
- 4. Гибридное кольцо периметра 3l/2
- 5. «Магические» Т-соединения.
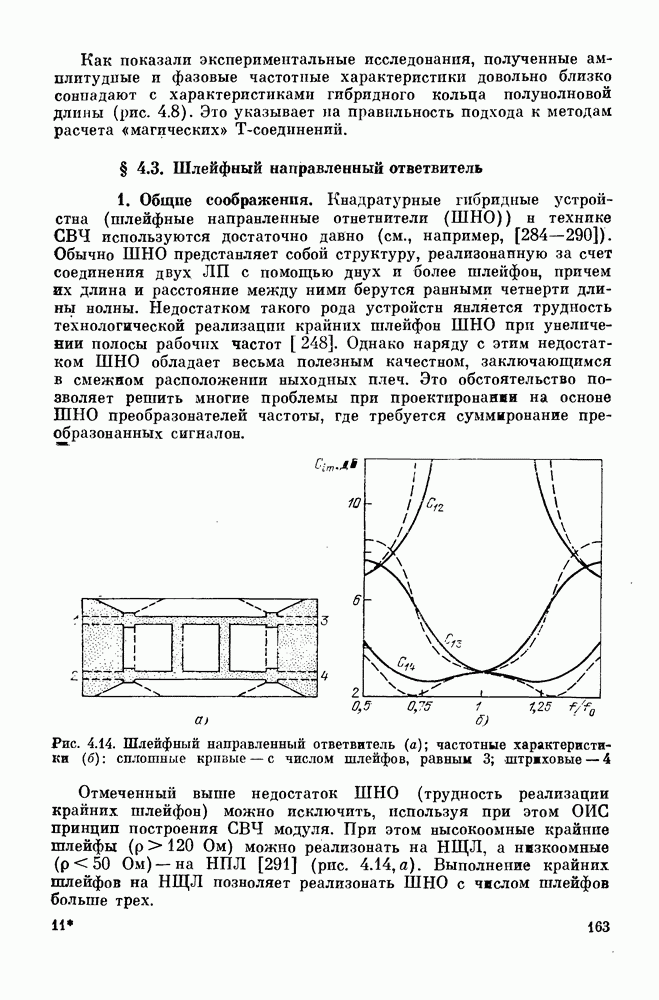
- § 4.3. Шлейфный направленный ответвитель
- § 4.4. Квадратурные направленные ответвители
- § 4.5. Связь двух полосковых линий с переменными параметрами и критическим сечением
- ГЛАВА 5. Объемные многослойные фильтры СВЧ
- § 5.2. Диэлектрические резонаторы
- § 5.3. Полосковые резонаторы
- § 5.4. Фильтры на ОИС СВЧ
- ГЛАВА 6. СВЧ устройства на ОИС
- § 6.1. Многоканальные делители мощности
- § 6.2. Фазовые манипуляторы
- § 6.3. Широкополосные модуляторы
- § 6.4. Приемно-передающие модули
- ГЛАВА 7. Применение ОИС СВЧ в измерительной технике
- § 7.1. Многозондовый датчик для измерения комплексных сопротивлений
- § 7.2. Экспресс-метод контроля диэлектрических проницаемостей подложек ОИС СВЧ
- § 7.3. Устройство дискретизации частотного масштаба
- Заключение