| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. СЩЛ типа «сэндвич».
Она представляет собой обычную СЩЛ, покрытую с двух сторон диэлектриком; схема ее приведена на рис. 1.11, в [71]. Дисперсионные характеристики неэкранированной структуры типа «сэндвич» анализировались в [72, 73].
Для ОИС СВЧ более важными являются, как мы уже неоднократно подчеркивали, экранированные структуры; Приведем некоторые результаты расчета по ним. Так, суммарная проводимость экранированной СЩЛ, расположенной между подложками диэлектрика, определяется следующим образом [70]:

где для действительных  имеем
имеем

Дисперсионные характеристики, рассчитанные для длины волны (20) и волнового сопротивления (16), приведены на рис. 1.14, а,

Рис. 1.14. Зависимость длины волны (сплошные линии) и волнового сопротивления (штриховые) в СЩЛ типа «сэндвич»: а) с удаленным экраном,  ; б) с близкорасположенным экраном,
; б) с близкорасположенным экраном, 
а влияние экрана — на рис. 1.14,6. Полученные результаты довольно хорошо совпадают с данными работы [74].
4. Экранированная СЩЛ. Этот вариант СЩЛ (рис. 1.11, г) представляет особый интерес, так как он наиболее просто вписывается в структуры на ОИС. Это объясняется возможностью ее использования в крайних слоях ОИС для параллельного включения в нее полупроводниковых приборов. Такое включение диодов упрощает настройку модуля и дает возможность практического решения задач теплоотвода, что в настоящее время является насущной проблемой.
Для физического понимания структуры электромагнитного поля различных типов волн в СЩЛ и распределения токов в проводниках воспользуемся численным расчетом по методу частичных областей. Разбиваем поперечное сечение СЩЛ на частичные области (рис. 1.11, г), в которых продольные компоненты векторов Герца, удовлетворяющие уравнению Гельмгольца и очевидным граничным условиям на проводниках, представимы в виде разложений по системам собственных функций этих областей [75]:
(см. скан)
где  диэлектрическая проницаемость в областях
диэлектрическая проницаемость в областях  в областях
в областях  в области
в области 
Рис. 1.15. (см. скан) Распределение электромагнитного поля в экранированной многослойной СЩЛ для волн четного  и нечетного
и нечетного  типов: сплошные линии — электрическое поле, штриховые — магнитное поле
типов: сплошные линии — электрическое поле, штриховые — магнитное поле
Векторы Герца в областях  получаются из соответствующих векторов в областях
получаются из соответствующих векторов в областях  заменами
заменами 
Выражая тангенциальные к границам «сшивания» компоненты полей через векторы Герца и используя свойство ортогональности на этих границах собственных функций частичных областей, образуем систему линейных однородных алгебраических уравнений относительно неизвестных амплитудных коэффициентов в разложениях полей. При выбранном разбиении на частичные области оказывается возможным выразить все неизвестные амплитудные
коэффициенты через коэффициенты разложения полей в области VII и получить систему уравнений относительно коэффициентов 

Система уравнений  неоднократно исследовалась на сходимость, устойчивость и т. д. [50, 57, 59, 60, 67, 88, 112, 218]. Показано, в частности, что учет особенностей на ребрах структуры позволяет существенно увеличить скорость сходимости решения к точному значению. На основе эвристической аппроксимации данных в отмеченных выше работах, а также некоторых других [81, 92, 189], на рис. .1.15 показаны структуры полей нескольких первых типов волн в экранированной многослойной
неоднократно исследовалась на сходимость, устойчивость и т. д. [50, 57, 59, 60, 67, 88, 112, 218]. Показано, в частности, что учет особенностей на ребрах структуры позволяет существенно увеличить скорость сходимости решения к точному значению. На основе эвристической аппроксимации данных в отмеченных выше работах, а также некоторых других [81, 92, 189], на рис. .1.15 показаны структуры полей нескольких первых типов волн в экранированной многослойной  масштаб по вертикальной оси несколько увеличен для удобства рассмотрения. Знание картины распределения полей позволяет разработчику ОИС СВЧ уверепио конструировать устройства, обеспечивать согласованное включение БЭ, а также активных элементов и элементов, управляемых проходящей СВЧ мощностью (параметрические элементы, ограничители мощности, преобразователи частоты и пр.).
масштаб по вертикальной оси несколько увеличен для удобства рассмотрения. Знание картины распределения полей позволяет разработчику ОИС СВЧ уверепио конструировать устройства, обеспечивать согласованное включение БЭ, а также активных элементов и элементов, управляемых проходящей СВЧ мощностью (параметрические элементы, ограничители мощности, преобразователи частоты и пр.).
По известному распределению электромагнитного поля в пространстве СЩЛ можно определить волновые сопротивления для каждого типа волны. Результаты расчета волновых сопротивлений и длины волны для основных типов колебаний представлепы на рис. 1.16 [32]. Здесь сплошные линии — четный тип колебаний, штриховые — нечетный.
Впервые приближенная модель СЩЛ на основе прямоугольного волновода, частично заполненного диэлектриком, была построена в работах [76—79]. Расчет ее основных характеристик в общем случае можно осуществлять численным методом с помощью уравнений (22). Для основной же волны  -типа из интегральных уравнений с использованием преобразований Швингера можно получить простое дисперсионное уравнение для структуры, приведенной на рис.
-типа из интегральных уравнений с использованием преобразований Швингера можно получить простое дисперсионное уравнение для структуры, приведенной на рис. 

где 
При достаточно узкой щели  выражение (23) переходит в известную формулу
выражение (23) переходит в известную формулу

при размерах щели, равной ширине волновода, (23) также переходит в известное соотношение


(кликните для просмотра скана)
что указывает на правильность рассуждений при выводе выражения (23).
На рис. 1.17 приведены расчетные кривые волнового сопротивления и длины волны в экранированной СЩЛ, однородно заполненной диэлектриком и расположенной симметрично в сечении экрана [79], причем дисперсионные кривые с графической точностью совпадают с результатами расчета по (23).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- 1. Основные тенденции развития современной радиоэлектроники.
- 2. Общие соображения о переходе к ОИС СВЧ.
- 3. Некоторые предварительные общие результаты.
- § В.2. Принципиальные основы подхода к автоматизированному проектированию ОИС СВЧ
- 2. Принцип декомпозиции.
- 3. Матрица рассеяния функционально-конструктивного узла РЭА.
- 4. Структура системы АП и режимы ее функционирования.
- ГЛАВА 1. Линии передачи для ОИС СВЧ
- 2. Учет реальных размеров СПЛ.
- 3. Потери в СПЛ.
- 4. Максимальная рабочая частота СПЛ
- § 1.2. Несимметричная полосковая линия
- § 1.3. Симметричная щелевая линия
- 2. Многослойная подвешенная СЩЛ.
- 3. СЩЛ типа «сэндвич».
- § 1.4. Несимметричная щелевая линия
- 2. Интегральные уравнения для НЩЛ. Собственные волны.
- 3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
- 4. Структура поля в НЩЛ.
- 5. Экспериментальные исследования НЩЛ.
- 6. Модификации НЩЛ.
- § 1.5. Копланарная линия передачи
- 2. Электродинамическое приближение в теории КЛ. Метод Галеркина. Численные результаты.
- 3. Экранированные КЛ.
- 4. Модификации экранированных КЛ.
- § 1.6. Линии передачи магнитостатических волн
- ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
- § 2.1. Метод Олинера и модели некоторых линий
- 2. Модели некоторых полосковых линий передачи.
- § 2.2. Неоднородности в ОИС СВЧ
- 2. Неоднородности в H-плоскости.
- 3. Неоднородности в Е-плоскости.
- 4. Неоднородности в копланарной линии.
- 5. Т-соединения различных типов линий в ОИС СВЧ.
- 6. Некоторые примеры тройников для ОИС СВЧ.
- ГЛАВА 3. Переходы между различными типами направляющих структур ОИС СВЧ
- § 3.1. Сверхширокополосные переходы — переходы с непосредственным гальваническим контактом
- § 3.2. Широкополосные шлейфные переходы
- § 3.3. Узкополосные резонансные переходы щелевого типа
- 2. Расчет щелевого перехода [226].
- 3. Согласование перехода.
- 4. Синтез перехода [224].
- 5. Частотные характеристики переходов.
- § 3.4. БЭ согласования ОИС СВЧ
- 2. Несинхронный трансформатор.
- 3. Шлейфный трансформатор.
- 4. Подстройка шлейфов согласующих трансформаторов.
- ГЛАВА 4. Гибридные мостовые устройства ОИС СВЧ
- § 4.1. Балансные делители (сумматоры) мощности
- § 4.2. Кольцевые мосты
- 2. Гибридный кольцевой мост с обращением фазы.
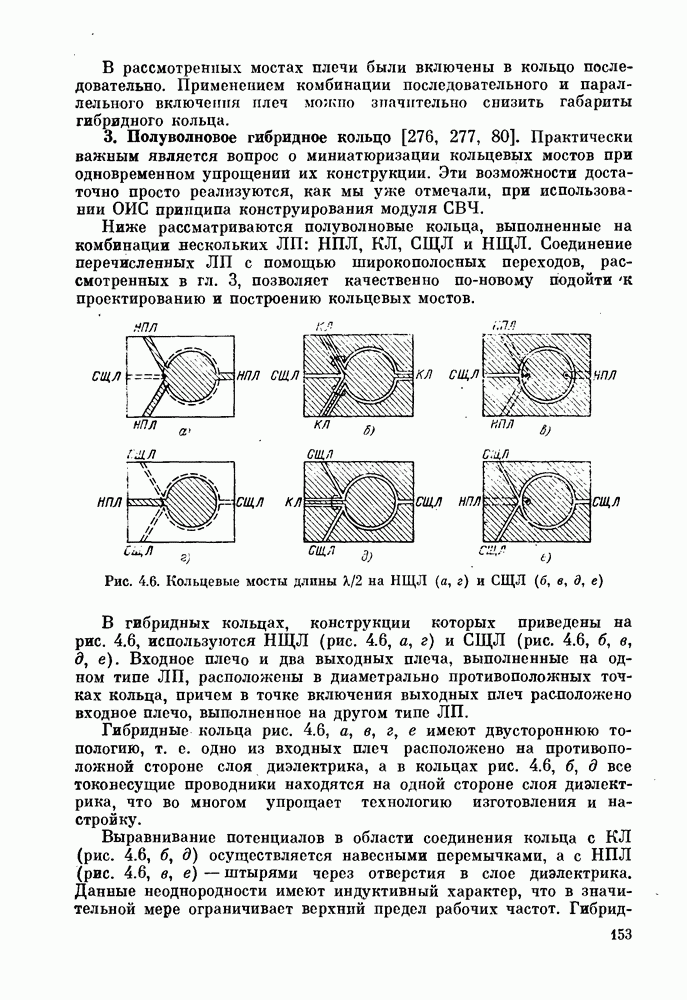
- 3. Полуволновое гибридное кольцо [276, 277, 80].
- 4. Гибридное кольцо периметра 3l/2
- 5. «Магические» Т-соединения.
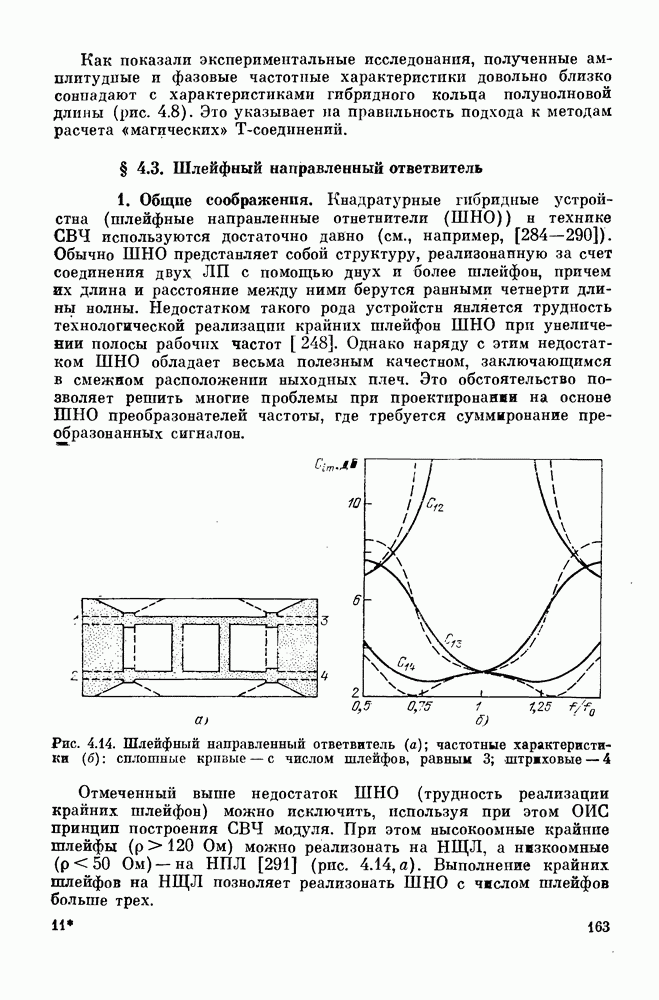
- § 4.3. Шлейфный направленный ответвитель
- § 4.4. Квадратурные направленные ответвители
- § 4.5. Связь двух полосковых линий с переменными параметрами и критическим сечением
- ГЛАВА 5. Объемные многослойные фильтры СВЧ
- § 5.2. Диэлектрические резонаторы
- § 5.3. Полосковые резонаторы
- § 5.4. Фильтры на ОИС СВЧ
- ГЛАВА 6. СВЧ устройства на ОИС
- § 6.1. Многоканальные делители мощности
- § 6.2. Фазовые манипуляторы
- § 6.3. Широкополосные модуляторы
- § 6.4. Приемно-передающие модули
- ГЛАВА 7. Применение ОИС СВЧ в измерительной технике
- § 7.1. Многозондовый датчик для измерения комплексных сопротивлений
- § 7.2. Экспресс-метод контроля диэлектрических проницаемостей подложек ОИС СВЧ
- § 7.3. Устройство дискретизации частотного масштаба
- Заключение