| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Неоднородности в Е-плоскости.
Выше неоднократно подчеркивалось, что щелевые направляющие структуры типа СЩЛ и НЩЛ представляют фундаментальную основу создания БЭ ОИС СВЧ. Для неоднородностей этого класса характерно, что они располагаются в Е-плоскости, т. е. в плоскости, перпендикулярной вектору  и являются в значительной степени порождением ОИС принципа конструирования СВЧ модулей РЭА. Естественно, что
и являются в значительной степени порождением ОИС принципа конструирования СВЧ модулей РЭА. Естественно, что  структуры изучены гораздо менее подробно, чем рассмотренные в п. 2. Наиболее полно, по-видимому, исследован скачок ширины СЩЛ [189, 190]. Классификация неоднородностей на СЩЛ (а также в копланарной линии (см. п. 2.2.4)) проведена в [191]. Ниже на основе модифицированного метода Олинера с использованием прототипов из [174] в квазистатическом приближении представлены эквивалентные схемы ряда типичных неоднородностей на СЩЛ.
структуры изучены гораздо менее подробно, чем рассмотренные в п. 2. Наиболее полно, по-видимому, исследован скачок ширины СЩЛ [189, 190]. Классификация неоднородностей на СЩЛ (а также в копланарной линии (см. п. 2.2.4)) проведена в [191]. Ниже на основе модифицированного метода Олинера с использованием прототипов из [174] в квазистатическом приближении представлены эквивалентные схемы ряда типичных неоднородностей на СЩЛ.
Закороченный и разомкнутый отрезки СЩЛ. Неоднородности такого вида довольно часто встречаются в фильтрах, направленных ответвителях и других БЭ. Рассмотрим закороченный отрезок СЩЛ (рис. 2.9);

Рис. 2.9. Закороченный копец симметричной щелевой лнпни (а); эквивалентная схема (б).
его эквивалентная схема состоит из индуктивной проводимости  и активной проводимости
и активной проводимости  значения которых приближенно определяются, согласно [174], так:
значения которых приближенно определяются, согласно [174], так:

где  размер
размер  определяемый из (2.1.6).
определяемый из (2.1.6).
Разомкнутый конец лпннн пмеет емкостной характер (рис. 2.10), значение реактивной проводимости которого приближенно определяется так:

где  а излучение с открытого конца СЩЛ равно
а излучение с открытого конца СЩЛ равно

Результаты экспериментальных исследований  показывают, что на излучение волны с разомкнутого конца во внешнее пространство и возбуждение им поверхностных волн сильное влияние оказывает форма экрана за пределами СЩЛ.
показывают, что на излучение волны с разомкнутого конца во внешнее пространство и возбуждение им поверхностных волн сильное влияние оказывает форма экрана за пределами СЩЛ.

Рис. 2.10. Обрыв СЩЛ на край полубесконечного металла (а) и на край вырезанного диска в металле (б); эквивалентная схема (в)
Для подавления излучения СЩЛ заканчивают разомкнутым кругом, вырезанным в слое металла (рис. 2.10,б). Радиус  выбирают из условия, чтобы круг не имел индуктивного характера
выбирают из условия, чтобы круг не имел индуктивного характера  и излучение было минимально возможным. При
и излучение было минимально возможным. При  схема рис. 2.10,б переходит в схему рис. 2.10, а.
схема рис. 2.10,б переходит в схему рис. 2.10, а.
Перемычка в СЩЛ, перпендикулярная краям щели. Наиболее часто этот тип неоднородности встречается при реализации полосовых фильтров (торцевая связь полуволновых резонаторов через веремычку [192]), шлейфпых направленных ответвлений и пр. (рис. 2.11, а).

Рис. 2.11. Перемычка в СЩЛ (а) и эквивалентная схема (б); смещение осей СЩЛ в металле (в)
Эквивалентная схема перемычки в СЩЛ показанана рис. 2.11, б. В данном случае перемычка замыкает края зазоров щели, имеющих преобладание индуктивной проводимости. Индуктивная и емкостная проводимости рассчитываются следующим образом [174]:

где

 - ширина ПВ, определяемая из уюавнения (2.1.6),
- ширина ПВ, определяемая из уюавнения (2.1.6),

Рис. 2.12. Скачок ширины щели в СЩЛ (а); эквивалентная схема (б)
Более точные результаты по расчету электрических характеристик перемычки в зависимости от ее ширины I и смещения осей  входной и выходной линий (рис. 2.11, в) приведены в [192].
входной и выходной линий (рис. 2.11, в) приведены в [192].
Скачок ширины СЩЛ. Симметричный скачок ширины СЩЛ реализуется при формировании фильтров нижних частот, устройств согласования и пр. Из анализа топологии скачка (рис. 2.12, а)
видно, что он осуществляет трансформацию волновых проводимостей (идеальный трансформатор  а в его реактивных компонентах преобладает емкостный характер
а в его реактивных компонентах преобладает емкостный характер  проводимость В с равна [174]
проводимость В с равна [174]

Формулы (20), (21) являются приближенными. Более точный расчет этой неоднородности проведен в [190]. При этом рассматривалась экранированная СЩЛ (на частотах до  На рис. 2.13 представлены зависимости коэффициента трансформации
На рис. 2.13 представлены зависимости коэффициента трансформации

Рис. 2.13. Частотная зависимость  эффициента трансформации (1) и проводимости (2) при постоянной геометрии скачка ширины щели СЩЛ: сплошная кривая — открытая; штриховая — экранированная
эффициента трансформации (1) и проводимости (2) при постоянной геометрии скачка ширины щели СЩЛ: сплошная кривая — открытая; штриховая — экранированная  и емкостной проводимости от геометрии скачка зазора. Для сравнения приведены случаи для скачка в открытой и экранированной ЩЛ. При небольших значениях ширины СЩЛ влияние экрана практически не сказывается.
и емкостной проводимости от геометрии скачка зазора. Для сравнения приведены случаи для скачка в открытой и экранированной ЩЛ. При небольших значениях ширины СЩЛ влияние экрана практически не сказывается.
При расчете двойного скачка ширины щели в СЩЛ необходимо учитывать индуктивную проводимость, образующуюся на ее длине (рис. 2.14, а). Частотные характеристики проводимостей в зависимо»  от геометрии скачка приведены на рис. 2.14, б. Очевидно, что, выбирая продольный размер расширенного участка щели кратным четверти длины волны, мы получим резонансный элемент. На такой неоднородности можно построить фильтры нижних частот и другие БЭ ОИС.
от геометрии скачка приведены на рис. 2.14, б. Очевидно, что, выбирая продольный размер расширенного участка щели кратным четверти длины волны, мы получим резонансный элемент. На такой неоднородности можно построить фильтры нижних частот и другие БЭ ОИС.
Поворот СЩЛ на произвольный угол. Симметричное соединение (под произвольным углом) двух одинаковых СЩЛ показано на рис. 2.15, а, а его эквивалентная схема — на рис. 2.15, б. Параметры
эквивалентной схемы суть

где  логарифмическая производная от
логарифмическая производная от 

Рис. 2.14. Двойной скачок ширины щели в СЩЛ и эквивалентная схема (а); частотная зависимость эквивалентных параметров СЩЛ (б):  ;
;
Из (22), (23) непосредственно следует, что в этой неоднородности преобладает индуктивная проводимость, которая значительно увеличивает коэффициент отражения.

Рис. 2.15. Излом СЩЛ (а); эквивалентная схема (б)  Уменьшение отражения достигается компенсацией индуктивности излома путем изменения его профиля. Минимальные значения отражения достигаются при металлизации участка
Уменьшение отражения достигается компенсацией индуктивности излома путем изменения его профиля. Минимальные значения отражения достигаются при металлизации участка  в изгибе (рис.
в изгибе (рис.  [1]).
[1]).
Т-соединение СЩЛ. Рассмотрим симметричное  -соединение СЩЛ (рис.
-соединение СЩЛ (рис.  Эквивалентная схема, построенная согласно [174], приведена на рис. 2.16, б. Параметры эквивалентной схемы при произвольных углах
Эквивалентная схема, построенная согласно [174], приведена на рис. 2.16, б. Параметры эквивалентной схемы при произвольных углах  между входным и выходным
между входным и выходным
плечами равны [193]:


Рис. 2.16. Т-соединение СЩЛ (а); эквивалентная схема (б)
В случае  и разложения логарифмической производной
и разложения логарифмической производной  в ряд получим более простые выражения для параметров эквивалентной схемы:
в ряд получим более простые выражения для параметров эквивалентной схемы:

где

Из этих выражений видно, что значения реактивных проводимостей  одного порядка (в предыдущих случаях реактивные сопротивления имели разный порядок). Следствием этого является возможное появление резонансов различных
одного порядка (в предыдущих случаях реактивные сопротивления имели разный порядок). Следствием этого является возможное появление резонансов различных
последовательных и параллельных цепочек. Поэтому ход кривых модулей и фаз коэффициентов отражения и прохождения в данном случае будет более сложным, чем ранее (ср. [1]).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- 1. Основные тенденции развития современной радиоэлектроники.
- 2. Общие соображения о переходе к ОИС СВЧ.
- 3. Некоторые предварительные общие результаты.
- § В.2. Принципиальные основы подхода к автоматизированному проектированию ОИС СВЧ
- 2. Принцип декомпозиции.
- 3. Матрица рассеяния функционально-конструктивного узла РЭА.
- 4. Структура системы АП и режимы ее функционирования.
- ГЛАВА 1. Линии передачи для ОИС СВЧ
- 2. Учет реальных размеров СПЛ.
- 3. Потери в СПЛ.
- 4. Максимальная рабочая частота СПЛ
- § 1.2. Несимметричная полосковая линия
- § 1.3. Симметричная щелевая линия
- 2. Многослойная подвешенная СЩЛ.
- 3. СЩЛ типа «сэндвич».
- § 1.4. Несимметричная щелевая линия
- 2. Интегральные уравнения для НЩЛ. Собственные волны.
- 3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
- 4. Структура поля в НЩЛ.
- 5. Экспериментальные исследования НЩЛ.
- 6. Модификации НЩЛ.
- § 1.5. Копланарная линия передачи
- 2. Электродинамическое приближение в теории КЛ. Метод Галеркина. Численные результаты.
- 3. Экранированные КЛ.
- 4. Модификации экранированных КЛ.
- § 1.6. Линии передачи магнитостатических волн
- ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
- § 2.1. Метод Олинера и модели некоторых линий
- 2. Модели некоторых полосковых линий передачи.
- § 2.2. Неоднородности в ОИС СВЧ
- 2. Неоднородности в H-плоскости.
- 3. Неоднородности в Е-плоскости.
- 4. Неоднородности в копланарной линии.
- 5. Т-соединения различных типов линий в ОИС СВЧ.
- 6. Некоторые примеры тройников для ОИС СВЧ.
- ГЛАВА 3. Переходы между различными типами направляющих структур ОИС СВЧ
- § 3.1. Сверхширокополосные переходы — переходы с непосредственным гальваническим контактом
- § 3.2. Широкополосные шлейфные переходы
- § 3.3. Узкополосные резонансные переходы щелевого типа
- 2. Расчет щелевого перехода [226].
- 3. Согласование перехода.
- 4. Синтез перехода [224].
- 5. Частотные характеристики переходов.
- § 3.4. БЭ согласования ОИС СВЧ
- 2. Несинхронный трансформатор.
- 3. Шлейфный трансформатор.
- 4. Подстройка шлейфов согласующих трансформаторов.
- ГЛАВА 4. Гибридные мостовые устройства ОИС СВЧ
- § 4.1. Балансные делители (сумматоры) мощности
- § 4.2. Кольцевые мосты
- 2. Гибридный кольцевой мост с обращением фазы.
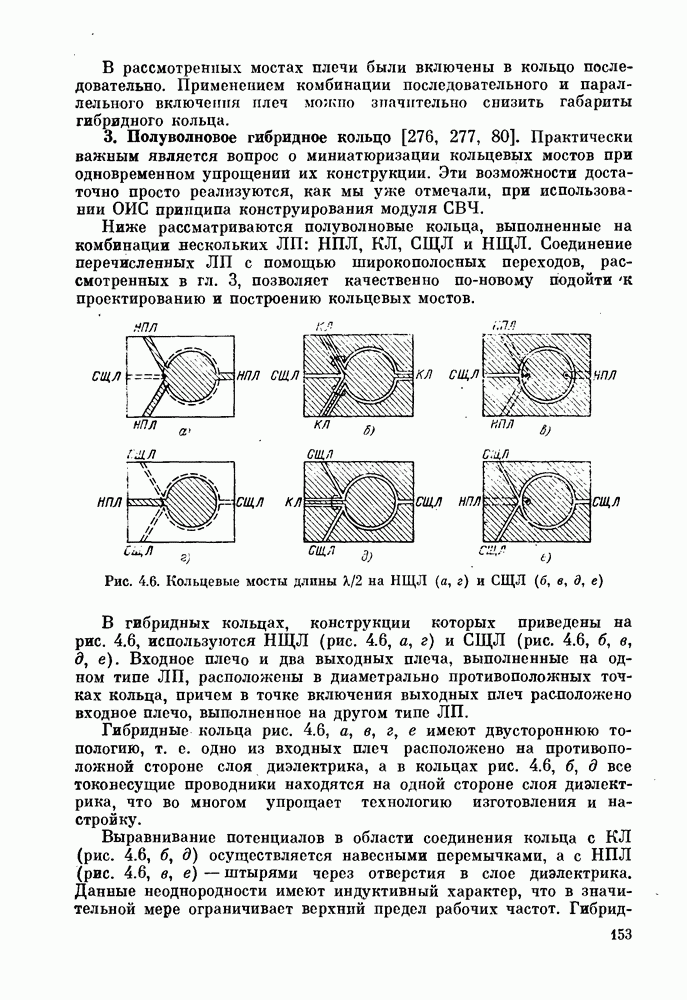
- 3. Полуволновое гибридное кольцо [276, 277, 80].
- 4. Гибридное кольцо периметра 3l/2
- 5. «Магические» Т-соединения.
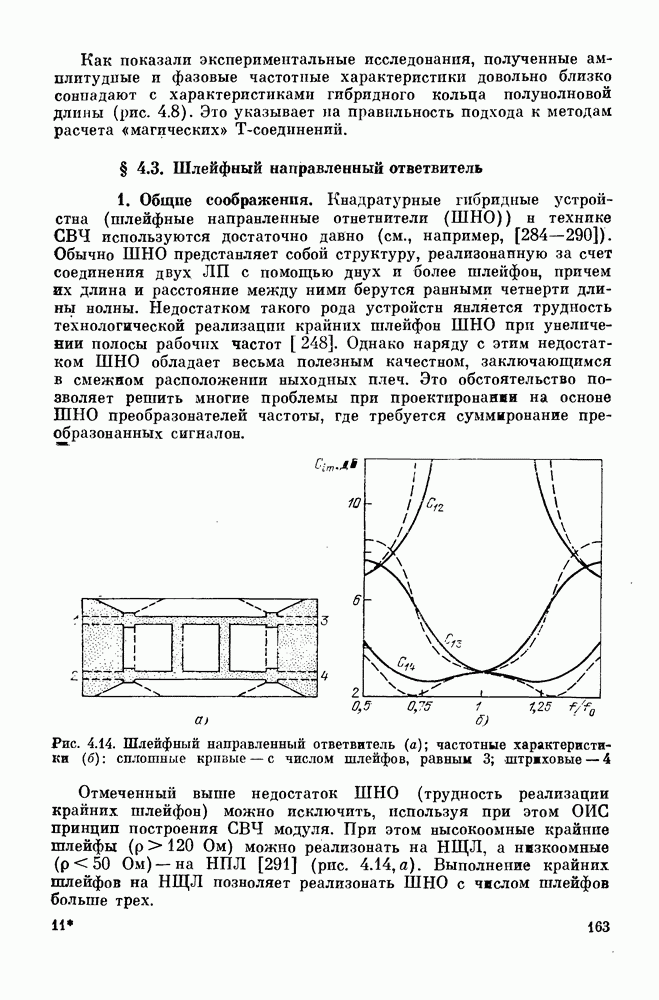
- § 4.3. Шлейфный направленный ответвитель
- § 4.4. Квадратурные направленные ответвители
- § 4.5. Связь двух полосковых линий с переменными параметрами и критическим сечением
- ГЛАВА 5. Объемные многослойные фильтры СВЧ
- § 5.2. Диэлектрические резонаторы
- § 5.3. Полосковые резонаторы
- § 5.4. Фильтры на ОИС СВЧ
- ГЛАВА 6. СВЧ устройства на ОИС
- § 6.1. Многоканальные делители мощности
- § 6.2. Фазовые манипуляторы
- § 6.3. Широкополосные модуляторы
- § 6.4. Приемно-передающие модули
- ГЛАВА 7. Применение ОИС СВЧ в измерительной технике
- § 7.1. Многозондовый датчик для измерения комплексных сопротивлений
- § 7.2. Экспресс-метод контроля диэлектрических проницаемостей подложек ОИС СВЧ
- § 7.3. Устройство дискретизации частотного масштаба
- Заключение