2. Интегральные уравнения для НЩЛ. Собственные волны.

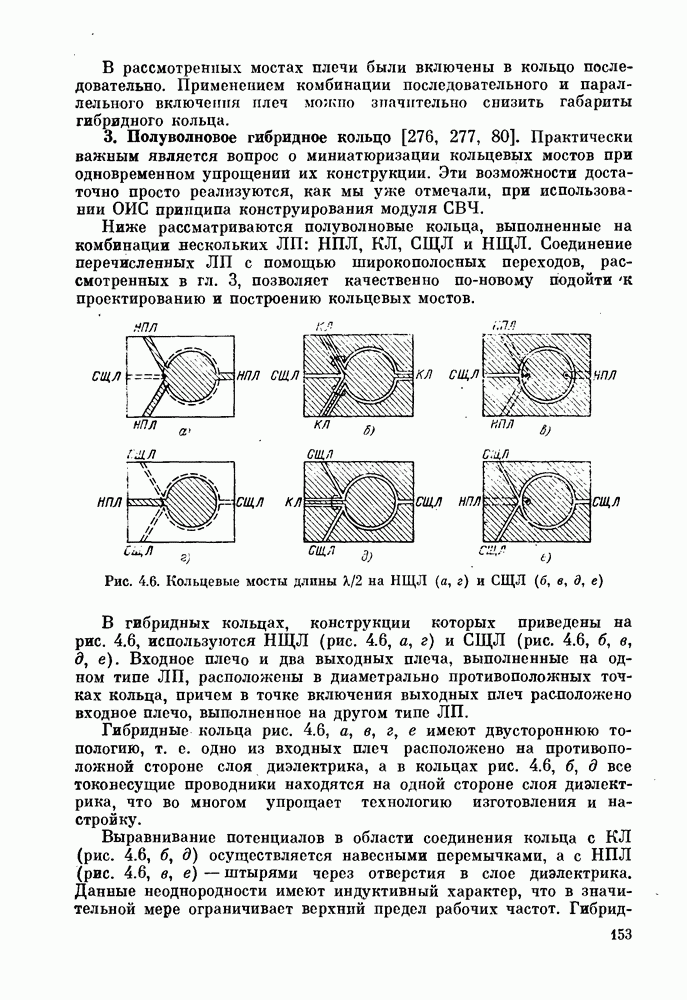
НЩЛ представляет собой волноведущую структуру, токонесущие проводники которой (в простейшем случае это полуплоскости) расположены в слоях диэлектрика в разных плоскостях (рис. 1.19). Наше рассмотрение мы начнем со случая экранированной модели ОИС, представляющей собой прямоугольный экран, заполненный

плоскопараллельными слоями диэлектрика одинаковой толщины. Некоторые части границ раздела слоев диэлектрика металлизированы — на них нанесены металлические слои с исчезающе малой толщиной и обладающие идеальной проводимостью. Для начала рассмотрим алгоритм вывода интегральных уравнений для направляющей структуры общего типа (рис. 1.19), а затем осуществим переход к собственно НЩЛ.

Общая методика получения интегральных уравнений относительно магнитных или электрических токов содержит два этапа: 1) выражение неизвестных коэффициентов в фурье-представлении и 2) разложение полей в слоях в ряды по фурье-трансформантам токов на их границах и подстановка этих коэффициентов в неиспользованные на первом этапе уравнения граничных условий. В случае ОИС первый этап целесообразно проводить отдельно для каждого слоя (поблочно удовлетворяя системе граничных условий [38, 83]), однако и это само по себе не гарантирует простоту записи искомых коэффициентов. С целью дальнейшего упрощения формы записи интегральных уравнений используем тот факт, что каждый слой диэлектрика с нанесенными на его поверхность слоями металла можно представить в виде волноводного трансформатора. Решение задачи о возбуждении такого трансформатора заключается в поочередном наложении условий короткого эамыкания или холостого хода на его входы и выражении неизвестных коэффициентов через соответствующие электрические или магнитные токи на границах. Повторяя эту операцию для каждого слоя, подставим найденные коэффициенты в оставшиеся граничные условия, не использованные на первом этапе, и тем самым получим интегральные уравнения относительно магнитных или электрических токов [63, 84]:

где тензорные функции Грина, -вектор магнитных токов, вектор электрических токов, а — размер основания экрана.

Рассмотрим интегральные уравнения относительно магнитных токов (1). Их эквивалентная функциональная форма имеет вид

Здесь — матрицы-столбцы фурье-трансформант магнитных и электрических токов соответственно:

где клеточно-диагональная матрица

проводимостей:

В (3) матричная клетка (размерностью 4X4) является матрицей проводимостей соответствующего диэлектрического слоя. Элементы ее суть 4

Элементы являются общими для матриц и а общими для матриц и В вышеприведенных формулах использовались следующие обозначения: волновое число в вакууме, номер диэлектрического слоя, у — постоянная распространения вдоль продольной оси постоянная распространения вдоль оси постоянная распространения вдоль оси

диэлектрическая проницаемость слоя диэлектрика, поперечное волновое число, толщина слоя диэлектрика.

Таким образом, вывод интегральных уравнений относительно магнитных токов для модели сводится к формальному составлению матрицы проводимости (За) из клеток элементы которых имеют простую аналитическую форму.