4. Структура поля в НЩЛ.

Расчет полей в волноведущих структурах представляет более сложную задачу, чем нахождение собственных чисел Это связано с тем, что система интегральных уравнений (1) является некорректной, вследствие чего в (10) матрица в некоторых случаях плохо обусловлена. В настоящее время отсутствует универсальный метод борьбы с этим явлением [88, 89]. Поэтому чаще всего прибегают к подбору базиса, обладающего, например, свойством минимальности [85], выбору метода решения а также, где возможно, устранению плохой обусловленности формы записи элементов матрицы

Итак, рассмотрим однородную Для решения ее один из неизвестных коэффициентов приравняем, например, к единице и соответствующий столбец вынесем в правую часть. Будем иметь прямоугольную систему линейных алгебраических уравнений:

Здесь матрица-столбец неизвестных коэффициентов, прямоугольная матрица, свободные члены. Учитывая некорректность поставленной задачи, будем искать такое решение, которое минимизирует квадрат невязки (12). Это приводит к необходимости

решения следующей СЛАУ [88, 89]:

Однако учитывая, что обусловленность (13) значительно хуже обусловленности (12), будем решать (12) методом сингулярного разложении матрицы Преимущество такого подхода состоит в возможности находить решения, минимизирующие квадрат невязки, без использования плохо обусловленной системы (13). Кроме того, в отличие от метода Гаусса, в процессе решения не меняются спектральные свойства матрицы т. е. не ухудшается ее исходная обусловленность [90, 91].

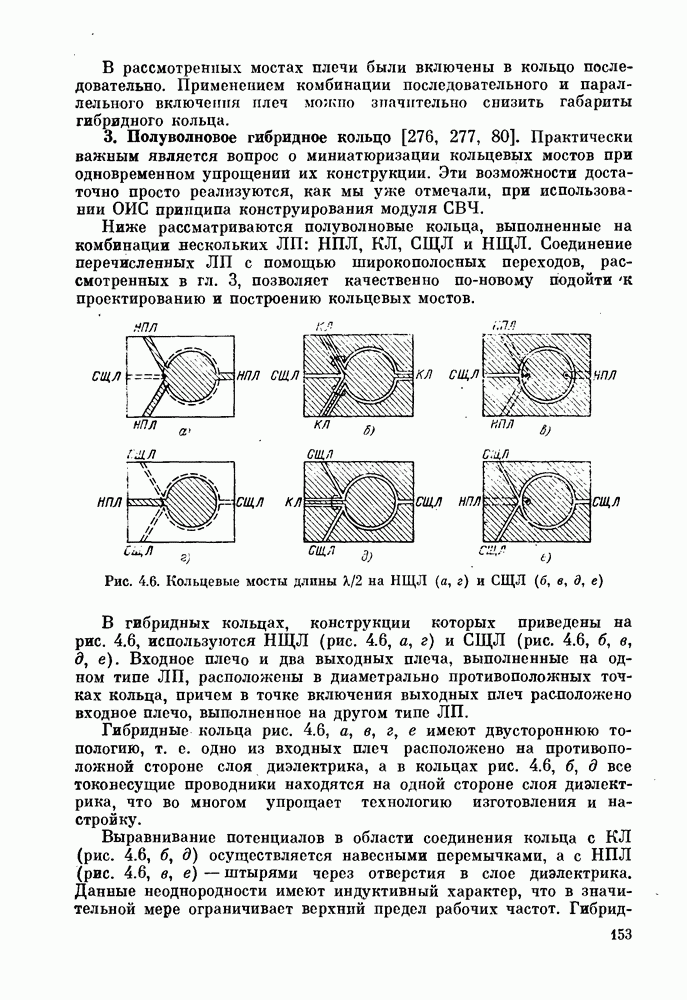
Результаты расчета распределения полей в НЩЛ изображены на рис. 1.21. Видно, что наличие некомпланарно расположенных ребер в случае разнесенных слоев металла существенно влияет на распределение магнитного тока на поверхности диэлектрика.

Рис. 1.21. Распределение плотности продольного и поперечного магнитных токов в НЩЛ при Стрелками отмечены координаты ребер

Установлено, что вблизи ребер существуют некоторые колебания магнитного тока, имеющие, по-видимому, дифракционную природу, вследствие чего существует хорошая обусловленность матрицы а ее элементы, представляющие собой тригонометрические ряды, имеют асимптотику поэтому решение для основной волны практически не зависит от предела суммирования начиная с

Проведенные эксперименты по исследованию сходимости алгоритма по полю показали, что влияние ошибок округления начинает

сказываться лишь при порядках решаемой Это связано в основном с возрастанием погрешностей счета тригонометрических функций малого аргумента, пропорционального шагу сетки, и возрастанием числа обусловленности СЛАУ (монотонным с увеличением порядка

Таким образом, машинные эксперименты по исследованию собственных волн в НЩЛ показали перспективность использования кусочно-определенных функций, обеспечивающих хорошую сходимость алгоритма и его устойчивость. Дальнейшее улучшение свойств решения возможно за счет использования полиномов старших степеней, учетом особенности на ребре и т. д.

Реализованная программа анализа собственных волн НЩЛ является основой для разработки алгоритмов проектирования перспективных элементов ОИС СВЧ.