| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1.3. Симметричная щелевая линия
1. Определение. Принцип действия. Волноводная модель СЩЛ.
Симметричная щелевая линия (СЩЛ) [54] представляет собой узкую щель, вырезанную в бесконечной металлической плоскости, расположенной на одной из сторон плоскопараллельного магнитодиэлектрического слоя, образующего подложку СЩЛ (рис. 1.10, а). Линии электрического поля (при  концентрируются в подложке, а магнитного поля — имеют вид эллипсов, переходящих в кривые типа «седло» (рис. 1.10,6), образуя таким образом основную волну СЩЛ, напоминающую конструкцию поля волны типа
концентрируются в подложке, а магнитного поля — имеют вид эллипсов, переходящих в кривые типа «седло» (рис. 1.10,6), образуя таким образом основную волну СЩЛ, напоминающую конструкцию поля волны типа  прямоугольного волновода. Распределение тока в слое на металлических полуплоскостях (рис. 1.10, в, г) — экспоненциальное.
прямоугольного волновода. Распределение тока в слое на металлических полуплоскостях (рис. 1.10, в, г) — экспоненциальное.
Необходимо отметить, что к настоящему времени не существует достаточно точной теории открытой СЩЛ (см., например, [1]
§§ 2.5, 2.6). Во всяком случае до сих пор нет еще такого отчетливого физического понимания принципа работы СЩЛ, которое характерно, например, для НПЛ (§ 1.2). Сказанное относится и к другим щелевым структурам, таким, как несимметричная щелевая линия (НЩЛ) (§ 1.4) и др. Здесь, в соответствии с задачами
нашей книги, мы приведем некоторые приближенные соотношения, поясняющие, с одной стороны, физику работы СЩЛ, а с другой — пригодные для использования в системах автоматизированного проектирования.
Для расчета параметров СЩЛ необходимо знать основные компоненты электрического и магнитного полей. При  напряжение между кромками бесконечно протяженной регулярной щели можно заменить эквивалентным линейным магнитным током.
напряжение между кромками бесконечно протяженной регулярной щели можно заменить эквивалентным линейным магнитным током.

Рис. 1.10. Симметричная щелевая линия: а), б) структура электромагнитного ноля; в), г) распределение продольных и полных токов; д), е) волноводная модель СЩЛ
При этом продольная составляющая магнитного поля для любой точки пространства вне щели записывается в виде уходящей волны [55]:

где  функция Ханкеля первого рода
функция Ханкеля первого рода  -го порядка,
-го порядка, 
 продольное волновое число,
продольное волновое число,  волновое число для воздуха,
волновое число для воздуха,  длина волны в
длина волны в  эффективная диэлектрическая проницаемость СЩЛ.
эффективная диэлектрическая проницаемость СЩЛ.
Поперечные составляющие поля СЩЛ в цилиндрических координатах определяются из уравнений Максвелла с помощью (1) следующим образом:

Используя свойства функции Ханкеля [56] и условие  определим расстояние
определим расстояние  от плоскости щели до места нахождения области круговой поляризации:
от плоскости щели до места нахождения области круговой поляризации:

Из формул (1) и (3) следует, что выражение (5) при стремится к единице. Поэтому на некотором расстоянии от щели электромагнитная волна имеет эллиптическую поляризацию (близкую, впрочем, к круговой).
Напряжение в произвольной точке слоя металла, нормированное на напряжение в щели, определяется следующей формулой:

При расчетах эффективной диэлектрической проницаемости и волнового сопротивления СЩЛ часто используется модель линии с электрическими и магнитными стенками (рис.  это позволяет с известной степенью точности представить СЩЛ в виде прямоугольного волновода и решать задачу в прямоугольных координатах. Волноводные модели, изображенные на рис.
это позволяет с известной степенью точности представить СЩЛ в виде прямоугольного волновода и решать задачу в прямоугольных координатах. Волноводные модели, изображенные на рис.  предполагают распространение волны без потерь в продольном направлении СЩЛ.
предполагают распространение волны без потерь в продольном направлении СЩЛ.
Введение электрических стенок на расстоянии а, равном половине длииы волны  и магнитных стенок симметрично осевой линии щели на достаточно большом расстоянии
и магнитных стенок симметрично осевой линии щели на достаточно большом расстоянии  не искажают в СЩЛ компоненты поля. В результате из первоначальной структуры (рис. 1.10, а) мы выделили участок, который можно рассматривать как прямоугольный волновод с емкостной диафрагмой, размещенной на диэлектрической подложке (рис. 1.10, д). В подобной структуре полный спектр волн, удовлетворяющих граничным условиям, состоит из волн
не искажают в СЩЛ компоненты поля. В результате из первоначальной структуры (рис. 1.10, а) мы выделили участок, который можно рассматривать как прямоугольный волновод с емкостной диафрагмой, размещенной на диэлектрической подложке (рис. 1.10, д). В подобной структуре полный спектр волн, удовлетворяющих граничным условиям, состоит из волн  для
для  для
для  .
.
Волны  и все высшие типы волн в волноводе без диэлектрика не распространяются, поскольку величина а меньше половины длины волны в воздухе. В диэлектрике распространяются волны
и все высшие типы волн в волноводе без диэлектрика не распространяются, поскольку величина а меньше половины длины волны в воздухе. В диэлектрике распространяются волны  а распространение высших типов волн зависит от ширины волновода а.
а распространение высших типов волн зависит от ширины волновода а.
При условии «поперечного резонанса» полей сумма реактивных проводимостей в плоскости диафрагмы должна быть равной нулю:

Здесь  реактивная проводимость в плоскости диафрагмы
реактивная проводимость в плоскости диафрагмы  со стороны подложки толщины
со стороны подложки толщины  — со стороны воздуха. Для получения решения уравнения (7) введем независимую переменную
— со стороны воздуха. Для получения решения уравнения (7) введем независимую переменную  При этом необходимо выполнить условия
При этом необходимо выполнить условия  позволяющие определить длину волны и частоту в зависимости от параметров СЩЛ.
позволяющие определить длину волны и частоту в зависимости от параметров СЩЛ.
Формула суммарной проводимости в плоскости диафрагмы [55] для электрической стенки  имеет вид
имеет вид

и для магнитной стенки 

где

Для действительных  имеем значения
имеем значения

где

Для мнимых  имеем значения
имеем значения

где

Волновое сопротивление СЩЛ определяется из уравнения энергетического баланса следующим образом [55]:

 находится из (8) при фиксированных значениях
находится из (8) при фиксированных значениях  а и для двух значений
а и для двух значений  взятых в окрестности
взятых в окрестности  при котором
при котором 
Результаты расчета (8) и (10) для эффективной диэлектрической проницаемости и волнового сопротивления открытой СЩЛ аппроксимированы с точностью до 2% в [58] следующими выражениями  :
:

Необходимо отметить, что волновое сопротивление в СЩЛ определяется неоднозначно, аналогично определению в теории закрытых волноводов. При выводе формулы (10) использовано «энергетическое» определение сопротивления. Структура же поля СЩЛ такова, что волновое сопротивление можно определить как отношение максимального напряжения в щели к току, текущему в продольном направлении по металлическим полуплоскостям:

Аналитическое выражение для волнового сопротивления СЩЛ в соответствии с (16) получено в работе [59]:

где  постоянная Эйлера.
постоянная Эйлера.
Формула (17) дает заниженные результаты по сравнению с формулами (13) и (15) примерно на 30% и лучше соответствует действительности в коротковолновой части сантиметрового и миллиметрового диапазонов волн. В дециметровом и длинноволновой части сантиметрового диапазонов методика Кона [55] дает более точное совпадение с экспериментом.
Существует более точный и достаточно хорошо разработанный метод частичных областей [60, 61]. Он также неоднократно использовался для расчета параметров экранированной СЩЛ с учетом толщины  токонесущих проводников [62—65], а также других полосковых линий [62—67]. Недостатком метода частичных областей является большое время счета на ЭВМ, увеличивающееся с усложнением структуры линии передачи. Поэтому этот метод, возможно, более пригоден для проведения исследования физических свойств и изучения липий сложных поперечных сечений, показанных на рис. 1.11.
токонесущих проводников [62—65], а также других полосковых линий [62—67]. Недостатком метода частичных областей является большое время счета на ЭВМ, увеличивающееся с усложнением структуры линии передачи. Поэтому этот метод, возможно, более пригоден для проведения исследования физических свойств и изучения липий сложных поперечных сечений, показанных на рис. 1.11.
Анализ СЩЛ с проводниками конечной толщины (рис. 1.11, а), но симметрично помещенной в экране прямоугольного сечения а  проведен в работе [62]. Волновое сопротивление при этом рассчитывалось по формуле (16).
проведен в работе [62]. Волновое сопротивление при этом рассчитывалось по формуле (16).
На рис. 1.12, а приведены дисперсионные кривые волнового сопротивления и длины волны в СЩЛ с достаточно удаленными стенками экрана, полученные в [62], а также результаты, рассчитанные в [68] по формулам (8)-(10).

Рис. 1.11. Наиболее распространенные варианты СЩЛ: а) подвешенная СЩЛ; б) многослойная подвешенная СЩЛ; в) СЩЛ типа «сэндвич»; г) экранированная СЩЛ с проводниками конечной толщины; д) СЩЛ, симметрично расположенная в экране
Из анализа кривых видно, что волновые сопротивления, полученные в [59], являются заниженными относительно сопротивлений, полученных из выражений (10), и результаты совпадают с данными формулы (17). Расчетные значения длины волны в СЩЛ совпадают с данными работ [25, 26], что указывает на правильность выбранных моделей для данного случая.
Влияние толщины металлических полуплоскостей на частотные характеристики волнового сопротивления и длииы волпы в СЩЛ
показано на рис. 1.12, б. При этом экраны были удалены достаточно далеко. Для узких щелей, как видно из кривых рис. 1.12,6, необходимо учитывать толщину металлических полуплоскостей. Для сравнения на рис. 1.12, б приведена кривая волнового сопротивления СЩЛ при нулевой толщипе проводников [68].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- 1. Основные тенденции развития современной радиоэлектроники.
- 2. Общие соображения о переходе к ОИС СВЧ.
- 3. Некоторые предварительные общие результаты.
- § В.2. Принципиальные основы подхода к автоматизированному проектированию ОИС СВЧ
- 2. Принцип декомпозиции.
- 3. Матрица рассеяния функционально-конструктивного узла РЭА.
- 4. Структура системы АП и режимы ее функционирования.
- ГЛАВА 1. Линии передачи для ОИС СВЧ
- 2. Учет реальных размеров СПЛ.
- 3. Потери в СПЛ.
- 4. Максимальная рабочая частота СПЛ
- § 1.2. Несимметричная полосковая линия
- § 1.3. Симметричная щелевая линия
- 2. Многослойная подвешенная СЩЛ.
- 3. СЩЛ типа «сэндвич».
- § 1.4. Несимметричная щелевая линия
- 2. Интегральные уравнения для НЩЛ. Собственные волны.
- 3. Алгебраизация системы интегральных уравнений. Дисперсионное уравнение.
- 4. Структура поля в НЩЛ.
- 5. Экспериментальные исследования НЩЛ.
- 6. Модификации НЩЛ.
- § 1.5. Копланарная линия передачи
- 2. Электродинамическое приближение в теории КЛ. Метод Галеркина. Численные результаты.
- 3. Экранированные КЛ.
- 4. Модификации экранированных КЛ.
- § 1.6. Линии передачи магнитостатических волн
- ГЛАВА 2. Моделирование и расчет регулярных полосковых линий и неоднородностей в них
- § 2.1. Метод Олинера и модели некоторых линий
- 2. Модели некоторых полосковых линий передачи.
- § 2.2. Неоднородности в ОИС СВЧ
- 2. Неоднородности в H-плоскости.
- 3. Неоднородности в Е-плоскости.
- 4. Неоднородности в копланарной линии.
- 5. Т-соединения различных типов линий в ОИС СВЧ.
- 6. Некоторые примеры тройников для ОИС СВЧ.
- ГЛАВА 3. Переходы между различными типами направляющих структур ОИС СВЧ
- § 3.1. Сверхширокополосные переходы — переходы с непосредственным гальваническим контактом
- § 3.2. Широкополосные шлейфные переходы
- § 3.3. Узкополосные резонансные переходы щелевого типа
- 2. Расчет щелевого перехода [226].
- 3. Согласование перехода.
- 4. Синтез перехода [224].
- 5. Частотные характеристики переходов.
- § 3.4. БЭ согласования ОИС СВЧ
- 2. Несинхронный трансформатор.
- 3. Шлейфный трансформатор.
- 4. Подстройка шлейфов согласующих трансформаторов.
- ГЛАВА 4. Гибридные мостовые устройства ОИС СВЧ
- § 4.1. Балансные делители (сумматоры) мощности
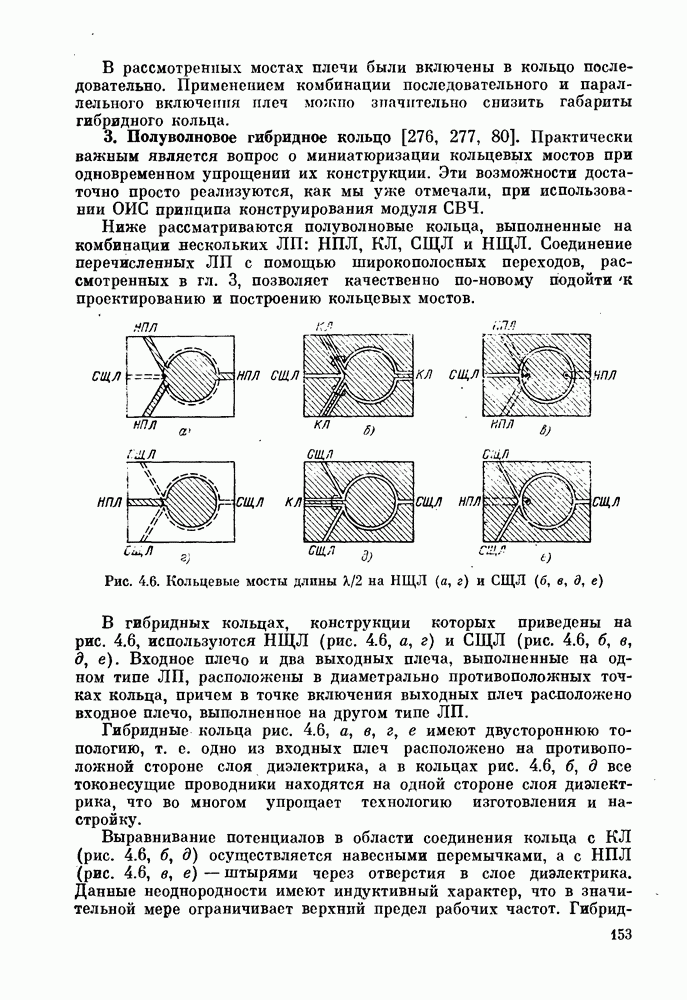
- § 4.2. Кольцевые мосты
- 2. Гибридный кольцевой мост с обращением фазы.
- 3. Полуволновое гибридное кольцо [276, 277, 80].
- 4. Гибридное кольцо периметра 3l/2
- 5. «Магические» Т-соединения.
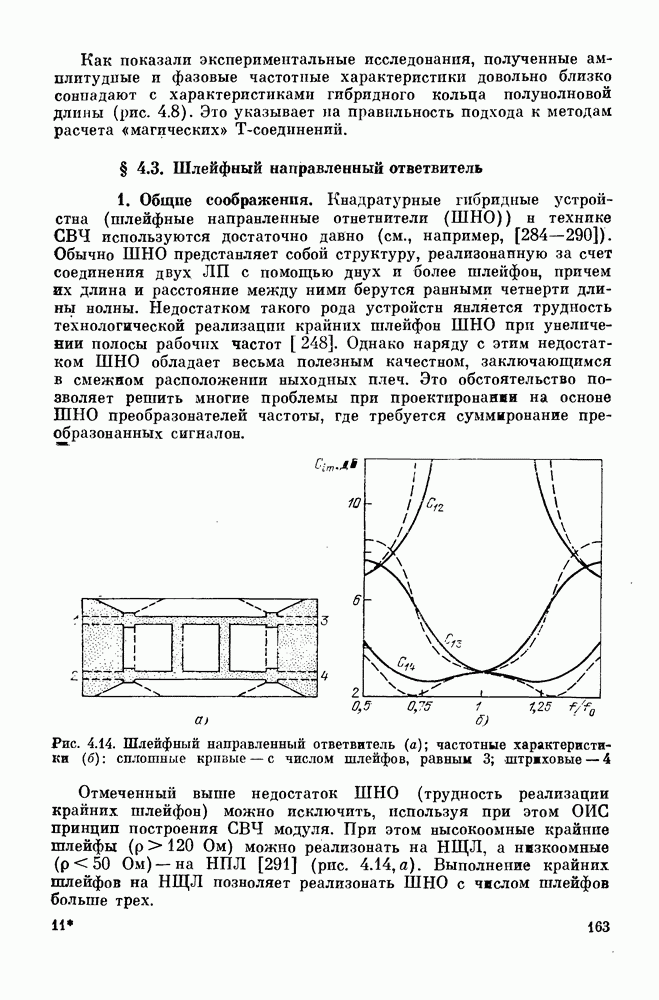
- § 4.3. Шлейфный направленный ответвитель
- § 4.4. Квадратурные направленные ответвители
- § 4.5. Связь двух полосковых линий с переменными параметрами и критическим сечением
- ГЛАВА 5. Объемные многослойные фильтры СВЧ
- § 5.2. Диэлектрические резонаторы
- § 5.3. Полосковые резонаторы
- § 5.4. Фильтры на ОИС СВЧ
- ГЛАВА 6. СВЧ устройства на ОИС
- § 6.1. Многоканальные делители мощности
- § 6.2. Фазовые манипуляторы
- § 6.3. Широкополосные модуляторы
- § 6.4. Приемно-передающие модули
- ГЛАВА 7. Применение ОИС СВЧ в измерительной технике
- § 7.1. Многозондовый датчик для измерения комплексных сопротивлений
- § 7.2. Экспресс-метод контроля диэлектрических проницаемостей подложек ОИС СВЧ
- § 7.3. Устройство дискретизации частотного масштаба
- Заключение