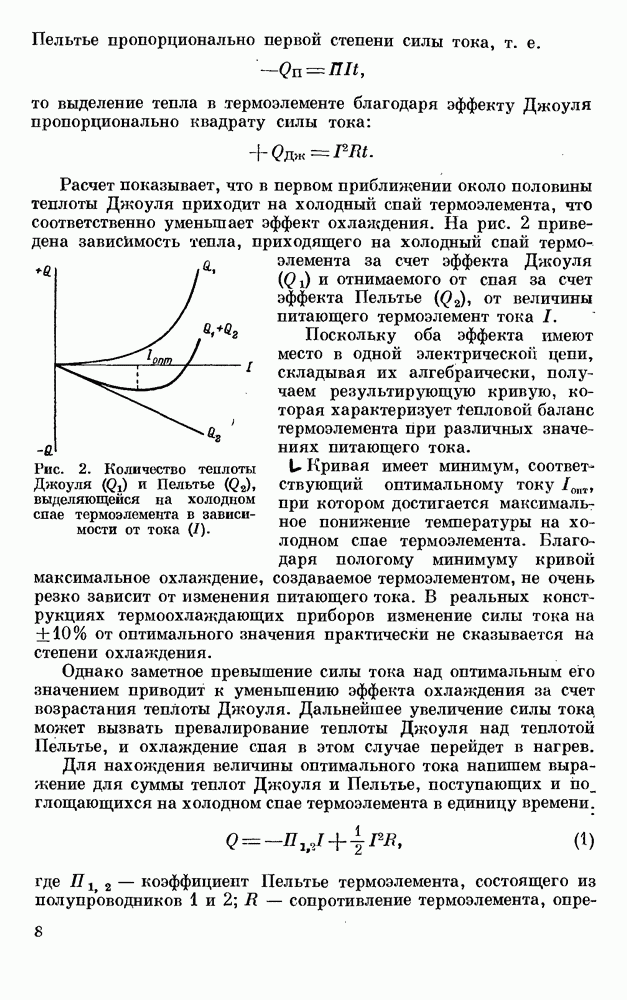
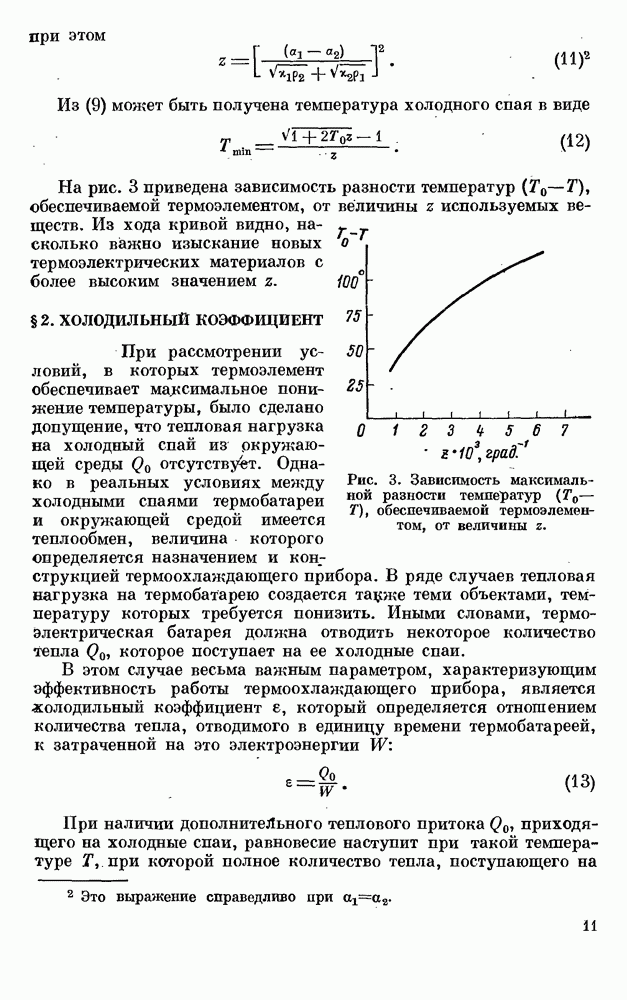
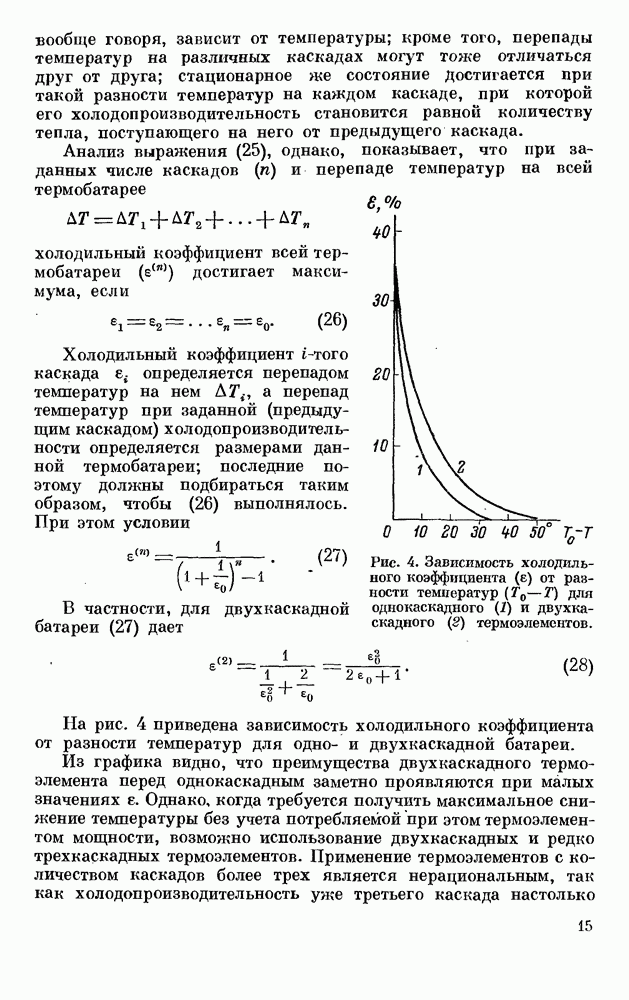
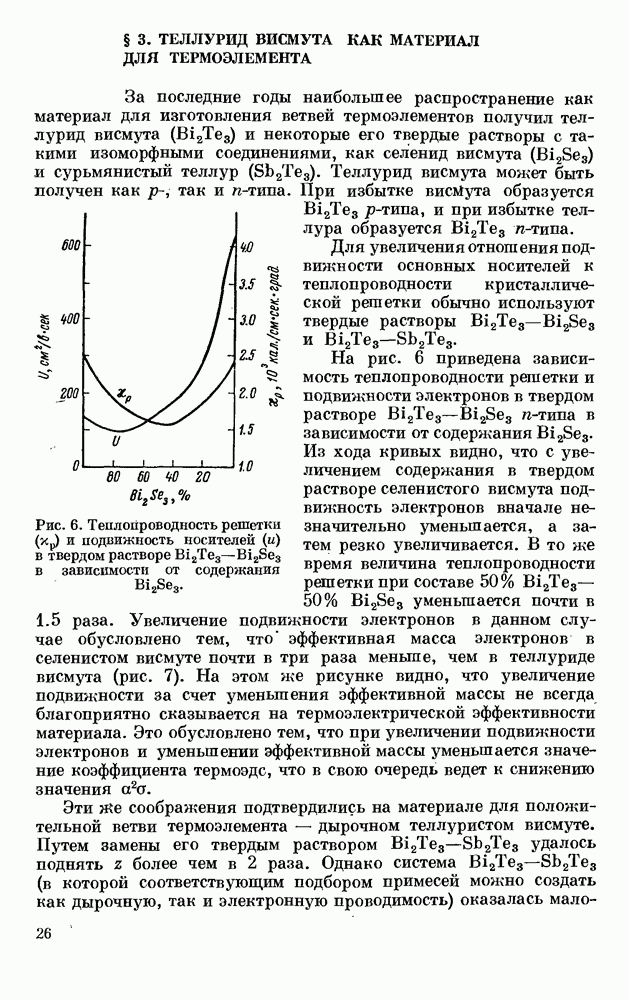
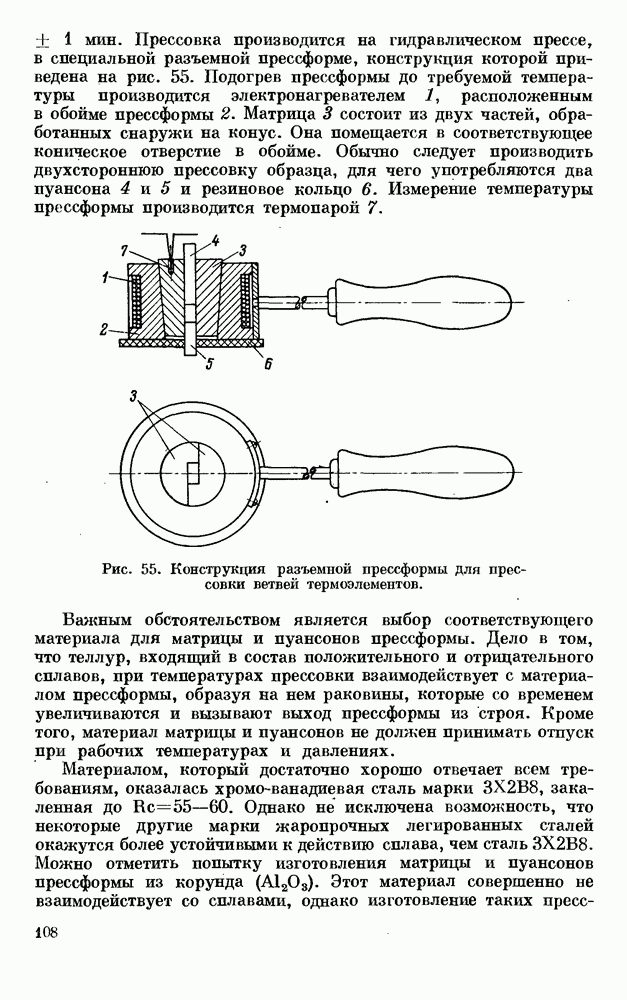
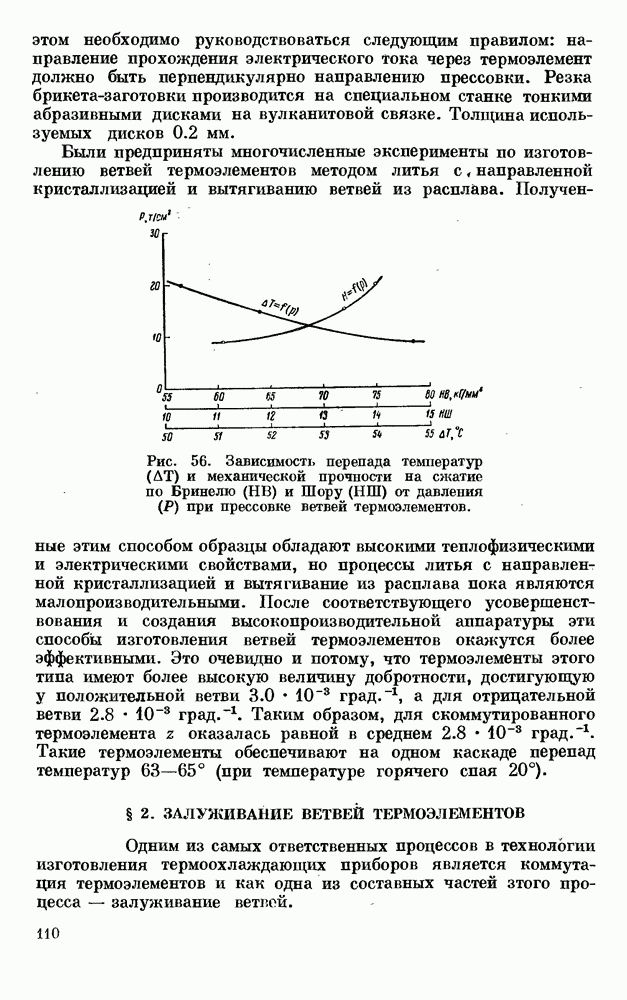
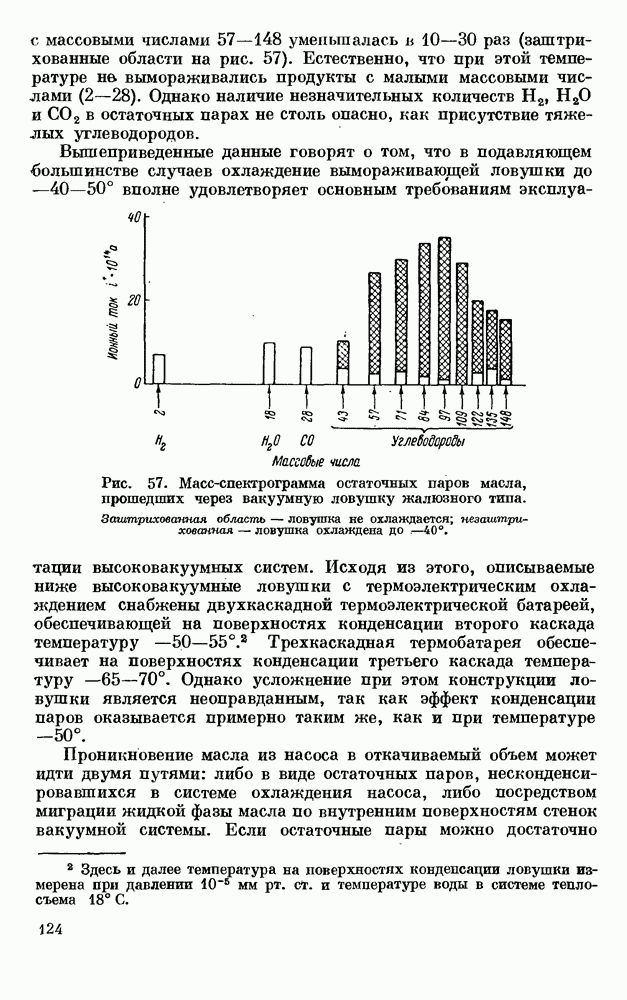
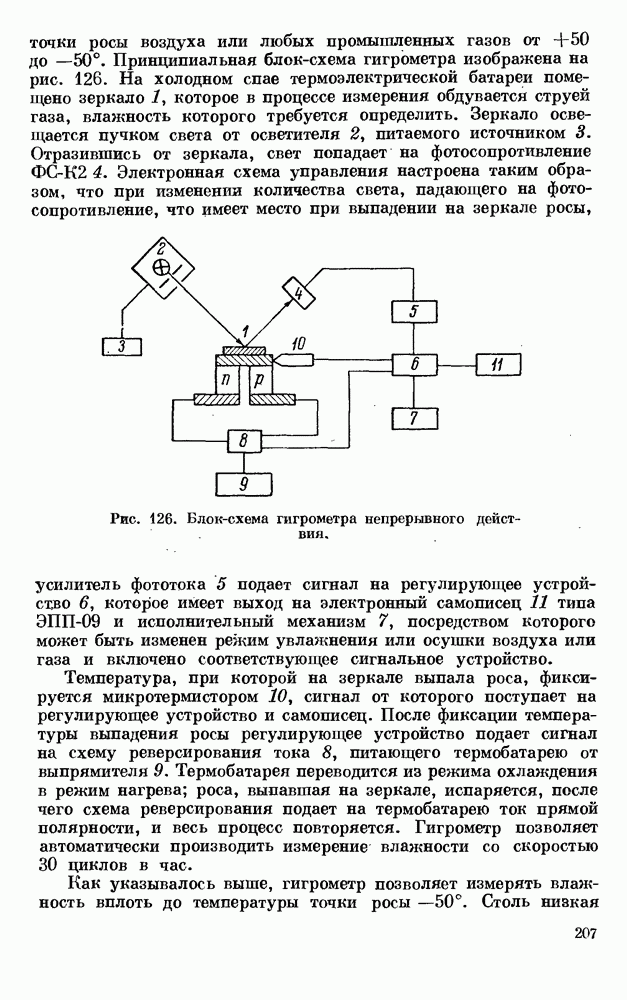
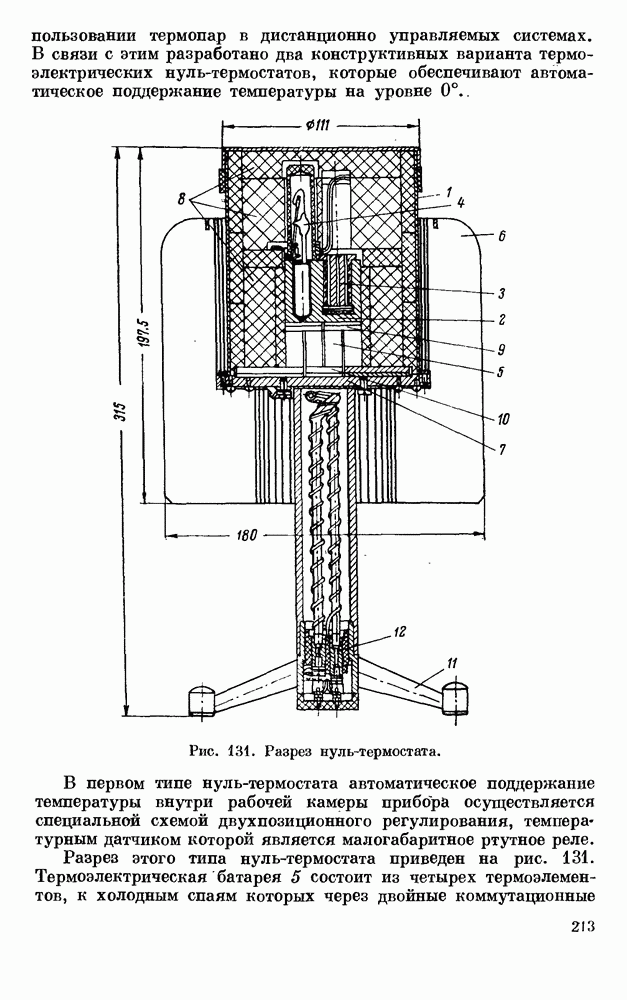
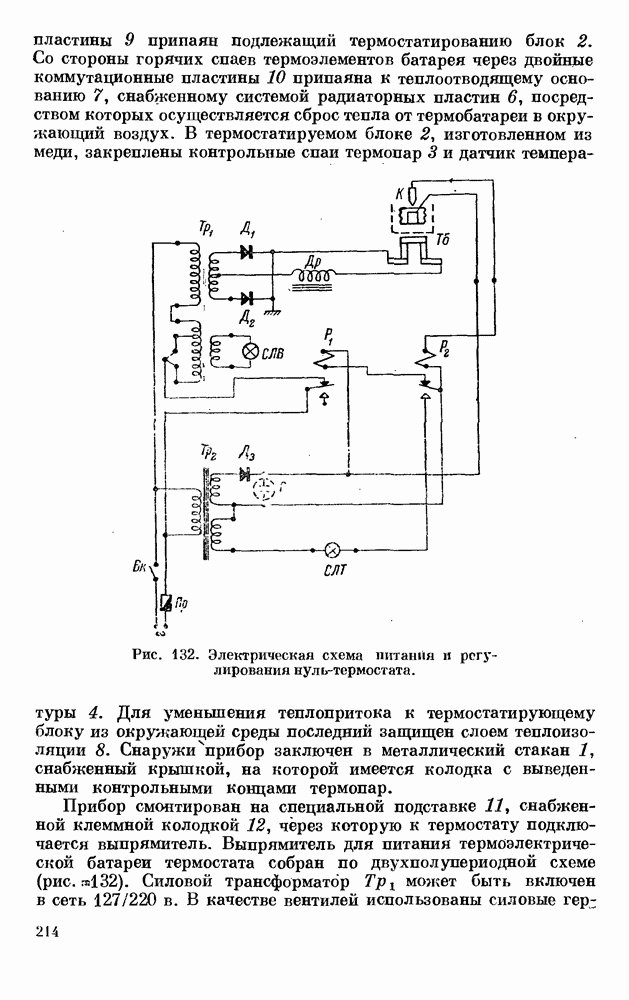
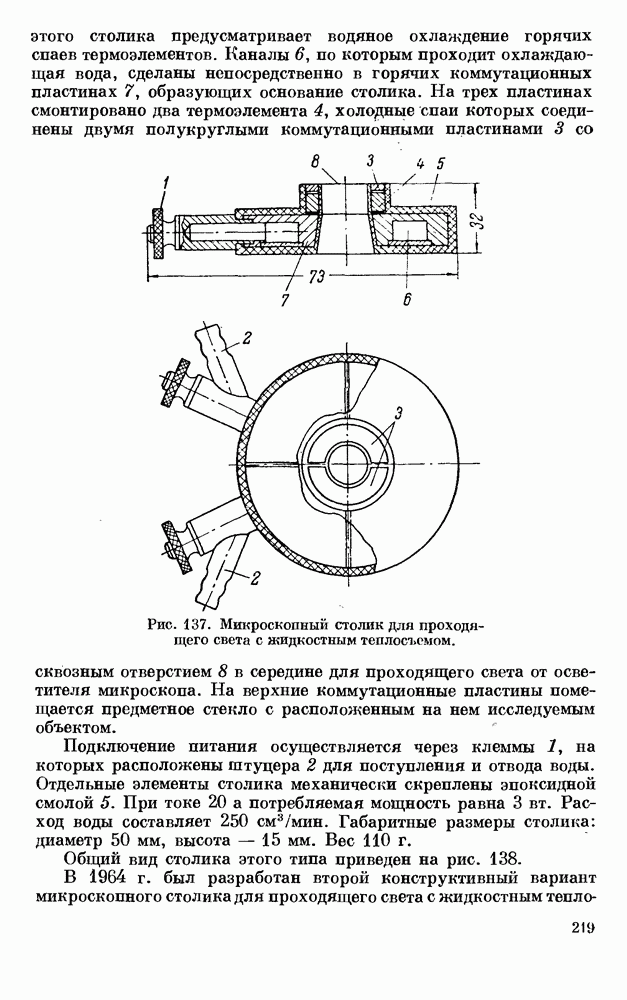
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. УЧЕТ ТЕПЛОТЫ ТОМСОНА В ЭНЕРГЕТИЧЕСКОМ БАЛАНСЕ ТЕРМОЭЛЕМЕНТА
Как следует из (34) и (35), наилучшими для полупроводниковых термоэлементов являются вещества, в которых коэффициент термоэдс постоянен:

а концентрация носителей меняется по закону

В теории, изложенной в гл. I и II, рассмотрены эти идеальные условия, при которых коэффициент Томсона

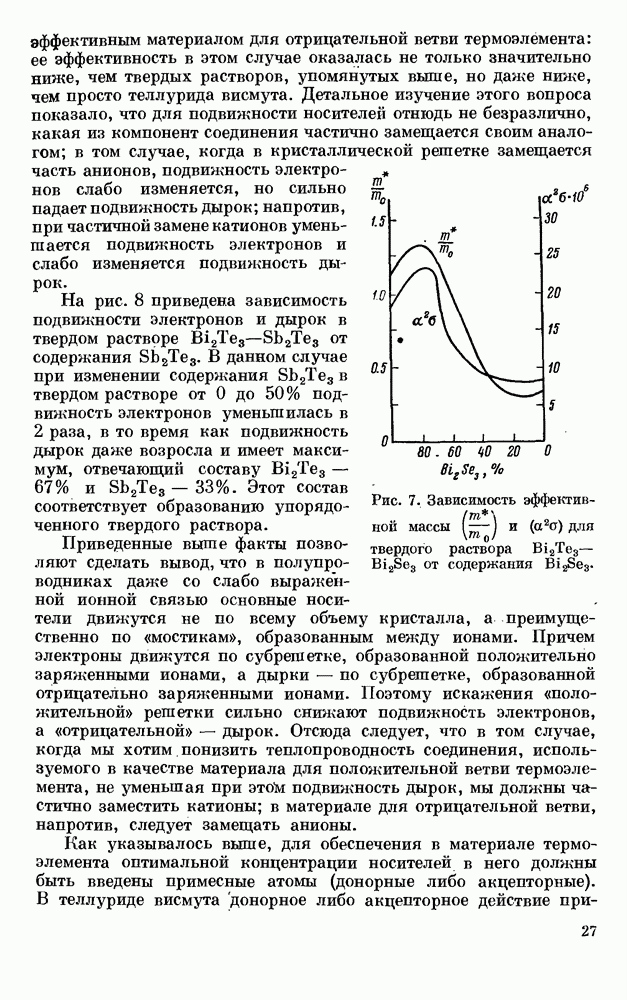
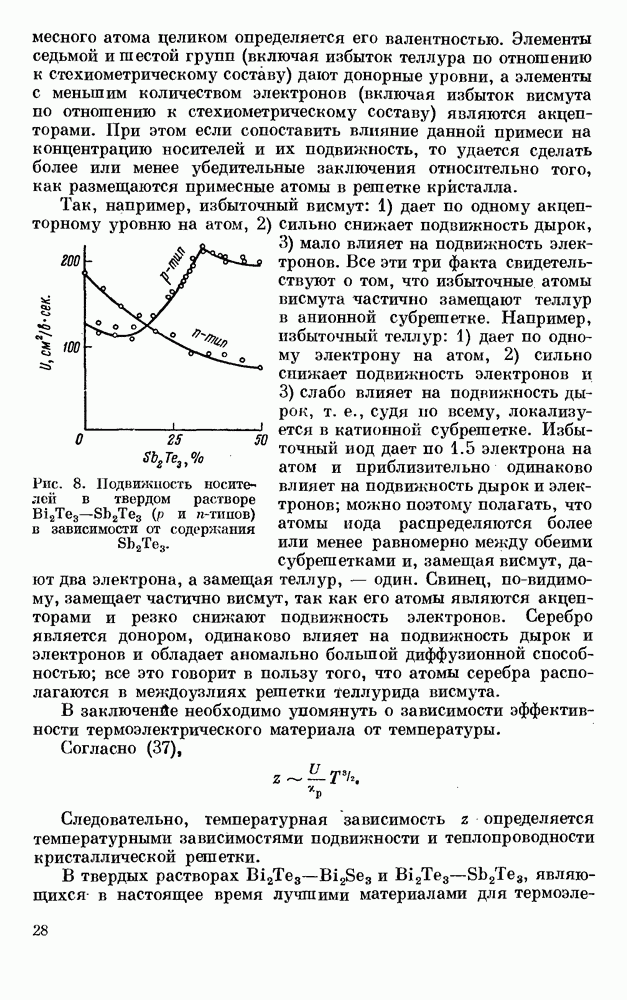
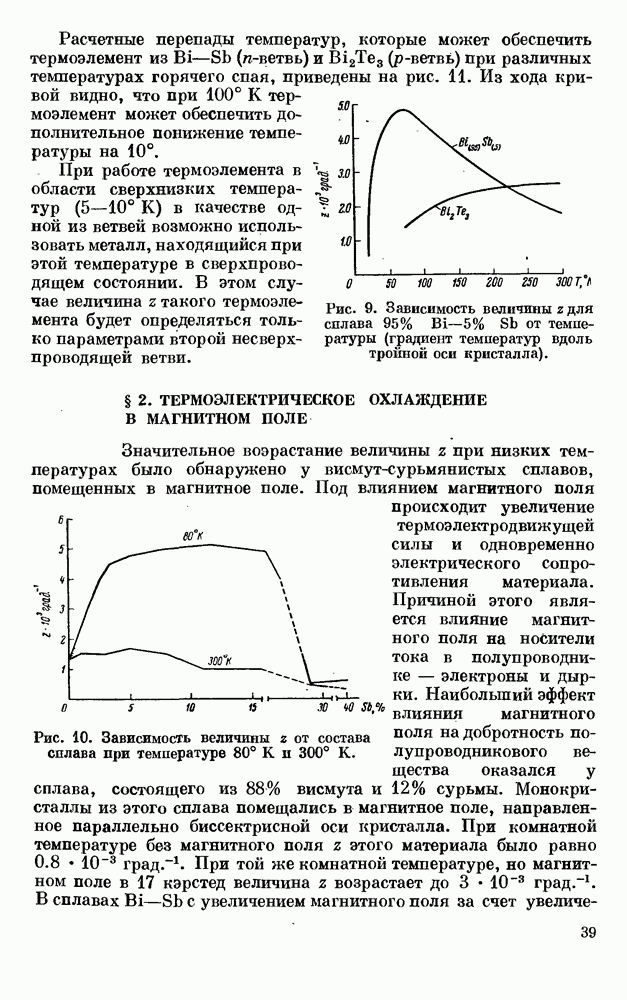
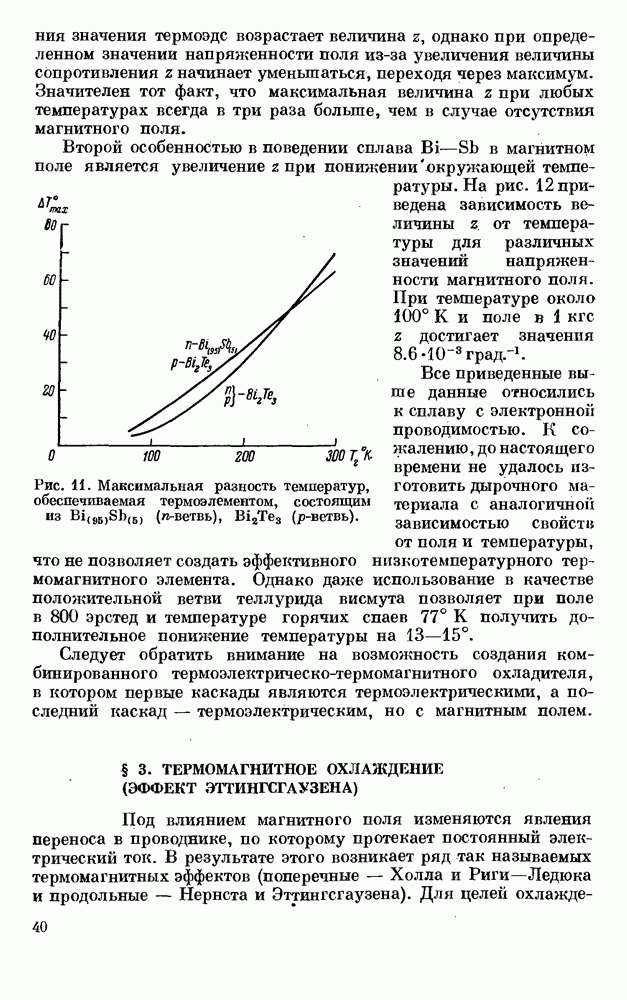
На практике же, как упоминалось выше, в качестве матерое для ветвей термоэлементов используются обычные
полуметаллы, т. е. вещества, в которых концентрация носителей постоянна, и термоэдс увеличивается с ростом температуры. В этом случае коэффициент Томсона отличен от нуля и выражается следующим образом:

Мы должны теперь учесть влияние теплоты Томсона на тепловой баланс термоэлемента. Это влияние скажется прежде всего на распределении температур вдоль ветвей термоэлемента. До сих пор мы предполагали, что градиент температуры вдоль ветвей термоэлемента постоянен и плотность теплового потока на холодный спай термоэлемента в соответствии с этим выражается формулой

Влияние теплоты Джоуля на распределение температуры учитывалось приближенно; полагалось, что половина ее поступает на горячий спай термоэлемента и половина — на холодный. Для тога чтобы решить задачу более строго, следует найти распределение температуры вдоль ветви термоэлемента с учетом теплоты Джоуля и Томсона и затем — плотность теплового потока по точной формуле:

Направим ось  вдоль ветви термоэлемента и совместим начало координат с холодным спаем термоэлемента; тогда (48) примет следующий вид:
вдоль ветви термоэлемента и совместим начало координат с холодным спаем термоэлемента; тогда (48) примет следующий вид:

Для вычисления  согласно (49) нам нужно узнать распре деление температуры вдоль ветви термоэлемента:
согласно (49) нам нужно узнать распре деление температуры вдоль ветви термоэлемента:

При этом по-прежнему не будем учитывать температурную зависимость теплопроводности и электропроводности, заменяя их истинные значения как функции температуры среднимрг значениями в рабочем интервале температур. В термоэлектрогенераторе и электроны, и дырки движутся от горячего спая к холодному; здесь во всем объеме ветви термоэлемента в дополнение к теплоте Джоуля выделяется теплота Томсона; в термоэлектро-холодильниках и электроны, и дырки движутся в обратном направлении, и поэтому теплота Томсона вычитается из теплоту Джоуля. Следовательно, условие стационарности для единицы
объема ветви термоэлемента в рассматриваемом нами случае будет иметь вид

где  плотность тока.
плотность тока.
Решение дифференциального уравнения (50) при учете граничных условий  при
при  при
при  имеет вид
имеет вид

где введены следующие обозначения:  Следовательно, согласно (49) и (51), поток тепла на холодный спай
Следовательно, согласно (49) и (51), поток тепла на холодный спай

Разлагая экспоненту в выражении (52) в ряд и ограничиваясь в разложении двумя первыми членами, лолучим

Мы, таким образом, доказали, что действительно в первом приближении половина теплоты Джоуля поступает на холодный спай; с помощью (53) можно теперь учесть влияние теплоты Томсона на холодильный коэффициент термоэлемента  Выражение (14) для холодопроизводительности термоэлемента с учетом (53) примет следующий вид:
Выражение (14) для холодопроизводительности термоэлемента с учетом (53) примет следующий вид:

где  значение коэффициента термоэдс при температуре Т. Следовательно, выражение (54) может быть переписано так:
значение коэффициента термоэдс при температуре Т. Следовательно, выражение (54) может быть переписано так:

где введено обозначение

Покажем, что а равно среднему значению коэффициента термоэдс в интервале температур 
Согласно второму соотношению Томсона

Подставляя (57) в (56), получим

С той же степенью точности можно считать электродвижущую силу

Следовательно, выражение (16) для холодильного коэффициента термоэлемента с учетом (58) и (65) примет вид

Выражение (59) - имеет тот же вид, что и (16), с той лишь разницей, что коэффициент термоэдс а, который мы раньше считали не зависящими от температуры, заменен его средним значением  в рабочем интервале температур. Следовательно, не повторяя выкладок, которые были приведены выше, мы вправе написать выражение для максимального холодильного коэффициента:
в рабочем интервале температур. Следовательно, не повторяя выкладок, которые были приведены выше, мы вправе написать выражение для максимального холодильного коэффициента:

где 
Можно также показать, что температурная зависимость электропроводности и теплопроводности может быть в первом приближении учтена заменой в выражении для  произведения
произведения  его средним значением в рабочем интервале температур:
его средним значением в рабочем интервале температур:

где

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Часть I. ТЕОРИЯ ТЕРМОЭЛЕКТРИЧЕСКОГО ОХЛАЖДЕНИЯ
- § 1. МАКСИМАЛЬНОЕ ПОНИЖЕНИЕ ТЕМПЕРАТУРЫ
- § 2. ХОЛОДИЛЬНЫЙ КОЭФФИЦИЕНТ
- § 3. МНОГОКАСКАДНЫЕ ТЕРМОБАТАРЕИ
- Глава II. МАТЕРИАЛЫ ДЛЯ ТЕРМОЭЛЕМЕНТОВ
- § 1. УСЛОВИЯ МАКСИМАЛЬНОЙ ЭФФЕКТИВНОСТИ ТЕРМОЭЛЕМЕНТА
- § 2. ВЫБОР МАТЕРИАЛОВ ДЛЯ ВЕТВЕЙ ТЕРМОЭЛЕМЕНТОВ
- § 3. ТЕЛЛУРИД ВИСМУТА КАК МАТЕРИАЛ ДЛЯ ТЕРМОЭЛЕМЕНТА
- Глава III. УЧЕТ ДОПОЛНИТЕЛЬНЫХ ФАКТОРОВ
- § 1. УЧЕТ ЭЛЕКТРОННОЙ ТЕПЛОПРОВОДНОСТИ
- § 2. УЧЕТ ТЕПЛОТЫ ТОМСОНА В ЭНЕРГЕТИЧЕСКОМ БАЛАНСЕ ТЕРМОЭЛЕМЕНТА
- § 3. ОТСТУПЛЕНИЯ ОТ ОПТИМАЛЬНЫХ УСЛОВИЙ
- Глава IV. ТЕРМОГАЛЬВАНОМАГНИТНЫЕ МЕТОДЫ ОХЛАЖДЕНИЯ
- § 2. ТЕРМОЭЛЕКТРИЧЕСКОЕ ОХЛАЖДЕНИЕ В МАГНИТНОМ ПОЛЕ
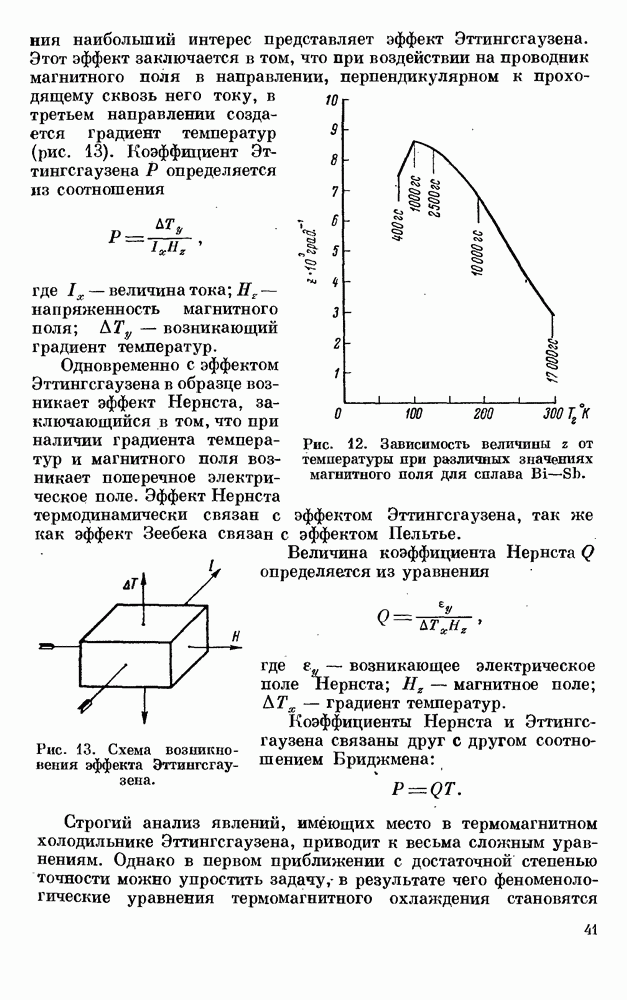
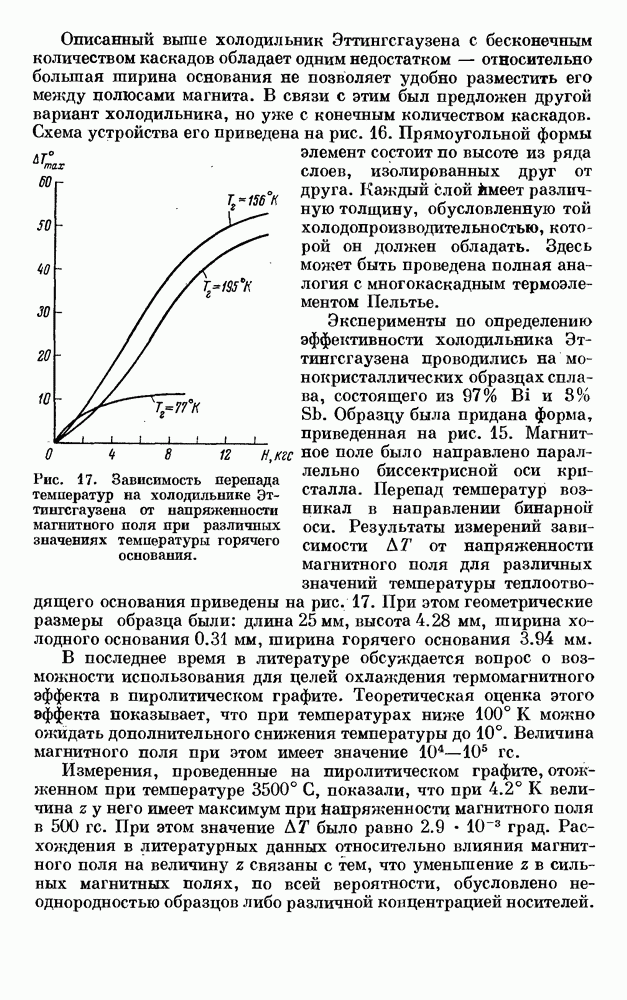
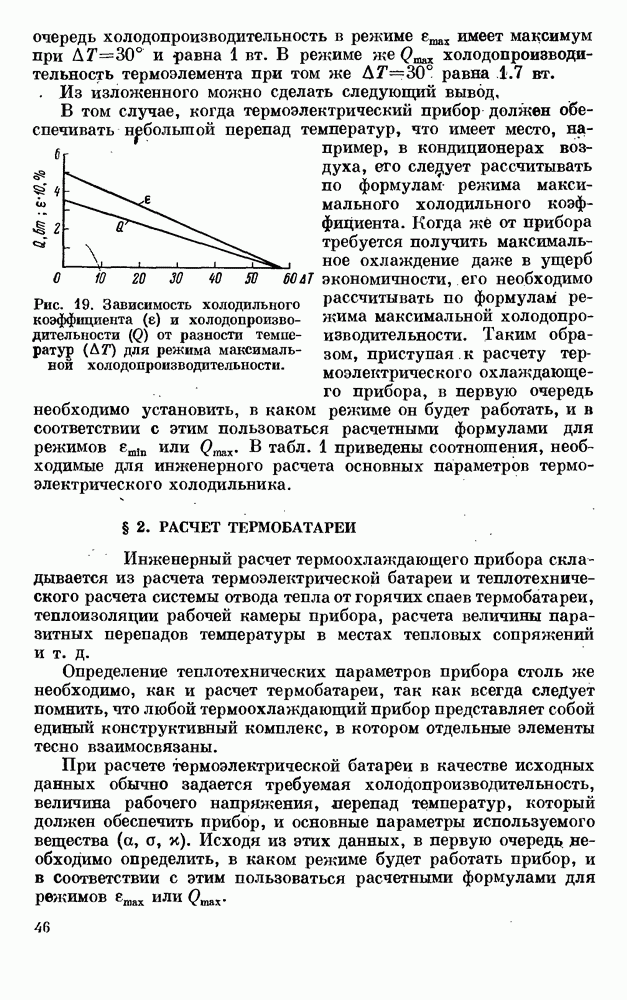
- § 3. ТЕРМОМАГНИТНОЕ ОХЛАЖДЕНИЕ (ЭФФЕКТ ЭТТИНГСГАУЗЕНА)
- Часть II. ИНЖЕНЕРНЫЕ ВОПРОСЫ ТЕХНИКИ ТЕРМОЭЛЕКТРИЧЕСКОГО ОХЛАЖДЕНИЯ
- Глава V. ОСНОВЫ РАСЧЕТА ТЕРМОЭЛЕКТРИЧЕСКИХ ОХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. РАСЧЕТ ТЕРМОБАТАРЕИ
- § 3. РАСЧЕТ РАДИАТОРА ТЕПЛОСЪЕМА
- Глава VI. КОНСТРУКТИВНЫЕ ЭЛЕМЕНТЫ ТЕРМОЭЛЕКТРИЧЕСКИХ ОХЛАЖДАЮЩИХ ПРИБОРОВ
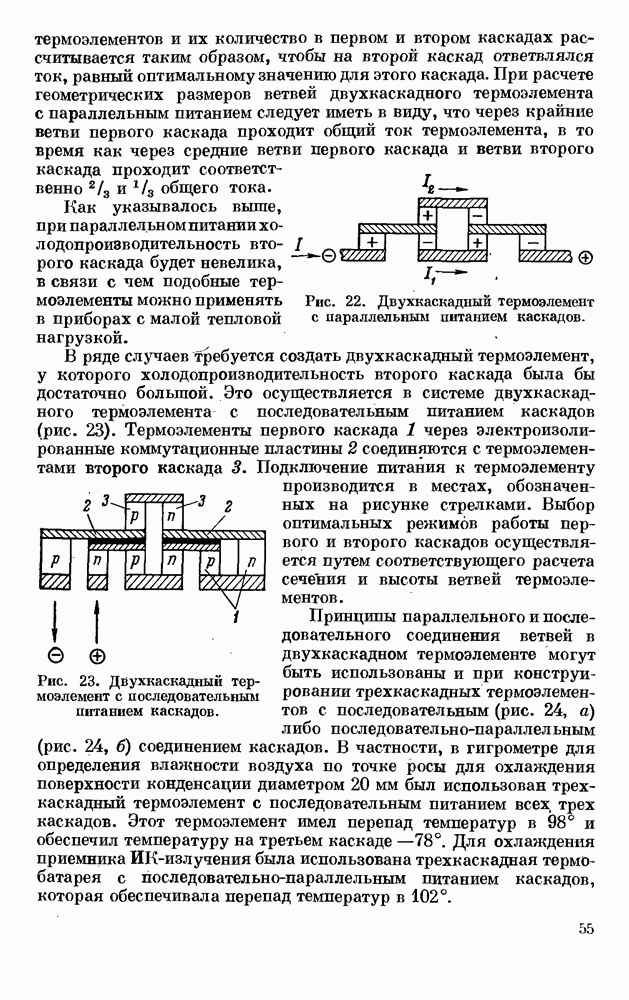
- § 2. МНОГОКАСКАДНЫЕ ТЕРМОЭЛЕМЕНТЫ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКАЯ БАТАРЕЯ
- § 4. ТЕПЛОВОЕ СОПРЯЖЕНИЕ ТЕРМОБАТАРЕИ
- § 5. КОНСТРУКЦИИ СИСТЕМ ТЕПЛООТВОДА
- § 6. РАБОЧАЯ КАМЕРА ПРИБОРА
- Глава VII. СПОСОБЫ ОТВОДА ТЕПЛА ОТ ТЕРМООХЛАЖДАЮЩИХ ПРИБОРОВ
- § 1. РАДИАТОРНАЯ СИСТЕМА С ЕСТЕСТВЕННОКОНВЕКЦИОННЫМ ТЕПЛООБМЕНОМ
- § 2. РАДИАТОРНАЯ СИСТЕМА С ПРИНУДИТЕЛЬНЫМ ТЕПЛОСЪЕМОМ
- § 3. ИГОЛЬЧАТЫЕ РАДИАТОРНЫЕ СИСТЕМЫ
- § 4. ЖИДКОСТНАЯ СИСТЕМА С ЕСТЕСТВЕННОЙ ЦИРКУЛЯЦИЕЙ
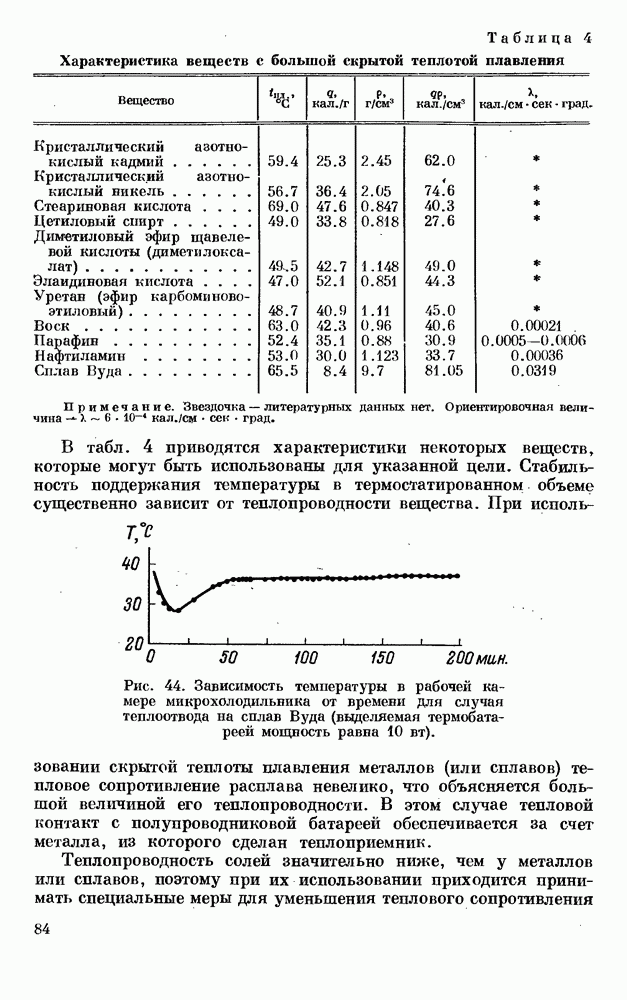
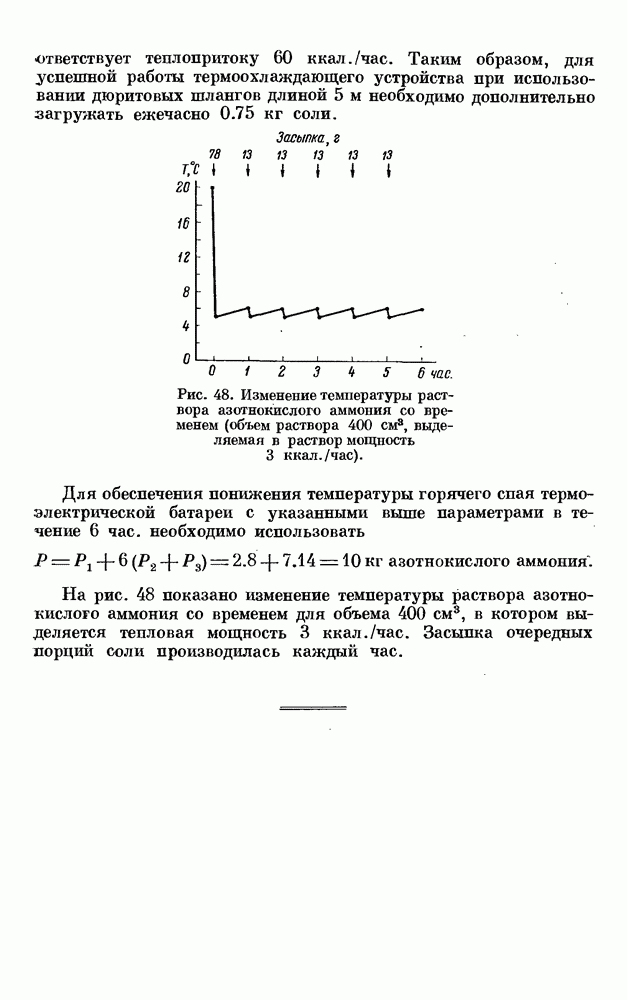
- § 5. ИСПОЛЬЗОВАНИЕ СКРЫТОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ
- § 6. ИСПОЛЬЗОВАНИЕ СКРЫТОЙ ТЕПЛОТЫ ИСПАРЕНИЯ
- § 7. ТЕПЛООТВОДЯЩАЯ СИСТЕМА С ИСПОЛЬЗОВАНИЕМ ТЕПЛОЕМКОСТИ
- § 8. ИСПОЛЬЗОВАНИЕ РАСТВОРОВ С НИЗКОЙ КРИОГИДРАТНОЙ ТЕМПЕРАТУРОЙ
- Глава VIII. ИСТОЧНИКИ ПИТАНИЯ ТЕРМОЭЛЕКТРИЧЕСКИХ ОХЛАЖДАЮЩИХ ПРИБОРОВ
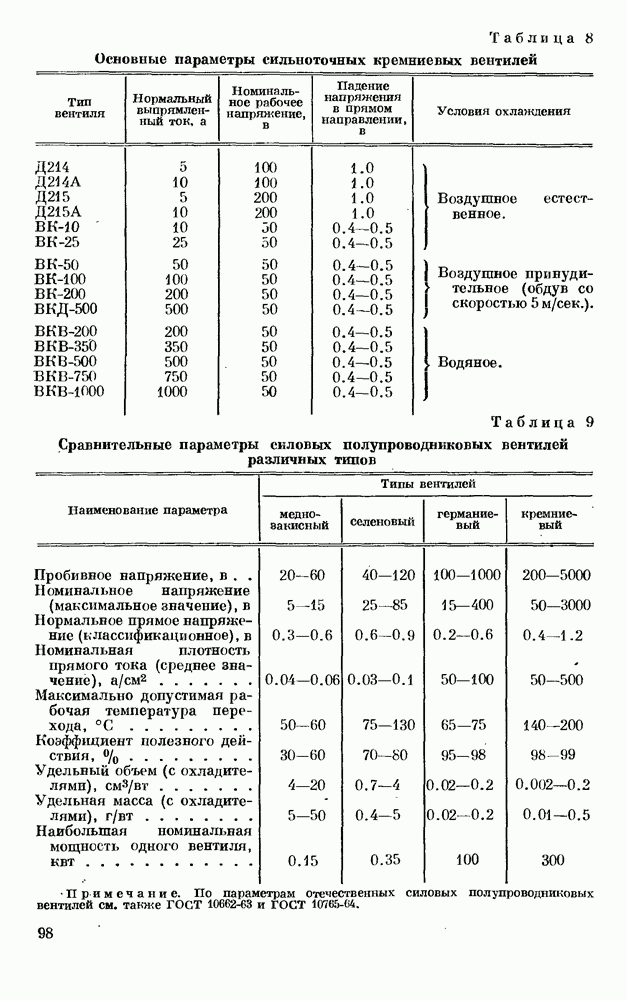
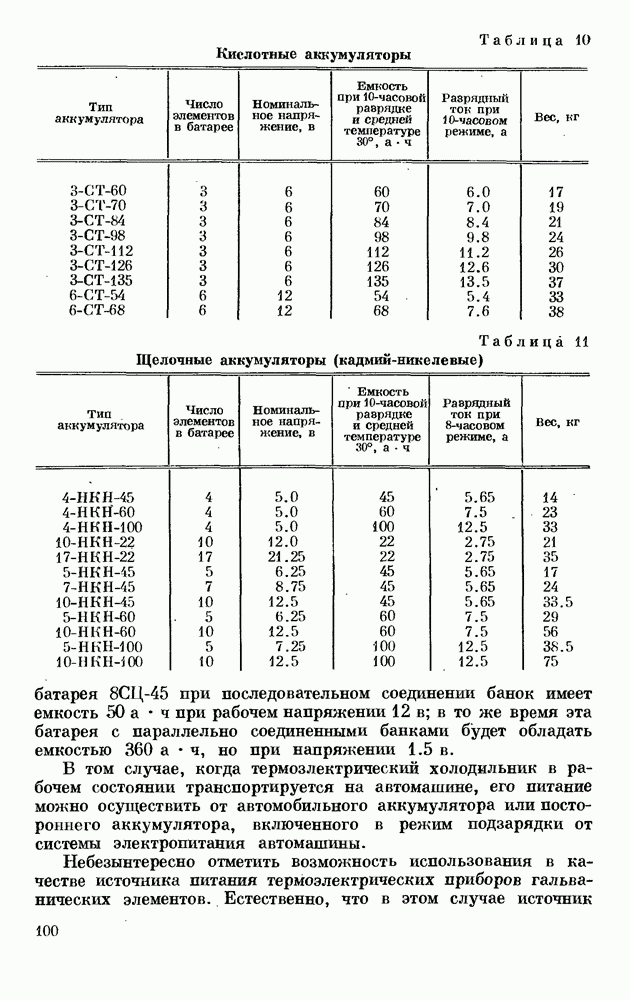
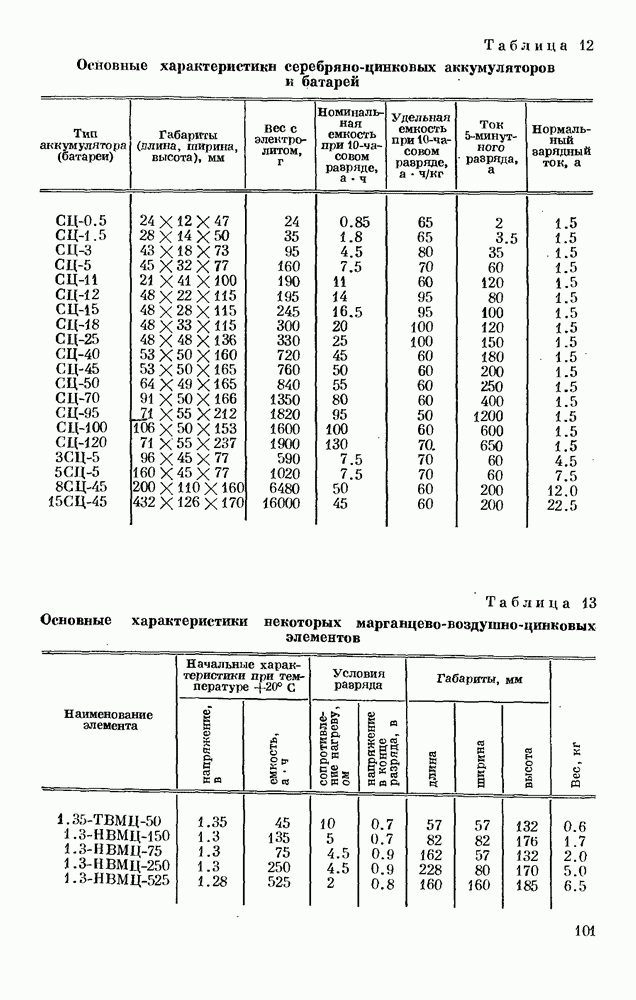
- § 2. АККУМУЛЯТОРЫ
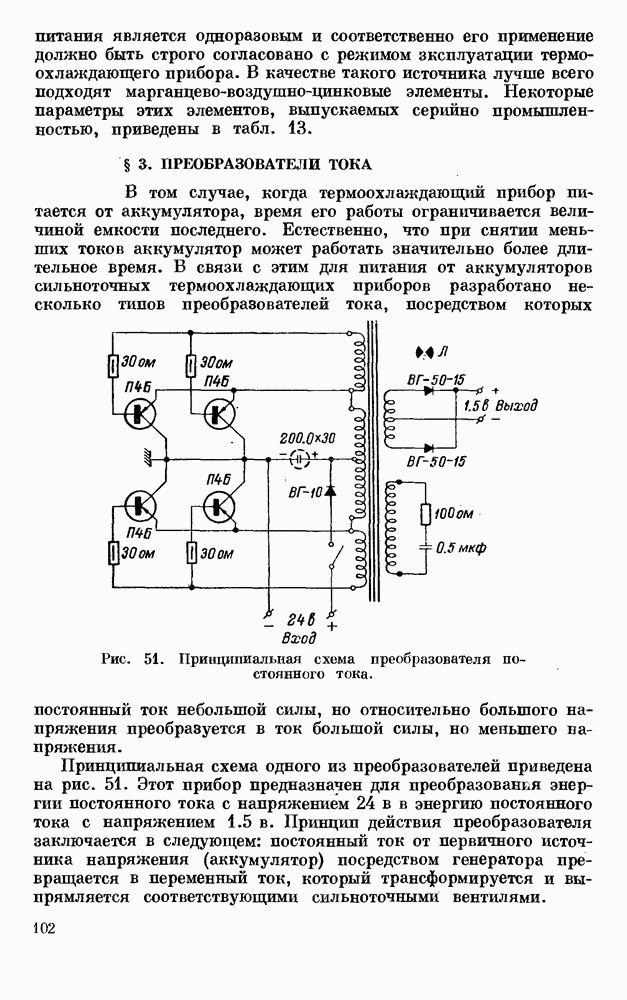
- § 3. ПРЕОБРАЗОВАТЕЛИ ТОКА
- § 4. ТЕРМОЭЛЕКТРОГЕНЕРАТОРЫ
- Глава IX. НЕКОТОРЫЕ ВОПРОСЫ ТЕХНОЛОГИИ ИЗГОТОВЛЕНИЯ ТЕРМООХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. ЗАЛУЖИВАНИЕ ВЕТВЕЙ ТЕРМОЭЛЕМЕНТОВ
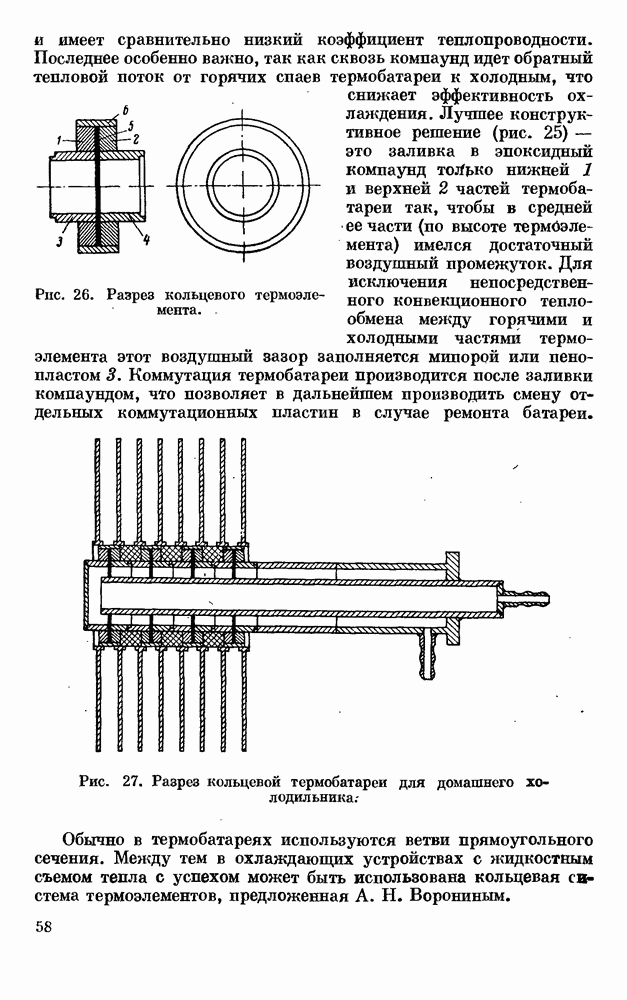
- § 3. КОММУТАЦИЯ ТЕРМОБАТАРЕИ
- § 4. ПРОЧИЕ ВОПРОСЫ ТЕХНОЛОГИИ
- Часть III. ПРАКТИКА ТЕРМОЭЛЕКТРИЧЕСКОГО ОХЛАЖДЕНИЯ
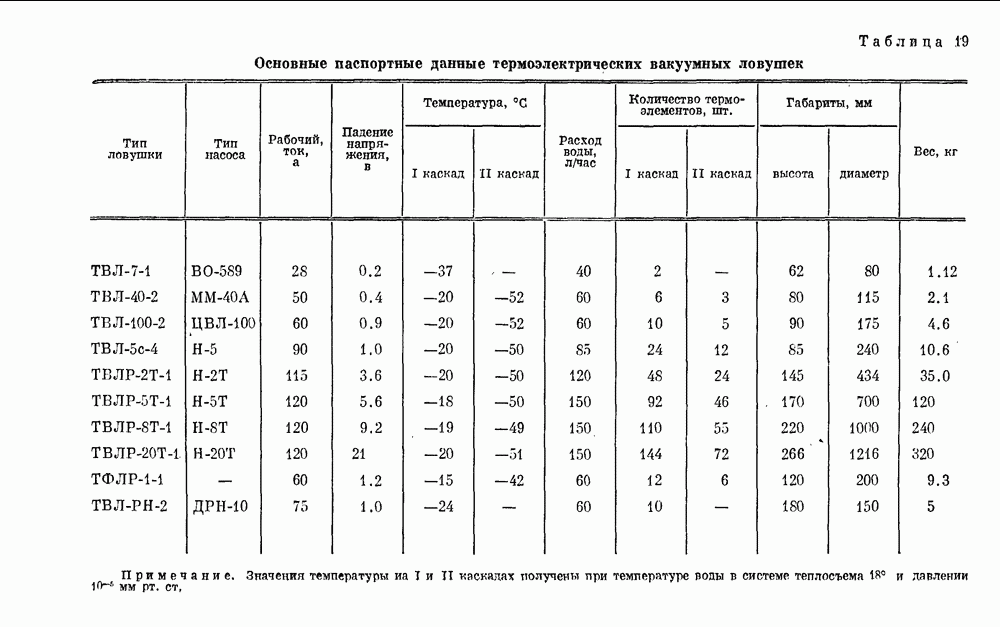
- Глава X. ВЫСОКОВАКУУМНЫЕ ЛОВУШКИ С ТЕРМОЭЛЕКТРИЧЕСКИМ ОХЛАЖДЕНИЕМ
- § 2. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЛОВУШКИ ДЛЯ ЕДИНОЙ СЕРИИ НАСОСОВ
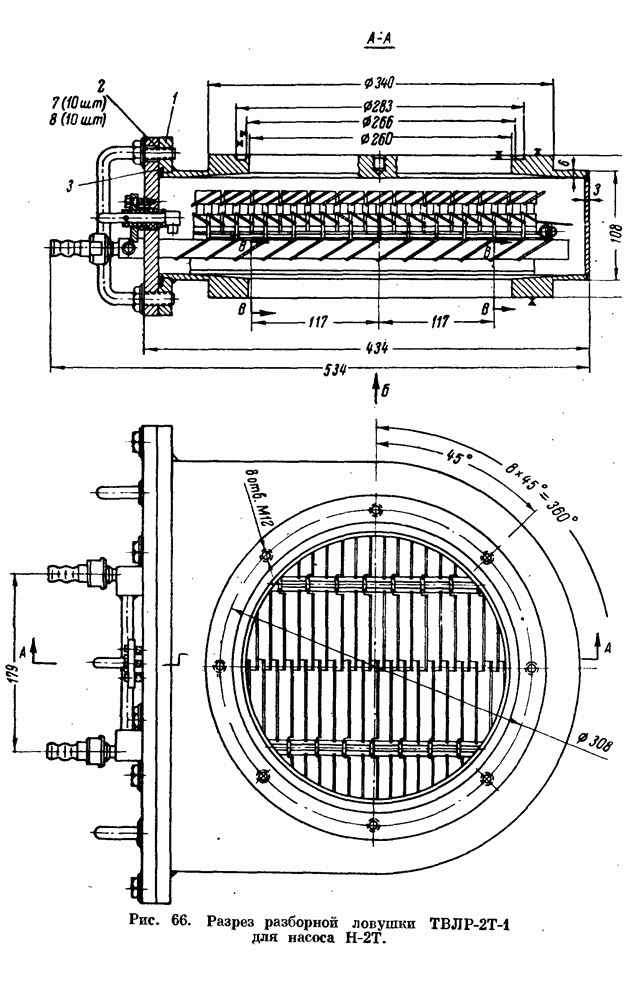
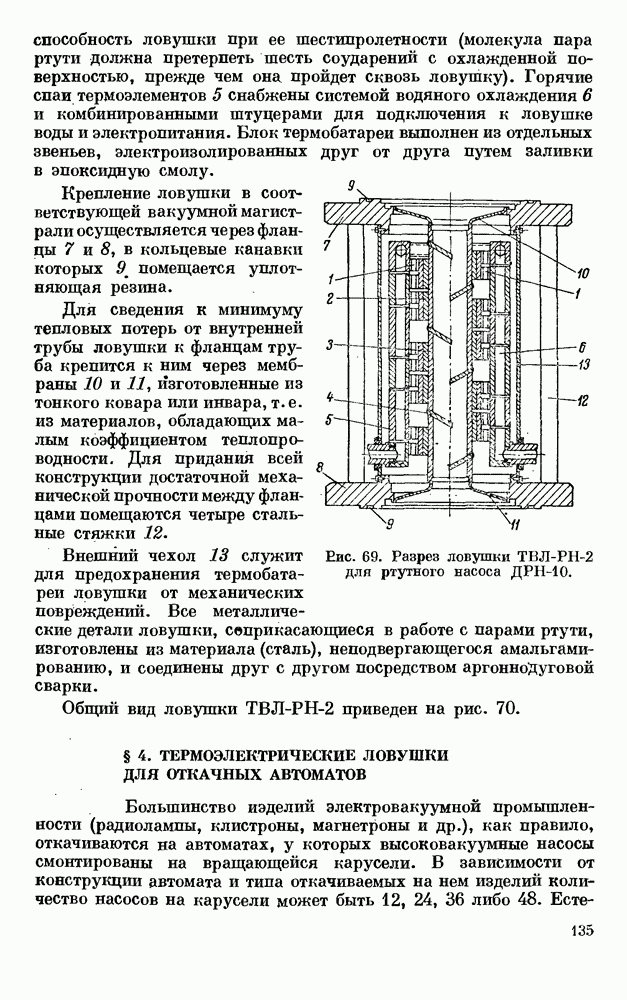
- § 3. ТЕРМОЭЛЕКТРИЧЕСКАЯ ЛОВУШКА ДЛЯ ПАРОРТУТНЫХ НАСОСОВ
- § 4. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЛОВУШКИ ДЛЯ ОТКАЧНЫХ АВТОМАТОВ
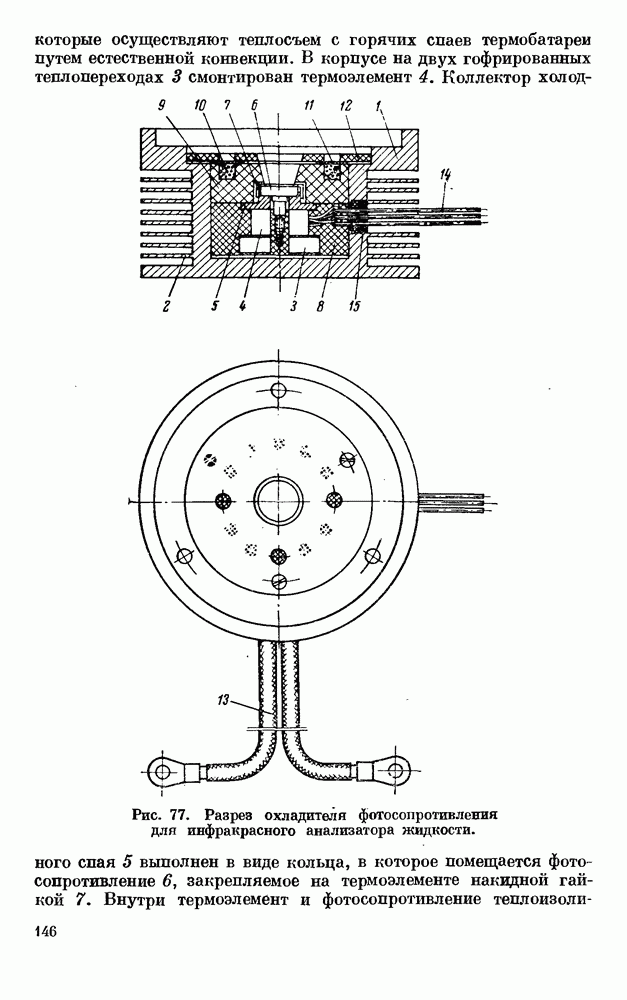
- Глава XI. ТЕРМОЭЛЕКТРИЧЕСКИЕ ОХЛАДИТЕЛИ ПРИЕМНИКОВ ЛУЧИСТОЙ ЭНЕРГИИ
- § 1. МИКРОТЕРМОСТАТЫ ДЛЯ ОХЛАЖДЕНИЯ ФОТОСОПРОТИВЛЕНИЙ
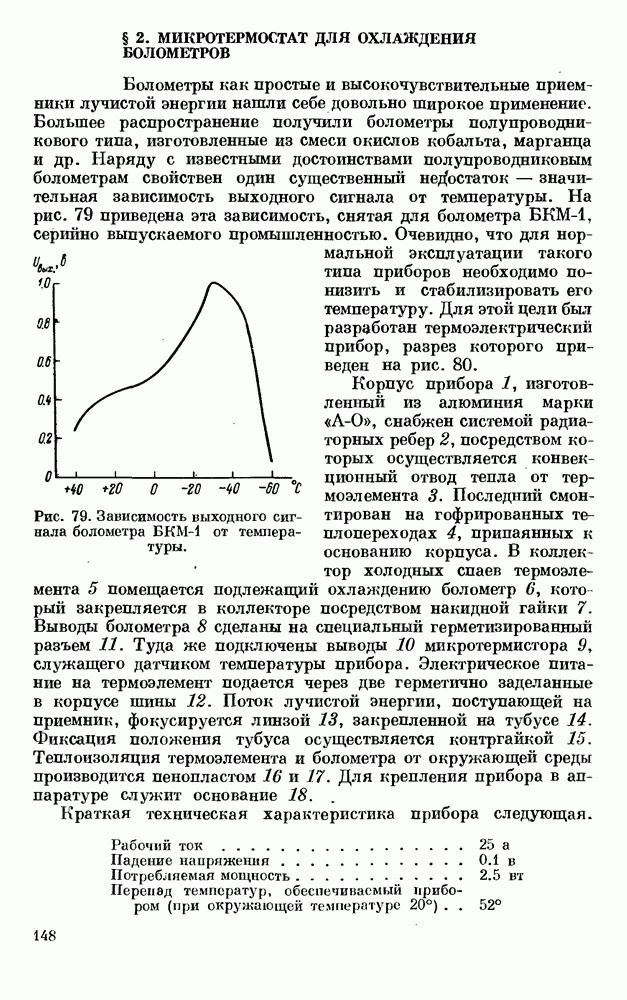
- § 2. МИКРОТЕРМОСТАТ ДЛЯ ОХЛАЖДЕНИЯ БОЛОМЕТРОВ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКИЙ ОХЛАДИТЕЛЬ ДЛЯ РАДИАЦИОННЫХ БАЛАНСОМЕРОВ
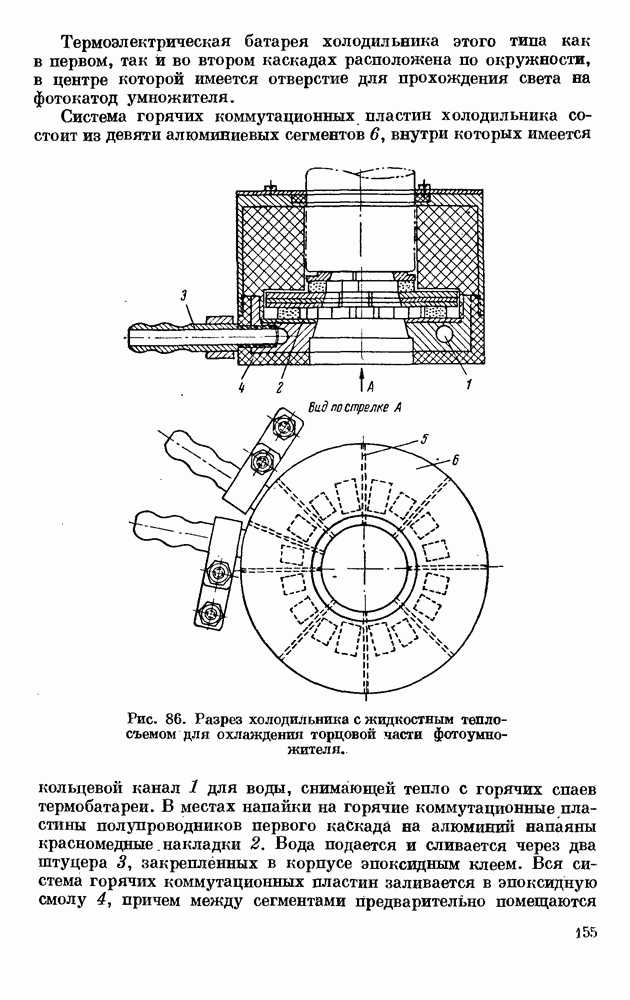
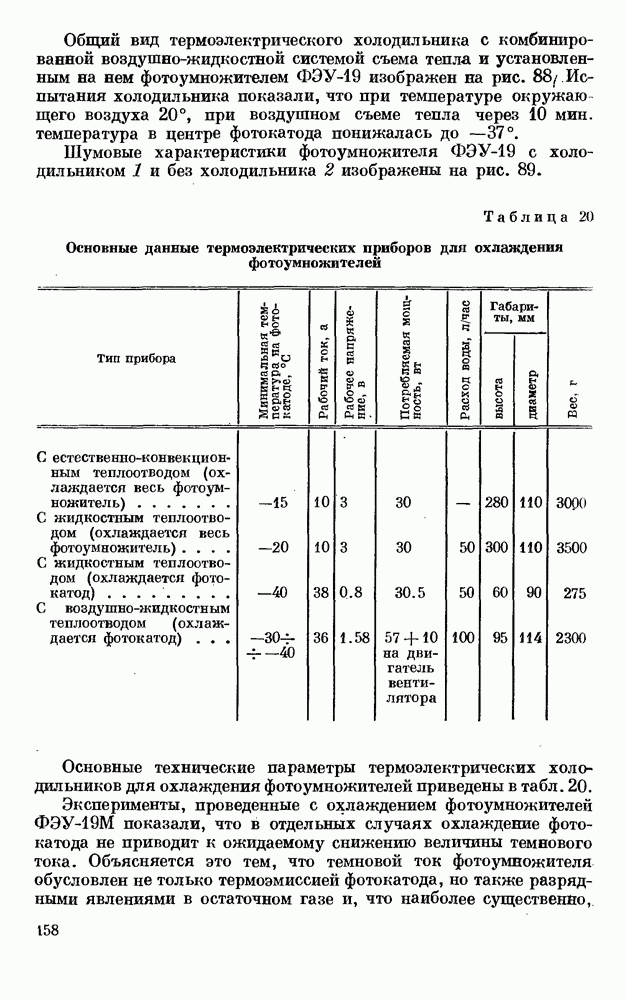
- § 4. ТЕРМОЭЛЕКТРИЧЕСКИЕ ХОЛОДИЛЬНИКИ ДЛЯ ФОТОУМНОЖИТЕЛЕЙ
- Глава XII. ТЕРМОЭЛЕКТРИЧЕСКИЕ ОХЛАЖДАЮЩИЕ ПРИБОРЫ ДЛЯ МЕДИЦИНЫ
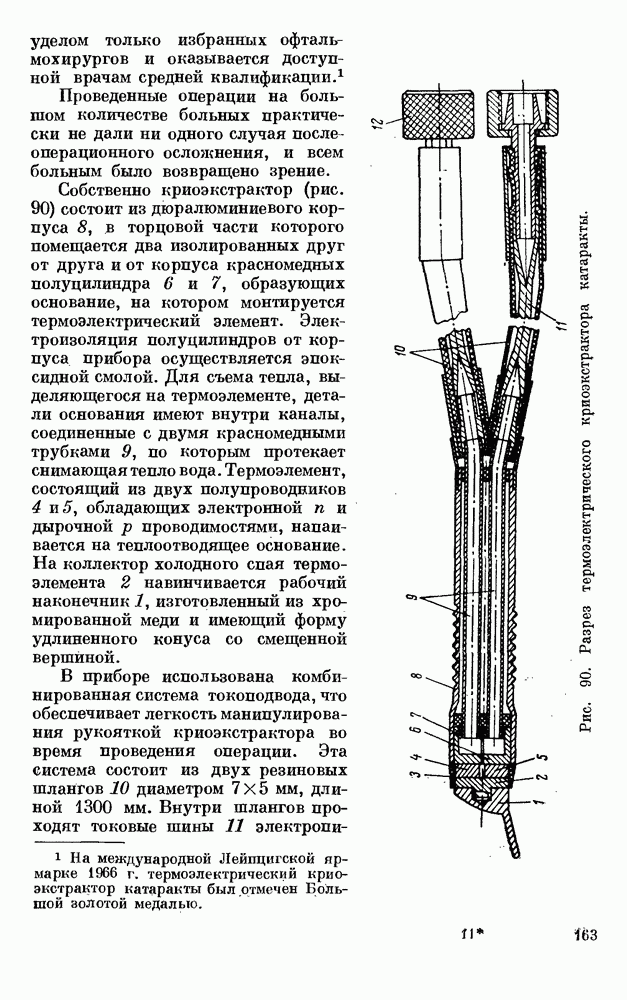
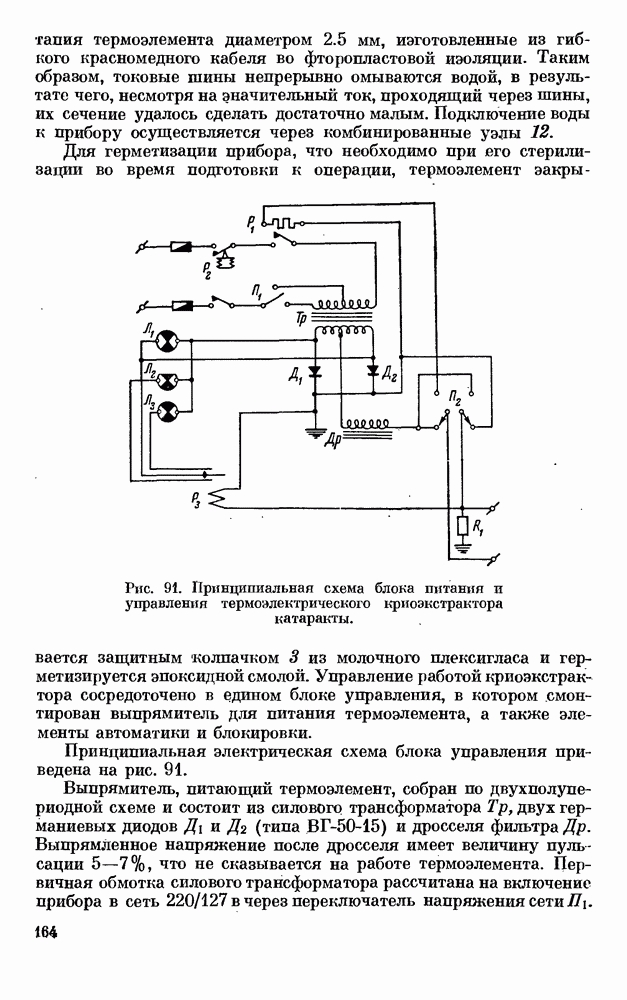
- § 1. ТЕРМОЭЛЕКТРИЧЕСКИЙ КРИОЭКСТРАКТОР КАТАРАКТЫ
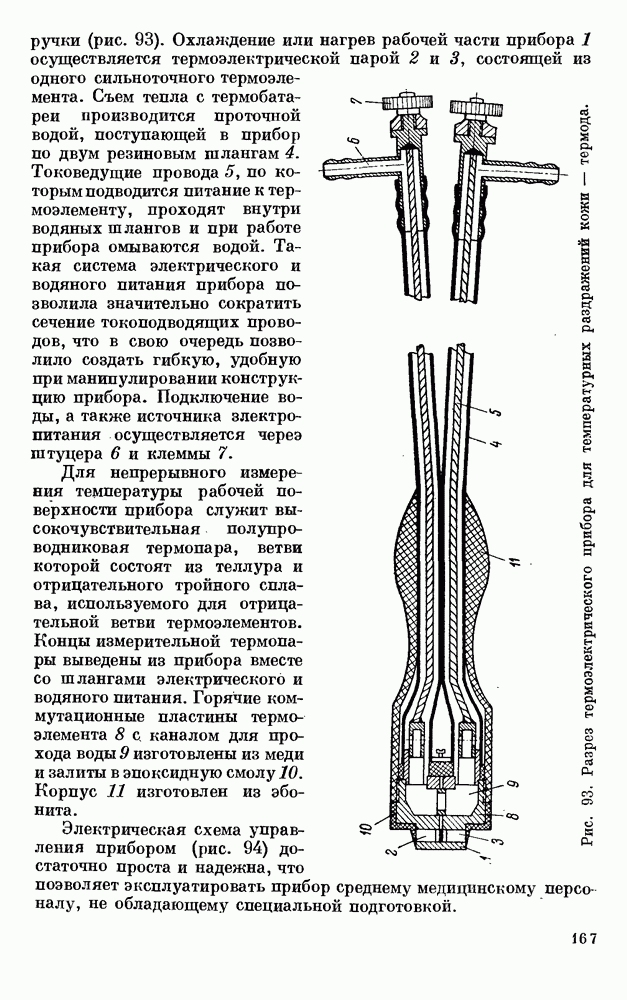
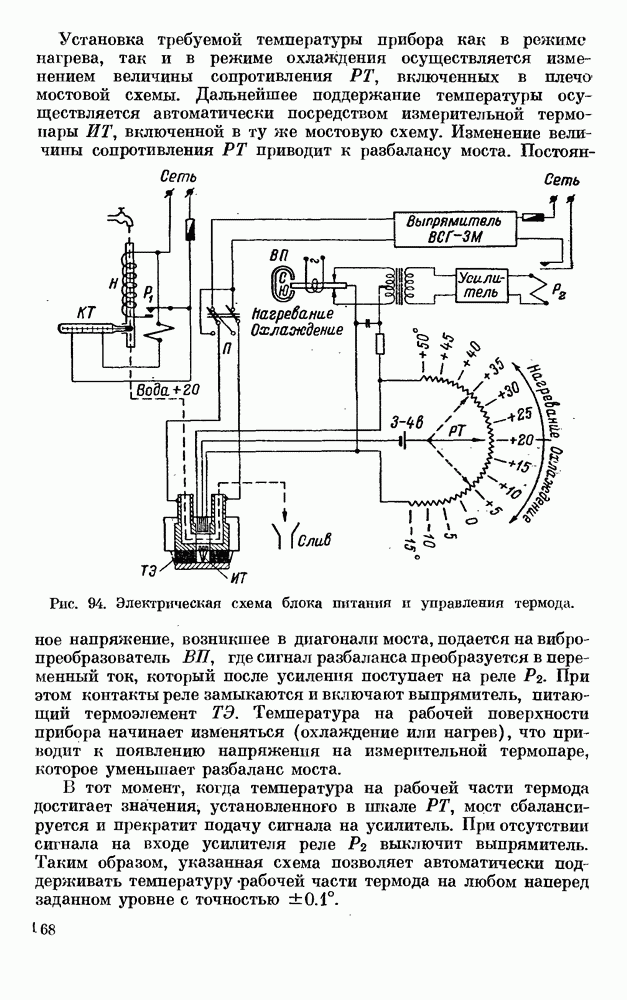
- § 2. ПРИБОР ДЛЯ ТЕМПЕРАТУРНЫХ РАЗДРАЖЕНИЙ КОЖИ — ТЕРМОД
- § 3. МИКРОХОЛОДИЛЬНИК ДЛЯ ЛЕЧЕНИЯ КОЖНЫХ ЗАБОЛЕВАНИЙ
- § 4. МИКРОТОМНЫЕ СТОЛИКИ С ТЕРМОЭЛЕКТРИЧЕСКИМ ОХЛАЖДЕНИЕМ
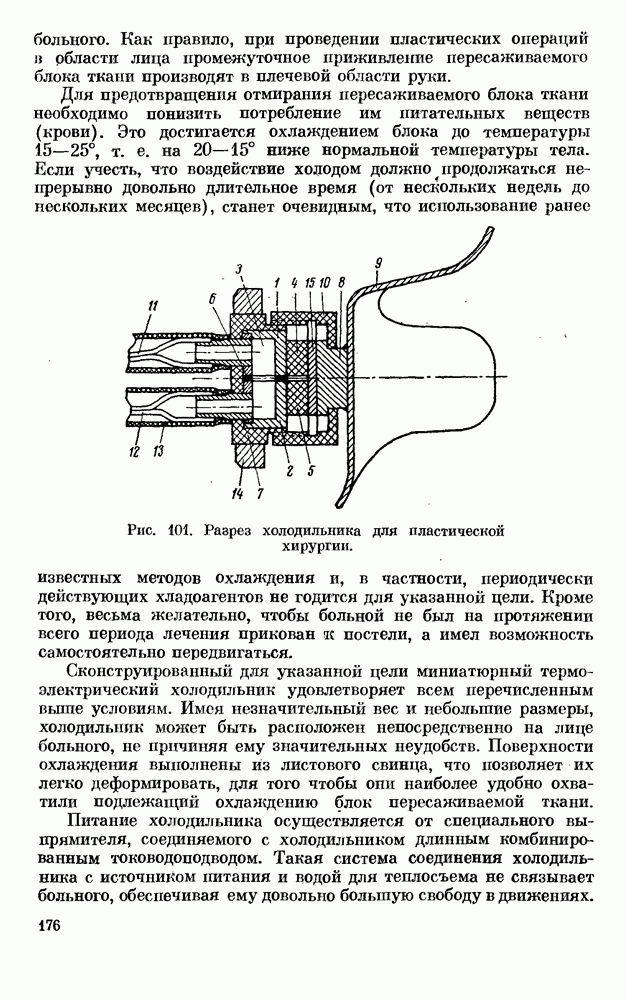
- § 5. ХОЛОДИЛЬНИК ДЛЯ ПЛАСТИЧЕСКОЙ ХИРУРГИИ
- Глава XIII. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ ДЛЯ РАДИОЭЛЕКТРОНИКИ
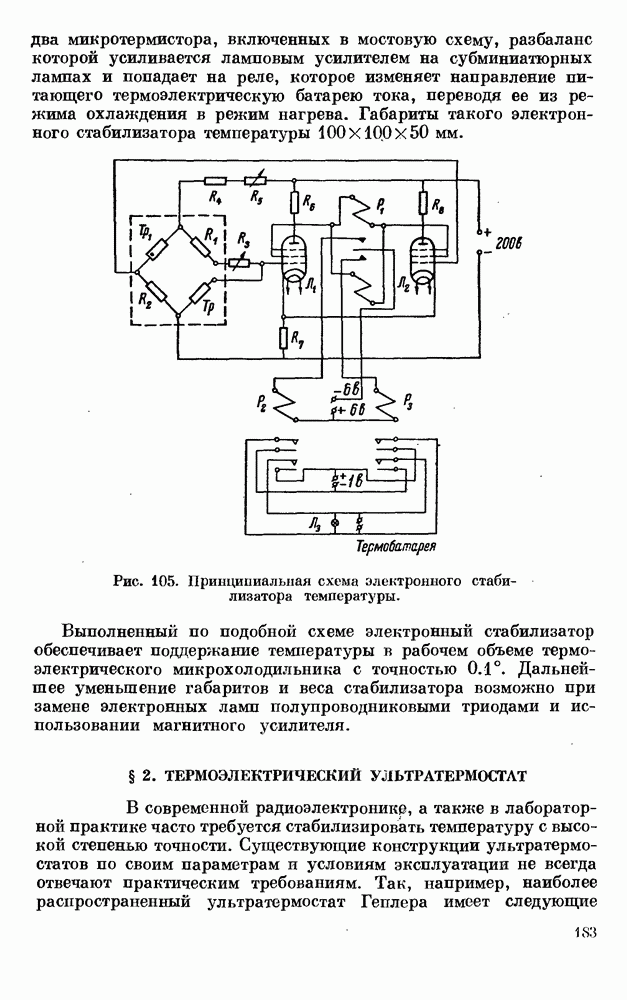
- § 2. ТЕРМОЭЛЕКТРИЧЕСКИЙ УЛЬТРАТЕРМОСТАТ
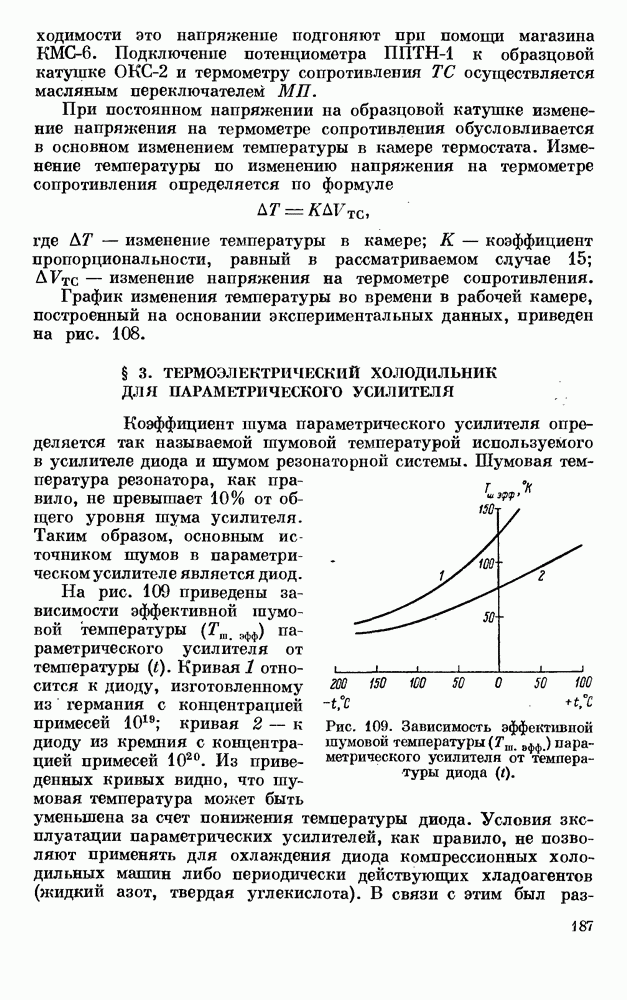
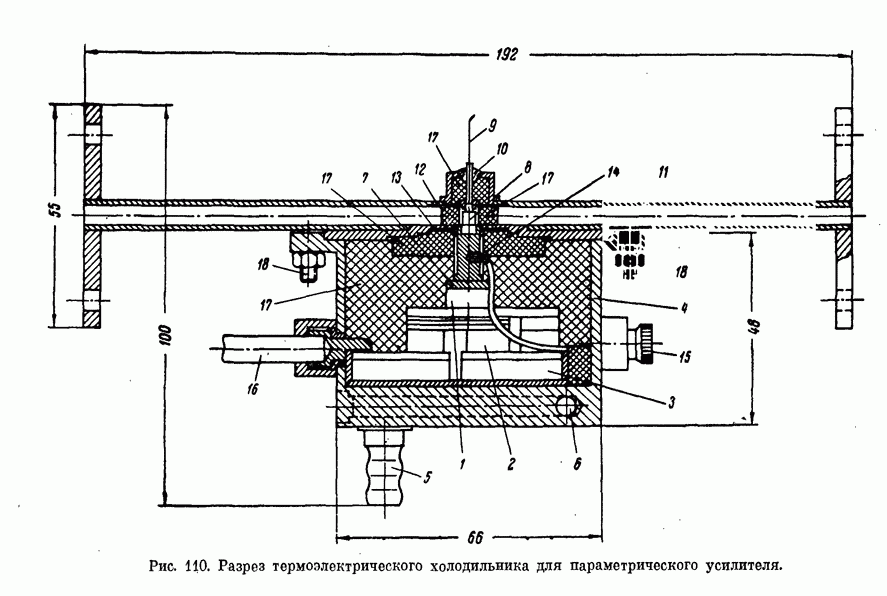
- § 3. ТЕРМОЭЛЕКТРИЧЕСКИЙ ХОЛОДИЛЬНИК ДЛЯ ПАРАМЕТРИЧЕСКОГО УСИЛИТЕЛЯ
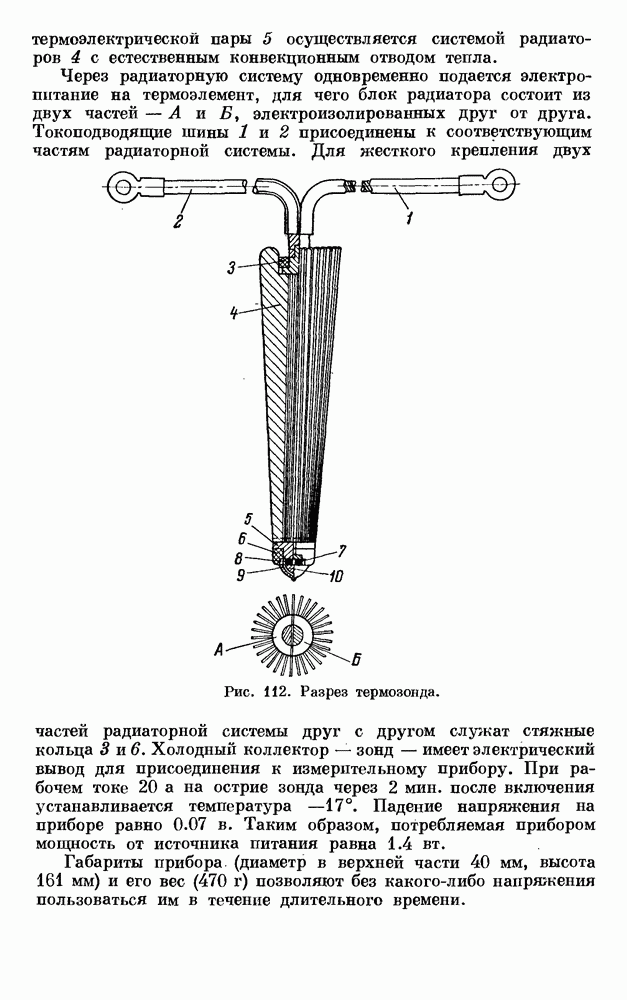
- § 4. ТЕРМОЗОНД
- Глава XIV. ТЕРМОЭЛЕКТРИЧЕСКИЕ ХОЛОДИЛЬНИКИ ОБЩЕГО НАЗНАЧЕНИЯ
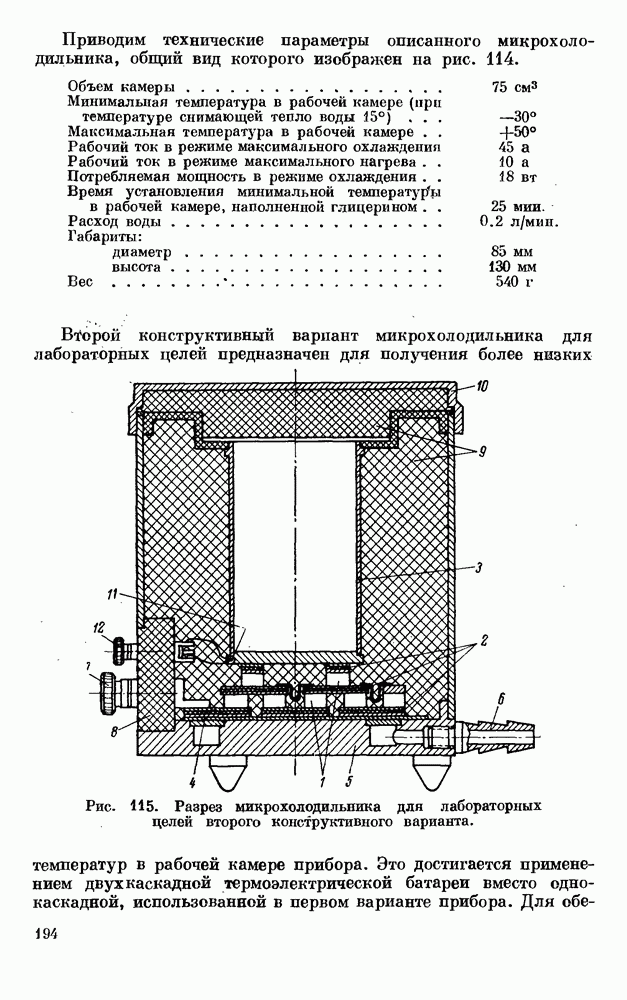
- § 1. МИКРОХОЛОДИЛЬНИКИ ДЛЯ ЛАБОРАТОРНЫХ ЦЕЛЕЙ
- § 2. ИСПЫТАТЕЛЬНЫЕ ТЕРМОЭЛЕКТРИЧЕСКИЕ МИКРОКАМЕРЫ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКИЕ КОНДЕНСАЦИОННЫЕ ГИГРОМЕТРЫ
- § 4. ПРИБОР ДЛЯ ТАРИРОВАНИЯ ТЕРМОМЕТРОВ
- § 5. ТЕРМОЭЛЕКТРИЧЕСКИЕ НУЛЬ-ТЕРМОСТАТЫ
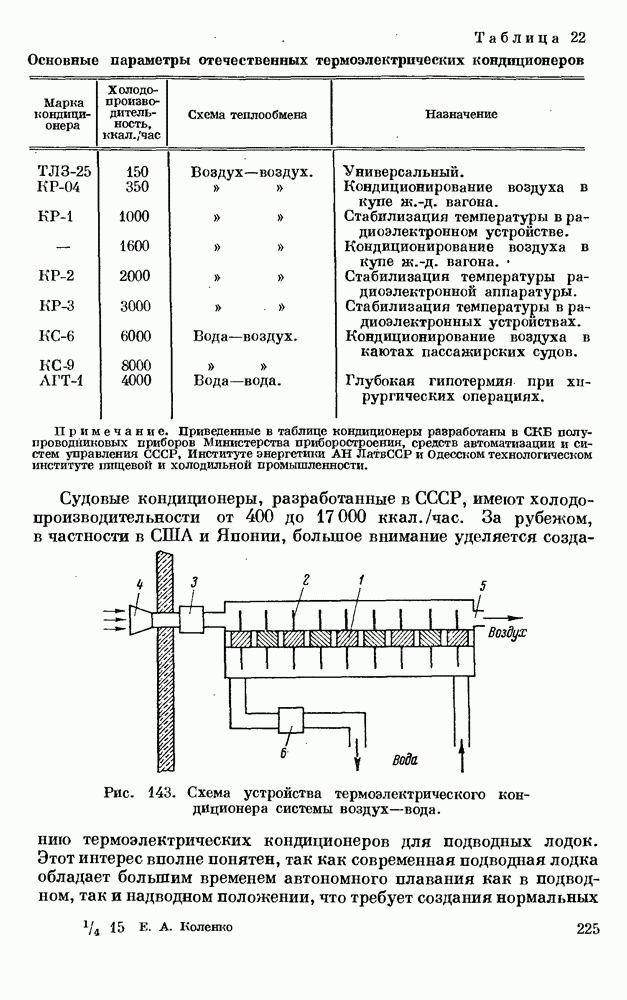
- § 6. МИКРОСКОПНЫЕ ПРЕДМЕТНЫЕ СТОЛИКИ С РЕГУЛИРУЕМОЙ ТЕМПЕРАТУРОЙ
- Глава XV. ТЕРМОЭЛЕКТРИЧЕСКИЕ КОНДИЦИОНЕРЫ И ДОМАШНИЕ ХОЛОДИЛЬНИКИ
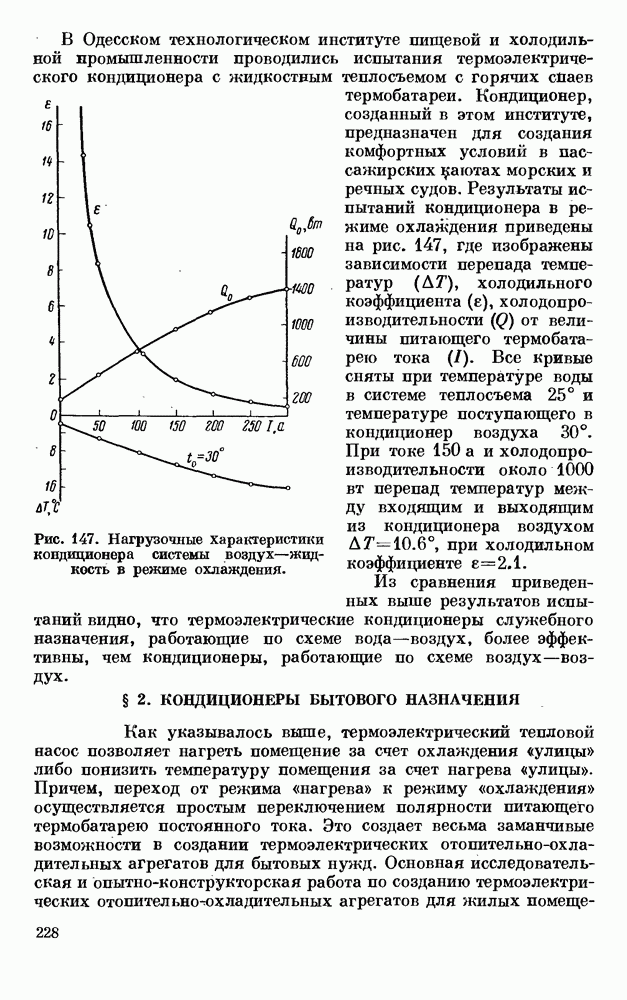
- § 1. КОНДИЦИОНЕРЫ СЛУЖЕБНОГО НАЗНАЧЕНИЯ
- § 2. КОНДИЦИОНЕРЫ БЫТОВОГО НАЗНАЧЕНИЯ
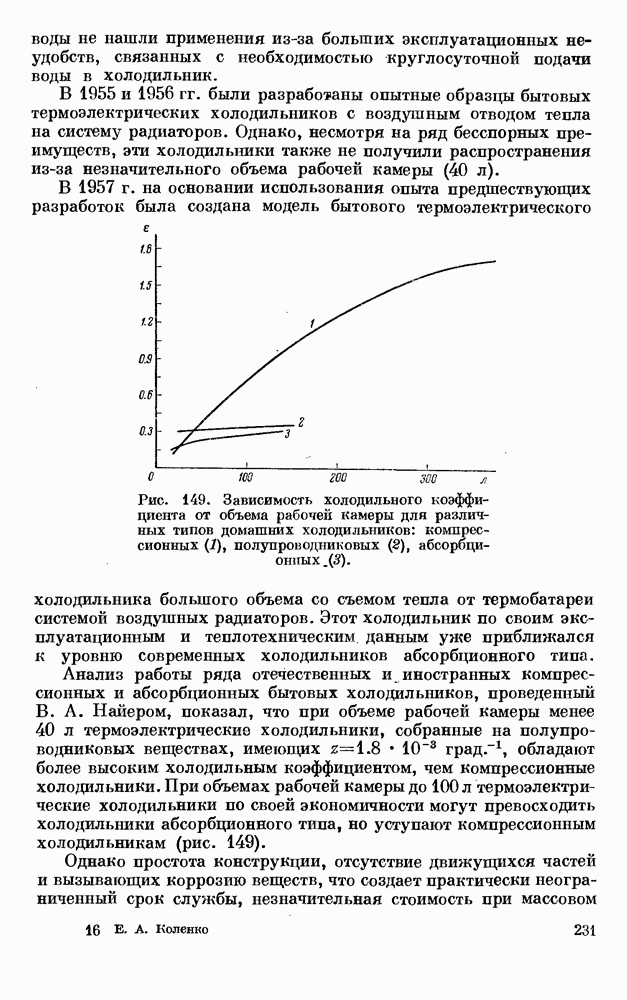
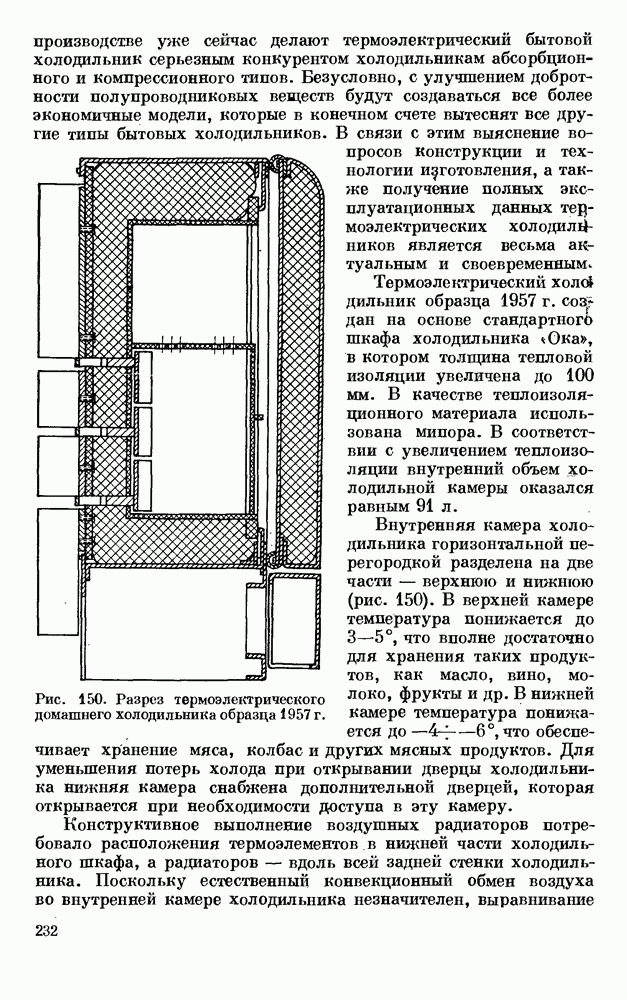
- § 3. ДОМАШНИЕ ХОЛОДИЛЬНИКИ БОЛЬШОГО ОБЪЕМА
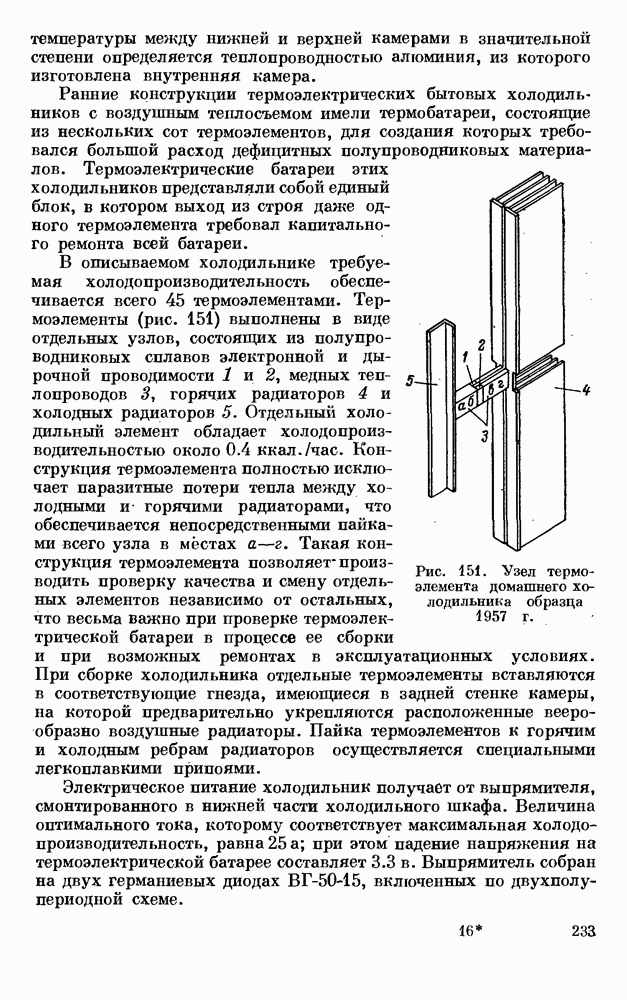
- § 4. ДОМАШНИЙ ХОЛОДИЛЬНИК МАЛОГО ОБЪЕМА
- Глава XVI. ПРИБОРЫ РАЗНОГО НАЗНАЧЕНИЯ
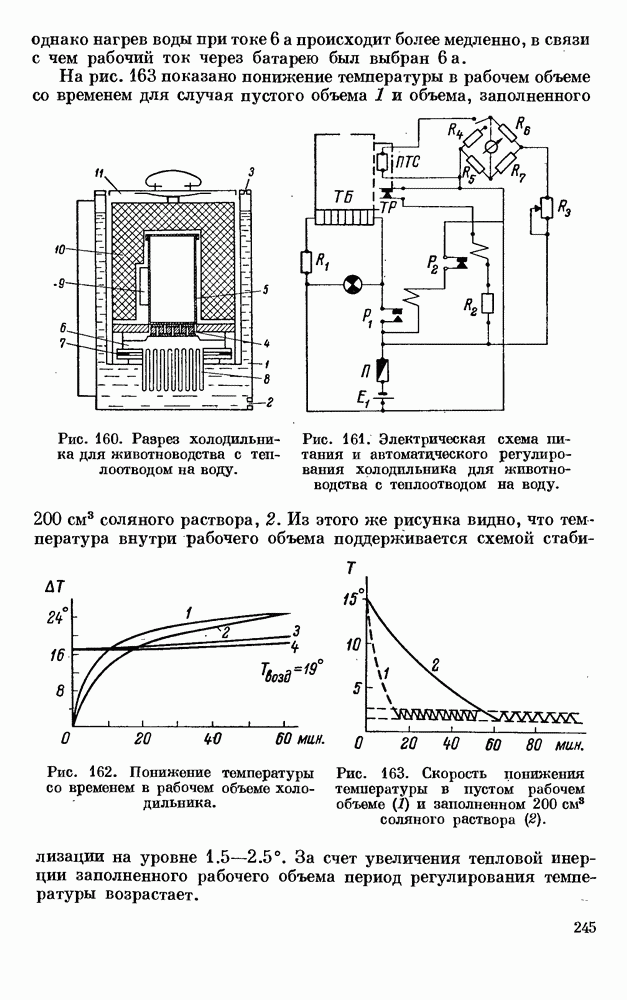
- § 1. ХОЛОДИЛЬНИКИ ДЛЯ ЖИВОТНОВОДСТВА
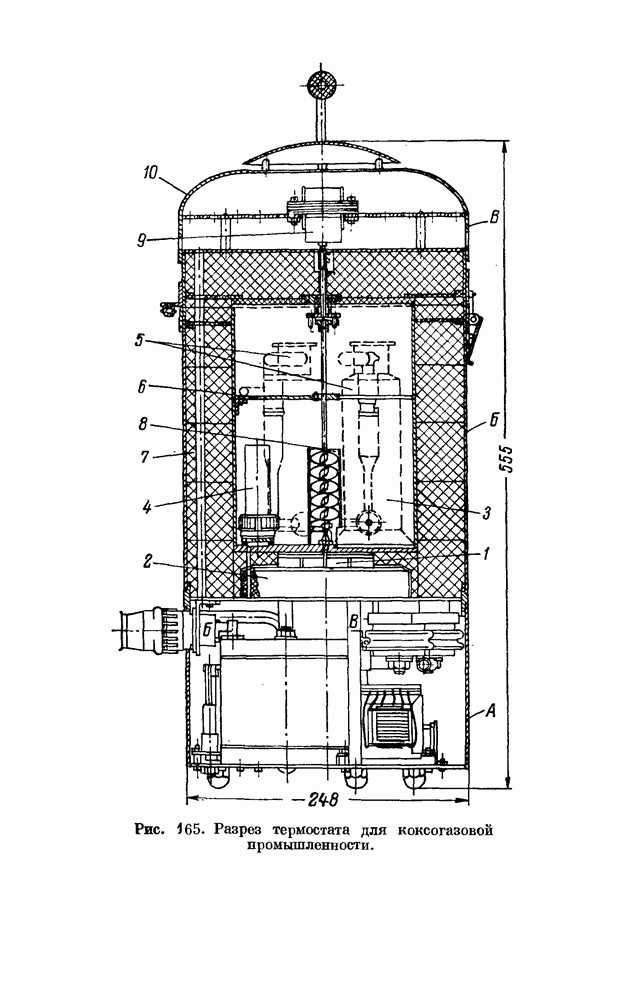
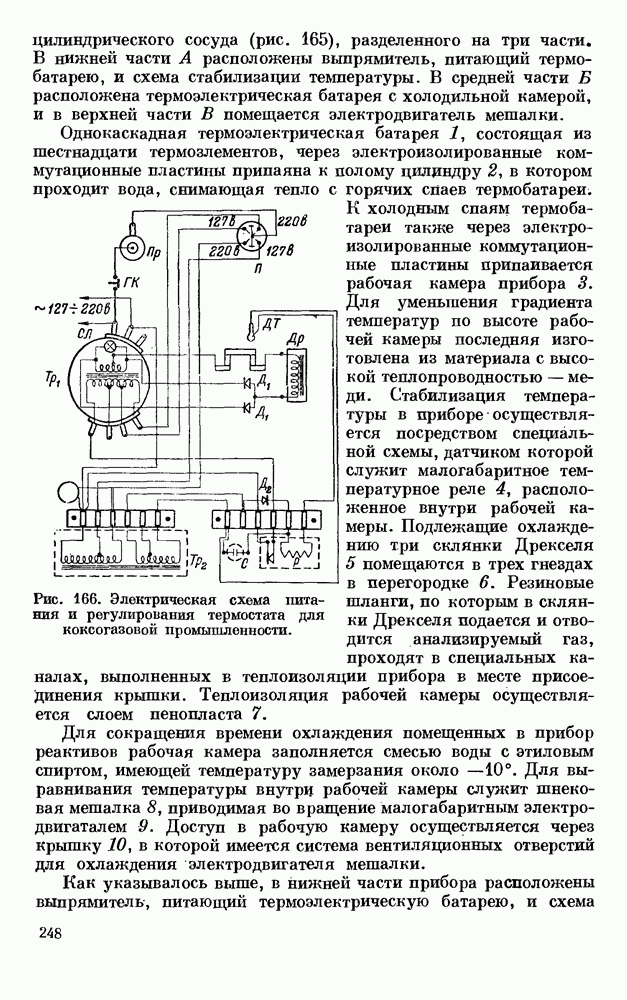
- § 2. ТЕРМОСТАТ ДЛЯ КОКСОГАЗОВОЙ ПРОМЫШЛЕННОСТИ
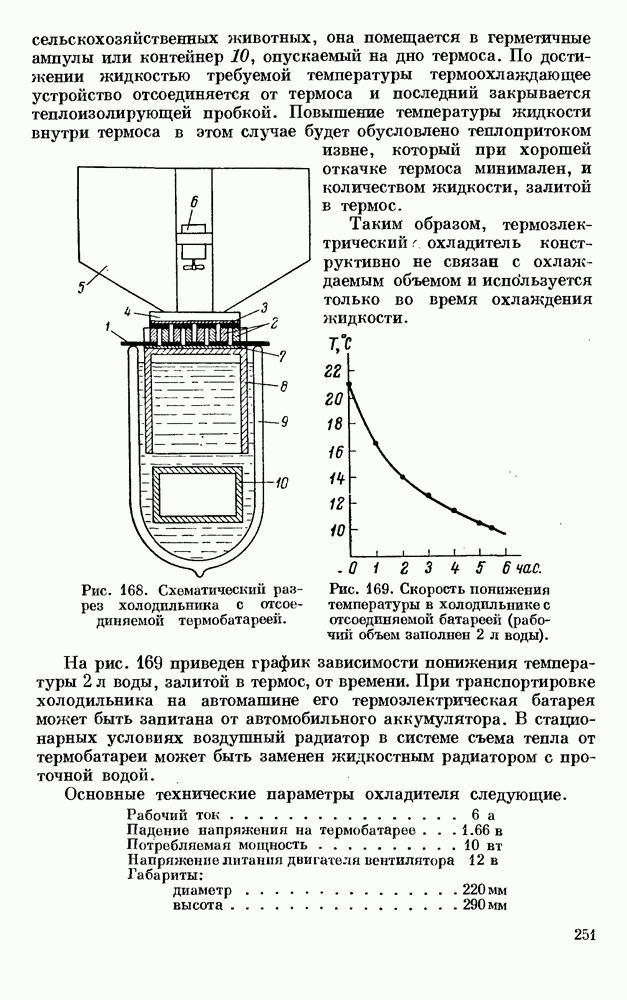
- § 3. ХОЛОДИЛЬНИК С ОТСОЕДИНЯЕМОЙ ТЕРМОБАТАРЕЕЙ
- § 4. ТЕРМОЭЛЕКТРИЧЕСКИЙ СТАБИЛИЗАТОР ТЕМПЕРАТУРЫ ФОТОРАСТВОРОВ
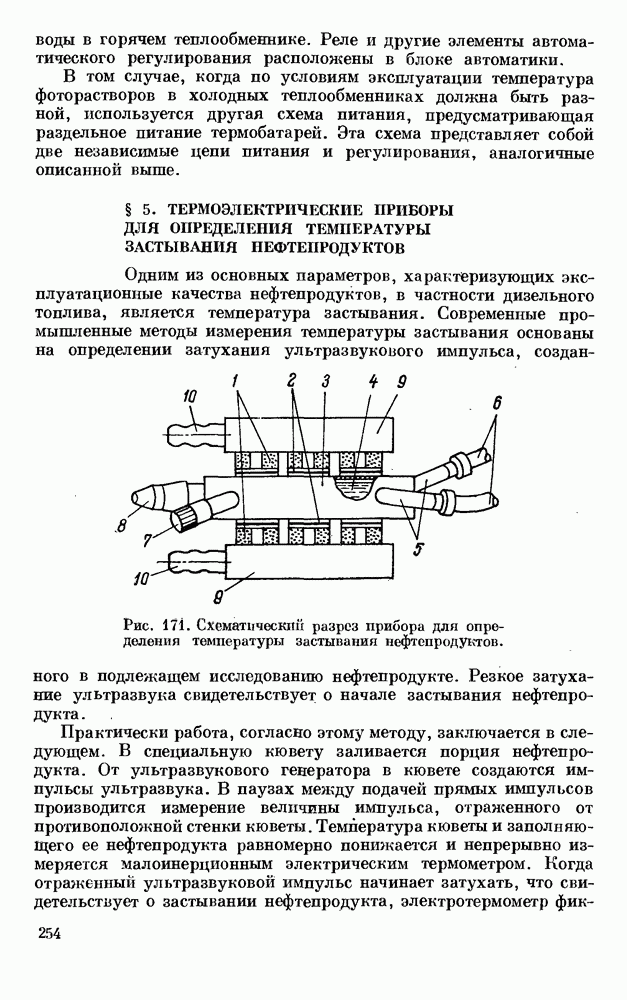
- § 5. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ ДЛЯ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ ЗАСТЫВАНИЯ НЕФТЕПРОДУКТОВ
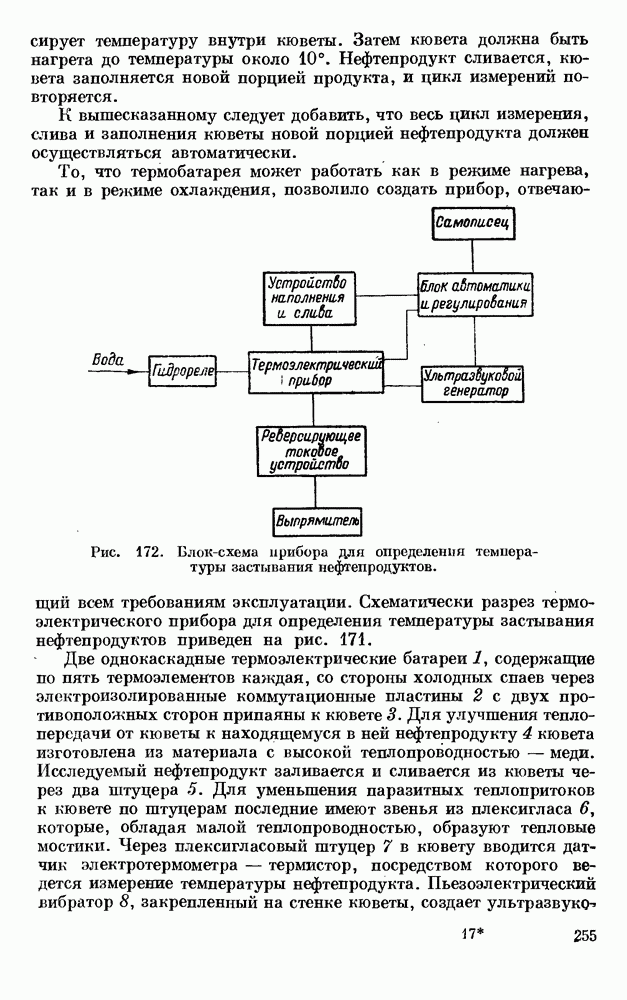
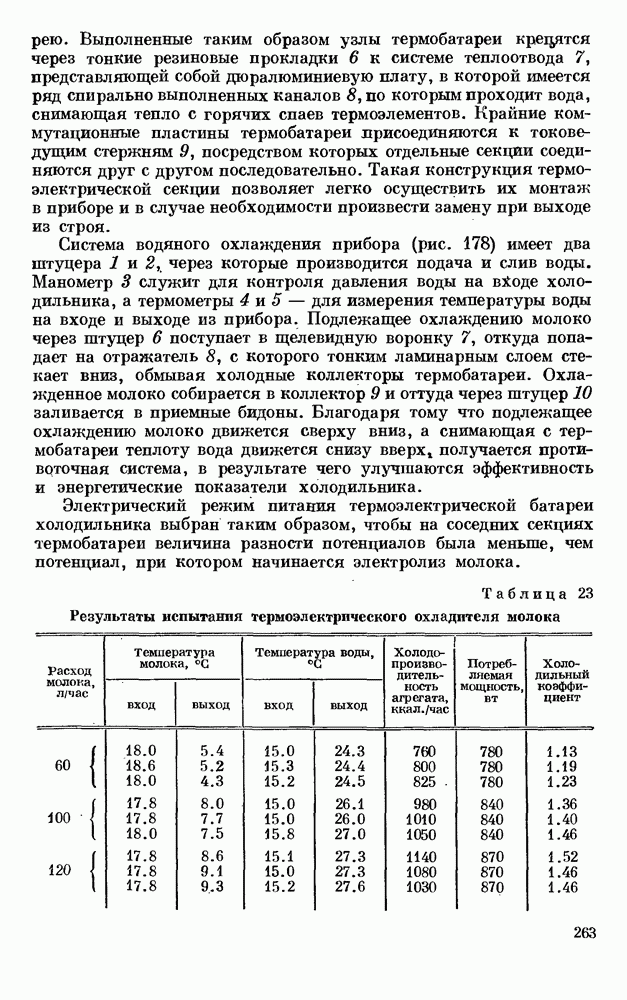
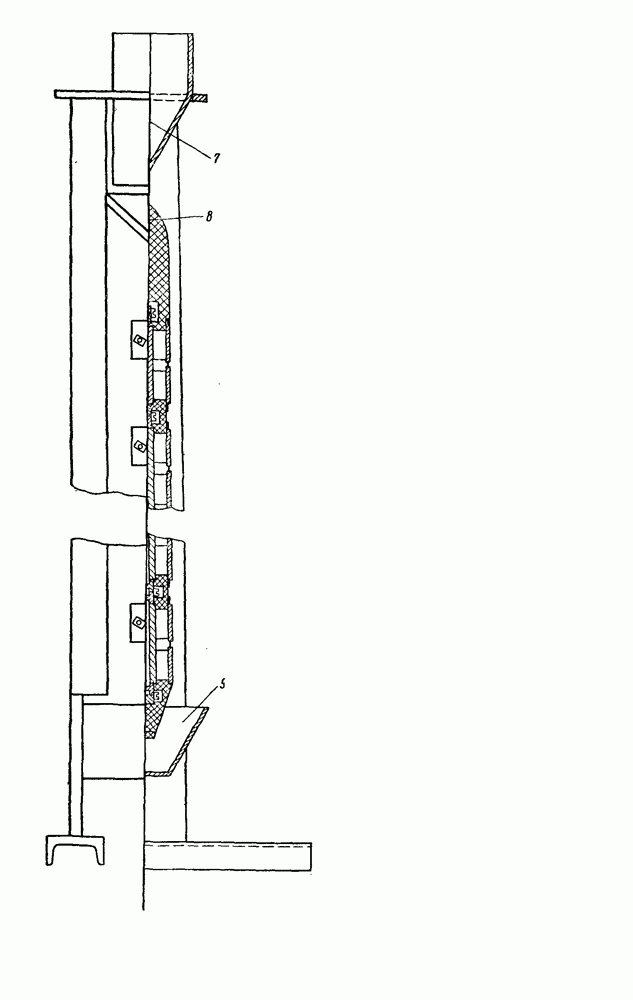
- § 6. ТЕРМОЭЛЕКТРИЧЕСКИЙ ОХЛАДИТЕЛЬ МОЛОКА
- § 7. ТЕРМОЭЛЕКТРИЧЕСКИЙ ОХЛАДИТЕЛЬ ПИТЬЕВОЙ ВОДЫ