| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
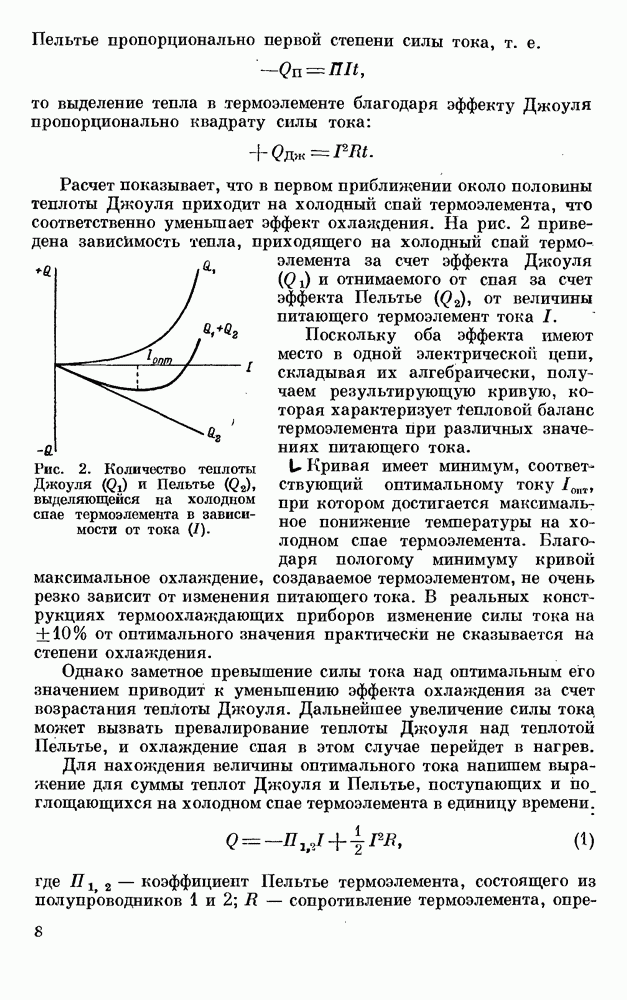
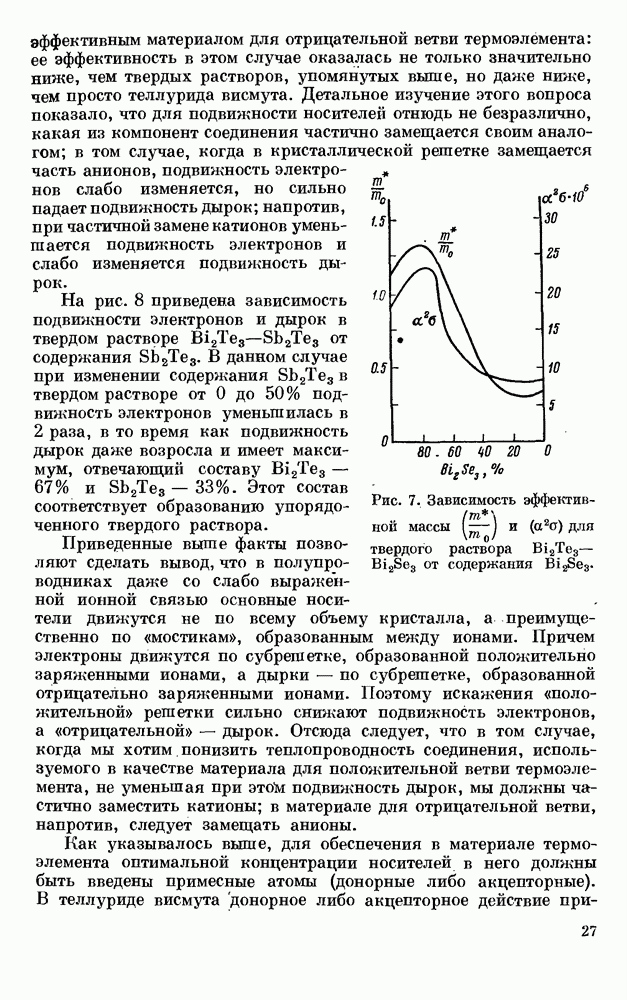
§ 3. ОТСТУПЛЕНИЯ ОТ ОПТИМАЛЬНЫХ УСЛОВИЙ
Выше мы нашли соотношение сечений ветвей термо-элемента, при котором  достигает максимального значения; были также найдены оптимальная электропроводность, оптимальный ток и т. д.
достигает максимального значения; были также найдены оптимальная электропроводность, оптимальный ток и т. д.
На практике в силу трудно контролируемых отклонений от технологического процесса ни одно из этих условий точно не выполняется. Поэтому важно установить, в какой мере отступления от оптимальных условий влияют на эффективность работы охлаждающего устройства.
Отступление от оптимального соотношения, сечений ветвей
Как указывалось выше,  обратно пропорционально произведению сопротивления термоэлемента на его теплопроводность:
обратно пропорционально произведению сопротивления термоэлемента на его теплопроводность:

где

достигает минимального значения при определенном соотношении сечений ветвей 

при

Выясним, насколько отступления от (63) влияют на  Согласно (62) и (64),
Согласно (62) и (64),

поделив числитель и знаменатель правой части (65) на  получим
получим

где коэффициент

а в подавляющем большинстве случаев с большой степенью точности равен 2.
Таким образом,

полагая, например,  получим
получим

Отступление от оптимальной концентрации носителей
Согласно (34), числитель  выражения для
выражения для  достигает максимального значения при определенной концентрации носителей и электропроводности. Выясним, насколько понизится эффективность термоэлемента, если электропроводность ветвей будет несколько отличаться от оптимального значения.
достигает максимального значения при определенной концентрации носителей и электропроводности. Выясним, насколько понизится эффективность термоэлемента, если электропроводность ветвей будет несколько отличаться от оптимального значения.
Простые вычисления, которые мы опускаем, дают следующий результат:

Соотношение (69) показывает, что зависимость  а следовательно, и
а следовательно, и  от
от  вблизи точки
вблизи точки  носит тот же характер, что и зависимость
носит тот же характер, что и зависимость  от
от  вблизи точки
вблизи точки  например, изменение
например, изменение  на
на  вызывает уменьшение
вызывает уменьшение  всего на
всего на 
Отступление от оптимального значения силы тока
При работе термоэлемента в условиях полной тепловой изоляции холодного спая, согласно (1) и (5),

Разлагая  в ряд Тейлора вблизи точки
в ряд Тейлора вблизи точки  получим после простых преобразований -
получим после простых преобразований -

Согласно (70), отступление плотности тока от оптимального значения на  обусловливает снижение
обусловливает снижение  на
на 
О значении z при отличающихся параметрах ветвей
Представляет интерес решить еще один вопрос. Предположим, что параметры ветвей термоэлемента неодинаковы:

и выясним, насколько  вычисленное согласно (11), меньше, чем
вычисленное согласно (11), меньше, чем  т. е. насколько показатели термоэлемента в целом хуже показателей лучшей ветви. Введем обозначения:
т. е. насколько показатели термоэлемента в целом хуже показателей лучшей ветви. Введем обозначения:

тогда

чем меньше удельное сопротивление данного материала, тем Меньше для него  в пределе эта величина стремится к постоянной в законе Видемана-Франца. Следовательно, чтобы худшая ветвь не снизила значительно
в пределе эта величина стремится к постоянной в законе Видемана-Франца. Следовательно, чтобы худшая ветвь не снизила значительно  мы должны таким образом подобрать концентрации носителей, чтобы выполнилось неравенство
мы должны таким образом подобрать концентрации носителей, чтобы выполнилось неравенство 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Часть I. ТЕОРИЯ ТЕРМОЭЛЕКТРИЧЕСКОГО ОХЛАЖДЕНИЯ
- § 1. МАКСИМАЛЬНОЕ ПОНИЖЕНИЕ ТЕМПЕРАТУРЫ
- § 2. ХОЛОДИЛЬНЫЙ КОЭФФИЦИЕНТ
- § 3. МНОГОКАСКАДНЫЕ ТЕРМОБАТАРЕИ
- Глава II. МАТЕРИАЛЫ ДЛЯ ТЕРМОЭЛЕМЕНТОВ
- § 1. УСЛОВИЯ МАКСИМАЛЬНОЙ ЭФФЕКТИВНОСТИ ТЕРМОЭЛЕМЕНТА
- § 2. ВЫБОР МАТЕРИАЛОВ ДЛЯ ВЕТВЕЙ ТЕРМОЭЛЕМЕНТОВ
- § 3. ТЕЛЛУРИД ВИСМУТА КАК МАТЕРИАЛ ДЛЯ ТЕРМОЭЛЕМЕНТА
- Глава III. УЧЕТ ДОПОЛНИТЕЛЬНЫХ ФАКТОРОВ
- § 1. УЧЕТ ЭЛЕКТРОННОЙ ТЕПЛОПРОВОДНОСТИ
- § 2. УЧЕТ ТЕПЛОТЫ ТОМСОНА В ЭНЕРГЕТИЧЕСКОМ БАЛАНСЕ ТЕРМОЭЛЕМЕНТА
- § 3. ОТСТУПЛЕНИЯ ОТ ОПТИМАЛЬНЫХ УСЛОВИЙ
- Глава IV. ТЕРМОГАЛЬВАНОМАГНИТНЫЕ МЕТОДЫ ОХЛАЖДЕНИЯ
- § 2. ТЕРМОЭЛЕКТРИЧЕСКОЕ ОХЛАЖДЕНИЕ В МАГНИТНОМ ПОЛЕ
- § 3. ТЕРМОМАГНИТНОЕ ОХЛАЖДЕНИЕ (ЭФФЕКТ ЭТТИНГСГАУЗЕНА)
- Часть II. ИНЖЕНЕРНЫЕ ВОПРОСЫ ТЕХНИКИ ТЕРМОЭЛЕКТРИЧЕСКОГО ОХЛАЖДЕНИЯ
- Глава V. ОСНОВЫ РАСЧЕТА ТЕРМОЭЛЕКТРИЧЕСКИХ ОХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. РАСЧЕТ ТЕРМОБАТАРЕИ
- § 3. РАСЧЕТ РАДИАТОРА ТЕПЛОСЪЕМА
- Глава VI. КОНСТРУКТИВНЫЕ ЭЛЕМЕНТЫ ТЕРМОЭЛЕКТРИЧЕСКИХ ОХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. МНОГОКАСКАДНЫЕ ТЕРМОЭЛЕМЕНТЫ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКАЯ БАТАРЕЯ
- § 4. ТЕПЛОВОЕ СОПРЯЖЕНИЕ ТЕРМОБАТАРЕИ
- § 5. КОНСТРУКЦИИ СИСТЕМ ТЕПЛООТВОДА
- § 6. РАБОЧАЯ КАМЕРА ПРИБОРА
- Глава VII. СПОСОБЫ ОТВОДА ТЕПЛА ОТ ТЕРМООХЛАЖДАЮЩИХ ПРИБОРОВ
- § 1. РАДИАТОРНАЯ СИСТЕМА С ЕСТЕСТВЕННОКОНВЕКЦИОННЫМ ТЕПЛООБМЕНОМ
- § 2. РАДИАТОРНАЯ СИСТЕМА С ПРИНУДИТЕЛЬНЫМ ТЕПЛОСЪЕМОМ
- § 3. ИГОЛЬЧАТЫЕ РАДИАТОРНЫЕ СИСТЕМЫ
- § 4. ЖИДКОСТНАЯ СИСТЕМА С ЕСТЕСТВЕННОЙ ЦИРКУЛЯЦИЕЙ
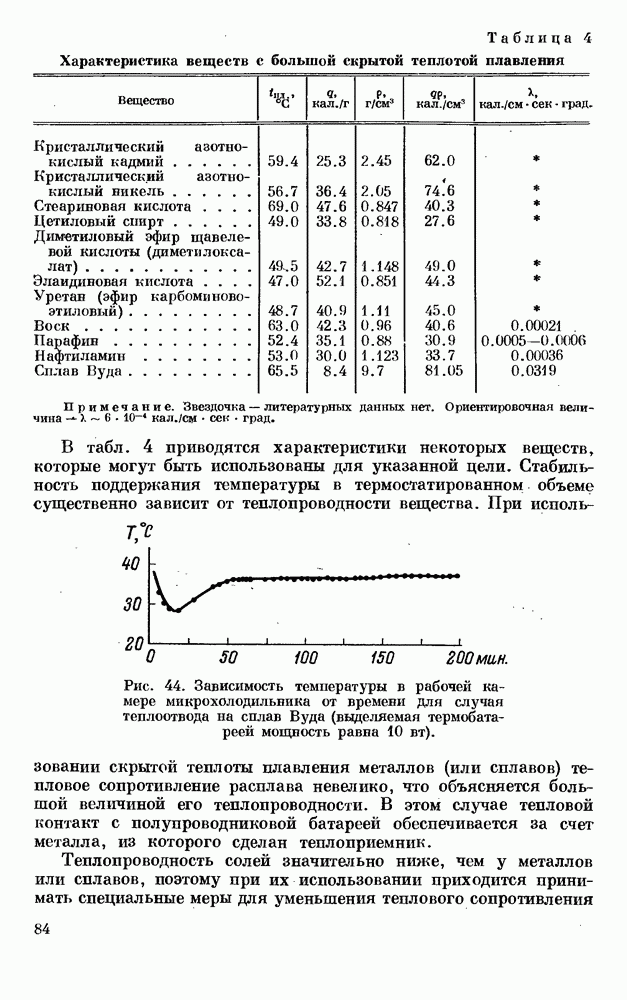
- § 5. ИСПОЛЬЗОВАНИЕ СКРЫТОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ
- § 6. ИСПОЛЬЗОВАНИЕ СКРЫТОЙ ТЕПЛОТЫ ИСПАРЕНИЯ
- § 7. ТЕПЛООТВОДЯЩАЯ СИСТЕМА С ИСПОЛЬЗОВАНИЕМ ТЕПЛОЕМКОСТИ
- § 8. ИСПОЛЬЗОВАНИЕ РАСТВОРОВ С НИЗКОЙ КРИОГИДРАТНОЙ ТЕМПЕРАТУРОЙ
- Глава VIII. ИСТОЧНИКИ ПИТАНИЯ ТЕРМОЭЛЕКТРИЧЕСКИХ ОХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. АККУМУЛЯТОРЫ
- § 3. ПРЕОБРАЗОВАТЕЛИ ТОКА
- § 4. ТЕРМОЭЛЕКТРОГЕНЕРАТОРЫ
- Глава IX. НЕКОТОРЫЕ ВОПРОСЫ ТЕХНОЛОГИИ ИЗГОТОВЛЕНИЯ ТЕРМООХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. ЗАЛУЖИВАНИЕ ВЕТВЕЙ ТЕРМОЭЛЕМЕНТОВ
- § 3. КОММУТАЦИЯ ТЕРМОБАТАРЕИ
- § 4. ПРОЧИЕ ВОПРОСЫ ТЕХНОЛОГИИ
- Часть III. ПРАКТИКА ТЕРМОЭЛЕКТРИЧЕСКОГО ОХЛАЖДЕНИЯ
- Глава X. ВЫСОКОВАКУУМНЫЕ ЛОВУШКИ С ТЕРМОЭЛЕКТРИЧЕСКИМ ОХЛАЖДЕНИЕМ
- § 2. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЛОВУШКИ ДЛЯ ЕДИНОЙ СЕРИИ НАСОСОВ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКАЯ ЛОВУШКА ДЛЯ ПАРОРТУТНЫХ НАСОСОВ
- § 4. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЛОВУШКИ ДЛЯ ОТКАЧНЫХ АВТОМАТОВ
- Глава XI. ТЕРМОЭЛЕКТРИЧЕСКИЕ ОХЛАДИТЕЛИ ПРИЕМНИКОВ ЛУЧИСТОЙ ЭНЕРГИИ
- § 1. МИКРОТЕРМОСТАТЫ ДЛЯ ОХЛАЖДЕНИЯ ФОТОСОПРОТИВЛЕНИЙ
- § 2. МИКРОТЕРМОСТАТ ДЛЯ ОХЛАЖДЕНИЯ БОЛОМЕТРОВ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКИЙ ОХЛАДИТЕЛЬ ДЛЯ РАДИАЦИОННЫХ БАЛАНСОМЕРОВ
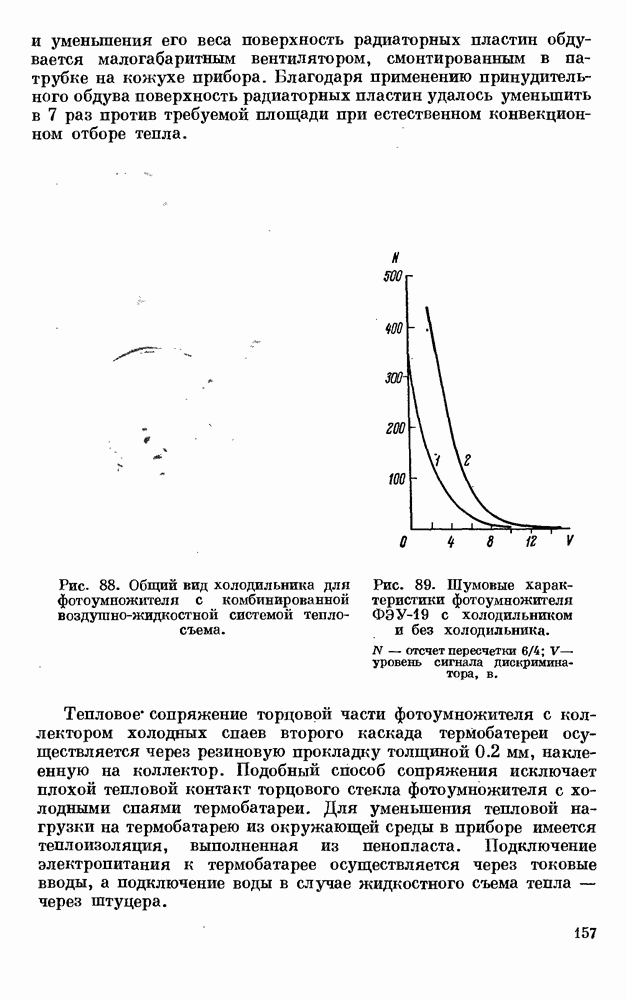
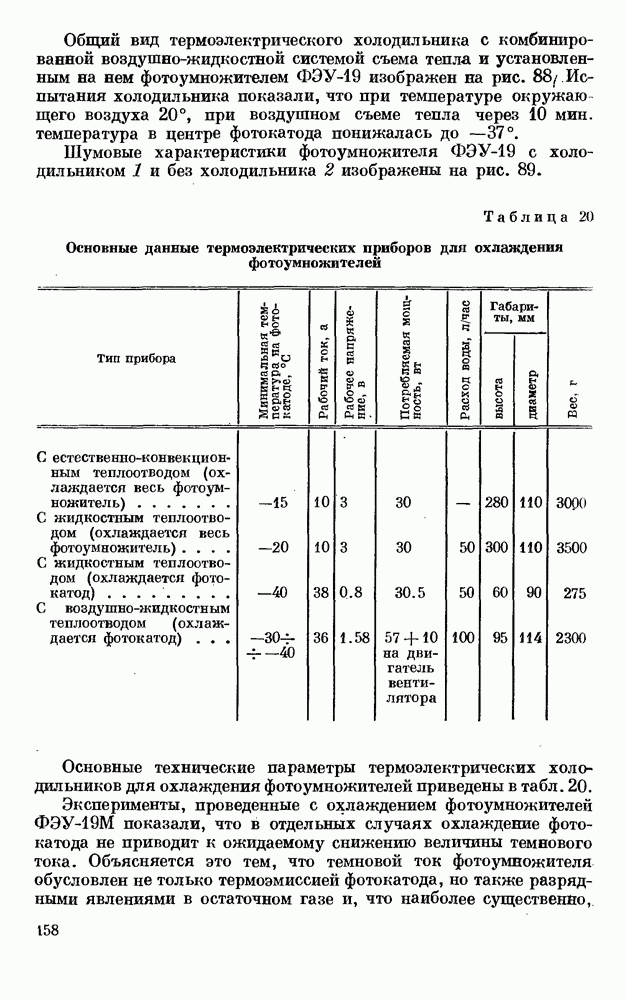
- § 4. ТЕРМОЭЛЕКТРИЧЕСКИЕ ХОЛОДИЛЬНИКИ ДЛЯ ФОТОУМНОЖИТЕЛЕЙ
- Глава XII. ТЕРМОЭЛЕКТРИЧЕСКИЕ ОХЛАЖДАЮЩИЕ ПРИБОРЫ ДЛЯ МЕДИЦИНЫ
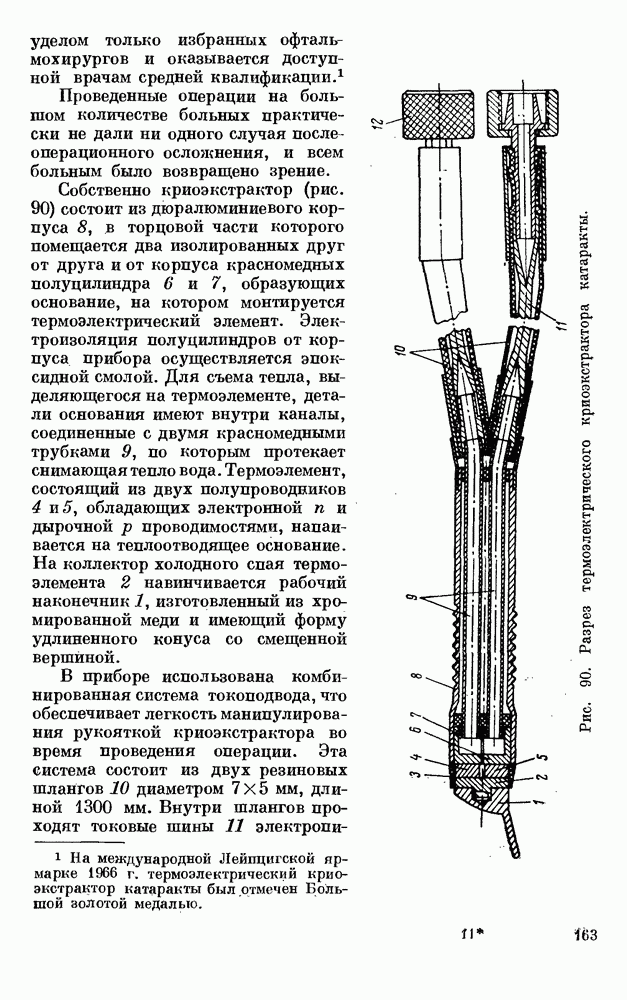
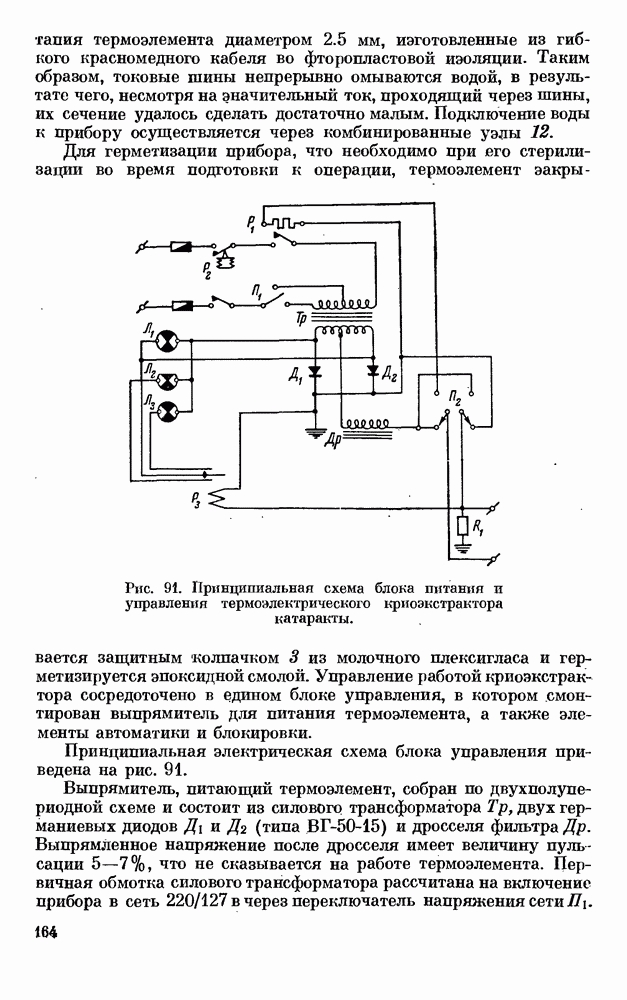
- § 1. ТЕРМОЭЛЕКТРИЧЕСКИЙ КРИОЭКСТРАКТОР КАТАРАКТЫ
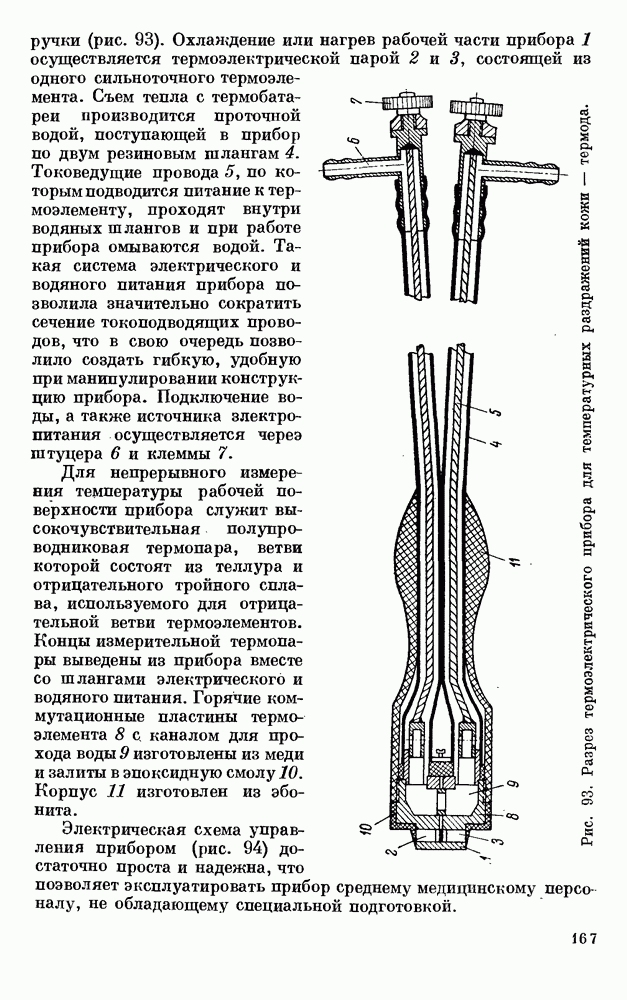
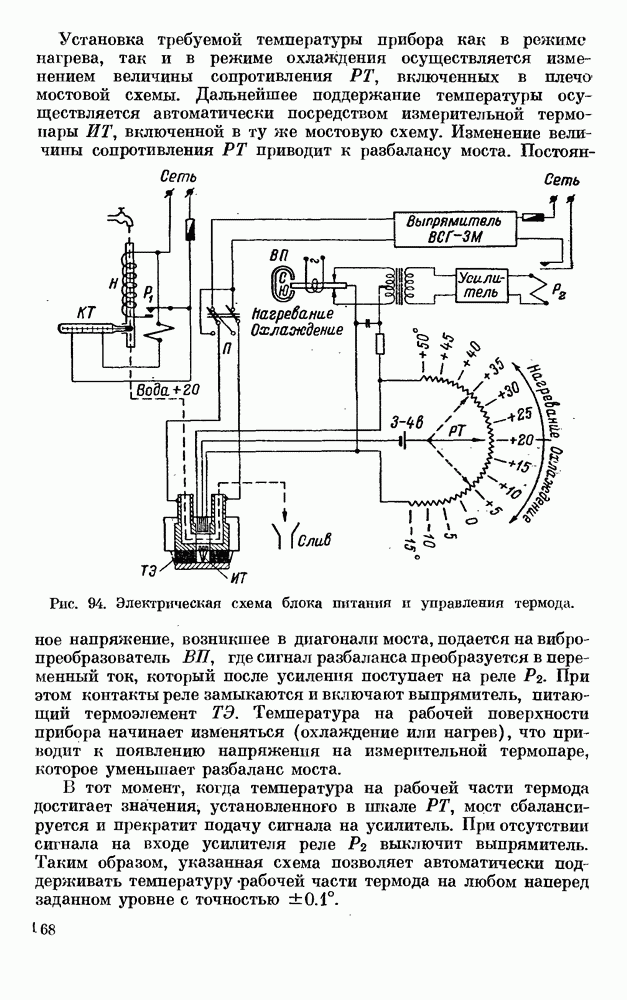
- § 2. ПРИБОР ДЛЯ ТЕМПЕРАТУРНЫХ РАЗДРАЖЕНИЙ КОЖИ — ТЕРМОД
- § 3. МИКРОХОЛОДИЛЬНИК ДЛЯ ЛЕЧЕНИЯ КОЖНЫХ ЗАБОЛЕВАНИЙ
- § 4. МИКРОТОМНЫЕ СТОЛИКИ С ТЕРМОЭЛЕКТРИЧЕСКИМ ОХЛАЖДЕНИЕМ
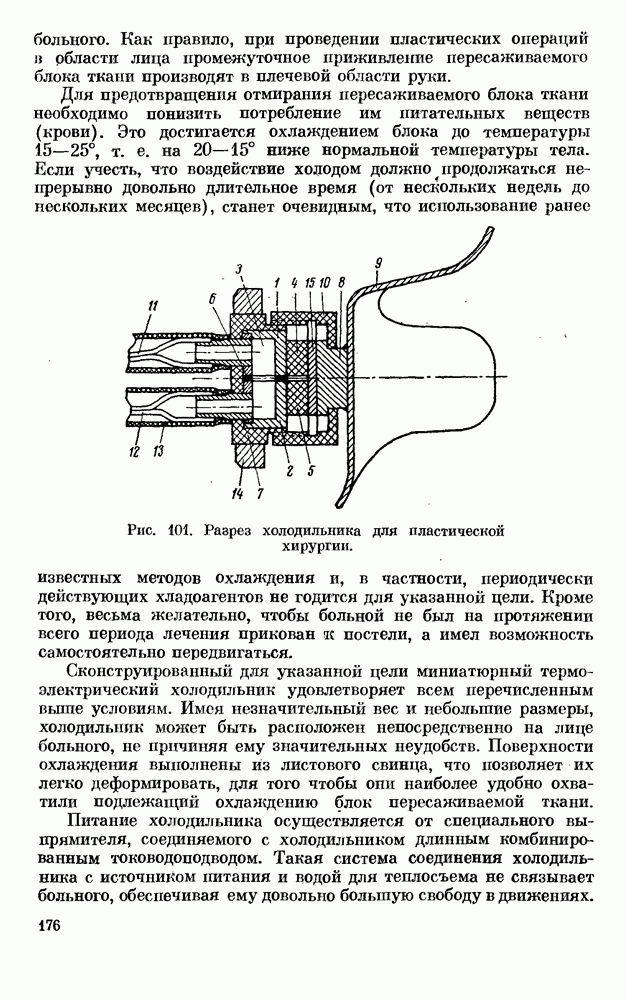
- § 5. ХОЛОДИЛЬНИК ДЛЯ ПЛАСТИЧЕСКОЙ ХИРУРГИИ
- Глава XIII. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ ДЛЯ РАДИОЭЛЕКТРОНИКИ
- § 2. ТЕРМОЭЛЕКТРИЧЕСКИЙ УЛЬТРАТЕРМОСТАТ
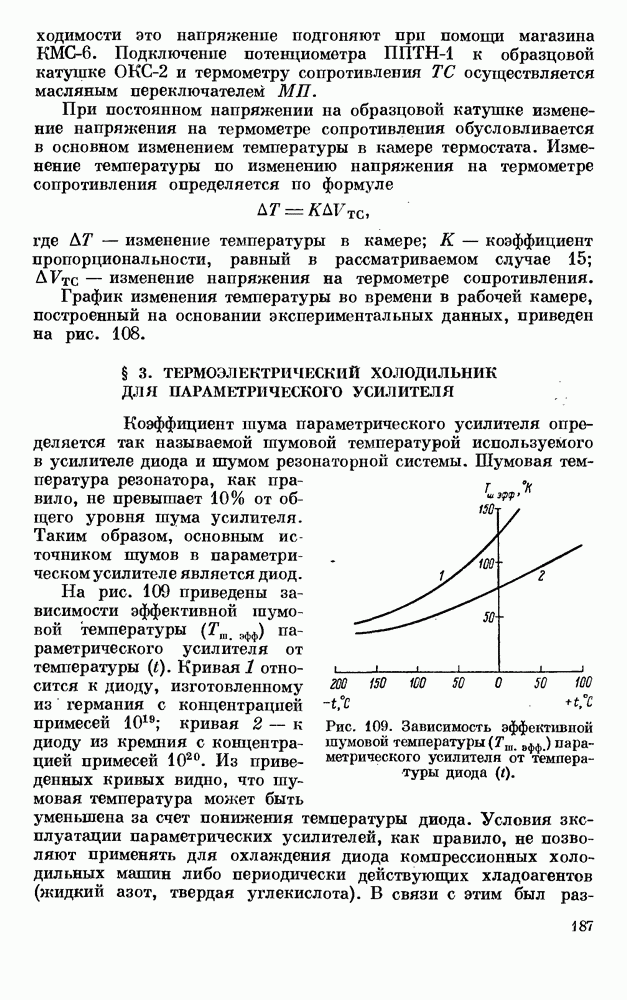
- § 3. ТЕРМОЭЛЕКТРИЧЕСКИЙ ХОЛОДИЛЬНИК ДЛЯ ПАРАМЕТРИЧЕСКОГО УСИЛИТЕЛЯ
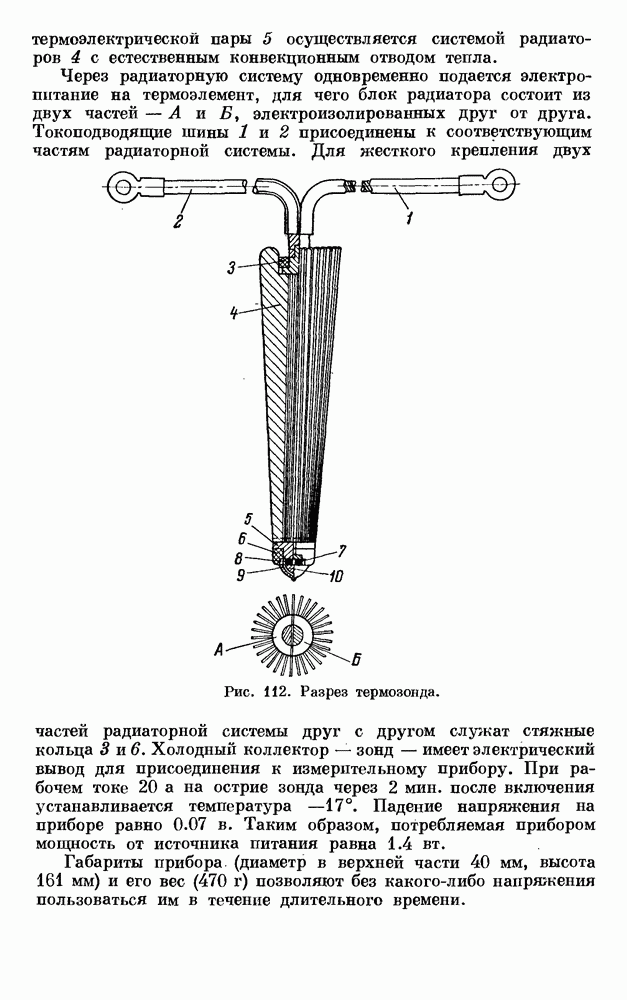
- § 4. ТЕРМОЗОНД
- Глава XIV. ТЕРМОЭЛЕКТРИЧЕСКИЕ ХОЛОДИЛЬНИКИ ОБЩЕГО НАЗНАЧЕНИЯ
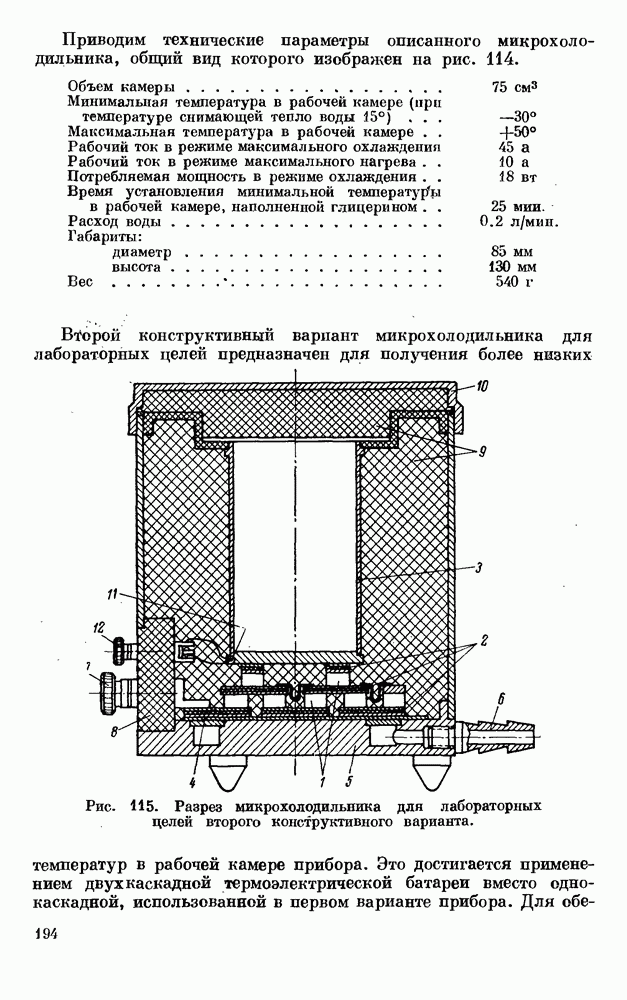
- § 1. МИКРОХОЛОДИЛЬНИКИ ДЛЯ ЛАБОРАТОРНЫХ ЦЕЛЕЙ
- § 2. ИСПЫТАТЕЛЬНЫЕ ТЕРМОЭЛЕКТРИЧЕСКИЕ МИКРОКАМЕРЫ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКИЕ КОНДЕНСАЦИОННЫЕ ГИГРОМЕТРЫ
- § 4. ПРИБОР ДЛЯ ТАРИРОВАНИЯ ТЕРМОМЕТРОВ
- § 5. ТЕРМОЭЛЕКТРИЧЕСКИЕ НУЛЬ-ТЕРМОСТАТЫ
- § 6. МИКРОСКОПНЫЕ ПРЕДМЕТНЫЕ СТОЛИКИ С РЕГУЛИРУЕМОЙ ТЕМПЕРАТУРОЙ
- Глава XV. ТЕРМОЭЛЕКТРИЧЕСКИЕ КОНДИЦИОНЕРЫ И ДОМАШНИЕ ХОЛОДИЛЬНИКИ
- § 1. КОНДИЦИОНЕРЫ СЛУЖЕБНОГО НАЗНАЧЕНИЯ
- § 2. КОНДИЦИОНЕРЫ БЫТОВОГО НАЗНАЧЕНИЯ
- § 3. ДОМАШНИЕ ХОЛОДИЛЬНИКИ БОЛЬШОГО ОБЪЕМА
- § 4. ДОМАШНИЙ ХОЛОДИЛЬНИК МАЛОГО ОБЪЕМА
- Глава XVI. ПРИБОРЫ РАЗНОГО НАЗНАЧЕНИЯ
- § 1. ХОЛОДИЛЬНИКИ ДЛЯ ЖИВОТНОВОДСТВА
- § 2. ТЕРМОСТАТ ДЛЯ КОКСОГАЗОВОЙ ПРОМЫШЛЕННОСТИ
- § 3. ХОЛОДИЛЬНИК С ОТСОЕДИНЯЕМОЙ ТЕРМОБАТАРЕЕЙ
- § 4. ТЕРМОЭЛЕКТРИЧЕСКИЙ СТАБИЛИЗАТОР ТЕМПЕРАТУРЫ ФОТОРАСТВОРОВ
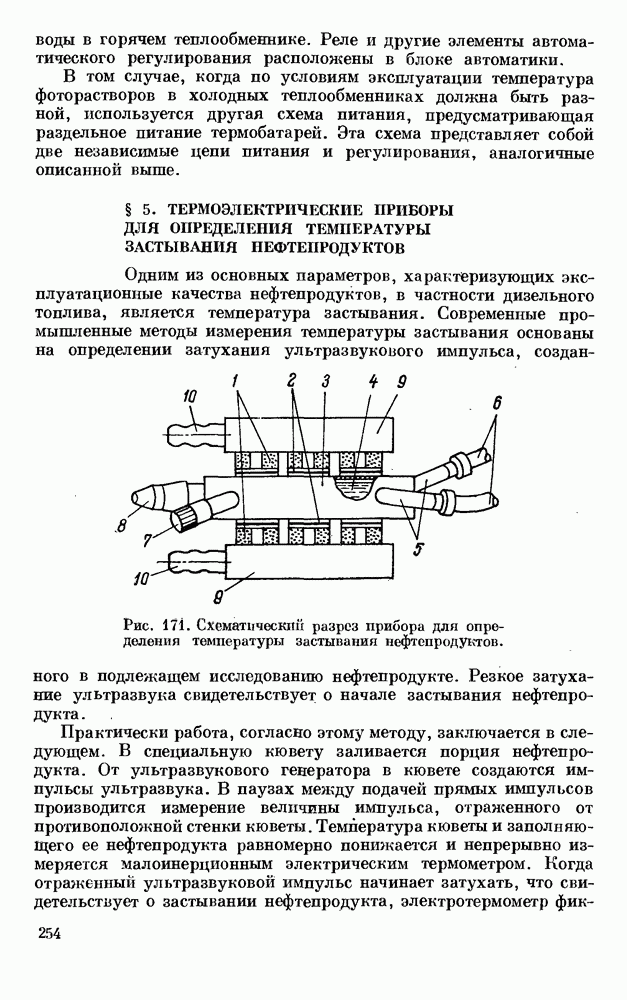
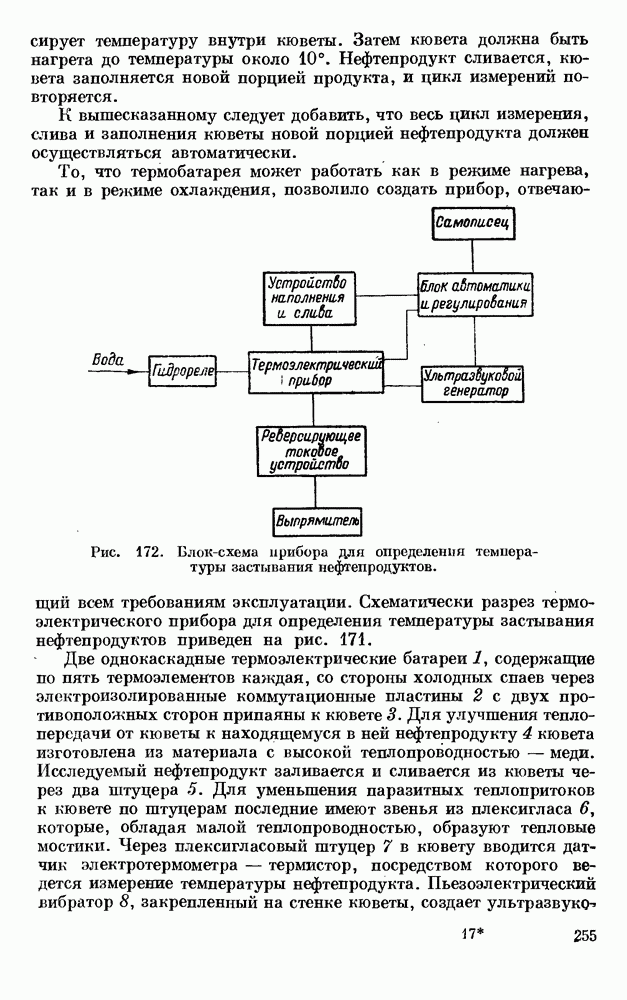
- § 5. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ ДЛЯ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ ЗАСТЫВАНИЯ НЕФТЕПРОДУКТОВ
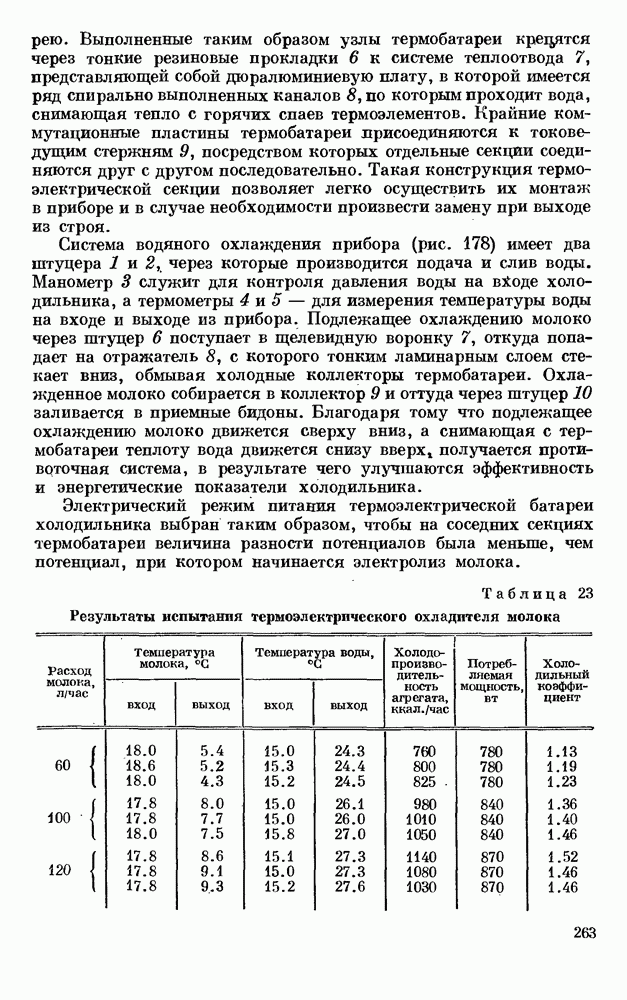
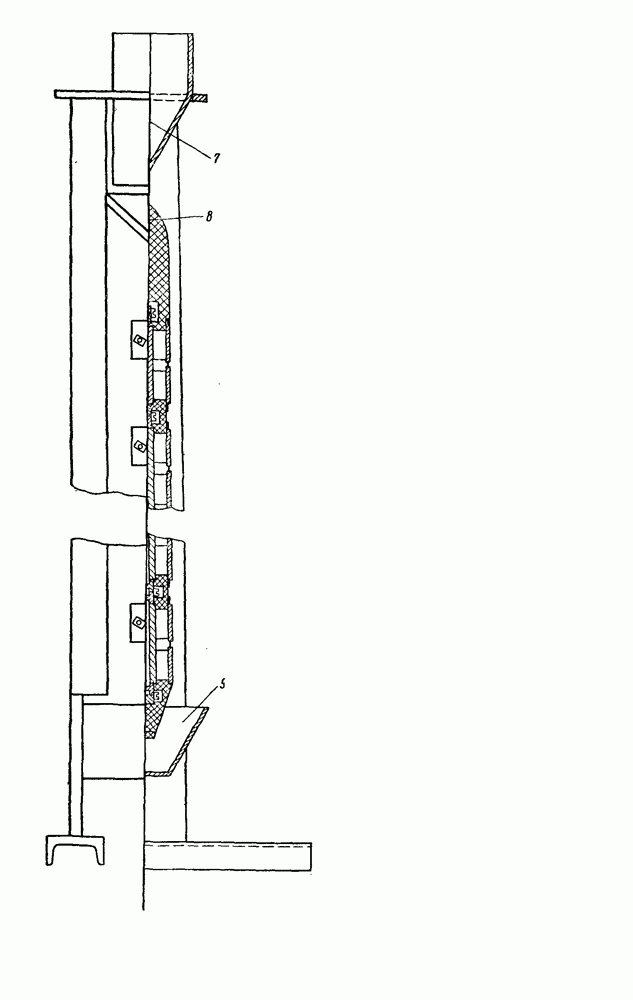
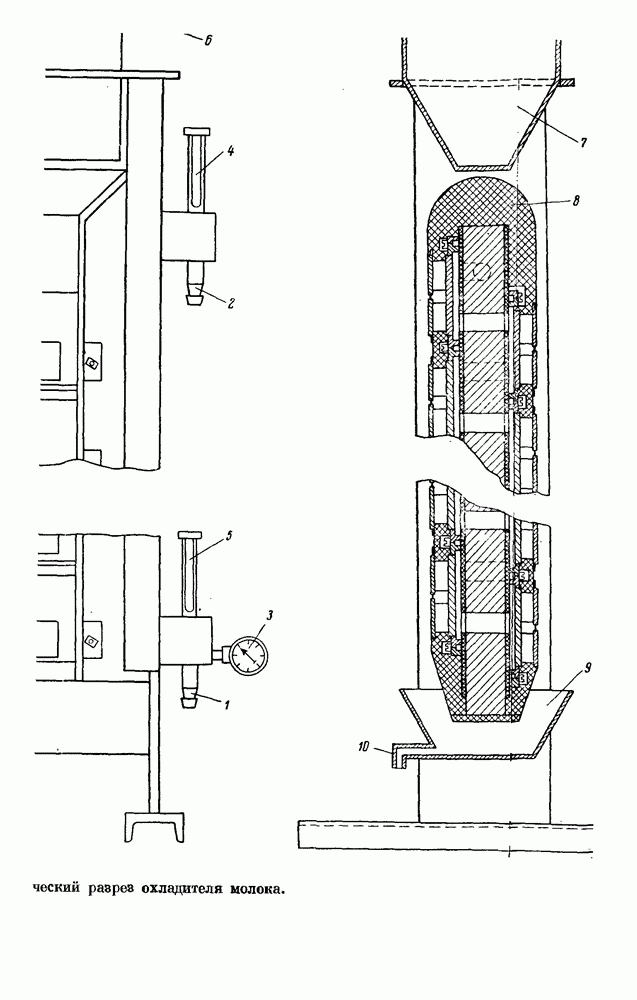
- § 6. ТЕРМОЭЛЕКТРИЧЕСКИЙ ОХЛАДИТЕЛЬ МОЛОКА
- § 7. ТЕРМОЭЛЕКТРИЧЕСКИЙ ОХЛАДИТЕЛЬ ПИТЬЕВОЙ ВОДЫ