| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава II. МАТЕРИАЛЫ ДЛЯ ТЕРМОЭЛЕМЕНТОВ
§ 1. УСЛОВИЯ МАКСИМАЛЬНОЙ ЭФФЕКТИВНОСТИ ТЕРМОЭЛЕМЕНТА
Параметры вещества, определяющие величину  как-то: коэффициент термоэдс а, удельная электропроводность а и удельная теплопроводность
как-то: коэффициент термоэдс а, удельная электропроводность а и удельная теплопроводность  , являются функциями концентрации свободных электронов (или дырок). Качественно эта зависимость представлена на рис.
, являются функциями концентрации свободных электронов (или дырок). Качественно эта зависимость представлена на рис.  Электропроводность пропорциональна
Электропроводность пропорциональна  термоэлектродвижущая сила, наоборот, стремится к нулю при возрастании числа носителей. Теплопроводность слагается из двух частей: теплопроводности кристаллической решетки —
термоэлектродвижущая сила, наоборот, стремится к нулю при возрастании числа носителей. Теплопроводность слагается из двух частей: теплопроводности кристаллической решетки —  и электронной теплопроводности —
и электронной теплопроводности —  рричем
рричем  Теплопроводность решетки в первом приближении не зависит от
Теплопроводность решетки в первом приближении не зависит от  пропорциональна
пропорциональна 

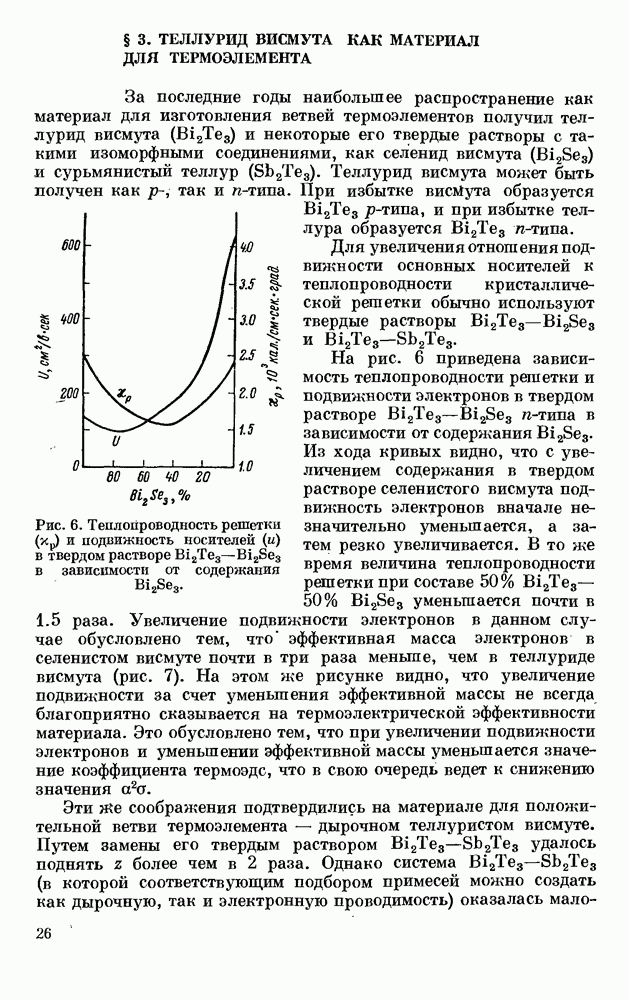
Рис. 5. Качественная зависимость электропроводности  коэффициента термоэдс (а) и
коэффициента термоэдс (а) и  от величины концентрации носителей
от величины концентрации носителей 
В металлах и металлических сплавах величина  очень мала за счет низкого коэффициента термоэдс, в диэлектриках стремится к нулю из-за ничтожно малой электропроводности; в области полупроводниковых концентраций носителей
очень мала за счет низкого коэффициента термоэдс, в диэлектриках стремится к нулю из-за ничтожно малой электропроводности; в области полупроводниковых концентраций носителей  достигает йвоего максимального значения. Эти качественные соображения позволяют понять, почему эффективность металлических термопар очень низка; именно этим объясняется то, что термоэлектрические генераторы и холодильники до последнего времени не находили сколько-нибудь значительного применения в технике. Если воспользоваться в качестве материалов для ветвей термопары полупроводниками (точнее, полуметаллами, см. ниже) и подобрать в них соответствующим образом концентрацию электронов (или
достигает йвоего максимального значения. Эти качественные соображения позволяют понять, почему эффективность металлических термопар очень низка; именно этим объясняется то, что термоэлектрические генераторы и холодильники до последнего времени не находили сколько-нибудь значительного применения в технике. Если воспользоваться в качестве материалов для ветвей термопары полупроводниками (точнее, полуметаллами, см. ниже) и подобрать в них соответствующим образом концентрацию электронов (или
дырок, если речь идет о положительной ветви), можно поднять эффективность термоэлементов в десятки раз.
Для того чтобы оформить эти соображения количественно, мы должны воспользоваться выражениями для коэффициента термоэдс, электропроводности и теплопроводности, подставить их в выражение для  и из условия экстремума
и из условия экстремума

найти оптимальную концентрацию носителей (электронов или дырок)  при которой
при которой  достигает максимума.
достигает максимума.
Нам важно получить решение в аналитической форме, а для этого придется сделать два допущения, упрощающих решение задачи.
1. Как видно из рис. 5, максимум числителя выражения для  оказывается лежащим в области концентрации носителей порядка
оказывается лежащим в области концентрации носителей порядка  т. е. приблизительно в 1000 раз меньшей, чем концентрация свободных электронов в металлах. Доля электронной теплопроводности по отношению к теплопроводности кристаллической решетки при этих условиях (обычно) уже невелика (в то время как в металлах
т. е. приблизительно в 1000 раз меньшей, чем концентрация свободных электронов в металлах. Доля электронной теплопроводности по отношению к теплопроводности кристаллической решетки при этих условиях (обычно) уже невелика (в то время как в металлах  играет преобладающую роль); поэтому в первом приближении мы можем заменить в выражении для
играет преобладающую роль); поэтому в первом приближении мы можем заменить в выражении для  полную теплопроводность
полную теплопроводность  теплопроводностью кристаллической решетки
теплопроводностью кристаллической решетки 

и, полагая, что  не зависит от
не зависит от  искать максимум
искать максимум  (как функции от
(как функции от  а не
а не  Предположение, что теплопроводность решетки не зависит от концентрации Свободных носителей, является, вообще говоря, не вполне строгим; во-первых, изменение концентрации носителей (при данной температуре) всегда требует введения примесей, а последние вызывают дополнительное рассеяние фононов и снижают теплопроводность решетки; во-вторых, фононы рассеиваются непосредственно на свободных электронах и дырках, — по этой причине теплопроводность кристаллической решетки металлов ничтожно мала. Однако при концентрациях носителей порядка
Предположение, что теплопроводность решетки не зависит от концентрации Свободных носителей, является, вообще говоря, не вполне строгим; во-первых, изменение концентрации носителей (при данной температуре) всегда требует введения примесей, а последние вызывают дополнительное рассеяние фононов и снижают теплопроводность решетки; во-вторых, фононы рассеиваются непосредственно на свободных электронах и дырках, — по этой причине теплопроводность кристаллической решетки металлов ничтожно мала. Однако при концентрациях носителей порядка  эти оба фактора играют ничтожную роль, и мы вправе поэтому считать
эти оба фактора играют ничтожную роль, и мы вправе поэтому считать  не зависящим от
не зависящим от 
2. Предположим далее, что при концентрации носителей, соответствующей максимальному значению  они (носители) находятся в невырожденном состоянии, и поэтому к ним применима классическая статистика. В этом случае функция распределения Ферми заменяется функцией распределения Максвелла
они (носители) находятся в невырожденном состоянии, и поэтому к ним применима классическая статистика. В этом случае функция распределения Ферми заменяется функцией распределения Максвелла

и выражения для термоэдс, концентрации носителей, электропроводности и теплопроводности чрезвычайно упрощаются:  могут быть выражены в виде явных функций от
могут быть выражены в виде явных функций от 

где

При этих условиях задача нахождения оптимальной концентрации носителей  и соответствующего ей максимального значения
и соответствующего ей максимального значения  решается чрезвычайно просто.
решается чрезвычайно просто.
В дальнейших рассуждениях сделаем допущение, что подвижность электронов не зависит от  что, вообще говоря, не совсем верно, так как: 1) с ростом
что, вообще говоря, не совсем верно, так как: 1) с ростом  одновременно растет число ионизированных доноров, являющихся дополнительными источниками рассеяния электронов; 2) при больших концентрациях электронов с ростом
одновременно растет число ионизированных доноров, являющихся дополнительными источниками рассеяния электронов; 2) при больших концентрациях электронов с ростом  начинает (за счет вырождения) расти их энергия, что также влияет на V (так как
начинает (за счет вырождения) расти их энергия, что также влияет на V (так как  является функцией от энергии
является функцией от энергии  Однако для качественного анализа, который является целью наших расчетов, можно пока этими зависимостями пренебречь (вопрос об учете вырождения будет рассмотрен ниже).
Однако для качественного анализа, который является целью наших расчетов, можно пока этими зависимостями пренебречь (вопрос об учете вырождения будет рассмотрен ниже).
Согласно (31) и (32),

Условие  дает оптимальную концентрацию носителей
дает оптимальную концентрацию носителей  соответствующую электропроводность
соответствующую электропроводность 

и оптимальную термоэдс

при этом выражение для максимального значения  принимает вид
принимает вид

и соответственно максимальное значение  приобретает вид
приобретает вид

где  масса свободного электрона, равная
масса свободного электрона, равная 
Как видно из (34), оптимальная концентрация носителей зависит от ряда факторов: эффективной массы  температуры
температуры  и механизма рассеяния
и механизма рассеяния 
Оптимальная же термоэдс  согласно (35), для всех веществ и при всех условиях остается постоянной. Поэтому при подборе нужной концентрации носителей удобнее ориентироваться по величине термоэдс, тем более что ее измерение несравненно проще, чем измерение концентрации свободных электронов.
согласно (35), для всех веществ и при всех условиях остается постоянной. Поэтому при подборе нужной концентрации носителей удобнее ориентироваться по величине термоэдс, тем более что ее измерение несравненно проще, чем измерение концентрации свободных электронов.
Согласно (34), оптимальная концентрация носителей, при которой  достигает максимального значения, есть функция от температуры; следовательно, концентрацию носителей нужно подбирать в соответствии с рабочим интервалом температур. С этой точки зрения наиболее выгодным для создания термопар было бы вещество, у которого концентрация электронов менялась бы с температурой по закону
достигает максимального значения, есть функция от температуры; следовательно, концентрацию носителей нужно подбирать в соответствии с рабочим интервалом температур. С этой точки зрения наиболее выгодным для создания термопар было бы вещество, у которого концентрация электронов менялась бы с температурой по закону  таким образом, условие оптимума (34) удовлетворялось бы во всем температурном интервале работы термопары для любого дифференциального участка ее ветви. К сожалению, таких веществ в природе не существует. В обычных полупроводниках в области примесной проводимости концентрация носителей растет по экспоненциальному закону
таким образом, условие оптимума (34) удовлетворялось бы во всем температурном интервале работы термопары для любого дифференциального участка ее ветви. К сожалению, таких веществ в природе не существует. В обычных полупроводниках в области примесной проводимости концентрация носителей растет по экспоненциальному закону  где
где  энергия активации примесных уровней, т. е. куда быстрее, чем требует условие (34).
энергия активации примесных уровней, т. е. куда быстрее, чем требует условие (34).
К счастью, в данном случае нам природа идет в известной степени навстречу. Дело в том, что энергия активации примесей  не есть величина постоянная, а, как правило, убывает с концентрацией
не есть величина постоянная, а, как правило, убывает с концентрацией  и обычно при
и обычно при  обращается в нуль. Полупроводник при этом обращается в так называемый полуметалл: уже вблизи абсолютного нуля все примеси оказываются ионизированными, и концентрация носителей остается постоянной
обращается в нуль. Полупроводник при этом обращается в так называемый полуметалл: уже вблизи абсолютного нуля все примеси оказываются ионизированными, и концентрация носителей остается постоянной  вплоть до температур, при. которых начинает проявляться собственная проводимость.
вплоть до температур, при. которых начинает проявляться собственная проводимость.
Таким образом, если в качестве материалов для ветвей термопары применить полуметаллы с достаточно широкой запретной зоной, то мы можем считать, что концентрация носителей остается постоянной. При этом условие (34) также не выполняется строго на всем протяжении ветви термоэлемента, и это приводит к некоторому снижению его эффективности. Однако, так как перепад температур на охлаждающей термопаре, как правило, не превышает нескольких десятков градусов, отступления от (34) и соответствующие потери эффективности обычно не превышают 10—20%. В этом отношении многокаскадные батареи приобретают еще одно преимущество: если общий рабочий перепад разделен на небольшие перепады температур, то в каждом каскаде условие (34) может быть удовлетворено более точно соответствующим подбором концентраций примесей. Можно также строго удовлетворить это условие, если обеспечить постепенное изменение концентрации примесей вдоль ветви термопары; это, однако, представляет большие технологические трудности, которые до настоящего времени полностью не преодолены.
Согласно (37), эффективность термопары  пропорциональна отношению подвижности носителей к теплопроводности кристаллической решетки;
пропорциональна отношению подвижности носителей к теплопроводности кристаллической решетки;  достигает максимального значения при определенной концентрации носителей. Таким образом, проведенный выше анализ показывает, что разработка материалов для ветвей термоэлементов сводится к решению следующих основных задач:
достигает максимального значения при определенной концентрации носителей. Таким образом, проведенный выше анализ показывает, что разработка материалов для ветвей термоэлементов сводится к решению следующих основных задач:
1) к отысканию веществ с максимальным отношением подвижности носителей к теплопроводности кристаллической решетки,
2) к созданию в этих веществах концентраций носителей, соответствующей (34).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Часть I. ТЕОРИЯ ТЕРМОЭЛЕКТРИЧЕСКОГО ОХЛАЖДЕНИЯ
- § 1. МАКСИМАЛЬНОЕ ПОНИЖЕНИЕ ТЕМПЕРАТУРЫ
- § 2. ХОЛОДИЛЬНЫЙ КОЭФФИЦИЕНТ
- § 3. МНОГОКАСКАДНЫЕ ТЕРМОБАТАРЕИ
- Глава II. МАТЕРИАЛЫ ДЛЯ ТЕРМОЭЛЕМЕНТОВ
- § 1. УСЛОВИЯ МАКСИМАЛЬНОЙ ЭФФЕКТИВНОСТИ ТЕРМОЭЛЕМЕНТА
- § 2. ВЫБОР МАТЕРИАЛОВ ДЛЯ ВЕТВЕЙ ТЕРМОЭЛЕМЕНТОВ
- § 3. ТЕЛЛУРИД ВИСМУТА КАК МАТЕРИАЛ ДЛЯ ТЕРМОЭЛЕМЕНТА
- Глава III. УЧЕТ ДОПОЛНИТЕЛЬНЫХ ФАКТОРОВ
- § 1. УЧЕТ ЭЛЕКТРОННОЙ ТЕПЛОПРОВОДНОСТИ
- § 2. УЧЕТ ТЕПЛОТЫ ТОМСОНА В ЭНЕРГЕТИЧЕСКОМ БАЛАНСЕ ТЕРМОЭЛЕМЕНТА
- § 3. ОТСТУПЛЕНИЯ ОТ ОПТИМАЛЬНЫХ УСЛОВИЙ
- Глава IV. ТЕРМОГАЛЬВАНОМАГНИТНЫЕ МЕТОДЫ ОХЛАЖДЕНИЯ
- § 2. ТЕРМОЭЛЕКТРИЧЕСКОЕ ОХЛАЖДЕНИЕ В МАГНИТНОМ ПОЛЕ
- § 3. ТЕРМОМАГНИТНОЕ ОХЛАЖДЕНИЕ (ЭФФЕКТ ЭТТИНГСГАУЗЕНА)
- Часть II. ИНЖЕНЕРНЫЕ ВОПРОСЫ ТЕХНИКИ ТЕРМОЭЛЕКТРИЧЕСКОГО ОХЛАЖДЕНИЯ
- Глава V. ОСНОВЫ РАСЧЕТА ТЕРМОЭЛЕКТРИЧЕСКИХ ОХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. РАСЧЕТ ТЕРМОБАТАРЕИ
- § 3. РАСЧЕТ РАДИАТОРА ТЕПЛОСЪЕМА
- Глава VI. КОНСТРУКТИВНЫЕ ЭЛЕМЕНТЫ ТЕРМОЭЛЕКТРИЧЕСКИХ ОХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. МНОГОКАСКАДНЫЕ ТЕРМОЭЛЕМЕНТЫ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКАЯ БАТАРЕЯ
- § 4. ТЕПЛОВОЕ СОПРЯЖЕНИЕ ТЕРМОБАТАРЕИ
- § 5. КОНСТРУКЦИИ СИСТЕМ ТЕПЛООТВОДА
- § 6. РАБОЧАЯ КАМЕРА ПРИБОРА
- Глава VII. СПОСОБЫ ОТВОДА ТЕПЛА ОТ ТЕРМООХЛАЖДАЮЩИХ ПРИБОРОВ
- § 1. РАДИАТОРНАЯ СИСТЕМА С ЕСТЕСТВЕННОКОНВЕКЦИОННЫМ ТЕПЛООБМЕНОМ
- § 2. РАДИАТОРНАЯ СИСТЕМА С ПРИНУДИТЕЛЬНЫМ ТЕПЛОСЪЕМОМ
- § 3. ИГОЛЬЧАТЫЕ РАДИАТОРНЫЕ СИСТЕМЫ
- § 4. ЖИДКОСТНАЯ СИСТЕМА С ЕСТЕСТВЕННОЙ ЦИРКУЛЯЦИЕЙ
- § 5. ИСПОЛЬЗОВАНИЕ СКРЫТОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ
- § 6. ИСПОЛЬЗОВАНИЕ СКРЫТОЙ ТЕПЛОТЫ ИСПАРЕНИЯ
- § 7. ТЕПЛООТВОДЯЩАЯ СИСТЕМА С ИСПОЛЬЗОВАНИЕМ ТЕПЛОЕМКОСТИ
- § 8. ИСПОЛЬЗОВАНИЕ РАСТВОРОВ С НИЗКОЙ КРИОГИДРАТНОЙ ТЕМПЕРАТУРОЙ
- Глава VIII. ИСТОЧНИКИ ПИТАНИЯ ТЕРМОЭЛЕКТРИЧЕСКИХ ОХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. АККУМУЛЯТОРЫ
- § 3. ПРЕОБРАЗОВАТЕЛИ ТОКА
- § 4. ТЕРМОЭЛЕКТРОГЕНЕРАТОРЫ
- Глава IX. НЕКОТОРЫЕ ВОПРОСЫ ТЕХНОЛОГИИ ИЗГОТОВЛЕНИЯ ТЕРМООХЛАЖДАЮЩИХ ПРИБОРОВ
- § 2. ЗАЛУЖИВАНИЕ ВЕТВЕЙ ТЕРМОЭЛЕМЕНТОВ
- § 3. КОММУТАЦИЯ ТЕРМОБАТАРЕИ
- § 4. ПРОЧИЕ ВОПРОСЫ ТЕХНОЛОГИИ
- Часть III. ПРАКТИКА ТЕРМОЭЛЕКТРИЧЕСКОГО ОХЛАЖДЕНИЯ
- Глава X. ВЫСОКОВАКУУМНЫЕ ЛОВУШКИ С ТЕРМОЭЛЕКТРИЧЕСКИМ ОХЛАЖДЕНИЕМ
- § 2. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЛОВУШКИ ДЛЯ ЕДИНОЙ СЕРИИ НАСОСОВ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКАЯ ЛОВУШКА ДЛЯ ПАРОРТУТНЫХ НАСОСОВ
- § 4. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЛОВУШКИ ДЛЯ ОТКАЧНЫХ АВТОМАТОВ
- Глава XI. ТЕРМОЭЛЕКТРИЧЕСКИЕ ОХЛАДИТЕЛИ ПРИЕМНИКОВ ЛУЧИСТОЙ ЭНЕРГИИ
- § 1. МИКРОТЕРМОСТАТЫ ДЛЯ ОХЛАЖДЕНИЯ ФОТОСОПРОТИВЛЕНИЙ
- § 2. МИКРОТЕРМОСТАТ ДЛЯ ОХЛАЖДЕНИЯ БОЛОМЕТРОВ
- § 3. ТЕРМОЭЛЕКТРИЧЕСКИЙ ОХЛАДИТЕЛЬ ДЛЯ РАДИАЦИОННЫХ БАЛАНСОМЕРОВ
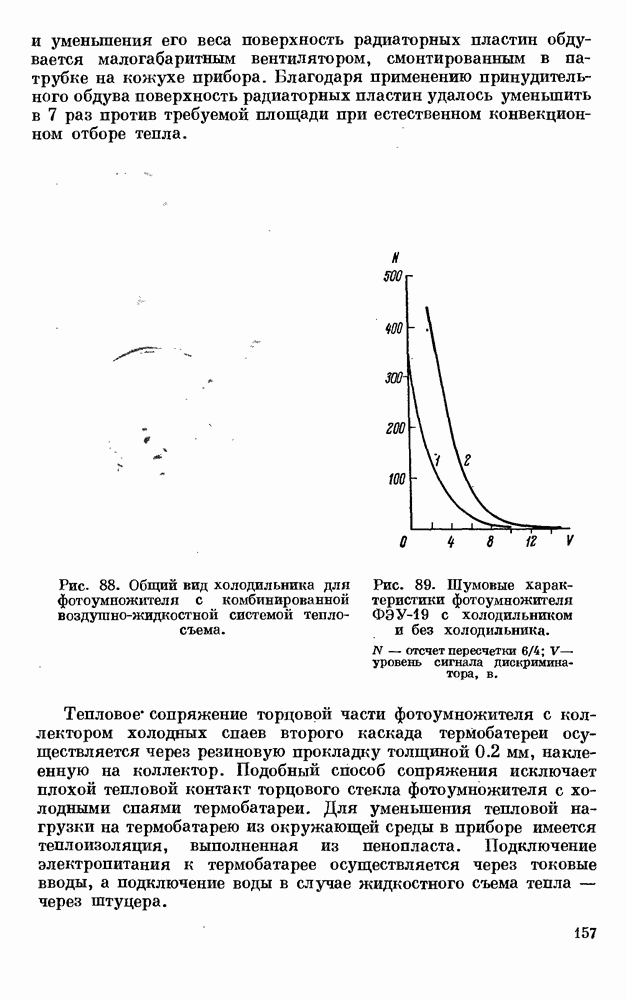
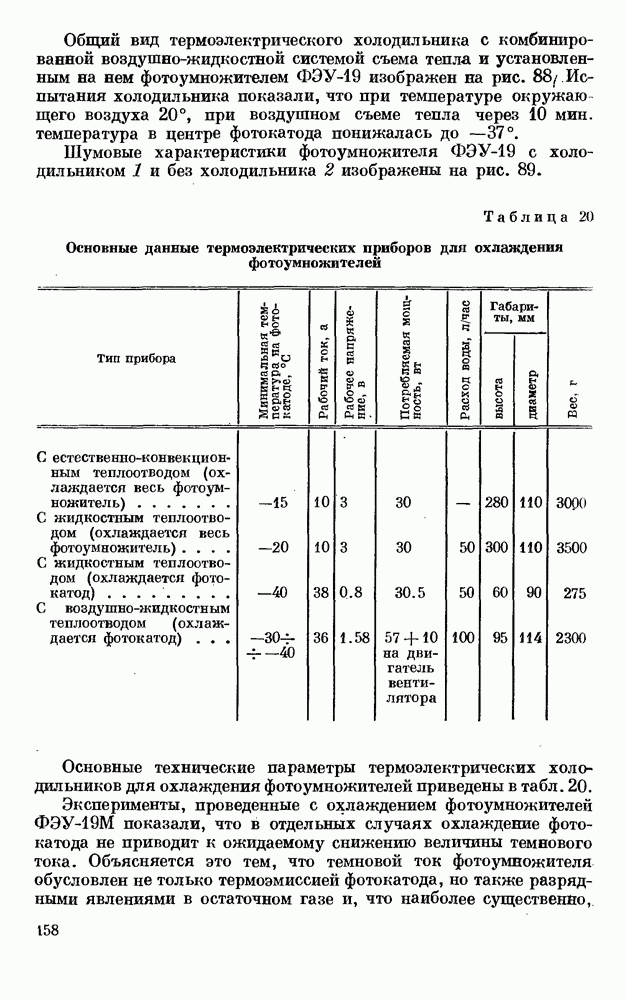
- § 4. ТЕРМОЭЛЕКТРИЧЕСКИЕ ХОЛОДИЛЬНИКИ ДЛЯ ФОТОУМНОЖИТЕЛЕЙ
- Глава XII. ТЕРМОЭЛЕКТРИЧЕСКИЕ ОХЛАЖДАЮЩИЕ ПРИБОРЫ ДЛЯ МЕДИЦИНЫ
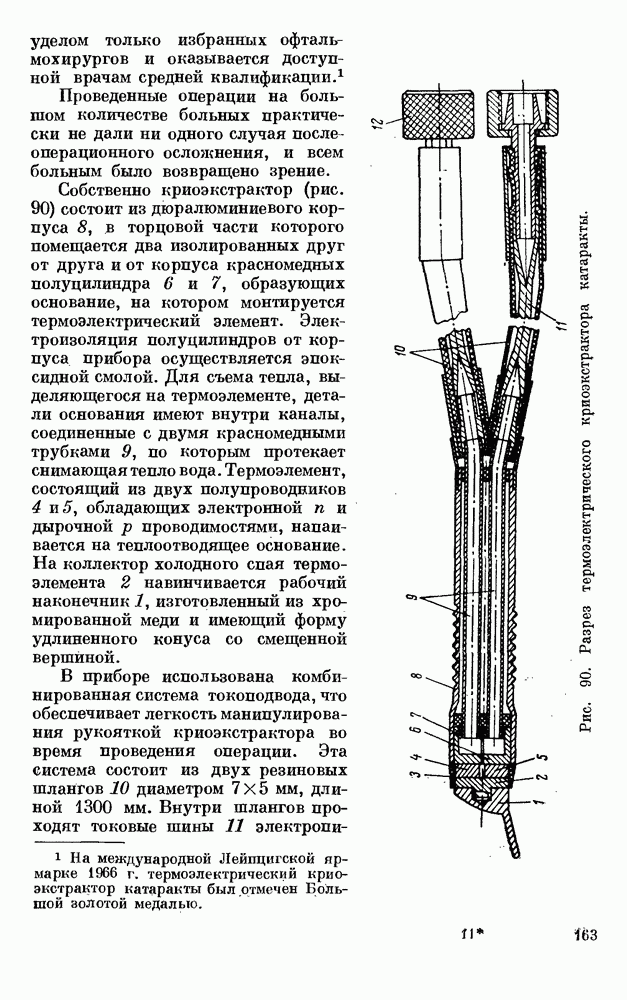
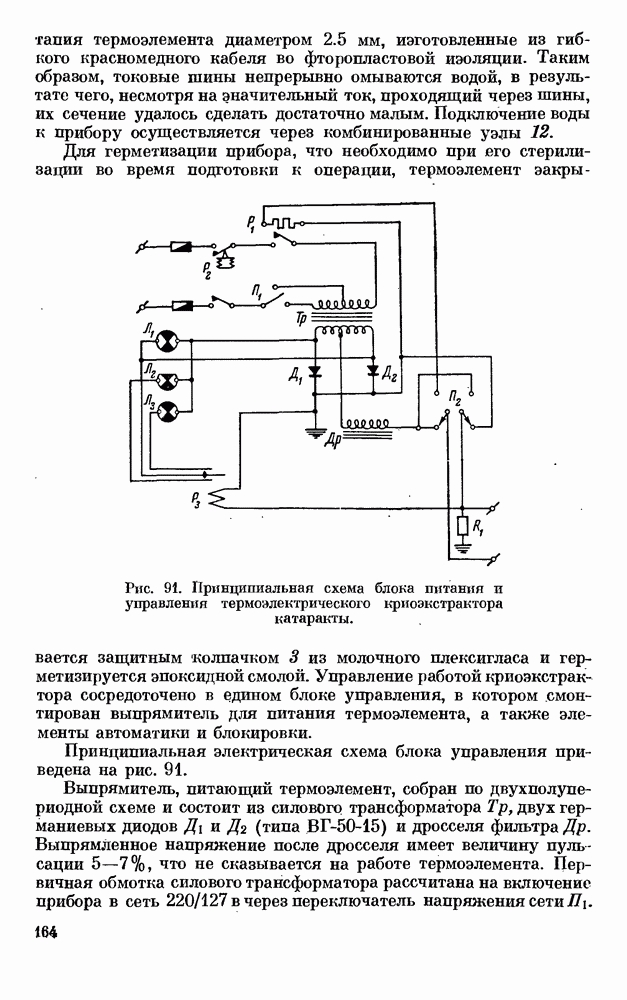
- § 1. ТЕРМОЭЛЕКТРИЧЕСКИЙ КРИОЭКСТРАКТОР КАТАРАКТЫ
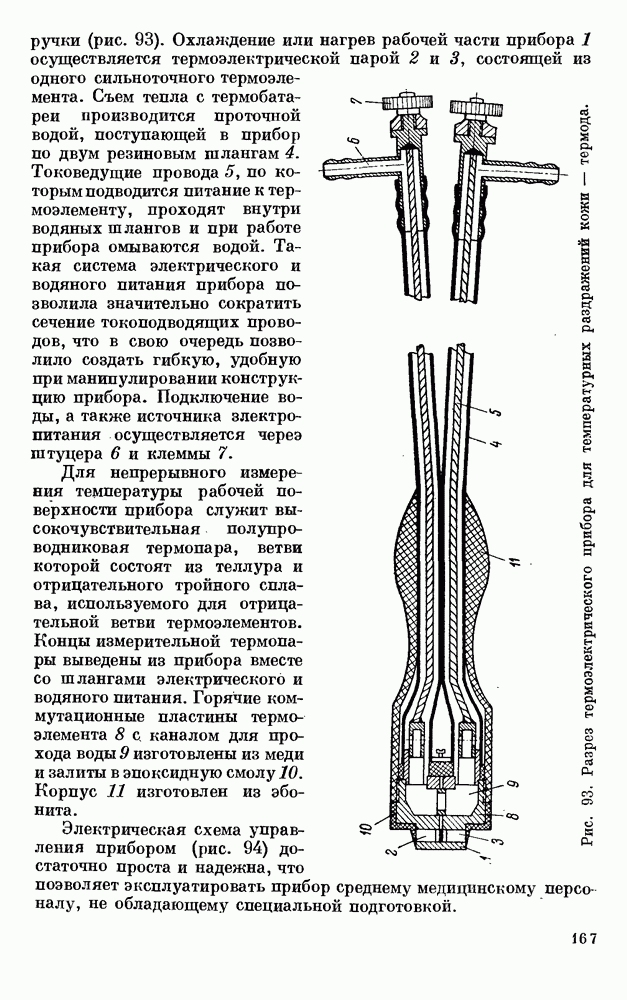
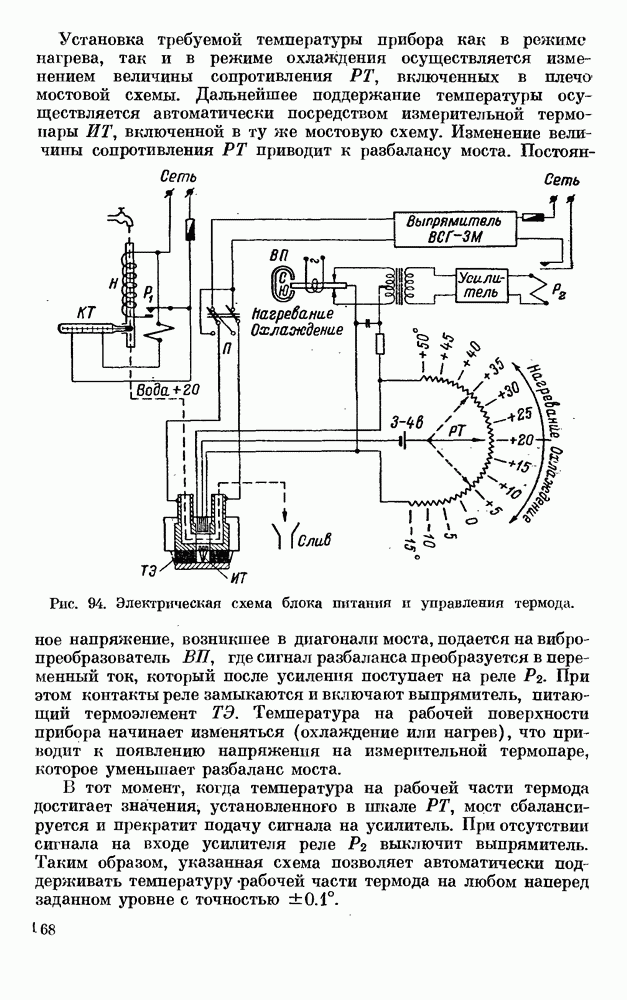
- § 2. ПРИБОР ДЛЯ ТЕМПЕРАТУРНЫХ РАЗДРАЖЕНИЙ КОЖИ — ТЕРМОД
- § 3. МИКРОХОЛОДИЛЬНИК ДЛЯ ЛЕЧЕНИЯ КОЖНЫХ ЗАБОЛЕВАНИЙ
- § 4. МИКРОТОМНЫЕ СТОЛИКИ С ТЕРМОЭЛЕКТРИЧЕСКИМ ОХЛАЖДЕНИЕМ
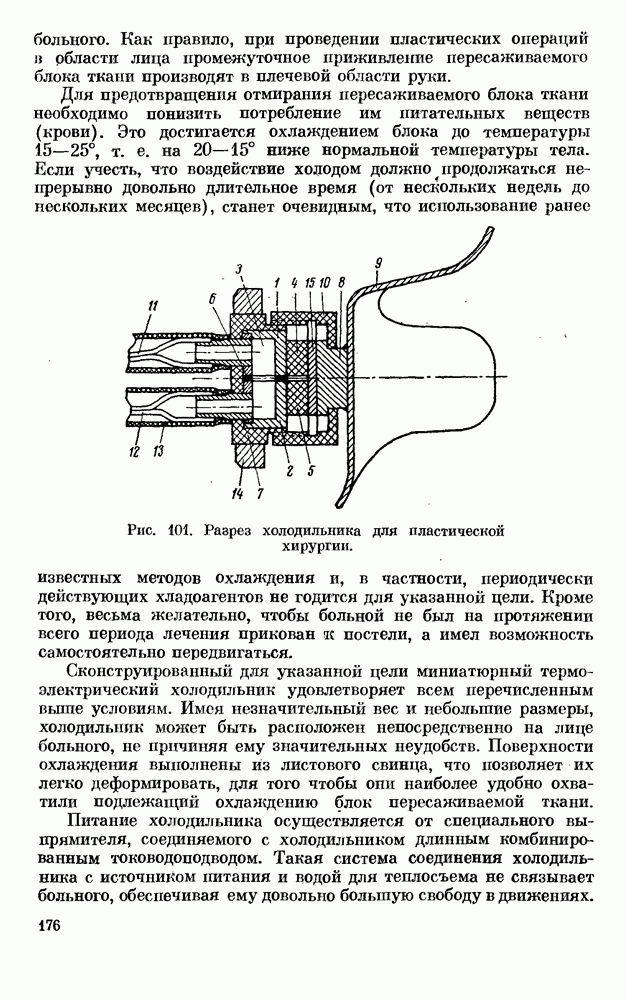
- § 5. ХОЛОДИЛЬНИК ДЛЯ ПЛАСТИЧЕСКОЙ ХИРУРГИИ
- Глава XIII. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ ДЛЯ РАДИОЭЛЕКТРОНИКИ
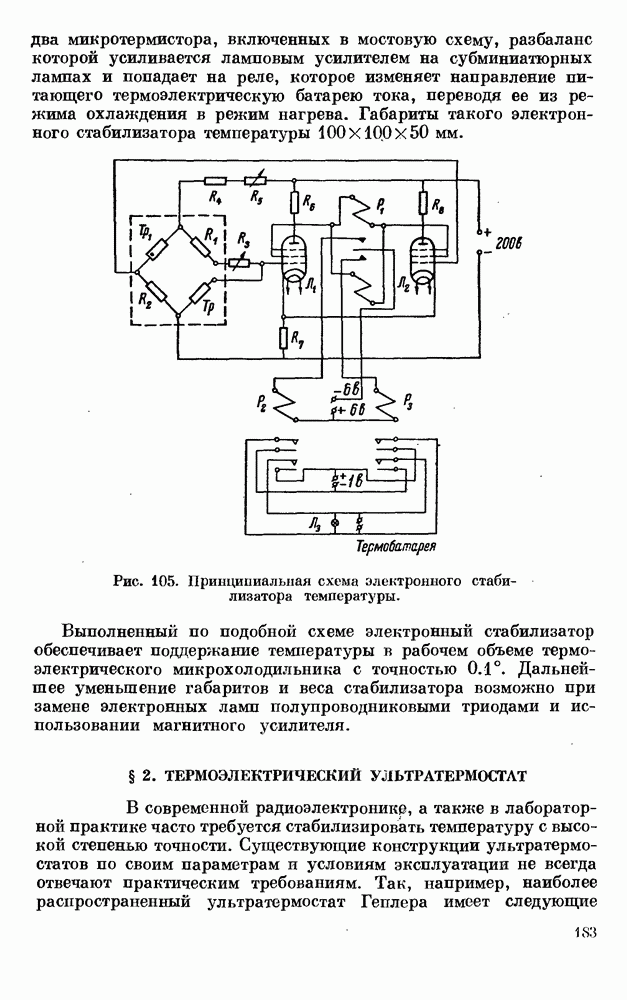
- § 2. ТЕРМОЭЛЕКТРИЧЕСКИЙ УЛЬТРАТЕРМОСТАТ
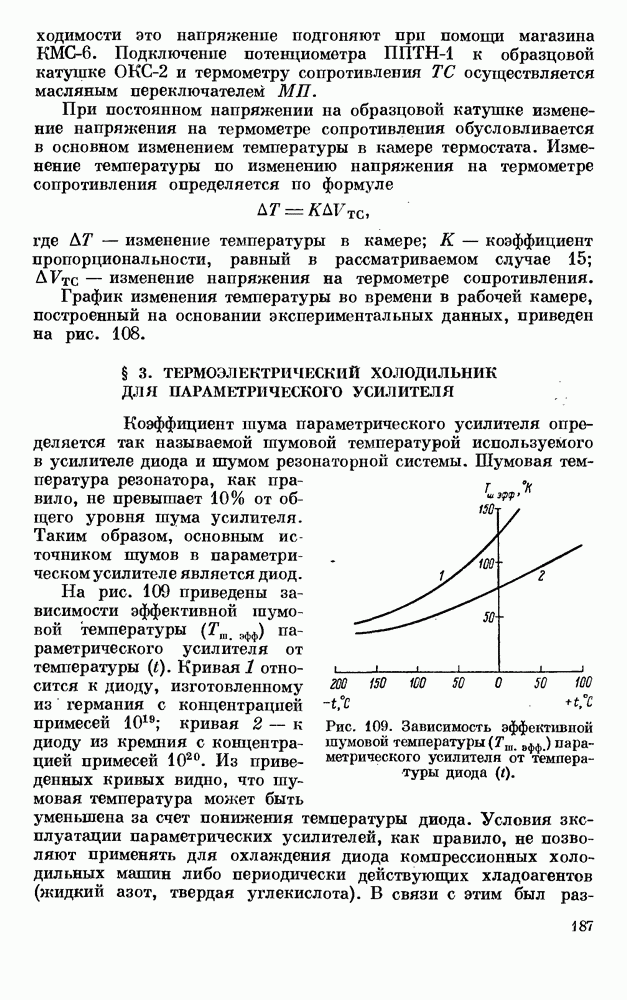
- § 3. ТЕРМОЭЛЕКТРИЧЕСКИЙ ХОЛОДИЛЬНИК ДЛЯ ПАРАМЕТРИЧЕСКОГО УСИЛИТЕЛЯ
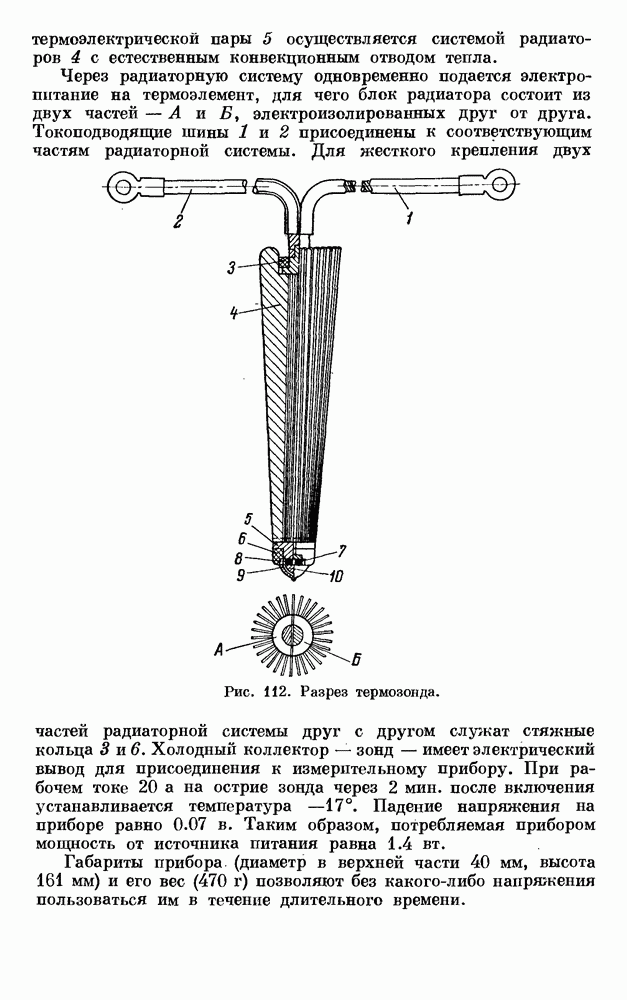
- § 4. ТЕРМОЗОНД
- Глава XIV. ТЕРМОЭЛЕКТРИЧЕСКИЕ ХОЛОДИЛЬНИКИ ОБЩЕГО НАЗНАЧЕНИЯ
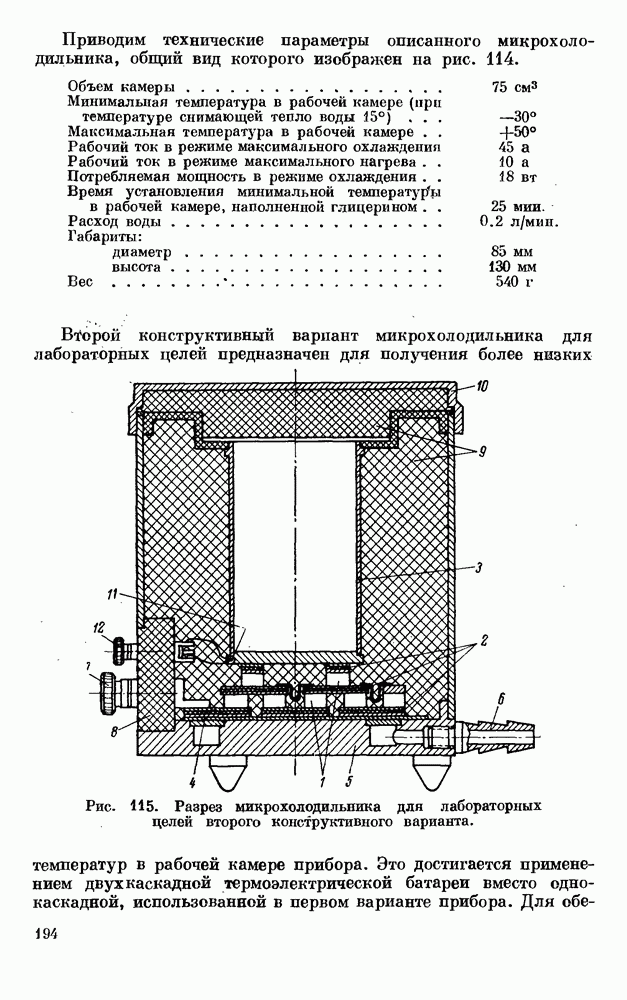
- § 1. МИКРОХОЛОДИЛЬНИКИ ДЛЯ ЛАБОРАТОРНЫХ ЦЕЛЕЙ
- § 2. ИСПЫТАТЕЛЬНЫЕ ТЕРМОЭЛЕКТРИЧЕСКИЕ МИКРОКАМЕРЫ
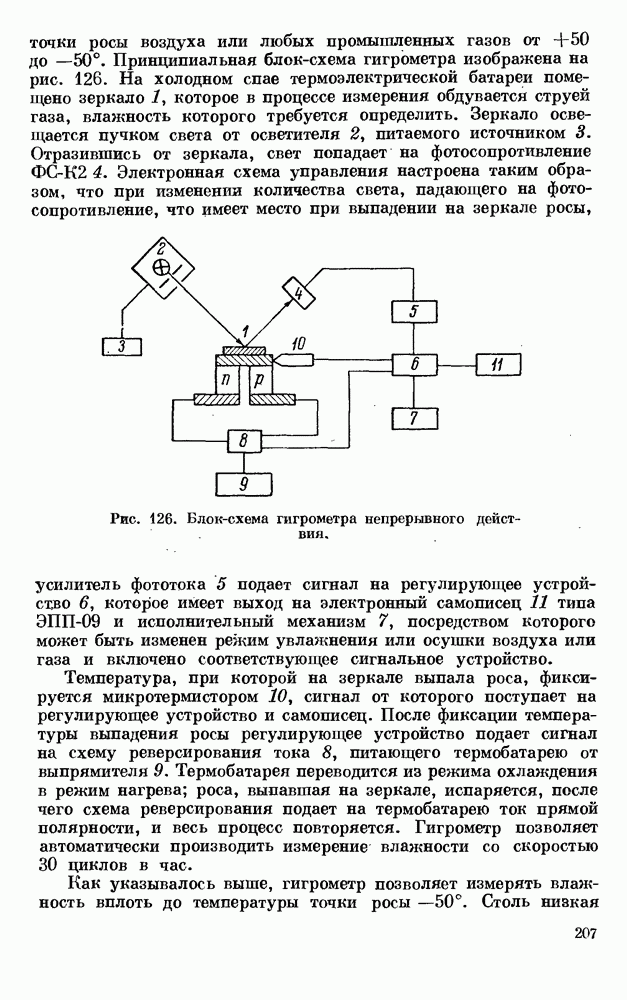
- § 3. ТЕРМОЭЛЕКТРИЧЕСКИЕ КОНДЕНСАЦИОННЫЕ ГИГРОМЕТРЫ
- § 4. ПРИБОР ДЛЯ ТАРИРОВАНИЯ ТЕРМОМЕТРОВ
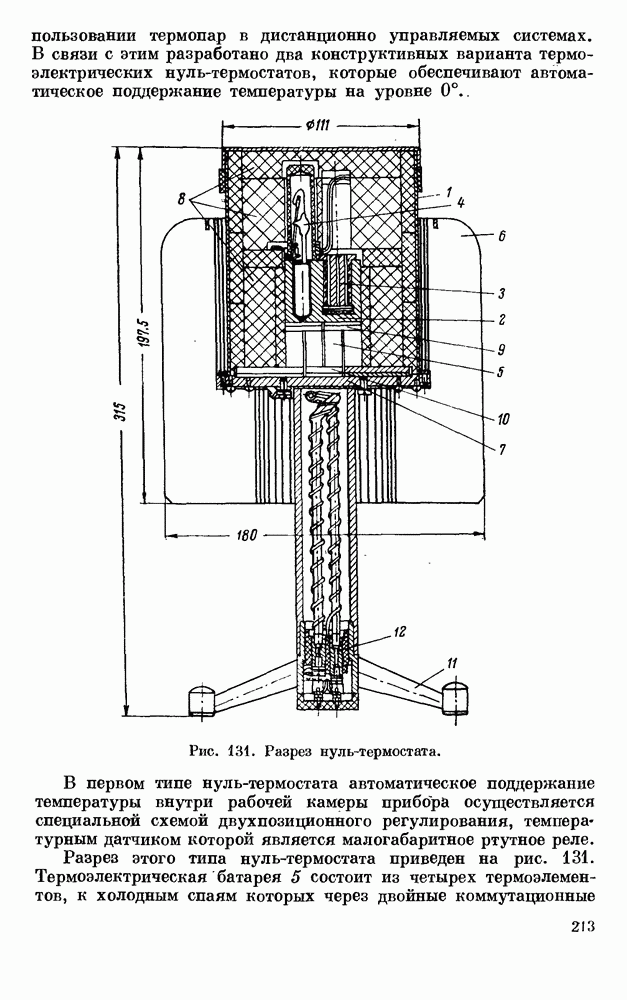
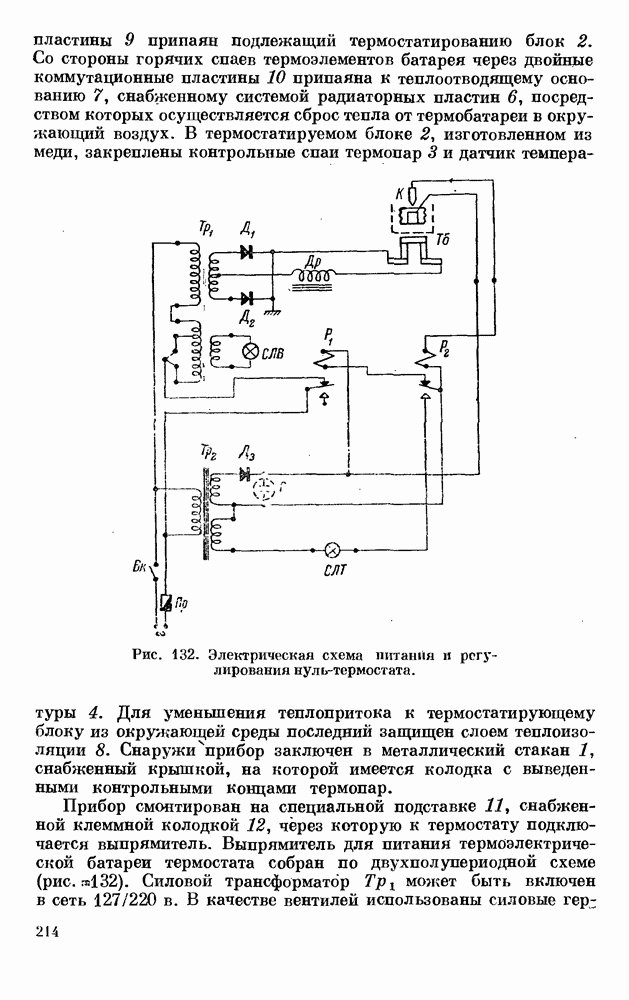
- § 5. ТЕРМОЭЛЕКТРИЧЕСКИЕ НУЛЬ-ТЕРМОСТАТЫ
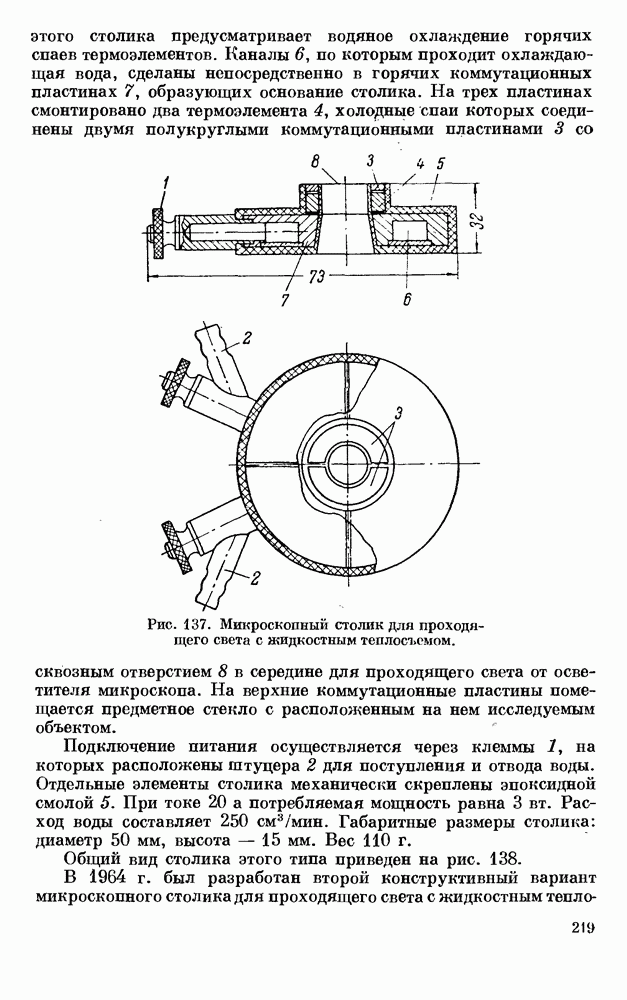
- § 6. МИКРОСКОПНЫЕ ПРЕДМЕТНЫЕ СТОЛИКИ С РЕГУЛИРУЕМОЙ ТЕМПЕРАТУРОЙ
- Глава XV. ТЕРМОЭЛЕКТРИЧЕСКИЕ КОНДИЦИОНЕРЫ И ДОМАШНИЕ ХОЛОДИЛЬНИКИ
- § 1. КОНДИЦИОНЕРЫ СЛУЖЕБНОГО НАЗНАЧЕНИЯ
- § 2. КОНДИЦИОНЕРЫ БЫТОВОГО НАЗНАЧЕНИЯ
- § 3. ДОМАШНИЕ ХОЛОДИЛЬНИКИ БОЛЬШОГО ОБЪЕМА
- § 4. ДОМАШНИЙ ХОЛОДИЛЬНИК МАЛОГО ОБЪЕМА
- Глава XVI. ПРИБОРЫ РАЗНОГО НАЗНАЧЕНИЯ
- § 1. ХОЛОДИЛЬНИКИ ДЛЯ ЖИВОТНОВОДСТВА
- § 2. ТЕРМОСТАТ ДЛЯ КОКСОГАЗОВОЙ ПРОМЫШЛЕННОСТИ
- § 3. ХОЛОДИЛЬНИК С ОТСОЕДИНЯЕМОЙ ТЕРМОБАТАРЕЕЙ
- § 4. ТЕРМОЭЛЕКТРИЧЕСКИЙ СТАБИЛИЗАТОР ТЕМПЕРАТУРЫ ФОТОРАСТВОРОВ
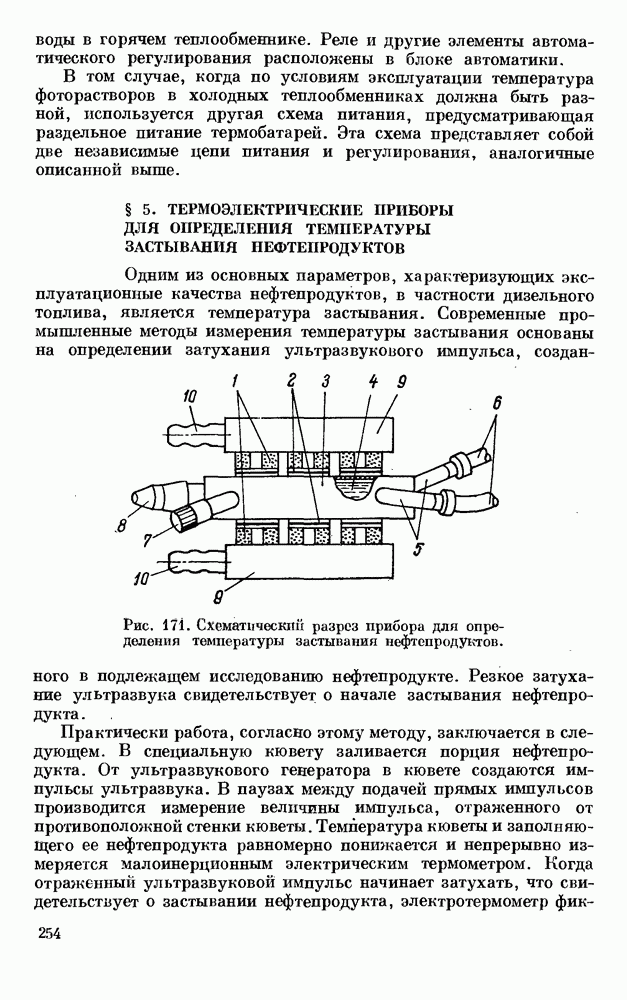
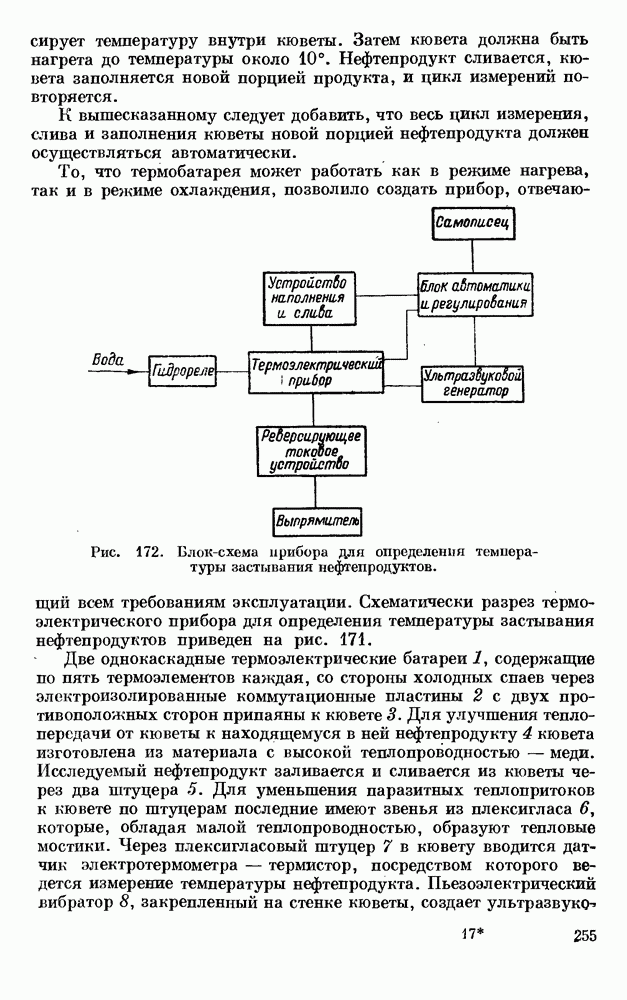
- § 5. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ ДЛЯ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ ЗАСТЫВАНИЯ НЕФТЕПРОДУКТОВ
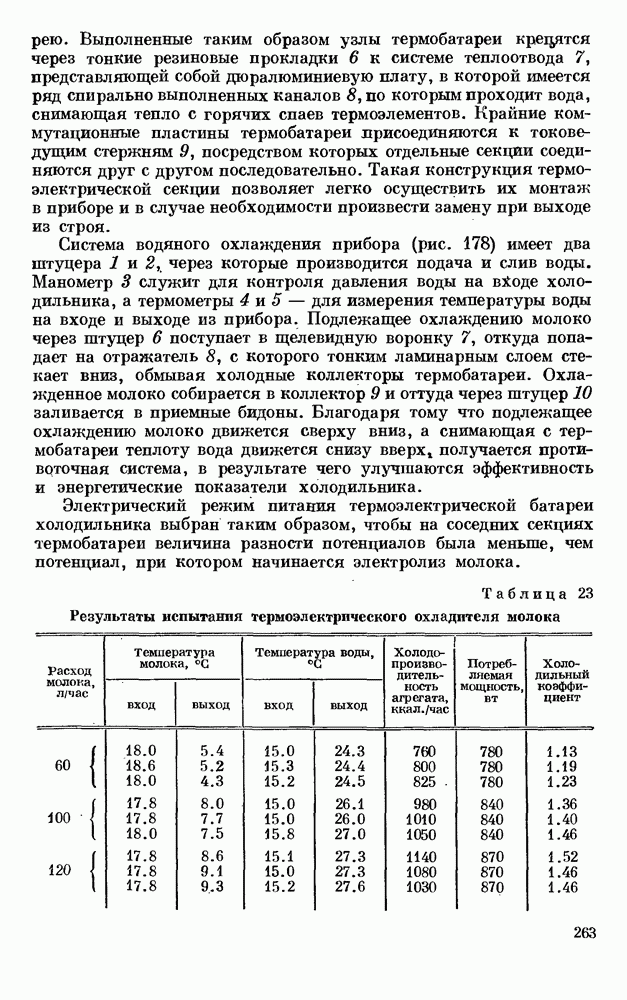
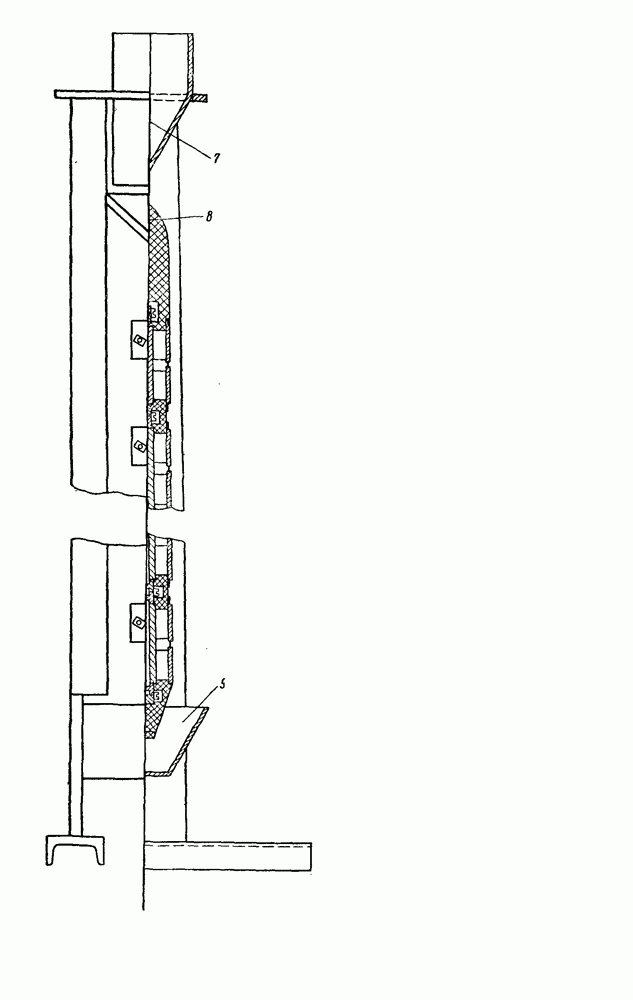
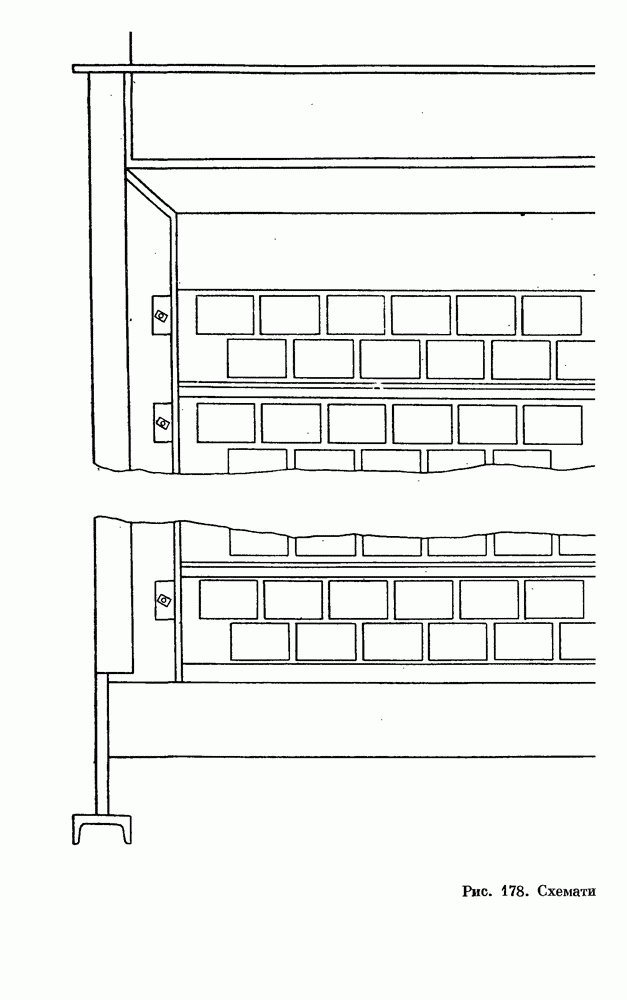
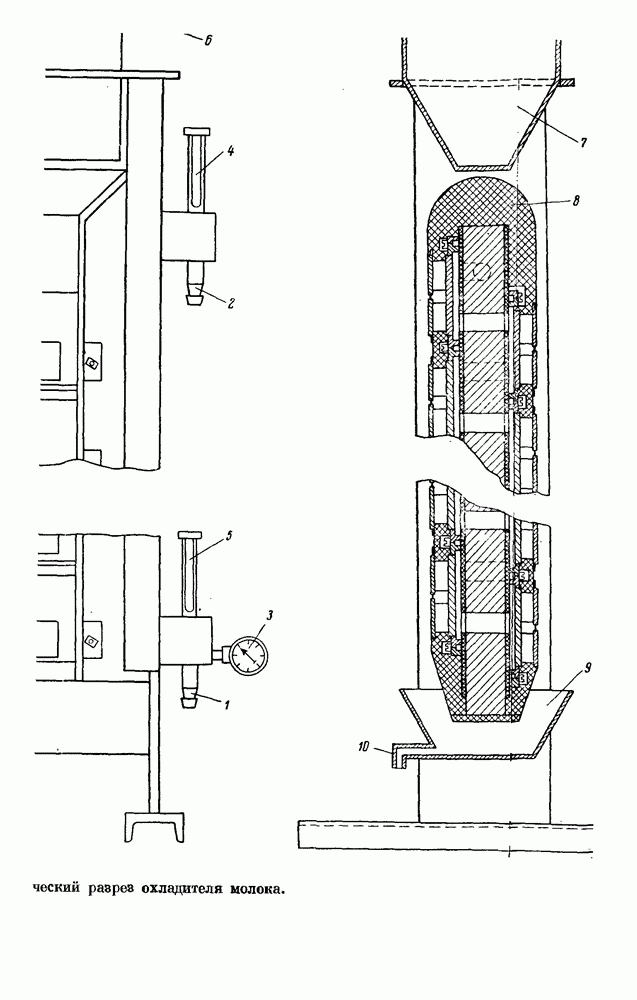
- § 6. ТЕРМОЭЛЕКТРИЧЕСКИЙ ОХЛАДИТЕЛЬ МОЛОКА
- § 7. ТЕРМОЭЛЕКТРИЧЕСКИЙ ОХЛАДИТЕЛЬ ПИТЬЕВОЙ ВОДЫ