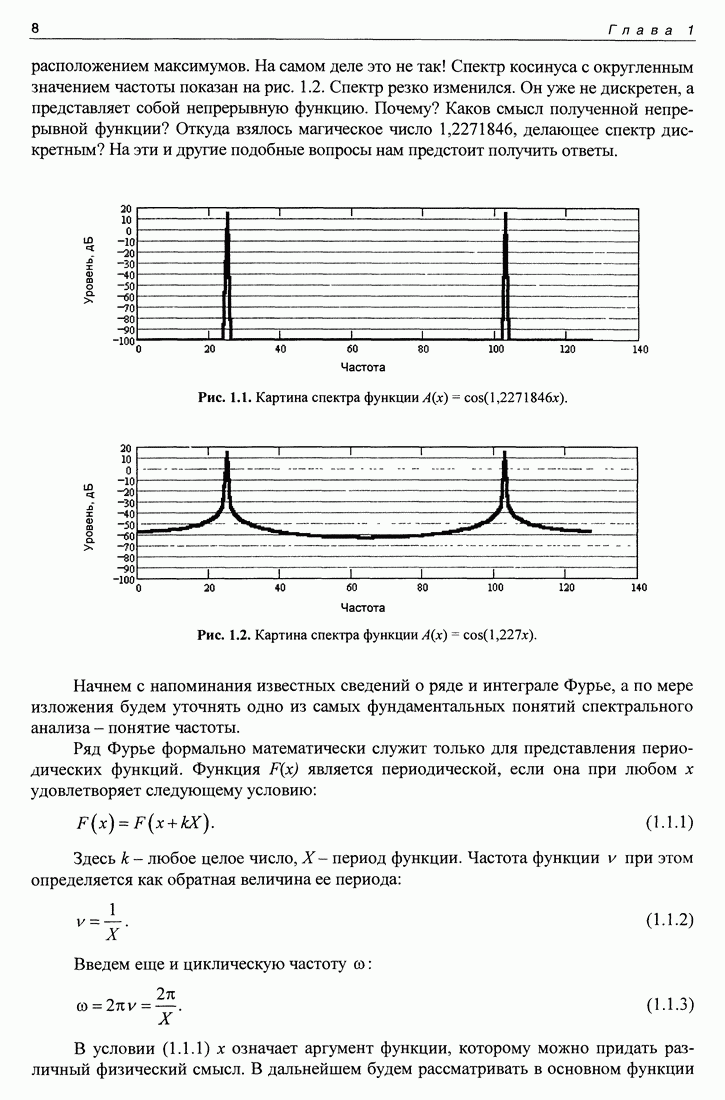
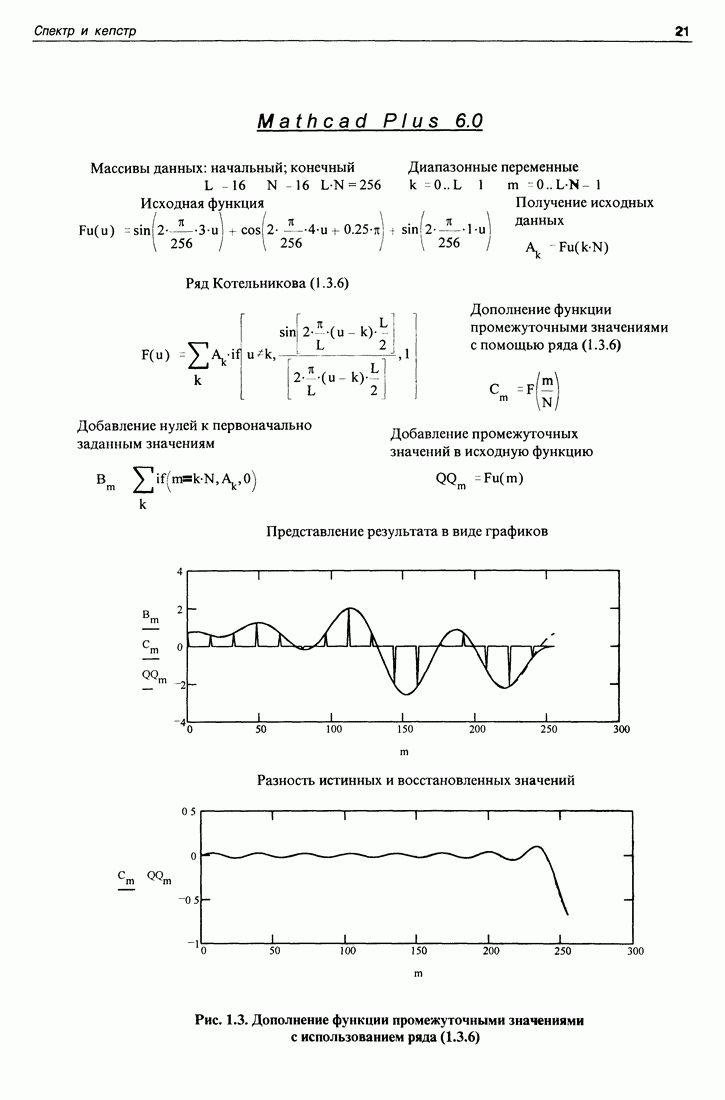
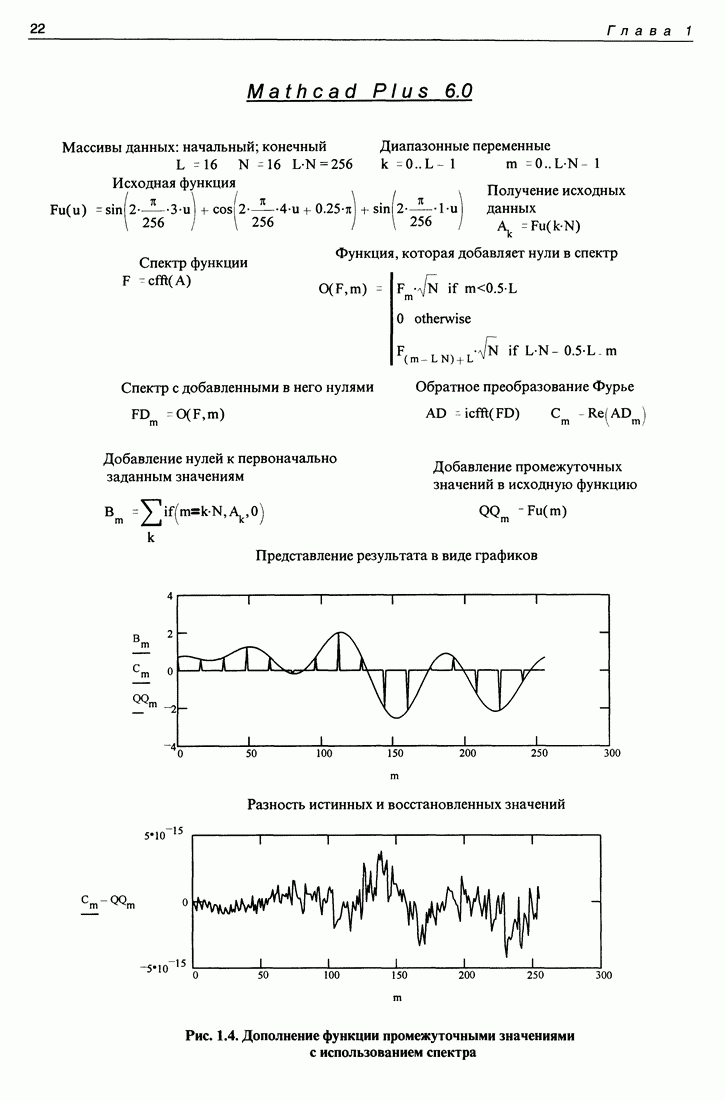
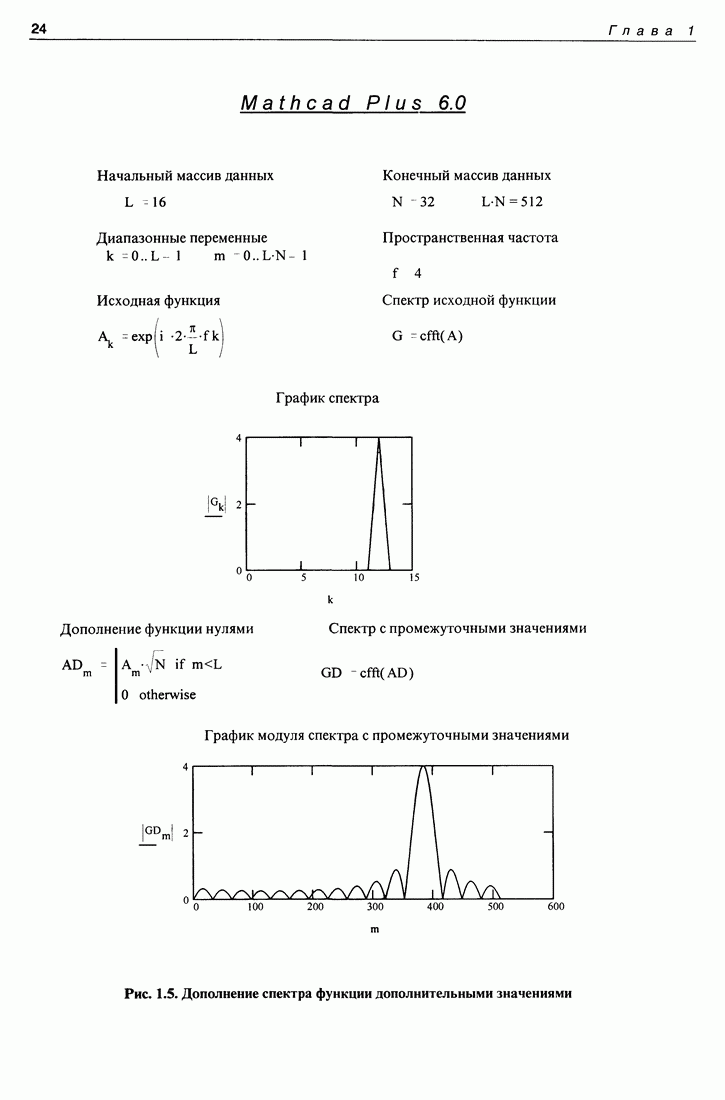
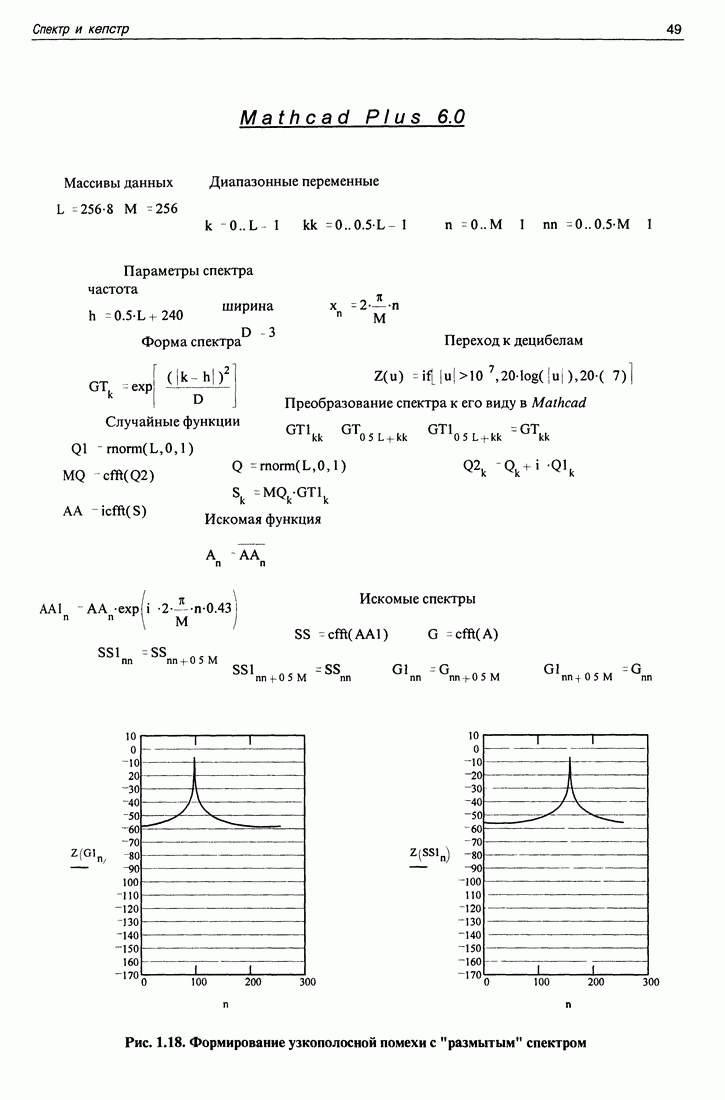
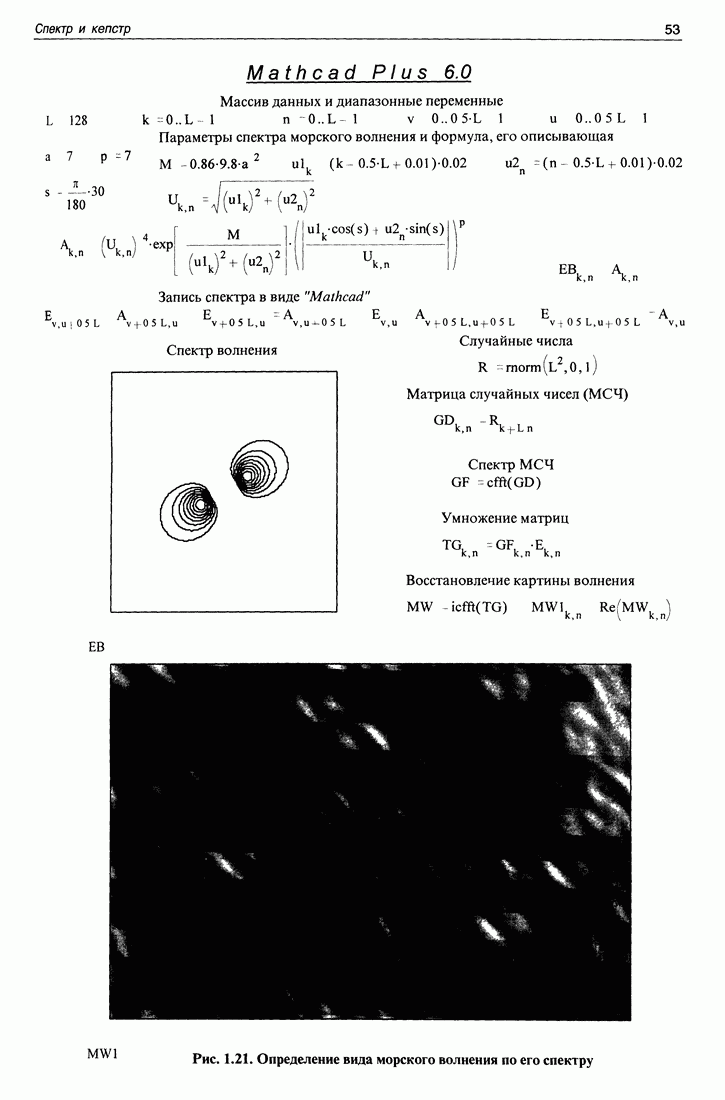
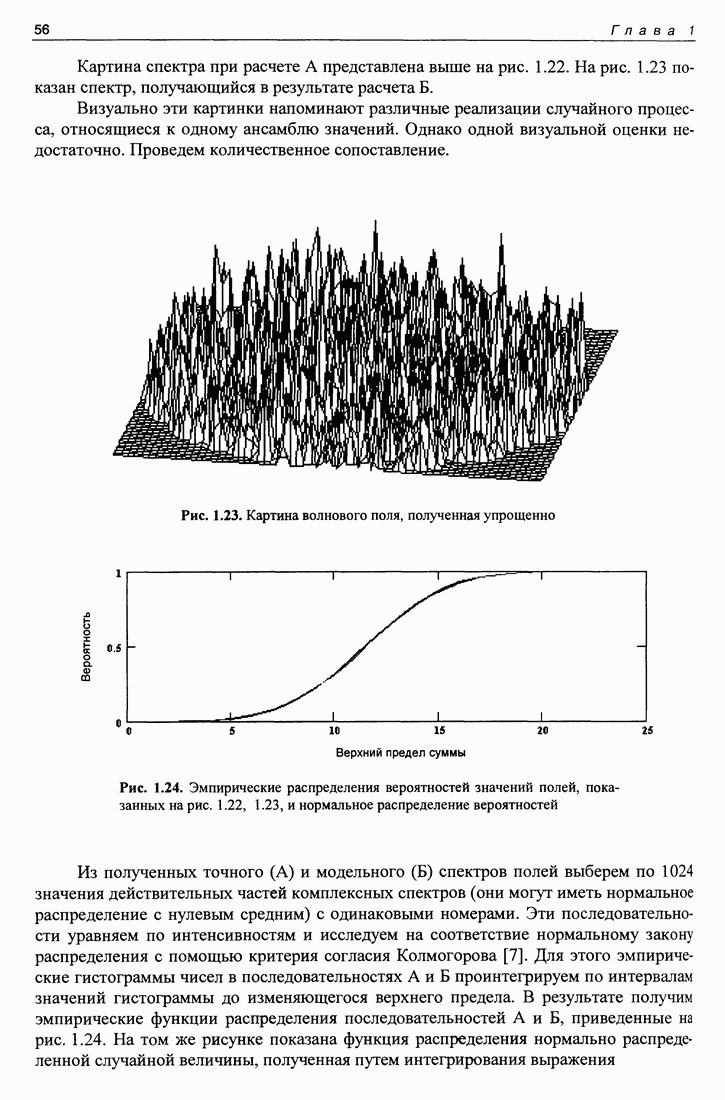
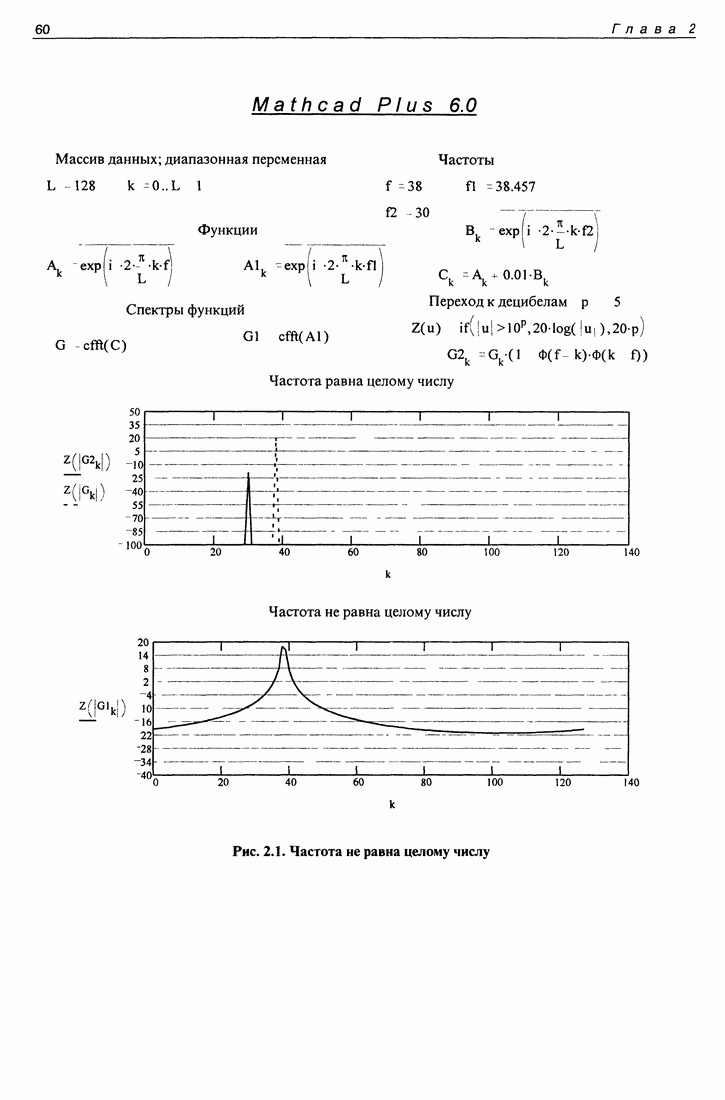
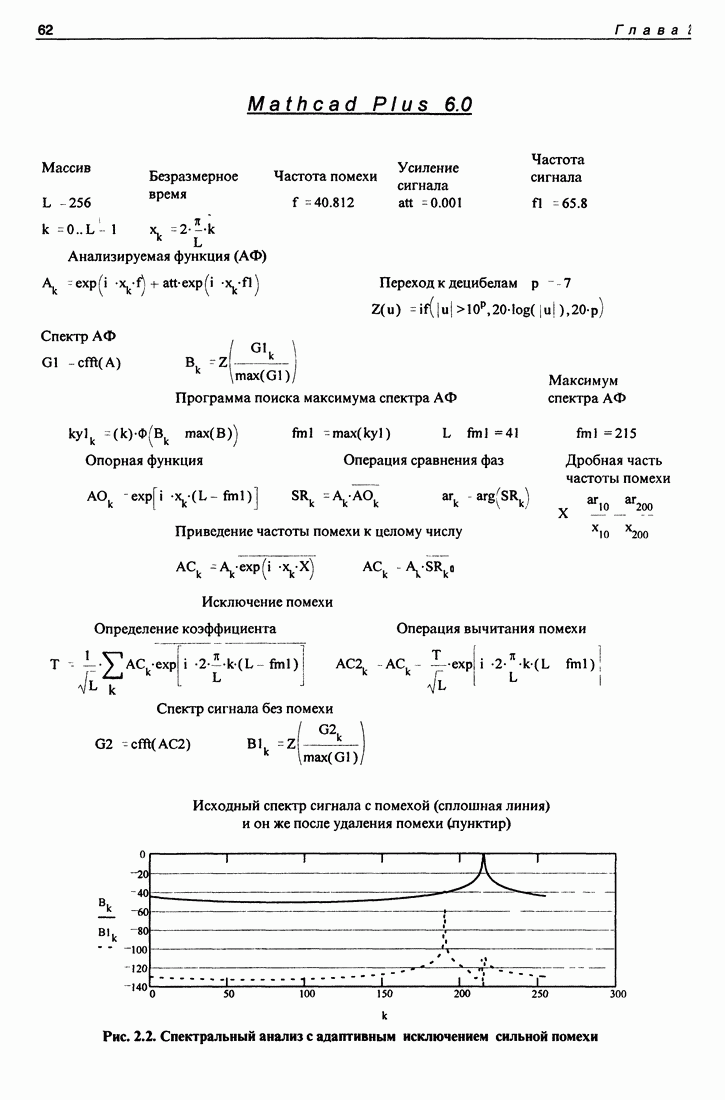
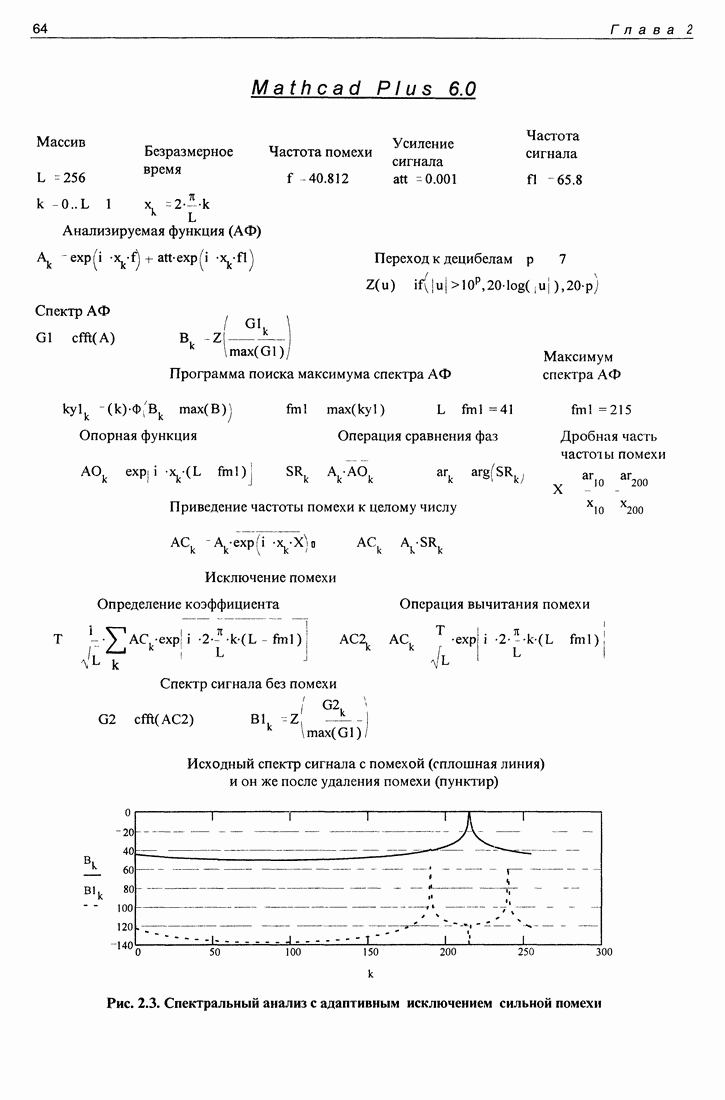
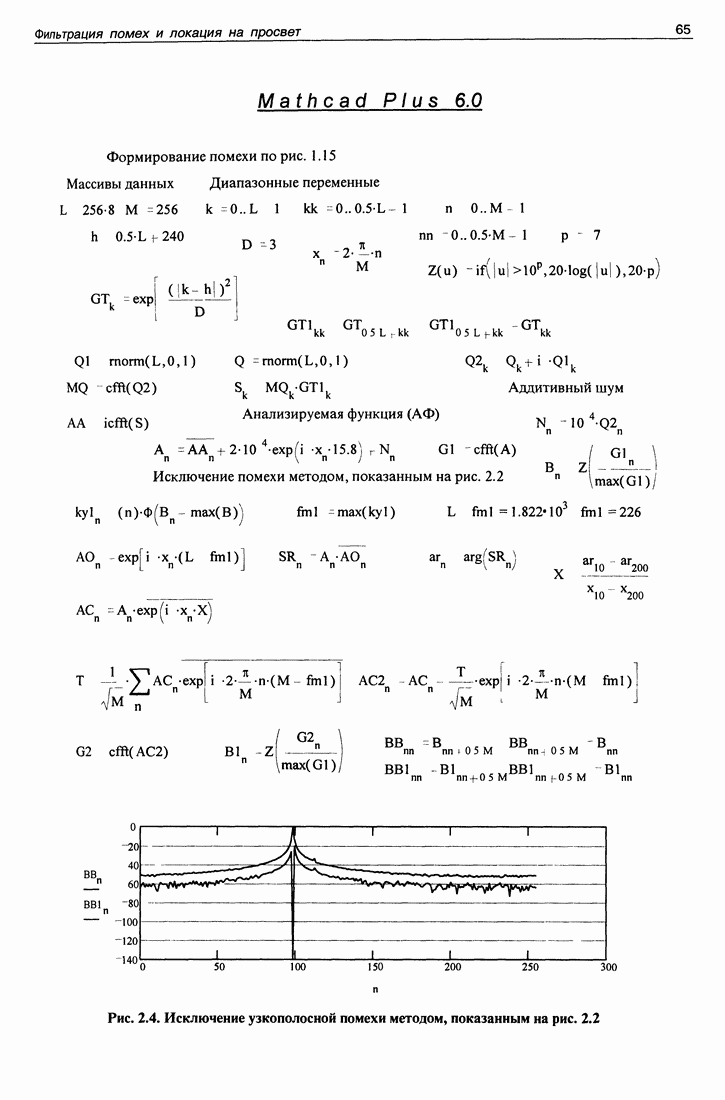
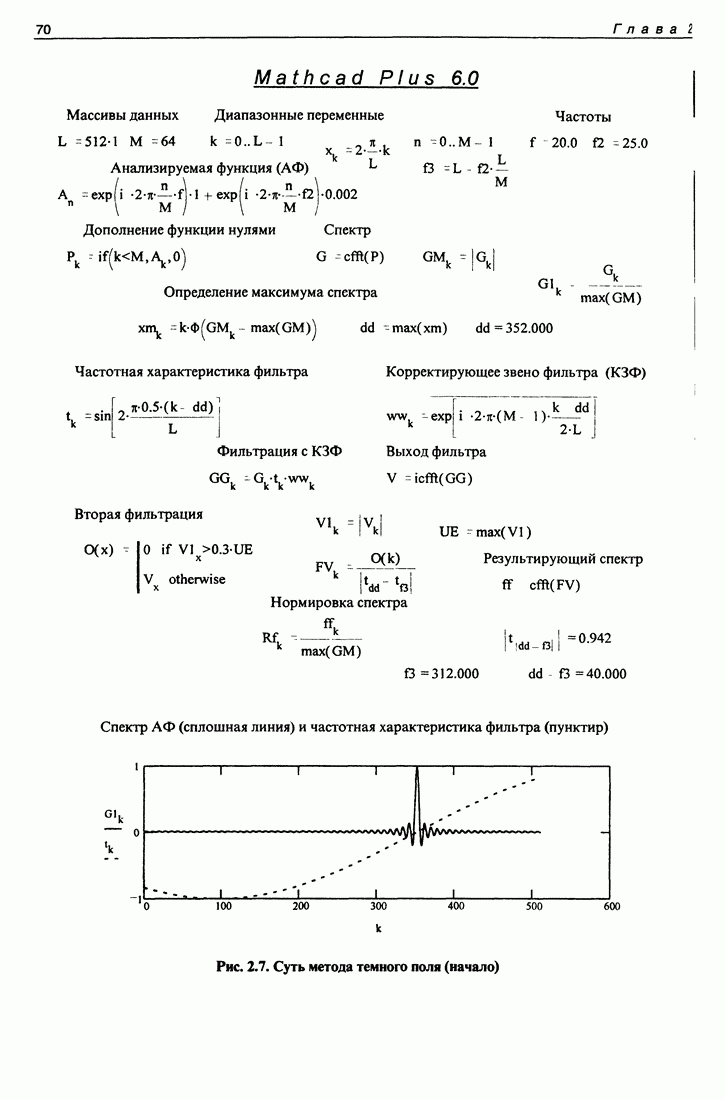
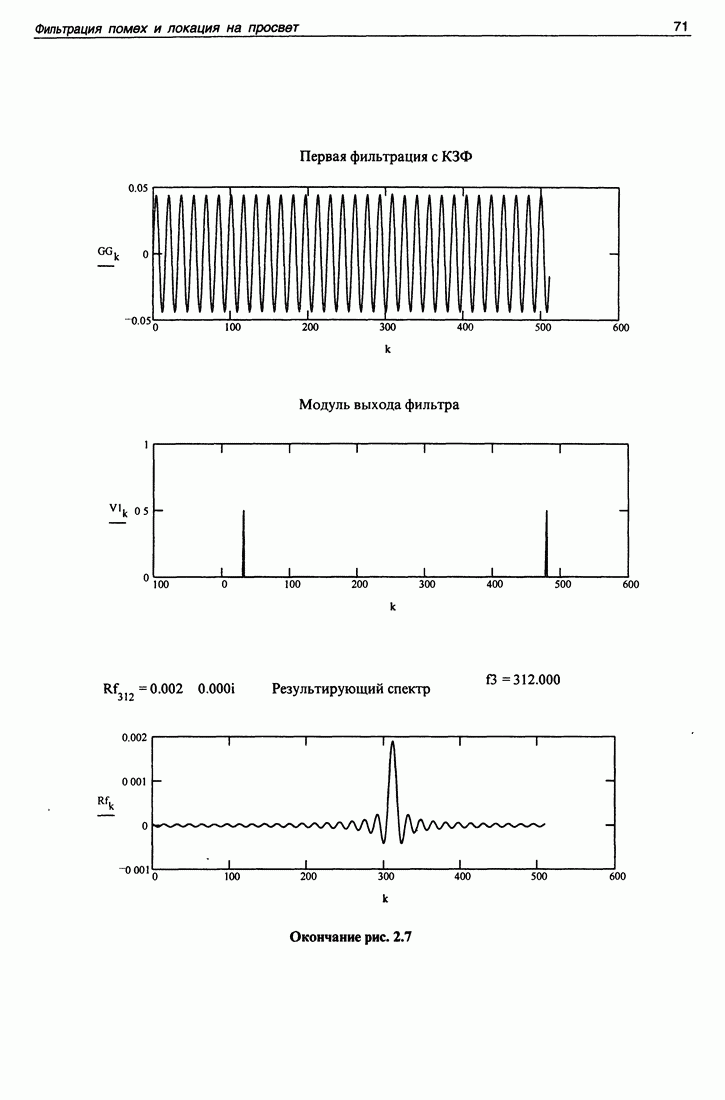
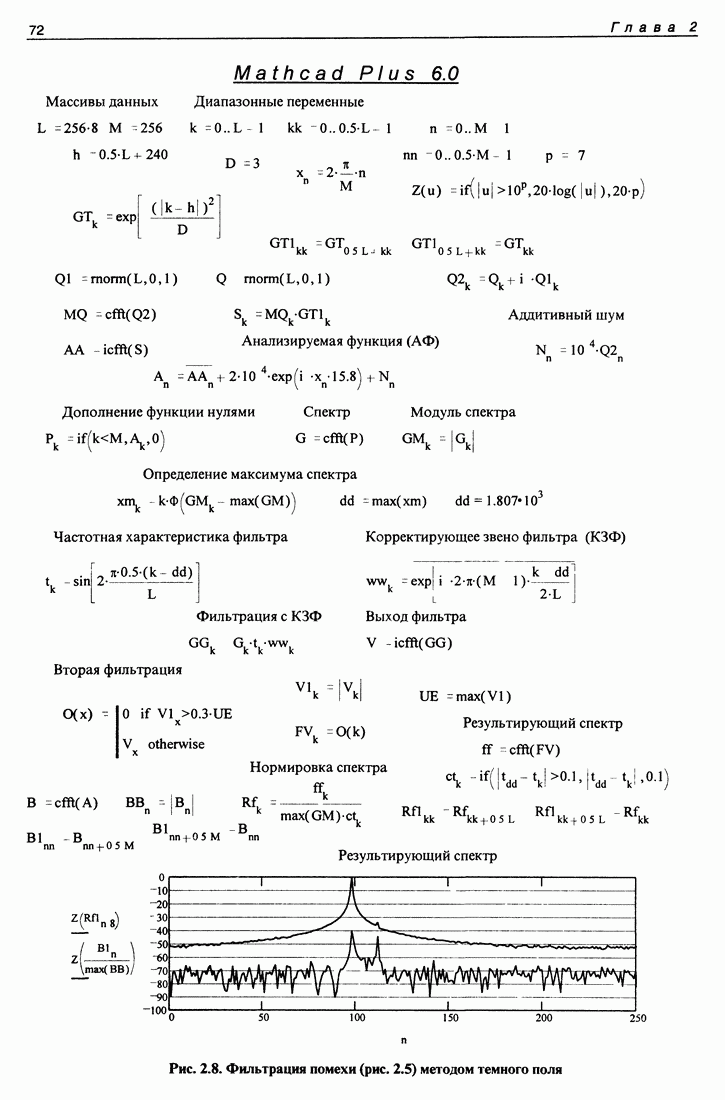
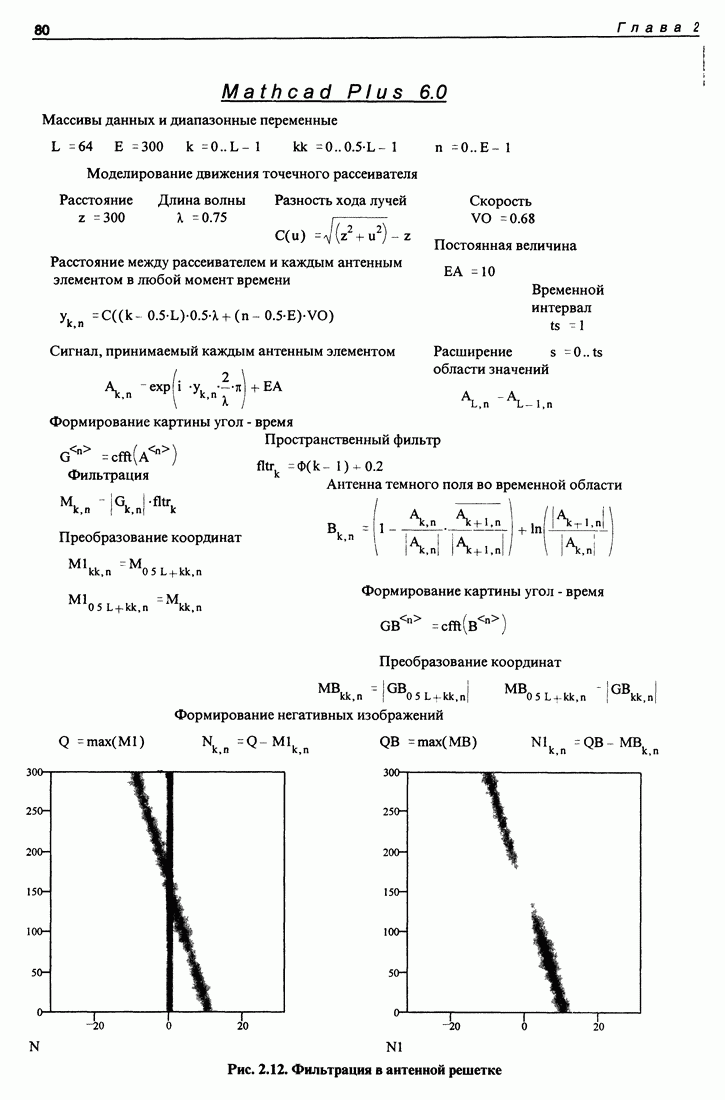
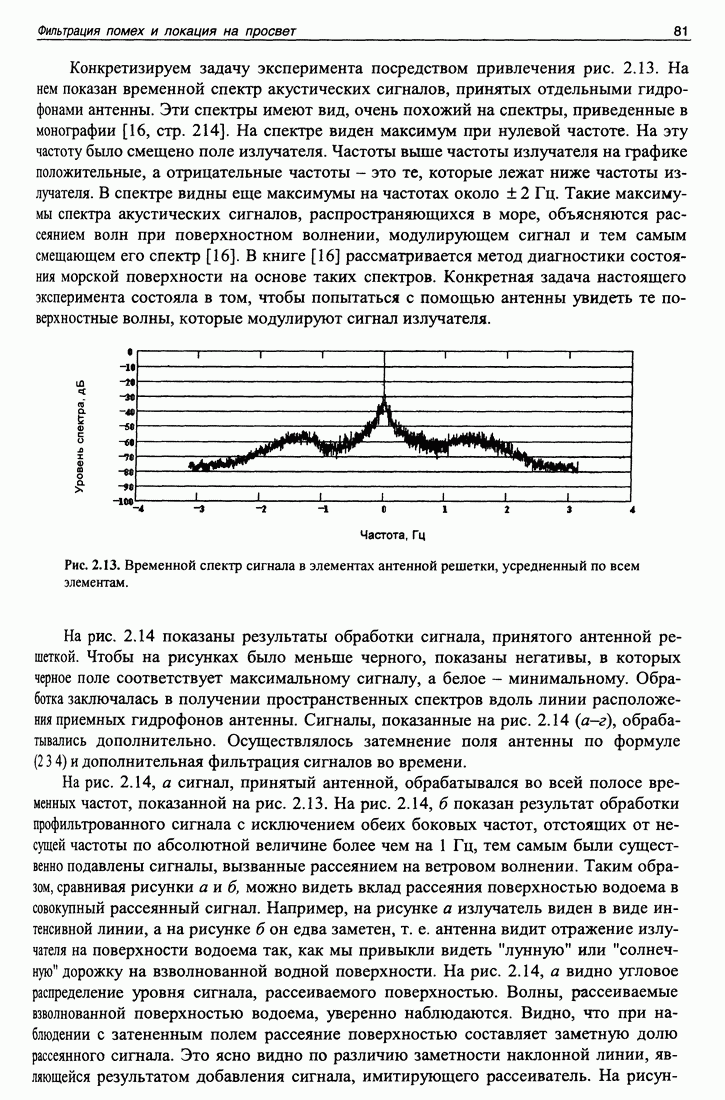
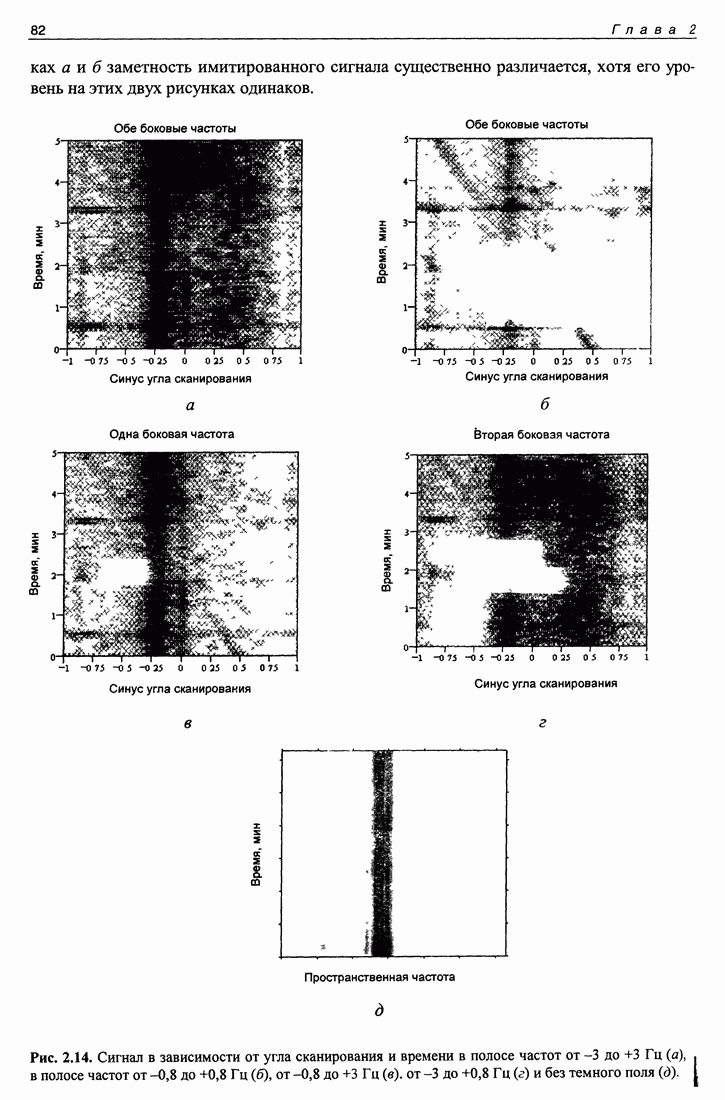
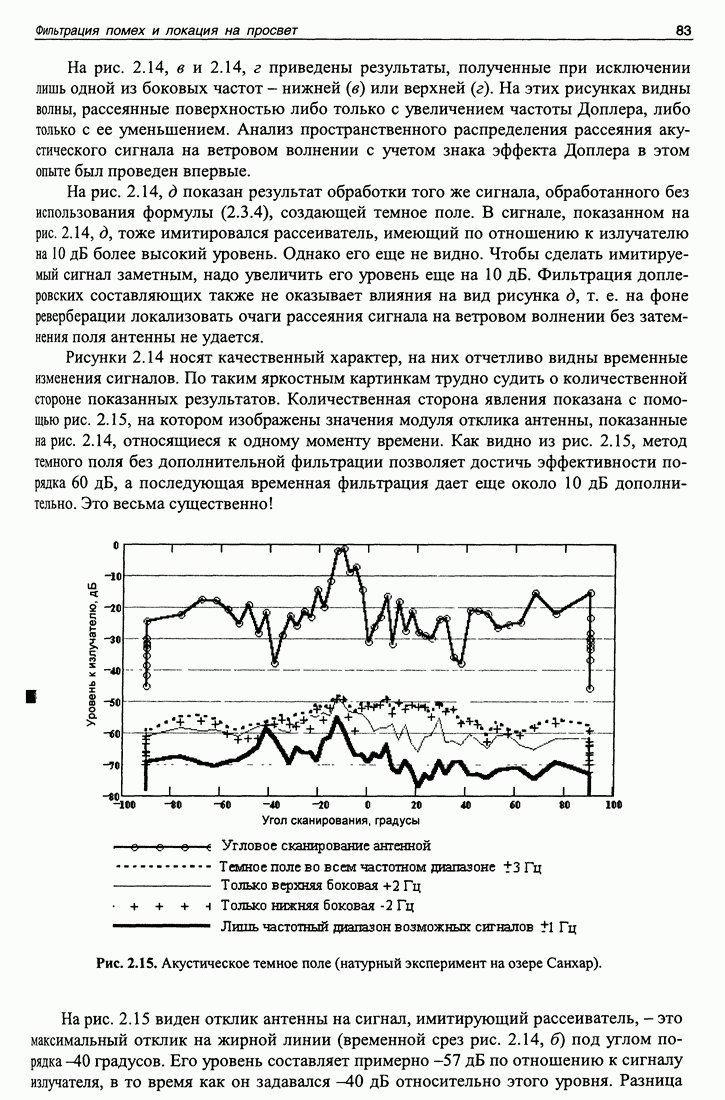
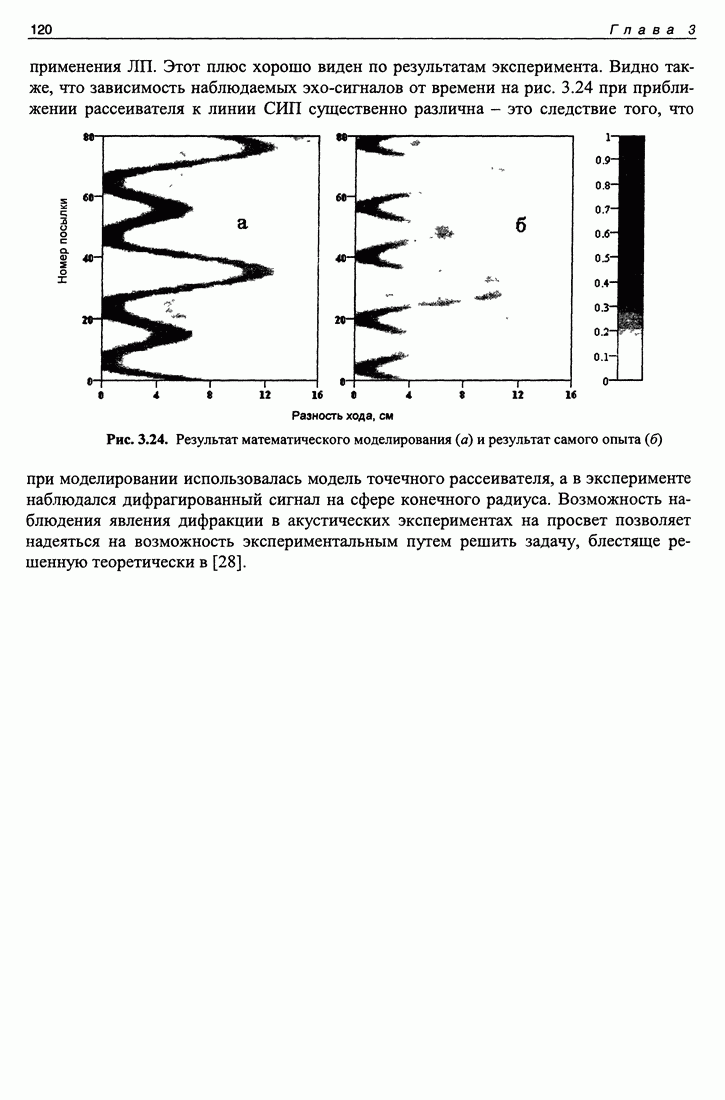
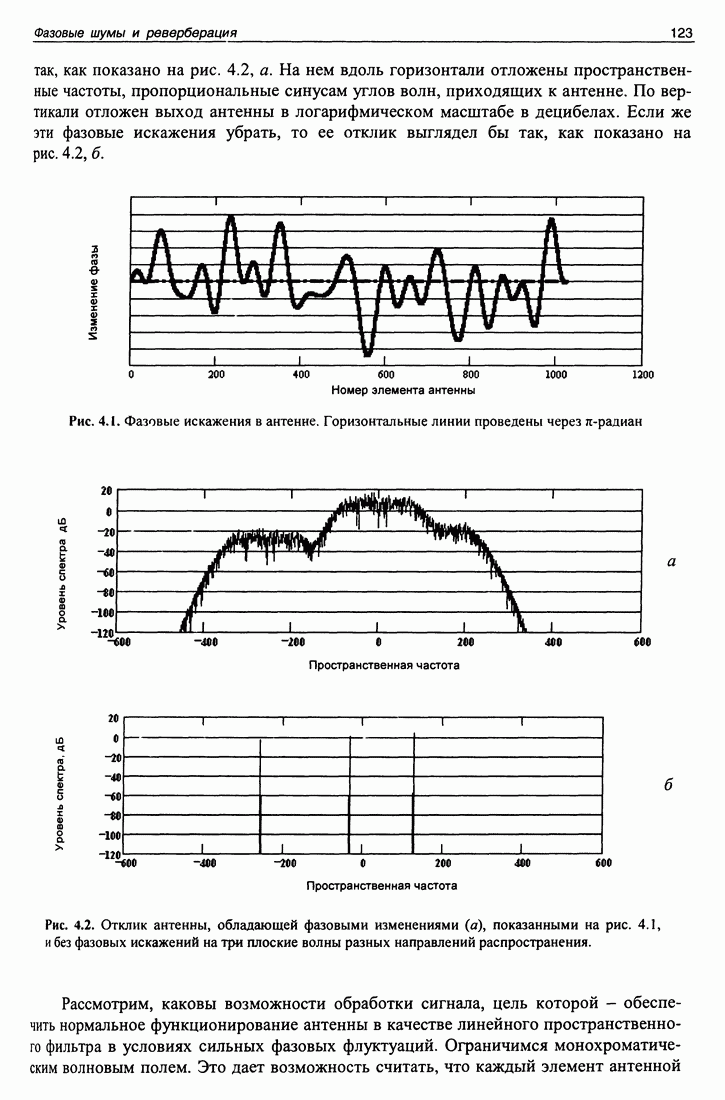
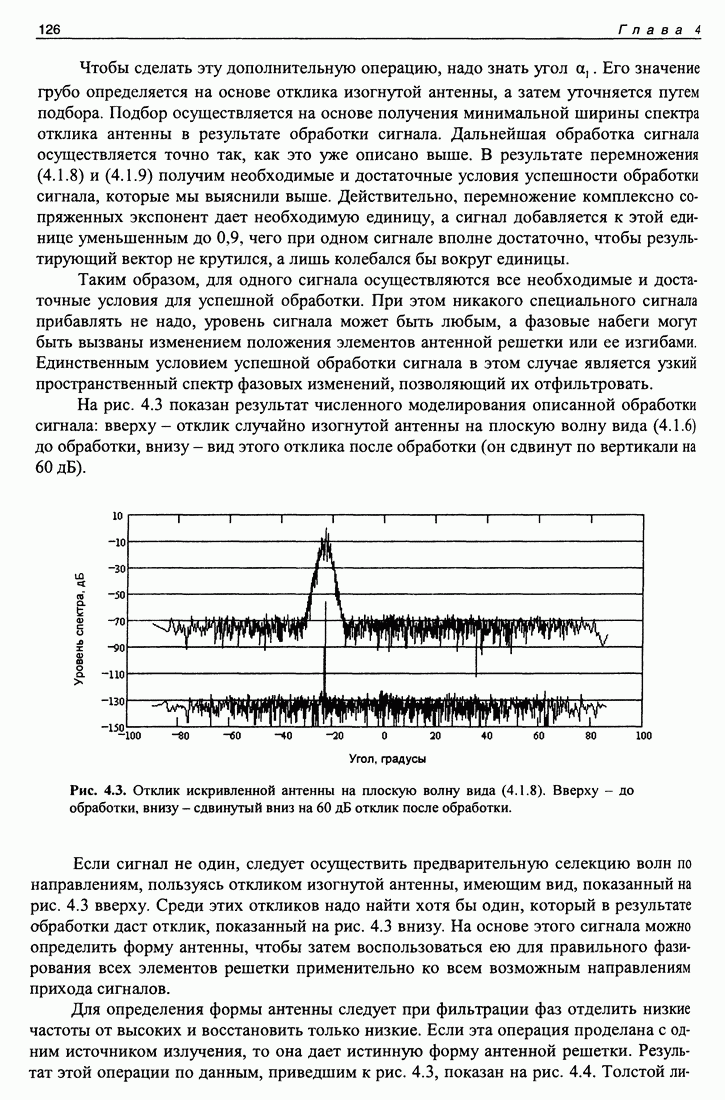
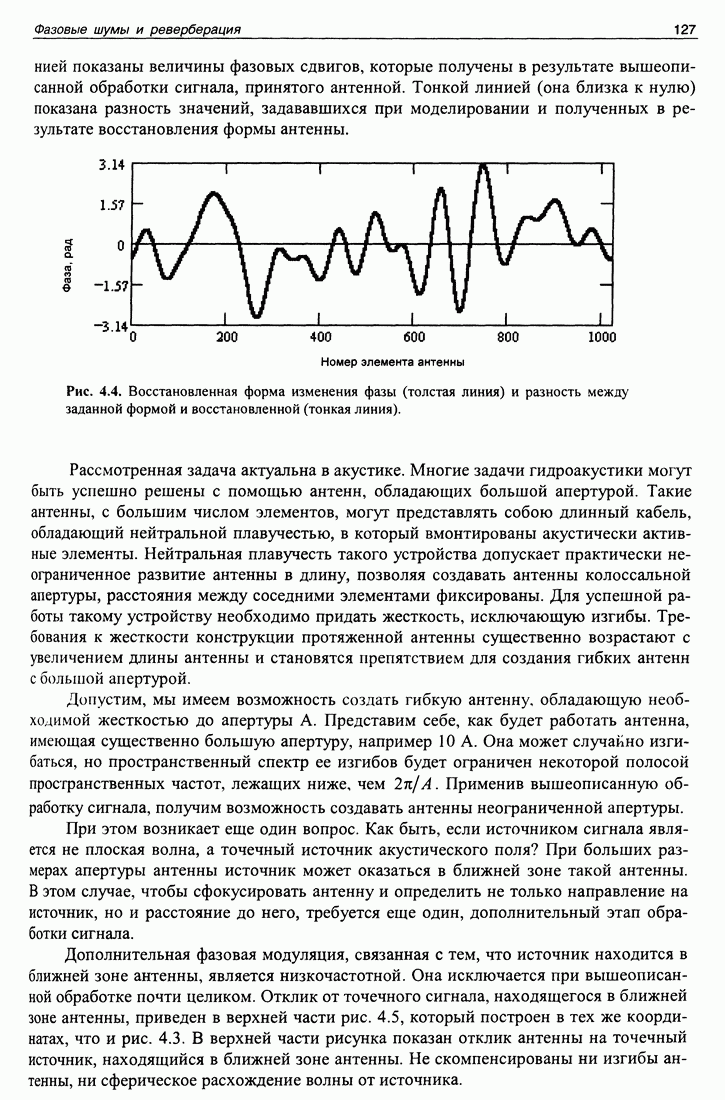
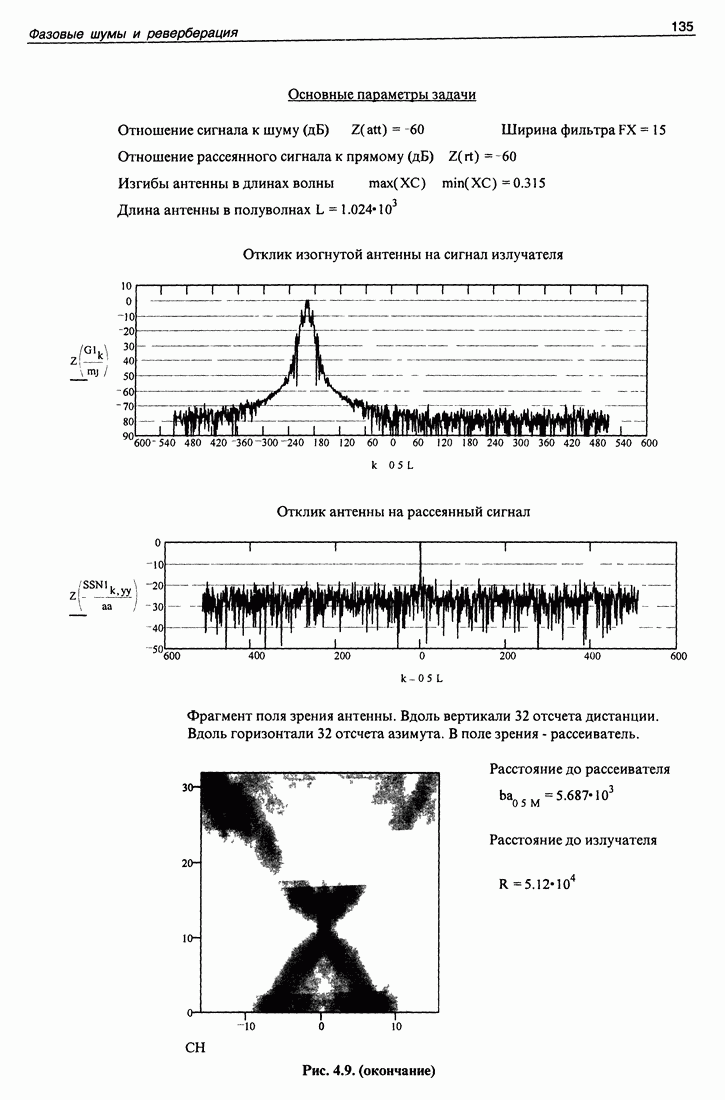
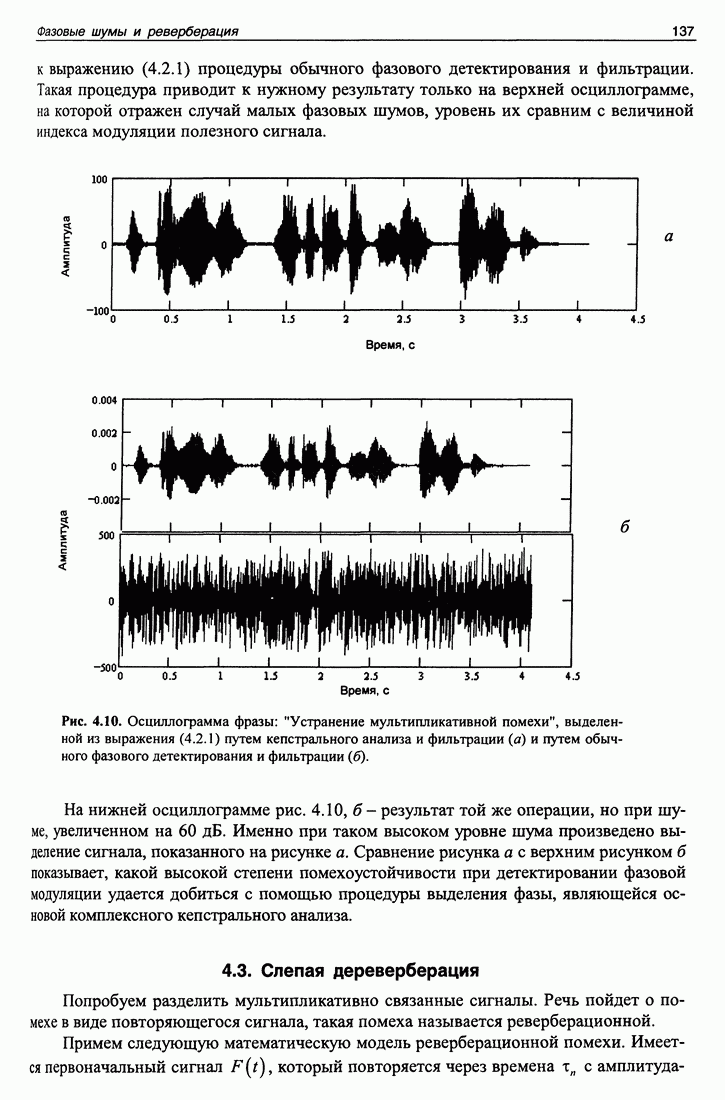
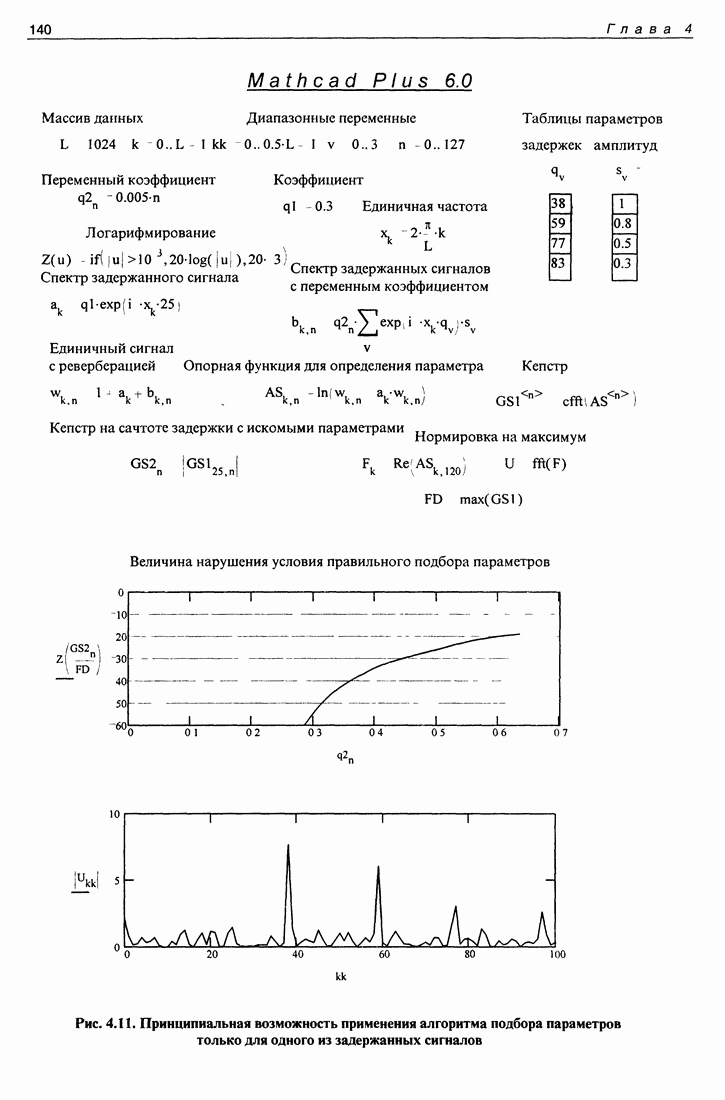
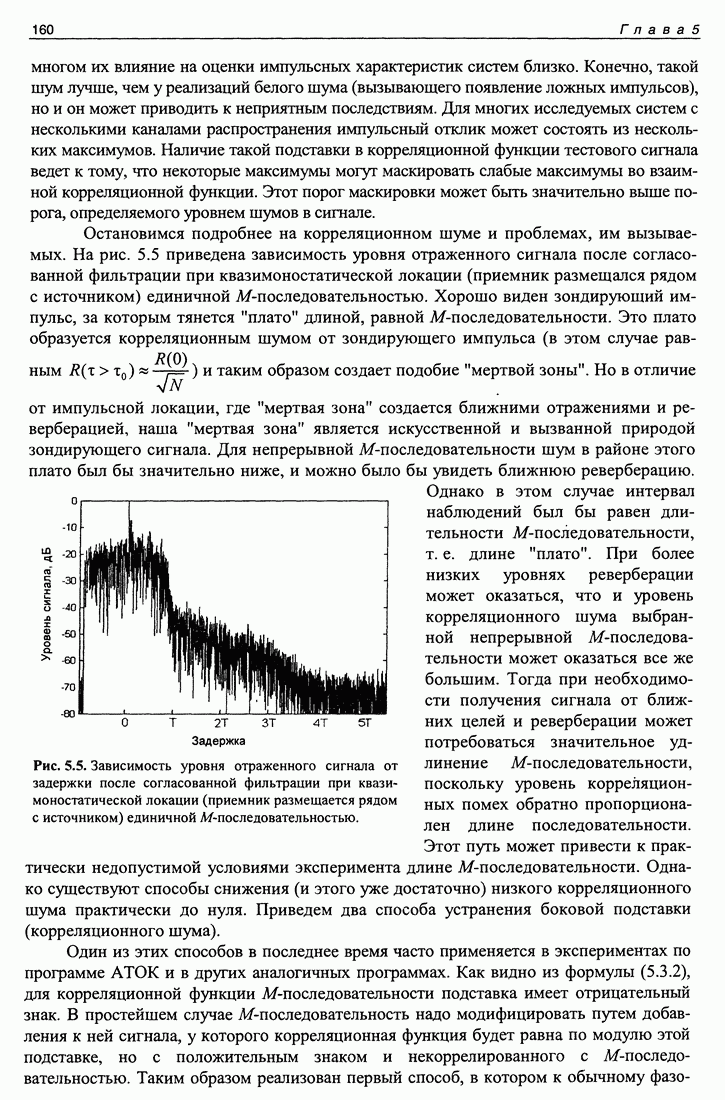
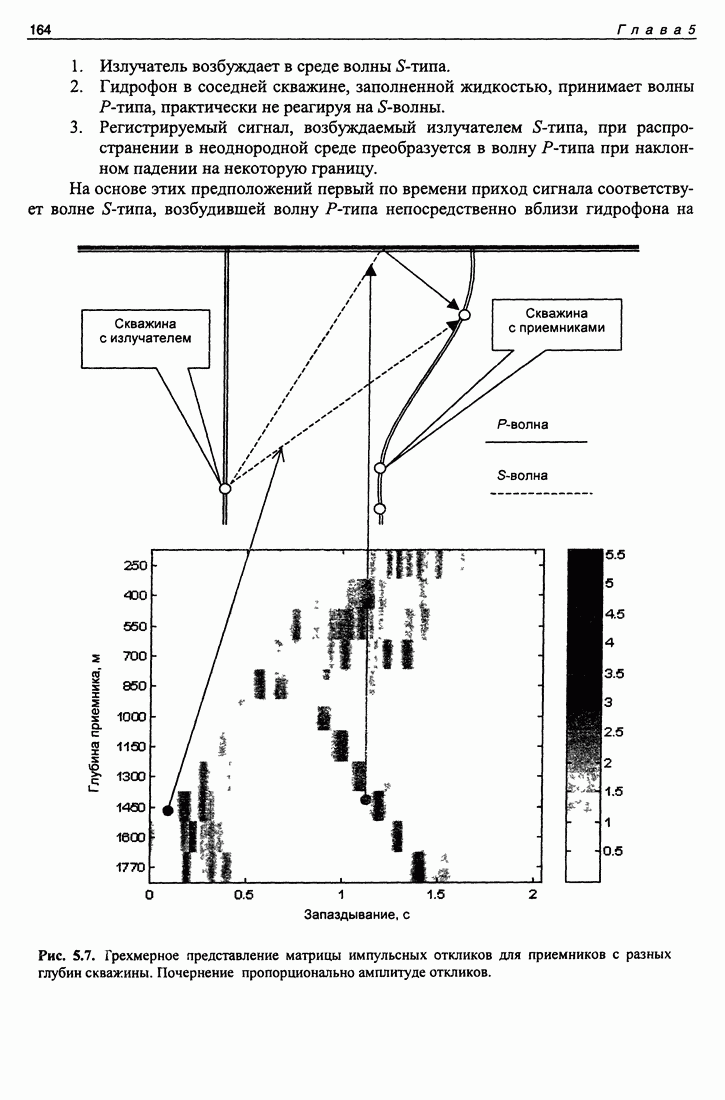
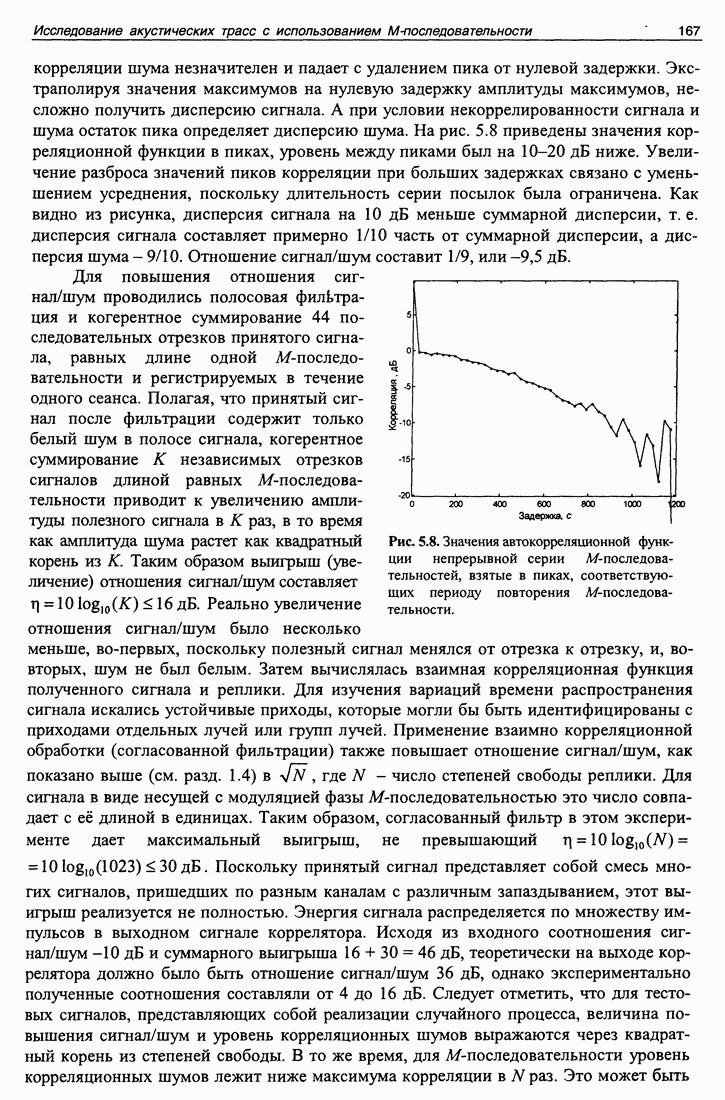
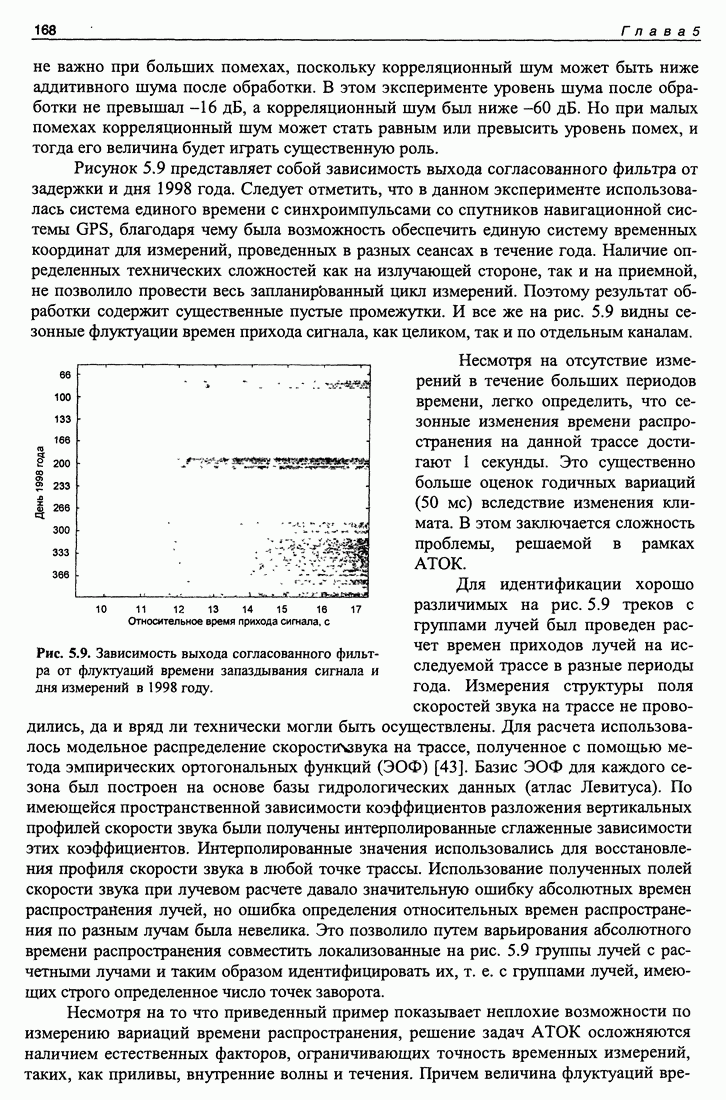
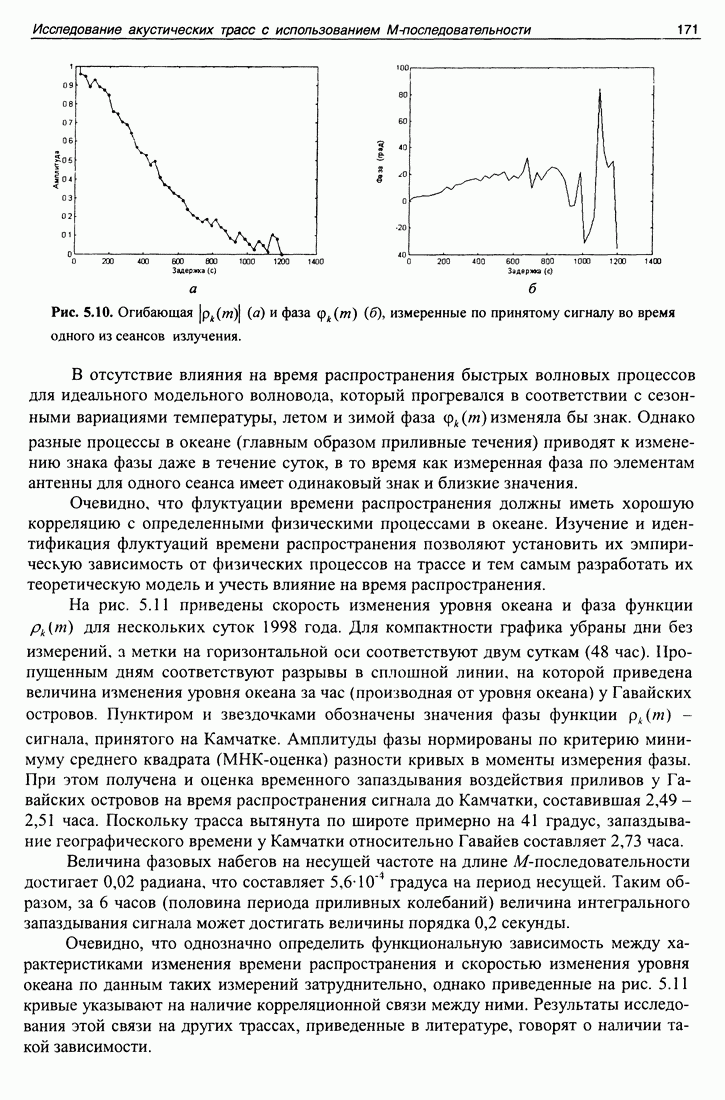
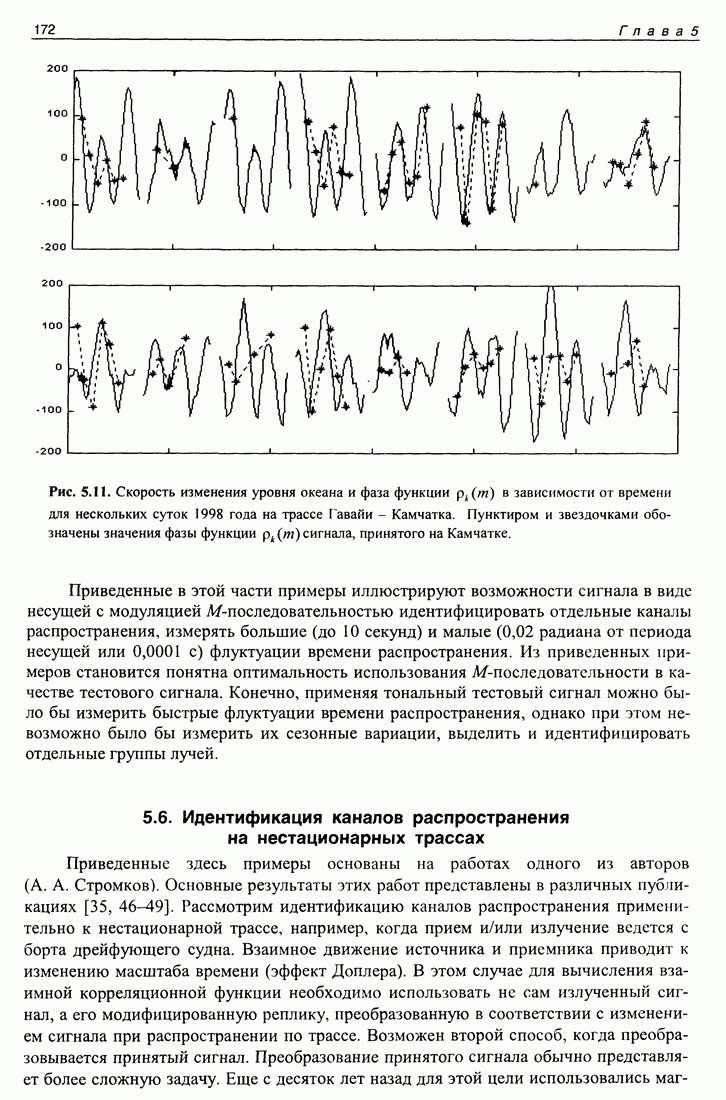
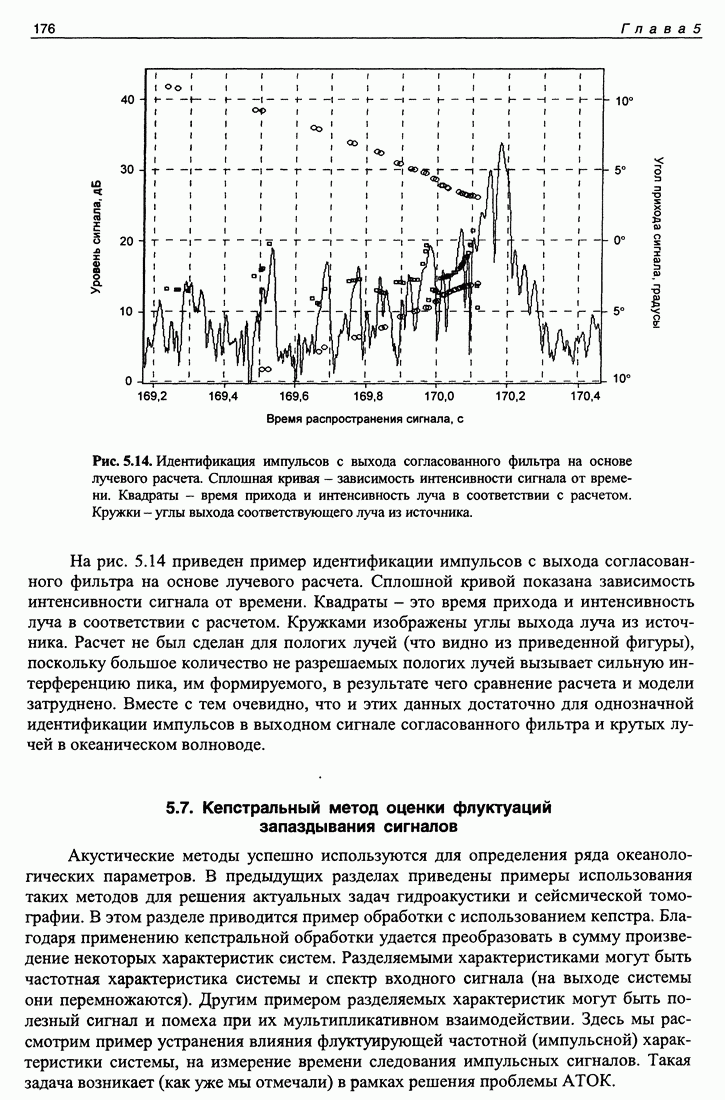
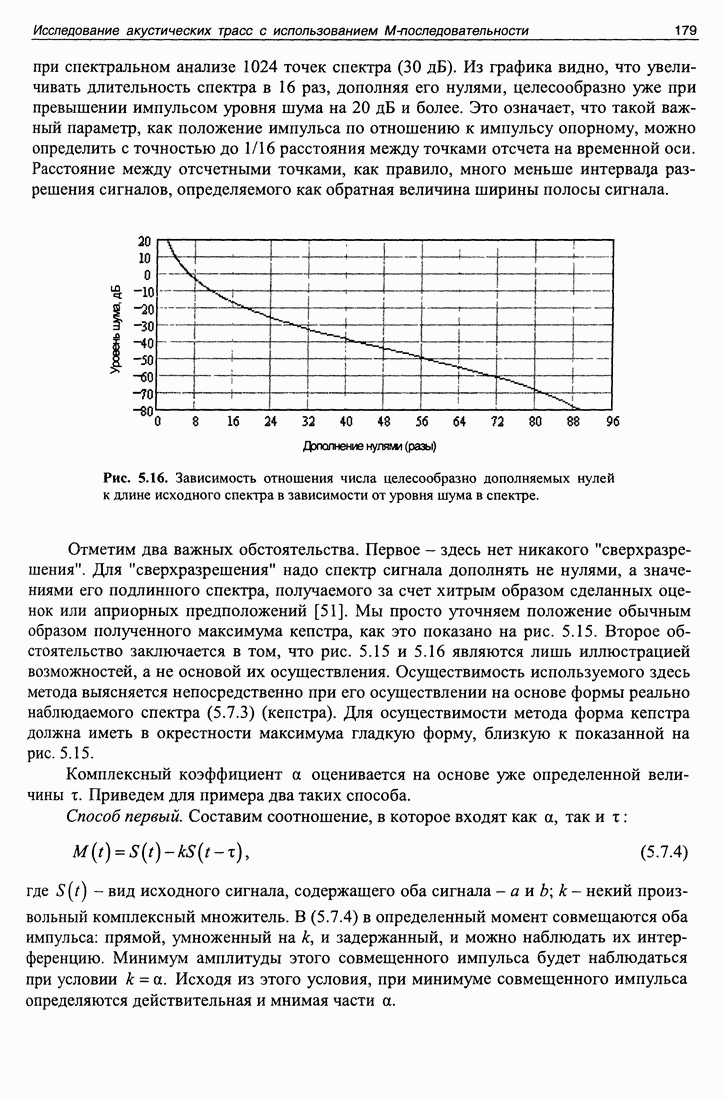
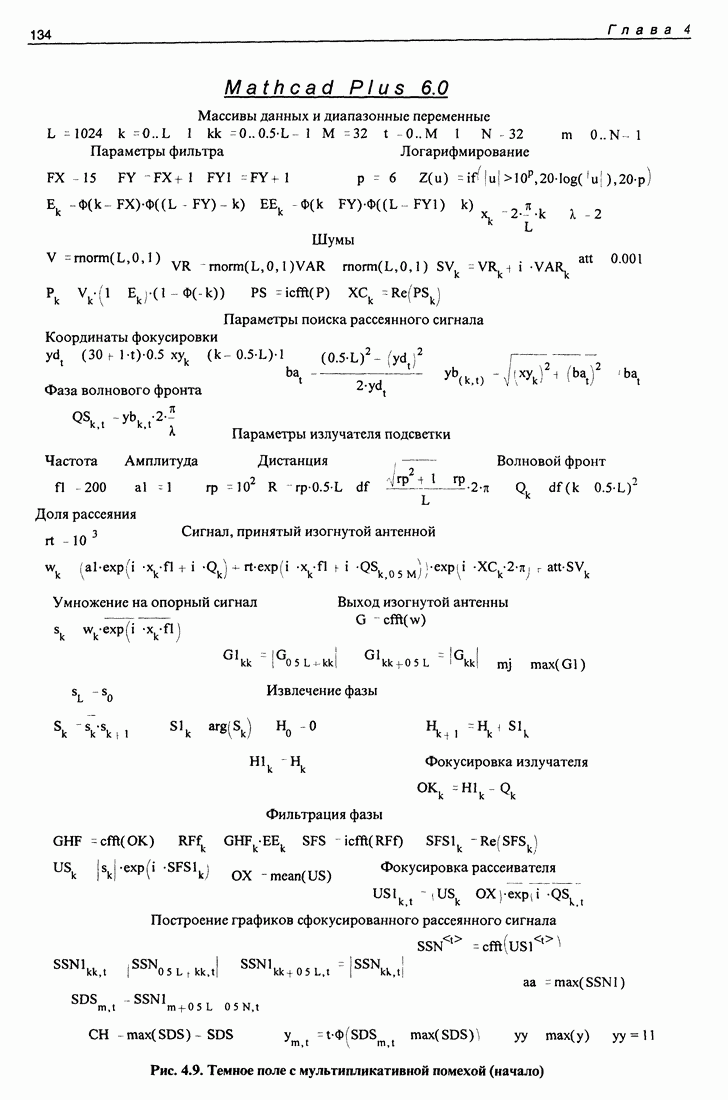| << Предыдущий параграф | Следующий параграф >> |
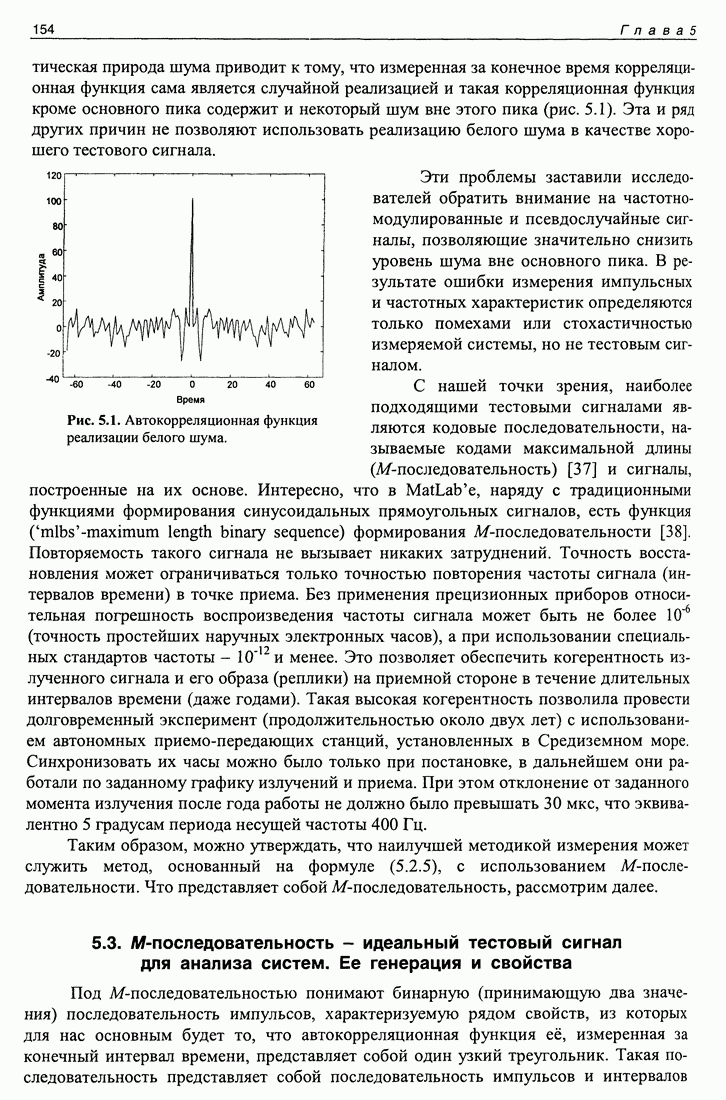
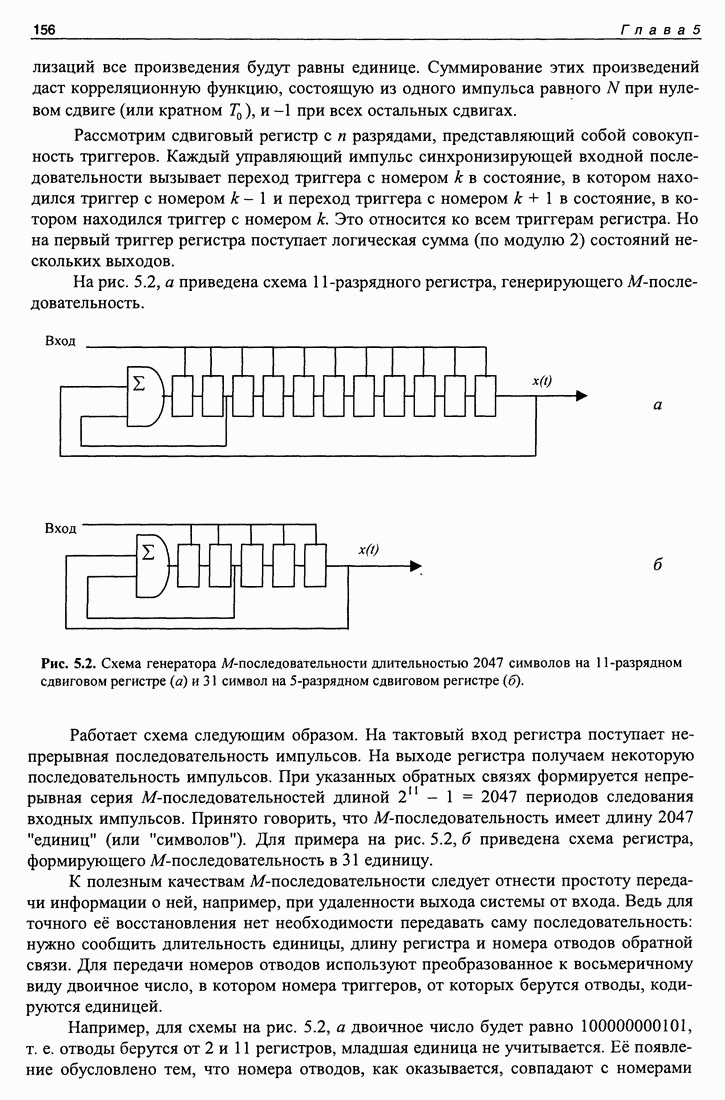
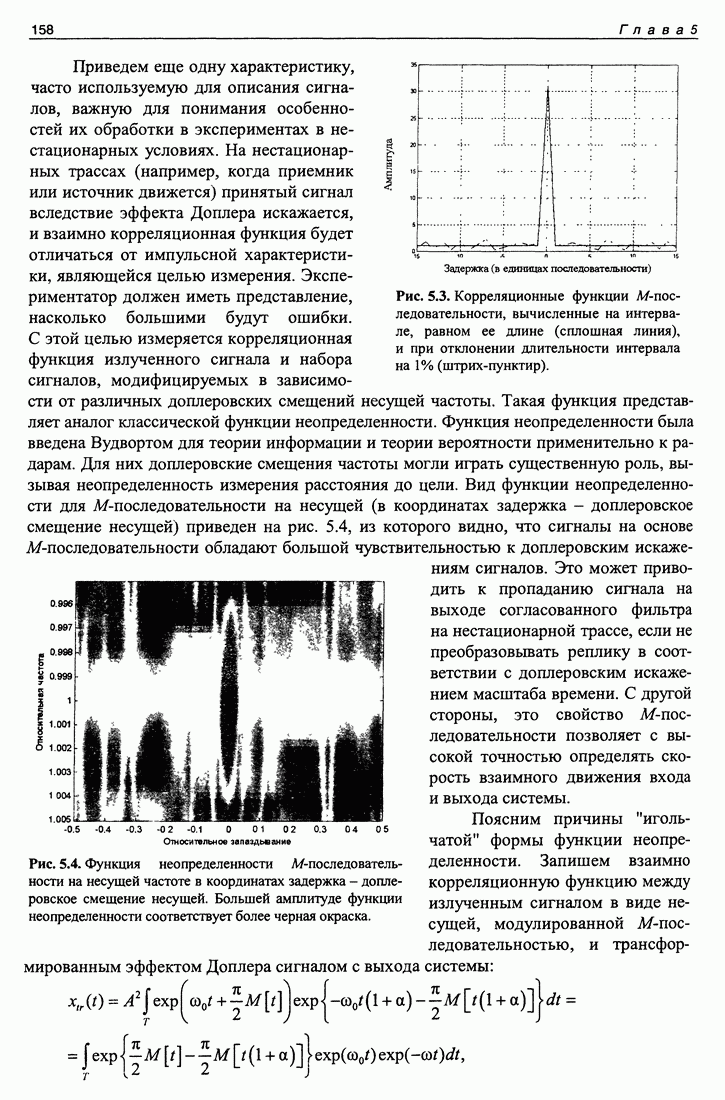
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 3. УВЕЛИЧЕНИЕ ПРОСТРАНСТВЕННОГО ИЛИ ВРЕМЕННОГО РАЗРЕШЕНИЯ
В этой главе рассмотрены методы, позволяющие повысить пространственно! или временное разрешение сигналов на примере решения конкретных задач. Первая задача - об увеличении пространственного разрешения при акустической локации в просвет. Для решения применен синтез апертуры антенны за счет движения рассеивателя, затем рассмотрены методы увеличения временного разрешения сигналов при локации путем сжатия во времени узкополосного сигнала, что получается при использовании зондирующего сигнала, длительность которого составляет много интервалов временного квантования. В результате обработки, заключающейся в выравниванш амплитуд и фаз спектра сигнала, длительность зондирующего сигнала сокращается до одного интервала временного квантования. Условия и тонкости этого метода показаны на примере задачи, решенной с помощью математического моделирования. Рассмотрена помехоустойчивость такого метода сжатия зондирующего сигнала. В за ключение главы рассмотрена задача, решенная как с помощью математического моделирования, так и экспериментально, - это задача о локации на просвет с отделена ем прямого и дифрагированного на цели сигналов по времени их прихода.
3.1. Наблюдение протяженного рассеивателя
В предыдущем разделе была сформулирована и решена задача о наблюдении точечного рассеивателя путем локации на просвет при непрерывном излучении В этом разделе, написанном на основе [19], задачей является наблюдение протяженного рассеивателя. Основное отличие от предыдущего раздела заключается в матема тической модели сигнала. На основе этой модели построен метод обработки сигнала, позволяющий существенно увеличить пространственное разрешение.
Выше было показано, что в условиях эксперимента на озере удается подавить мультипликативную помеху, вызванную флуктуациями амплитуды и фазы сигнала излучателя, на 60 дБ [12]. В результате появилась принципиальная возможность не только выделить рассеянный сигнал, но и рассмотреть форму протяженного рассеива теля. Здесь предлагается дополнить предложенную выше методику фильтрации специальной обработкой выделенного рассеянного сигнала с целью определения разме ров рассеивателя и оценки акустических параметров трассы. Основная особенность обработки сигнала, позволяющая решить поставленную задачу, состоит в таком фази ровании протяженной акустической антенны, при котором она все время нацелена на
движущийся акустический экран. Условие постоянной нацеленности антенны на экран позволяет сделать процедуру помехоустойчивой и дает дополнительное уравнение для определения акустических параметров эксперимента.
Поясним общую схему опыта и методику обработки полученных в его ходе экспериментальных данных. Принципиальная возможность визуализации акустического поля на протяженном рассеивателе вытекает из следующих очевидных соображений. Волновое поле в плоскости, включающей поверхность акустического экрана, может быть вычислено по полю, наблюдаемому в плоскости, находящейся на расстоянии  от него. Успех решения такой задачи на основе измеренного поля определяется двумя факторами: первый заключается в достаточной точности измерений; второй - в том, что значения должны быть зафиксированы на большой пространственной протяженности (достаточной апертуре).
от него. Успех решения такой задачи на основе измеренного поля определяется двумя факторами: первый заключается в достаточной точности измерений; второй - в том, что значения должны быть зафиксированы на большой пространственной протяженности (достаточной апертуре).
Опыт состоял в том, что акустически непрозрачный экран протягивался между акустическим излучателем и приемной антенной, содержащей 64 приемных элемента, расположенных горизонтально в линию на апертуре размером А = 12 м. Расстояние  от трассы движения экрана до антенны составляло 150 м. При размере экрана порядка 4 м, а длине акустической волны порядка 0,5 м это обеспечивало выполнение условий дифракции Фраунгофера для поля за экраном в месте расположения антенны. Антенна в пределах своей апертуры также была в зоне дифракции Фраунгофера, что не позволяло непосредственно с помощью антенны определять распределение поля вдоль экрана, антенна позволяла определять лишь направление на экран, представлявшийся в виде точечного объекта. Однако экран двигался, и значения поля на антенне многократно фиксировались за время перемещения экрана. Эти данные можно было использовать для увеличения эффективной апертуры антенны путем ее синтеза.
от трассы движения экрана до антенны составляло 150 м. При размере экрана порядка 4 м, а длине акустической волны порядка 0,5 м это обеспечивало выполнение условий дифракции Фраунгофера для поля за экраном в месте расположения антенны. Антенна в пределах своей апертуры также была в зоне дифракции Фраунгофера, что не позволяло непосредственно с помощью антенны определять распределение поля вдоль экрана, антенна позволяла определять лишь направление на экран, представлявшийся в виде точечного объекта. Однако экран двигался, и значения поля на антенне многократно фиксировались за время перемещения экрана. Эти данные можно было использовать для увеличения эффективной апертуры антенны путем ее синтеза.
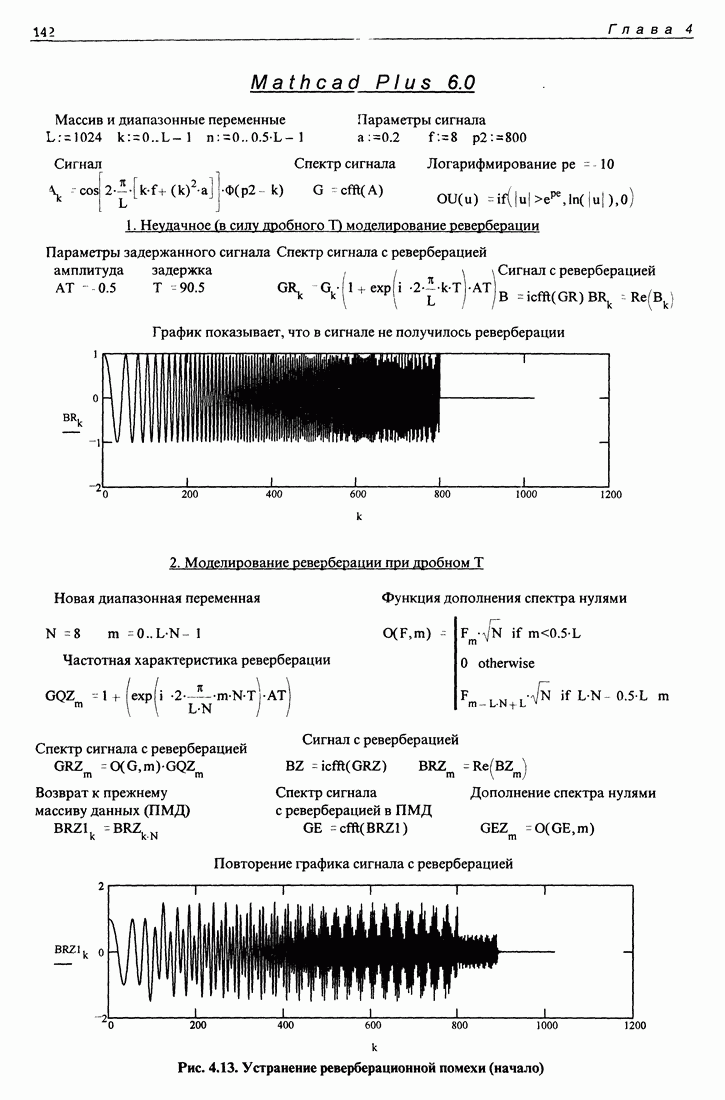
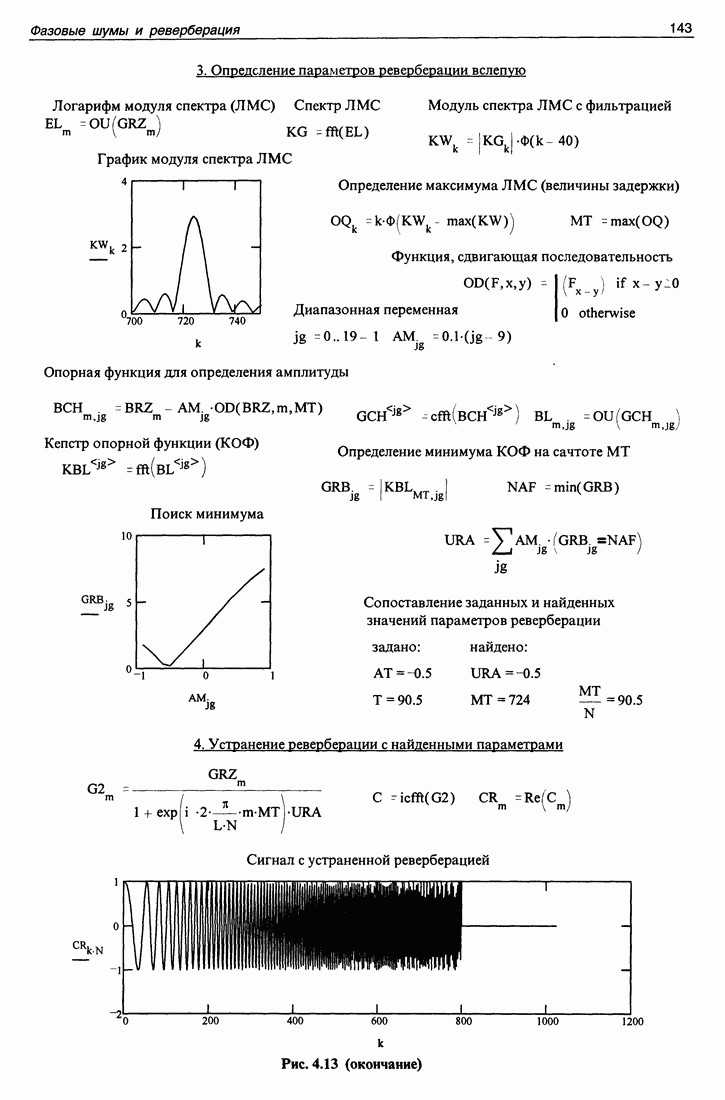
С целью проверки этой возможности было выполнено математическое моделирование процесса измерения. Волновое поле на движущемся экране было математически смоделировано и вычислено на антенне в пределах ее апертуры А для всех фиксируемых в ходе эксперимента 1024 положений экрана. При этом была учтена геометрия эксперимента и сделаны предположения, что волна распространяется в свободном пространстве, а поле непосредственно за акустически непрозрачным экраном в соответствии с известным правилом Кирхгофа равно нулю, а вне экрана остается невозмущенным. Такие правила, подменяющие решение дифракционной задачи, в дальнейшем будем называть правилом Кирхгофа. Правило Кирхгофа является хорошим приближением для экранов больших волновых размеров в пределах малых углов дифракции. По вычисленным 64 х 1024 значениям волнового поля в дальней зоне была численно решена задача о восстановлении значений волнового поля в непосредственной близости за экраном. Результат решения этой задачи показан на рис. 3.1 и напоминает форму экрана, предполагавшегося в расчетах прямоугольным.
Это не означает, что столь же успешным будет реальный эксперимент.
В реальном эксперименте волна распространяется не в свободном

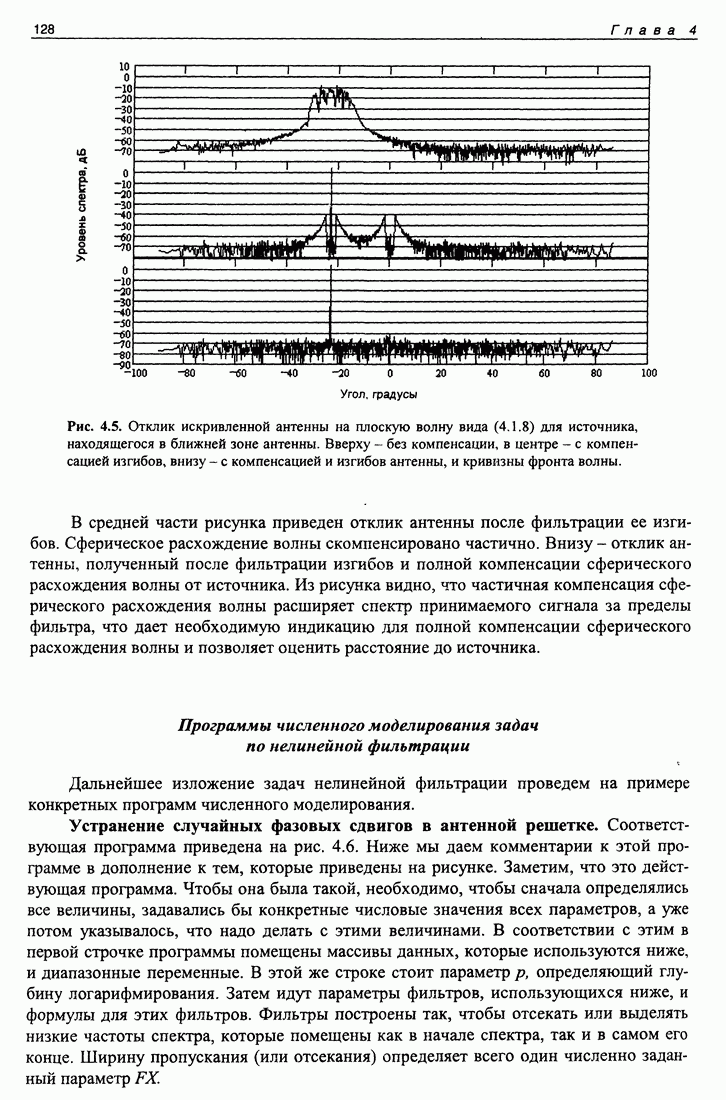
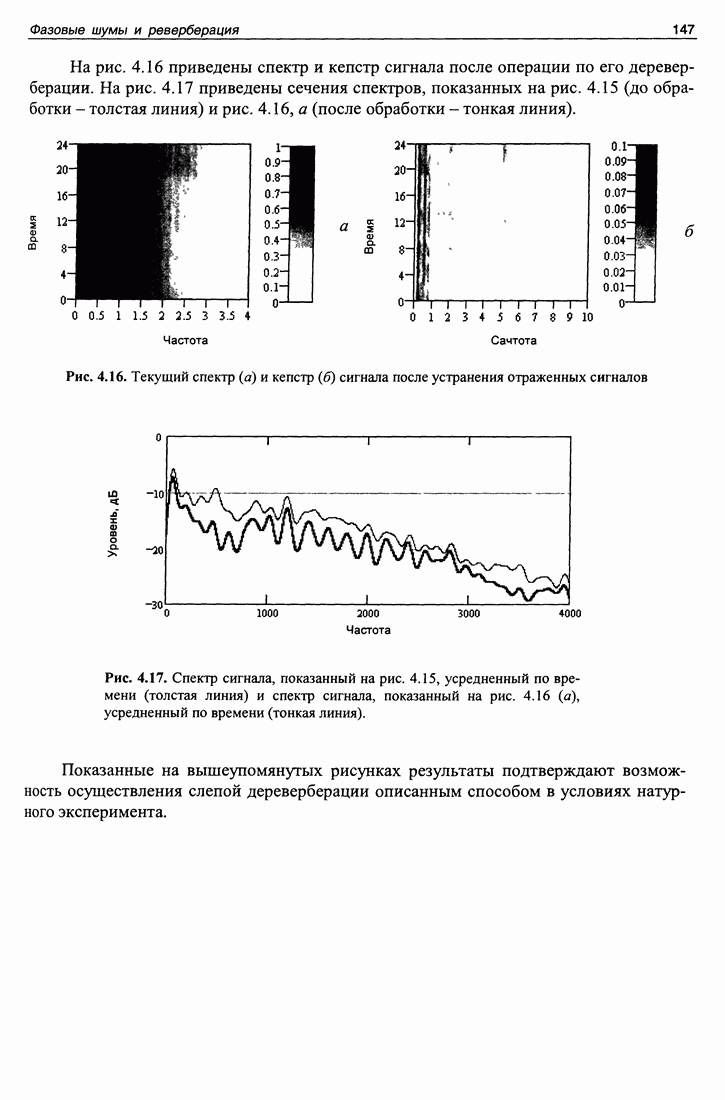
Рис. 3.1. Изображение поля на рассеивателе. Сверху - действительная часть поля, в середине - мнимая часть, внизу - модуль.
пространстве, а в природном волноводе, отражаясь от дна и поверхности озера. На результат может оказать влияние межмодовая интерференция, модуляция сигнала поверхностным волнением, внутренние волны и ряд других факторов. Кроме того, трудно ожидать, что справедливо правило Кирхгофа, так как экран обладает волновым размером, который меньше 10 длин волн.
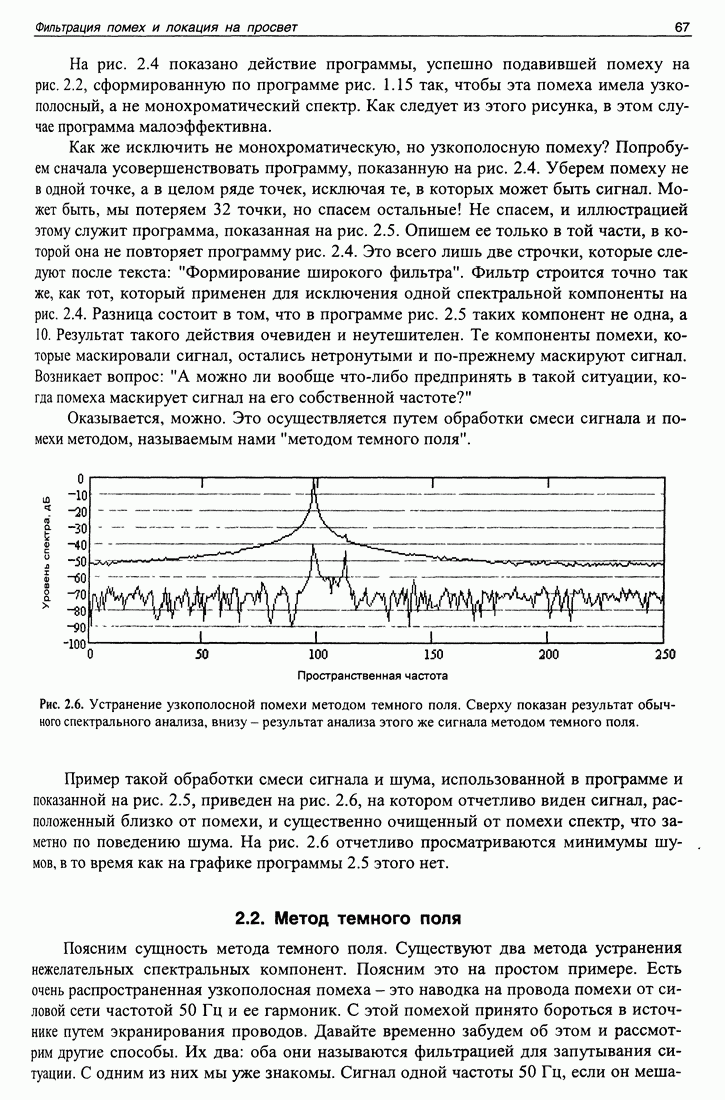
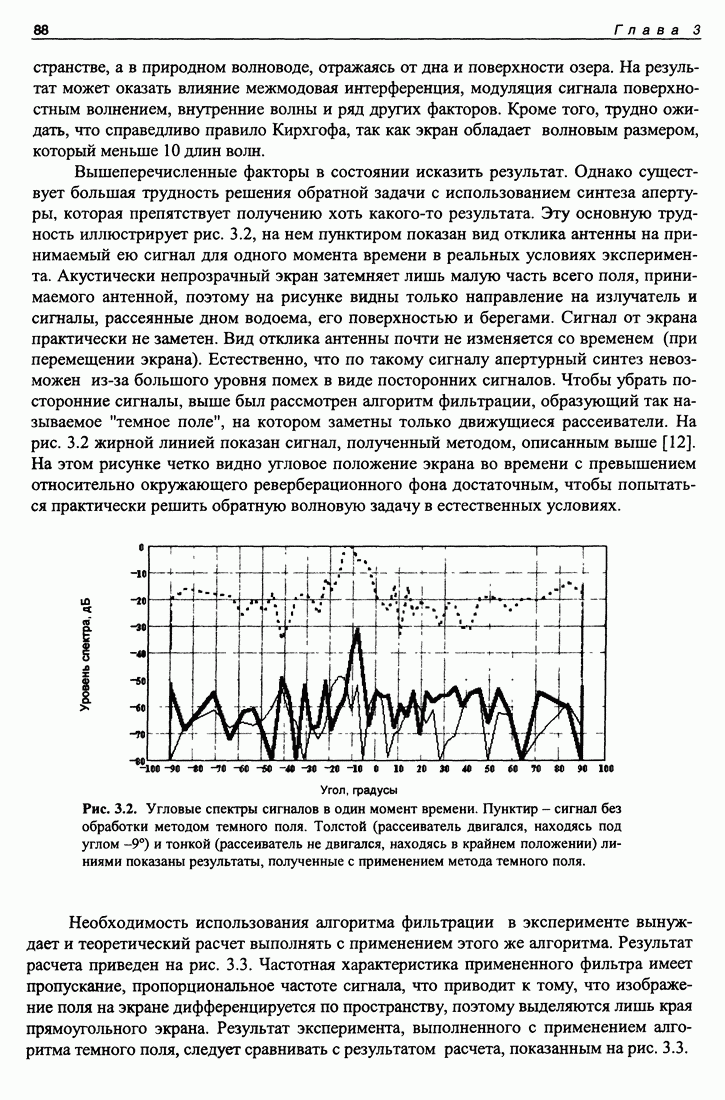
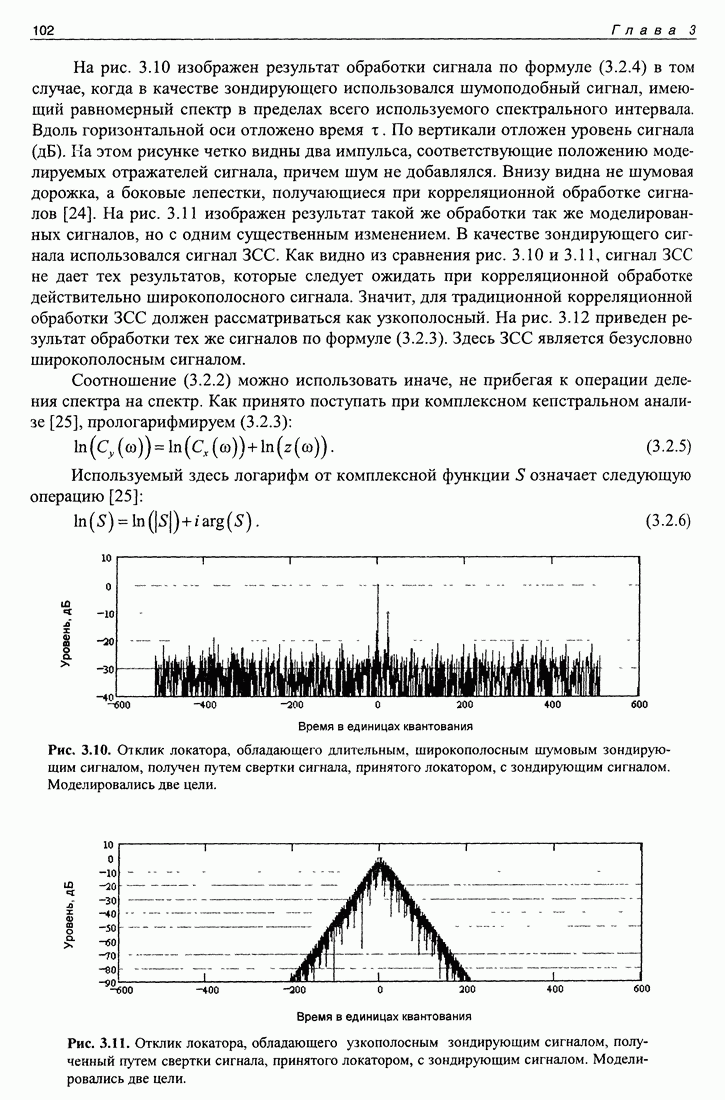
Вышеперечисленные факторы в состоянии исказить результат. Однако существует большая трудность решения обратной задачи с использованием синтеза апертуры, которая препятствует получению хоть какого-то результата. Эту основную трудность иллюстрирует рис. 3.2, на нем пунктиром показан вид отклика антенны на принимаемый ею сигнал для одного момента времени в реальных условиях эксперимента. Акустически непрозрачный экран затемняет лишь малую часть всего поля, принимаемого антенной, поэтому на рисунке видны только направление на излучатель и сигналы, рассеянные дном водоема, его поверхностью и берегами. Сигнал от экрана практически не заметен. Вид отклика антенны почти не изменяется со временем (при перемещении экрана). Естественно, что по такому сигналу апертурный синтез невозможен из-за большого уровня помех в виде посторонних сигналов. Чтобы убрать посторонние сигналы, выше был рассмотрен алгоритм фильтрации, образующий так называемое "темное поле”, на котором заметны только движущиеся рассеиватели. На рис. 3.2 жирной линией показан сигнал, полученный методом, описанным выше [12]. На этом рисунке четко видно угловое положение экрана во времени с превышением относительно окружающего реверберационного фона достаточным, чтобы попытаться практически решить обратную волновую задачу в естественных условиях.

Рис. 3.2. Угловые спектры сигналов в один момент времени. Пунктир - сигнал без обработки методом темного поля. Толстой (рассеиватель двигался, находясь под углом -9°) и тонкой (рассеиватель не двигался, находясь в крайнем положении) линиями показаны результаты, полученные с применением метода темного поля.
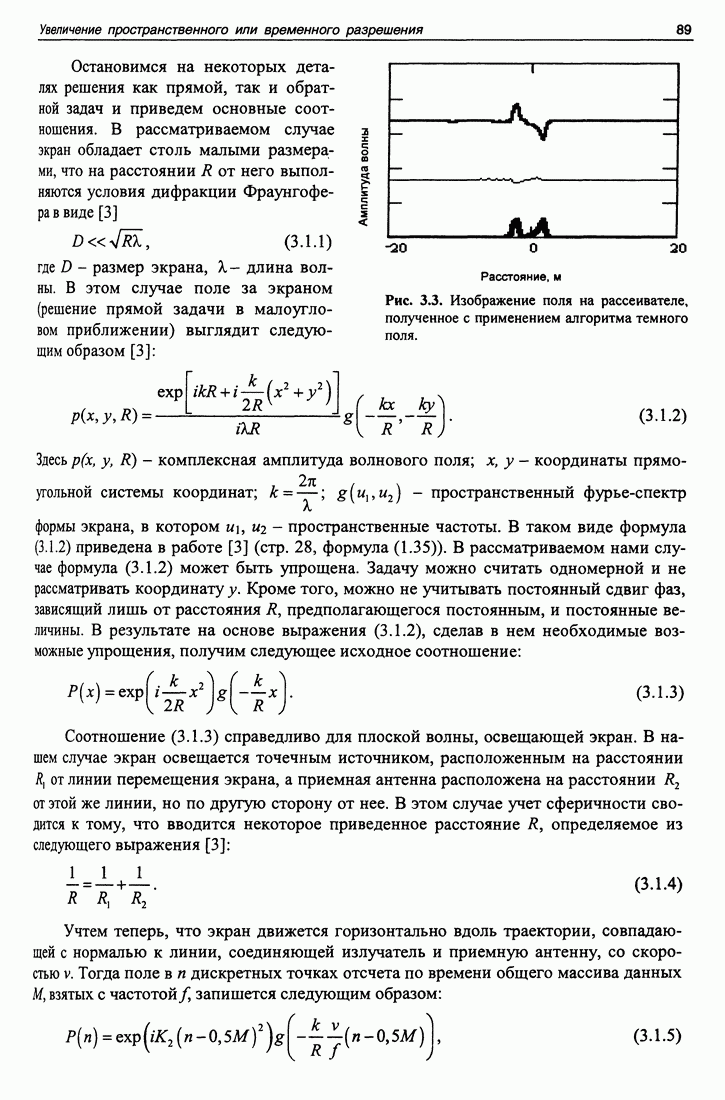
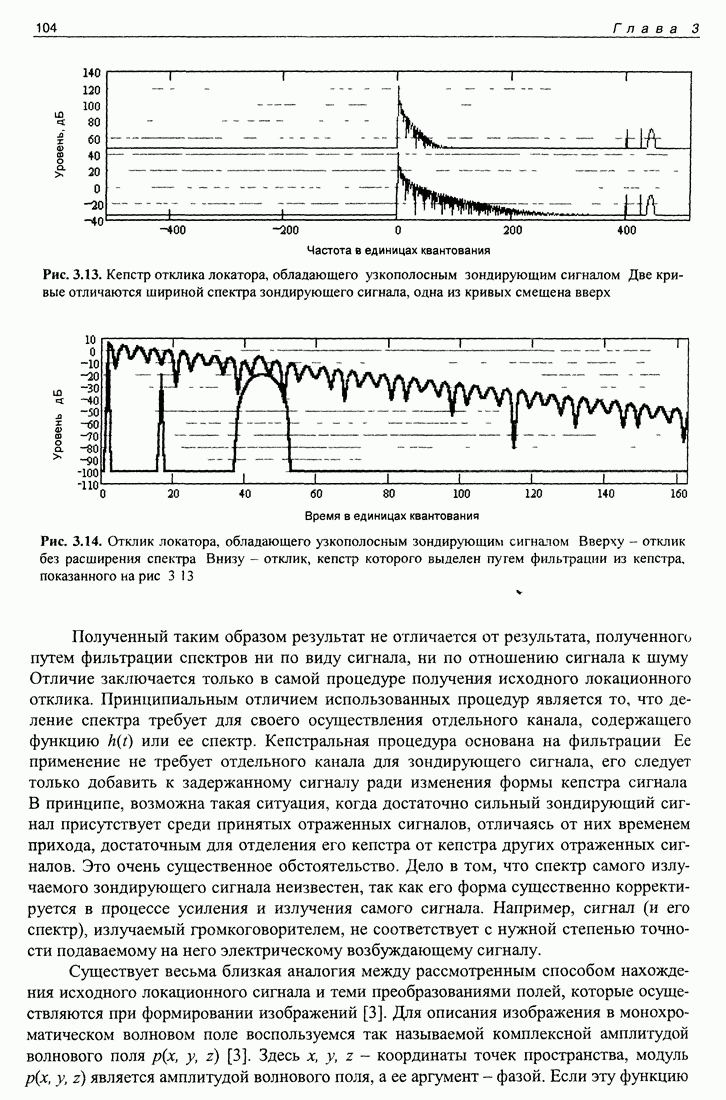
Необходимость использования алгоритма фильтрации в эксперименте вынуждает и теоретический расчет выполнять с применением этого же алгоритма. Результат расчета приведен на рис. 3.3. Частотная характеристика примененного фильтра имеет пропускание, пропорциональное частоте сигнала, что приводит к тому, что изображение поля на экране дифференцируется по пространству, поэтому выделяются лишь края прямоугольного экрана. Результат эксперимента, выполненного с применением алгоритма темного поля, следует сравнивать с результатом расчета, показанным на рис. 3.3.

Рис. 3.3. Изображение поля на рассеивателе, полученное с применением алгоритма темного поля.
Остановимся на некоторых деталях решения как прямой, так и обратной задач и приведем основные соотношения. В рассматриваемом случае экран обладает столь малыми размерами, что на расстоянии  от него выполняются условия дифракции Фраунгофера в виде [3]
от него выполняются условия дифракции Фраунгофера в виде [3]

где  - размер экрана, X - длина волны. В этом случае поле за экраном (решение прямой задачи в малоугловом приближении) выглядит следующим образом [3]:
- размер экрана, X - длина волны. В этом случае поле за экраном (решение прямой задачи в малоугловом приближении) выглядит следующим образом [3]:

Здесь  - комплексная амплитуда волнового поля;
- комплексная амплитуда волнового поля;  - координаты прямоугольной системы координат;
- координаты прямоугольной системы координат;  - пространственный фурье-спектр формы экрана, в котором
- пространственный фурье-спектр формы экрана, в котором  - пространственные частоты. В таком виде формула (3.1.2) приведена в работе [3] (стр. 28, формула (1.35)). В рассматриваемом нами случае формула (3.1.2) может быть упрощена. Задачу можно считать одномерной и не рассматривать координату
- пространственные частоты. В таком виде формула (3.1.2) приведена в работе [3] (стр. 28, формула (1.35)). В рассматриваемом нами случае формула (3.1.2) может быть упрощена. Задачу можно считать одномерной и не рассматривать координату  . Кроме того, можно не учитывать постоянный сдвиг фаз, зависящий лишь от расстояния
. Кроме того, можно не учитывать постоянный сдвиг фаз, зависящий лишь от расстояния  предполагающегося постоянным, и постоянные величины. В результате на основе выражения (3.1.2), сделав в нем необходимые возможные упрощения, получим следующее исходное соотношение:
предполагающегося постоянным, и постоянные величины. В результате на основе выражения (3.1.2), сделав в нем необходимые возможные упрощения, получим следующее исходное соотношение:

Соотношение (3.1.3) справедливо для плоской волны, освещающей экран. В нашем случае экран освещается точечным источником, расположенным на расстоянии  от линии перемещения экрана, а приемная антенна расположена на расстоянии
от линии перемещения экрана, а приемная антенна расположена на расстоянии  от этой же линии, но по другую сторону от нее. В этом случае учет сферичности сводится к тому, что вводится некоторое приведенное расстояние
от этой же линии, но по другую сторону от нее. В этом случае учет сферичности сводится к тому, что вводится некоторое приведенное расстояние  определяемое из следующего выражения [3]:
определяемое из следующего выражения [3]:

Учтем теперь, что экран движется горизонтально вдоль траектории, совпадающей с нормалью к линии, соединяющей излучатель и приемную антенну, со скоростью  Тогда поле в
Тогда поле в  дискретных точках отсчета по времени общего массива данных М, взятых с частотой
дискретных точках отсчета по времени общего массива данных М, взятых с частотой  запишется следующим образом:
запишется следующим образом:

где

Выражение (3.1.5) справедливо для одиночного приемника излучения. В нашем случае прием осуществляется с помощью ряда отдельных гидрофонов акустической антенны. Соотношение (3.1.5) справедливо для каждого гидрофона антенны при учете фаз принимаемых ими сигналов, определяемых геометрией расположения гидрофонов.
Ниже показано, как сделать так, чтобы сигналы с отдельных гидрофонов антенны суммировались с такими фазовыми соотношениями, которые обеспечивают синфазное сложение сигналов, принимаемых от движущегося экрана при любом  Пока примем, что это условие выполнено. Оно обеспечивает помехоустойчивость обработки сигнала. Кроме того, при его выполнении антенна по отношению к сигналу, рассеянному экраном, становится эквивалентной ненаправленному гидрофону. Последнее очень важно, так как направленность приема ограничивает разрешающую способность, достигаемую путем синтеза апертуры. К сигналу антенны, сфазированному указанным выше образом, применима формула (3.1.5).
Пока примем, что это условие выполнено. Оно обеспечивает помехоустойчивость обработки сигнала. Кроме того, при его выполнении антенна по отношению к сигналу, рассеянному экраном, становится эквивалентной ненаправленному гидрофону. Последнее очень важно, так как направленность приема ограничивает разрешающую способность, достигаемую путем синтеза апертуры. К сигналу антенны, сфазированному указанным выше образом, применима формула (3.1.5).
Получим требуемое условие фазировки сигналов, принимаемых отдельными гидрофонами антенны. Поле от экрана в пределах апертуры антенны представляет собою плоскую волну (в этом состоит условие дифракции Фраунгофера) вида

где  - число гидрофонов антенны, совпадающее с числом дискретных отсчетов, приходящихся на апертуру антенны А;
- число гидрофонов антенны, совпадающее с числом дискретных отсчетов, приходящихся на апертуру антенны А;  - номер дискретного отсчета волнового поля, взятого вдоль апертуры антенны, или номер приемного гидрофона, расположенного в этой точке; и - пространственная частота, определяемая углом, под которым плоская волна падает на антенну, нормированная на
- номер дискретного отсчета волнового поля, взятого вдоль апертуры антенны, или номер приемного гидрофона, расположенного в этой точке; и - пространственная частота, определяемая углом, под которым плоская волна падает на антенну, нормированная на 

Через  обозначена длина волны, которая в условиях градиента скорости звука в воде имеет место на горизонте антенны. В нашем случае угол, под которым от
обозначена длина волны, которая в условиях градиента скорости звука в воде имеет место на горизонте антенны. В нашем случае угол, под которым от  тенны наблюдается движущийся экран, можно записать следующим образом: I
тенны наблюдается движущийся экран, можно записать следующим образом: I

где  - угол в вертикальной плоскости, под которым сигнал от экрана подходит к
- угол в вертикальной плоскости, под которым сигнал от экрана подходит к  тенне.
тенне.
Считая угол 8 малым, подставляя (3.1.9) в (3.1.8), а (3.1.8) в (3.1.7), получим

где

Сделаем следующее замечание. Формула (3.1.2), а следовательно и (3.1.3), справедлива в условиях малоуглового приближения [3]. Множитель  уменьшает эквивалентный угол падения волны на антенну в горизонтальной плоскости, облегчает
уменьшает эквивалентный угол падения волны на антенну в горизонтальной плоскости, облегчает
выполнение условия малоуглового приближения по сравнению с распространением волны в свободном пространстве.
Для фазировки антенны на экран следует сигнал, принятый антенной и представленный в виде матрицы от переменных  умножить на комплексно сопряженную матрицу для матрицы (3.1.10).
умножить на комплексно сопряженную матрицу для матрицы (3.1.10).
По формулам (3.1.5) и (3.1.10) были получены 64 х 1024 значения комплексных амплитуд поля, имитирующих экспериментальные данные.
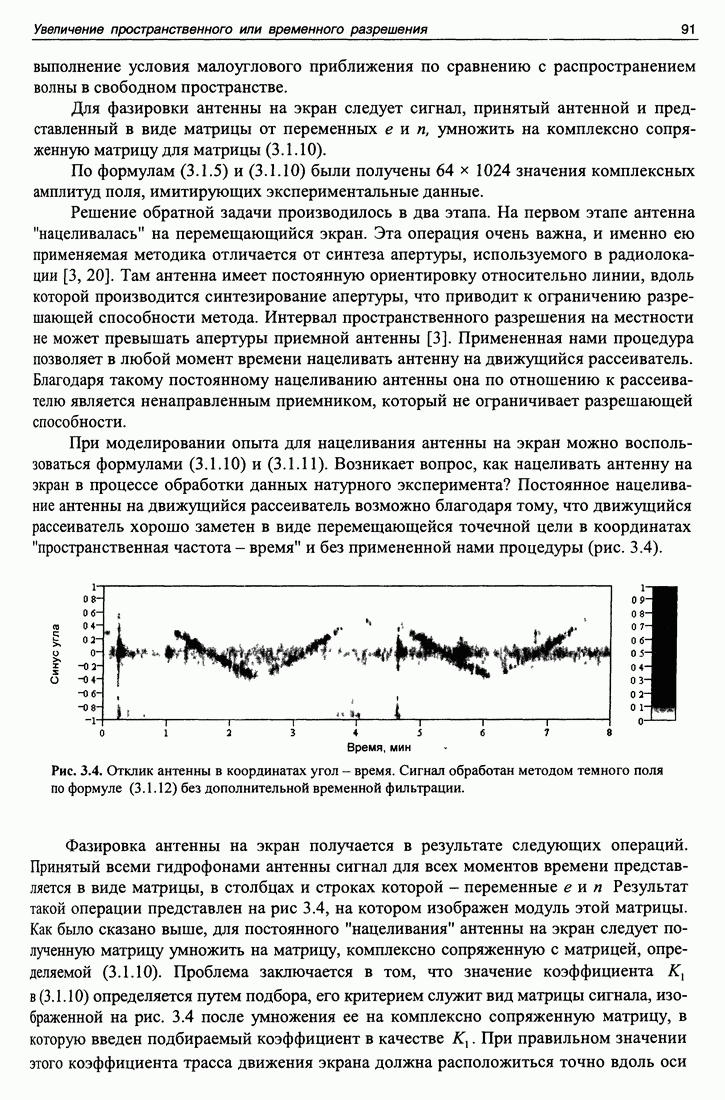
Решение обратной задачи производилось в два этапа. На первом этапе антенна "нацеливалась" на перемещающийся экран. Эта операция очень важна, и именно ею применяемая методика отличается от синтеза апертуры, используемого в радиолокации [3, 20]. Там антенна имеет постоянную ориентировку относительно линии, вдоль которой производится синтезирование апертуры, что приводит к ограничению разрешающей способности метода. Интервал пространственного разрешения на местности не может превышать апертуры приемной антенны [3]. Примененная нами процедура позволяет в любой момент времени нацеливать антенну на движущийся рассеиватель. Благодаря такому постоянному нацеливанию антенны она по отношению к рассеивателю является ненаправленным приемником, который не ограничивает разрешающей способности.
При моделировании опыта для нацеливания антенны на экран можно воспользоваться формулами (3.1.10) и (3.1.11). Возникает вопрос, как нацеливать антенну на экран в процессе обработки данных натурного эксперимента? Постоянное нацеливание антенны на движущийся рассеиватель возможно благодаря тому, что движущийся рассеиватель хорошо заметен в виде перемещающейся точечной цели в координатах "пространственная частота - время" и без примененной нами процедуры (рис. 3.4).

Рис. 3.4. Отклик антенны в координатах угол - время. Сигнал обработан методом темного поля по формуле (3.1.12) без дополнительной временной фильтрации.
Фазировка антенны на экран получается в результате следующих операций. Принятый всеми гидрофонами антенны сигнал для всех моментов времени представляется в виде матрицы, в столбцах и строках которой - переменные  Результат такой операции представлен на рис 3.4, на котором изображен модуль этой матрицы. Как было сказано выше, для постоянного "нацеливания" антенны на экран следует полученную матрицу умножить на матрицу, комплексно сопряженную с матрицей, определяемой (3.1.10). Проблема заключается в том, что значение коэффициента
Результат такой операции представлен на рис 3.4, на котором изображен модуль этой матрицы. Как было сказано выше, для постоянного "нацеливания" антенны на экран следует полученную матрицу умножить на матрицу, комплексно сопряженную с матрицей, определяемой (3.1.10). Проблема заключается в том, что значение коэффициента  в (3.1.10) определяется путем подбора, его критерием служит вид матрицы сигнала, изображенной на рис. 3.4 после умножения ее на комплексно сопряженную матрицу, в которую введен подбираемый коэффициент в качестве
в (3.1.10) определяется путем подбора, его критерием служит вид матрицы сигнала, изображенной на рис. 3.4 после умножения ее на комплексно сопряженную матрицу, в которую введен подбираемый коэффициент в качестве  При правильном значении этого коэффициента трасса движения экрана должна расположиться точно вдоль оси
При правильном значении этого коэффициента трасса движения экрана должна расположиться точно вдоль оси
времени. Для получения сфазированного сигнала остается считать значения сигнала вдоль той строки оси времени получившейся матрицы, вдоль которой наблюдается сигнал от экрана. Указанная процедура применима в случае достаточного превышения сигнала от экрана над уровнем шумов и помех. В нашем случае, как показывает количественно рис. 3.1.2 и качественно рис. 3.1.5, это условие выполняется.
На втором этапе обработки используем из всей матрицы значений лишь одну строку, содержащую сигнал, зависящий только от времени. Вид этого сигнала определяется формулой (3.1.5). Обработка сигнала предполагает его умножение на экспоненту, комплексно сопряженную с экспонентой, входящей в (3.1.5). После этого, как следует из (3.1.5), форма волнового поля непосредственно за экраном определяется с помощью преобразования Фурье.
Использование метода темного поля заключалось в преобразовании матрицы исходных данных  по формуле, приведенной выше с увеличенным интервалом вычитания (см. гл. 2):
по формуле, приведенной выше с увеличенным интервалом вычитания (см. гл. 2):

Эксперимент проводился на озере Санхар во Владимирской области. Излучатель располагался на расстоянии 300 метров от приемной антенны и излучал в непрерывном режиме монохроматический сигнал. Данные с антенны считывались так, как описано в работе [12]. Экран протягивался с постоянной скоростью по трассе, расположенной посередине между излучателем и приемной антенной.
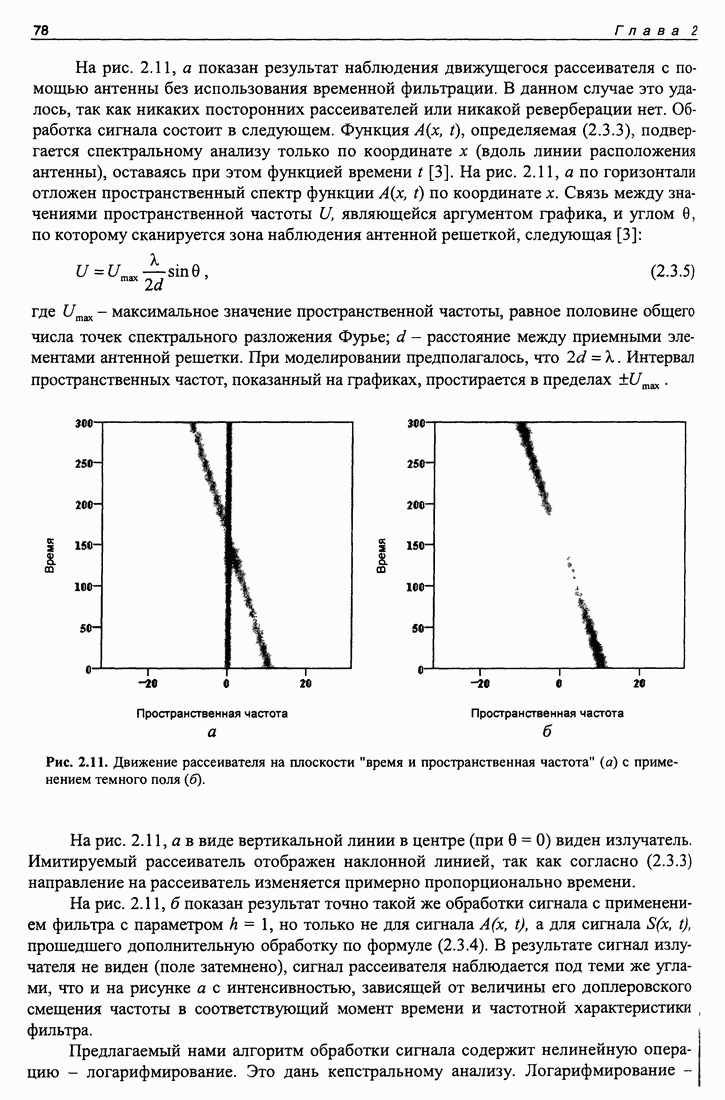
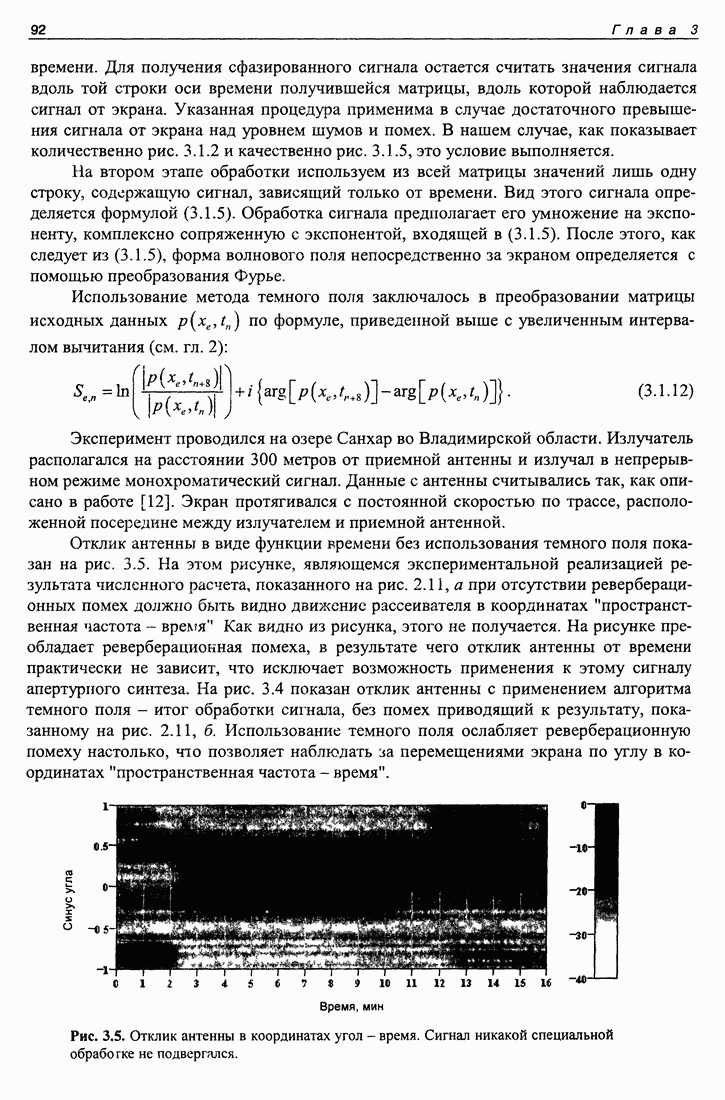
Отклик антенны в виде функции времени без использования темного поля показан на рис. 3.5. На этом рисунке, являющемся экспериментальной реализацией результата численного расчета, показанного на рис. 2.11, а при отсутствии реверберационных помех должно быть видно движение рассеивателя в координатах "пространственная частота - время" Как видно из рисунка, этого не получается. На рисунке преобладает реверберациокная помеха, в результате чего отклик антенны от времени практически не зависит, что исключает возможность применения к этому сигналу апертурного синтеза. На рис. 3.4 показан отклик антенны с применением алгоритма темного поля - итог обработки сигнала, без помех приводящий к результату, показанному на рис. 2.11, б. Использование темного поля ослабляет реверберационную помеху настолько, что позволяет наблюдать за перемещениями экрана по углу в координатах "пространственная частота - время".

Рис. 3.5. Отклик антенны в координатах угол - время. Сигнал никакой специальной обработке не подвергался.
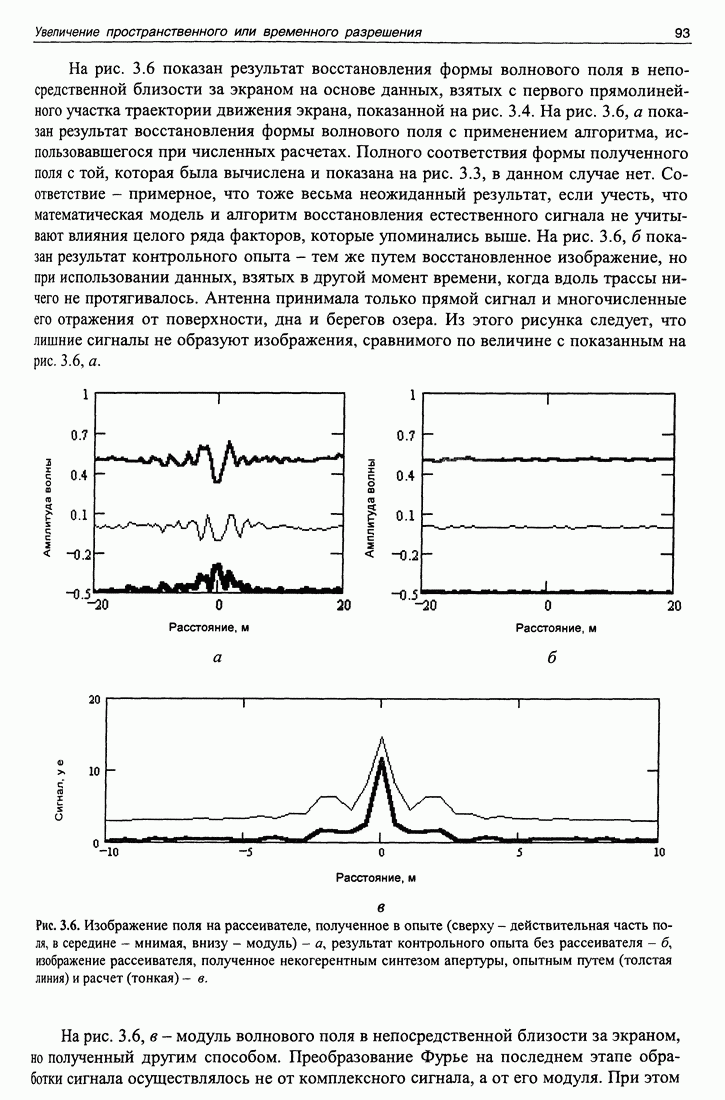
На рис. 3.6 показан результат восстановления формы волнового поля в непосредственной близости за экраном на основе данных, взятых с первого прямолинейного участка траектории движения экрана, показанной на рис. 3.4. На рис. 3.6, а показан результат восстановления формы волнового поля с применением алгоритма, использовавшегося при численных расчетах. Полного соответствия формы полученного поля с той, которая была вычислена и показана на рис. 3.3, в данном случае нет. Соответствие - примерное, что тоже весьма неожиданный результат, если учесть, что математическая модель и алгоритм восстановления естественного сигнала не учитывают влияния целого ряда факторов, которые упоминались выше. На рис. 3.6, б показан результат контрольного опыта - тем же путем восстановленное изображение, но при использовании данных, взятых в другой момент времени, когда вдоль трассы ничего не протягивалось. Антенна принимала только прямой сигнал и многочисленные его отражения от поверхности, дна и берегов озера. Из этого рисунка следует, что лишние сигналы не образуют изображения, сравнимого по величине с показанным на рис. 3.6, а.
Рис. 3.6. (см. скан) Изображение поля на рассеивателе, полученное в опыте (сверху - действительная часть поля, в середине - мнимая, внизу - модуль) - а, результат контрольного опыта без рассеивателя - б, изображение рассеивателя, полученное некогерентным синтезом апертуры, опытным путем (толстая линия) и расчет (тонкая) - в.
На рис. 3.6, в - модуль волнового поля в непосредственной близости за экраном, но полученный другим способом. Преобразование Фурье на последнем этапе обработки сигнала осуществлялось не от комплексного сигнала, а от его модуля. При этом
исключаются некоторые фазовые соотношения. На рисунке показаны одновременно как результаты теоретического расчета, так и результаты обработки данных эксперимента. Видно, что они удовлетворительно согласуются. Очевидно, что при такой обработке влияние факторов распространения сигнала не является существенным. Такой некогерентный апертурный синтез не дает возможности восстановления формы экрана, позволяя судить о его размерах, что также существенно.
Некогерентный апертурный синтез возможен не всегда. В нашем случае он получается благодаря тому, что антенна хорошо выделяет сигнал, рассеиваемый движущимся экраном на фоне сигнала излучателя и других рассеивателей. Без соблюдения этого условия некогерентный апертурный синтез из-за влияния интерференции ряда рассеивателей приведет к иному результату, который трудно сопоставить с теорией.
На основе эксперимента удалось оценить ряд интересных параметров, характеризующих акустические условия, в которых проводился опыт. Ключом к этому являются экспоненты, входящие в формулу (3.1.5) и (3.1.10). Из эксперимента оцениваются безразмерные коэффициенты, входящие в выражения под знаком экспонент. В формуле (3.1.10) - это коэффициент  определяемый (3.1.10). В формуле (3.1.5) - коэффициент
определяемый (3.1.10). В формуле (3.1.5) - коэффициент  перед множителем
перед множителем  определяемый (3.1.6).
определяемый (3.1.6).
Коэффициент  на основании формулы (3.1.6) следующим образом связан с параметрами эксперимента:
на основании формулы (3.1.6) следующим образом связан с параметрами эксперимента:

Из двух уравнений, (3.1.11) и (3.1.13), можно определить два входящих в эти уравнения параметра при условии, что остальные параметры известны. Алгоритмы, использовавшиеся ранее [21, 22], позволяют оценивать параметры эксперимента только на основе формулы (3.1.5).
В нашем случае параметры  а также
а также  известны. Поэтому нами оценивались другие акустические параметры трассы распространения волн, входящие в
известны. Поэтому нами оценивались другие акустические параметры трассы распространения волн, входящие в 
Известные и измеренные параметры приведены в таблице.

Точность определения величин коэффициентов путем их подбора в этом опыте получается порядка 10%.
Интересно оценить точность, с которой горизонтально ориентированная антенна селектирует излучение, приходящее к ней, в вертикальном направлении. Имеем

В нашем случае  Следовательно, в этом опыте горизонтальная антенна способна селектировать излучение в вертикальном направлении примерно с вдвое меньшей точностью, чем в горизонтальном.
Следовательно, в этом опыте горизонтальная антенна способна селектировать излучение в вертикальном направлении примерно с вдвое меньшей точностью, чем в горизонтальном.
Итак, проведенное экспериментальное исследование позволяет сделать некоторые выводы.
Алгоритм акустического темного поля обеспечивает выделение движущегося слабого рассеивателя на уровне, достаточном для использования специальной
процедуры апертурного синтеза. Специальная процедура апертурного синтеза, примененная в настоящей работе, отличается тем, что позволяет использовать весь потенциал акустической антенны без потери разрешающей способности.
Направленная антенна с ее полным потенциалом по разрешению и помехоустойчивости позволяет применить некогерентный апертурный синтез. Проведенный эксперимент показал реальную возможность оценки двух параметров эксперимента. Эти возможности являются новыми сравнительно с существующими. В частности, показано, что есть возможность определения и селекции излучения, приходящего к горизонтальной антенне в вертикальной плоскости.
Предлагаемая методика может применяться в томографическом режиме. Имеется в виду режим согласованного перемещения излучателя и приемника, так что может быть определена форма рассеивателей, находящихся внутри трассы движения, а также оценены некоторые акустические параметры трассы.
В последнее время появились работы, в которых теоретически уточняются дифракционные явления на телах простой формы [7, 8, 9]. Методы, использованные в этой работе, могут оказаться полезными при экспериментальной проверке выводов теории.
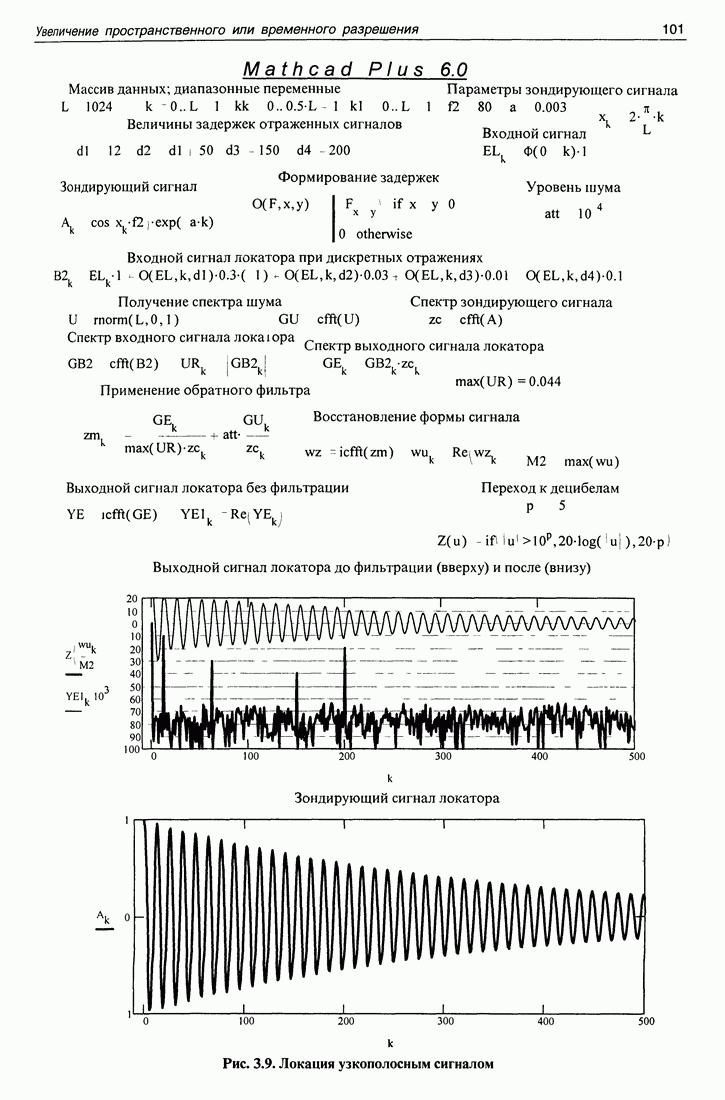
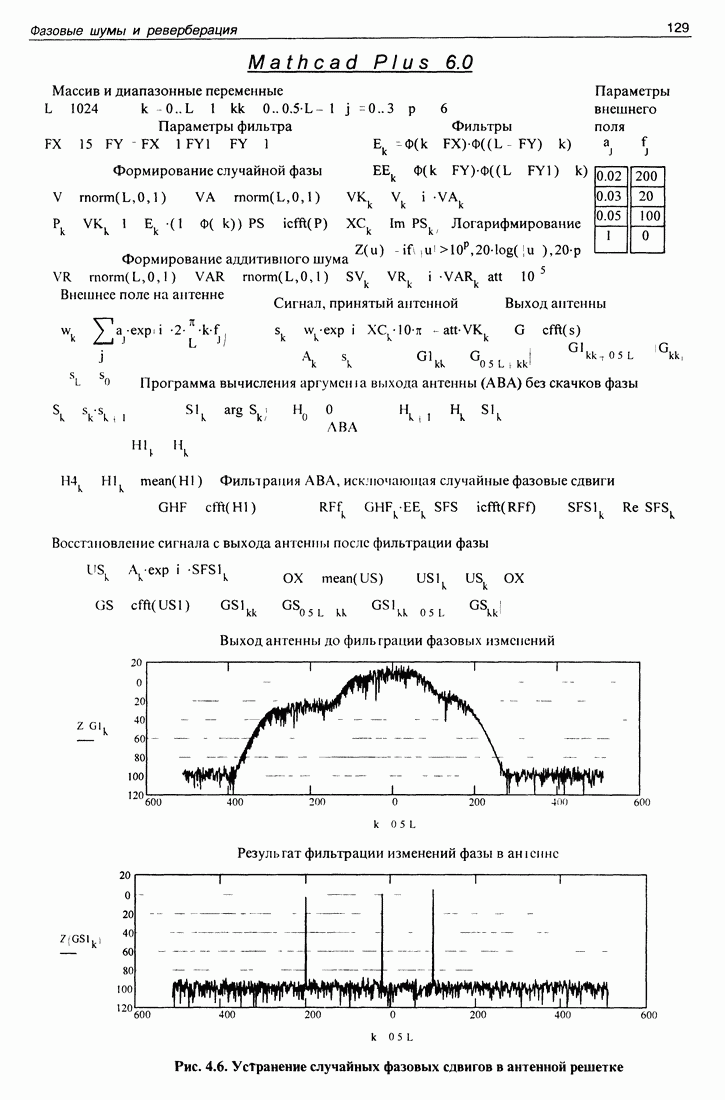
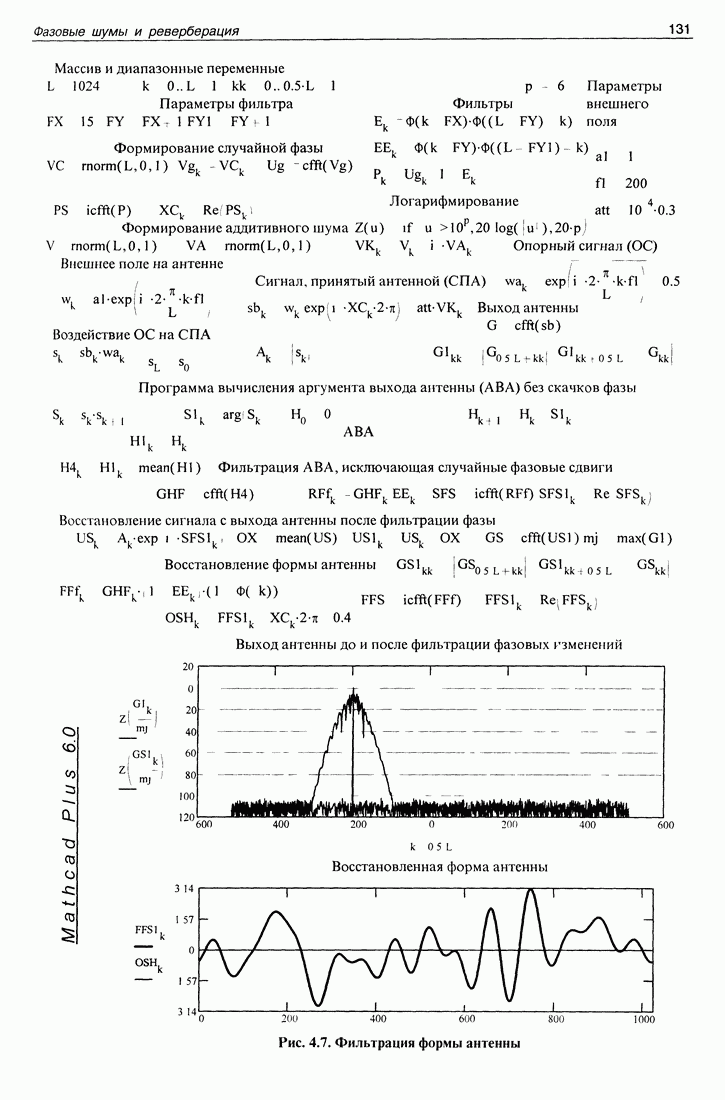
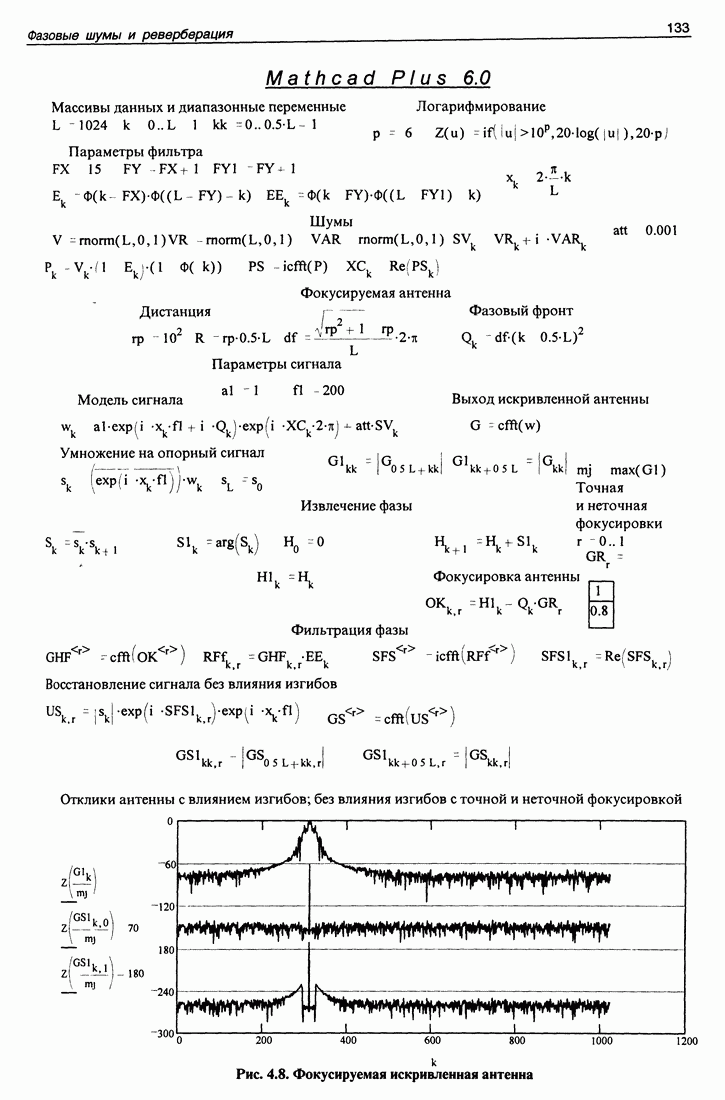
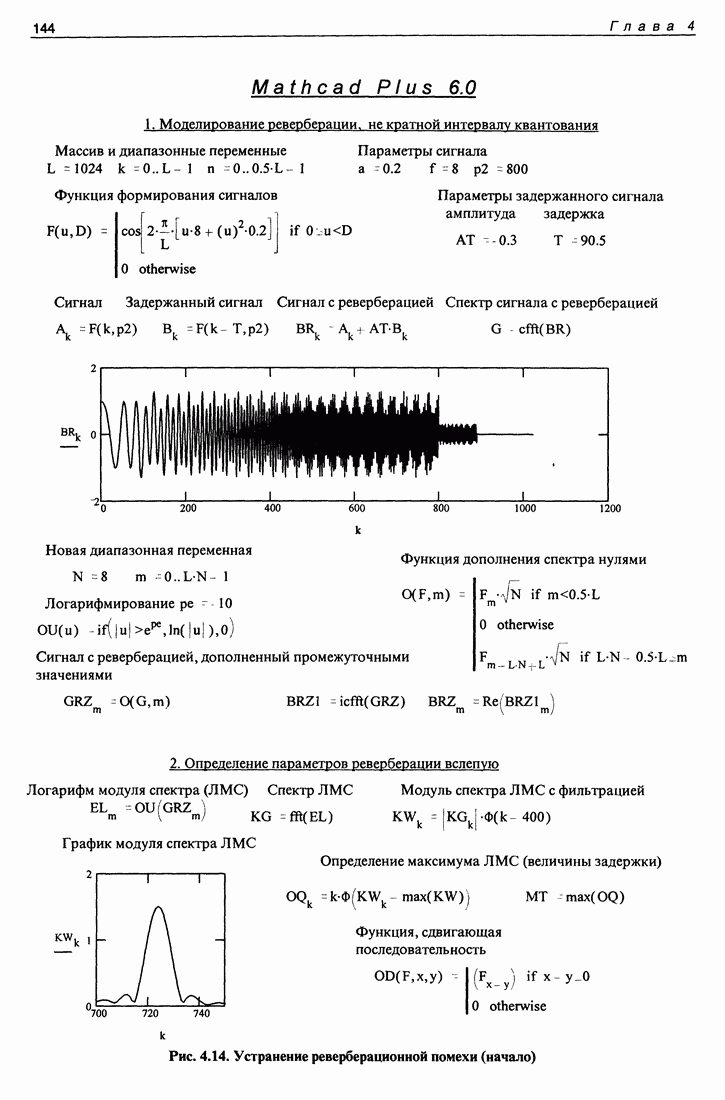
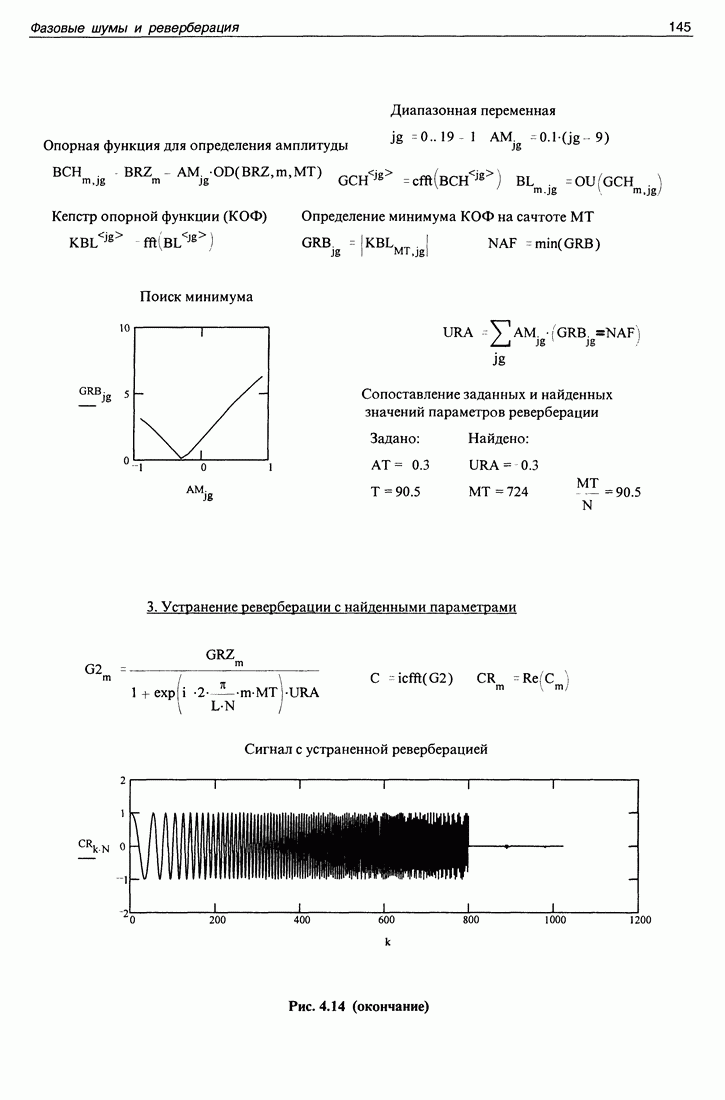
Мы не можем здесь привести математическую программу, работающую с данными натурного эксперимента по двум причинам. Во-первых, данные эксперимента занимают большой объем, сравнимый с общим объемом книги. Во-вторых, в книге невозможно привести эти данные в такой форме, чтобы их можно было автоматически ввести в компьютер. Поэтому приводим точно такую же программу, работающую с данными, получаемыми путем математического моделирования задачи. Все особенности программирования обработки реальных данных при этом сохраняются, а сами исходные данные получаются в самом компьютере.
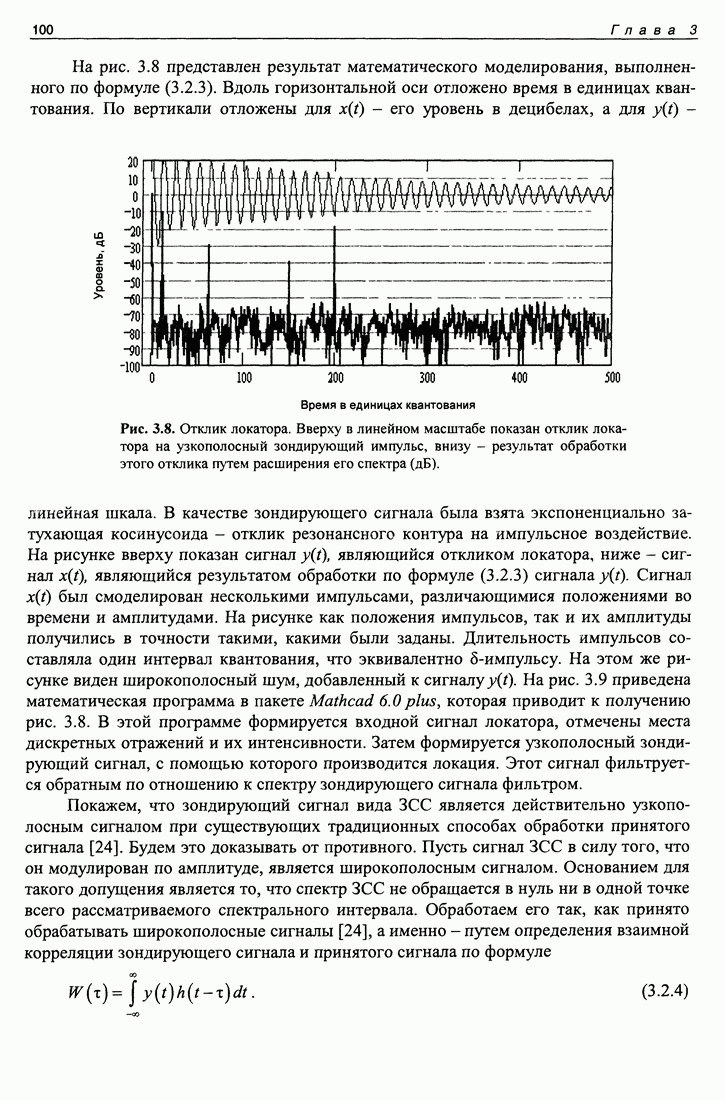
Эта программа приведена на рис. 3.7. На первой странице помещена полная программа получения и обработки данных, на второй странице помещены графики (они приведены и в тексте настоящего раздела (это рис. 3.1, 3.3, частично 3.6).
Как обычно, дадим некоторые комментарии к приведенной программе. Вначале приведены массивы используемых данных и диапазонные переменные. Затем идут параметры эксперимента, существенные для моделирования. Апертура антенны  расстояния
расстояния  в метрах от излучателя 1 (см. рис. 2.10 в гл. 2) до линии 3-3 200 м и от линии 3-3 до линии
в метрах от излучателя 1 (см. рис. 2.10 в гл. 2) до линии 3-3 200 м и от линии 3-3 до линии  длина волны, на которой производился опыт, равнялась 0,584 м; величина интервала между приемниками антенны -
длина волны, на которой производился опыт, равнялась 0,584 м; величина интервала между приемниками антенны -  скорость протяжки рассеивателя вдоль линии
скорость протяжки рассеивателя вдоль линии  частота квантования
частота квантования  размер рассеивателя
размер рассеивателя  параметр фильтра
параметр фильтра  определяющий интервал в отсчетных точках, через который производится вычитание логарифмов значений поля. Введено приведенное расстояние по формуле (3.1.4). Далее приведено выражение для координаты вдоль антенны и смещение рассеивателя вдоль линии его движения в метрах.
определяющий интервал в отсчетных точках, через который производится вычитание логарифмов значений поля. Введено приведенное расстояние по формуле (3.1.4). Далее приведено выражение для координаты вдоль антенны и смещение рассеивателя вдоль линии его движения в метрах.
Далее программа строится в точном соответствии с теоретическими формулами. Приведена функция  входящая в (3.1.2) и в (3.1.3). Приведены формулы для коэффициентов, входящих в формулы (3.1.5) и (3.1.10). Согласно этим формулам численно создается такой сигнал, который может быть получен экспериментально. При обработке сигнала модуляция, определяемая как коэффициентом, входящим в (3.1.5), так и коэффициентом, входящим в (3.1.10), убирается путем умножения на комплексно сопряженный множитель. Для обработки сигнала, полученного в эксперименте, иного пути нет. В условиях эксперимента приходится подбирать коэффициенты соответствующих выражений. В условиях моделирования все коэффициенты точно известны. Поэтому вроде бы нет смысла сначала множить функцию на какую-то функцию, а потом
входящая в (3.1.2) и в (3.1.3). Приведены формулы для коэффициентов, входящих в формулы (3.1.5) и (3.1.10). Согласно этим формулам численно создается такой сигнал, который может быть получен экспериментально. При обработке сигнала модуляция, определяемая как коэффициентом, входящим в (3.1.5), так и коэффициентом, входящим в (3.1.10), убирается путем умножения на комплексно сопряженный множитель. Для обработки сигнала, полученного в эксперименте, иного пути нет. В условиях эксперимента приходится подбирать коэффициенты соответствующих выражений. В условиях моделирования все коэффициенты точно известны. Поэтому вроде бы нет смысла сначала множить функцию на какую-то функцию, а потом

(кликните для просмотра скана)

(кликните для просмотра скана)
ликвидировать результат этой операции умножением на комплексно сопряженную функцию. Эти, казалось бы, бессмысленные действия, результат которых не должен зависеть от того, как точно мы промоделируем ситуацию, на самом деле присутствуют в программе. Почему? Если бы сигнал не подвергался в ходе обработки фильтрации, то разумного ответа на этот вопрос не было бы. В программе есть две параллельно идущие ветви, одна из которых включает фильтрацию (она слева), а другая (правая) обходится без нее. В правой ветви действительно можно обойтись без точного соблюдения формул (3.1.5) и (3.1.10) и даже игнорировать их. Однако этого ни в коем случае нельзя делать в левой части программы, включающей фильтрацию. Предлагаем в этом убедиться, изменив значения коэффициентов, входящих в формулы (3.1.5) и (3.1.10). В правой части программы не произойдет ничего, а результат левой изменится. Это происходит оттого, что для фильтрации важен спектр функции, а он в результате модуляции сильно изменяется. Устранение модуляции путем умножения на комплексно сопряженный множитель происходит после прохождения сигнала через фильтр. Чтобы моделируемый сигнал фильтровался точно так же, как и экспериментальный, необходимо строгое соблюдение значений всех параметров, входящих в формулы (3.1.5) и (3.1.10).
Две последние строчки программы посвящены операции некогерентного апертурного синтеза.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. СПЕКТР И КЕПСТР
- 1.1. Ряд и интеграл Фурье
- 1.2. Математические свойства преобразования Фурье
- 1.3. Знаменитая теорема отсчетов
- 1.4. Как выполняется преобразование Фурье численно
- 1.5. Линейные системы
- 1.6. Кепструм
- 1.7. Численное представление случайных сигналов
- Глава 2. ФИЛЬТРАЦИЯ ПОМЕХ И ЛОКАЦИЯ НА ПРОСВЕТ
- 2.1. Устранение узкополосной помехи
- 2.2. Метод темного поля
- 2.3. Эксперимент по наблюдению точечного рассеивателя
- Глава 3. УВЕЛИЧЕНИЕ ПРОСТРАНСТВЕННОГО ИЛИ ВРЕМЕННОГО РАЗРЕШЕНИЯ
- 3.2. Увеличение временного разрешения сигналов
- 3.3. Локация на просвет с разделением прямого и дифрагированного сигналов по времени
- Глава 4. ФАЗОВЫЕ ШУМЫ И РЕВЕРБЕРАЦИЯ
- 4.1. Фильтрация мультипликативно связанных сигналов
- 4.2. Устранение влияния фазовых шумов в параметрическом микрофоне
- 4.3. Слепая дереверберация
- Глава 5. ИССЛЕДОВАНИЕ АКУСТИЧЕСКИХ ТРАСС С ИСПОЛЬЗОВАНИЕМ М-ПОСЛЕДОВАТЕЛЬНОСТИ
- 5.1. Акустические задачи, решаемые с помощью M-последовательности
- 5.2. Выбор оптимальной методики анализа линейной системы
- 5.3. М-последовательность — идеальный тестовый сигнал для анализа систем. Ее генерация и свойства
- 5.4. Применение М-последовательности на стационарной сейсмической трассе
- 5.5. Применение М-последовательности на сверхдлинных океанических трассах
- 5.6. Идентификация каналов распространения на нестационарных трассах
- 5.7. Кепстральный метод оценки флуктуаций запаздывания сигналов
- Литература