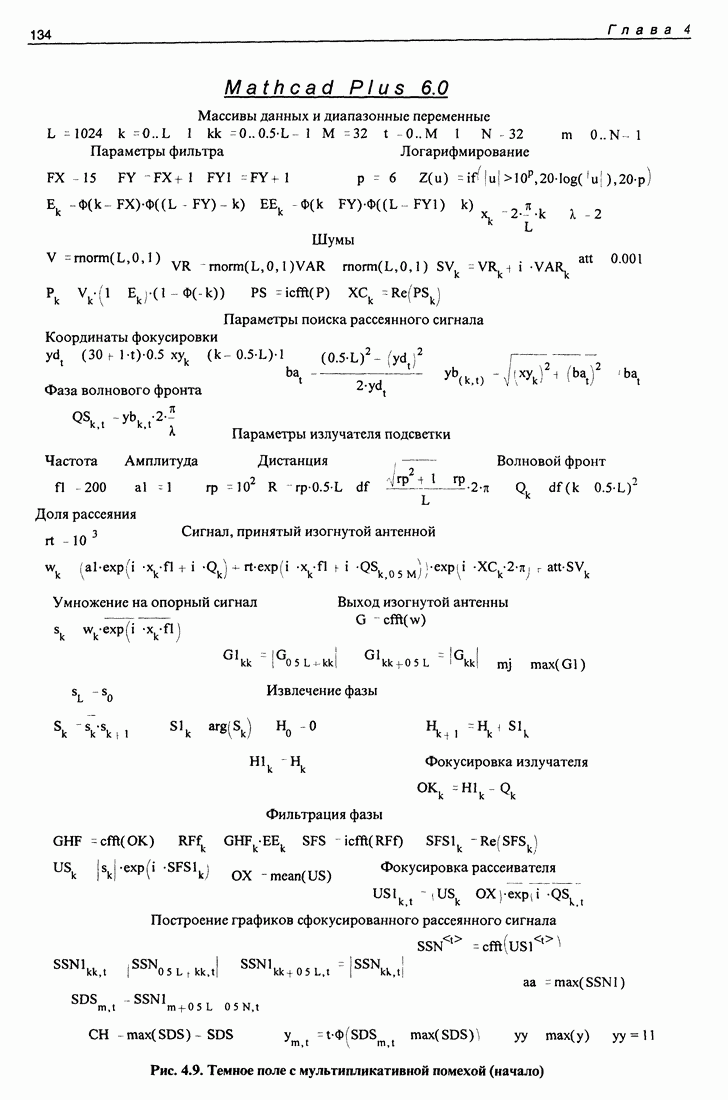| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5. Линейные системы
Свойства так называемых линейных систем успешно используются при выделении сигналов. Более того, вся линейная обработка сигналов с целью выделения нужных сигналов и подавления ненужных (шумов) основана на свойствах линейных систем. Поэтому выделим свойства линейных систем в отдельный раздел.
Свое название описываемые нами системы получили вследствие того, что они математически описываются системами линейных дифференциальных уравнений с постоянными коэффициентами. К таким системам относятся радиотехнические устройства, осуществляющие усиление или фильтрацию сигналов, механические устройства (рычаги, пружины, диссипативные элементы), оптические устройства (объективы, многоканальные антенные решетки) и многое другое. Рассмотрим математические свойства подобных систем, общие для всех случаев.
Чтобы сразу перейти к свойствам, дадим иное определение линейных систем. Систему, способную совершать колебания под действием внешней силы, будем называть линейной, если она обладает следующими двумя математическими свойствами. Чтобы перейти к ним дадим два определения. Определим, что будем называть выходом системы, а что - входом. С точки зрения линейных дифференциальных уравнений, описывающих систему, выход системы - это та переменная или те переменные (если их несколько), которые являются переменными, входящими в левую часть уравнения, которые надо найти, решая уравнения. Входом системы является переменная или совокупность многих переменных, входящих в правую часть уравнения, которые являются заданными и их искать не надо.
Определим это на примере линейного радиотехнического фильтра, выполненного в виде четырехполюсника. У этого устройства два полюса представляют собою вход, а два других - выход. Сигнал, поданный на вход четырехполюсника, будем называть входным сигналом, он не зависит от того, как устроен четырехполюсник. Сигнал, снимаемый с других двух полюсов этого четырехполюсника, назовем выходным сигналом. Этот сигнал изменяется при изменении параметров четырехполюсника.
Итак, систему будем считать линейной, если она удовлетворяет свойству суперпозиции и свойству транспозиции. Поясним, что мы имеем в виду под этими свойствами. Пусть система откликается на входное воздействие вида  откликом
откликом  при любых
при любых  Свойство суперпозиции заключается в том, что на сумму входных сигналов
Свойство суперпозиции заключается в том, что на сумму входных сигналов  система откликается суммой выходных сигналов
система откликается суммой выходных сигналов  Условимся обозначать действие системы стрелочкой
Условимся обозначать действие системы стрелочкой  . Тогда свойство суперпозиции можно записать следующим образом:
. Тогда свойство суперпозиции можно записать следующим образом:

Заметим, что в этом определении существенны как (1.5.1), так и (1.5.2), т. е. важно, чтобы отклик мог быть представлен в виде суммы откликов, каждый из которых является откликом на соответствующее слагаемое в сумме входных сигналов.
Перейдем теперь к свойству транспозиции. Его можно дать сразу в виде математической формулы:

Это равенство должно быть справедливо при любых  их, которые участвуют в формулировке и решении задачи. Иными словами, форма любого отклика системы не должна зависеть от момента подачи входного воздействия. Иначе это свойство можно определить так: линейная система в процессе ее функционирования не стареет.
их, которые участвуют в формулировке и решении задачи. Иными словами, форма любого отклика системы не должна зависеть от момента подачи входного воздействия. Иначе это свойство можно определить так: линейная система в процессе ее функционирования не стареет.
На практике оба этих свойства линейных систем выполняются приблизительно. Поэтому выводы, основанные на их свойствах, надо проверять и перепроверять. Однако есть существенное для нас исключение. Линейные системы, построенные численными методами, обладают этими свойствами с такой точностью, что ничего проверять не надо. Этим во многом объясняется преимущество в точности, достигаемое численными методами перед аналоговыми, действие которых основано на вышеприведенных свойствах линейных систем.
Исходя из сформулированных математических свойств линейных систем, можно связать их с преобразованием Фурье и ввести функцию, полностью определяющую отклик линейной системы на любое входное воздействие.
Сначала заметим, что отклик линейной системы на монохроматическое входное воздействие обязательно будет тоже монохроматическим, той же частоты. Это следует из того, что в системе все параметры постоянны (иначе будет несправедливо свойство транспозиции), и нет причин, по которым частота входного воздействия может измениться. Кроме того, если фаза входного воздействия изменится, то точно на эту же величину должна измениться и фаза выходного воздействия, что является прямым следствием свойства транспозиции, так как фаза монохроматического сигнала может быть сведена к его задержке на соответствующую долю периода. Это можно выразить следующей формулой:

Здесь  представляет собою комплексное число, модуль которого определяет изменение выходного сигнала с частотой, а аргумент определяет изменение фазы выходного сигнала с частотой. Соотношение (1.5.4) удается записать в таком виде только благодаря свойству транспозиции. Если бы фаза выходного сигнала зависела от фазы входного, то понадобился бы еще третий параметр, появление которого изменило бы ситуацию кардинальным образом.
представляет собою комплексное число, модуль которого определяет изменение выходного сигнала с частотой, а аргумент определяет изменение фазы выходного сигнала с частотой. Соотношение (1.5.4) удается записать в таком виде только благодаря свойству транспозиции. Если бы фаза выходного сигнала зависела от фазы входного, то понадобился бы еще третий параметр, появление которого изменило бы ситуацию кардинальным образом.
Теперь представим входное воздействие в виде разложения в частотный спектр по формуле (1.1.14):

Чтобы найти отклик системы на входное воздействие (1.5.5), воспользуемся формулой (1.5.4). Каждое слагаемое интеграла (1.5.5) будет иметь в виде отклика следующее выражение:

Здесь также использовано свойство транспозиции. Изменения фаз и амплитуд входного сигнала, вызванные комплексным множителем с  переходят без изменений в выходное воздействие. Воспользуемся свойством суперпозиции, чтобы написать выражение для отклика системы на весь интеграл:
переходят без изменений в выходное воздействие. Воспользуемся свойством суперпозиции, чтобы написать выражение для отклика системы на весь интеграл:

Полученное соотношение важно вдвойне. Во-первых, оно определяет функцию  называемую частотной характеристикой линейной системы, которая, в свою очередь, определяет отклик этой системы на любое входное воздействие. Во-вторых, отклик линейной системы представлен в виде преобразования Фурье, следовательно, он обладает математическими свойствами этого преобразования.
называемую частотной характеристикой линейной системы, которая, в свою очередь, определяет отклик этой системы на любое входное воздействие. Во-вторых, отклик линейной системы представлен в виде преобразования Фурье, следовательно, он обладает математическими свойствами этого преобразования.
Воспользуемся последним обстоятельством, чтобы представить отклик линейной системы иначе. Заметим, что выражение (1.5.7) представляет собою преобразование Фурье от произведения двух функций. На основе обратной теоремы о свертке (1.2.8) выражение (1.5.7) может быть представлено как свертка спектров функций сомножителей. Для этого введем спектр частотной характеристики, называемой откликом линейной системы, посредством равенства


Тогда на основе (1.2.8) и (1.2.4) запишем

Пользуясь (1.5.10), можно интерпретировать отклик линейной системы как выходной сигнал системы при подаче на вход  -функции. В самом деле, вместо
-функции. В самом деле, вместо  подставив в (1.5.10)
подставив в (1.5.10)  , на основании (1.2.17) получим
, на основании (1.2.17) получим 
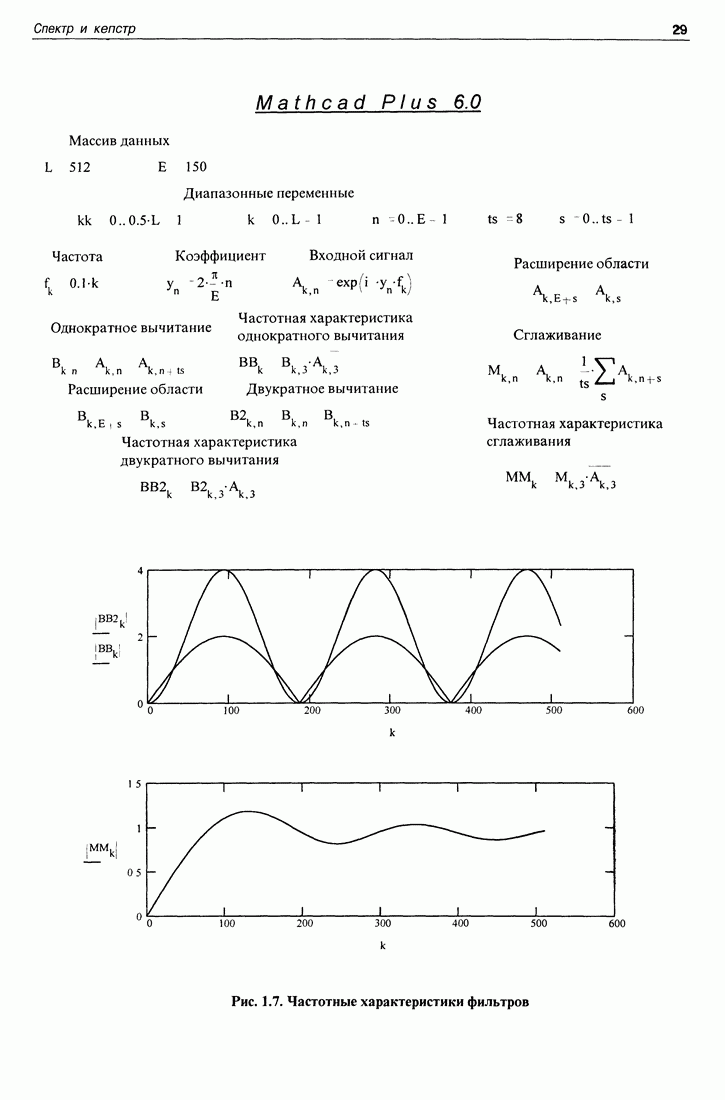
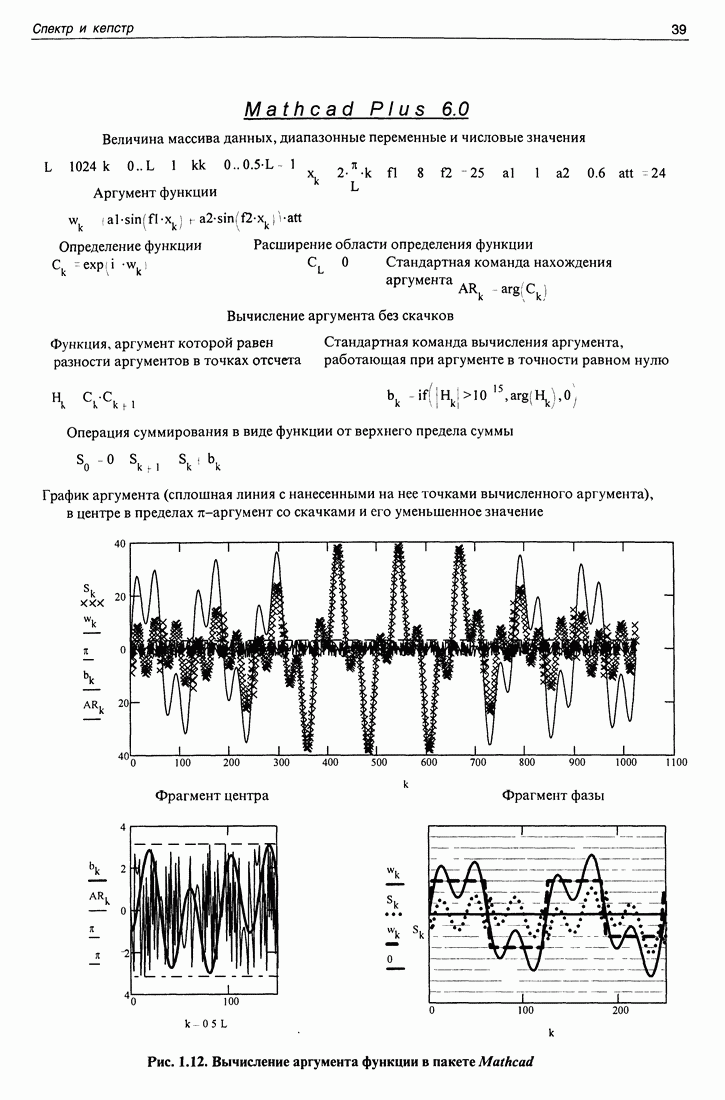
На рис. 1.7 приведен пример численного формирования частотных характеристик линейных систем и метод численного их определения. В начале программы помещены 2 массива данных. Массив  определяет количество частот, участвующих в определении частотной характеристики. Массив Е определяет длительность временного отклика системы в процессе формирования и определения частотной характеристики. Ниже идут диапазонные переменные: к - частотная;
определяет количество частот, участвующих в определении частотной характеристики. Массив Е определяет длительность временного отклика системы в процессе формирования и определения частотной характеристики. Ниже идут диапазонные переменные: к - частотная;  - временная;
- временная;  - переменная, используемая для получения систем, имеющих частотные характеристики различной формы. На следующей строке программы формируется сигнал, используемый для определения формы частотной характеристики. По определению (1.5.4) частотная характеристика содержится в виде множителя в отклике системы на экспоненциальный сигнал от мнимого аргумента. В соответствующей строке программы и формируется такой сигнал, в котором есть коэффициент, зависящий от времени, и множитель, зависящий от частоты. Далее в программе формируются три линейные системы с различными частотными характеристиками: система однократного вычитания, в которой выходной сигнал образуется в результате вычитания входных сигналов через фиксированный интервал времени
- переменная, используемая для получения систем, имеющих частотные характеристики различной формы. На следующей строке программы формируется сигнал, используемый для определения формы частотной характеристики. По определению (1.5.4) частотная характеристика содержится в виде множителя в отклике системы на экспоненциальный сигнал от мнимого аргумента. В соответствующей строке программы и формируется такой сигнал, в котором есть коэффициент, зависящий от времени, и множитель, зависящий от частоты. Далее в программе формируются три линейные системы с различными частотными характеристиками: система однократного вычитания, в которой выходной сигнал образуется в результате вычитания входных сигналов через фиксированный интервал времени  система двукратного вычитания, в которой вычитанию через тот же фиксированный интервал
система двукратного вычитания, в которой вычитанию через тот же фиксированный интервал  подвергается выход системы однократного вычитания; система, образованная вычитанием из входного сигнала скользящего среднего значения того же сигнала.
подвергается выход системы однократного вычитания; система, образованная вычитанием из входного сигнала скользящего среднего значения того же сигнала.

(кликните для просмотра скана)
Формирование этих систем требует расширения области определения входных данных, что показано в программе. Сама частотная характеристика, в соответствии с формулой (1.5.4), получается в результате деления отклика системы на экспоненциальное входное воздействие от комплексного аргумента на само это входное воздействие. Это показано в программе в виде умножения отклика на комплексно сопряженный входной сигнал (что эквивалентно делению на него). Таким путем в программе получаются частотные характеристики всех 3 формируемых систем. Получаемая частотная характеристика не зависит от времени  поэтому ее можно получать при произвольном значении этой переменной. В программе взято значение
поэтому ее можно получать при произвольном значении этой переменной. В программе взято значение  На графиках приведены модули частотных характеристик всех трех систем.
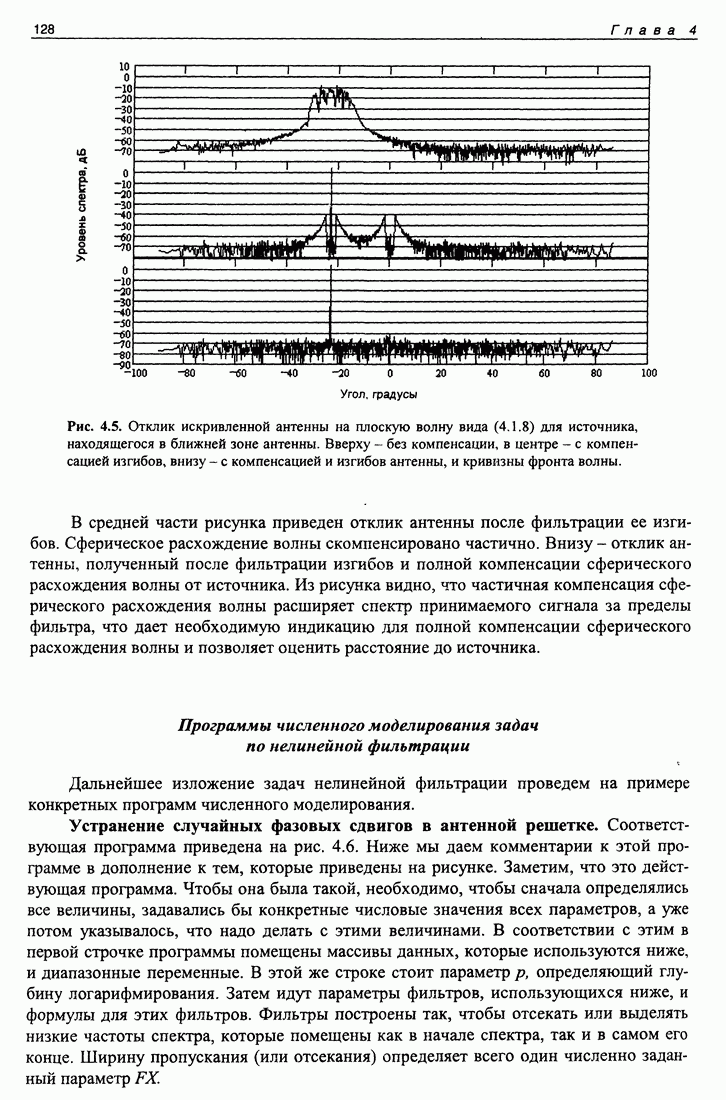
На графиках приведены модули частотных характеристик всех трех систем.
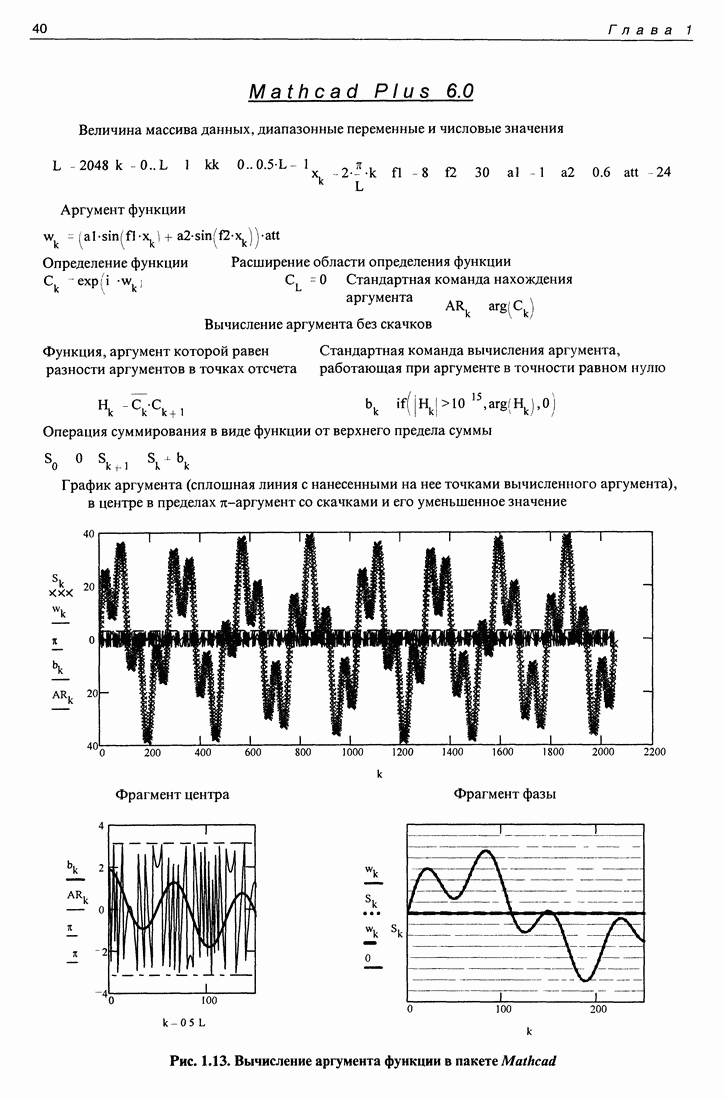
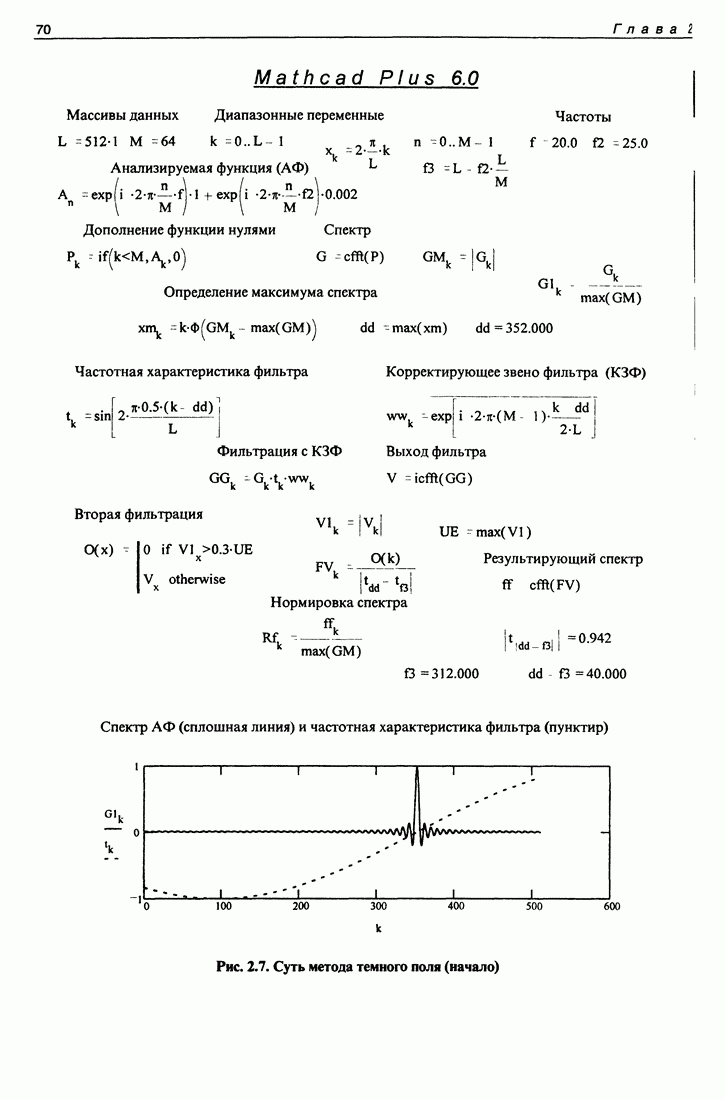
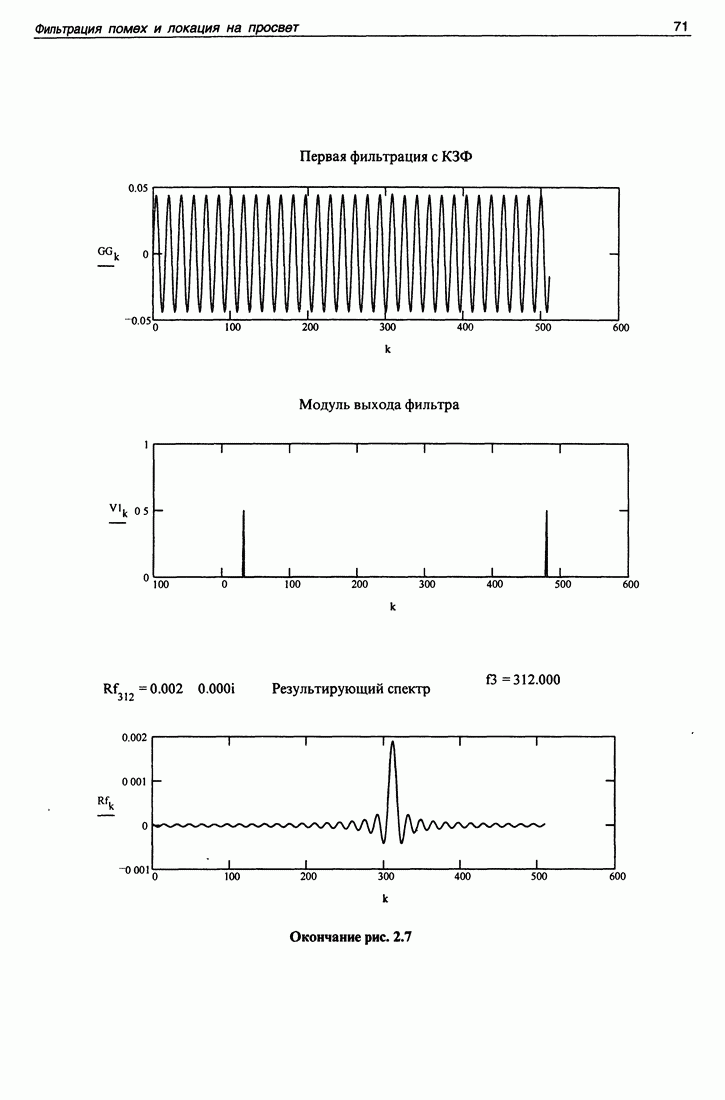
На рис. 1.8 приведен наиболее употребительный способ формирования заданных частотных характеристик. Частотная характеристика формируется с помощью преобразования Фурье на основании соотношения (1.5.7). Согласно (1.5.7) спектр на выходе линейной системы равен произведению спектра входного сигнала на частотную характеристику системы. Формирование входного сигнала, за исключением ряда обозначений, совпадает с программой, показанной на рис. 1.7. Частотная характеристика формируется в виде спектрального окна, которое пропускает частоты в некоторой области, определяемой комбинацией чисел  Спектр выходного сигнала формируется перемножением спектра входного сигнала и "спектрального окна". Затем восстанавливается выходной сигнал и определяется частотная характеристика получившейся линейной системы точно так же, как это сделано в программе, показанной на рис. 1.7. Форма характеристики получилась в точности повторяющей форму заданного спектрального окна. Возможность формирования частотных характеристик заданной формы весьма привлекательна. Благодаря этому свойству спектральный метод формирования частотных характеристик получил большое распространение, хотя это свойство в более общих условиях выполняется лишь приблизительно, так как спектр экспоненты от мнимого аргумента при дробной частоте простирается весьма широко. Об этом идет речь в следующей программе.
Спектр выходного сигнала формируется перемножением спектра входного сигнала и "спектрального окна". Затем восстанавливается выходной сигнал и определяется частотная характеристика получившейся линейной системы точно так же, как это сделано в программе, показанной на рис. 1.7. Форма характеристики получилась в точности повторяющей форму заданного спектрального окна. Возможность формирования частотных характеристик заданной формы весьма привлекательна. Благодаря этому свойству спектральный метод формирования частотных характеристик получил большое распространение, хотя это свойство в более общих условиях выполняется лишь приблизительно, так как спектр экспоненты от мнимого аргумента при дробной частоте простирается весьма широко. Об этом идет речь в следующей программе.
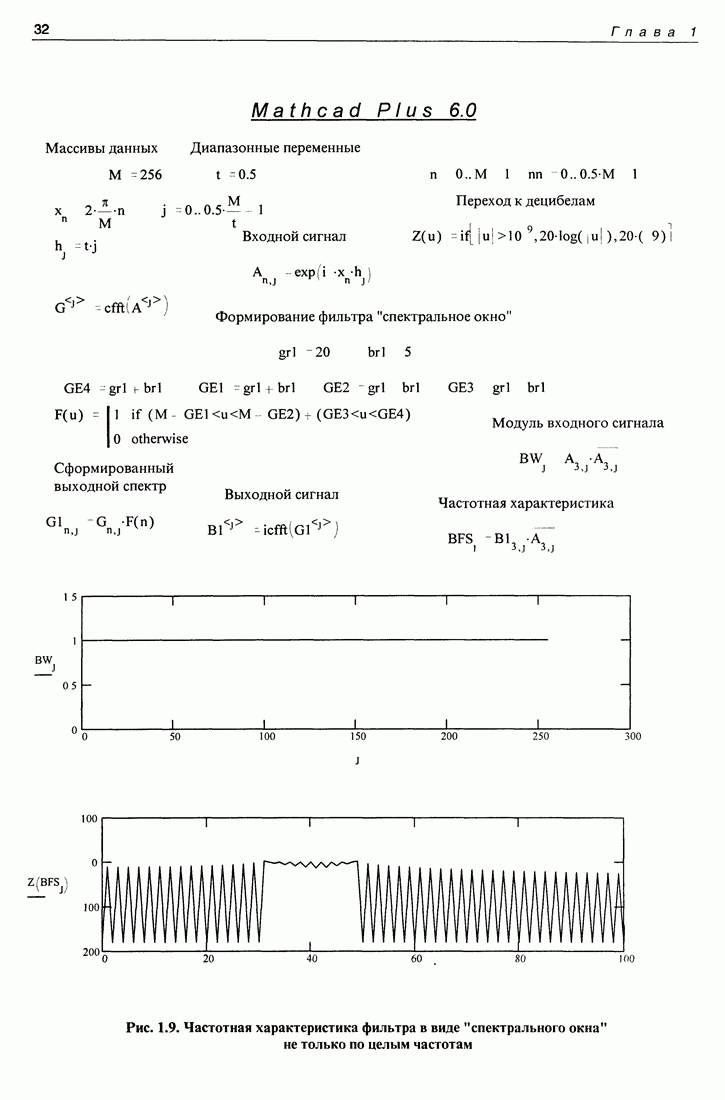
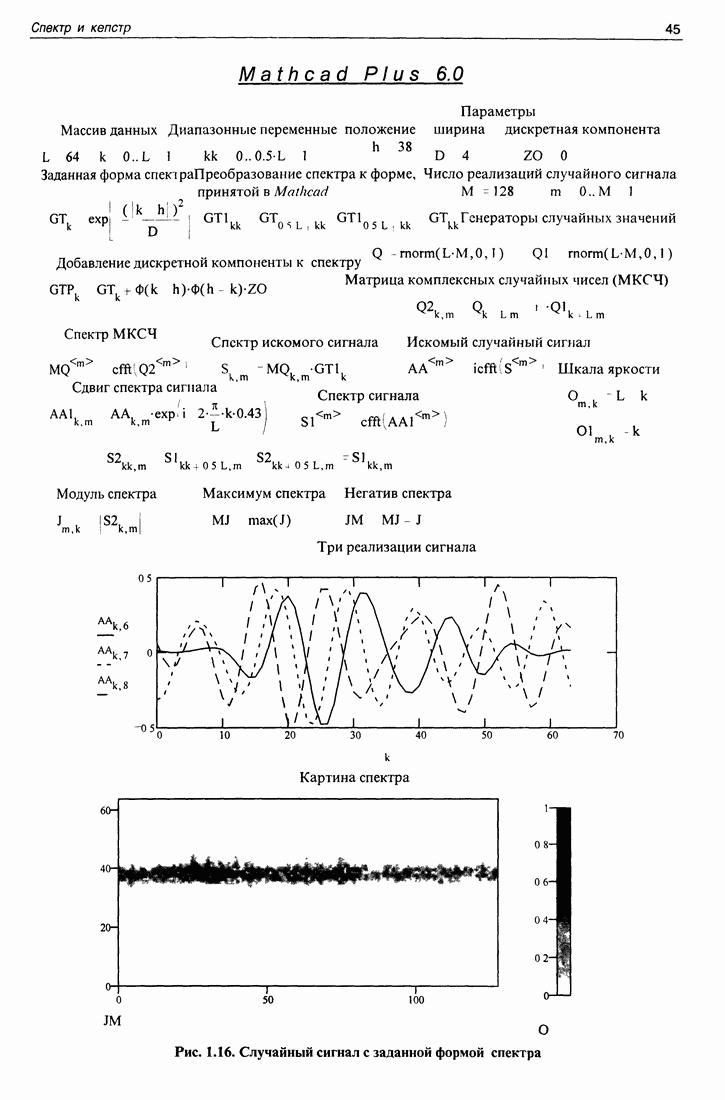
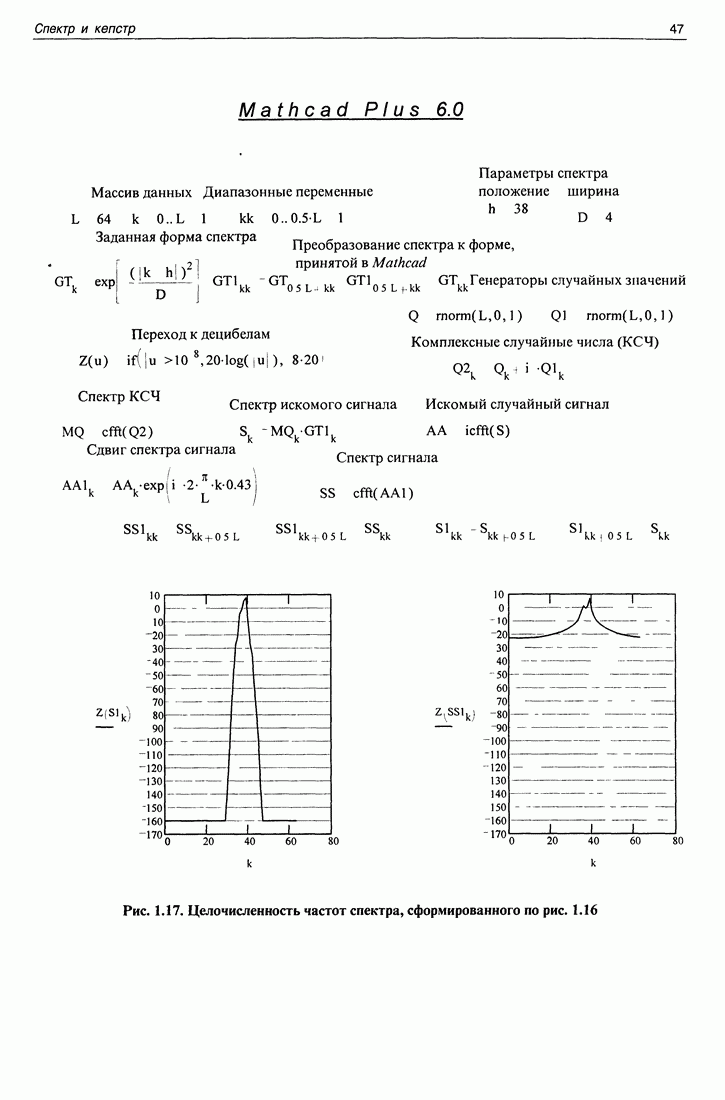
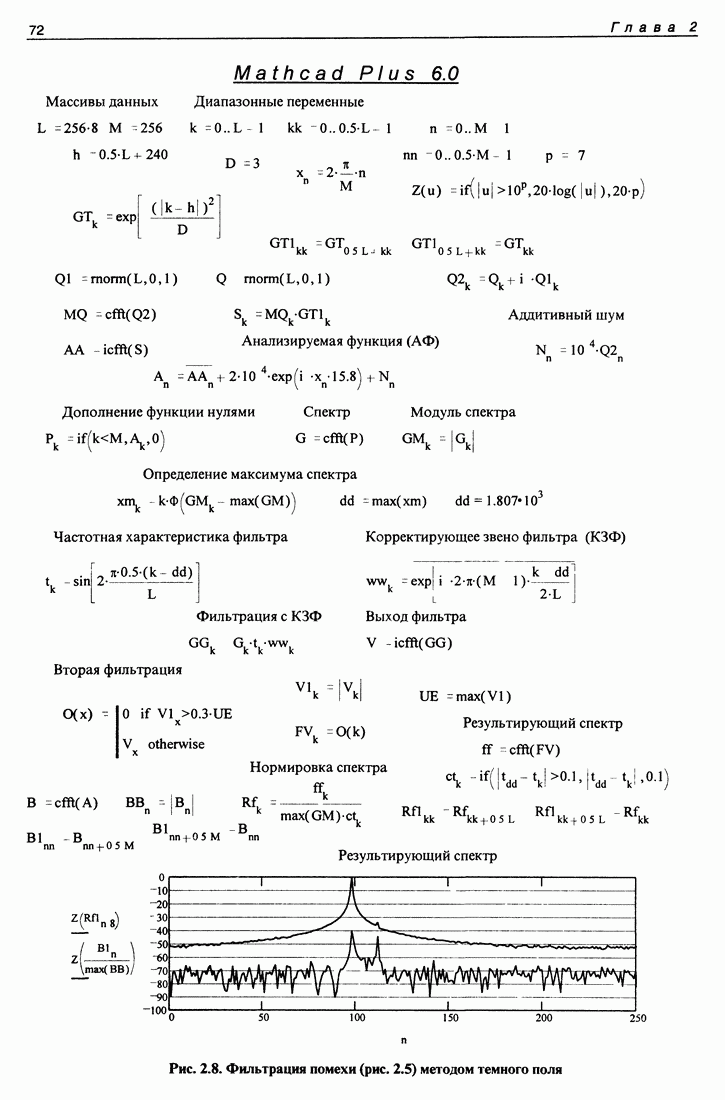
Форма частотной характеристики, сформированной в спектре, при использовании дробных значений частоты показана в программе, приведенной на рис. 1.9. Эта программа отличается от предыдущей тем, что в процессе определения формы частотной характеристики используются и дробные частоты, и форма получившейся частотной характеристики уже не совпадает полностью с формой "спектрального окна". Это объясняется тем, что спектр комплексной экспоненты в случае дробной частоты занимает всю частотную ось. Поэтому дробные частоты "пролезают" в "окно прозрачности" фильтра, находясь далеко за пределами этого окна. Это обстоятельство следует учитывать при спектральном способе формирования фильтров.
Для нас особое значение будут иметь свойства линейных систем как согласованных фильтров. Фильтром, согласованным с сигналом  называется линейная система, частотная характеристика которой равна комплексно сопряженному спектру
называется линейная система, частотная характеристика которой равна комплексно сопряженному спектру 
Рассмотрим ряд свойств согласованных фильтров. Отклик фильтра на сигнал, с которым он согласован, выглядит так:


(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
где выход фильтра представлен как спектр от произведения двух функций (здесь и далее черта сверху означает комплексное сопряжение). Преобразовав это выражение на основании обратной теоремы свертки (1.2.8), получим

Функция в правой части (1.5.12) называется корреляционной функцией. В отличие от свертки у нее переменные, по которым ведется интегрирование, в обоих сомножителях одного знака.
На основе (1.5.12) рассмотрим выход согласованного фильтра на сигнал, имеющий равные амплитуды а во всех точках отсчета, а знак - случайный. При  величина
величина  Далее будем перемещаться на одну отсчетную точку и смотреть выход фильтра. При сдвиге из-за случайности знаков сумма будет стремиться в среднем к пути, который проделывает абсолютно пьяный человек за
Далее будем перемещаться на одну отсчетную точку и смотреть выход фильтра. При сдвиге из-за случайности знаков сумма будет стремиться в среднем к пути, который проделывает абсолютно пьяный человек за  шагов. Эта величина в среднем равна
шагов. Эта величина в среднем равна  Учитывая это, а также то, что число членов последовательности при каждом сдвиге сокращается на единицу, получим
Учитывая это, а также то, что число членов последовательности при каждом сдвиге сокращается на единицу, получим  Этот результат не зависит от величины смещения, поэтому в нуле в одной точке отсчета сигнал превышает средние значения во всех иных точках в
Этот результат не зависит от величины смещения, поэтому в нуле в одной точке отсчета сигнал превышает средние значения во всех иных точках в  раз. Примерно такая же картина получается при сигнале, обладающем случайной амплитудой.
раз. Примерно такая же картина получается при сигнале, обладающем случайной амплитудой.
Выход согласованного фильтра на сигнал, с которым он согласован, и сигнал, с которым он не согласован, показан на рис. 1.10, на котором приведена и программа расчета.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. СПЕКТР И КЕПСТР
- 1.1. Ряд и интеграл Фурье
- 1.2. Математические свойства преобразования Фурье
- 1.3. Знаменитая теорема отсчетов
- 1.4. Как выполняется преобразование Фурье численно
- 1.5. Линейные системы
- 1.6. Кепструм
- 1.7. Численное представление случайных сигналов
- Глава 2. ФИЛЬТРАЦИЯ ПОМЕХ И ЛОКАЦИЯ НА ПРОСВЕТ
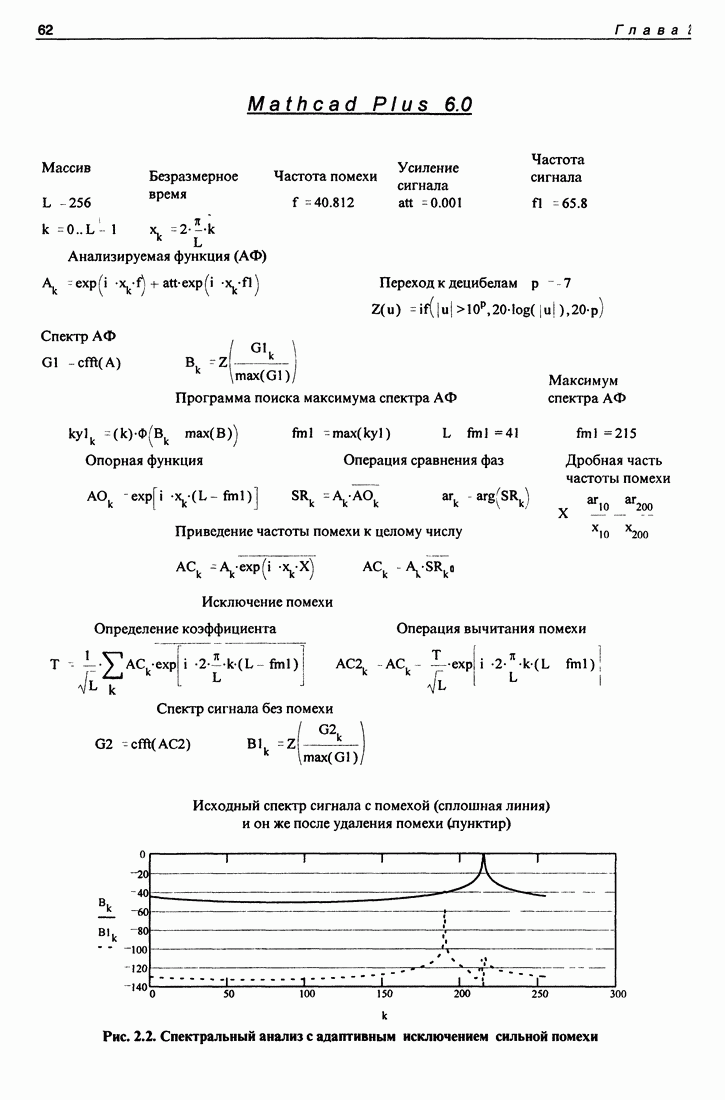
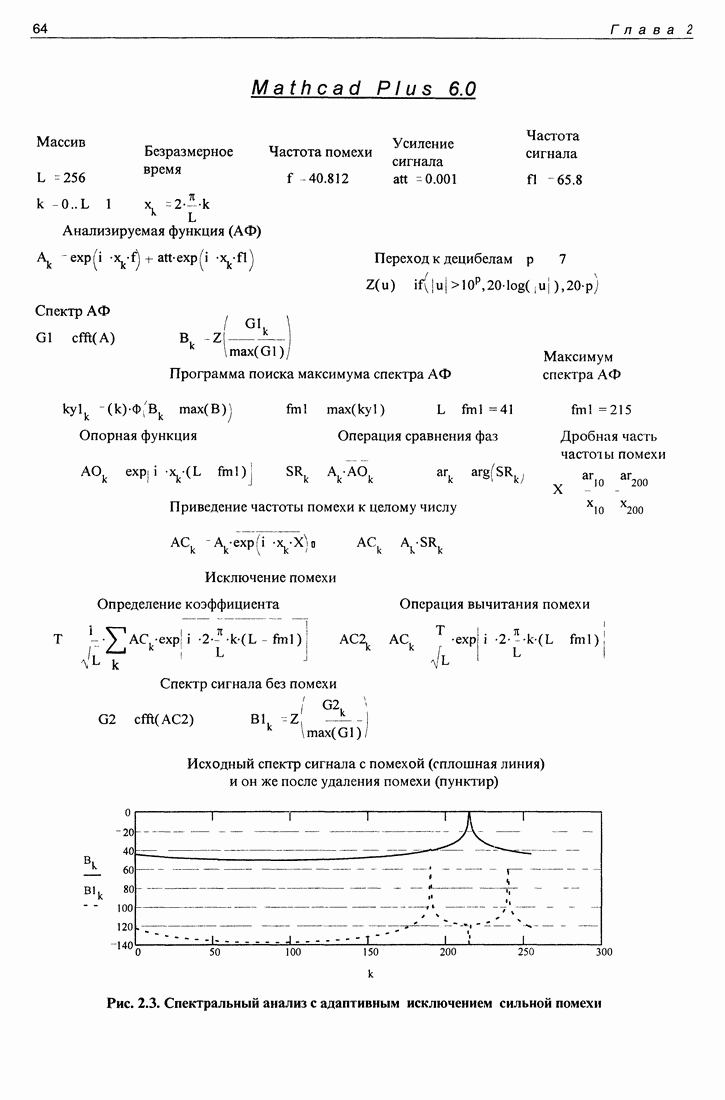
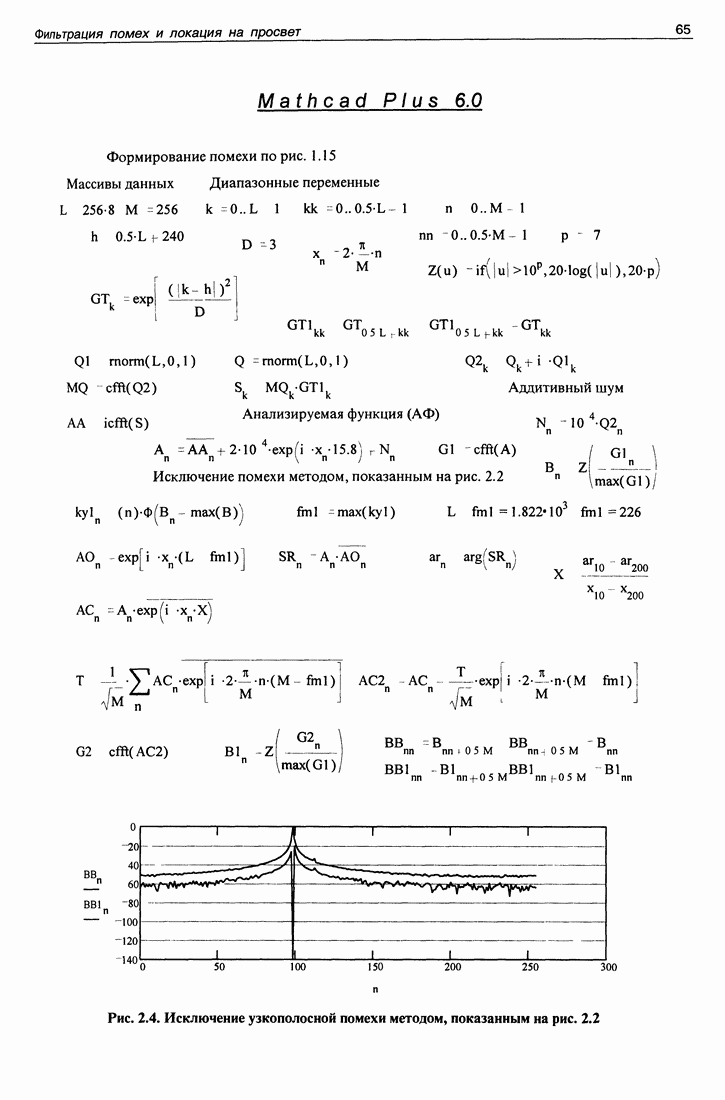
- 2.1. Устранение узкополосной помехи
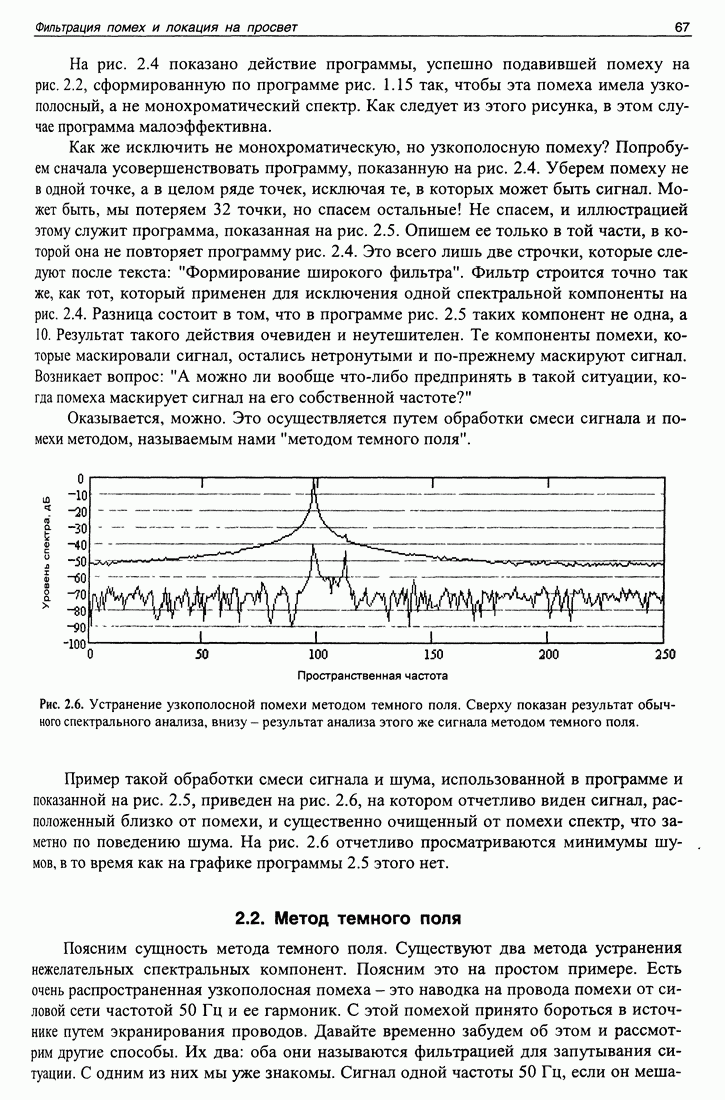
- 2.2. Метод темного поля
- 2.3. Эксперимент по наблюдению точечного рассеивателя
- Глава 3. УВЕЛИЧЕНИЕ ПРОСТРАНСТВЕННОГО ИЛИ ВРЕМЕННОГО РАЗРЕШЕНИЯ
- 3.2. Увеличение временного разрешения сигналов
- 3.3. Локация на просвет с разделением прямого и дифрагированного сигналов по времени
- Глава 4. ФАЗОВЫЕ ШУМЫ И РЕВЕРБЕРАЦИЯ
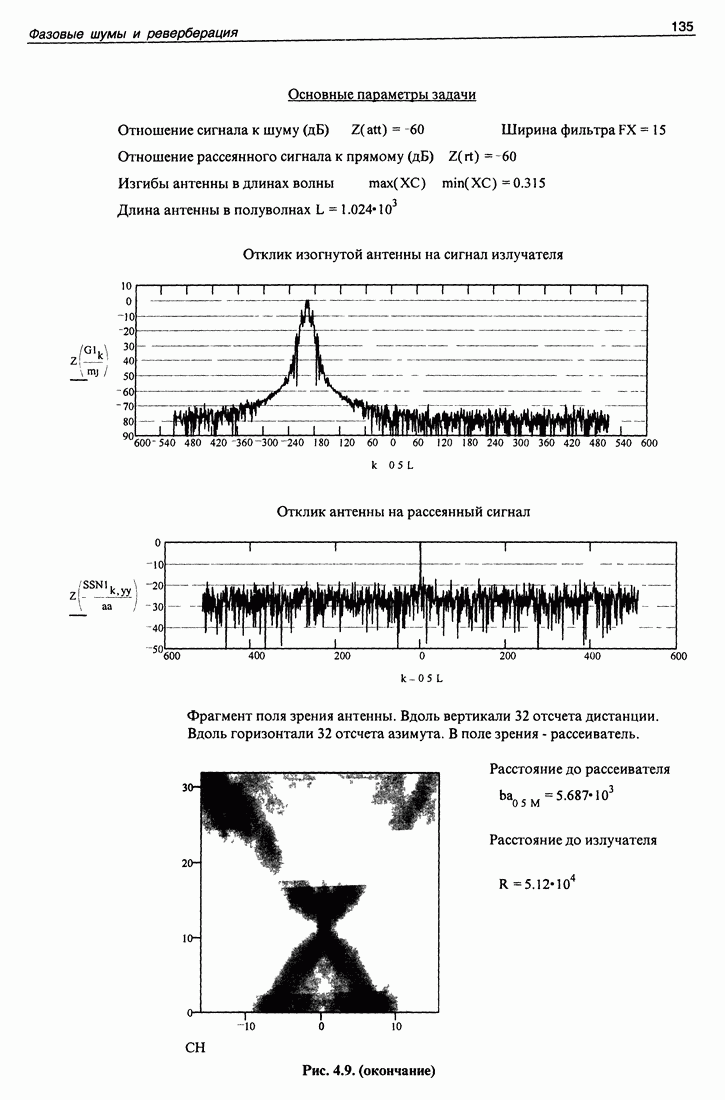
- 4.1. Фильтрация мультипликативно связанных сигналов
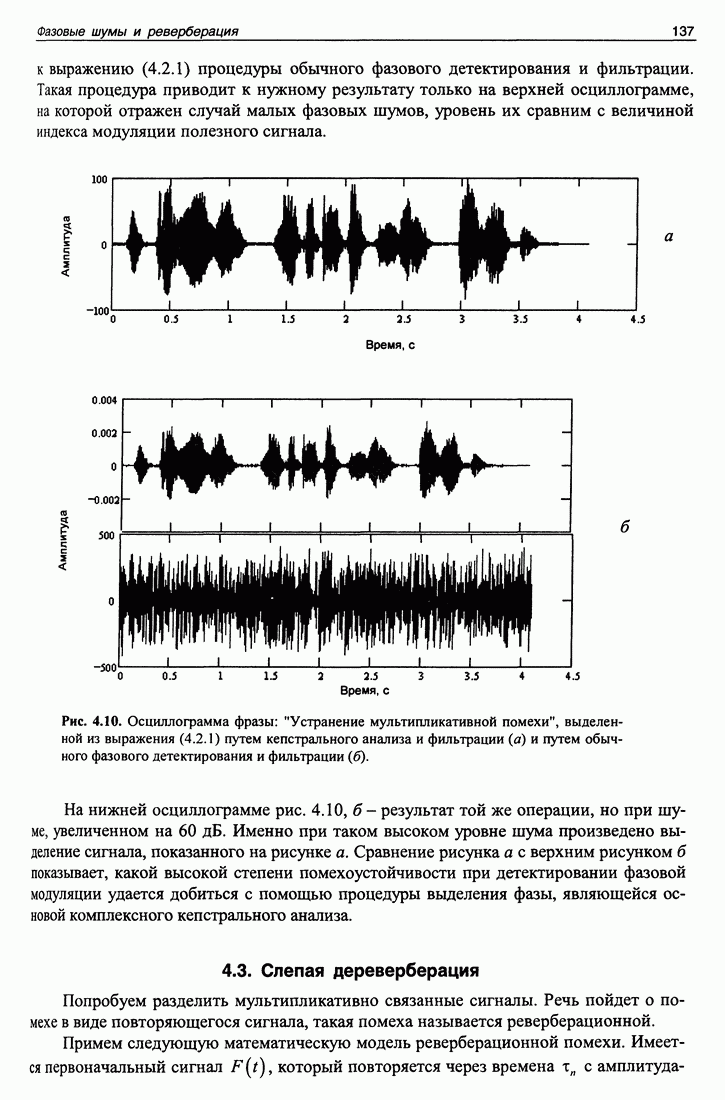
- 4.2. Устранение влияния фазовых шумов в параметрическом микрофоне
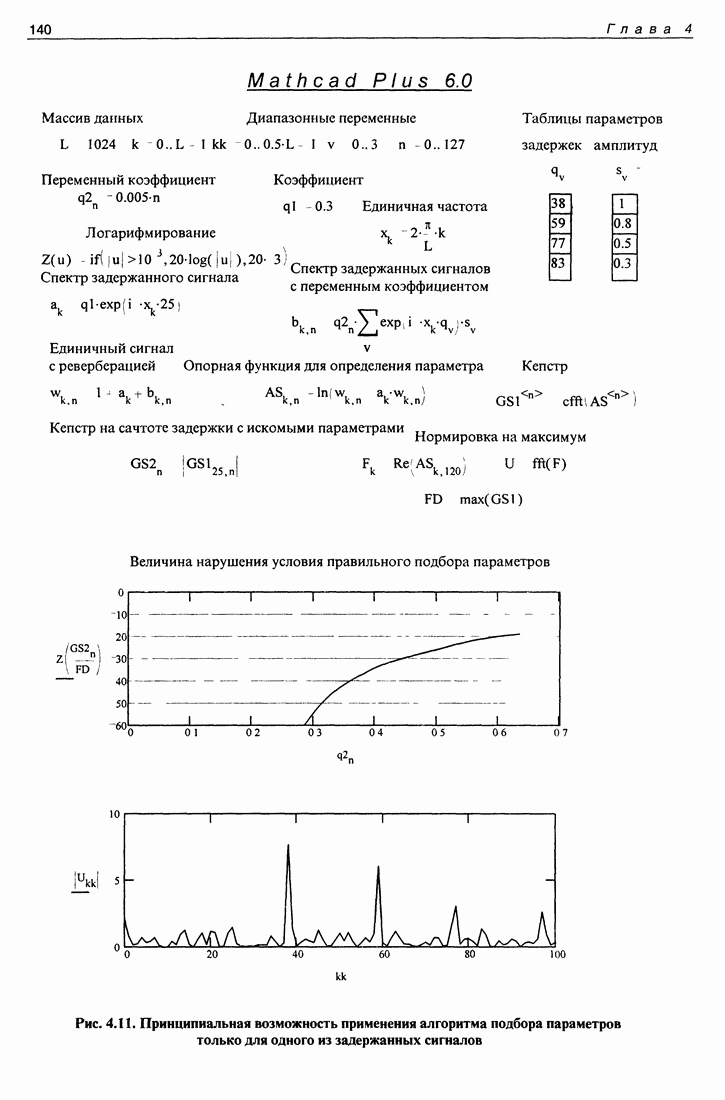
- 4.3. Слепая дереверберация
- Глава 5. ИССЛЕДОВАНИЕ АКУСТИЧЕСКИХ ТРАСС С ИСПОЛЬЗОВАНИЕМ М-ПОСЛЕДОВАТЕЛЬНОСТИ
- 5.1. Акустические задачи, решаемые с помощью M-последовательности
- 5.2. Выбор оптимальной методики анализа линейной системы
- 5.3. М-последовательность — идеальный тестовый сигнал для анализа систем. Ее генерация и свойства
- 5.4. Применение М-последовательности на стационарной сейсмической трассе
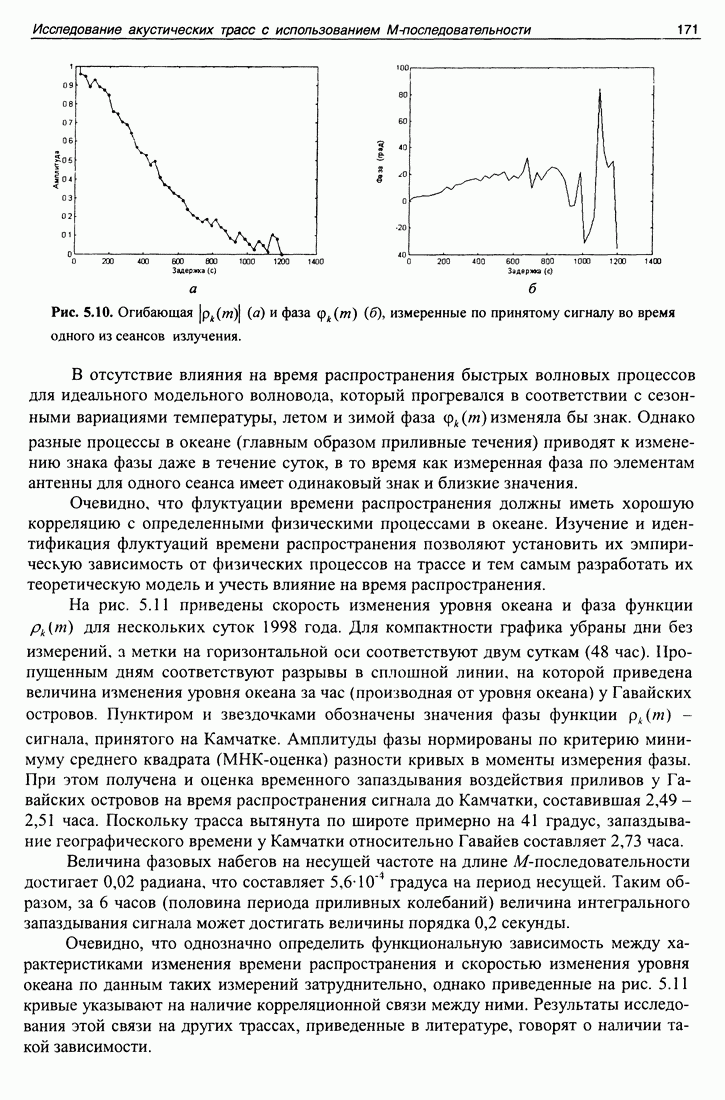
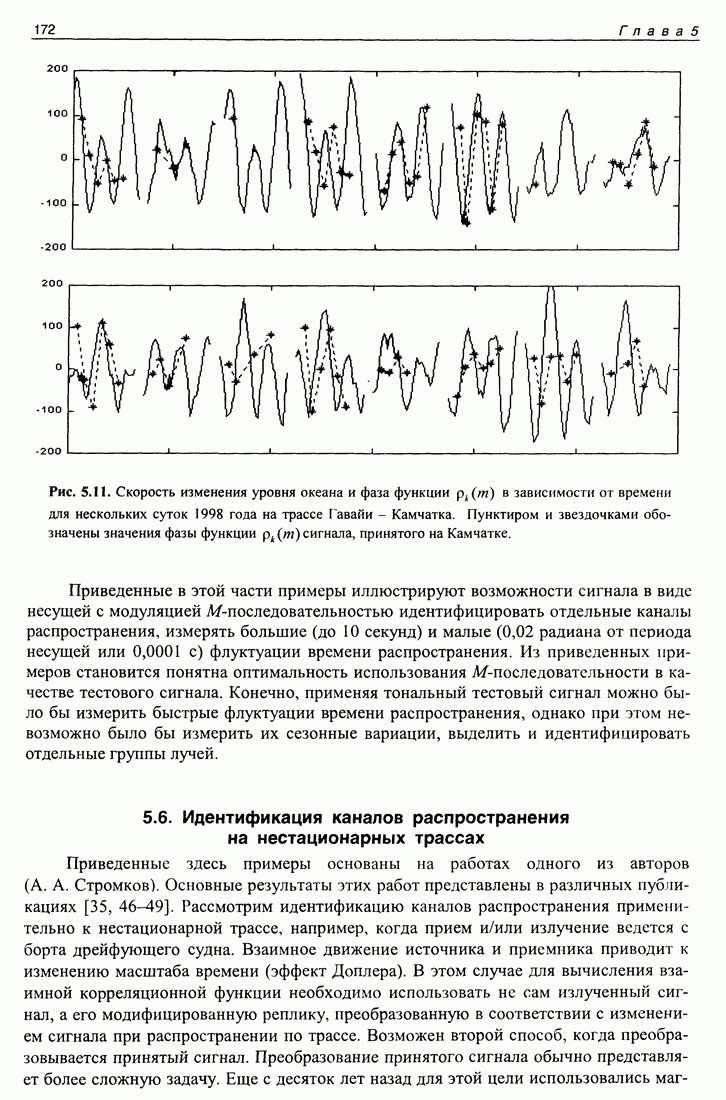
- 5.5. Применение М-последовательности на сверхдлинных океанических трассах
- 5.6. Идентификация каналов распространения на нестационарных трассах
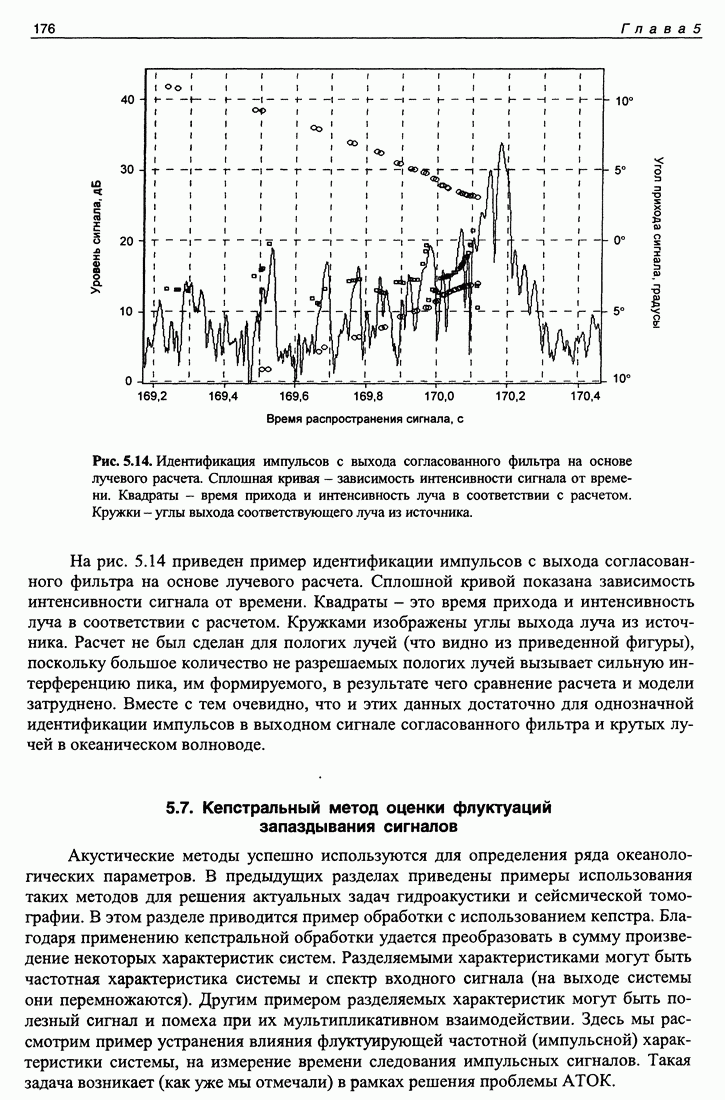
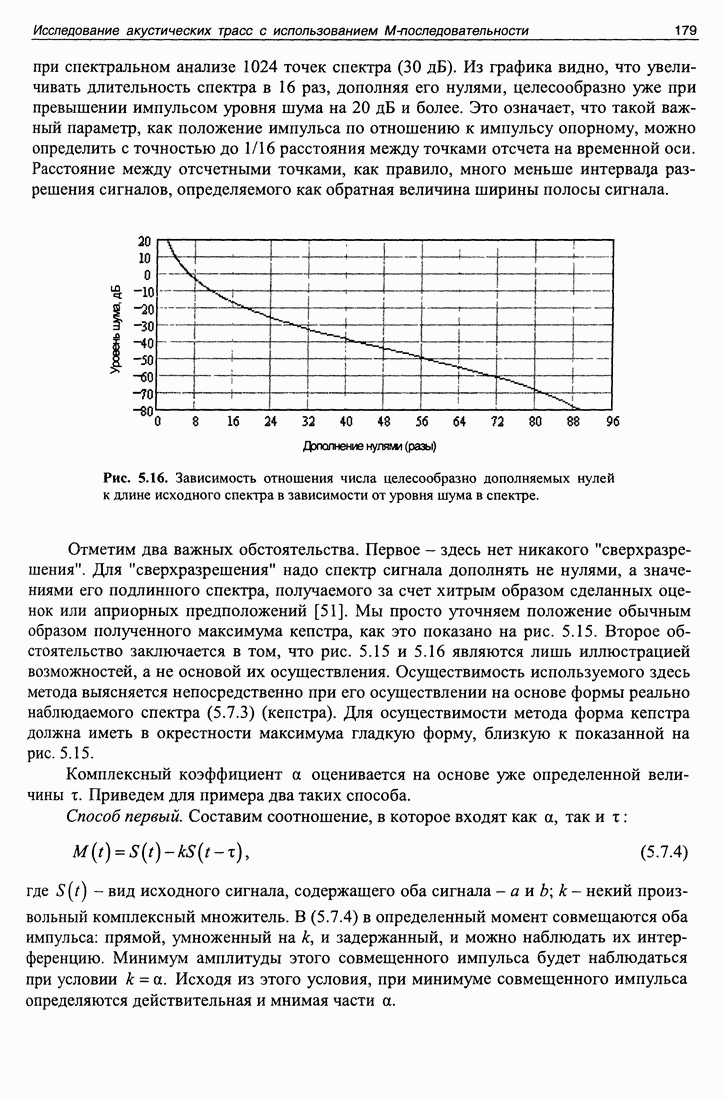
- 5.7. Кепстральный метод оценки флуктуаций запаздывания сигналов
- Литература