1.3. Знаменитая теорема отсчетов

Окончательный вид преобразованию Фурье и возможность его использования для любых, а не только периодических функций, мы получили благодаря предельному переходу от ряда Фурье (1.1.13) к интегралу (1.1.14). Численный счет осуществляется на основе дискретной сетки значений, не допускающих, вообще говоря,

предельных переходов. Не потеряем ли мы всех плюсов и возможностей преобразования Фурье, записанного в интегральной форме, не имея реальной возможности осуществить предельный переход к бесконечному периоду? На этот вопрос мы пока ответим следующим замечанием. Численными методами можно практически с любой точностью оценивать интегралы. Поэтому преобразования Фурье можно представлять себе в удобной интегральной форме не только тогда, когда производятся вычисления на бумаге, но и тогда, когда подключаются численные методы. Однако в действительности дело обстоит куда проще. Чтобы пояснить это, необходима так называемая теорема отсчетов.

Теорема отсчетов тоже является одним из математических свойств преобразования Фурье. Выделим ее в специальный раздел и даже докажем, поскольку это одна из самых замечательных и наиболее используемых теорем 20 века. Она имеет три названия. В 1935 г. эту теорему сформулировал, доказал и показал ее выдающуюся роль в теории связи В. А. Котельников. Она получила название теоремы Котельникова. В 1945 г. известный ученый Клод Шеннон построил фундамент современной теории связи. В основу этого фундамента легла та же теорема, доказанная К. Шенноном независимо от Котельникова. После этого было обнаружено доказательство этой же теоремы в работах известного математика Уиттекера. Работа Уиттекера относится к 1915 г. Тогда в литературе эта теорема стала появляться как теорема Уиттекера - Шеннона, так как Уиттекер доказал теорему только как относящуюся к теории преобразования Фурье, не помышляя о том, что она станет фундаментом теории связи. Мы будем придерживаться названия, связанного с существом теоремы, называя ее теоремой отсчетов.

Чтобы сформулировать теорему и приступить к ее доказательству, необходимо ввести еще одно понятие, связанное с преобразованием Фурье. Это понятие о функции, обладающей ограниченным спектром. Функцией с ограниченным спектром называется такая функция, спектр которой по модулю обращается в нуль на всех частотах, начиная с частоты, которая называется граничной частотой. Теперь сформулируем теорему.

Непрерывная функция, имеющая ограниченный спектр с граничной частотой может быть представлена в любой точке на основании своих значений, взятых в дискретных точках отсчета этой функции. Расстояние между точками отсчета при этом не должно превышать значения

Прежде чем доказывать эту теорему, обсудим ее практическое значение. Все функции, имеющие какой-то физический смысл, обладают ограниченным спектром. Поэтому по условиям теоремы отсчетов любая непрерывная функция представима дискретным рядом значений. Это позволяет представлять информацию о любых непрерывно протекающих явлениях в виде дискретного набора значений, используемого при численном счете. Без этого в условиях, когда любой конечный отрезок непрерывной функции определяется бесконечной совокупностью значений, численный счет и передача таких данных по каналам связи была бы невозможной.

Теперь докажем эту теорему. Доказательство привлекательно тем, что дает прекрасную возможность проиллюстрировать то, как практически при этом работают сформулированные выше математические свойства преобразования Фурье.

Пусть функция имеет ограниченный спектр. Запишем спектр этой функции в таком виде, чтобы ограничения ширины спектра функции были бы явно видны:

Здесь использована специальная функция определяемая (1.2.14). Эта запись (1.3.1) дает нам возможность доопределять спектр за пределами любым образом. Примем, что за пределами граничной частоты спектр является периодической функцией. Такое предположение мы имеем право делать, только пользуясь для спектра представлением (1.3.1). Теперь подвергнем обе части (1.3.1) преобразованию Фурье и получим выражение

которое на основании обратной теоремы свертки (1.2.8) можно записать в виде

Вычислим каждую функцию, входящую в свертку (1.3.3), а затем выполним преобразование свертки.

На основании предположения о периодичности функции обратное преобразование от нее будет содержать дельта-функцию:

От второй функции обратное преобразование Фурье находится непосредственным вычислением:

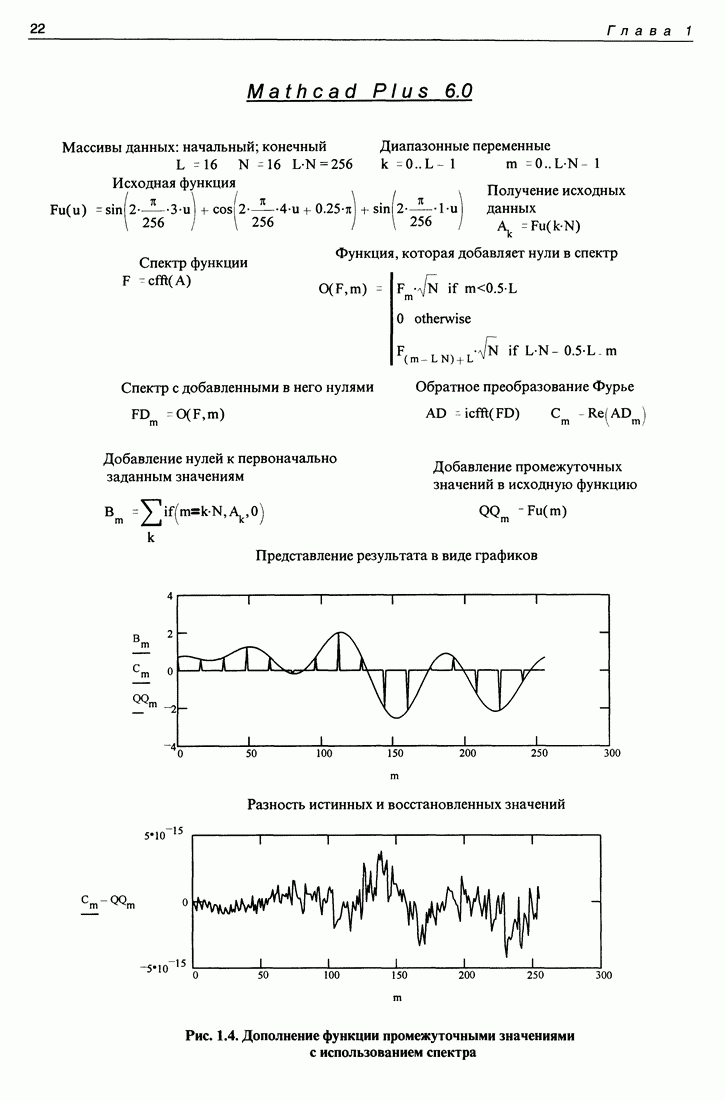
Выполняя преобразование свертки с учетом свойств дельта-функции, окончательно получим следующий ряд Котельникова:

Этот ряд позволяет вычислить с любой точностью значения непрерывной функции по ее значениям в дискретных точках отсчета, определяемых следующим образом:

Интегральные уравнения преобразования Фурье практически симметричны относительно функции и ее спектра. Поэтому существует еще одна симметричная теорема отсчетов, относящаяся к спектру функции. Она формулируется аналогично доказанной теореме и утверждает, что непрерывный спектр функции может быть задан дискретными отсчетами, если значения функции точно равны нулю вне конечной области ненулевых значений.

Введем понятие о степенях свободы сигнала, являющееся важнейшим для практики следствием теоремы отсчетов. Пусть спектр сигнала ограничен. На этом основании можно строго математически показать, что значения непрерывной функции достаточно знать лишь в точках отсчета. Число значений функции, которые надо вводить в вычислительное устройство, вроде бы существенно сократилось, но не совсем. Есть

же еще и спектр функции. Чтобы и спектр функции мог быть задан значениями в дискретных точках, значения самой функции должны быть заданы в пределах некоторого ограниченного отрезка области значений функции. Иными словами, задание функции значениями в дискретных точках еще не гарантирует нам возможности представления этой функции конечным набором чисел. Должна быть ограничена и область задания функции. Если это сделано, т. е. ограничен спектр функции и область ее задания ненулевыми значениями, то тогда непрерывная функция может быть задана конечным числом своих значений, взятых в точках отсчета. Это число называется числом степеней свободы функции, так как любые ее изменения должны быть связаны с изменением только этих конечных значений.

Пусть число степеней свободы функции будет ширина ее спектра, простирающаяся от одной граничной частоты до другой, будет а область задания значений функции обозначим Тогда число степеней свободы функции, равное отношению интервала к расстоянию между отсчетными точками, определится как

Выражение (1.3.8) является настолько важным в приложениях, что одно его существование среди всех математических свойств преобразования Фурье обеспечивало бы этому преобразованию широкое применение в исследованиях.