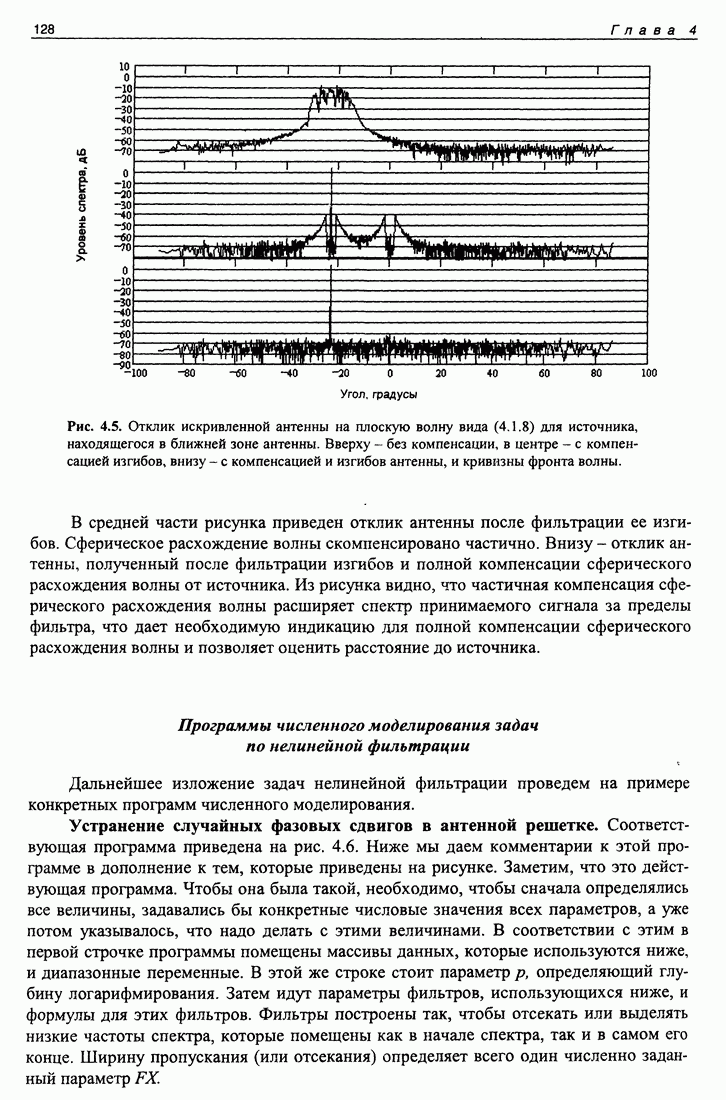
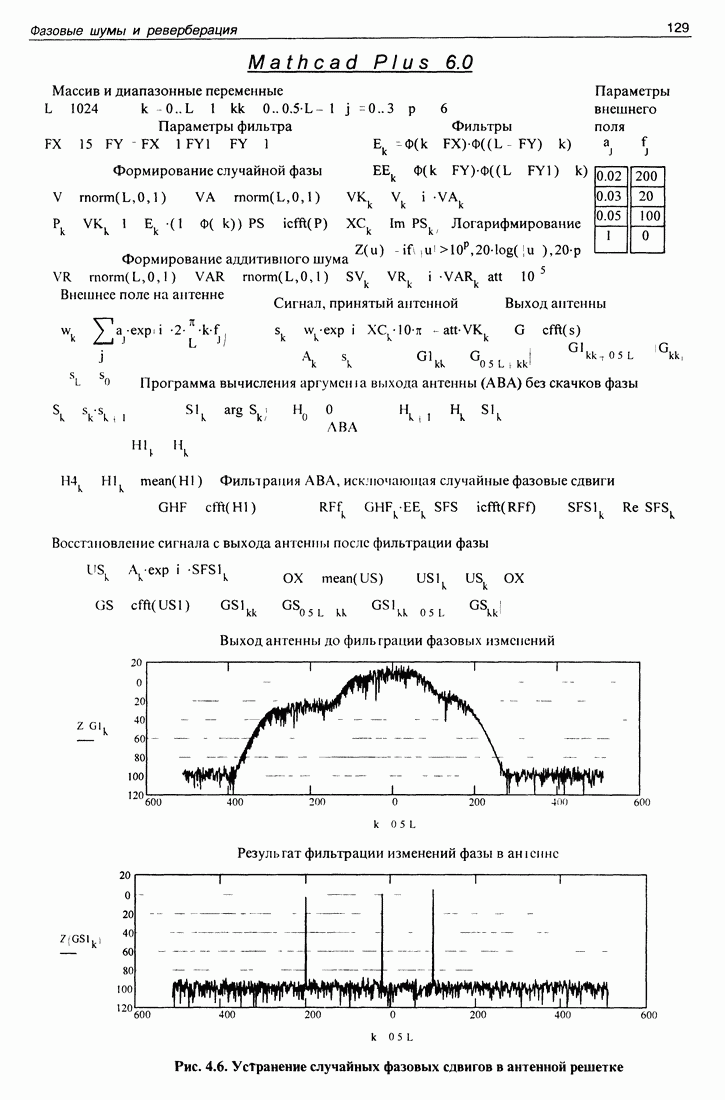
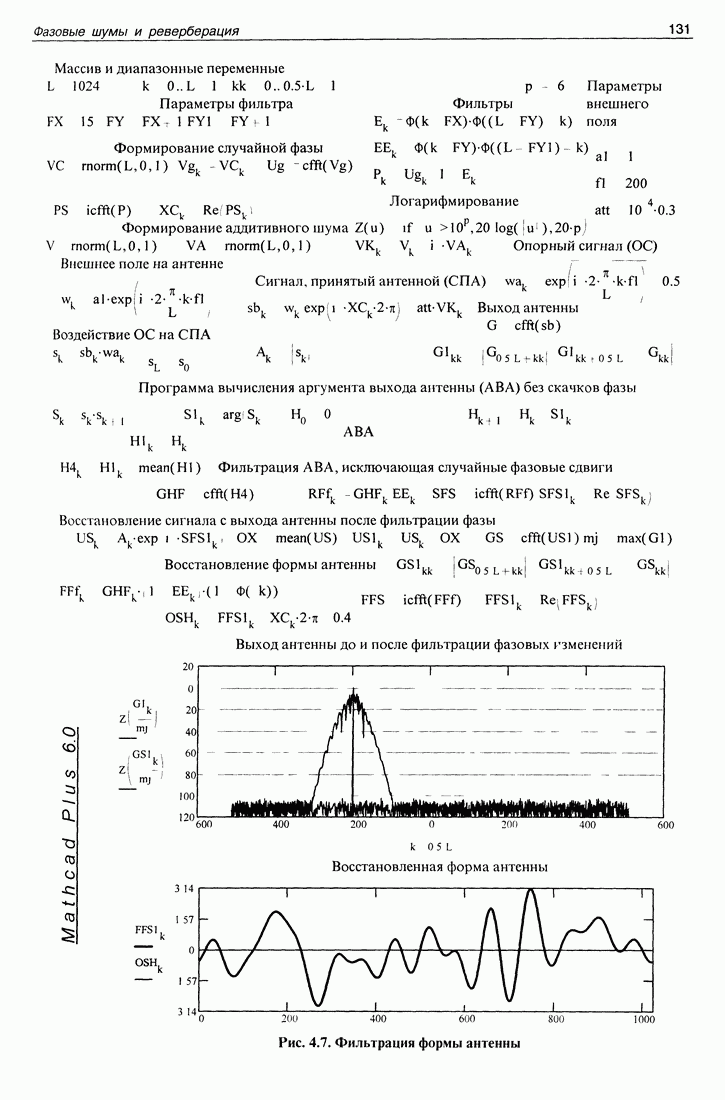
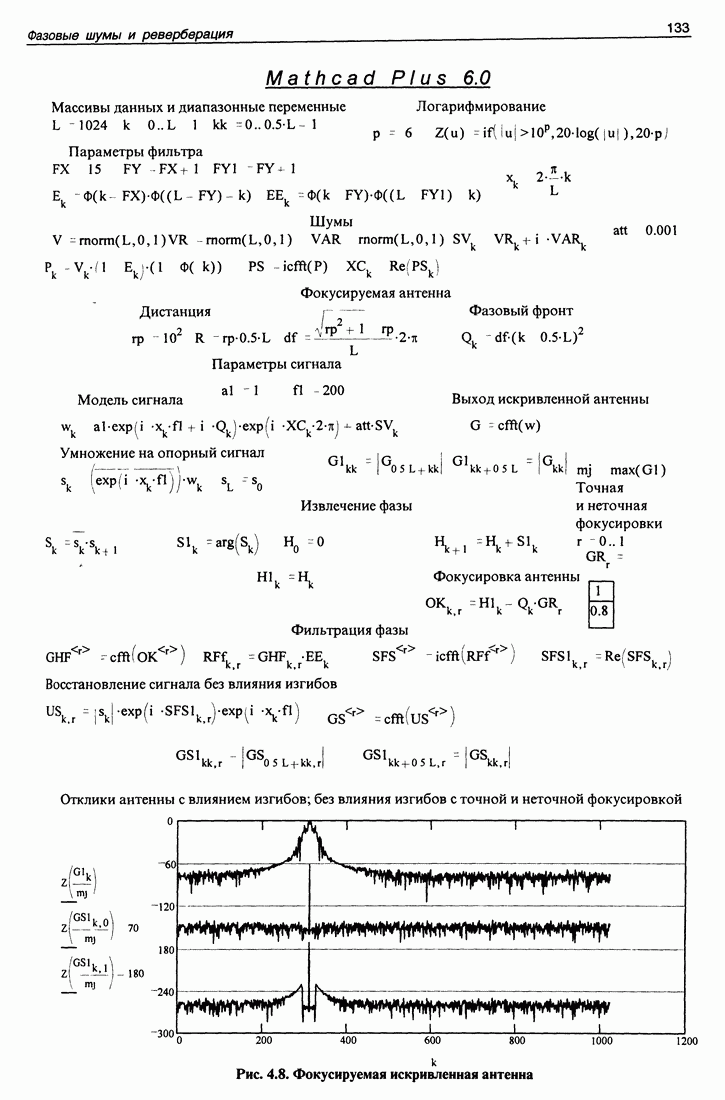
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
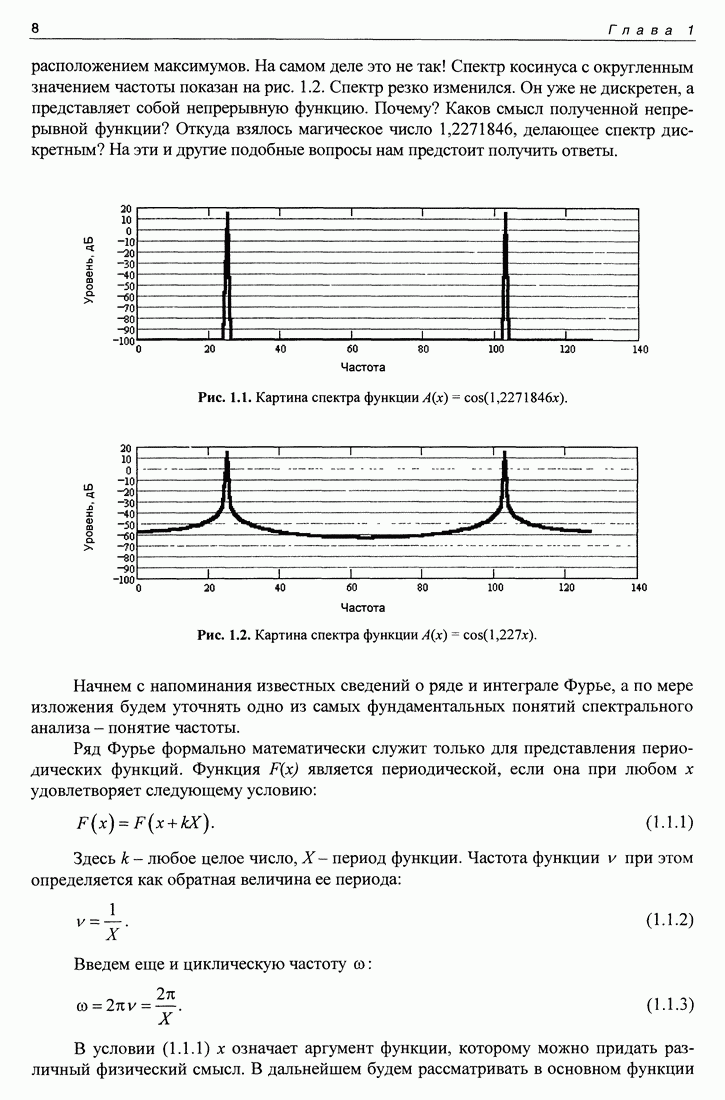
1.2. Математические свойства преобразования Фурье
Приведем здесь основные математические свойства преобразования Фурье, не останавливаясь на их доказательствах.
1. Главное математическое свойство преобразования Фурье состоит в том, что оно однозначно. Каждой функции соответствует только ей присущий частотный спектр, по которому можно восстановить эту функцию однозначно. Отсюда следует, что преобразование Фурье, примененное к одной и той же функции дважды (сначала к самой функции, а затем к ее спектру), дает в результате исходную функцию. Так построены и математические специальные программы, позволяющие выполнять преобразование Фурье.
С помощью принятой нами символики математически это свойство преобразования Фурье может быть записано следующим образом:

2. Важнейшее свойство преобразования Фурье - это его аддитивность. Преобразование Фурье от суммы двух функций равно сумме преобразований Фурье от каждой из них в отдельности, или

Когда складываются функции, то суммируются и их частотные спектры. Это свойство легко обобщается на любое число слагаемых.
3. Более сложным является выражение преобразования Фурье от произведения функций через преобразования Фурье от сомножителей. На этот счет существуют две теоремы свертки (прямая и обратная). Сверткой двух функций называется следующее интегральное преобразование:

Для преобразования (1.2.4) существует специальное обозначение в виде косого крестика в кружочке. Вот как оно выглядит:

Прямая теорема свертки формулируется так: фурье-преобразование от свертки двух функций равно произведению преобразований Фурье от этих функций:


Черта сверху здесь и далее означает операцию перехода к комплексно сопряженному выражению. Обратная теорема свертки: фурье-преобразование от произведения функций равно свертке их преобразований Фурье:


4. Теорема смещения. Это свойство преобразования Фурье чрезвычайно широко используется в приложениях для смещения спектров функций. Свойство выглядит следующим образом:


5. Преобразования Фурье от некоторых специальных функций. В приложениях ряда и интеграла Фурье к практическим задачам существенную роль играют некоторые специальные функции. Эти функции обладают математическими особенностями в виде разрывов и расходимости. Поэтому они не могут быть вычислены непосредственно по формулам, описывающим преобразования Фурье. Во многих руководствах и математической литературе большое внимание уделяется преобразованиям Фурье от специальных функций. Учитывая, что это уже сделано и есть почти в каждой книге, посвященной преобразованиям Фурье, мы дадим эти свойства без доказательств.
Одна из самых употребительных функций - так называемая дельта-функция 
Эту функцию мы определим через ее фурье-спектр. Фурье-спектр дельта-функции равен единице:


Из (1.2.12) и (1.2.13) следует, что  всюду равна нулю за исключением всего одной точки, а именно нуля. В нуле функция
всюду равна нулю за исключением всего одной точки, а именно нуля. В нуле функция  обращается в бесконечность, но так, что интеграл от нее остается конечным и равным единице.
обращается в бесконечность, но так, что интеграл от нее остается конечным и равным единице.
Следующей специальной функцией, которую мы рассмотрим, будет так называемая прямоугольная функция. Она определяется так:

Между прямоугольной и дельта-функцией существует связь:

6. В качестве следующего свойства преобразования Фурье отметим следствие определения дельта-функции. Хотя это простое и легко устанавливаемое следствие, однако ввиду его важности мы его выделяем. Это свойство касается результата свертки какой-либо функции с дельта-функцией:

Подвергая (1.2.16) преобразованию Фурье дважды (сначала прямому, а затем обратному) и пользуясь теоремой свертки, получим, что

Пользуясь этим свойством дельта-функции, легко доказывать другие. В качестве примера рассмотрим прямую теорему свертки.
Свертку функций запишем в виде (1.2.4). В этом выражении функцию  заменим ее преобразованием Фурье. Получим
заменим ее преобразованием Фурье. Получим

Здесь мы употребили очень удобное обозначение для спектра функции  пометив его той же буквой с добавлением внизу индекса
пометив его той же буквой с добавлением внизу индекса  - сразу видно, от какой именно функции взято прямое преобразование Фурье. Конечно, это видно и при символическом написании, но символическое написание ввиду его громоздкости и символичности не всегда удобно подставлять в формулы. В (1.2.18) можно выполнить
- сразу видно, от какой именно функции взято прямое преобразование Фурье. Конечно, это видно и при символическом написании, но символическое написание ввиду его громоздкости и символичности не всегда удобно подставлять в формулы. В (1.2.18) можно выполнить

интегрирование по переменной  в результате чего получается спектр
в результате чего получается спектр 
Поскольку нам надо найти спектр свертки, совершим прямое преобразование Фурье над обеими частями (1.2.19). Это преобразование надо совершить по переменной  так как переменная
так как переменная  у нас уже занята в (1.2.19). Совершив это преобразование, получим:
у нас уже занята в (1.2.19). Совершив это преобразование, получим:

Интегрируя (1.2.20) по  получаем дельта-функцию:
получаем дельта-функцию:

Используя (1.2.16), получаем прямую теорему свертки.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. СПЕКТР И КЕПСТР
- 1.1. Ряд и интеграл Фурье
- 1.2. Математические свойства преобразования Фурье
- 1.3. Знаменитая теорема отсчетов
- 1.4. Как выполняется преобразование Фурье численно
- 1.5. Линейные системы
- 1.6. Кепструм
- 1.7. Численное представление случайных сигналов
- Глава 2. ФИЛЬТРАЦИЯ ПОМЕХ И ЛОКАЦИЯ НА ПРОСВЕТ
- 2.1. Устранение узкополосной помехи
- 2.2. Метод темного поля
- 2.3. Эксперимент по наблюдению точечного рассеивателя
- Глава 3. УВЕЛИЧЕНИЕ ПРОСТРАНСТВЕННОГО ИЛИ ВРЕМЕННОГО РАЗРЕШЕНИЯ
- 3.2. Увеличение временного разрешения сигналов
- 3.3. Локация на просвет с разделением прямого и дифрагированного сигналов по времени
- Глава 4. ФАЗОВЫЕ ШУМЫ И РЕВЕРБЕРАЦИЯ
- 4.1. Фильтрация мультипликативно связанных сигналов
- 4.2. Устранение влияния фазовых шумов в параметрическом микрофоне
- 4.3. Слепая дереверберация
- Глава 5. ИССЛЕДОВАНИЕ АКУСТИЧЕСКИХ ТРАСС С ИСПОЛЬЗОВАНИЕМ М-ПОСЛЕДОВАТЕЛЬНОСТИ
- 5.1. Акустические задачи, решаемые с помощью M-последовательности
- 5.2. Выбор оптимальной методики анализа линейной системы
- 5.3. М-последовательность — идеальный тестовый сигнал для анализа систем. Ее генерация и свойства
- 5.4. Применение М-последовательности на стационарной сейсмической трассе
- 5.5. Применение М-последовательности на сверхдлинных океанических трассах
- 5.6. Идентификация каналов распространения на нестационарных трассах
- 5.7. Кепстральный метод оценки флуктуаций запаздывания сигналов
- Литература