| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.6. Кепструм
Кепстральный анализ является математической основой нелинейных методов выделения сигналов. Остановимся на тех математических свойствах этого преобразования сигналов, которые нам понадобятся в дальнейшем. Кепструм - это такое математическое преобразование, когда спектральному преобразованию подвергается спектр функции. Если взять спектр от спектра в виде (1.2.2), то получится сама первоначальная функция. Это неинтересно. Чтобы был иной результат, имеющий какой-то смысл, надо не просто взять спектр от спектра, а предварительно преобразовать этот спектр.
В качестве такого преобразования принято логарифмировать спектр. Логарифм можно взять от модуля спектра - при таком преобразовании спектра получается обычный кепструм. Можно взять логарифм от комплексного спектра - получится комплексный кепструм. Примем, что логарифм берется при основании е.
Остановимся сначала на математических особенностях преобразования "обычный кепструм”. Математическое определение операции "кепструм" следующее:

где  означает вводимую нами функциональную операцию - кепструм от функции
означает вводимую нами функциональную операцию - кепструм от функции  Остальные обозначения те же, что и в разд. 1, посвященном ряду и интегралу Фурье.
Остальные обозначения те же, что и в разд. 1, посвященном ряду и интегралу Фурье.
Название функциональной операции "кепструм" происходит от латинского слова spectrum. Если в этом слове первые четыре подчеркнутые буквы поставить в обратном порядке, то получится cepstrum. Такой принцип применяется для обозначения всех операций, в которых используется второе преобразование Фурье. Так, частота, полученная в результате второго спектрального преобразования, называется "сачтота". Также поступают и с другими терминами, относящимися ко второму спектральному анализу. Это упрощает описание процедуры, придавая ему точность. Сразу становится ясно, о какой частоте идет речь, о той, которая еще должна подвергнуться спектральному преобразованию, или о той, которая уже получена в результате второго преобразования Фурье.
Выделим существенные для нас математические свойства кепструма.
1. Главное - это кепструм от произведения спектров двух функций. На основе свойства логарифма превращать произведение в сумму и аддитивности преобразования получается, что, если  то
то

Это очень важное свойство. Именно из-за него в операцию вводится логарифмирование.
2. Пусть

где  - комплексная функция, но такая, что
- комплексная функция, но такая, что

Тогда

Это тоже чрезвычайно полезное свойство преобразования.
3. Кепструм суммы спектров двух функций через кепструмы слагаемых не выражается. Однако на основании свойства 2, выраженного (1.6.5), можно оценить кепструм суммы спектров двух функций, из которых один спектр много меньше другого по модулю.
Пусть

тогда

4. Если частота образует гармонический ряд, состоящий из суммы гармоник, то такому ряду соответствует единственная сачтота кепструма. Это свойство очень важно в приложениях для выделения гармонических составляющих.
5. Каждой частоте, имеющей период  в колебании, модулирующем спектр функции, соответствует частота
в колебании, модулирующем спектр функции, соответствует частота

Теперь перейдем к комплексному кепструму. Его отличает то, что логарифм берется не от модуля спектра, а от самого комплексного спектра. Логарифм от комплексной функции определяется как

Свойства первого слагаемого (1.6.9) мы уже рассмотрели. Теперь посмотрим на второе слагаемое - аргумент функции.
Здесь основная проблема состоит в том, чтобы суметь вычислить этот аргумент. Многие математические программы предоставляют возможность вычислять аргументы комплексных функций. Этими возможностями обладают и использующиеся нами пакеты программ Mathcad и Matlab.
Вычисление аргумента функции основано на его выражении через арктангенс отношения мнимой части комплексного числа к его действительной части. При этом в пакете Mathcad значение аргумента, вычисляемого по команде  дает значение аргумента только в пределах
дает значение аргумента только в пределах  поэтому вычисляемый аргумент испытывает скачки на
поэтому вычисляемый аргумент испытывает скачки на  или
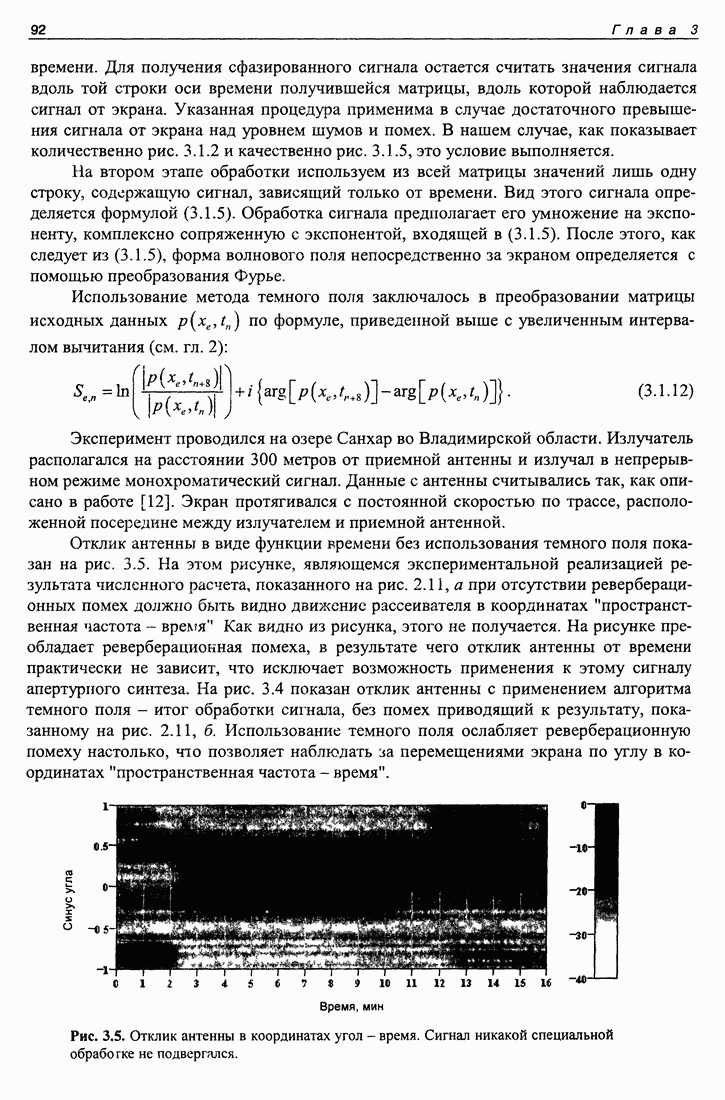
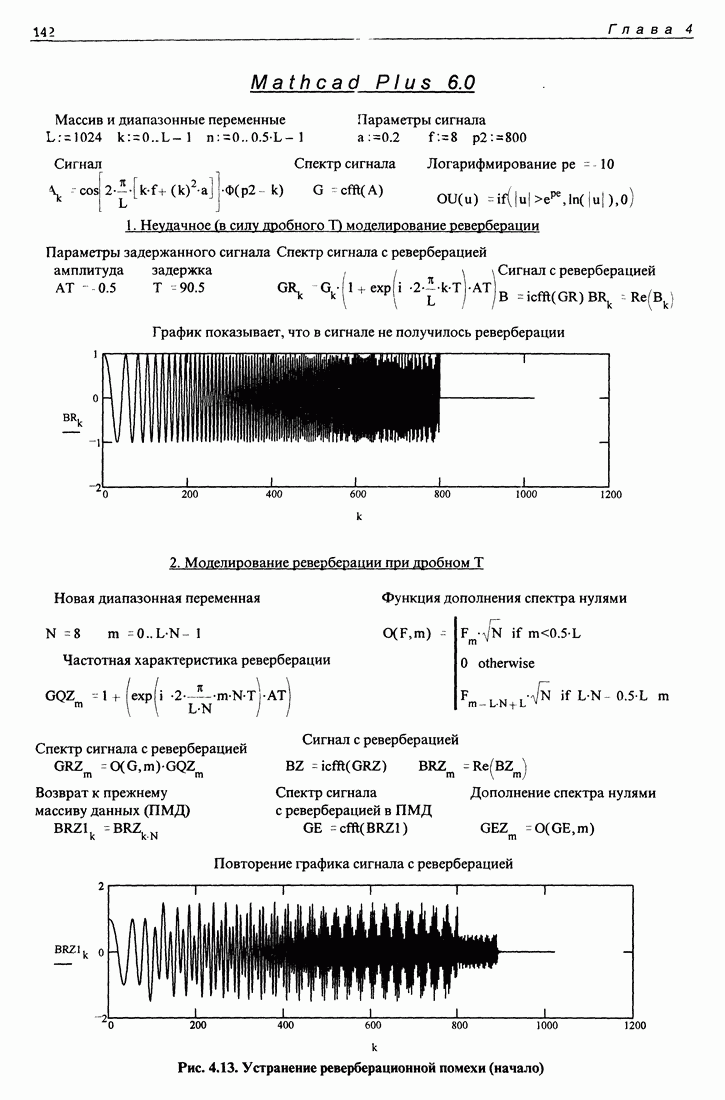
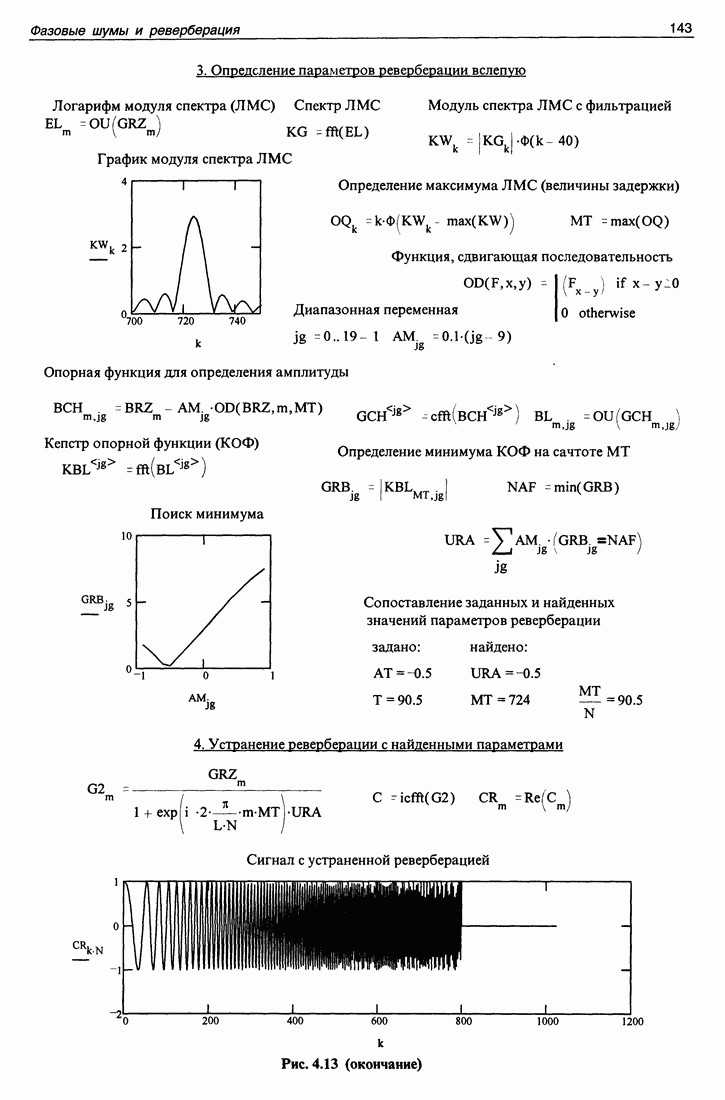
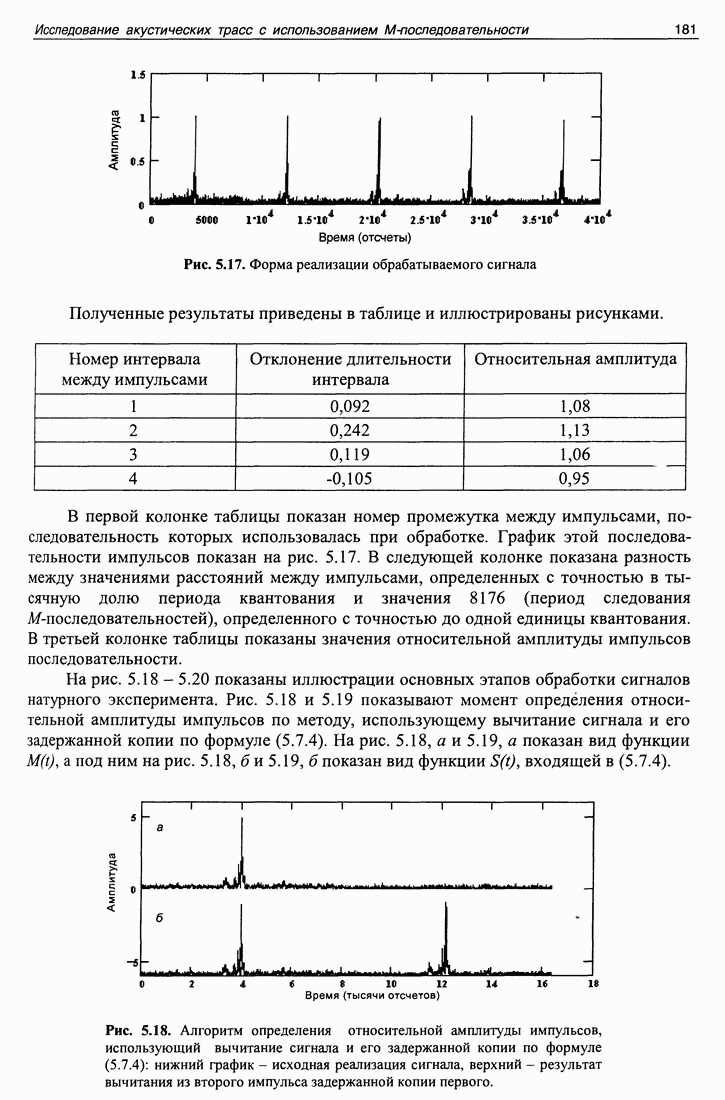
или  Такие скачки влияют на спектр аргумента, а следовательно, на кепструм. Скачки следует устранять. Как это сделать - мы рассмотрим на примере конкретной программы, изображенной на рис. 1.11.
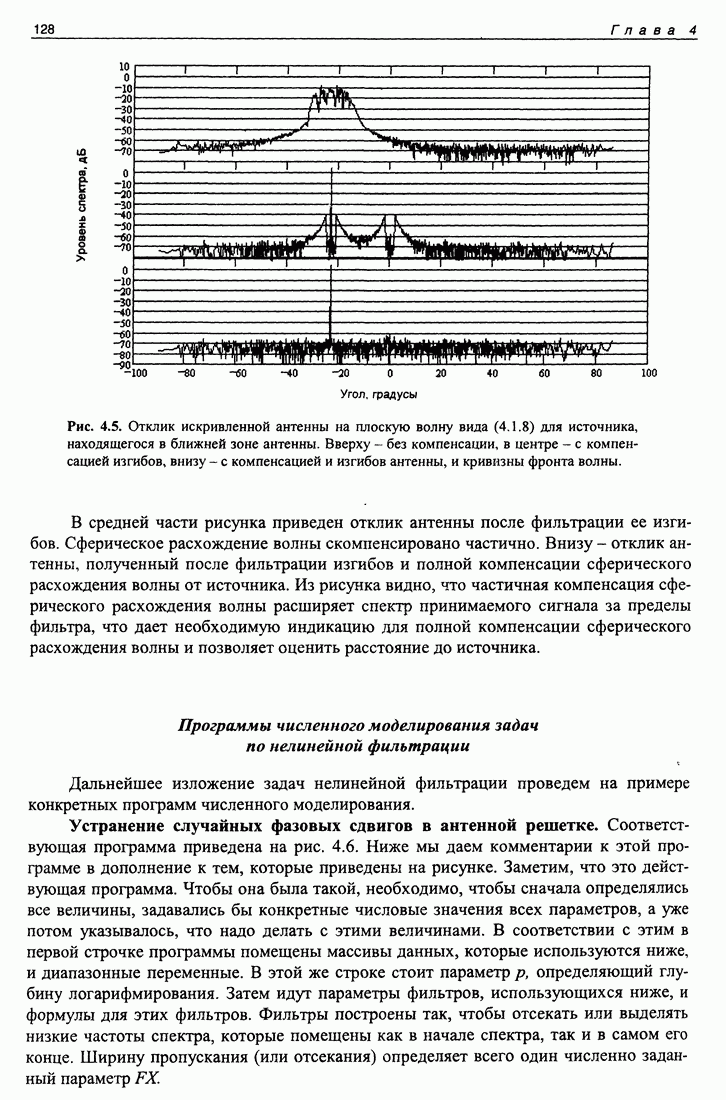
Такие скачки влияют на спектр аргумента, а следовательно, на кепструм. Скачки следует устранять. Как это сделать - мы рассмотрим на примере конкретной программы, изображенной на рис. 1.11.
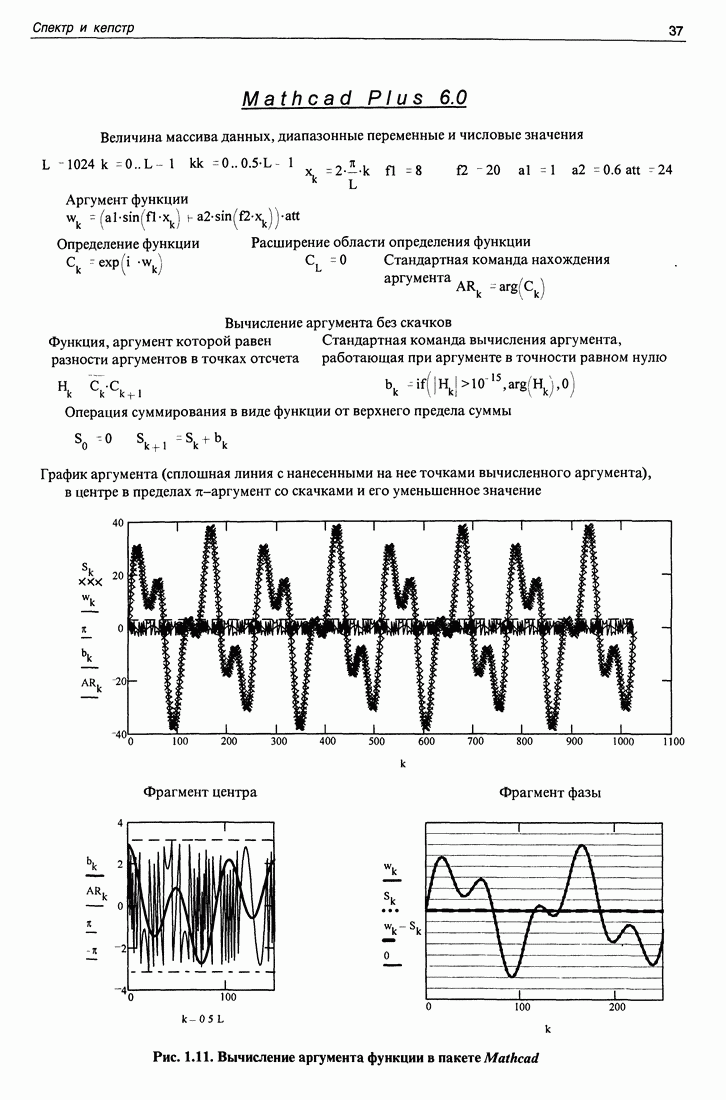
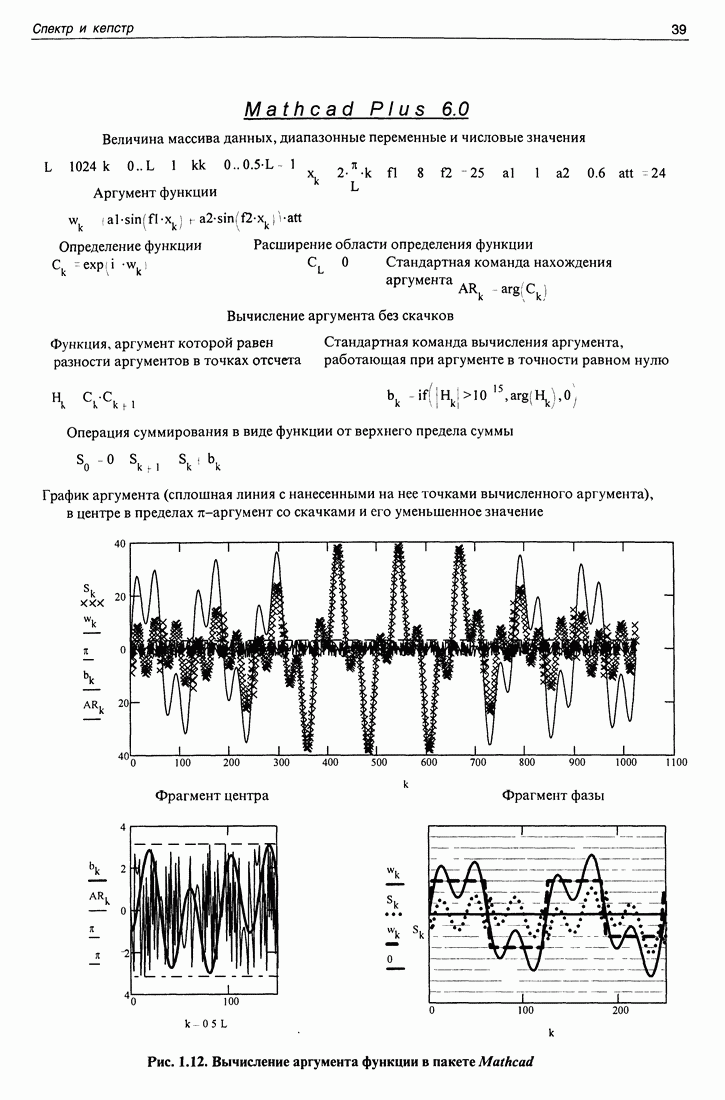
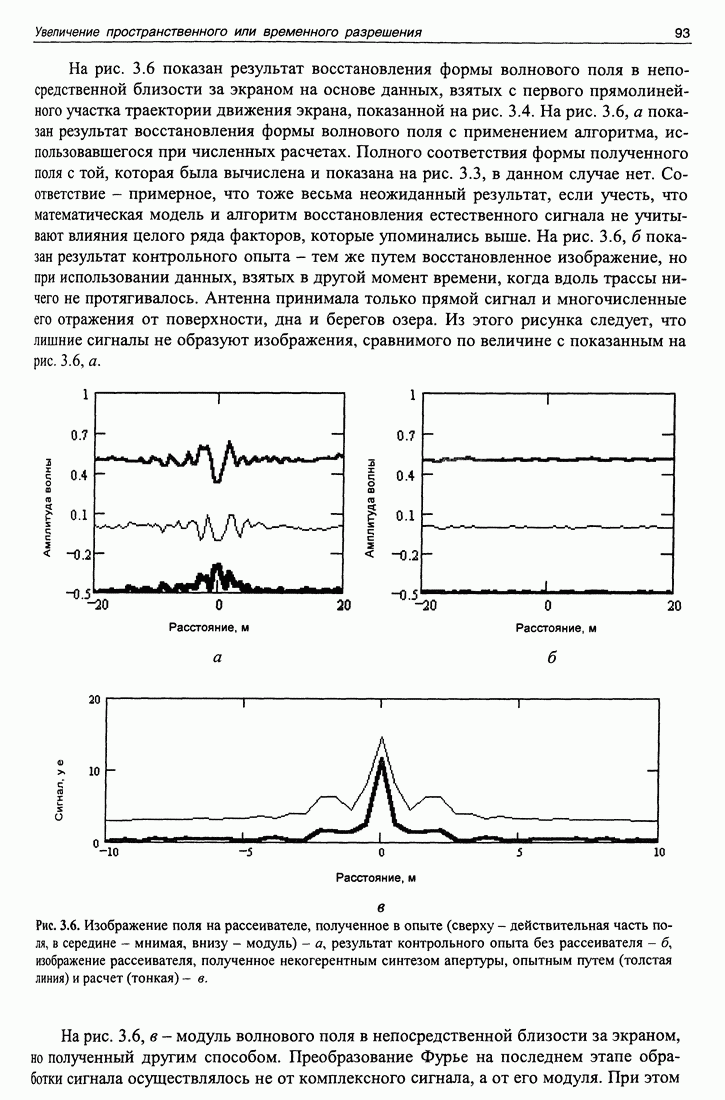
На этом рисунке верхняя строчка отведена массиву данных, диапазонным переменным и числовым значениям параметров функций, используемых для вычислений. На следующей строчке помещено выражение для истинного аргумента функции. Значения входящих в это выражение констант выбраны таким образом, чтобы значения аргумента существенно превосходили интервал от  до
до  На следующей строчке приведено выражение для комплексной функции, аргументом которой является заданная нами функция. Задача заключается в определении значения аргумента этой функции, пользуясь лишь ее значениями. Решив эту задачу, можно сравнить полученное решение с той функцией, которая была задана в качестве аргумента. Для успешной работы алгоритма область значений функции расширена на одно значение, принятое равным нулю. На следующей строчке показана команда аргумент, входящая в пакет Mathcad, примененная ко всем значениям функции. График, полученный в результате выполнения этой программы, показан в центре большого рисунка сплошной линией. Внизу показан фрагмент этого же рисунка. Результат выполнения команды "аргумент" виден на рисунке в виде кривой, имеющей множество зубцов. Эта кривая явно не соответствует заданным значениям аргумента функции. Результат этой операции в данном случае (большого значения аргумента) нельзя использовать для получения комплексного кепструма.
На следующей строчке приведено выражение для комплексной функции, аргументом которой является заданная нами функция. Задача заключается в определении значения аргумента этой функции, пользуясь лишь ее значениями. Решив эту задачу, можно сравнить полученное решение с той функцией, которая была задана в качестве аргумента. Для успешной работы алгоритма область значений функции расширена на одно значение, принятое равным нулю. На следующей строчке показана команда аргумент, входящая в пакет Mathcad, примененная ко всем значениям функции. График, полученный в результате выполнения этой программы, показан в центре большого рисунка сплошной линией. Внизу показан фрагмент этого же рисунка. Результат выполнения команды "аргумент" виден на рисунке в виде кривой, имеющей множество зубцов. Эта кривая явно не соответствует заданным значениям аргумента функции. Результат этой операции в данном случае (большого значения аргумента) нельзя использовать для получения комплексного кепструма.

(кликните для просмотра скана)
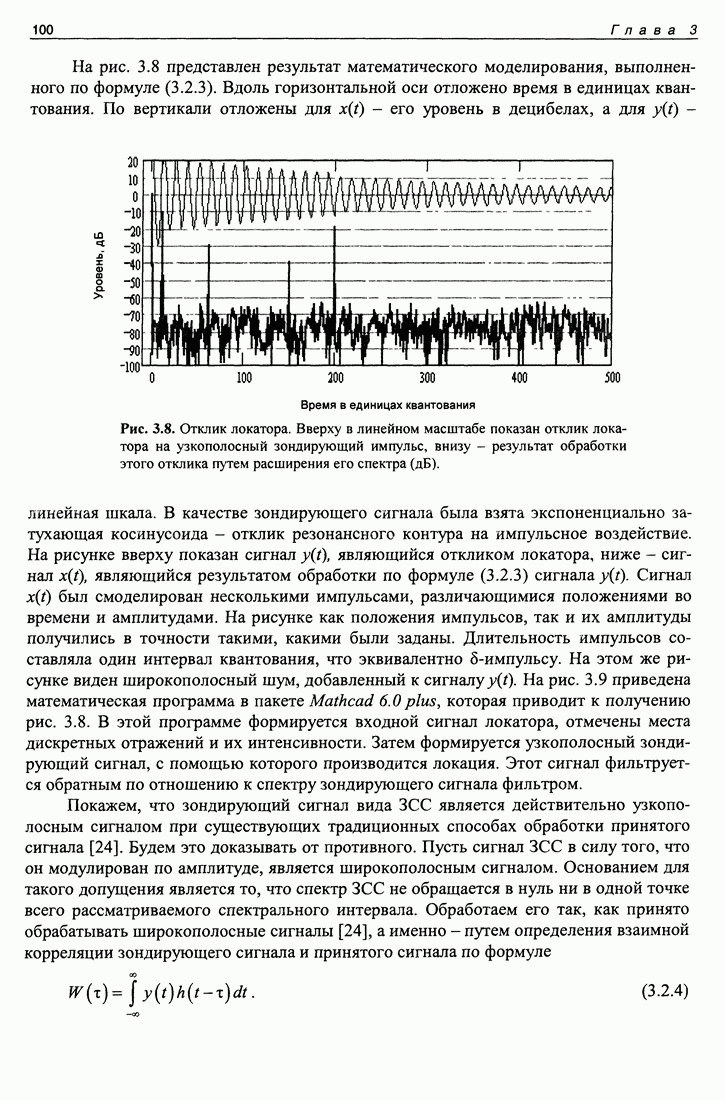
Программа, позволяющая получить значение аргумента без скачков, включает три операции. Первая операция заключается в образовании новой функции, аргумент которой существенно уменьшен и не выходит за рамки  Это делается путем умножения значений функции на ее же комплексно сопряженное значение (чтобы их аргументы вычитались), взятое в соседней точке отсчета функции. Взять в той же точке нельзя, так как аргумент будет тождественно равен нулю. Взять через большее число точек отсчета, а не в соседней отсчетной точке нежелательно, так как это увеличит значение аргумента. К этой новой функции применяется стандартная операция вычисления аргумента. В результате получается совокупность значений разностей аргументов. Чтобы получить само значение аргумента, требуется сложить эти разности как функцию верхнего предела. В пакете Mathcad есть такая стандартная операция, она работает, но крайне медленно. Дело в том, что стандартная процедура нахождения суммы как верхнего предела устроена так, что для нахождения следующего члена суммы, который равен предыдущей плюс еще одно значение, это значение почему-то не прибавляется, а вся сумма вычисляется вновь. В предлагаемой программе этот недостаток исправлен. Она составлена так, что к предыдущей сумме добавляется всего одно следующее слагаемое. Результат фиксируется каждый раз после прибавления нового слагаемого. Эта программа работает очень быстро.
Это делается путем умножения значений функции на ее же комплексно сопряженное значение (чтобы их аргументы вычитались), взятое в соседней точке отсчета функции. Взять в той же точке нельзя, так как аргумент будет тождественно равен нулю. Взять через большее число точек отсчета, а не в соседней отсчетной точке нежелательно, так как это увеличит значение аргумента. К этой новой функции применяется стандартная операция вычисления аргумента. В результате получается совокупность значений разностей аргументов. Чтобы получить само значение аргумента, требуется сложить эти разности как функцию верхнего предела. В пакете Mathcad есть такая стандартная операция, она работает, но крайне медленно. Дело в том, что стандартная процедура нахождения суммы как верхнего предела устроена так, что для нахождения следующего члена суммы, который равен предыдущей плюс еще одно значение, это значение почему-то не прибавляется, а вся сумма вычисляется вновь. В предлагаемой программе этот недостаток исправлен. Она составлена так, что к предыдущей сумме добавляется всего одно следующее слагаемое. Результат фиксируется каждый раз после прибавления нового слагаемого. Эта программа работает очень быстро.
Результат вычислений по этой программе приведен в виде точек, нанесенных на график функции, которая задавалась в качестве аргумента. Совпадение результата вычисления аргумента функции с его заданным значением получается очень хорошим при любых значениях аргумента, включающих большие. На фрагменте этого графика приведена разность между вычисленными и заданными значениями аргумента функции. Эта разность обращается в нуль.
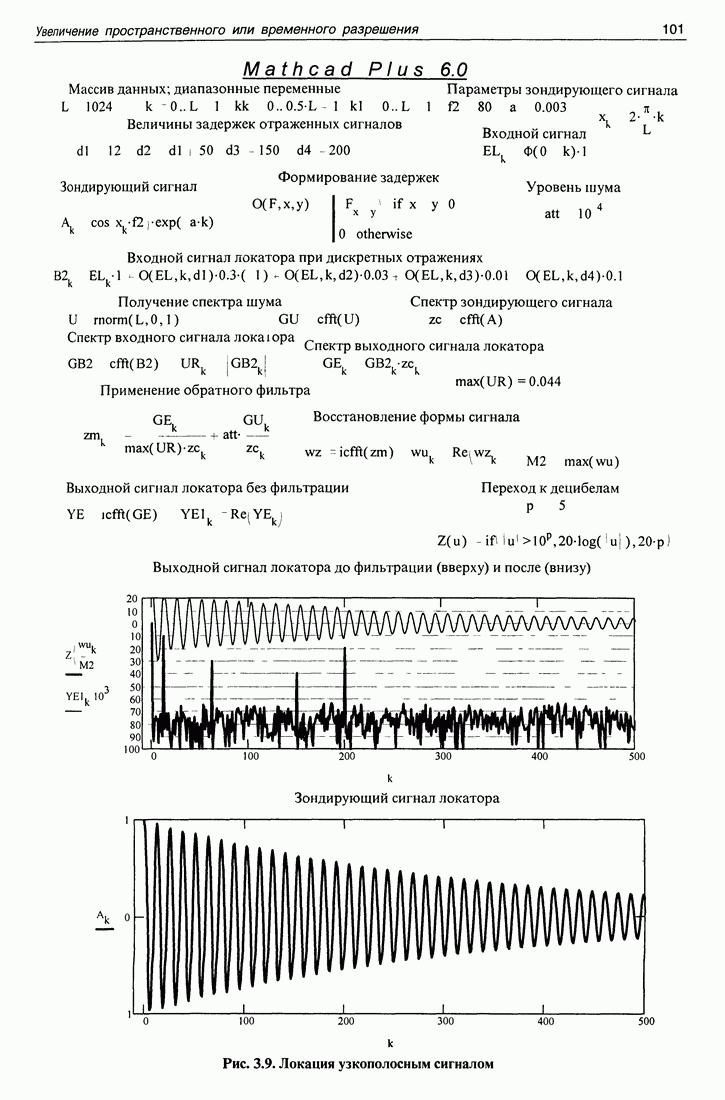
Все, вроде бы, хорошо. Однако обратите внимание на рис. 1.12, на котором приведена та же самая программа. Увеличено значение всего одного параметра функции, заданной в виде аргумента. На рис. 1.11 - параметр  а на рис. 1.12 - параметр
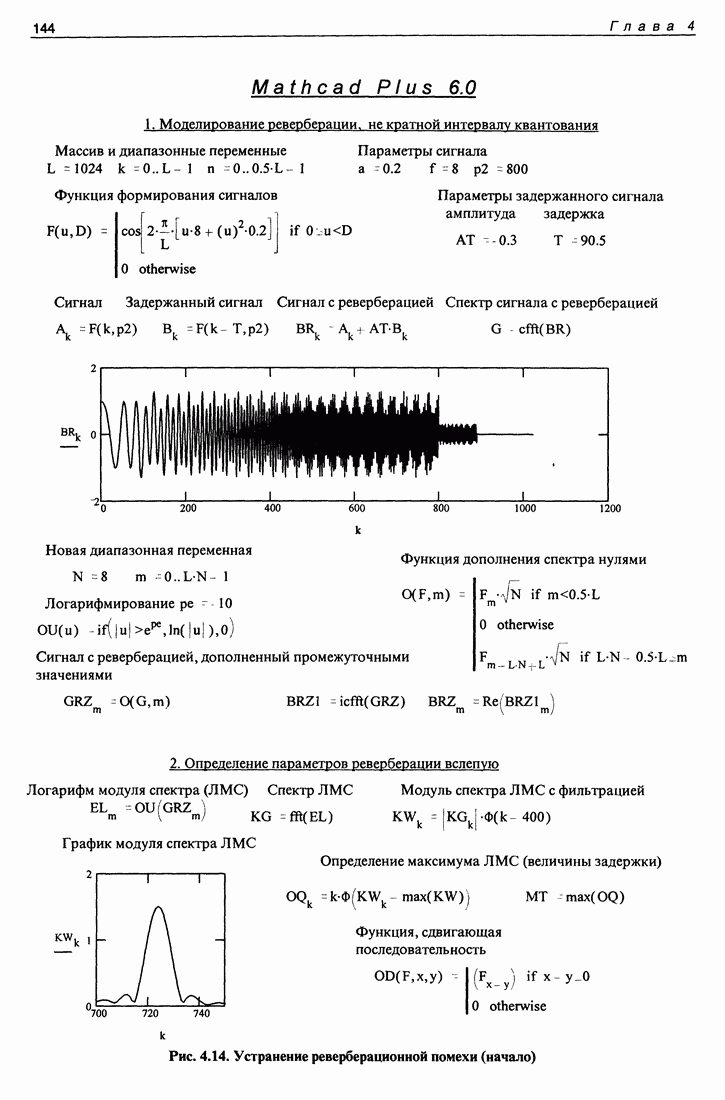
а на рис. 1.12 - параметр  Совпадения вычисленного и заданного значений аргумента уже не наблюдается. В чем дело? Обычно в нашем распоряжении нет никакой заданной функции и проверить правильность вычислений нельзя. Надо найти условие, гарантирующее правильность результата. Для нахождения этого условия полезно обратиться к программе, изображенной на рис. 1.13. На нем значение параметра
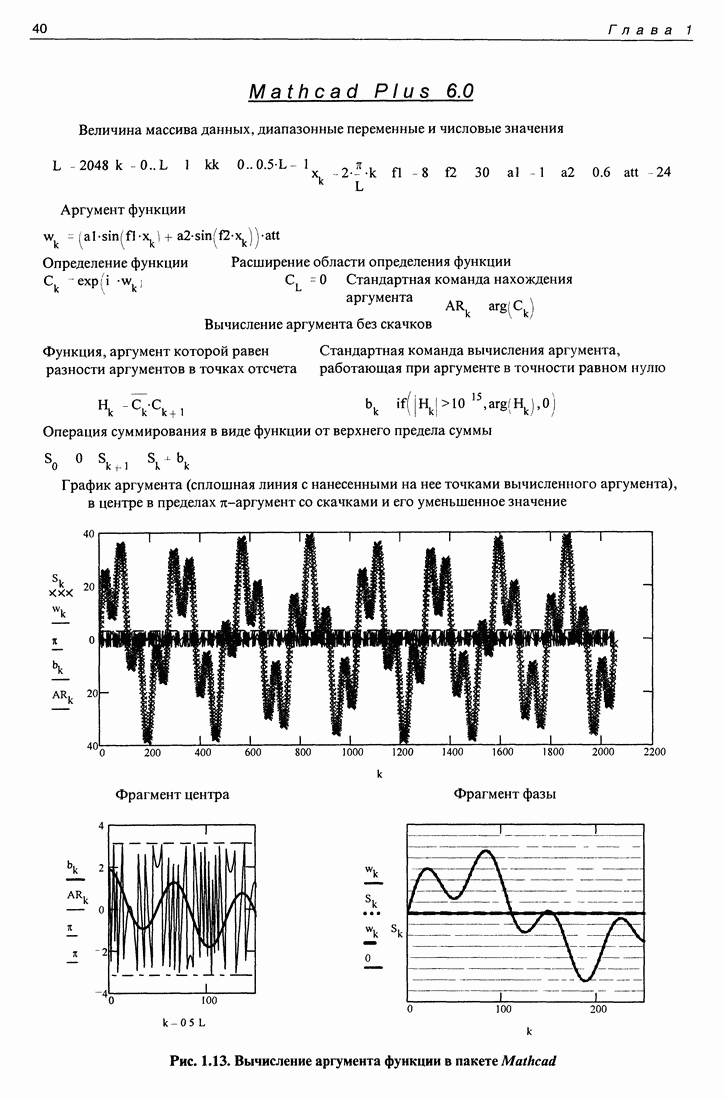
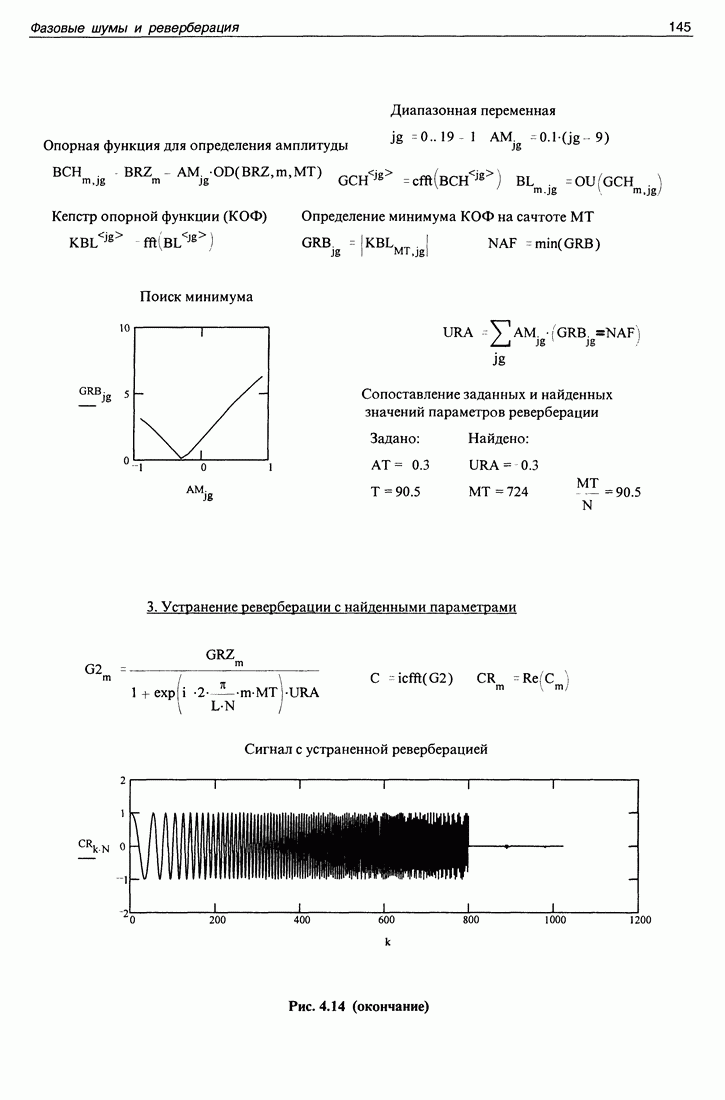
Совпадения вычисленного и заданного значений аргумента уже не наблюдается. В чем дело? Обычно в нашем распоряжении нет никакой заданной функции и проверить правильность вычислений нельзя. Надо найти условие, гарантирующее правильность результата. Для нахождения этого условия полезно обратиться к программе, изображенной на рис. 1.13. На нем значение параметра  т. е. оно еще больше увеличено. Если такое значение параметра придать рис. 1.12, то получающееся несоответствие должно существенно возрасти. Однако на рис. 1.13 этого не наблюдается. Почему? Дело в том, что на рис. 1.13 увеличено вдвое значение еще одного параметра - массива данных
т. е. оно еще больше увеличено. Если такое значение параметра придать рис. 1.12, то получающееся несоответствие должно существенно возрасти. Однако на рис. 1.13 этого не наблюдается. Почему? Дело в том, что на рис. 1.13 увеличено вдвое значение еще одного параметра - массива данных  Увеличение массива данных привело к сокращению вдвое расстояния между точками отсчета функции. При этом существенно уменьшилось значение аргумента, получаемого в результате второй операции - получения значений аргумента между соседними точками отсчета.
Увеличение массива данных привело к сокращению вдвое расстояния между точками отсчета функции. При этом существенно уменьшилось значение аргумента, получаемого в результате второй операции - получения значений аргумента между соседними точками отсчета.
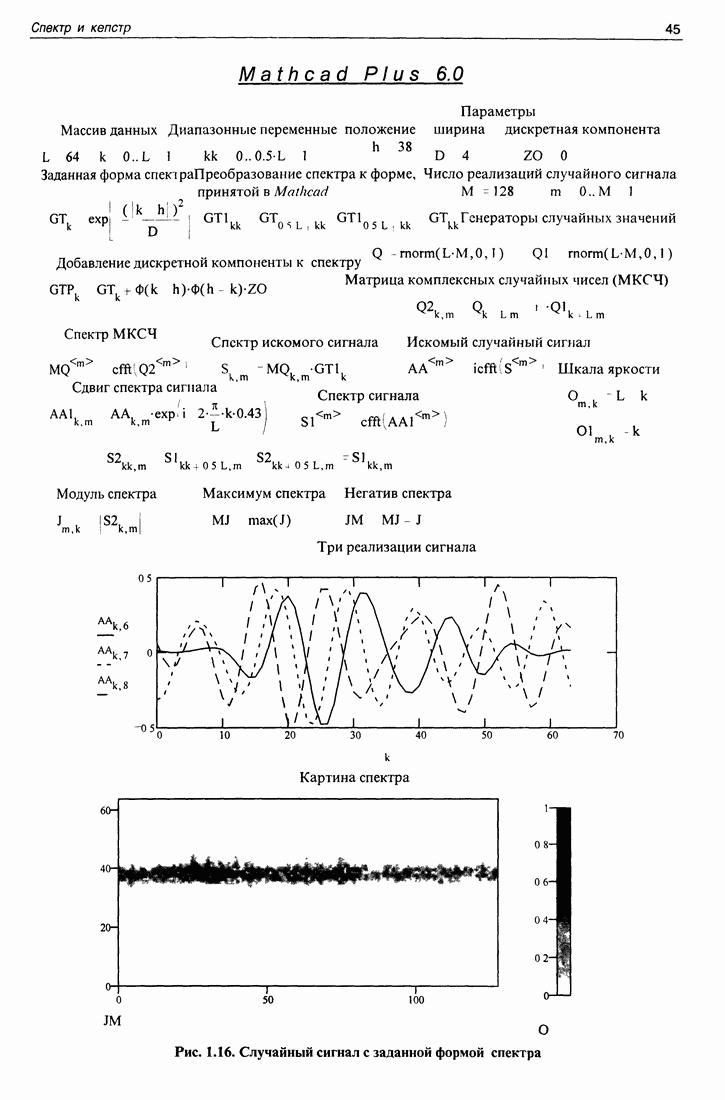
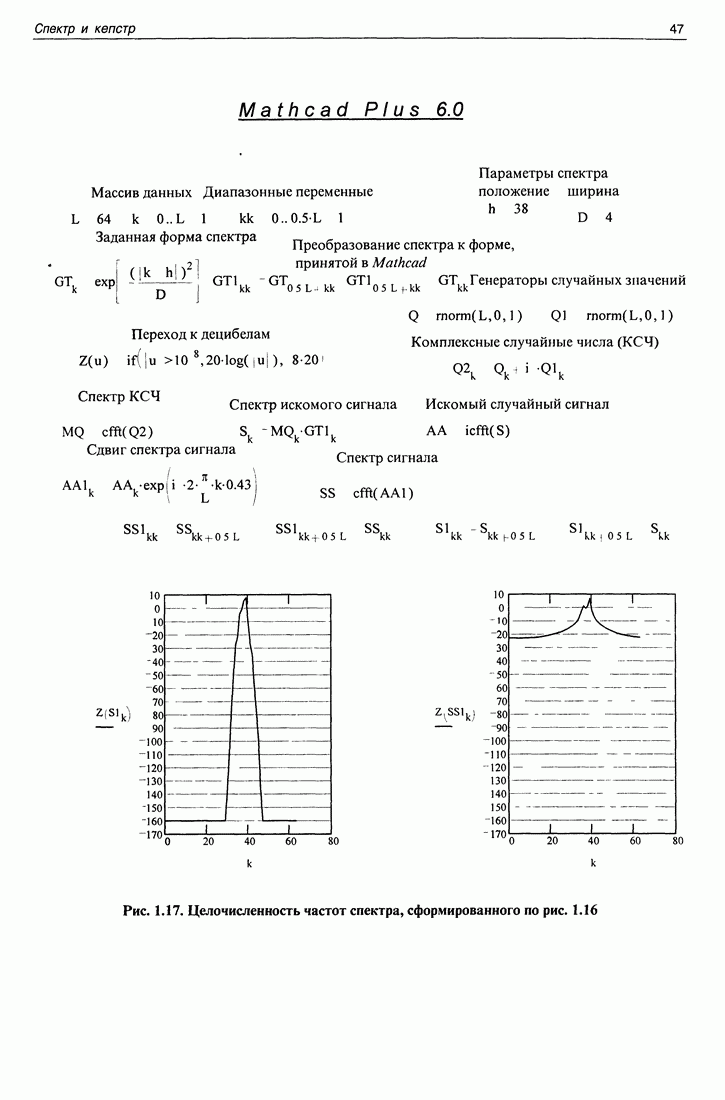
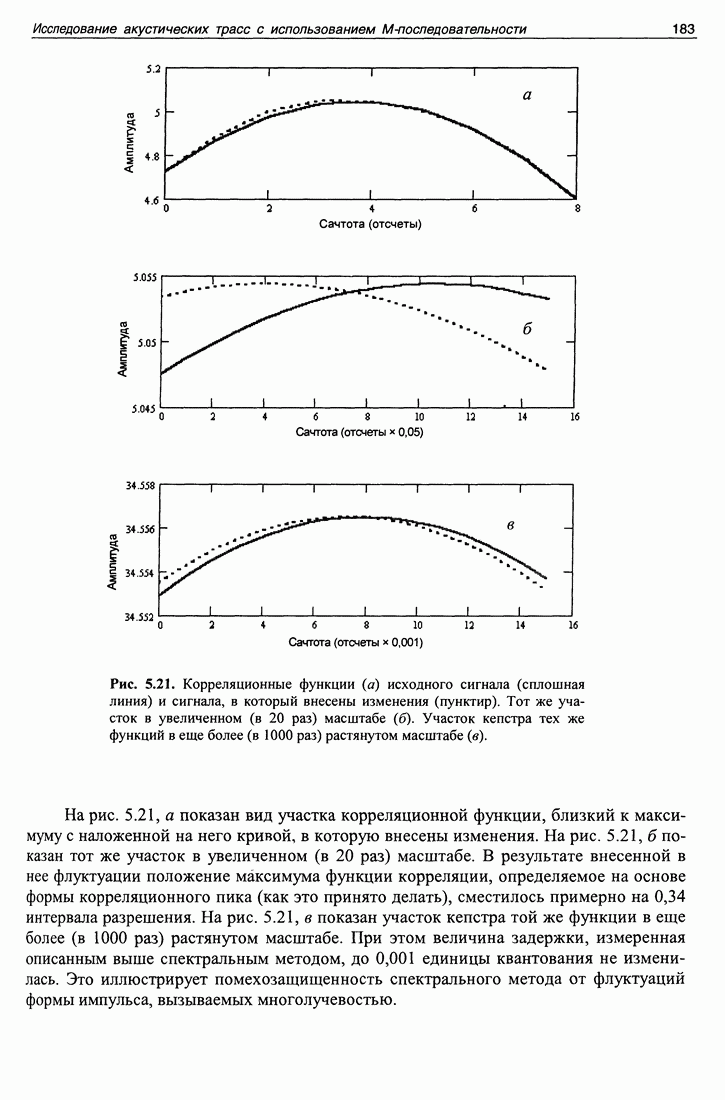
Необходимое и достаточное условие правильной работы вышеприведенного алгоритма (и всех иных тоже) заключается в том, чтобы спектр функции был ограничен, а расстояние между точками отсчета функции удовлетворяло бы условиям теоремы отсчетов. Это можно показать, пользуясь рассмотренным примером. На рис. 1.14 показан результат вычисления спектра функции, аргумент которой мы ищем, в зависимости от значений параметра  отложенных на рис. 1.14 вдоль горизонтали. Вдоль вертикали отложена ширина спектра функции в числах точек отсчета, нормированных на число степеней свободы функции, длительность которой
отложенных на рис. 1.14 вдоль горизонтали. Вдоль вертикали отложена ширина спектра функции в числах точек отсчета, нормированных на число степеней свободы функции, длительность которой 

(кликните для просмотра скана)

(кликните для просмотра скана)
Это означает, что функция, ширина спектра которой единица, удовлетворяет условию теоремы отсчетов при  а если ширина спектра превышает единицу, то не удовлетворяет. Из рисунка видно, что значения параметра
а если ширина спектра превышает единицу, то не удовлетворяет. Из рисунка видно, что значения параметра  еле-еле удовлетворяют условию, а при
еле-еле удовлетворяют условию, а при  или тем более
или тем более  не удовлетворяют. Очень важно отметить, что увеличивать число значений функции путем вставления промежуточных значений в этом случае бесполезно, необходимо увеличивать число дискретных отсчетных точек, представляющих функцию.
не удовлетворяют. Очень важно отметить, что увеличивать число значений функции путем вставления промежуточных значений в этом случае бесполезно, необходимо увеличивать число дискретных отсчетных точек, представляющих функцию.

Рис. 1.14. Ширина спектра функции, аргумент которой определяется в зависимости от параметра  (см. рис. 1.11).
(см. рис. 1.11).
Это положение имеет простое физическое истолкование: дискретные точки отсчета должны быть так близко друг от друга, чтобы между ними не происходило скачков фазы более чем на 
Возможен другой способ нахождения истинного значения аргумента. Этот способ основан на исключении уже получившихся скачков, для чего может служить программа, содержащая несколько операций. Первая - стандартное вычисление аргумента со скачками. Вторая операция определяет функцию, равную величине скачка фазы. Эта программа в пакете Mathcad 6.0 plus выглядит следующим образом:

Третья операция представляет собою сложение значений функции (1.6.10) до верхнего предела, осуществляемое посредством


Заключительная операция представляет собою исключение скачков аргумента функции посредством

где в качестве второго слагаемого входит аргумент функции со скачками. Сложение этой функции с (1.6.12) устраняет скачки. Как уже говорилось выше, условие того, что этот алгоритм работает, остается прежним. Необходимо, чтобы спектр функции был ограничен, а точки отсчета расположены достаточно часто (в соответствии с требованиями теоремы отсчетов).
В пакете программ Matlab имеется программа, позволяющая получать значения аргумента функции без скачков.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. СПЕКТР И КЕПСТР
- 1.1. Ряд и интеграл Фурье
- 1.2. Математические свойства преобразования Фурье
- 1.3. Знаменитая теорема отсчетов
- 1.4. Как выполняется преобразование Фурье численно
- 1.5. Линейные системы
- 1.6. Кепструм
- 1.7. Численное представление случайных сигналов
- Глава 2. ФИЛЬТРАЦИЯ ПОМЕХ И ЛОКАЦИЯ НА ПРОСВЕТ
- 2.1. Устранение узкополосной помехи
- 2.2. Метод темного поля
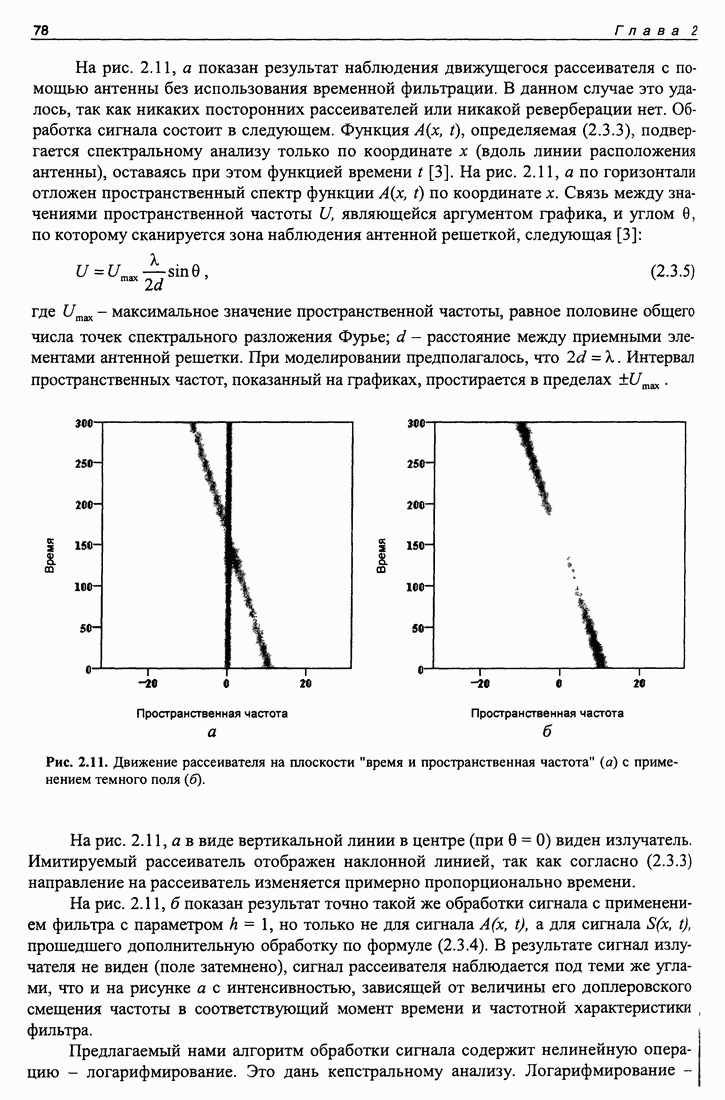
- 2.3. Эксперимент по наблюдению точечного рассеивателя
- Глава 3. УВЕЛИЧЕНИЕ ПРОСТРАНСТВЕННОГО ИЛИ ВРЕМЕННОГО РАЗРЕШЕНИЯ
- 3.2. Увеличение временного разрешения сигналов
- 3.3. Локация на просвет с разделением прямого и дифрагированного сигналов по времени
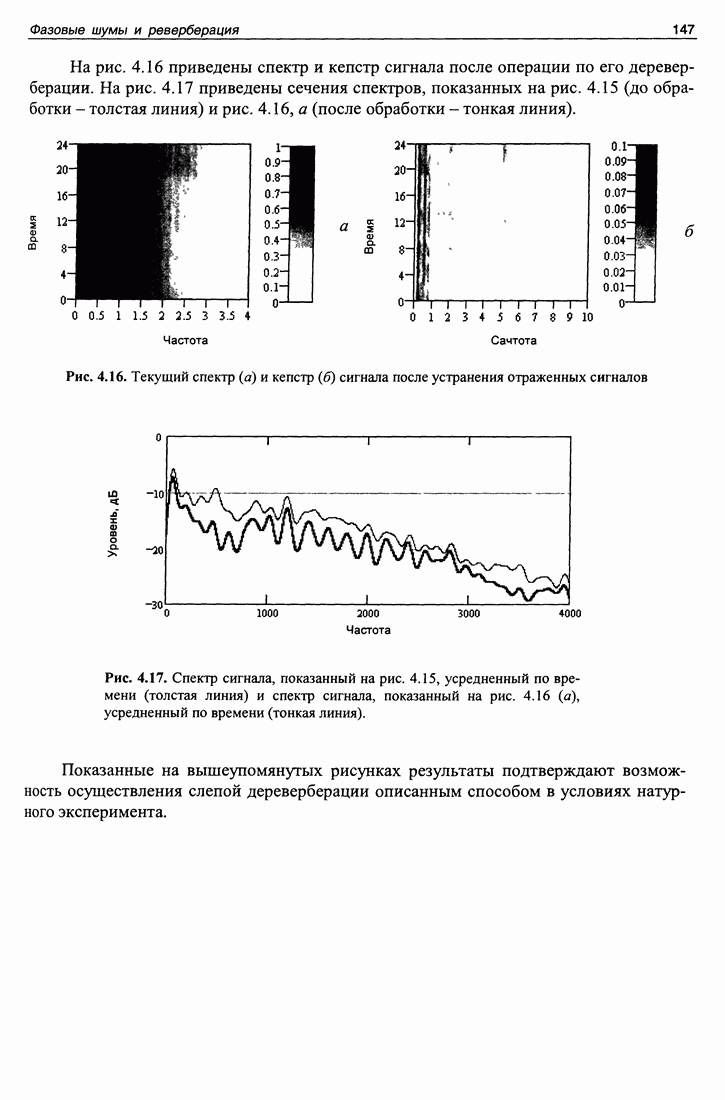
- Глава 4. ФАЗОВЫЕ ШУМЫ И РЕВЕРБЕРАЦИЯ
- 4.1. Фильтрация мультипликативно связанных сигналов
- 4.2. Устранение влияния фазовых шумов в параметрическом микрофоне
- 4.3. Слепая дереверберация
- Глава 5. ИССЛЕДОВАНИЕ АКУСТИЧЕСКИХ ТРАСС С ИСПОЛЬЗОВАНИЕМ М-ПОСЛЕДОВАТЕЛЬНОСТИ
- 5.1. Акустические задачи, решаемые с помощью M-последовательности
- 5.2. Выбор оптимальной методики анализа линейной системы
- 5.3. М-последовательность — идеальный тестовый сигнал для анализа систем. Ее генерация и свойства
- 5.4. Применение М-последовательности на стационарной сейсмической трассе
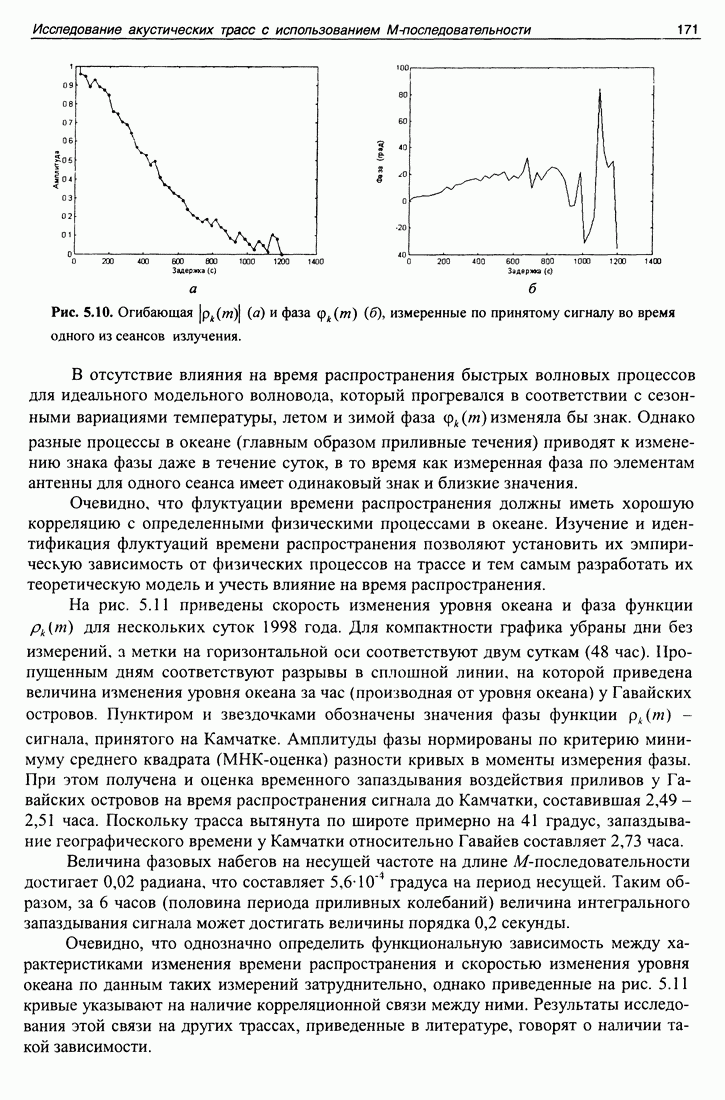
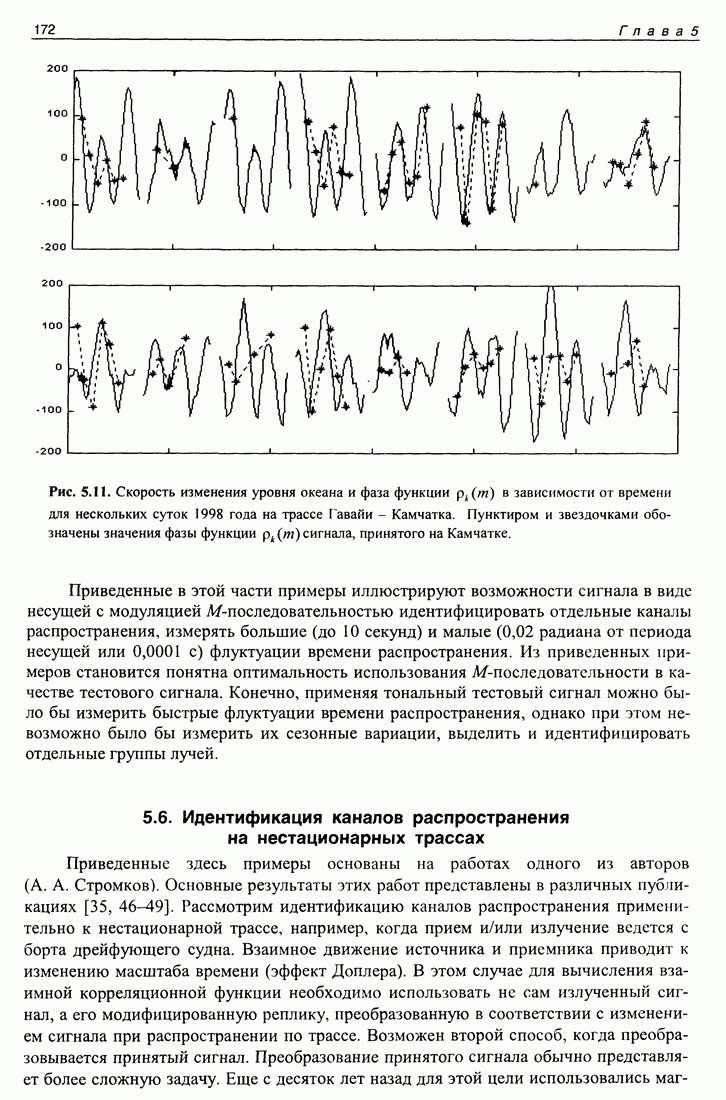
- 5.5. Применение М-последовательности на сверхдлинных океанических трассах
- 5.6. Идентификация каналов распространения на нестационарных трассах
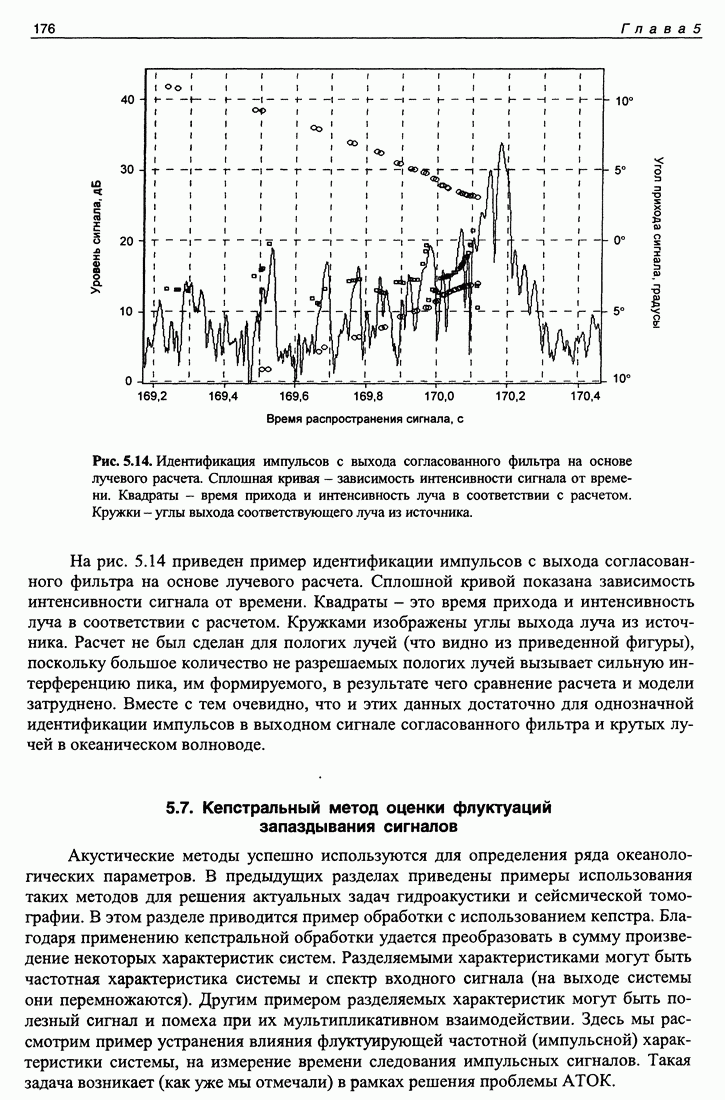
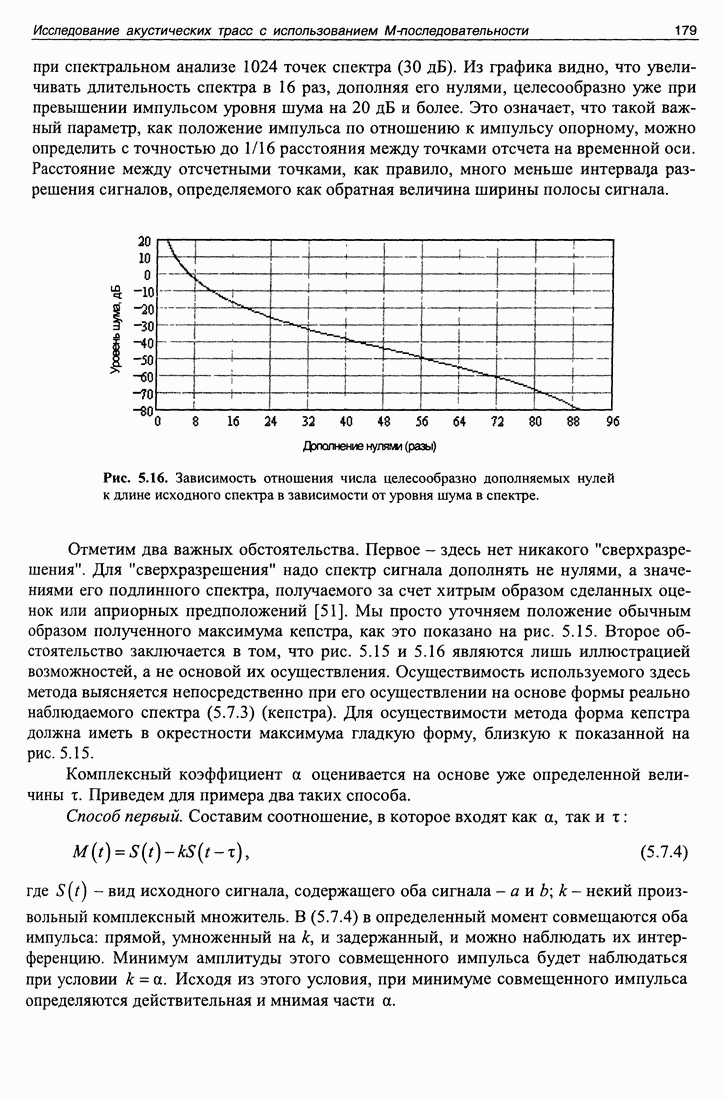
- 5.7. Кепстральный метод оценки флуктуаций запаздывания сигналов
- Литература