1.4. Как выполняется преобразование Фурье численно

Преобразования Фурье (1.1.16) и (1.1.17) настолько широко используются в физике, математике и других точных науках, что для их выполнения численными методами созданы специальные программы. Непосредственно по формулам (1.1.14), (1.1.15) численное преобразование Фурье не выполняется, так как эти формулы получены в результате предельного перехода от интегральных сумм (1.1.13) к интегралам, чего численными методами точно сделать нельзя. Нам предстоит выяснить, каковы особенности преобразования Фурье, совершаемые численно.

Численными методами осуществляется представление функций в виде ряда Фурье, но так, что результаты могут быть истолкованы точно так же, как если бы совершалось точное интегральное преобразование Фурье. Достигается это следующими приемами.

Входные данные поступают в виде набора действительных или комплексных (в ряде программ, в частности тех, которые мы предполагаем использовать в дальнейшем) чисел. Эти числа можно трактовать как значения непрерывной функции, взятые в точках отсчета. Совокупность всех введенных значений образует вектор. Форму этого вектора можно представить себе в виде графика или таблицы значений.

Пусть имеется значений, отстоящих одно от другого через единицу. Таким образом, длина числовой оси тоже равна Функция, представленная дискретными равноотстоящими друг от друга отсчетами, имеет ограниченный спектр, ее фурье-спектр состоит из бесконечного числа слагаемых. Он вовсе не конечен, но значения модуля спектра равны нулю вне некоторого интервала значений спектра. Границы этого интервала, согласно теореме отсчетов, равны

где интервал между точками отсчета. Полная ширина спектра (область возможных ненулевых членов) простирается от до что составляет С учетом (1.4.1) и того, что интервал в нашем случае равен единице, размер области возможных ненулевых значений спектра будет равен

Доопределим нашу функцию за пределы того интервала на котором она задана. Пусть это будет периодическая функция с периодом, равным интервалу ее задания, т. е. Периодическая функция раскладывается в дискретный ряд Фурье. Частоты этого ряда (значения ) определяются на основании (1.5) как

Как мы уже выяснили, ненулевые значения располагаются только на интервале Сколько ненулевых компонент будет содержать спектр функции? Для ответа на этот вопрос надо поделить интервал на расстояние между дискретными частотами спектра функции, равное Тогда спектр нашей функции будет содержать дискретных частот, т. е. ровно столько, сколько задано значений функции. Повторяем, что это есть следствие двух положений. Первое заключается в том, что мы задали функцию только дискретными значениями, а второе состоит в том, что мы продолжили заданную функцию за пределы ее задания периодически до бесконечности.

Сделаем еще один важный шаг - учтем дискретность при вычислении спектров. Примем, что мы вычисляем спектр лишь при тех значениях частот, которые записаны в формуле (1.4.2). Такова специфика дискретного счета. Вычисляем ровно значений спектра, по числу заданных значений функции. Отсюда следует вывод: если функция задается дискретным рядом значений (не важно, спектр это или функция), то ее спектр ограничен. Спектр от спектра - это сама функция. Значит, сама функция должна быть ограничена и равна нулю вне области ее задания. Продолжать функцию можно только нулями, если мы ограничиваемся вычислениями только дискретных равноотстоящих друг от друга точек спектра. Значит, обе функции, как сама функция, так и ее спектр, являются ограниченными функциями. Это можно представить в таком виде, что первоначально периодическая функция, имеющая период умножается на такую функцию прямоугольной формы, которая на всем интервале задания функции равна единице, а за пределами этого интервала равна нулю.

Чрезвычайно важен вопрос: каков спектр чистой экспоненты? Выражение для экспоненты запишем, используя (1.4.2) в виде

В связи с тем, что спектр вычисляется только при целых значениях к, будут различаться две области возможных значений коэффициента Первая область значений, когда коэффициент/представлен целым числом. Это целое число в этом случае имеет смысл номера той единственной точки отсчета спектра, в которой будет наблюдаться спектр нашей экспоненты. Программа численного преобразования Фурье устроена так, что на картине, изображающей спектр, вдоль горизонтали отложены целые значения коэффициента Это является достаточным основанием для того, чтобы значение коэффициента/назвать частотой. Заметим, что если мы имеем дело с дискретной частотой, то, продолжая функцию периодически за пределы ее задания, получим чистую экспоненту бесконечной длительности. Ее разложение в ряд Фурье состоит всего из одного члена, который бесконечен в этой точке. Учтем теперь, что наша функция

умножена на прямоугольную функцию. Спектр произведения функций представляет собой свертку спектров, спектр прямоугольной функции - функцию (формула (1.3.5))

Эта функция при равна единице, а при всех остальных целых значениях к она равна нулю. Умножение прямоугольной функции на экспоненту смещает ее спектр, определяемый формулой (1.4.4), . В случае целочисленной частоты спектр сдвинется на целое число отсчетных точек спектра. По-прежнему в одной точке будет значение единица, а во всех остальных отсчетных точках будет нуль.

Вторая область значений коэффициента или частоты, представляет собою все остальные дробные значения. Эту область значений частоты будем называть дробной. Как будет выглядеть спектр в этом случае? Спектр (1.4.4) сместится на дробное число отсчетных точек, а значения спектра будут определяться по-прежнему лишь в отсчетных точках. Теперь уже нигде не будет нулевых значений, а значения во всех отсчетных точках определятся формулой (1.4.4) при смещении ее на величину частоты, включая ее дробную часть.

Заметим, что введенное нами определение частоты как номера соответствующей отсчетной точки спектра удобно лишь в случае численного счета. В иных задачах принято частотой считать не коэффициент/в (1.4.3), а значение другого коэффициента, стоящего перед к.

Поясним это подробнее для весьма употребительного случая, когда переменная к трактуется как номер отсчета точки во времени. Интервал времени в секундах между последовательно взятыми точками составляет в этом случае где - это частота временного квантования в циклах в секунду. Разделим и умножим показатель экспоненты в (1.4.3) на тогда (1.4.3) можно переписать в виде функции времени следующим образом:

Частотой, измеряемой в радианах в секунду, будет являться весь коэффициент, стоящий перед исключая мнимую единицу, а частотой, измеряемой в герцах, будет

Другая важная особенность численного преобразования Фурье состоит в использовании так называемого быстрого преобразования Фурье. Если число значений равно где - любое положительное целое число, то при вычислении спектра функции многие действия в точности повторяются. Существует специальная математическая программа, позволяющая исключить повторы и тем самым существенно сократить объем вычислений. Эта программа называется быстрым преобразованием Фурье (БПФ). Пользуясь БПФ, мы осуществляем только логарифм от общего числа необходимых операций. Поэтому выигрыш от использования БПФ быстро растет с ростом

Число операций можно дополнительно сократить вдвое при вычислении спектра от действительной функции. В случае действительной функции члены ряда Фурье с положительными и отрицательными частотами равны друг другу, и тогда можно ограничиться вычислениями коэффициентов ряда только при положительных частотах. Такая программа тоже имеется в пакете программ БПФ.

В пакете программ Mathcad преобразование Фурье от комплексной функции (с вычислением всех коэффициентов Фурье) обозначается как (обозначение функции в виде вектора или матрицы значений). Преобразование от действительной функции (с вычислением коэффициентов) обозначается как указанием вектора или матрицы). Преобразование от комплексной функции устроено так, что выдает значения коэффициентов Фурье сначала для частот одного знака в порядке возрастания значений частот. Затем к ним пристраиваются значения частот другого знака в порядке убывания. Итак, оказывается, что по краям картины спектра располагаются низкие частоты, а высокие частоты занимают середину спектра. В центре спектра оказываются самые высокие частоты. Этот порядок размещения частот можно изменить только путем построения соответствующей программы. Ниже будут даны примеры таких программ. В пакете Mat lab можно получить сразу спектр с желательным размещением частот (в центре либо высокие, либо низкие частоты).

Из вышеизложенного следует, что для задания непрерывной комплексной функции на конечном участке X необходимо задать на этом участке значений комплексных чисел, разделенных интервалом При этом спектр функции вычисляется тоже в точках в виде комплексных коэффициентов Фурье. Исходя из условия, что спектр функции ограничен интервалом можно получить значения заданной функции в промежуточных точках. Такая операция необходима и часто используется в дальнейшем как при численном моделировании сигналов, так и при их выделении, поэтому остановимся на ней подробнее.

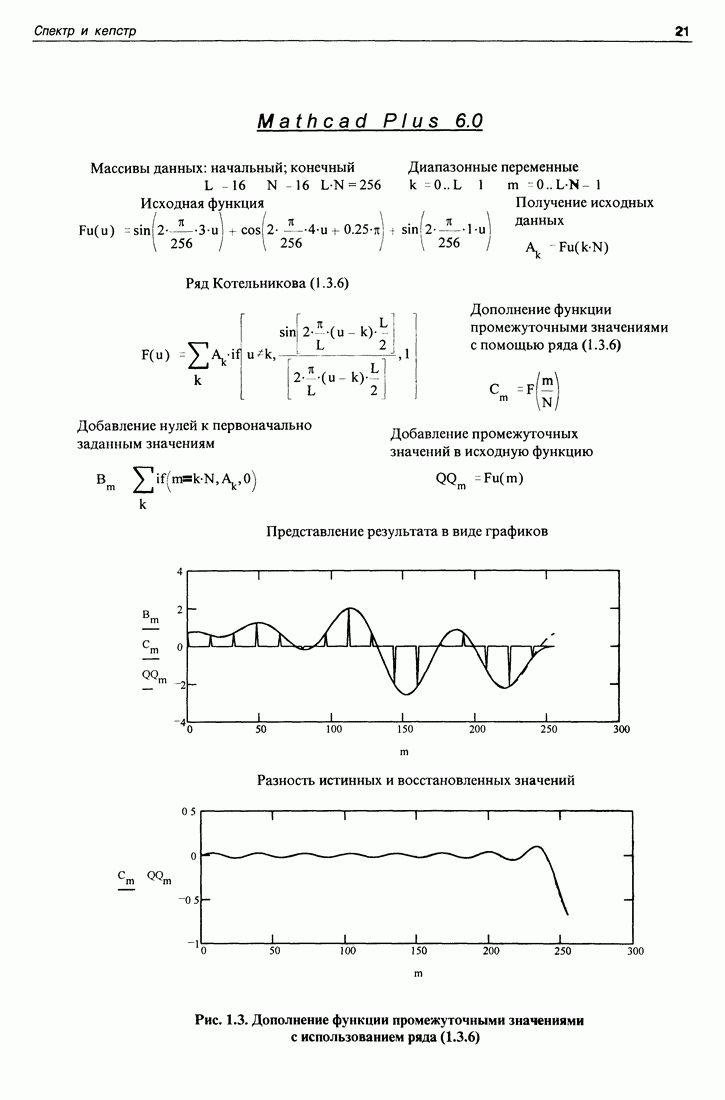
Для получения промежуточных значений функции можно действовать двумя путями. Наиболее естественный путь - применение для этой цели формулы (1.3.6), определяющей значение функции в любой точке посредством ряда. Такая программа приведена на рис. 1.3.

В начале программы обозначены так называемые диапазонные переменные [1]. которые используются в вычислениях. Далее идет процедура задания исходных 16 дискретных значений, которые должны быть дополнены промежуточными значениями. В качестве исходных могут быть взяты любые числа, но при этом сравнивать полученные промежуточные значения будет не с чем. Чтобы иметь возможность сравнить полученные нами промежуточные значения функции с истинными промежуточными значениями той же функции, она задана в виде непрерывной функции переменной и. Эта функция не может быть полностью произвольной, а должна иметь ограниченный спектр. Это условие обеспечивается тем, что функция составлена из суммы синусоид, каждая из которых низкочастотна. Далее в программе приведен ряд Котельникова (1.3.6) в виде некоторой функции переменной и. Коэффициентами этого ряда являются исходные 16 значений функции. Придавая какое-то конкретное значение переменной и, являющейся аргументом ряда можно получить любое промежуточное значение функции, заданной лишь дискретными значениями. Далее определяются 256 промежуточных значений путем их подстановки в ряд (1.3.6). Поясним подробнее получившийся конечный результат и форму его представления. Обе функции, как первоначальная, так и дополненная промежуточными значениями, приведены на одном графике. Чтобы это сделать в пакете Mathcad, обе функции вдоль горизонтали должны иметь одну и ту же переменную, т. е. вдоль горизонтали у обеих функций должно быть равное число значений. Чтобы удовлетворить этому условию, пришлось первоначальные 16 значений функции дополнить нулями, они помещены в промежуточных точках функции с помощью специальной программы. Эта программа содержит условие [1], которое помещено в скобках в самом начале и отделено запятой. После запятой приведено

значение функции, которое она должна принять при выполнении этого условия, это значение также отделено запятой. После второй запятой приведено значение функции, которое она должна принять в случае нарушения условия. Знак суммы необходим, чтобы задействовать диапазонную переменную к, которая не входит в левую часть программы и поэтому не может быть задействована иначе. Приведенный прием полезен при необходимости представить в пакете Mathcad две или более функций с разным числом значений вдоль оси абсцисс. На том же рисунке приведен график исходной заданной функции, определенной для всех 256 значений посредством формулы Разность между восстановленными промежуточными значениями и истинными приведена на отдельном графике.

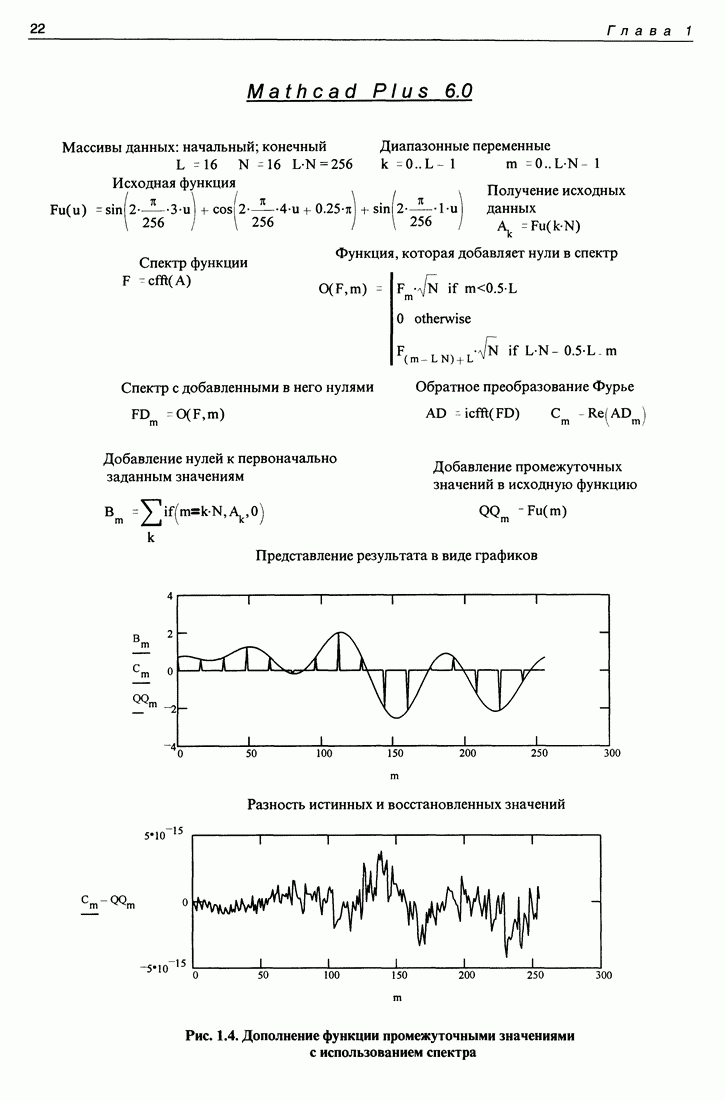
Следующая программа, ведущая к той же цели иным путем, приведена на рис. 1.4. Это гораздо более быстрая программа, так как она не содержит суммирования. В ее основе лежит ограничение спектра восстанавливаемой функции. Для получения промежуточных значений функции достаточно выполнить три операции: 1) вычислить спектр функции в точках; 2) дополнить получившийся спектр нулями, получив точек спектра; 3) совершить обратное преобразование Фурье. Из этих операций новой для нас является вторая - добавление нулей в спектр. Остановимся на ней подробнее.

Нули следует вставлять взамен высоких частот, которые выше уже представленных в спектре. Если значения частот выведены так, как это принято в пакете Mathcad (низкие частоты по краям интервала, а высокие в центре), то нули следует добавлять в центральную область спектра, не трогая уже выведенных значений. Вот как выглядит программа добавления нулей в спектр в пакете Mathcad 6 0 plus (удобство пакета Mathcad состоит в том, что используемая символика приближена к обычной практике математической записи формул):

Здесь специальная функция, обеспечивающая вставление нужного числа нулей в спектр, - матрица спектра функции. В этой матрице столбцов и строк. В столбцах располагаются значения спектра функции (комплексные коэффициенты Фурье), а в строках значения некоторого параметра, от которого может зависеть спектр функции. Если такого параметра нет, а есть только спектр функции, то переменную надо исключить из формулы (1.4.6). Первоначальное число точек в спектре За счет добавления нулей требуется расширить спектр в раз. Нижняя и верхняя строки в правой части (1.4.6) обеспечивают сохранение значений спектра функции с неизменной амплитудой (изменение амплитуд в раз обеспечивает сохранение амплитуды сигнала после выполнения обратного преобразования Фурье по увеличенному в раз числу точек).

Действие этой программы (см. рис. 1.4) покажем на том же исходном массиве значений, использовавшемся в программе, представленной на рис. 1.3. В каждый промежуток между этими 16 значениями вставим 16 дополнительных точек.

(кликните для просмотра скана)

(кликните для просмотра скана)

После получения исходных данных следуют иные действия, чем в предыдущей программе. Исходные данные представляются в виде спектра, который дополняется нулями по формуле (1.4.6). В результате обратного преобразования Фурье к исходным данным добавляются промежуточные значения.

Этот способ восстановления промежуточных значений оказывается не только более быстродействующим, но и гораздо более точным, как видно из приведенного графика в конце программы.

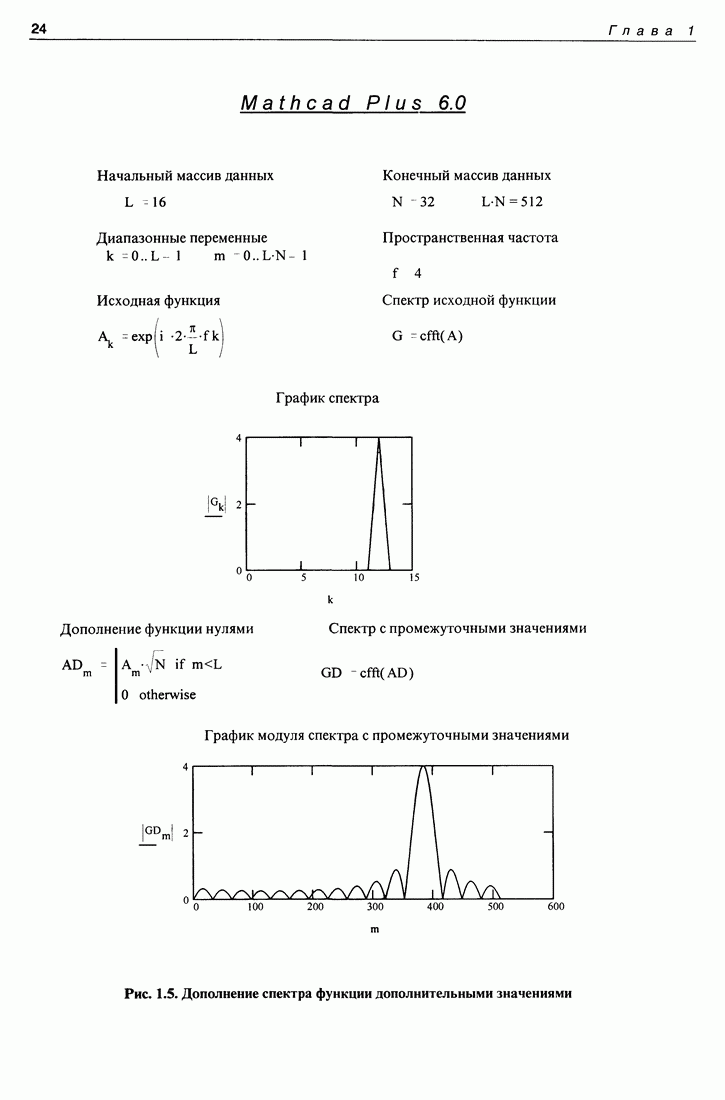
На рис. 1.5 приведена программа, позволяющая получать промежуточные значения в спектре функции. В качестве примера взята экспоненциальная функция от мнимого аргумента при целочисленной частоте. В этом случае спектр функции, не дополняемый промежуточными точками, содержит всего одну точку. Все остальные значения приходятся точно на нули функции

Для получения промежуточных значений спектра функции она должна быть дополнена нулями, что и сделано в прилагаемой программе (см. рис. 1.5).

Заметим, что спектр чистой экспоненты всегда определяется по формуле (1.4.3) как При целочисленных частотах отдельные точки приходятся на нули этой функции. Иногда бывает важно не делать кардинальной разницы между целочисленными и дробными частотами, для чего достаточно спектр дополнить промежуточными значениями, т. е. функцию в пределах ее задания следует дополнить нулями. Сколько нулей мы вставим в функцию, столько промежуточных значений получим.

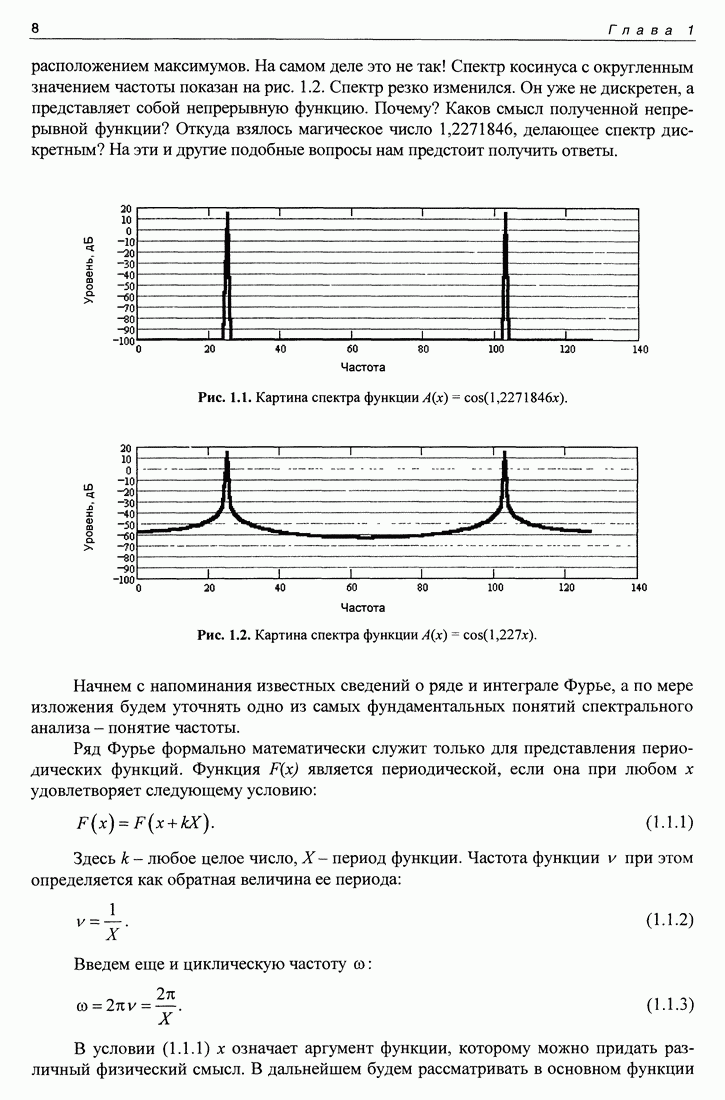
Теперь мы можем ответить на все вопросы, поставленные в разд. 1.1 (см. рис. 1.1 и 1.2).

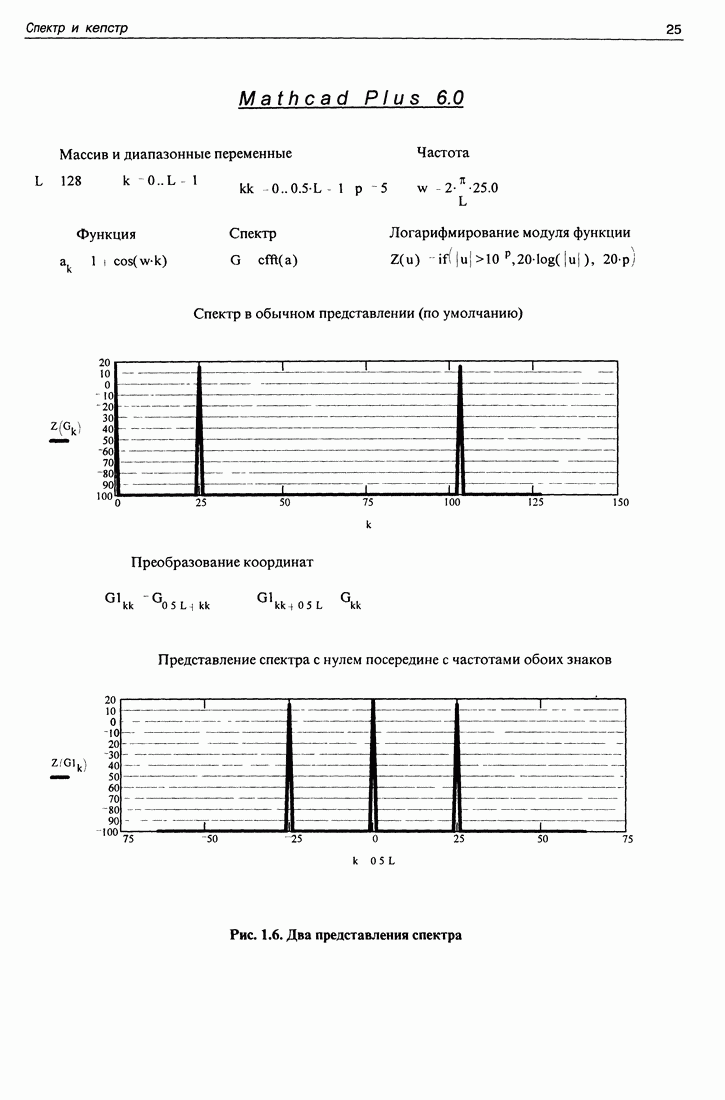
Первый. Что отложено вдоль горизонтальной оси рисунка, на котором изображен спектр? На этот вопрос выше ответ уже был дан, но здесь остановимся подробнее. Вдоль горизонтальной оси отложено целое число являющееся номером отсчетной точки спектра. К отрицательным значениям в пакете программ "Mathcad 6 plus" прибавляется число равное половине длины массива данных, в результате чего они оказываются во второй половине спектра. Положительные значения/откладываются в самом начале спектра до его середины. Такое представление спектра в упомянутом пакете программ получается по умолчанию. Это представление можно преобразовать в иное, являющееся в ряде случаев более удобным, как показано на рис. 1.6, где программа представлена в виде спектра функции единица плюс косинус целочисленной частоты, равной 25. На верхней картинке изображен спектр таким, каким он обычно получается в пакете Mathcad Plus 6.0. Все частоты положительные, их число в точности равно числу заданных дискретных значений самой функции. На нижнем графике координаты преобразованы. Левая часть рисунка до его середины перемещена в правую посредством прибавления к номеру числа Правая часть рисунка передвинута в левую путем вычитания из номеров чисел того же числа Тем самым мы поместили нулевую частоту в центр, от которого идет в обе стороны увеличение частот. Чтобы придать правильный знак частотам, включив отрицательные значения, следует от значений к отнять то же число Таким образом, использовав три раза число мы получили представление спектра, показанное на нижнем графике рис. 1.6, вдоль горизонтальной оси отложены как отрицательные, так и положительные частоты.

Второй. О магическом числе 1,2231856, при округлении которого происходит качественное изменение картины спектра. Это магическое число равно с точностью до восьми знаков Таким образом, это число представляет собою целое значение частоты, равное 25, что и видно на рисунке. Если это число округлить всего до четырех знаков, то частота будет целой лишь приблизительно, т. е. она будет дробной, что и сказывается на виде спектра.

(кликните для просмотра скана)

(кликните для просмотра скана)