| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.3. М-последовательность - идеальный тестовый сигнал для анализа систем. Ее генерация и свойства
Под М-последовательностью понимают бинарную (принимающую два значения) последовательность импульсов, характеризуемую рядом свойств, из которых для нас основным будет то, что автокорреляционная функция её, измеренная за конечный интервал времени, представляет собой один узкий треугольник. Такая последовательность представляет собой последовательность импульсов и интервалов
между ними разной ширины. Длина импульсов и интервалов следования кратны некоторому временному интервалу  часто называемому "единицей последовательности". Общие времена нахождения сигнала в одном из состояний на интервале длины М-последовательности отличаются на величину
часто называемому "единицей последовательности". Общие времена нахождения сигнала в одном из состояний на интервале длины М-последовательности отличаются на величину  поскольку длина М-последовательности равна нечетному числу единиц
поскольку длина М-последовательности равна нечетному числу единиц  При большой длине М-последовательности эти времена почти равны. Мы будем полагать, что последовательность принимает два значения: -1 и 1.
При большой длине М-последовательности эти времена почти равны. Мы будем полагать, что последовательность принимает два значения: -1 и 1.
Корреляционная функция непрерывной М-последовательности состоит из треугольника, высотой равного  - дисперсии последовательности и константе
- дисперсии последовательности и константе  где
где  - длина М-последовательности в единицах [39]. При вычислении корреляционной функции апериодической М-последовательности вне треугольника вместо константы появляется квазислучайный шум, для которого становится справедливым соотношение
- длина М-последовательности в единицах [39]. При вычислении корреляционной функции апериодической М-последовательности вне треугольника вместо константы появляется квазислучайный шум, для которого становится справедливым соотношение 
При вычислении (измерении) корреляционной функции серии из нескольких  -последовательностей через её спектр на интервале, равном длине
-последовательностей через её спектр на интервале, равном длине  корреляционная функция эквивалентна корреляционной функции непрерывной М-последовательности. В дальнейшем в книге рассматривается применение непрерывной М-последовательности (или серий М-последовательностей, следующих друг за другом без интервалов), поскольку только в этом случае удаётся получить при обработке корреляционный шум в виде константы равной
корреляционная функция эквивалентна корреляционной функции непрерывной М-последовательности. В дальнейшем в книге рассматривается применение непрерывной М-последовательности (или серий М-последовательностей, следующих друг за другом без интервалов), поскольку только в этом случае удаётся получить при обработке корреляционный шум в виде константы равной  где
где  - длина
- длина  -последовательности в единицах [39].
-последовательности в единицах [39].
Итак, измеряя импульсный отклик системы с помощью тестового сигнала в виде М-последовательности на интервале  можно быть уверенным, что мы не получим ложных пиков, вызванных корреляционным шумом. В то же время использование реализаций белого шума требует проведения измерений на бесконечных интервалах времени для достижения такого же результата.
можно быть уверенным, что мы не получим ложных пиков, вызванных корреляционным шумом. В то же время использование реализаций белого шума требует проведения измерений на бесконечных интервалах времени для достижения такого же результата.
Генерирование М-последовательности не представляет никаких проблем, что также сыграло большую роль в широком её использовании в радиосвязи и в акустических экспериментах. Практически М-последовательность генерируется схемой на основе сдвигового регистра с обратными связями, на тактовый вход которой подается последовательность импульсов с периодом повторения  . В зависимости от набора обратных связей на выходе могут формироваться сигналы разного вида (от меандра до псевдослучайных последовательностей), повторяющиеся через определенный интервал. Сигнал, имеющий самый большой период, называется кодом максимальной длины или М-последовательностью. Обычно в литературе обратные связи, реализующие М-последовательность на выходе регистра, приводятся в виде таблиц [37]. Если регистр состоит из
. В зависимости от набора обратных связей на выходе могут формироваться сигналы разного вида (от меандра до псевдослучайных последовательностей), повторяющиеся через определенный интервал. Сигнал, имеющий самый большой период, называется кодом максимальной длины или М-последовательностью. Обычно в литературе обратные связи, реализующие М-последовательность на выходе регистра, приводятся в виде таблиц [37]. Если регистр состоит из  триггеров, то длина такой последовательности будет равна
триггеров, то длина такой последовательности будет равна 
Пусть на выходе сдвигового регистра сигнал принимает два значения:  При определенных обратных связях формируется сигнал, интервал повторения которого максимален для регистра данной длины. Последовательность состояний на выходе такова, что посимвольное перемножение двух любых реализаций длины Т, вырезанных из сигнала на выходе регистра, даст на единицу больше отрицательных произведений всегда, кроме полностью совпадающих реализаций. Для совпадающих
При определенных обратных связях формируется сигнал, интервал повторения которого максимален для регистра данной длины. Последовательность состояний на выходе такова, что посимвольное перемножение двух любых реализаций длины Т, вырезанных из сигнала на выходе регистра, даст на единицу больше отрицательных произведений всегда, кроме полностью совпадающих реализаций. Для совпадающих
реализаций все произведения будут равны единице. Суммирование этих произведений даст корреляционную функцию, состоящую из одного импульса равного  при нулевом сдвиге (или кратном
при нулевом сдвиге (или кратном  при всех остальных сдвигах.
при всех остальных сдвигах.
Рассмотрим сдвиговый регистр с  разрядами, представляющий собой совокупность триггеров. Каждый управляющий импульс синхронизирующей входной последовательности вызывает переход триггера с номером к в состояние, в котором находился триггер с номером
разрядами, представляющий собой совокупность триггеров. Каждый управляющий импульс синхронизирующей входной последовательности вызывает переход триггера с номером к в состояние, в котором находился триггер с номером  и переход триггера с номером к
и переход триггера с номером к  в состояние, в котором находился триггер с номером к. Это относится ко всем триггерам регистра. Но на первый триггер регистра поступает логическая сумма (по модулю 2) состояний нескольких выходов.
в состояние, в котором находился триггер с номером к. Это относится ко всем триггерам регистра. Но на первый триггер регистра поступает логическая сумма (по модулю 2) состояний нескольких выходов.
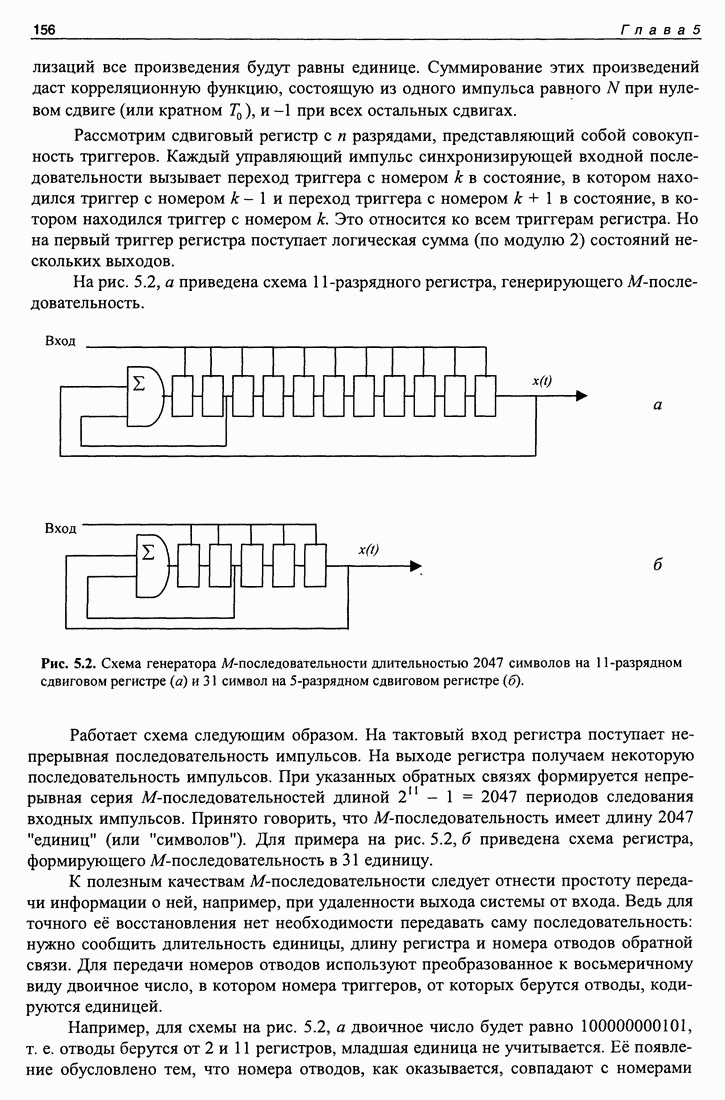
На рис. 5.2, а приведена схема  -разрядного регистра, генерирующего М-после-довательность.
-разрядного регистра, генерирующего М-после-довательность.

Рис. 5.2. Схема генератора М-последовательности длительностью 2047 символов на  -разрядном сдвиговом регистре
-разрядном сдвиговом регистре  и 31 символ на
и 31 символ на  -разрядном сдвиговом регистре
-разрядном сдвиговом регистре 
Работает схема следующим образом. На тактовый вход регистра поступает непрерывная последовательность импульсов. На выходе регистра получаем некоторую последовательность импульсов. При указанных обратных связях формируется непрерывная серия М-последовательностей длиной  периодов следования входных импульсов. Принято говорить, что М-последовательность имеет длину 2047 "единиц" (или "символов"). Для примера на рис. 5.2, б приведена схема регистра, формирующего М-последовательность в 31 единицу.
периодов следования входных импульсов. Принято говорить, что М-последовательность имеет длину 2047 "единиц" (или "символов"). Для примера на рис. 5.2, б приведена схема регистра, формирующего М-последовательность в 31 единицу.
К полезным качествам М-последовательности следует отнести простоту передачи информации о ней, например, при удаленности выхода системы от входа. Ведь для точного её восстановления нет необходимости передавать саму последовательность: нужно сообщить длительность единицы, длину регистра и номера отводов обратной связи. Для передачи номеров отводов используют преобразованное к восьмеричному виду двоичное число, в котором номера триггеров, от которых берутся отводы, кодируются единицей.
Например, для схемы на рис. 5.2, а двоичное число будет равно 100000000101, т. е. отводы берутся от 2 и 11 регистров, младшая единица не учитывается. Её появление обусловлено тем, что номера отводов, как оказывается, совпадают с номерами
ненулевых членов неприводимых полиномов. Для этой М-последовательности такой полином будет  ненулевые члены со степенями 0, 2 и 11. В восьмеричном виде это число 4005. Благодаря такой кодировке, для восстановления входной
ненулевые члены со степенями 0, 2 и 11. В восьмеричном виде это число 4005. Благодаря такой кодировке, для восстановления входной  -последовательности на выходе системы достаточно передать с входа системы восьмеричный код последовательности и длину ее единицы.
-последовательности на выходе системы достаточно передать с входа системы восьмеричный код последовательности и длину ее единицы.
Пусть период следования тактовых импульсов  а последовательность принимает значения -1 и 1, тогда корреляционную функцию М-последовательности
а последовательность принимает значения -1 и 1, тогда корреляционную функцию М-последовательности  для всех значений задержки (а не только кратных
для всех значений задержки (а не только кратных  можно записать в виде
можно записать в виде

Как видно, корреляционная функция М-последовательности представляет собой узкий треугольник с высотой, равной длине кодовой последовательности, расположенный на ненулевой  подставке.
подставке.
Спектр М-последовательности сосредоточен вблизи нуля частот. Поэтому для изучения свойств распространения акустических сигналов в определенных диапазонах частот используются сигналы с модуляцией  -последовательностью. Чаще всего используют сигналы в виде несущей, фаза которых манипулирована М-последовательностью (в англоязычной литературе такой сигнал называют М-после-дователъностъю на несущей):
-последовательностью. Чаще всего используют сигналы в виде несущей, фаза которых манипулирована М-последовательностью (в англоязычной литературе такой сигнал называют М-после-дователъностъю на несущей):

Такой сигнал обладает практически теми же свойствами, что и модулирующая последовательность. Корреляционная функция такого сигнала имеет вид

Отметим еще раз особенность обработки непрерывных сигналов на основе М-последовательности. Вычисление спектров и корреляционных функций следует производить на интервалах, кратных длине М-последовательности  Эти процедуры удобно выполнять, используя дискретное преобразование Фурье именно на интервале равном длине М-последовательности. Только в этом случае корреляционная функция определяется вышеприведенной формулой. Невыполнение этого условия приводит к появлению корреляционного шума, аналогичного шуму корреляционных функций случайных сигналов, для уровня которых справедлива оценка
Эти процедуры удобно выполнять, используя дискретное преобразование Фурье именно на интервале равном длине М-последовательности. Только в этом случае корреляционная функция определяется вышеприведенной формулой. Невыполнение этого условия приводит к появлению корреляционного шума, аналогичного шуму корреляционных функций случайных сигналов, для уровня которых справедлива оценка  от максимума корреляционной функции. В этом случае, как видно из уровня корреляционного шума, он не только в
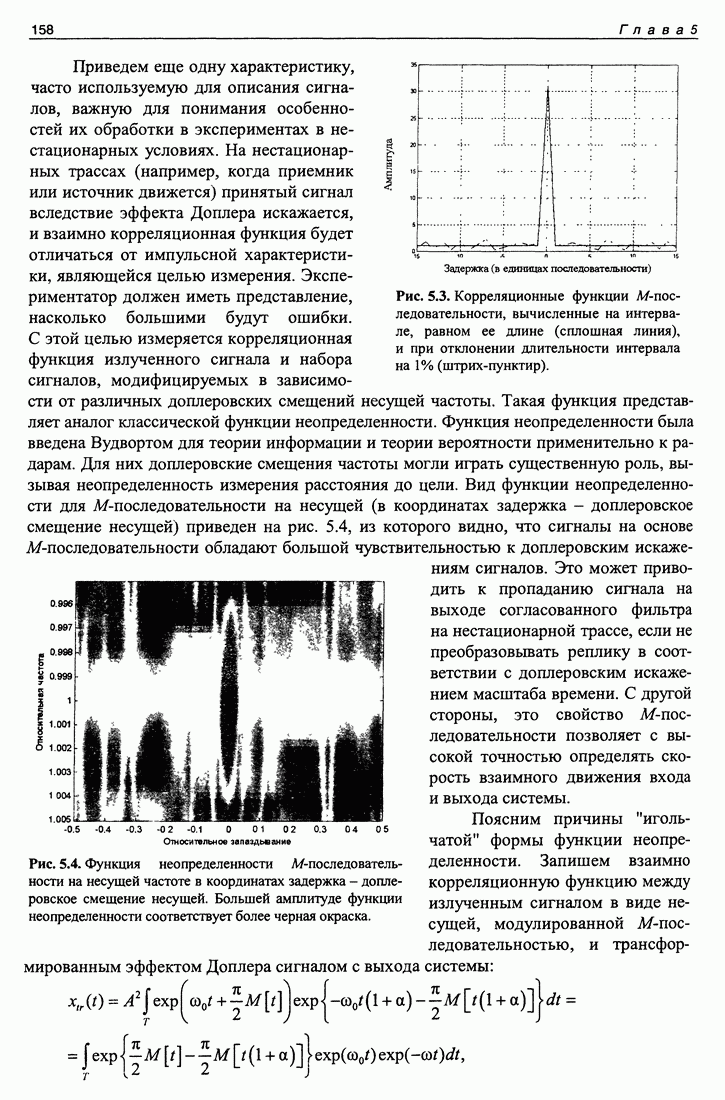
от максимума корреляционной функции. В этом случае, как видно из уровня корреляционного шума, он не только в  раз становится больше, но и уже не является константой, что существенно повышает его маскирующие свойства. На рис. 5.3 приведены корреляционные функции
раз становится больше, но и уже не является константой, что существенно повышает его маскирующие свойства. На рис. 5.3 приведены корреляционные функции  -последовательности, вычисленные на интервале, равном ее длине (сплошная линия), и при отклонении длительности интервала на 1 % (штрих-пунктир).
-последовательности, вычисленные на интервале, равном ее длине (сплошная линия), и при отклонении длительности интервала на 1 % (штрих-пунктир).

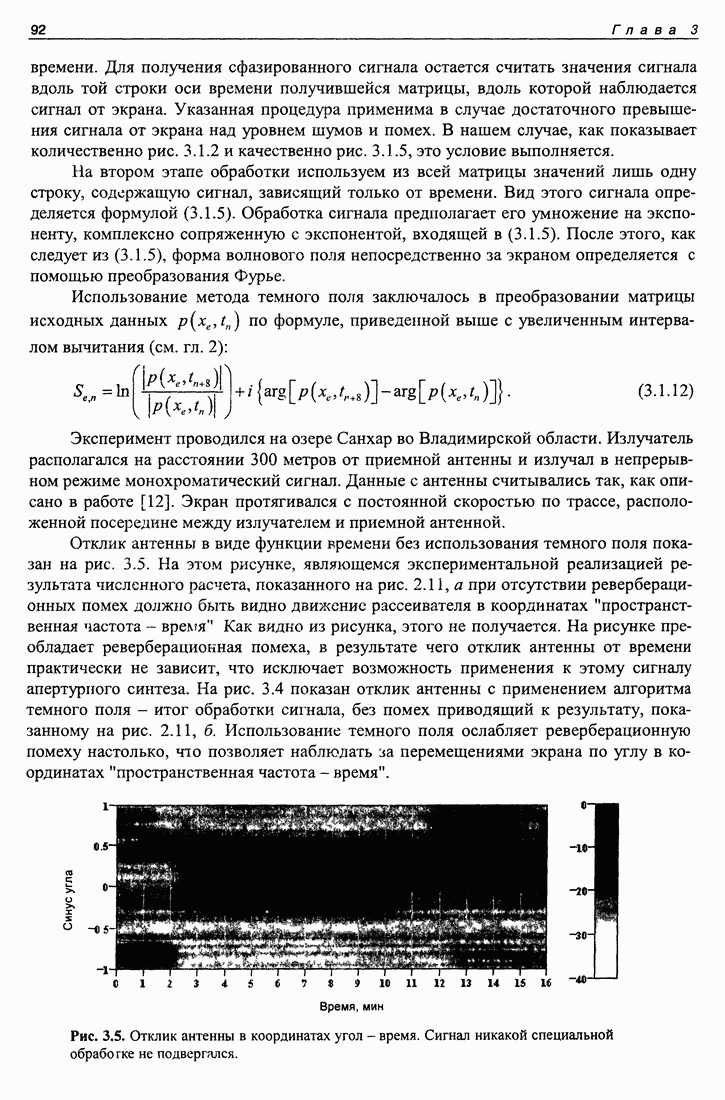
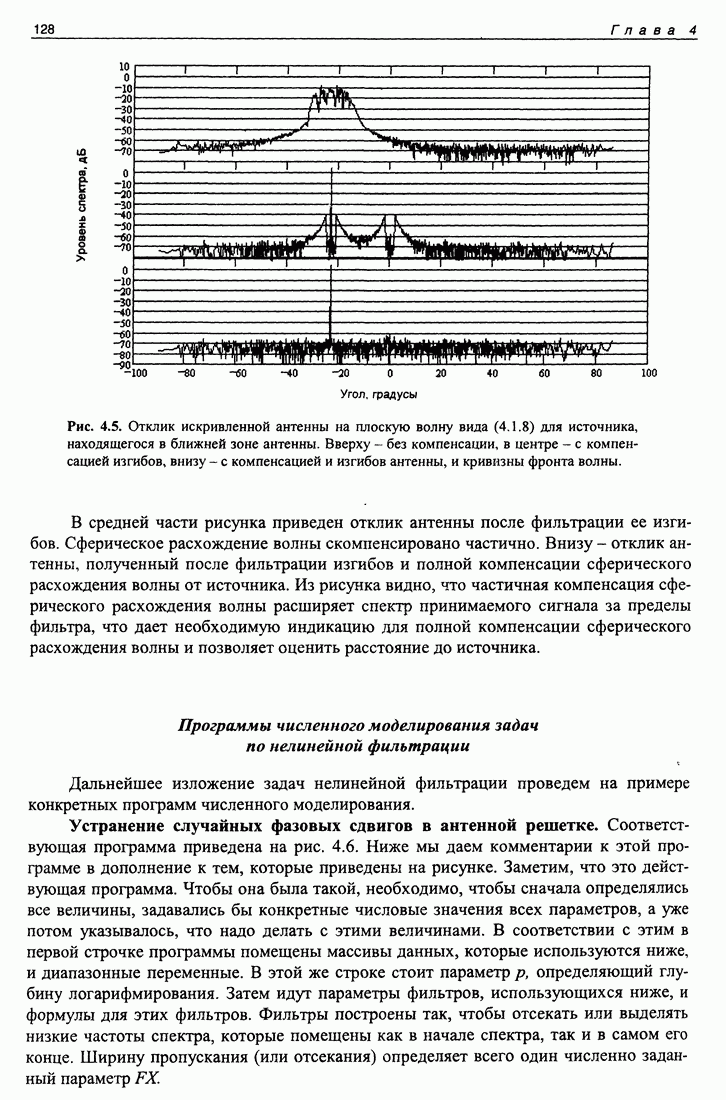
Рис. 5.3. Корреляционные функции М-последовательности, вычисленные на интервале, равном ее длине (сплошная линия), и при отклонении длительности интервала на 1% (штрих-пунктир).
Приведем еще одну характеристику, часто используемую для описания сигналов, важную для понимания особенностей их обработки в экспериментах в нестационарных условиях. На нестационарных трассах (например, когда приемник или источник движется) принятый сигнал вследствие эффекта Доплера искажается, и взаимно корреляционная функция будет отличаться от импульсной характеристики, являющейся целью измерения. Экспериментатор должен иметь представление, насколько большими будут ошибки.
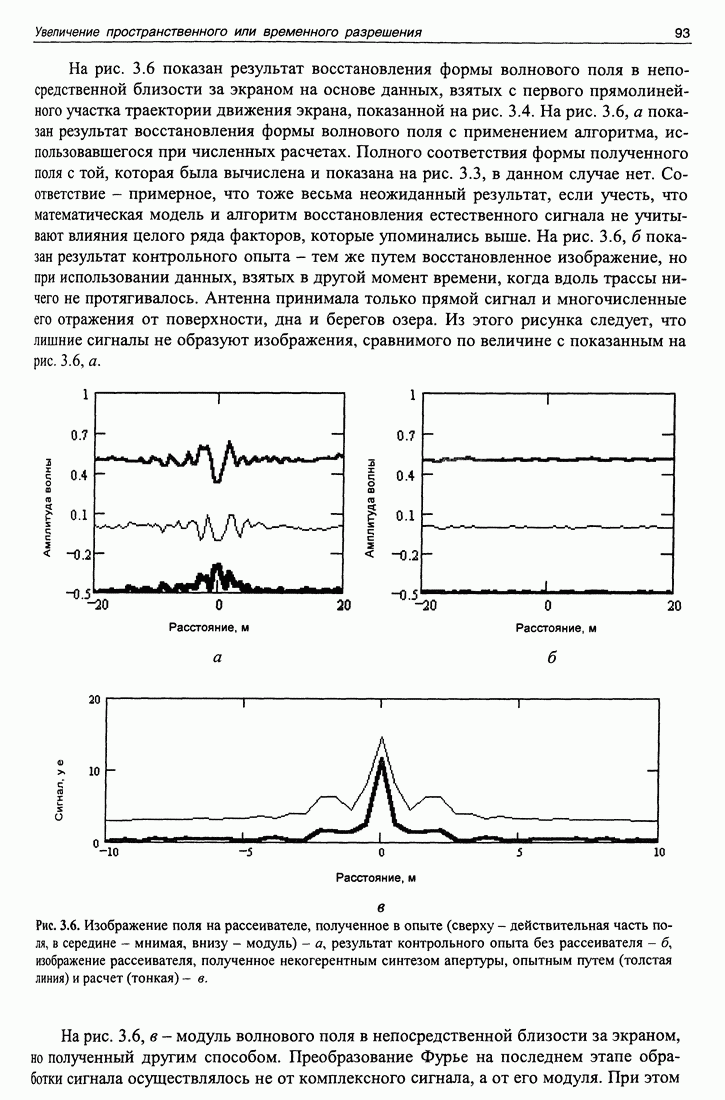
С этой целью измеряется корреляционная функция излученного сигнала и набора сигналов, модифицируемых в зависимости от различных доплеровских смещений несущей частоты. Такая функция представляет аналог классической функции неопределенности. Функция неопределенности была введена Вудвортом для теории информации и теории вероятности применительно к радарам. Для них доплеровские смещения частоты могли играть существенную роль, вызывая неопределенность измерения расстояния до цели. Вид функции неопределенности для М-последовательности на несущей (в координатах задержка - доплеровское смещение несущей) приведен на рис. 5.4, из которого видно, что сигналы на основе М-последовательности обладают большой чувствительностью к доплеровским искажениям сигналов. Это может приводить к пропаданию сигнала на выходе согласованного фильтра на нестационарной трассе, если не преобразовывать реплику в соответствии с доплеровским искажением масштаба времени. С другой стороны, это свойство М-последовательности позволяет с высокой точностью определять скорость взаимного движения входа и выхода системы.
Поясним причины "игольчатой" формы функции неопределенности. Запишем взаимно корреляционную функцию между излученным сигналом в виде несущей, модулированной М-последовательностью, и трансформированным эффектом Доплера сигналом с выхода системы:


Рис. 5.4. Функция неопределенности М-последователь-ности на несущей частоте в координатах задержка - доплеровское смещение несущей. Большей амплитуде функции неопределенности соответствует более черная окраска.
где  - коэффициент трансформации, очевидно имеющий малые значения, а
- коэффициент трансформации, очевидно имеющий малые значения, а  - доплеровская частота. Как нетрудно заметить, выражение представляет собой преобразование Фурье по
- доплеровская частота. Как нетрудно заметить, выражение представляет собой преобразование Фурье по  . В предположении малости а функция, от которой определяется преобразование Фурье, представляет собой просто гармонический сигнал. И ширина отклика по частоте для такого сигнала равна
. В предположении малости а функция, от которой определяется преобразование Фурье, представляет собой просто гармонический сигнал. И ширина отклика по частоте для такого сигнала равна  . В примере на рис. 5.4 длина М-последовательности равна 31 единице. Единица последовательности равна восьми периодам несущей сигнала, т. е.
. В примере на рис. 5.4 длина М-последовательности равна 31 единице. Единица последовательности равна восьми периодам несущей сигнала, т. е.  Таким образом, разрешение по Доплеру составляет
Таким образом, разрешение по Доплеру составляет  Для несущей с частотой равной единице спад корреляционного отклика до нуля происходит на частотах
Для несущей с частотой равной единице спад корреляционного отклика до нуля происходит на частотах  или 1.004 и 0.996, что хорошо видно на рис. 5.4.
или 1.004 и 0.996, что хорошо видно на рис. 5.4.
Проведенный анализ - приближенный, но, как видно, дающий правильную оценку ширины функции неопределенности по Доплеру. Конечно, при необходимости можно сделать точный анализ формы функции неопределенности, однако более сложные выкладки могут содержать ошибки, а приближенный анализ позволяет легко их отследить. Это удивительное свойство несущей, модулированной М-после-довательностью, обладающей такой же чувствительностью к смещению по частоте, как и тональный сигнал, позволяет получить также хорошее временное разрешение.
Ошибки оценки корреляционной функции обычно называют корреляционным шумом. Как показано в работе [39], его дисперсия зависит от многих параметров, но для белого шума имеет достаточно простое выражение и может служить приближенной оценкой в большинстве случаев. Эта формула уже была приведена:  где
где  - дисперсия корреляционного шума,
- дисперсия корреляционного шума,  уже определена выше,
уже определена выше,  - корреляционная функция сигнала. Аналогичное выражение определяет и дисперсию для взаимно корреляционной функции, только в числителе стоит произведение значений автокорреляционной функции в нуле. Значение корреляционного шума велико. Пусть мы исследуем канал распространения с импульсной характеристикой в виде дельтафункции. Подавая на вход системы реализацию белого шума и измеряя взаимно корреляционную функцию, можно получить оценку импульсной характеристики, имеющую кроме основного (истинного) пика еще множество дополнительных пиков, хотя и меньшего уровня, т. е. вместо истинной импульсной характеристики мы получаем оценку, отличающуюся от искомой. Важно то, что погрешность эта вызвана причиной, на которую вполне мог бы воздействовать экспериментатор, подобрав более подходящую реализацию, в отличие от ошибок, вызванных аддитивными помехами, в основном находящихся вне власти исследователей. Часто для уменьшения этой ошибки опыт повторяют несколько раз с различными реализациями шума с последующим усреднением результатов. При этом дисперсия корреляционного шума уменьшается обратно пропорционально квадратному корню из числа опытов. Но такой подход требует априорной информации о стационарности системы и такого проведения измерений, чтобы за время проведения опытов не произошло изменения импульсной характеристики системы.
- корреляционная функция сигнала. Аналогичное выражение определяет и дисперсию для взаимно корреляционной функции, только в числителе стоит произведение значений автокорреляционной функции в нуле. Значение корреляционного шума велико. Пусть мы исследуем канал распространения с импульсной характеристикой в виде дельтафункции. Подавая на вход системы реализацию белого шума и измеряя взаимно корреляционную функцию, можно получить оценку импульсной характеристики, имеющую кроме основного (истинного) пика еще множество дополнительных пиков, хотя и меньшего уровня, т. е. вместо истинной импульсной характеристики мы получаем оценку, отличающуюся от искомой. Важно то, что погрешность эта вызвана причиной, на которую вполне мог бы воздействовать экспериментатор, подобрав более подходящую реализацию, в отличие от ошибок, вызванных аддитивными помехами, в основном находящихся вне власти исследователей. Часто для уменьшения этой ошибки опыт повторяют несколько раз с различными реализациями шума с последующим усреднением результатов. При этом дисперсия корреляционного шума уменьшается обратно пропорционально квадратному корню из числа опытов. Но такой подход требует априорной информации о стационарности системы и такого проведения измерений, чтобы за время проведения опытов не произошло изменения импульсной характеристики системы.
Фактически М-последовательность имеет корреляционный шум в виде константы. Хотя природа его иная, нежели природа корреляционного шума случайных сигналов, во
многом их влияние на оценки импульсных характеристик систем близко. Конечно, такой шум лучше, чем у реализаций белого шума (вызывающего появление ложных импульсов), но и он может приводить к неприятным последствиям. Для многих исследуемых систем с несколькими каналами распространения импульсный отклик может состоять из нескольких максимумов. Наличие такой подставки в корреляционной функции тестового сигнала ведет к тому, что некоторые максимумы могут маскировать слабые максимумы во взаимной корреляционной функции. Этот порог маскировки может быть значительно выше порога, определяемого уровнем шумов в сигнале.
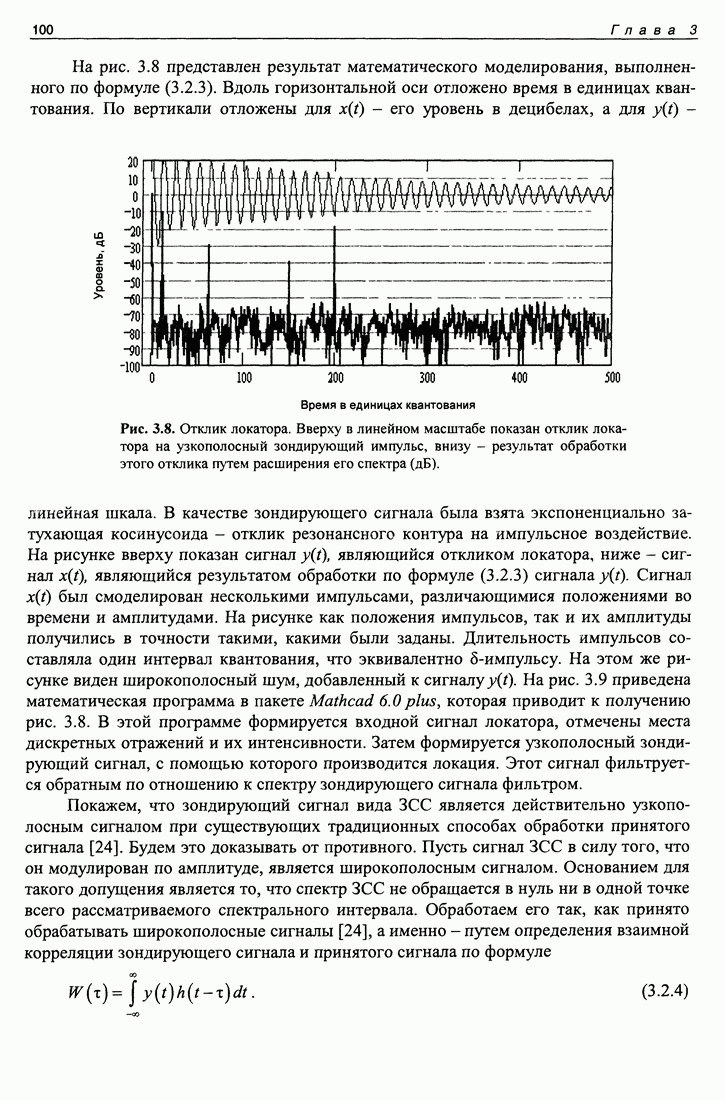
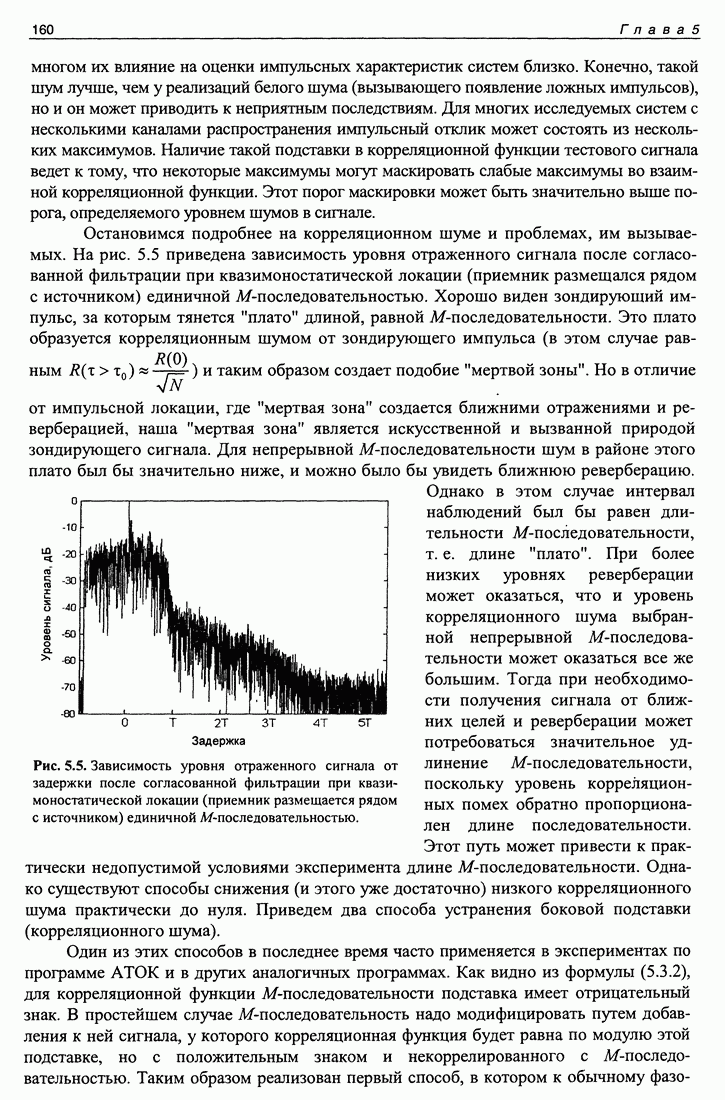
Остановимся подробнее на корреляционном шуме и проблемах, им вызываемых. На рис. 5.5 приведена зависимость уровня отраженного сигнала после согласованной фильтрации при квазимоностатической локации (приемник размещался рядом с источником) единичной  -последовательностью. Хорошо виден зондирующий импульс, за которым тянется "плато" длиной, равной М-последовательности. Это плато образуется корреляционным шумом от зондирующего импульса (в этом случае равным
-последовательностью. Хорошо виден зондирующий импульс, за которым тянется "плато" длиной, равной М-последовательности. Это плато образуется корреляционным шумом от зондирующего импульса (в этом случае равным  и таким образом создает подобие "мертвой зоны". Но в отличие от импульсной локации, где "мертвая зона" создается ближними отражениями и реверберацией, наша "мертвая зона" является искусственной и вызванной природой зондирующего сигнала. Для непрерывной М-последовательности шум в районе этого плато был бы значительно ниже, и можно было бы увидеть ближнюю реверберацию.
и таким образом создает подобие "мертвой зоны". Но в отличие от импульсной локации, где "мертвая зона" создается ближними отражениями и реверберацией, наша "мертвая зона" является искусственной и вызванной природой зондирующего сигнала. Для непрерывной М-последовательности шум в районе этого плато был бы значительно ниже, и можно было бы увидеть ближнюю реверберацию.
Однако в этом случае интервал наблюдений был бы равен длительности М-последовательности, т. е. длине "плато". При более низких уровнях реверберации может оказаться, что и уровень корреляционного шума выбранной непрерывной М-последовательности может оказаться все же большим. Тогда при необходимости получения сигнала от ближних целей и реверберации может потребоваться значительное удлинение М-последовательности, поскольку уровень корреляционных помех обратно пропорционален длине последовательности. Этот путь может привести к практически недопустимой условиями эксперимента длине М-последовательности. Однако существуют способы снижения (и этого уже достаточно) низкого корреляционного шума практически до нуля. Приведем два способа устранения боковой подставки (корреляционного шума).
Один из этих способов в последнее время часто применяется в экспериментах по программе АТОК и в других аналогичных программах. Как видно из формулы (5.3.2), для корреляционной функции М-последовательности подставка имеет отрицательный знак. В простейшем случае М-последовательность надо модифицировать путем добавления к ней сигнала, у которого корреляционная функция будет равна по модулю этой подставке, но с положительным знаком и некоррелированного с М-последовательностью. Таким образом реализован первый способ, в котором к обычному

Рис. 5.5. Зависимость уровня отраженного сигнала от задержки после согласованной фильтрации при квазимоностатической локации (приемник размещается рядом с источником) единичной М-последовательностью.
фазоманипулированному сигналу добавлен гармонический сигнал с частотой, равной частоте несущей. Этот способ - фазовая манипуляция с амплитудной модуляцией:

где  - длина регистра, генерирующего
- длина регистра, генерирующего  -последовательность.
-последовательность.
Второй способ интуитивно не так прозрачен, но он приводит к тем же результатам и основан на фазовой модуляции

Такие псевдослучайные сигналы имеют корреляционную функцию

Использование этих сигналов позволяет полностью избавиться от корреляционного шума и таким образом устранить основной недостаток М-последовательности. Теоретически нет никаких препятствий к получению у таких сигналов нулевого корреляционного шума, но реально неточность модуляции амплитуды или фазы приводит к невозможности полного отсутствия корреляционного шума. Реализация подобных сигналов часто бывает затруднена в синтезаторах с дискретным квантованием и в аналоговых системах с нарушением линейности. Дискретный синтез может давать значения коэффициентов модуляции фазы и амплитуды, не совпадающие с требуемыми в соответствии с формулами для полного устранения корреляционного шума, т. е. избавиться от корреляционной подставки полностью обычно не удается. Однако уменьшение подставки такими методами гораздо эффективнее. Например, снижение подставки у последовательности длиной 1023 на 20 дБ (исходно подставка имеет уровень -60 дБ) и первым, и вторым способом не представляет труда, в то время как для сигнала с фазовой манипуляцией потребуется увеличение длины последовательности в 10 раз. Для получения корреляционной подставки у такого сигнала на уровне -80 дБ длина последовательности должна быть около 10000.
Кроме того, линейные системы, вообще говоря, являются обычно некоторой идеализацией, физически не реализуемой, но в пределах точности измерений допустимой. Поэтому даже в линейных системах коэффициент модуляции может изменяться от заданной величины вследствие её нелинейности. Исследования показали, что эти изменения могут приводить к изменению корреляционного шума. На рис. 5.6 приведена зависимость уровня корреляционного шума от коэффициента нелинейности

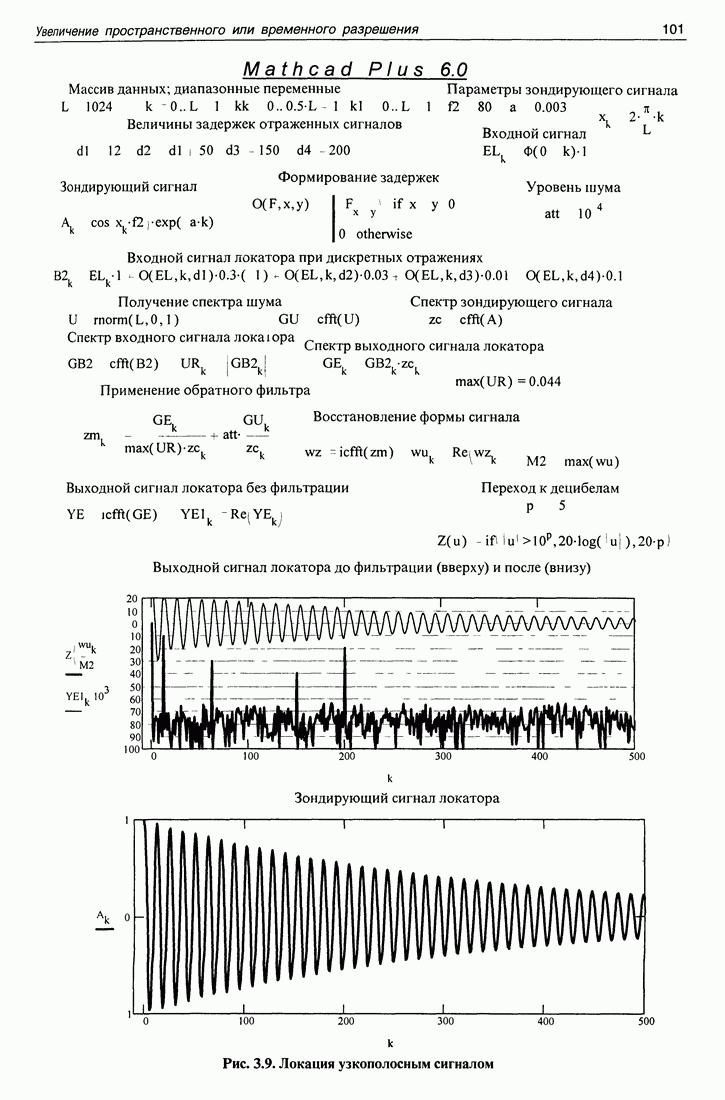
Рис. 5.6. Зависимость уровня корреляционного шума от коэффициента нелинейности регистрирующей системы.
системы. Из рисунка хорошо видно, что зависимость велика. Этот коэффициент определен как квадратный корень из отношения суммы мощностей дополнительных гармоник тонального сигнала к мощности первой. Очевидно, что только применение высококачественной звуковой аппаратуры может позволить максимально реализовать преимущества сигналов без корреляционного шума.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. СПЕКТР И КЕПСТР
- 1.1. Ряд и интеграл Фурье
- 1.2. Математические свойства преобразования Фурье
- 1.3. Знаменитая теорема отсчетов
- 1.4. Как выполняется преобразование Фурье численно
- 1.5. Линейные системы
- 1.6. Кепструм
- 1.7. Численное представление случайных сигналов
- Глава 2. ФИЛЬТРАЦИЯ ПОМЕХ И ЛОКАЦИЯ НА ПРОСВЕТ
- 2.1. Устранение узкополосной помехи
- 2.2. Метод темного поля
- 2.3. Эксперимент по наблюдению точечного рассеивателя
- Глава 3. УВЕЛИЧЕНИЕ ПРОСТРАНСТВЕННОГО ИЛИ ВРЕМЕННОГО РАЗРЕШЕНИЯ
- 3.2. Увеличение временного разрешения сигналов
- 3.3. Локация на просвет с разделением прямого и дифрагированного сигналов по времени
- Глава 4. ФАЗОВЫЕ ШУМЫ И РЕВЕРБЕРАЦИЯ
- 4.1. Фильтрация мультипликативно связанных сигналов
- 4.2. Устранение влияния фазовых шумов в параметрическом микрофоне
- 4.3. Слепая дереверберация
- Глава 5. ИССЛЕДОВАНИЕ АКУСТИЧЕСКИХ ТРАСС С ИСПОЛЬЗОВАНИЕМ М-ПОСЛЕДОВАТЕЛЬНОСТИ
- 5.1. Акустические задачи, решаемые с помощью M-последовательности
- 5.2. Выбор оптимальной методики анализа линейной системы
- 5.3. М-последовательность — идеальный тестовый сигнал для анализа систем. Ее генерация и свойства
- 5.4. Применение М-последовательности на стационарной сейсмической трассе
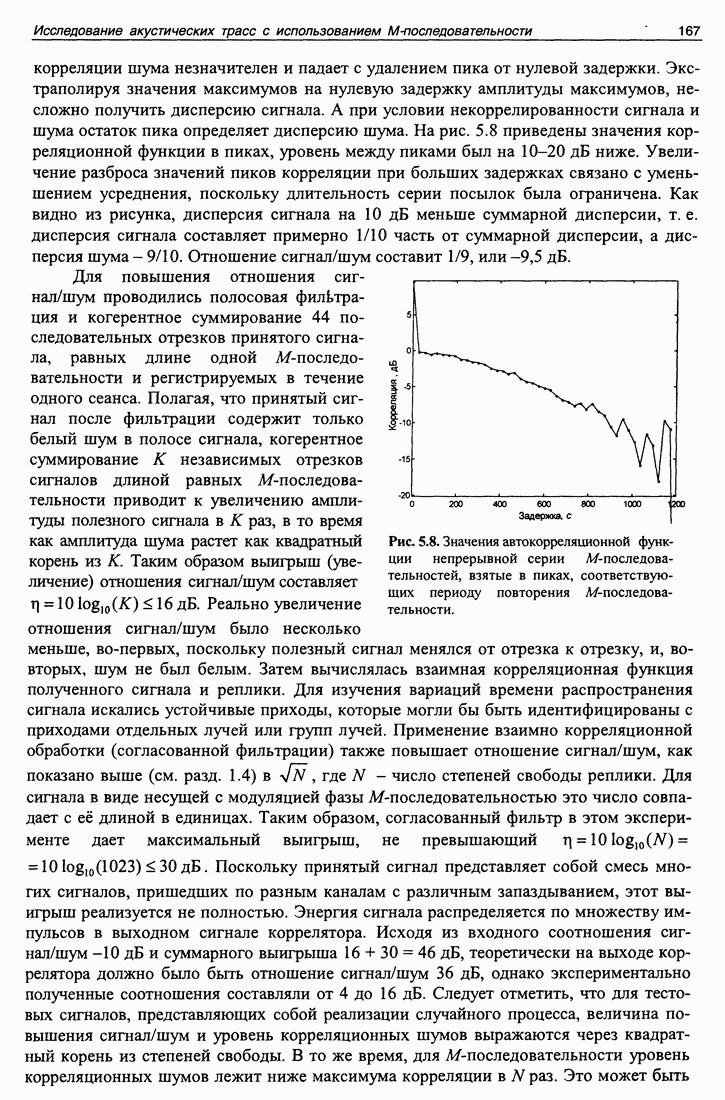
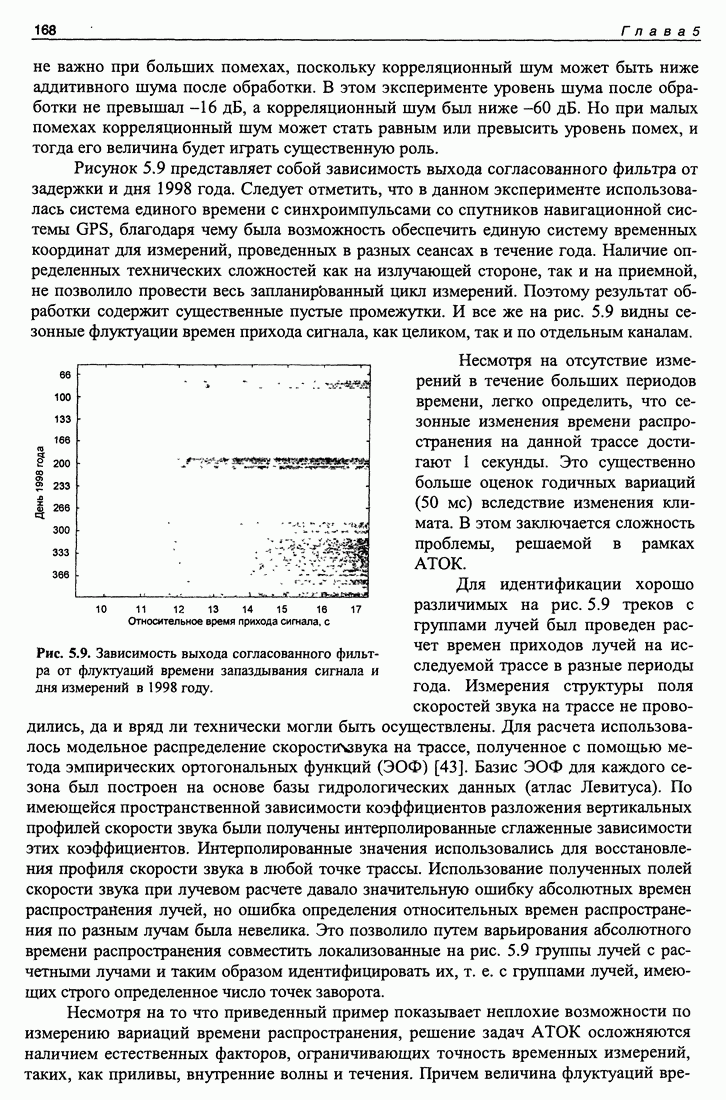
- 5.5. Применение М-последовательности на сверхдлинных океанических трассах
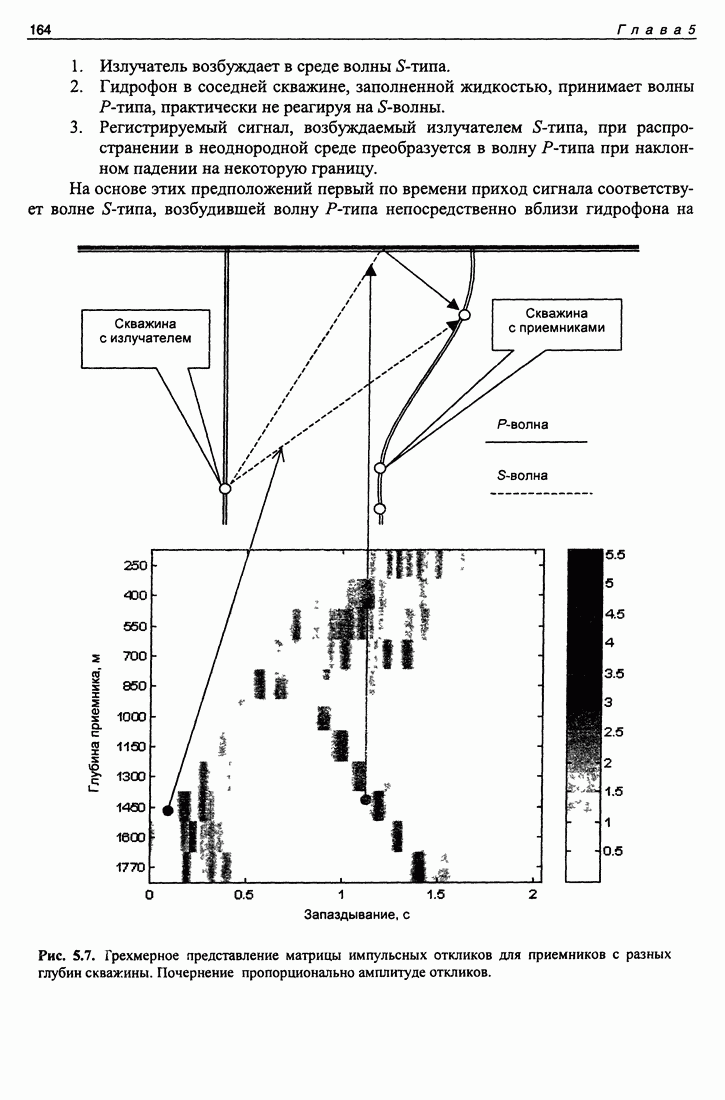
- 5.6. Идентификация каналов распространения на нестационарных трассах
- 5.7. Кепстральный метод оценки флуктуаций запаздывания сигналов
- Литература