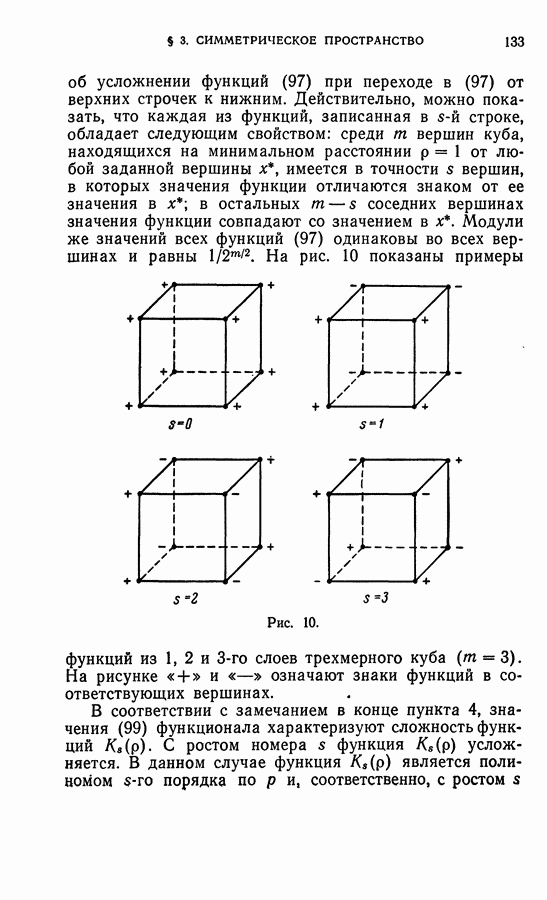
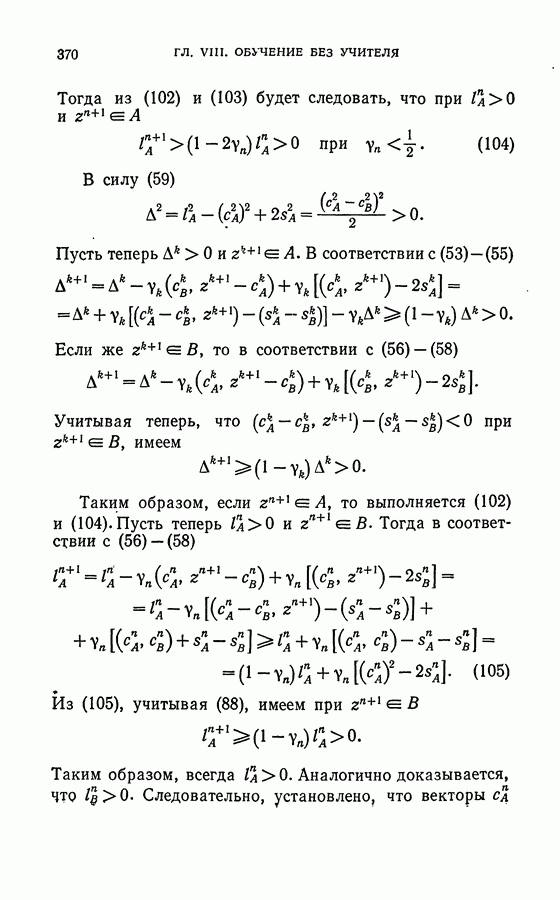| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Условия сходимости процедур метода потенциальных функций
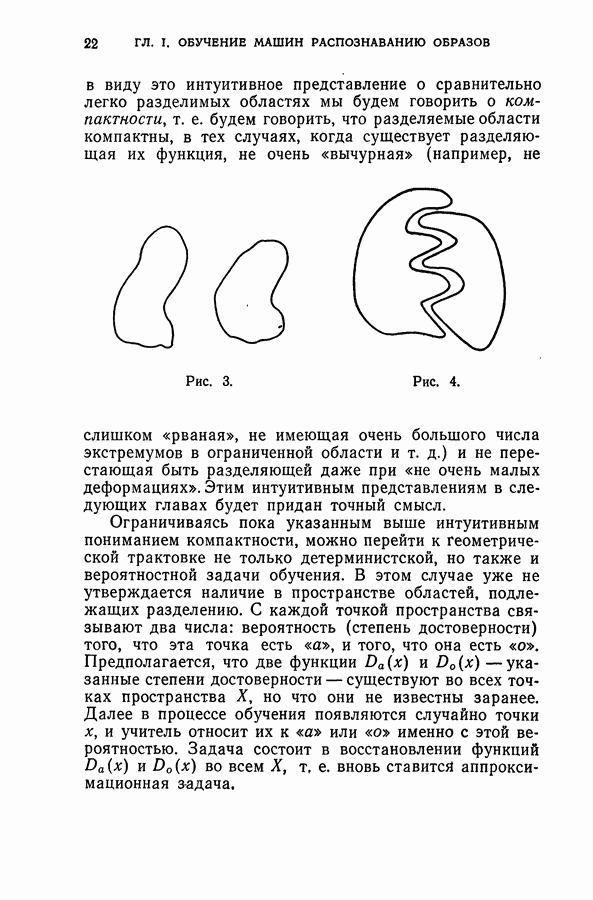
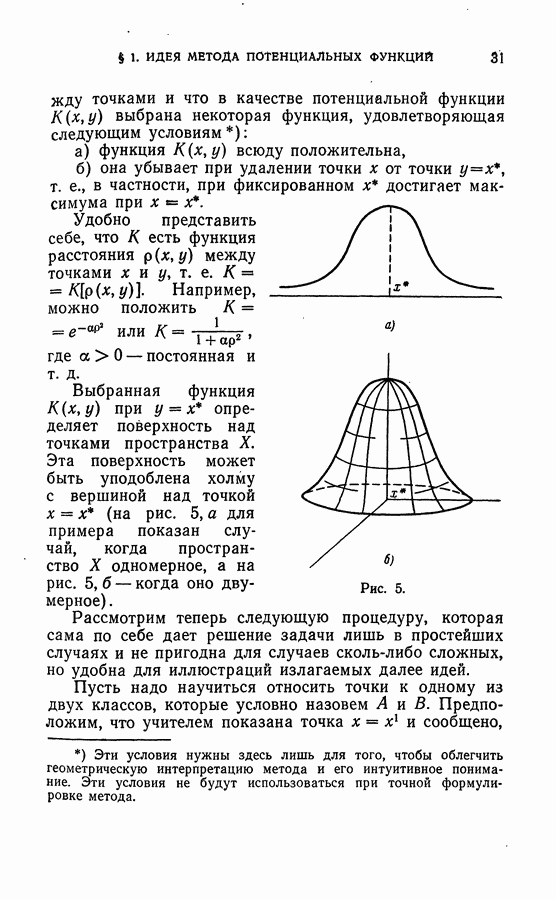
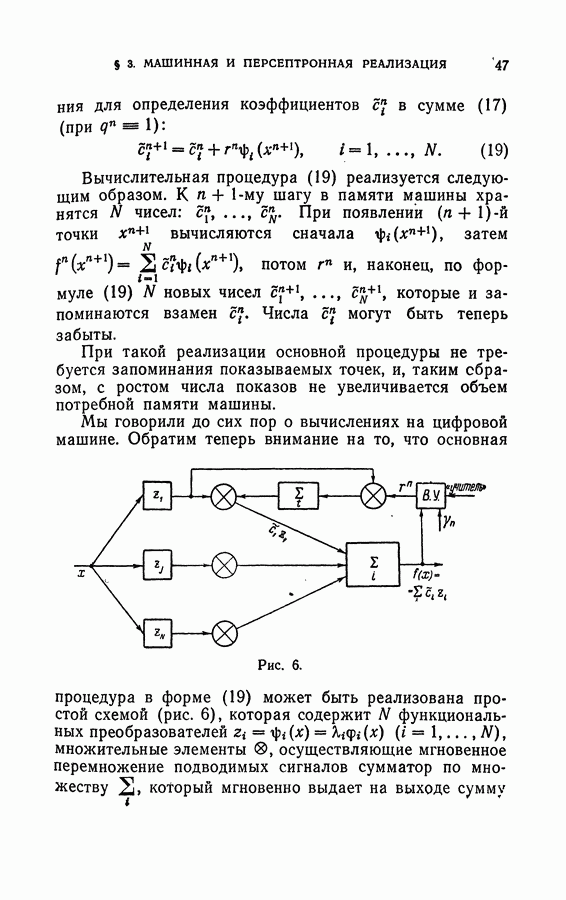
В настоящем параграфе устанавливаются теоремы, из которых следуют условия сходимости процедур метода потенциальных функций (см. гл. II)

в тех случаях, когда

Как показано в главе II, процедура (101) может быть записана с учетом (102) в эквивалентном «персептрон-ном» виде:

где вектор  бесконечномерный, если потенциальная функция представима бесконечным рядом
бесконечномерный, если потенциальная функция представима бесконечным рядом

Процедура (103) является частным случаем процедуры (4). Поэтому в тех случаях, когда ряд (104) конечен и вектор  конечномерный, к процедуре (103) применимы условия сходимости, доказанные в § 4. Однако, как показано в главе II, особенность процедуры (103) как в конечно, так и в бесконечномерном случае (в отличие от общей процедуры
конечномерный, к процедуре (103) применимы условия сходимости, доказанные в § 4. Однако, как показано в главе II, особенность процедуры (103) как в конечно, так и в бесконечномерном случае (в отличие от общей процедуры  заключается в том, что можно определить функционал, экстремизируемый этой процедурой. Эта особенность процедуры (103) и позволяет дать специфические для нее условия сходимости, которым и посвящен настоящий параграф.
заключается в том, что можно определить функционал, экстремизируемый этой процедурой. Эта особенность процедуры (103) и позволяет дать специфические для нее условия сходимости, которым и посвящен настоящий параграф.
Вернемся к основной процедуре (4). Будем считать, что вектор-функция  такова, что
такова, что

при  и при любом фиксированном х.
и при любом фиксированном х.
Легко видеть, что при этом в силу процедуры  если только
если только  (сравни аналогичное утверждение в § 4 главы II относительно общей процедуры
(сравни аналогичное утверждение в § 4 главы II относительно общей процедуры 
Наложим теперь такие ограничения на вид функций  которые учитывают отмеченную выше специфику соотношений (103).
которые учитывают отмеченную выше специфику соотношений (103).
Рассмотрим математическое ожидание

и определим интеграл

как интеграл по отрезку прямой  соединяющему точки
соединяющему точки  следующим образом:
следующим образом:

Будем говорить, что интеграл  не зависит от пути, если для любых трех точек
не зависит от пути, если для любых трех точек  имеет место равенство
имеет место равенство

Введем в рассмотрение функцию

В тех случаях, когда функция  такова, что интеграл
такова, что интеграл  не зависит от пути, имеет место равенство
не зависит от пути, имеет место равенство

Функция  при выполнении условия (109), как это будет видно в последующих главах, и будет играть роль экстремизируемого функционала в конкретных применениях процедур метода потенциальных функций.
при выполнении условия (109), как это будет видно в последующих главах, и будет играть роль экстремизируемого функционала в конкретных применениях процедур метода потенциальных функций.
Будем говорить, что функция  монотонна, если для любой пары точек
монотонна, если для любой пары точек  справедливо неравенство
справедливо неравенство

В отношении функции  всюду далее в этом параграфе мы будем требовать лишь существования интеграла по прямой и монотонность; каких-либо дополнительных требований непрерывности на функцию
всюду далее в этом параграфе мы будем требовать лишь существования интеграла по прямой и монотонность; каких-либо дополнительных требований непрерывности на функцию  не накладывается (функция
не накладывается (функция  может иметь разрывы).
может иметь разрывы).
Покажем, что если функция  монотонна и интеграл
монотонна и интеграл  не зависит от пути, то функция
не зависит от пути, то функция  является выпуклой. Действительно, вычислим значение функции
является выпуклой. Действительно, вычислим значение функции  в точке
в точке

Учитывая условие (109) и определение (106), имеем 1

Но в силу монотонности функции  справедливо неравенство
справедливо неравенство

Действительно, в силу (110)

Поскольку же  то
то

а последнее неравенство эквивалентно неравенству (112).
Подставляя теперь неравенство (112) в соотношение (111) и вспоминая снова (109) и определение (106), получаем

а это и есть определение выпуклости функции 
При использовании в следующих главах метода потенциальных функций для решения конкретных задач функция  монотонна, и, следовательно, функция
монотонна, и, следовательно, функция  выпуклая. Более того, при этом оказывается, что монотонной является и функция
выпуклая. Более того, при этом оказывается, что монотонной является и функция  (при каждом фиксированном
(при каждом фиксированном  Если распределение вероятностей случайной величины х, входящее в определение (105), не зависит от у (а это предположение обычно выполняется в задачах, рассмотренных в последующих главах), то из монотонности
Если распределение вероятностей случайной величины х, входящее в определение (105), не зависит от у (а это предположение обычно выполняется в задачах, рассмотренных в последующих главах), то из монотонности  очевидным образом следует монотонность
очевидным образом следует монотонность  а следовательно, и выпуклость
а следовательно, и выпуклость 
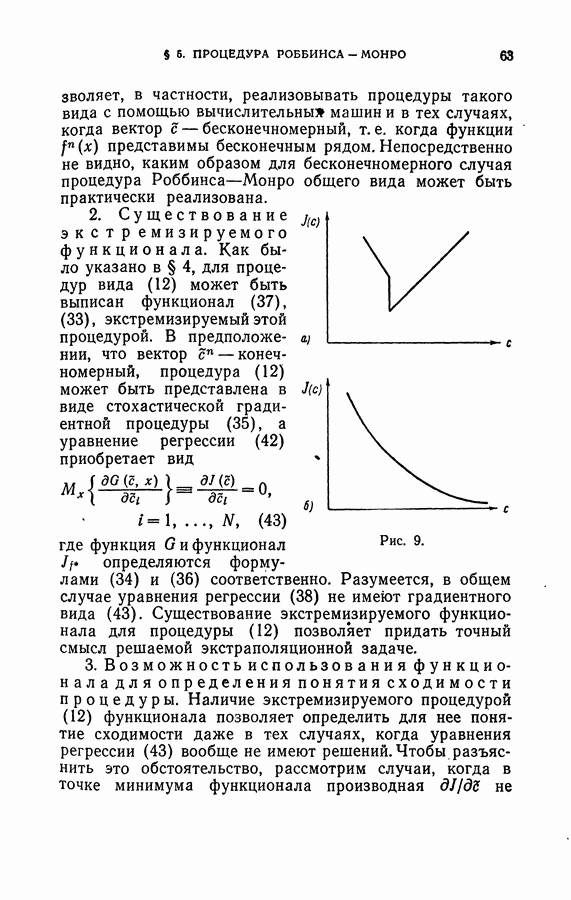
Особенность теорем настоящего параграфа заключается в том, что они, в отличие от теорем § 4, устанавливают сходимость значений функционала  к минимальному значению, а не сходимость последовательности
к минимальному значению, а не сходимость последовательности  Более того, при этом последовательность
Более того, при этом последовательность  вообще может не сходиться, например, в том случае, когда минимальное значение
вообще может не сходиться, например, в том случае, когда минимальное значение  достигается на бесконечности. В теореме XIII для конечномерного случая будут определены условия, при которых и
достигается на бесконечности. В теореме XIII для конечномерного случая будут определены условия, при которых и  сходится к области значений, обеспечивающих минимум функционала
сходится к области значений, обеспечивающих минимум функционала  Заметим также, что, говоря выше о выпуклости
Заметим также, что, говоря выше о выпуклости  мы нигде не требовали строгой выпуклости, и поэтому минимум
мы нигде не требовали строгой выпуклости, и поэтому минимум  может достигаться не в одной точке, а на целом множестве.
может достигаться не в одной точке, а на целом множестве.
Прежде чем сформулировать интересующие нас теоремы, докажем вспомогательное неравенство, которое будет далее использовано при доказательстве этих теорем:

Из (109) и (106) имеем

Но из условия монотонности функции  следует, что
следует, что

и, следовательно,

Поскольку  из последнего неравенства следует
из последнего неравенства следует

Подставляя (115) в (114), получаем неравенство (113). Сформулируем и докажем следующую теорему. Теорема XII. Пусть в рекуррентных соотношениях (4) вектор  таков, что функция
таков, что функция

монотонна, а интеграл  не зависит от пути. Пусть, далее,
не зависит от пути. Пусть, далее,

где  константы.
константы.
Тогда в силу рекуррентной процедуры (4) и условий (87)

при 
Доказательство теоремы XII основано на использовании теоремы III § 3 этой главы.
Рассмотрим множество  точек у таких, что
точек у таких, что

Это множество не пусто по определению точной нижней грани: 
Расстояние  точки
точки  до множества Г» определим как:
до множества Г» определим как:

Очевидно, число  существует для любого
существует для любого  и любого
и любого  такого, что
такого, что  так как
так как

при любом 
Ниже будет показано, что для любого фиксированного  последовательности
последовательности

в силу рекуррентной процедуры (4) и условий (87) удовлетворяют условиям теоремы III, если только выполнены условия теоремы XII. Поэтому в силу теоремы III при 

Кроме того, далее доказывается, что в условиях теоремы XII последовательность  ограничена почти наверное.
ограничена почти наверное.
Используя неравенство (113), положив в нем  и взяв в качестве
и взяв в качестве  точку
точку  например, такую, что
например, такую, что  получим
получим

Отсюда в силу (119) при ограниченности  следует, что
следует, что

а поскольку  произвольно, то и
произвольно, то и

Таким образом, для доказательства теоремы XII достаточно установить следующие факты:
1. Последовательности функций (118) удовлетворяют условиям теоремы III; 2. Последовательность  ограничена почти наверное.
ограничена почти наверное.
Проверим сначала выполнение условий теоремы III. Займемся проверкой первого условия этой теоремы. Для произвольной точки  имеем в силу процедуры (4):
имеем в силу процедуры (4):

Переходя здесь к условным математическим ожиданиям и используя затем (116), получим неравенство

Используя определение (117), можно написать очевидное неравенство

так что из (120) следует

Рассмотрим точную нижнюю грань

и последовательность  такую, что
такую, что

Если  то можно положить
то можно положить 
так что

Если же  то, учитывая неравенство (113) (положив в нем
то, учитывая неравенство (113) (положив в нем  и тот факт, что
и тот факт, что  и поэтому
и поэтому  , получим
, получим

Объединяя соотношения (123) и (124) для любого  имеем
имеем

Воспользовавшись неравенствами (121) и (125), после простых преобразований получим для любого 

При выводе (126) из (121) мы воспользовались очевидным неравенством

Переходя в (126) к пределу при  и учитывая соотношения (122), получаем
и учитывая соотношения (122), получаем

или, вспоминая обозначения (118),

которое совместно с условиями (87) гарантирует выполнение условия 1° теоремы III, начиная с некоторого 
Перейдем к проверке условия 2° теоремы III. С этой целью рассмотрим множество  и неравенство (127), заменив в нем
и неравенство (127), заменив в нем  на
на  и усилив его при достаточно больших
и усилив его при достаточно больших  за счет отбрасывания неположительного второго
за счет отбрасывания неположительного второго
члена в правой части:

В силу (129) и условий (87) (сходимость последовательность  удовлетворяет условиям леммы II (§ 3 этой главы), так что последовательность
удовлетворяет условиям леммы II (§ 3 этой главы), так что последовательность  сходится почти наверное к некоторой случайной величине и, следовательно, ограничена почти наверное. Поэтому для любого 8 найдется такое
сходится почти наверное к некоторой случайной величине и, следовательно, ограничена почти наверное. Поэтому для любого 8 найдется такое  что с вероятностью, большей
что с вероятностью, большей  последовательность
последовательность  удовлетворяет условию
удовлетворяет условию

Покажем, что на последовательностях, удовлетворяющих условию (130), выполнено неравенство

Действительно, пусть сначала  и удовлетворяет условию (130). Рассмотрим в этом случае последовательность
и удовлетворяет условию (130). Рассмотрим в этом случае последовательность  такую,
такую, 

Для каждого  рассмотрим отрезок
рассмотрим отрезок

и функцию

Функция  непрерывна в силу определения (108), причем
непрерывна в силу определения (108), причем

Рассмотрим такое  что
что

и точку

так что в силу (134)

Из (135) следует, что

и, поскольку  (в силу (136)),
(в силу (136)),  (в силу (135)), то
(в силу (135)), то

В силу выпуклости функции  имеем
имеем

Используя теперь соотношения (133), (134) и (137), получим

Переходя в неравенстве (138) к пределу при  учитывая при этом соотношения (132) и (130), получим, что в случае
учитывая при этом соотношения (132) и (130), получим, что в случае 

и, следовательно, в этом случае неравенство (131) выполнено.
Если же  то выполнение неравенства (131) очевидно.
то выполнение неравенства (131) очевидно.
Таким образом, неравенство (131) установлено.
Из неравенства (131) следует, что на множестве реализаций вероятности, большей  из того, что
из того, что  следует, что и
следует, что и  В силу произвольности
В силу произвольности  это означает, что выполнено условие 2° теоремы III. Таким образом, проверка выполнения условий теоремы III завершена.
это означает, что выполнено условие 2° теоремы III. Таким образом, проверка выполнения условий теоремы III завершена.
Приступим к установлению того факта, что последовательность  ограничена почти наверное. В силу условия (116) теоремы и очевидного неравенства
ограничена почти наверное. В силу условия (116) теоремы и очевидного неравенства

имеем

Возьмем последовательность точек  и используем неравенство (113), положив в нем
и используем неравенство (113), положив в нем 

откуда

Подставляя последнее неравенство в (139), имеем квадратичное неравенство для 

Из (140) следует, что при любом 

Выбирая последовательность  такой, что
такой, что 

и переходя в (141) к пределу при  получаем
получаем

Поскольку последовательность  ограничена почти наверное (см. текст после формулы (129)), то тем самым ограничена почти наверное и последовательность
ограничена почти наверное (см. текст после формулы (129)), то тем самым ограничена почти наверное и последовательность  Это последнее замечание и исчерпывает доказательство теоремы XII.
Это последнее замечание и исчерпывает доказательство теоремы XII.
Заметим, что в условиях теоремы XII не требуется, чтобы точная нижняя грань  значений функционала
значений функционала  достигалась при каких-либо значениях у. Если же, однако, точная нижняя грань
достигалась при каких-либо значениях у. Если же, однако, точная нижняя грань  и достигается на некоторых точках у, образующих множество У, то теорема XII не утверждает, что последовательность
и достигается на некоторых точках у, образующих множество У, то теорема XII не утверждает, что последовательность  сходится к нулю. Условия, при которых, наряду со
сходится к нулю. Условия, при которых, наряду со
сходимостью  к точной нижней грани утверждается сходимостью к нулю
к точной нижней грани утверждается сходимостью к нулю  , даются теоремой XIII.
, даются теоремой XIII.
Теорема XIII. Пусть  -конечномерный вектор, и в рекуррентных соотношениях (4) вектор
-конечномерный вектор, и в рекуррентных соотношениях (4) вектор  таков, что функция
таков, что функция

монотонна, а интеграл  не зависит от пути. Пусть, далее,
не зависит от пути. Пусть, далее,

существует множество  такое, что
такое, что

и

где  константы. Тогда в силу рекуррентной процедуры (4) и условий (87) при
константы. Тогда в силу рекуррентной процедуры (4) и условий (87) при 

Прежде чем перейти к доказательству теоремы XIII, сделаем следующие два замечания.
Замечание 1. Условие (116) предыдущей теоремы XII более сильное, нежели условие (143) теоремы XIII. Действительно, покажем, что из неравенства (116) следует неравенство (143). С этой целью выберем произвольную точку  и используем неравенство (113), положив в нем
и используем неравенство (113), положив в нем 

Возводя это неравенство в квадрат, используя неравенство Коши — Буняковского и учитывая, что в силу (116)

получим

Из этого квадратичного неравенства следует, что

Подставляя это неравенство в (116), получаем окончательно неравенство

имеющее вид (143).
Замечание 2. Слегка изменив доказательство предыдущей теоремы XII, можно доказать, что и в бесконечномерном случае условие (116) может быть заменено более слабым условием (143), если только потребовать существования множества  на котором достигается точная нижняя грань
на котором достигается точная нижняя грань  При этом, однако, нельзя было бы гарантировать, что
При этом, однако, нельзя было бы гарантировать, что  Возможность доказательства в теореме XIII последнего факта обеспечивается требованием конечномерности вектора у.
Возможность доказательства в теореме XIII последнего факта обеспечивается требованием конечномерности вектора у.
Доказательство теоремы XIII. Доказательство основано на использовании теоремы III § 3 этой главы. Покажем, что последовательности

удовлетворяют условиям 1° и 2° теоремы III.
Проверим выполнение условия 1° теоремы III. Для каждой точки  рассмотрим точку
рассмотрим точку  такую, что
такую, что

(точка  существует, так как множество
существует, так как множество  замкнуто как множество минимумов непрерывной функции). В силу рекуррентной процедуры (4), воспользовавшись очевидным соотношением
замкнуто как множество минимумов непрерывной функции). В силу рекуррентной процедуры (4), воспользовавшись очевидным соотношением

имеем

Переходя в этом соотношении к условным математическим ожиданиям и используя неравенство (113), получим неравенство

Используя условие (143) и обозначения (144), получаем

Поскольку в силу условия (87) ряд  сходится, для завершения проверки выполнения условия 1° теоремы III остается доказать, что
сходится, для завершения проверки выполнения условия 1° теоремы III остается доказать, что

С этой целью выберем произвольную точку  и докажем сначала, что
и докажем сначала, что

Из неравенства (148) неравенство (147) будет следовать тогда в силу очевидного неравенства

Для доказательства неравенства (148) запишем в силу рекуррентной процедуры (4)

Переходя к условным математическим ожиданиям, учитывая неравенство (113) и условия (143), получим

Учитывая неравенство (149) и неотрицательность  получим
получим

Переходя теперь к безусловным математическим ожиданиям, легко убедиться, что в силу (150)

Из сходимости ряда  следует, что при любых
следует, что при любых  величины
величины  ограничены одной и той же константой. Это и гарантирует выполнение условия (148). Тем самым проверка выполнения условия 1° теоремы III завершена.
ограничены одной и той же константой. Это и гарантирует выполнение условия (148). Тем самым проверка выполнения условия 1° теоремы III завершена.
Приступим к проверке выполнения условия 2° теоремы III. С этой целью докажем сначала, что почти все реализации случайного процесса  ограничены. Действительно, обращаясь к неравенству (150) и вводя последовательность функций
ограничены. Действительно, обращаясь к неравенству (150) и вводя последовательность функций

которая является бесконечно большой, имеем в силу (150)

Используя теперь лемму II (§ 3 этой главы), убеждаемся, что почти все реализации случайного процесса  действительно ограничены. Поскольку векторы
действительно ограничены. Поскольку векторы  конечномерные, а функция
конечномерные, а функция  непрерывна, на каждой ограниченной последовательности
непрерывна, на каждой ограниченной последовательности  из того факта, что
из того факта, что  стремится к нулю, следует, что и
стремится к нулю, следует, что и  также стремится к нулю. Сопоставляя это обстоятельство с доказаной выше ограниченностью почти всех реализаций, убеждаемся в том, что условие. 2° теоремы III выполнено.
также стремится к нулю. Сопоставляя это обстоятельство с доказаной выше ограниченностью почти всех реализаций, убеждаемся в том, что условие. 2° теоремы III выполнено.
Таким образом, в силу теоремы III оказывается, что при 

Тот факт, что и  следует теперь из
следует теперь из
(153), если учесть, что функция  непрерывна, а почти все реализации конечномерного случайного процесса
непрерывна, а почти все реализации конечномерного случайного процесса  ограничены. Теорема XIII доказана.
ограничены. Теорема XIII доказана.
Обратимся теперь непосредственно к установлению условий сходимости процедуры метода потенциальных функций вида

Для установления условий сходимости процедуры (154) могут быть использованы теоремы XII и XIII. Однако при непосредственном использовании этих теорем для проверки выполнения их условий надо проделать ряд предварительных вычислений, чтобы установить факт существования минимизируемого функционала, его вид, а также вид функции 
Для того чтобы облегчить установление сходимости конкретных алгоритмов, желательно иметь критерии сходимости, задаваемые в форме требований, наложенных непосредственно на величины, входящие в рекуррентную процедуру. Условия подобного типа дает формулируемая ниже теорема XIV, доказательство которой основано на использовании теорем XII и XIII.
Теорема XIV (Б. М. Литваков [5]). Пусть в рекуррентных соотношениях  есть последовательность независимых случайных величин с одним и тем же распределением вероятностей, последовательность
есть последовательность независимых случайных величин с одним и тем же распределением вероятностей, последовательность  удовлетворяет условиям
удовлетворяет условиям

где  некоторая константа, а числовая последовательность
некоторая константа, а числовая последовательность  удовлетворяет условиям (87). Пусть, далее, вектор
удовлетворяет условиям (87). Пусть, далее, вектор  ограничен константой, не зависящей от х,
ограничен константой, не зависящей от х,

а функция  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
I°.  убывает (не обязательно строго) по и при любом х, причем для любых их и
убывает (не обязательно строго) по и при любом х, причем для любых их и  имеет место неравенство
имеет место неравенство

где константы  не зависят от х.
не зависят от х.
2°. Математическое ожидание

существует.
3°. Функция

где

ограничена снизу при 

Тогда в силу рекуррентной процедуры (154) и условий (87) при 

Если, кроме того, векторы  конечномерны, а минимум функции
конечномерны, а минимум функции  достигается на некотором множестве
достигается на некотором множестве  при
при 

Сделаем два замечания к теореме XIV.
Замечание 1. Поскольку функция

есть аппроксимирующая функция, выстраиваемая процедурой (154), функционал, минимизируемый этой процедурой, имеет в соответствии с формулой (159) вид

Разумеется, утверждение теоремы остается в силе, если к этому функционалу прибавить произвольную константу. В частности, если математическое ожидание величины  существует, т. е.
существует, т. е.

то минимизируемый функционал можно записать в виде

Тем самым при выполнении условия (161) проверка условия (160) теоремы XIV сводится к проверке ограниченности снизу функционала (162). Ограниченность же снизу функционала (162) обеспечивается, в частности, в том случае, когда функция  удовлетворяет естественному условию (см. гл. II, § 2)
удовлетворяет естественному условию (см. гл. II, § 2)

Это условие выполнено во всех конкретных алгоритмах типа (154), используемых в настоящей книге. В силу этого условия функционал (162) неотрицателен

и, следовательно, ограничен снизу.
Замечание 2. Условие (157) означает ограниченность потенциальной функции  так как (см. гл. 11)
так как (см. гл. 11)

и

так что

Прежде чем перейти непосредственно к доказательству теоремы XIV, сформулируем и докажем следующую лемму IV, устанавливающую неравенство, которое используется в доказательстве теоремы XIV.
Лемма IV. Пусть  - возрастающая (не обязательно строго) на отрезке [0, 1] функция, удовлетворяющая при любых
- возрастающая (не обязательно строго) на отрезке [0, 1] функция, удовлетворяющая при любых  условию
условию

где  некоторые константы. Тогда
некоторые константы. Тогда

где

Доказательство леммы IV. Рассмотрим вспомогательную функцию

где  определяется соотношением (165). Очевидно, что
определяется соотношением (165). Очевидно, что

В соответствии с определением функции и 

и в силу выпуклости функции 

Из (168) и (169) следует, что

функция и  является вогнутой, т. е.
является вогнутой, т. е.

что следует сразу из определения (166), если учесть, что  выпукла. Заметим, что в соответствии с определениями (165), (166) из неравенства (163) следует
выпукла. Заметим, что в соответствии с определениями (165), (166) из неравенства (163) следует

и, в частности,

Поскольку  не убывает, в силу (170) получаем из (173)
не убывает, в силу (170) получаем из (173)

и

Для доказательства утверждения (164) леммы IV рассмотрим два случая:

В случае (176) утверждение (164) верно, так как в силу (174) и (176)

а в силу (167) и (169)

Перейдем к доказательству неравенства (164) в случае (177). Рассмотрим наибольшую из двух величин I и  (если
(если  рассмотрим любую из них). Пусть, например,
рассмотрим любую из них). Пусть, например,

Тогда, очевидно,

и, поскольку  то
то

Воспользовавшись неравенством (172) и учитывая, что  получаем неравенство
получаем неравенство

или, учитывая (180), неравенство

Интегрируя это неравенство в пределах от некоторого Я до 1, получим после простых преобразований

Учитывая, что  получаем отсюда
получаем отсюда

Положим

Поскольку  (см. формулу
(см. формулу  (см. формулу (176)), то
(см. формулу (176)), то

Из (182) имеем поэтому, что при некотором 

и, следовательно, для максимального значения функции и  на отрезке [0, 1] получаем неравенство
на отрезке [0, 1] получаем неравенство

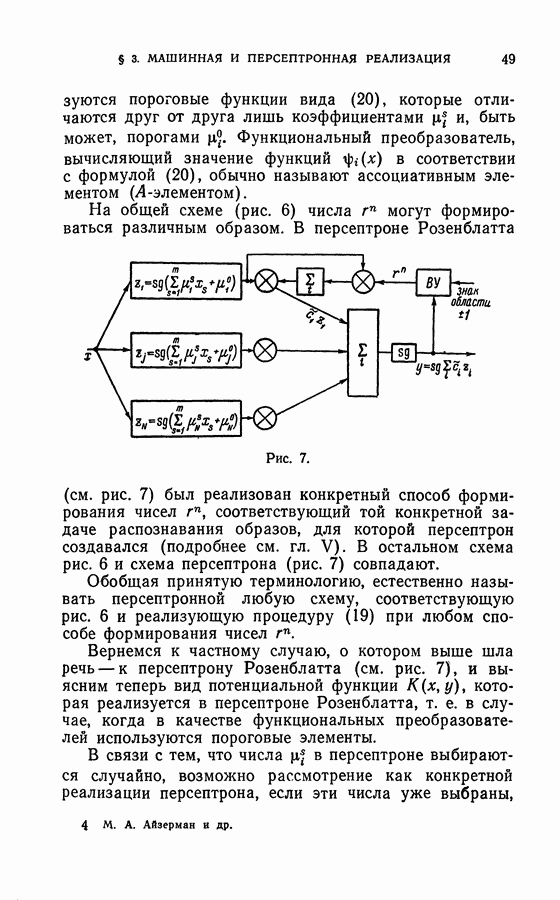
Для любой неотрицательной вогнутой функции  заданной на отрезке
заданной на отрезке  справедливо неравенство
справедливо неравенство

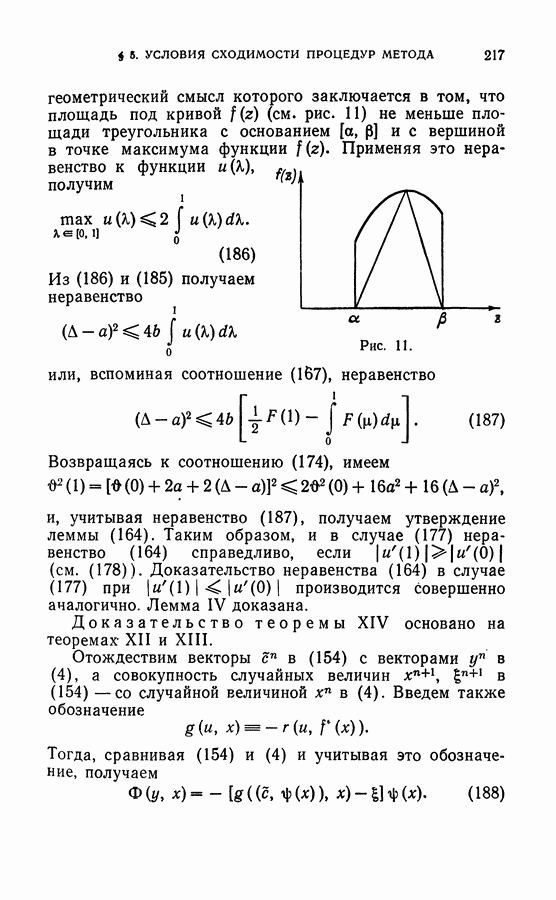
геометрический смысл которого заключается в том, что площадь под кривой  рис. 11) не меньше площади треугольника с основанием
рис. 11) не меньше площади треугольника с основанием  и с вершиной в точке максимума функции
и с вершиной в точке максимума функции  Применяя это неравенство к функции
Применяя это неравенство к функции  получим
получим


Рис. 11.
Из (186) и (185) получаем неравенство

или, вспоминая соотношение  неравенство
неравенство

Возвращаясь к соотношению (174), имеем

и, учитывая неравенство (187), получаем утверждение леммы (164). Таким образом, и в случае (177) неравенство (164) справедливо, если  (см.
(см.  Доказательство неравенства (164) в случае (177) при
Доказательство неравенства (164) в случае (177) при  производится совершенно аналогично. Лемма IV доказана.
производится совершенно аналогично. Лемма IV доказана.
Доказательство теоремы XIV основано на теоремах XII и XIII.
Отождествим векторы  в (154) с векторами
в (154) с векторами  в (4), а совокупность случайных величин
в (4), а совокупность случайных величин  в (154) - со случайной величиной
в (154) - со случайной величиной  в (4). Введем также обозначение
в (4). Введем также обозначение

Тогда, сравнивая (154) и (4) и учитывая это обозначение, получаем

В силу (188)

и, учитывая (155), получаем

Для того, чтобы убедиться, что функция  монотонна, а интеграл
монотонна, а интеграл

не зависит от пути, покажем, что подынтегральная функция  монотонна по с, а интеграл
монотонна по с, а интеграл

не зависит от пути при любом фиксированном х. Тогда в силу соотношений (189) и (190) будет следовать, что функция  и интеграл (190) обладают соответствующими свойствами. Монотонность функции
и интеграл (190) обладают соответствующими свойствами. Монотонность функции  следует из соотношения
следует из соотношения

если учесть, что функция  в силу условия 1° теоремы XIV возрастающая и поэтому для любых
в силу условия 1° теоремы XIV возрастающая и поэтому для любых 

Независимость интеграла (191) от пути следует из непосредственно проверяемого тождества 

где функция  определяется соотношением (159).
определяется соотношением (159).
Таким образом, функция

определена и в силу условия 3° теоремы XIV ограничена снизу.
Для того чтобы завершить проверку выполнения условий теоремы XII, остается показать справедливость неравенства (116). Из (188) следует, что в силу условий

Поэтому, если теперь показать, что существуют константы  такие, что
такие, что

то тем самым справедливость неравенства (116) будет доказана.
Для доказательства неравенства (195) зафиксируем некоторое с и для любого фиксированного х такого, что  рассмотрим функцию
рассмотрим функцию

где независимая переменная  принимает значения из отрезка [0, 1]. Покажем, что функция
принимает значения из отрезка [0, 1]. Покажем, что функция  удовлетворяет условиям леммы IV. Действительно,
удовлетворяет условиям леммы IV. Действительно,  -возрастающая функция, так как функция
-возрастающая функция, так как функция  есть возрастающая функция по и при любом фиксированном х. Выполнение условия (163) леммы IV гарантируется тем, что в силу условия (158) теоремы XIV
есть возрастающая функция по и при любом фиксированном х. Выполнение условия (163) леммы IV гарантируется тем, что в силу условия (158) теоремы XIV

так что в условии (163)

Поскольку функция  фигурирующая в лемме IV, в рассматриваемом случае имеет вид
фигурирующая в лемме IV, в рассматриваемом случае имеет вид

то в силу утверждения (164) леммы получим

Переходя в (198) к математическим ожиданиям по х и вспоминая соотношение (193), получим

Принимая во внимание, что

и что в силу условия 2° теоремы XIV математическое ожидание  существует, убеждаемся в справедливости неравенства (116). Тем самым доказано выполнение всех условий теоремы XII и поэтому доказано, что
существует, убеждаемся в справедливости неравенства (116). Тем самым доказано выполнение всех условий теоремы XII и поэтому доказано, что

Если теперь векторы  конечномерны, а минимум функции
конечномерны, а минимум функции  достигается на некотором множестве С, то выполнены все условия теоремы XIII. Условие (143)
достигается на некотором множестве С, то выполнены все условия теоремы XIII. Условие (143)
теоремы XIII следует, как показано в замечании 1 к теореме XIII, из условия (116). В силу теоремы XIII выполняется соотношение  Теорема XIV доказана.
Теорема XIV доказана.
В случае, когда функция  ограничена некоторой константой (а такой случай реализуется в некоторых алгоритмах, рассмотренных в главах VI, VII), доказательство утверждений теоремы XIV может быть существенно упрощено, так как при этом не возникает необходимости в применении леммы IV, и проверка выполнения условий теорем XII и XIII производится непосредственно. В этом случае существование математического ожидания
ограничена некоторой константой (а такой случай реализуется в некоторых алгоритмах, рассмотренных в главах VI, VII), доказательство утверждений теоремы XIV может быть существенно упрощено, так как при этом не возникает необходимости в применении леммы IV, и проверка выполнения условий теорем XII и XIII производится непосредственно. В этом случае существование математического ожидания  очевидно, а условие (157) может быть заменено более слабым условием
очевидно, а условие (157) может быть заменено более слабым условием

Рассмотрим теперь вытекающие из теоремы XIV следствия, которые могут быть использованы при решении задач о приближении и восстановлении функций  с помощью процедуры (154).
с помощью процедуры (154).
В. соответствии с замечанием 1 к теореме XIV, если выполнены условия

и

то функционал (162) существует, если существует функция  и неотрицателен. Поскольку при этом
и неотрицателен. Поскольку при этом  то функционал (162) принадлежит к тому классу функционалов, которые обсуждались в § 4 главы II в связи с определением понятий приближения и восстановления функции
то функционал (162) принадлежит к тому классу функционалов, которые обсуждались в § 4 главы II в связи с определением понятий приближения и восстановления функции  В силу теоремы XIV значения
В силу теоремы XIV значения  этого функционала стремятся к точной нижней грани функции
этого функционала стремятся к точной нижней грани функции  при условии
при условии  Вспоминая определение класса функций
Вспоминая определение класса функций  (см. § 4 гл. II), замечаем поэтому, что теорема XIV утверждает, по существу,
(см. § 4 гл. II), замечаем поэтому, что теорема XIV утверждает, по существу,
что значения функционала (162) стремятся почти наверное к точной нижней грани функционала на функциях из

Однако это утверждение еще не означает, что процедура (154) решает задачу приближения или восстановления функции  в том смысле, который был придан этим терминам в § 4 главы II. Действительно, для решения задачи приближения необходимого определению, стремление значений
в том смысле, который был придан этим терминам в § 4 главы II. Действительно, для решения задачи приближения необходимого определению, стремление значений  функционала (162) к точной нижней грани не на классе функций
функционала (162) к точной нижней грани не на классе функций  а на классе
а на классе  Для решения же задачи восстановления нужно убедиться, что
Для решения же задачи восстановления нужно убедиться, что

Ниже будет доказана лемма V, из которой следует, что при выполнении условий теоремы XIV и условия (201) функционал (162) определен для любой функции  и его точные нижние грани на функциях из
и его точные нижние грани на функциях из  и совпадают:
и совпадают:

Поэтому из утверждения (204) следует, что

т. е. что процедура (154) при выполнении условий теоремы XIV и условия (201) решает задачу приближения функции 
Рассмотрим теперь условие, при котором процедура (154) гарантирует не только приближение, но и восстановление функции  Пусть
Пусть  Поскольку функционал (162) неотрицателен и вместе с тем
Поскольку функционал (162) неотрицателен и вместе с тем

то при 

Тем самым при  соотношение (205) гарантирует, что
соотношение (205) гарантирует, что

т. е. что процедура (154) решает задачу восстановления функции 
Таким образом, мы приходим к следующей теореме, устанавливающей условия, при которых процедура (154) решает задачи приближения и восстановления функции 
Теорема XV. Пусть выполнены условия теоремы
XIV и, кроме того, условия:

Тогда в силу рекуррентной процедуры (154) иусловия (87) при 

 процедура (154) приближает функцию
процедура (154) приближает функцию 
Если же дополнительно предположить, что  то при
то при 

т. е. процедура (154) восстанавливает функцию 
Замечаниектеореме XV. Поскольку условия 1° и 2° теоремы XV гарантируют ограниченность снизу функции  фигурирующей в теореме XIV (см. замечание 1 к этой теореме), то при использовании теоремы
фигурирующей в теореме XIV (см. замечание 1 к этой теореме), то при использовании теоремы
XV условие 3° теоремы XIV можно не проверять.
Как следует из приведенных выше рассуждений, для доказательства теоремы XV достаточно установить лишь, что при выполнении условий теоремы XIV и (201) имеет место соотношение (204). Этот факт непосредственно следует из леммы V, так как условия леммы всегда выполнены, если выполнены условия 1° и 2° теоремы XIV и (201).
Лемма V. Пусть в функционале (162) функция  удовлетворяет условиям:
удовлетворяет условиям:
1°. Для любых  выполняется неравенство
выполняется неравенство

где  константы, не зависящие от х.
константы, не зависящие от х.

Тогда функционал (162) существует для всех 

Доказательство леммы  Докажем сначала существование функционала (162) при
Докажем сначала существование функционала (162) при  В силу условия 3° для этого достаточно установить ограниченность величины
В силу условия 3° для этого достаточно установить ограниченность величины  при Очевидно, что
при Очевидно, что

Используя условие 1° леммы и производя затем интегрирование, получаем

Используя далее неравенство Коши — Буняковского и условие 2°, убеждаемся, что

если

что по определению имеет место при  Существование функционала (163) при доказано.
Существование функционала (163) при доказано.
Докажем теперь справедливость соотношения (204). Для этого достаточно показать, что для любой функции  и любого
и любого 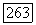 существует такая функция
существует такая функция 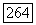
что 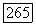 Действительно, если это будет показано, то для любой последовательности функций из
Действительно, если это будет показано, то для любой последовательности функций из 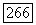 таких, что на этой последовательности функционал
таких, что на этой последовательности функционал 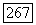 стремится к своей точной нижней грани, можно указать последовательность функций из значение функционала для которой также стремится к этой точной нижней грани.
стремится к своей точной нижней грани, можно указать последовательность функций из значение функционала для которой также стремится к этой точной нижней грани.
Пусть функция 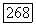 представлена рядом
представлена рядом

Рассмотрим последовательность функций

Очевидно, что 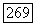 при любом
при любом 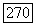 По смыслу ряда (206)
По смыслу ряда (206)

Оценим величину 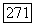 Очевидно, что
Очевидно, что

Используя условие 1° леммы и производя интегрирование, получаем

В (210) учтено, что при любых а и 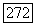

Учитывая, что 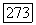 и используя неравенство Коши — Буняковского, получаем из (210)
и используя неравенство Коши — Буняковского, получаем из (210)

Вспоминая условие 2° леммы и учитывая, что 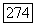 при получаем в силу (208) и (211)
при получаем в силу (208) и (211)

Отсюда следует, что всегда найдется такой номер 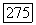 что
что

Таким образом, для любого 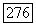 существует функция
существует функция 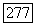 такая, что имеет место соотношение (212). Лемма доказана.
такая, что имеет место соотношение (212). Лемма доказана.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ АВТОРОВ
- Глава I. ПРОБЛЕМА ОБУЧЕНИЯ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ (СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ)
- § 1. О задаче обучения машин распознаванию образов
- § 2. Геометрическая интерпретация задачи
- § 3. Разделение сложных образов. Признаки. Лингвистический подход к задачам распознавания
- Глава II. МЕТОД ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ
- § 2. Общая рекуррентная процедура
- § 3. Машинная и персептронная реализация процедуры метода потенциальных функций
- § 4. Функционалы, экстремизируемые процедурами метода потенциальных функций
- § 5. Процедура Роббинса — Монро метода стохастической аппроксимации и процедура метода потенциальных функций
- § 6. Некоторые замечания о методе потенциальных функций
- Глава III. О ВЫБОРЕ СИСТЕМЫ ФУНКЦИЙ И ПОТЕНЦИАЛЬНОЙ ФУНКЦИИ
- § 2. О выборе вида потенциальной функции К(х,у)
- 2. Выбор потенциальной функции в евклидовом пространстве.
- 3. Выбор потенциальной функции в случае, когда пространство X — множество вершин m-мерного куба.
- § 3. О выборе потенциальной функции в симметрических пространствах
- 2. Квадратичные функционалы качества на симметрических пространствах.
- 3. Выделение классов функций одинакового качества.
- 4. Разложение функций расстояния в ряд.
- 5. Вид потенциальной функции в симметрическом пространстве.
- 6. О выборе потенциальной функции в пространстве вершин m-мерного куба.
- Глава IV. СХОДИМОСТЬ ОСНОВНОЙ ПРОЦЕДУРЫ МЕТОДА ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ
- § 2. Особенности исследования случайных процессов, порождаемых методом потенциальных функций
- § 3. Основные теоремы о сходимости
- § 4. Условия сходимости процедуры Роббинса — Монро метода стохастической аппроксимации
- § 5. Условия сходимости процедур метода потенциальных функций
- § 6. Оценка скорости сходимости
- Глава V. ПРИМЕНЕНИЕ МЕТОДА ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ К ЗАДАЧЕ ОБ ОБУЧЕНИИ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ (ДЕТЕРМИНИСТСКАЯ ПОСТАНОВКА ЗАДАЧИ)
- § 2. Алгоритм, решающий задачу
- § 3. Два метода реализации алгоритма
- § 4. Экстремизируемый функционал
- § 5. Сходимость процедуры
- § 6. Условия остановки алгоритма
- Глава VI. ПРИМЕНЕНИЕ МЕТОДА ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ К ЗАДАЧЕ АППРОКСИМАЦИИ ФУНКЦИИ ПО ЕЕ ЗНАЧЕНИЯМ В СЛУЧАЙНО ВЫБРАННЫХ ТОЧКАХ
- § 1. Аппроксимация функции при отсутствии помех
- 2. Алгоритмы аппроксимации функции при отсутствии помех.
- § 2. Аппроксимация функции при наличии помех
- § 3. Сходимость алгоритмов
- § 4. Оценка скорости сходимости алгоритмов
- Глава VII. ВЕРОЯТНОСТНАЯ ЗАДАЧА ОБ ОБУЧЕНИИ МАШИН РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Аппроксимация плотности вероятности р(х)
- § 3. Описание алгоритмов непосредственной аппроксимации степени достоверности.
- § 4. Минимизируемые функционалы и сходимость второго и третьего алгоритмов
- § 5. Сравнение второго и третьего алгоритмов с другими алгоритмами метода потенциальных функций
- § 6. Оценка скорости сходимости
- Глава VIII. ОБУЧЕНИЕ БЕЗ УЧИТЕЛЯ
- § 2. Связь между видом экстремизирующей разделяющей функции и видом функционала
- § 3. Применение метода потенциальных функций к задаче обучения машины без учителя
- 2. Описание алгоритма метода потенциальных функций для восстановления экстремизирующей функции.
- § 4. Условия сходимости алгоритма
- ЛИТЕРАТУРА