| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
Для реализации детерминированной процедуры маршрутизации программное обеспечение узлов коммутации должно включать программу вычисления вектора кратчайших маршрутов. Наиболее совершенными методами решения этой задачи являются методы Флойда и Дийкстры, базирующиеся на принципе оптимальности.
Метод Флойда основан на двух понятиях [35]: базисной липни связи и тернарной операции.
Линия связи  называется базисной, если она является кратчайшим маршрутом из узла
называется базисной, если она является кратчайшим маршрутом из узла  в узел у. Заметим, что дерево кратчайших маршрутов состоит только из базисных линий связи.
в узел у. Заметим, что дерево кратчайших маршрутов состоит только из базисных линий связи.
Метод обеспечивает выявление базисных линий сети путем сравнения веса каждой линии связи  с весами всех маршрутов между узлами
с весами всех маршрутов между узлами  Если сеть не содержит маршрутов с весом менее то линия
Если сеть не содержит маршрутов с весом менее то линия  является базисной.
является базисной.
В процессе поиска базисных линий связи для всех  используются так называемые тернарные операции над элементами матрицы весов
используются так называемые тернарные операции над элементами матрицы весов

При этом вес каждой линии связи  сравнивается с длиной маршрута из узла
сравнивается с длиной маршрута из узла  в узел
в узел  проходящего через
проходящего через  Если
Если  то в качестве элемента матрицы весов заносится
то в качестве элемента матрицы весов заносится 
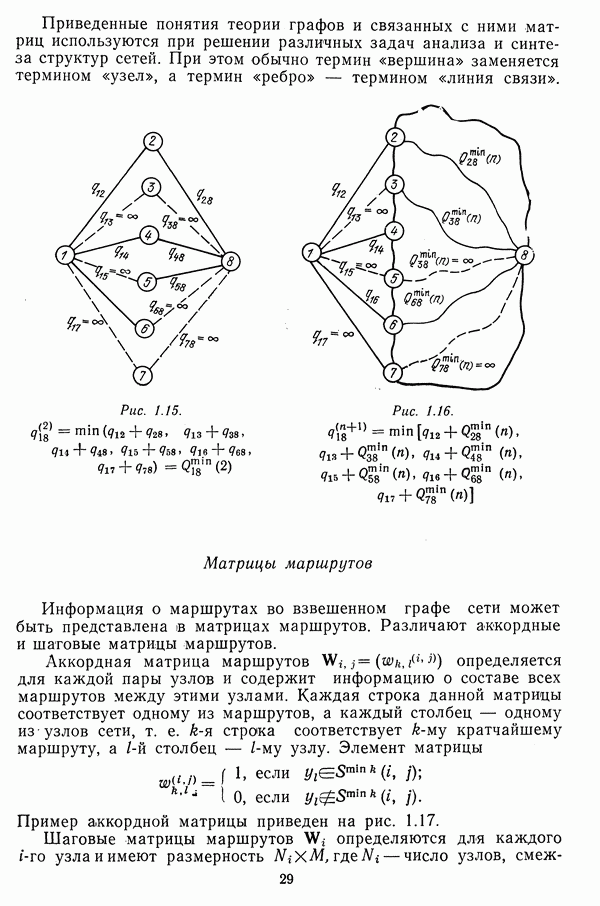
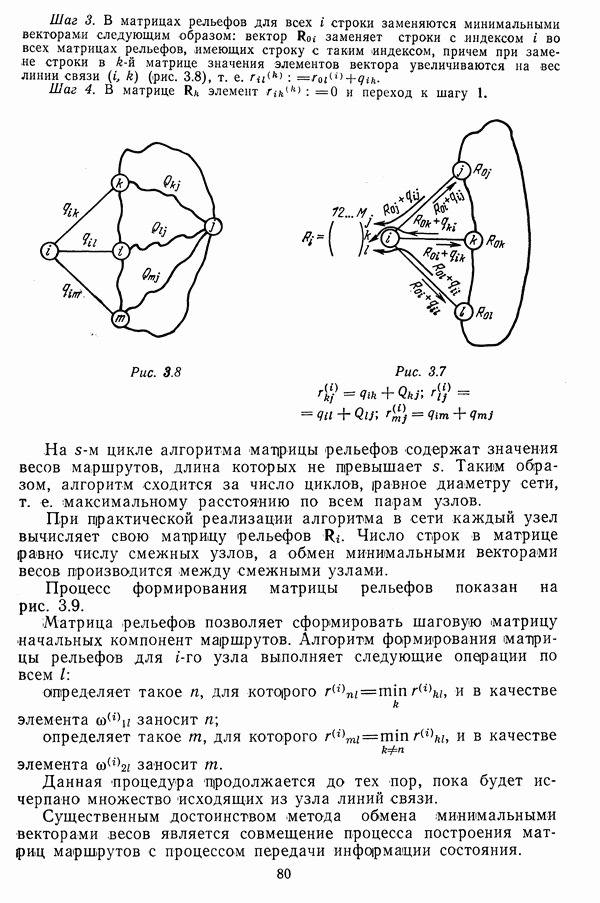
При выполнении тернарных операций по всем парам узлов полученные значения  будут весами кратчайших маршрутов между соответствующими узлами. Доказательство этого утверждения приведено в [35]. Смысл тернарных операций пояснен на рис. 3.1.
будут весами кратчайших маршрутов между соответствующими узлами. Доказательство этого утверждения приведено в [35]. Смысл тернарных операций пояснен на рис. 3.1.

Рис. 3.1.

Векторы кратчайших маршрутов заполняются в процессе вычислений. При этом одновременно можно строить векторы для всех узлов сети. Вначале все элементы векторов полагаются нулевыми для несмежных узлов  и у а на позициях, соответствующих смежным узлам
и у а на позициях, соответствующих смежным узлам  заносятся
заносятся  Далее при выполнении каждой тернарной операции осуществляется корректирование следующим образом:
Далее при выполнении каждой тернарной операции осуществляется корректирование следующим образом:

Таким образом, алгоритм, реализующий метод Флойда, состоит в выполнении для всех пар узлов  цикла, в каждом из которых поочередно осуществляется сначала операция (3.1), а затем (3.2). Результатом является совокупность векторов начальных компонент кратчайших маршрутов для всех М узлов сети. Общее число требуемых операций составляет
цикла, в каждом из которых поочередно осуществляется сначала операция (3.1), а затем (3.2). Результатом является совокупность векторов начальных компонент кратчайших маршрутов для всех М узлов сети. Общее число требуемых операций составляет 
Достоинства данного метода — простота реализующего алгоритма и возможность получения маршрутной информации сразу
для всех узлов сети. Последнее делает целесообразным его использование при централизованных структурах управления внутренними потоками. Для децентрализованного управления, когда каждый узел строит маршруты только от себя, метод Флойда неэкономичен.
Метод Дийкстры [35] состоит в поэтапном наращивании дерева кратчайших маршрутов от исходного узла. При этом необходимо, чтобы после добавления на каждом этапе линии связи и узла вновь образуемый кратчайший маршрут был минимально возможным по всем оконечным узлам, еще не вошедшим в дерево. В процессе построения дерева кратчайших маршрутов вычисляются «векторы весов маршрутов и корректируются векторы начальных Компонент кратчайших маршрутов.
Введем ряд понятий и обозначений, используемых при описании алгоритма, реализующего метод Дийкстры.
Некоторую часть дерева кратчайших маршрутов  будем называть текущим деревом. Последнее включает
будем называть текущим деревом. Последнее включает  линий связи. Узлы, не входящие в это дерево,
линий связи. Узлы, не входящие в это дерево,  образуют множество соседних узлов
образуют множество соседних узлов 
Как и ранее,  вес линии связи из
вес линии связи из  — элемент шагового вектора начальных компонент маршрутов (номер первого промежуточного узла в кратчайшем маршруте из
— элемент шагового вектора начальных компонент маршрутов (номер первого промежуточного узла в кратчайшем маршруте из  — вес кратчайшего маршрута между
— вес кратчайшего маршрута между  все узлы и линии связи которого принадлежат текущему дереву;
все узлы и линии связи которого принадлежат текущему дереву;  — вес кратчайшего маршрута между
— вес кратчайшего маршрута между  все узлы и линии связи которого принадлежат текущему дереву, кроме одного узла у .и одной линии связи
все узлы и линии связи которого принадлежат текущему дереву, кроме одного узла у .и одной линии связи  которые дереву не принадлежат.
которые дереву не принадлежат.
Теперь рассмотрим сам алгоритм для некоторого узла  в сети с
в сети с  линиями связи и М узлами.
линиями связи и М узлами.
Шаг 0. Ввод исходных данных: номер исходного узла  матрица весов
матрица весов 
Шаг 1. Присвоение начальных значений переменным и массивам:

Шаг 2. Находится такая линия связи  не принадлежащая текущему дереву, которая позволяет построить, используя уже имеющееся дерево
не принадлежащая текущему дереву, которая позволяет построить, используя уже имеющееся дерево  самый короткий маршрут от узла
самый короткий маршрут от узла  к любому из соседних узлов
к любому из соседних узлов  Иначе, ищется такой узел
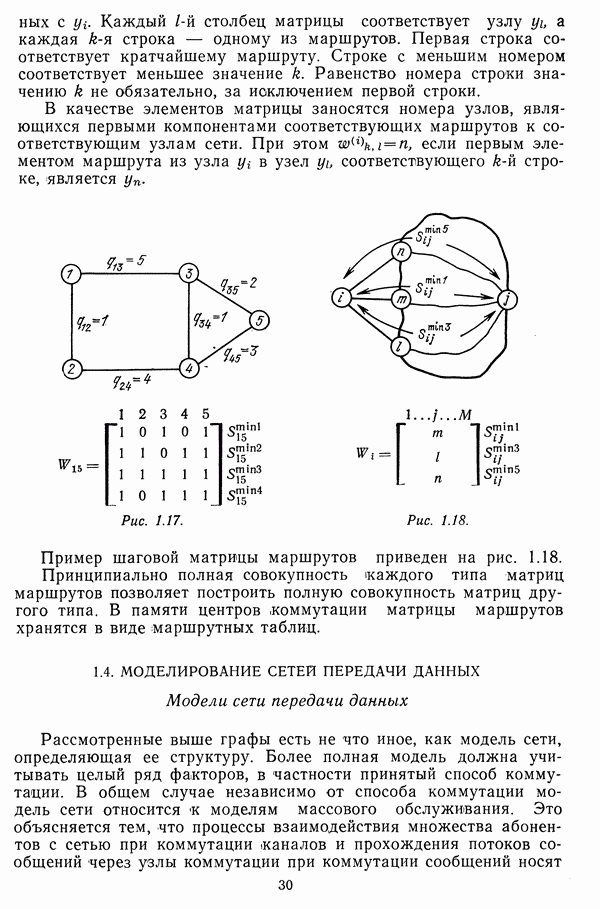
Иначе, ищется такой узел  для которого выполняется условие (рис. 3.2)
для которого выполняется условие (рис. 3.2) 
В соответствии с определением  Поэтому в состав текущего дерева на данном этапе включаются линия связи
Поэтому в состав текущего дерева на данном этапе включаются линия связи  и узел
и узел  Общее число линий связи в текущем дереве при этом увеличивается на единицу:
Общее число линий связи в текущем дереве при этом увеличивается на единицу: 
Узел  исключается из множества
исключается из множества 
Далее производится перерасчет значения  с учетом изменений в дереве:
с учетом изменений в дереве: 
Шаг 3. Проверяется окончание процесса построения дерева кратчайших маршрутов.
Так как любое остовное дерево графа с М узлами имеет  линию связи, то проверяется условие
линию связи, то проверяется условие 
Если это условие выполняется, то процесс заканчивается и следует переход к шагу 5, иначе переход к шагу 4.
Шаг 4. Осуществляется перерасчет значений  для всех узлов При этом для каждого узла с сравнивается имеющееся значение
для всех узлов При этом для каждого узла с сравнивается имеющееся значение  со значением, которое получается, если в качестве участка маршрута, принадлежащего дереву, использовать кратчайший маршрут, вес которого
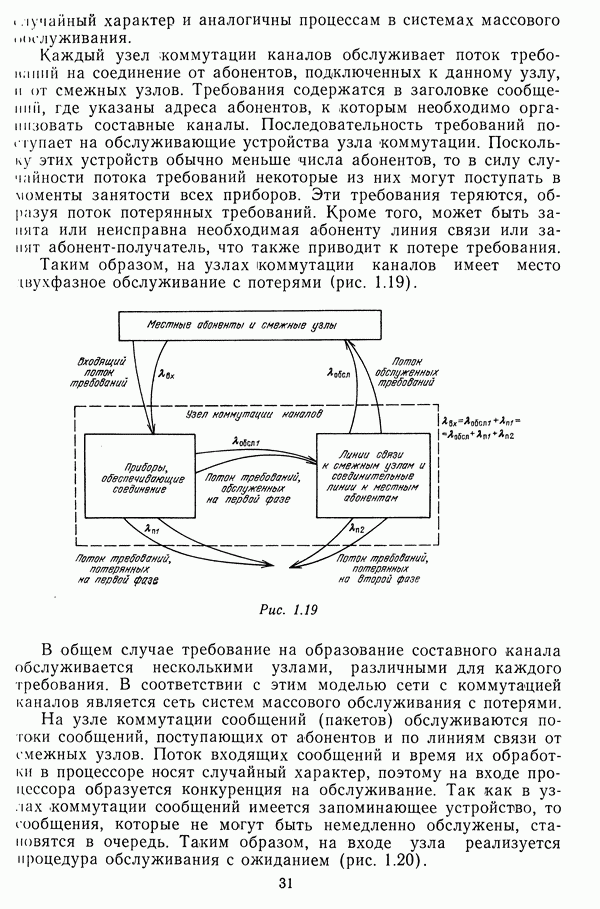
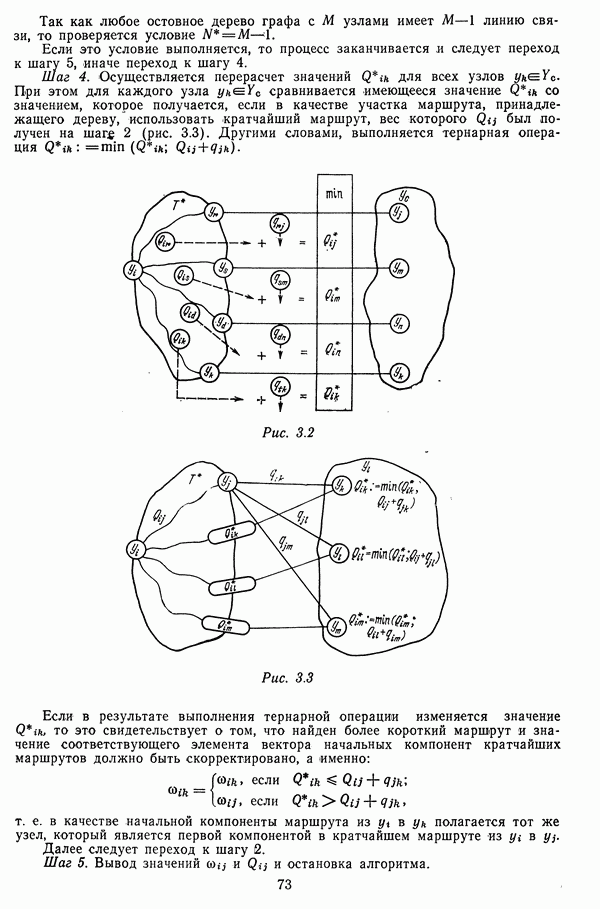
со значением, которое получается, если в качестве участка маршрута, принадлежащего дереву, использовать кратчайший маршрут, вес которого  был получен на шаг? 2 (рис. 3.3). Другими словами, выполняется тернарная операция
был получен на шаг? 2 (рис. 3.3). Другими словами, выполняется тернарная операция 

Рис. 3.2

Рис. 3.3
Если в результате выполнения тернарной операции изменяется значение  то это свидетельствует о том, что найден более короткий маршрут и значение соответствующего элемента вектора начальных компонент кратчайших маршрутов должно быть скорректировано, а именно:
то это свидетельствует о том, что найден более короткий маршрут и значение соответствующего элемента вектора начальных компонент кратчайших маршрутов должно быть скорректировано, а именно:

т. e. в качестве начальной компоненты маршрута из  полагается тот же узел, который является первой компонентой в кратчайшем маршруте из
полагается тот же узел, который является первой компонентой в кратчайшем маршруте из  Далее следует переход к шагу 2.
Далее следует переход к шагу 2.
Шаг 5. Вывод значений  и остановка алгоритма.
и остановка алгоритма.
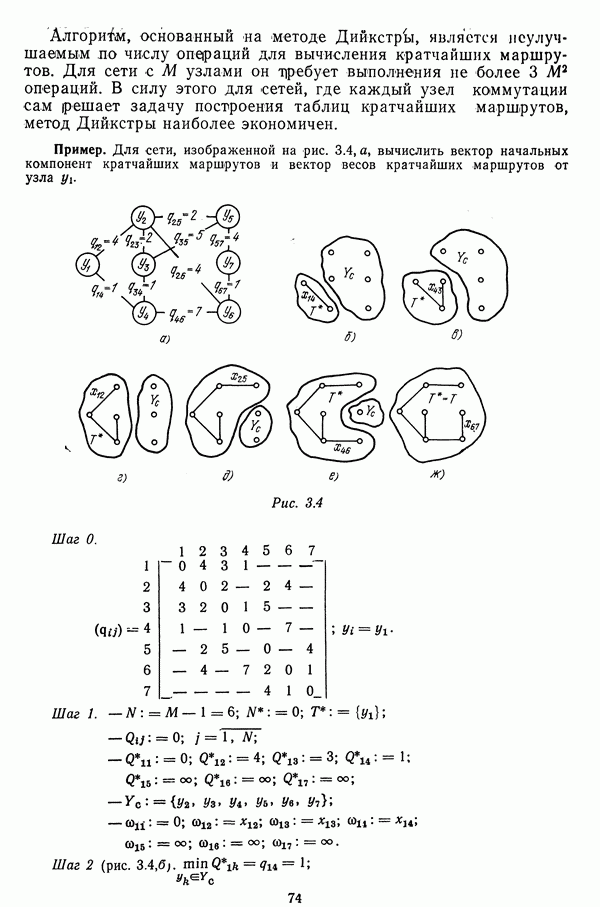
Алгоритм, основанный на методе Дийкстрк, является неулучшаемым по числу операций для вычисления кратчайших маршрутов. Для сети с М узлами он требует выполнения не более  операций. В силу этого для сетей, где каждый узел коммутации сам решает задачу построения таблиц кратчайших маршрутов, метод Дийкстры наиболее экономичен.
операций. В силу этого для сетей, где каждый узел коммутации сам решает задачу построения таблиц кратчайших маршрутов, метод Дийкстры наиболее экономичен.
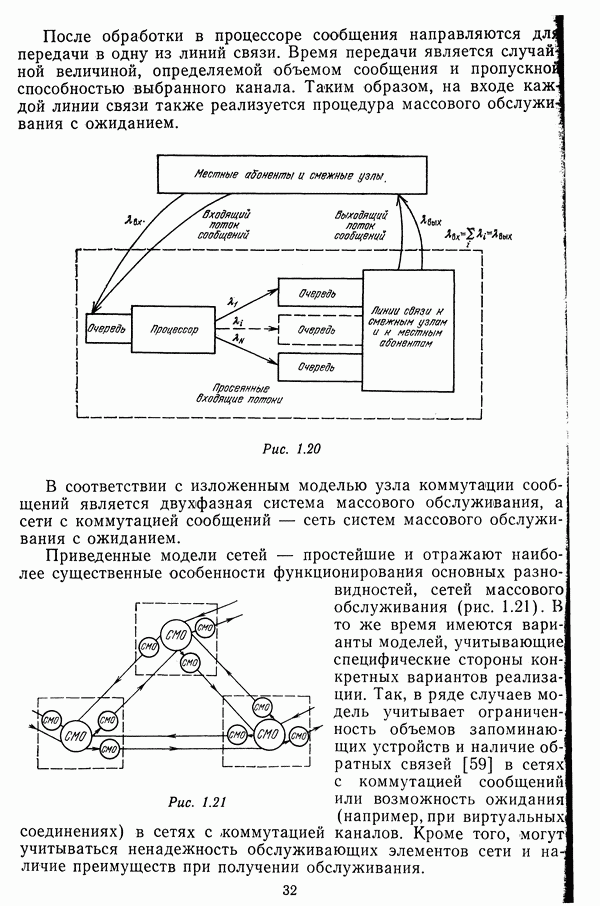
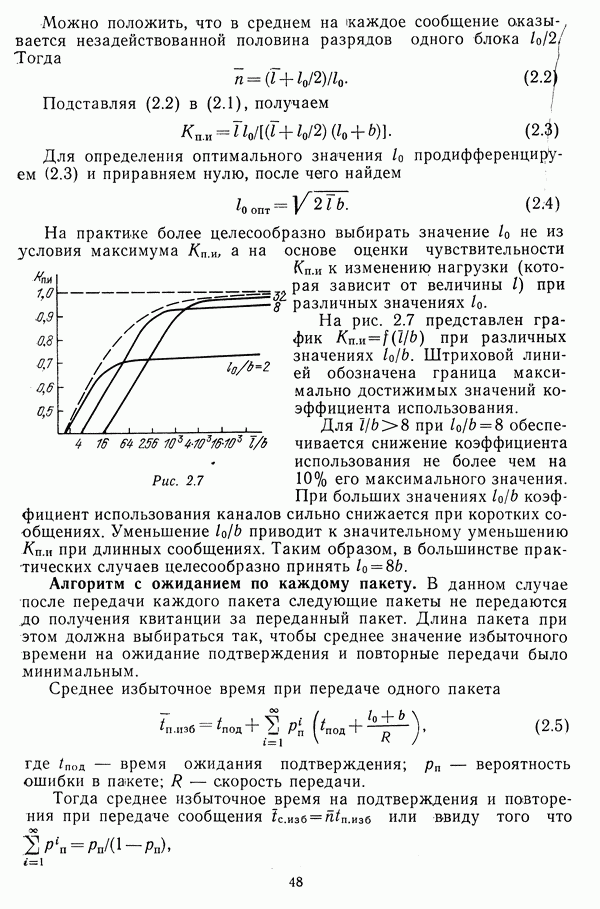
Пример. Для сети, изображенной на рис. 3.4, а, вычислить вектор начальных компонент кратчайших маршрутов и вектор весов кратчайших маршрутов от узла 

Рис. 3.4


(кликните для просмотра скана)

Переход к шагу 2.
Шаг 2 (рис. 3.4,д). 

Шаг 3. Так как  переход к шагу 4.
переход к шагу 4.

Переход к шагу 2.
Шаг 2 (рис. 3.4,е). 

Шаг 3 Так как  переход к шагу 4.
переход к шагу 4.

Переход к шагу 2.
Шаг 2 (рис. 3.4,ж), 

Шаг 3. Так как  то переход к шагу 5.
то переход к шагу 5.

Конец.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1 ОБЩАЯ ХАРАКТЕРИСТИКА СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 1.1. СЕТЬ СВЯЗИ КАК ПОДСИСТЕМА СИСТЕМЫ УПРАВЛЕНИЯ
- 1.2. ПРИНЦИПЫ ПОСТРОЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 1.3. ПРЕДСТАВЛЕНИЕ СТРУКТУР СЕТЕЙ
- Кратчайшие маршруты во взвешенных графах
- Матрицы, определяющие структуру сетей
- Матрицы маршрутов
- 1.4. МОДЕЛИРОВАНИЕ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- Математические модели, используемые при расчете сетей
- Потоки в сетях передачи данных
- ГЛАВА 2. ПРИНЦИПЫ ФУНКЦИОНИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.1. СТРУКТУРА ФУНКЦИОНАЛЬНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.2. ФОРМАЛИЗАЦИЯ СООБЩЕНИИ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 2.3. АДРЕСОВАНИЕ СООБЩЕНИЙ
- 2.4. ПРОЦЕДУРЫ ВЫБОРА МАРШРУТОВ
- 2.5. РЕГУЛИРОВАНИЕ ПОТОКОВ СООБЩЕНИЙ ПО ПРИОРИТЕТАМ
- 2.6. УПРАВЛЕНИЕ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- Глава 3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ МАРШРУТИЗАЦИИ И УПРАВЛЕНИЯ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 3.2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПОИСКОВЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.4. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КВАЗИСЛУЧАИНЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.5. ФИЗИЧЕСКИЕ ВЕРСИИ ВЕСОВ ЭЛЕМЕНТОВ СЕТИ
- 3.6. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УПРАВЛЕНИЯ ВНЕШНИМИ ПОТОКАМИ СООБЩЕНИЙ
- Глава 4. ВОПРОСЫ ПРОЕКТИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 4.1. ЗАДАЧИ СИСТЕМНОГО ПРОЕКТИРОВАНИЯ СЕТЕЙ
- 4.2. РАЗМЕЩЕНИЕ УЗЛОВ КОММУТАЦИИ
- Оптимизация числа узлов и их размещения при независимом положении абонентов
- Размещение узлов для связи с мобильными абонентами
- Размещение центра управления сетью
- 4.3. СИНТЕЗ СТРУКТУРЫ СЕТИ
- Синтез структуры сети минимальной стоимости при заданной связности
- 4.4. РАСЧЕТ МОЩНОСТИ ЛИНИИ СВЯЗИ СЕТИ
- Оптимизация мощности линий связи при произвольном виде функций затрат
- Методика выбора каналов передачи данных для линий связи с заданной мощностью
- 4.5. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ЖИВУЧЕСТИ ЭЛЕМЕНТОВ СЕТИ
- 4.6. ВЫБОР ПАРАМЕТРОВ НАДЕЖНОСТИ ЭЛЕМЕНТОВ СЕТИ
- Методы вычисления вероятности связности сети
- Выбор параметров надежности центров коммутации
- Аналитическая оптимизация внутренних показателей надежности элементов сети
- Оптимизация внутренних показателей надежности при произвольном виде функций затрат
- СПИСОК ЛИТЕРАТУРЫ