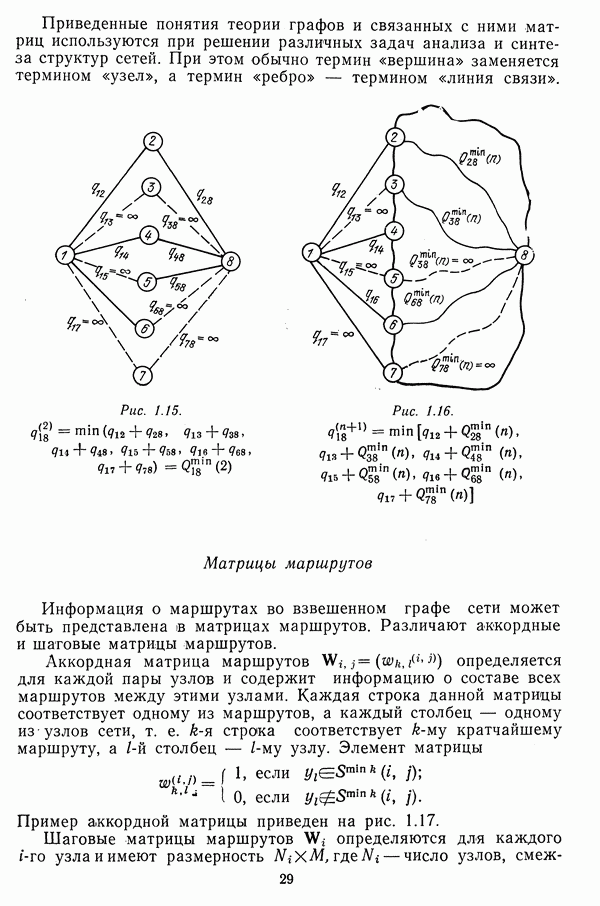
Кратчайшие маршруты во взвешенных графах

Если каждому ребру графа поставить в соответствие некоторое, в общем случае произвольное, число — вес, то такой граф будет взвешенным.

В приложении к сетям в качестве весов ребер обычно используются неотрицательные числа, соответствующие значениям какого-либо из физических параметров. При этом может не выполняться неравенство треугольника

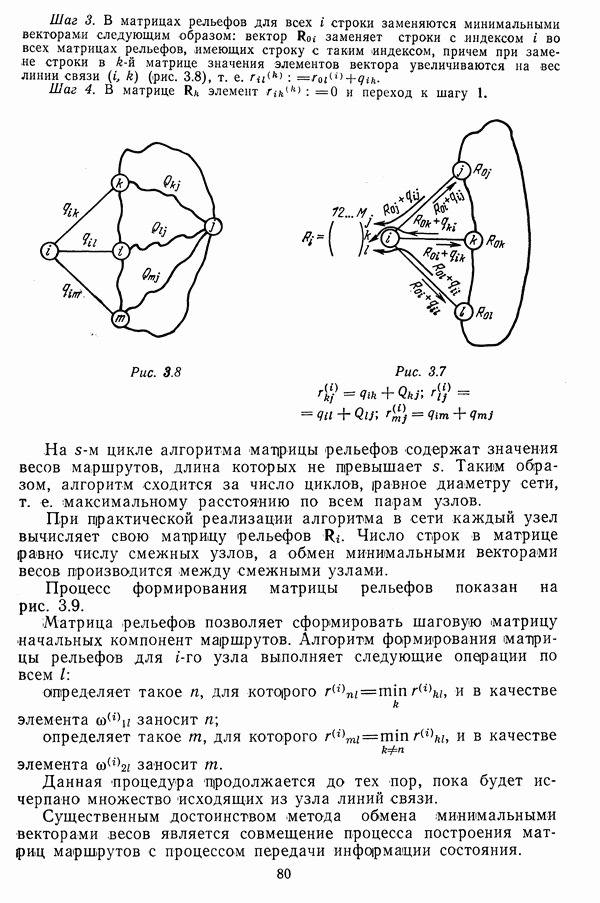
В помеченном графе каждый маршрут имеет вес

Маршрут, имеющий минимальный вес среди всех маршрутов для некоторой пары вершин и у и называется кратчайшим. Такой маршрут будем обозначать а соответствующий ему вес — При соответствующей интерпретации кратчайший маршрут будет физически кратчайшим. В общем случае понятие кратчайшего маршрута, как и понятие его веса, является условным. Для кратчайших маршрутов в теории сетей формируются два важных положения, которые представим в виде теорем.

Теорема (принцип оптимальности) [35]. Если кратчайший маршрут из с весом включает вершину то каждый из двух участков маршрута: свесом и от до с весом — также будет кратчайшим между соответствующими вершинами, т. е. . При этом где .

Доказательство [40]. Проведем его от противного для

Пусть Тогда должен существовать некоторый маршрут вес которого . В этом случае что невозможно, так как по условию .

Таким образом, Основным следствием данной теоремы является то, что если определен кратчайший маршрут между некоторой парой вершин, то при этом оказываются известными кратчайшие маршруты между всеми промежуточными вершинами.

Теорема. Граф, включающий только кратчайшие маршруты между вершиной и остальными вершинами сети, является остовным деревом.

Доказательство. В соответствии с одним из определений остовным деревом является граф, для которого удаление любого ребра приводит к несвязному графу.

Доказательство проведем от противного. Пусть граф, состоящий только из кратчайших маршрутов, не является остовным деревом. Тогда из него может быть удалено некоторое ребро

Поскольку исходный граф состоит только из кратчайших маршрутов, то удаленное ребро должно принадлежать хотя бы одному кратчайшему маршруту, например

В соответствии с исходными предпосылками рассматриваемый граф не имеет других маршрутов между вершинами и а операция удаления ребра приводит к разрыву этого маршрута, т. е. вершины а следовательно, и граф оказываются несвязанными. Таким образом, из графа, образованного только кратчайшими маршрутами, нельзя удалить ни одного ребра, не нарушив связности. Таким графом, в соответствии с определением, является остовнос дерево, что и требовалось доказать.

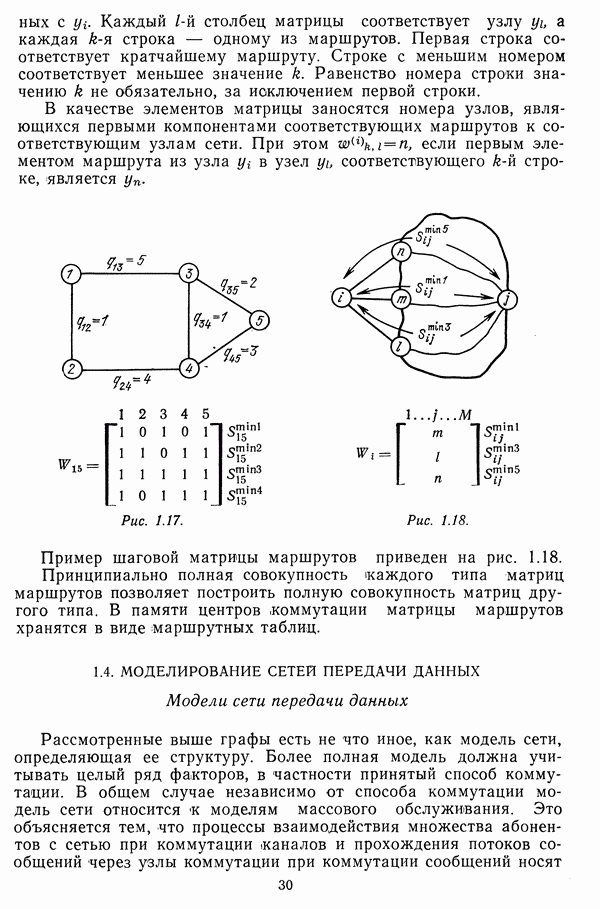
Если во взвешенном графе упорядочить множество маршрутов для некоторой пары вершин в соответствии с их весом, то маршрут в этой последовательности будет кратчайшим маршрутом и обозначается Значение К каждого маршрута зависит от параметров, используемых в качестве весов ребер.