| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.5. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ЖИВУЧЕСТИ ЭЛЕМЕНТОВ СЕТИ
Постановка задачи оптимизации параметров живучести сети
В данном параграфе под живучестью будем понимать способность сети обеспечить передачу одиночного сообщения между определенным множеством абонентов после внешнего воздействия с целью нарушения связности. Надежностью сети является ее способность обеспечить установленные значения вероятностно-временных характеристик при передаче заданных потоков сообщений с учетом отказов и восстановлений узлов и линий связи.
В то время, как надежность сети полностью определяется безусловной надежностью ее элементов, живучесть зависит от соотношения ресурсов воздействия и защищенности элементов сети.
Как известно, живучесть сети обеспечивается ее структурной избыточностью и защищенностью элементов.
Пусть имеются две противоборствующие стороны — А и В. Положим, что структура сети, создаваемой стороной А, определена на предварительном этапе проектирования по заданным детерминированным параметрам.
Требования по живучести заданы одним из следующих способов:
1) по допустимой вероятности нарушения связности сети;
2) по допустимой вероятности нарушения связности некоторого узла более чем с заданным числом узлов;
3) по среднему числу узлов, связь (Которых с определенным узлом может быть потеряна.
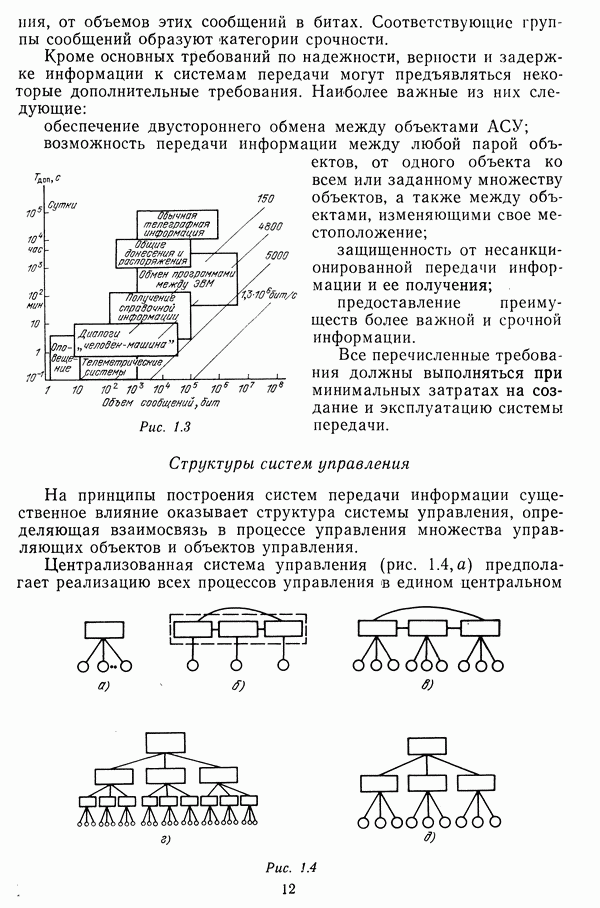
Заданные требования к живучести сети могут быть выполнены три различных вероятностях вывода  строя элементов сети. Эти вероятности определяются защищенностью и избыточностью и, таким образом, являются функциями затрат
строя элементов сети. Эти вероятности определяются защищенностью и избыточностью и, таким образом, являются функциями затрат 
Задача стороны Б заключается в том, чтобы нарушить связность сети при минимальных затратах на основе имеющихся сведений о структуре и априорных вероятностях вывода элементов сети из строя.
Задача стороны Л состоит в выборе и обеспечении таких значений  при которых:
при которых:
суммарные затраты на сеть минимальны;
обеспечиваются требования по живучести сети;
сторона Б вынуждена выделить максимальные средства на вывод сети из строя по установленному критерию.
Для нарушения связности сети достаточно вывести из строя одно или некоторое множество сечений в зависимости от критерия нарушения связности. Поскольку сторона Б должна стремиться нарушить связность минимальными средствами, то она выбирает в качестве объекта воздействия одно или некоторый набор простых сечений. При выборе наиболее слабых сечений может быть использована априорная информация о сети.
В качестве критерия слабости сечения может рассматриваться

Степень неопределенности при выборе нарушаемого сечения стороной Б характеризуется энтропией

где  — число рассматриваемых простых сечений;
— число рассматриваемых простых сечений; 
Таким образом, сторона А должна обеспечить такие априорные вероятности нарушения сечений, (при которых неопределенность, а следовательно, и затраты стороны Б будут максимальны. Формально это соответствует максимуму энтропии при ограничениях, определяемых требованиями к живучести сети. Для каждого сечения распределение априорных вероятностей вывода из строя отдельных элементов не влияет на затраты, необходимые для нарушения сечения в целом. (Поэтому при оптимизации априорных вероятностей вывода элементов сети из строя в качестве критерия оптимальности сторона А может использовать минимум затрат на обеспечение защищенности.
Варианты оптимизации параметров живучести сечений
Пусть требования к живучести заданы по допустимой вероятности нарушения связности  Тогда сеть считается вышедшей из строя, если нарушено хотя бы одно сечение.
Тогда сеть считается вышедшей из строя, если нарушено хотя бы одно сечение.
При целенаправленном выборе сечения стороной Б вероятности нарушения сечений можно принять независимыми. В этом случае задача оптимизации априорных вероятностей нарушения сечений формулируется следующим образом: наити такие значения  , при которых обеспечивается
, при которых обеспечивается

и выполняется ограничение

где  — число рассматриваемых простых сечений.
— число рассматриваемых простых сечений.
Для решения используем метод неопределенных множителей Лагранжа. Функция Лагранжа

Дифференцируя  и приравнивая нулю, получаем систему уравнений
и приравнивая нулю, получаем систему уравнений

Отсюда 
Если для сети определена допустимая вероятность отрыва заданного числа узлов  то решение остается аналогичным, однако рассматриваются только те сечения, нарушение которых приводит к отрыву от сети М узлов. При этом
то решение остается аналогичным, однако рассматриваются только те сечения, нарушение которых приводит к отрыву от сети М узлов. При этом
Для определения множества простых сечений, связанных с различными наборами из М по  может быть использовано понятие кограницы. В соответствии с определением [34] кограница набора вершин графа есть множество ребер, удаление которых приводит к отрыву от сети всех вершин данного набора. Таким образом, найдя кограницы наборов по М узлов, получим множество интересующих нас простых сечений.
может быть использовано понятие кограницы. В соответствии с определением [34] кограница набора вершин графа есть множество ребер, удаление которых приводит к отрыву от сети всех вершин данного набора. Таким образом, найдя кограницы наборов по М узлов, получим множество интересующих нас простых сечений.
При определении кограницы для некоторого набора узлов  можно использовать матрицу инциденций. При этом необходимо произвести векторное сложение по модулю 2 строк
можно использовать матрицу инциденций. При этом необходимо произвести векторное сложение по модулю 2 строк
матрицы инциденций, соответствующих узлам, входящим в данный набор:

В том случае, когда для сети определено допустимое среднее число узлов, между которыми невозможна передача информации М, ограничение (4.53) заменяется на

где  — число узлов, отрываемых от сети при нарушении сечения
— число узлов, отрываемых от сети при нарушении сечения  Соответствующая функция Лалранжа имеет вид
Соответствующая функция Лалранжа имеет вид

После дифференцирования получим систему уравнений 

Решение этой системы имеет вид трансцендентного уравнения

положительный корень которого является значением множителя Лалранжа. Окончательно получаем

Решение приведенного уравнения может быть получено любым известным численным методом.

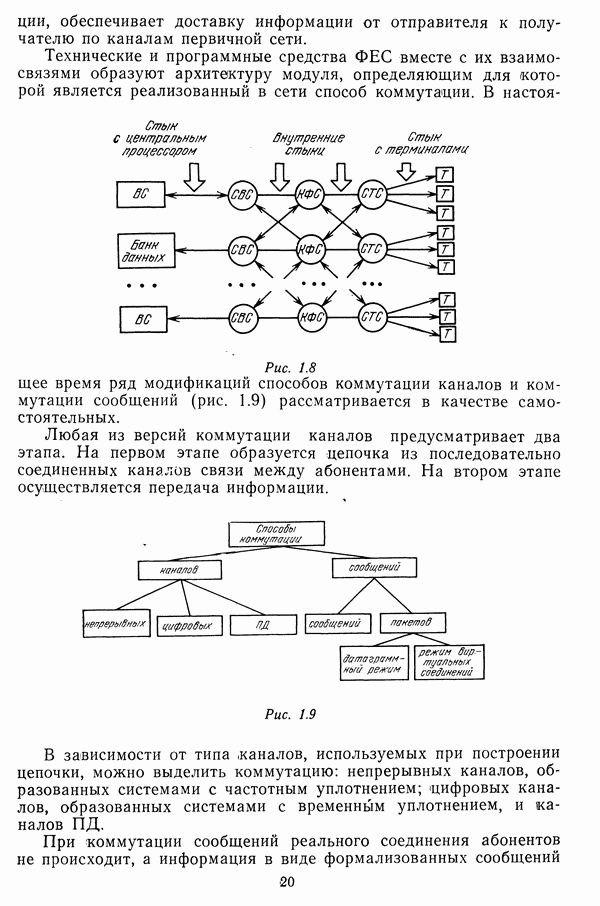
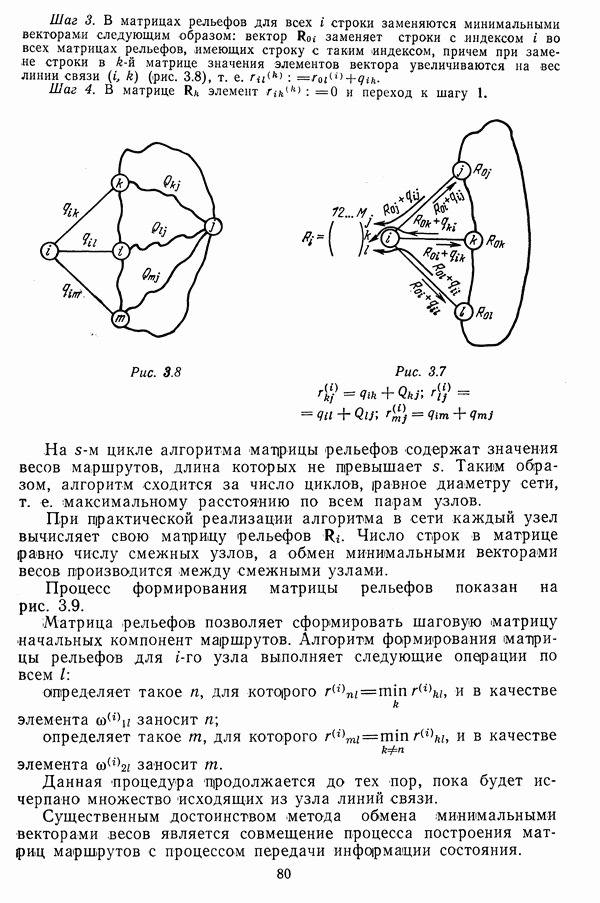
Рис. 4.8
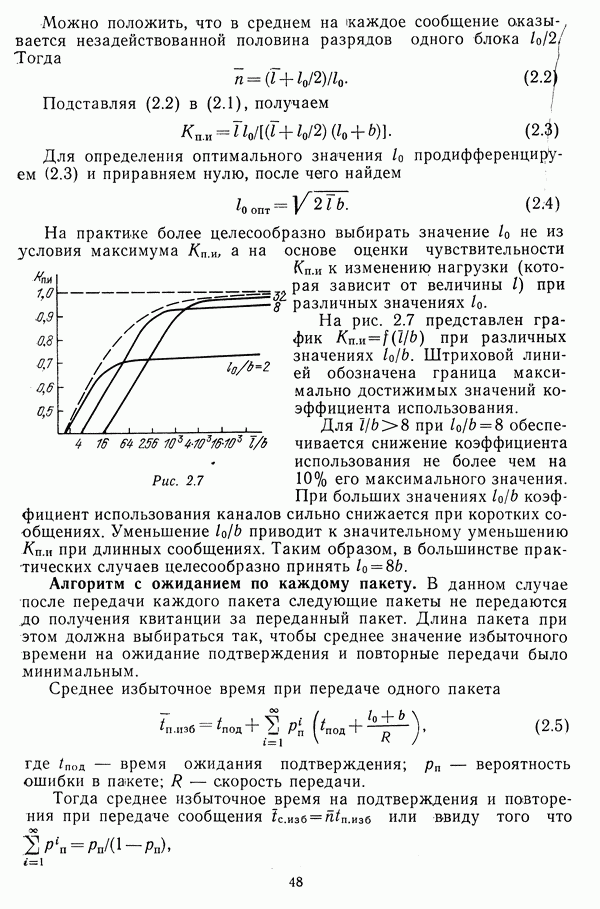
В качестве простой иллюстрации рассмотрим следующий пример.
Вариант 1. Заданы структура сети (рис. 4.8) и допустимая вероятность нарушения связности  Тогда в соответствии с
Тогда в соответствии с 
Вариант 2. С узлом  совмещен управляющий объект. В среднем из
совмещен управляющий объект. В среднем из  должна обеспечиваться связь хотя бы с одним узлом, т. е. М= 1. Из
должна обеспечиваться связь хотя бы с одним узлом, т. е. М= 1. Из  Положительный корень уравнения
Положительный корень уравнения  Тогда получаем
Тогда получаем 
Оптимизация значений априорных вероятностей вывода из строя элементов сечений
Априорные вероятности вывода из строя элементов сети являются функциями затрат  имеющими произвольный, но принципиально невозрастающий характер. Оптимальными будем
имеющими произвольный, но принципиально невозрастающий характер. Оптимальными будем
считать такие значения  элементов сети, при которых для множества сечений обеспечивается допустимая вероятность их нарушения
элементов сети, при которых для множества сечений обеспечивается допустимая вероятность их нарушения  а суммарные затраты минимальны.
а суммарные затраты минимальны.
Другими словами, эти значения обеспечивают

при выполнении ограничения

где  — элемент матрицы сечений.
— элемент матрицы сечений.
Логарифмируя ограничения, получаем

При выпуклом характере функции  данная задача является задачей выпуклого программирования, которая может быть решена методом нормированных функций. Необходимыми условиями при этом являются [2]
данная задача является задачей выпуклого программирования, которая может быть решена методом нормированных функций. Необходимыми условиями при этом являются [2]

Первое может быть выполнено выбором соответствующего шага измерения затрат. Второе условие, как правило, не выполняется. Для того чтобы его обойти, преобразуем ограничения к виду

Таким образом, окончательно задача примет следующий вид: найти  , при которых обеспечивается
, при которых обеспечивается  и выполняются ограничения
и выполняются ограничения

Основная идея используемого метода оптимизации состоит в том, что на каждом этапе процесса последовательного распределения средств связи очередная единица выделяется тому элементу сети, повышение живучести которого на данном этапе оказывает наиболее существенное (влияние на живучесть сети в целом.
Поскольку необходимым условием окончания процесса оптимизации является выполнение всех граничных условий, то для удобства контроля за процессом в смысле приближения к границам целесообразно, чтобы эти ограничения были одинаковыми. Этого
можно достигнуть нормированием с использованием приведенной границы

Тогда система ограничений примет вид

или, если сомножитель перед суммой обозначить как

Поскольку каждый элемент сети может входить в состав нескольких простых сечений, то при оценке эффективности внесения затрат на элемент необходимо учитывать состояние на данном этапе процесса оптимизации сечений, включающих данный элемент.
При использовании метода нормированных функций это осуществляется умножением абсолютного Прироста эффективности при внесении единицы затрат на элемент на коэффициент  где
где  на первом этапе оптимизации и уменьшается по мере убывания
на первом этапе оптимизации и уменьшается по мере убывания  если
если  элемент принадлежит
элемент принадлежит  сечению.
сечению.
Выполнение условия  означает, что требования по живучести
означает, что требования по живучести  сечения выполнены и соответствующее ограничение должно быть выведено из задачи. Об окончании процесса оптимизации свидетельствует выполнение данного условия для всех
сечения выполнены и соответствующее ограничение должно быть выведено из задачи. Об окончании процесса оптимизации свидетельствует выполнение данного условия для всех  Таким образом, алгоритм включает следующую последовательность шагов.
Таким образом, алгоритм включает следующую последовательность шагов.
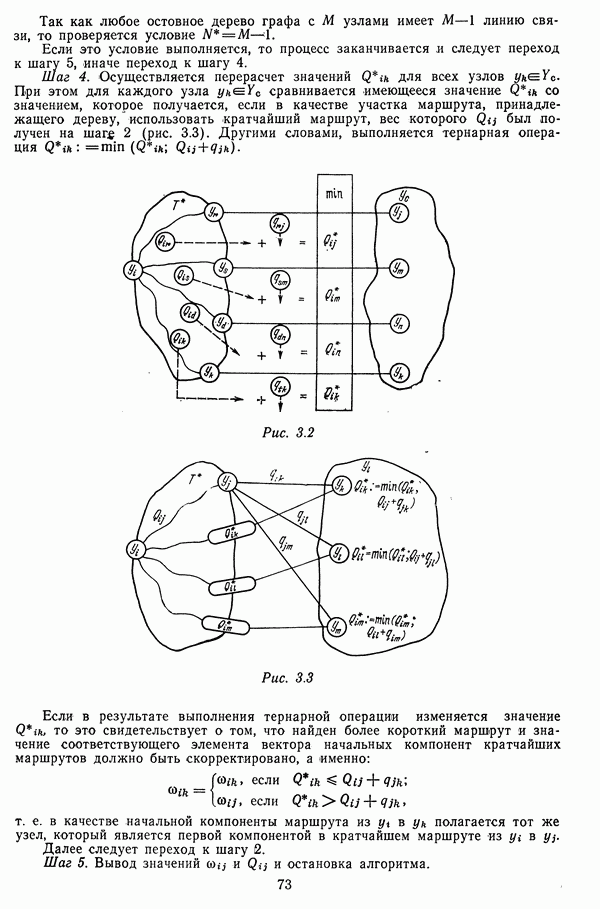
Шаг 0. Ввод исходных данных:  — массив сечений;
— массив сечений;  — массивы функций затрат;
— массивы функций затрат;  — массив требований к сечениям.
— массив требований к сечениям.
Вычисление исходных величин:  — число ограничений;
— число ограничений;  затраты на 6-й элемент; В — по соотношению (4.63);
затраты на 6-й элемент; В — по соотношению (4.63);  — по соотношению (4.64);
— по соотношению (4.64); 
Шаг 1. Для каждой линии связи поочередно для всех сечений вычислить эффективность внесения единицы затрат

Шаг 2. Вычислить прирост эффективности в смысле повышения живучести сети в целом при внесении единицы затрат на  элемент:
элемент: 
Шаг 3. Определить, на какой элемент сети целесообразно выделять очередную единицу средств, т. е. найти такое  для которого
для которого 
Шаг 4. Увеличить затраты на  элемент:
элемент:  Произвести корректировку значений
Произвести корректировку значений  характеризующих степень удовлетворения ограничений на данном этапе:
характеризующих степень удовлетворения ограничений на данном этапе: 
Шаг 5. Определить сечения, для которых требования выполнены, и вывести соответствующие ограничения из рассмотрения. Для  проверить условие Если да, то
проверить условие Если да, то  перейти к шагу 6, иначе перейти к шагу 1.
перейти к шагу 6, иначе перейти к шагу 1.
Шаг 6. Проверить наличие сечений, требования по которым не выполнены:  Если да, то перейти к шагу 7, иначе перейти к шагу 1.
Если да, то перейти к шагу 7, иначе перейти к шагу 1.
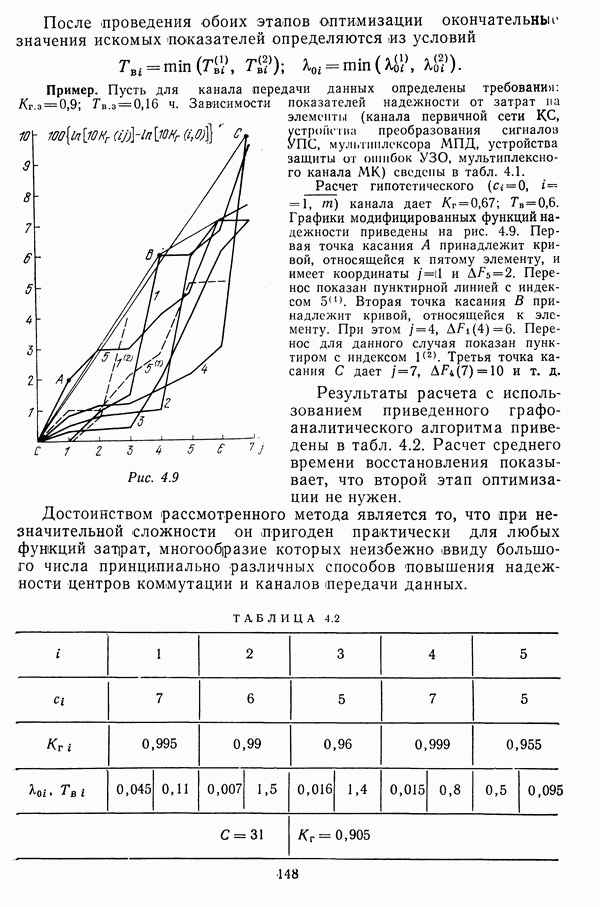
Шаг 7. Вывести результаты: 
Грубая оценка числа операций, необходимых для реализации алгоритма, может производиться по формуле  где
где  — число операций, необходимое для вычислений на шаге
— число операций, необходимое для вычислений на шаге  число единиц затрат, требуемое для выполнения приведенной границы путем внесения затрат на повышение живучести условного элемента, для которого
число единиц затрат, требуемое для выполнения приведенной границы путем внесения затрат на повышение живучести условного элемента, для которого 
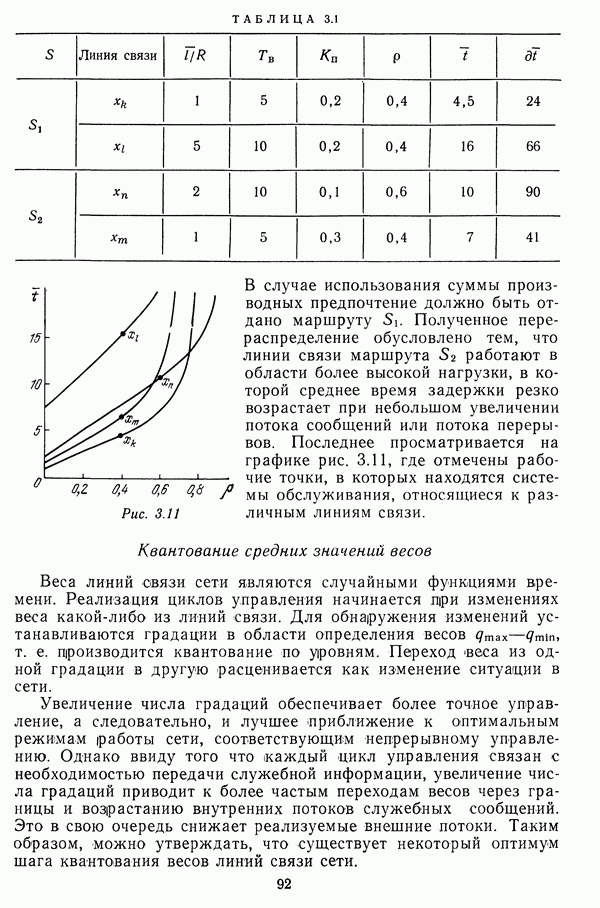
Пример. Для сети, структура которой приведена на рис. 4.8, задано  Зависимости вероятностей выживания линий связи от внесенных затрат определяются соотношениями
Зависимости вероятностей выживания линий связи от внесенных затрат определяются соотношениями

Решение данной задачи с использованием изложенного алгоритма дает следующие оптимальные по критерию минимума затрат значения допустимой вероятности вывода из строя линий связи:  Суммарные затраты составляют 10 единиц.
Суммарные затраты составляют 10 единиц.
При равных значениях этих вероятностей обеспечение требований к живучести сети выполняются, если  Соответствующие суммарные затраты в данном случае будут составлять 15 единиц.
Соответствующие суммарные затраты в данном случае будут составлять 15 единиц.
Число произведенных операций равно 240.
В общем случае функции, определяющие зависимость живучести элементов сети от затрат, могут иметь характер, отличный от выпуклого. Однако по очевидным соображениям вид этих функций ограничивается классом линейно-ломаных невозрастающих кривых. Линейно-ломаные функции могут быть заданы в виде таблиц, а задача в этом случае является задачей аддитивного программирования. Решение ее возможно на базе приведенного алгоритма с использованием идей, лежащих в основе метода выпуклых оболочек. В соответствии с этим методом на каждом этапе решения задачи осуществляется поиск оптимальной длины шага приращения затрат (в отличие от выпуклых функций, когда приращение производится с постоянным шагом).
Необходимые операции состоят в вычислении для диапазона существования функции затрат массивов

Величина  характеризует границу области определение функций затрат.
характеризует границу области определение функций затрат.
Далее для каждого этапа решения определяются оптимальные величины приращения затрат на каждый из элементов, а именно находятся такие  для которых выполняются условия
для которых выполняются условия

Выделение ресурсов на шаге 1 осуществляется в соответствии со значениями 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1 ОБЩАЯ ХАРАКТЕРИСТИКА СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 1.1. СЕТЬ СВЯЗИ КАК ПОДСИСТЕМА СИСТЕМЫ УПРАВЛЕНИЯ
- 1.2. ПРИНЦИПЫ ПОСТРОЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 1.3. ПРЕДСТАВЛЕНИЕ СТРУКТУР СЕТЕЙ
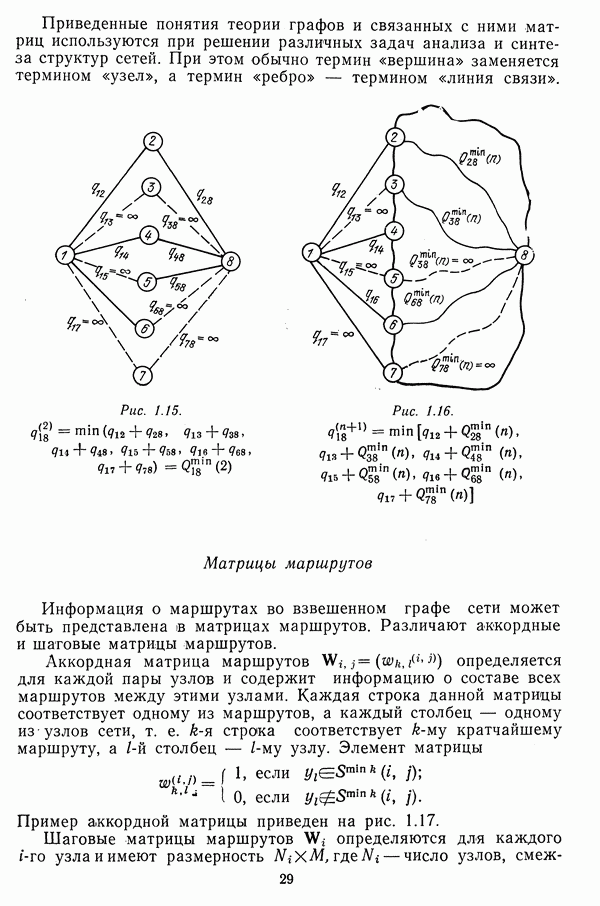
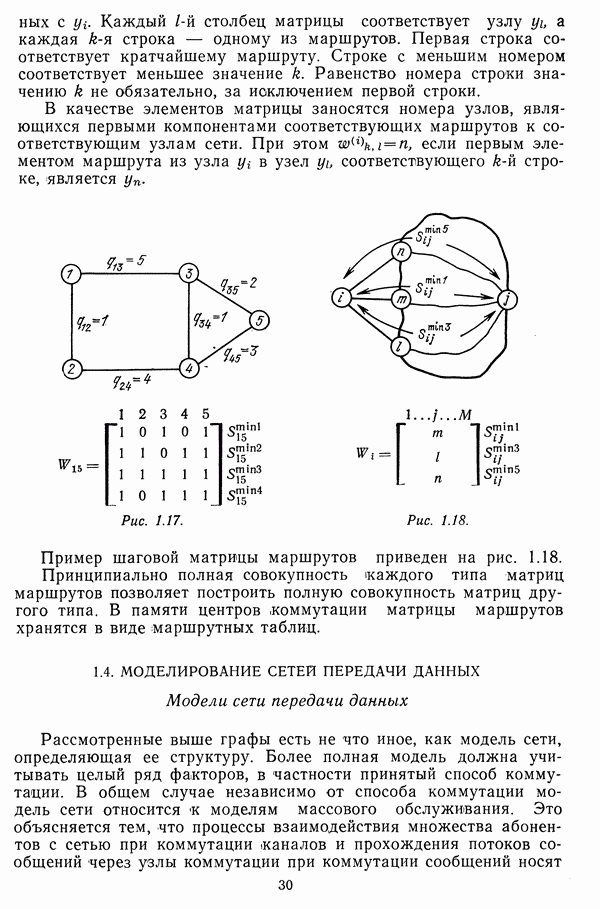
- Кратчайшие маршруты во взвешенных графах
- Матрицы, определяющие структуру сетей
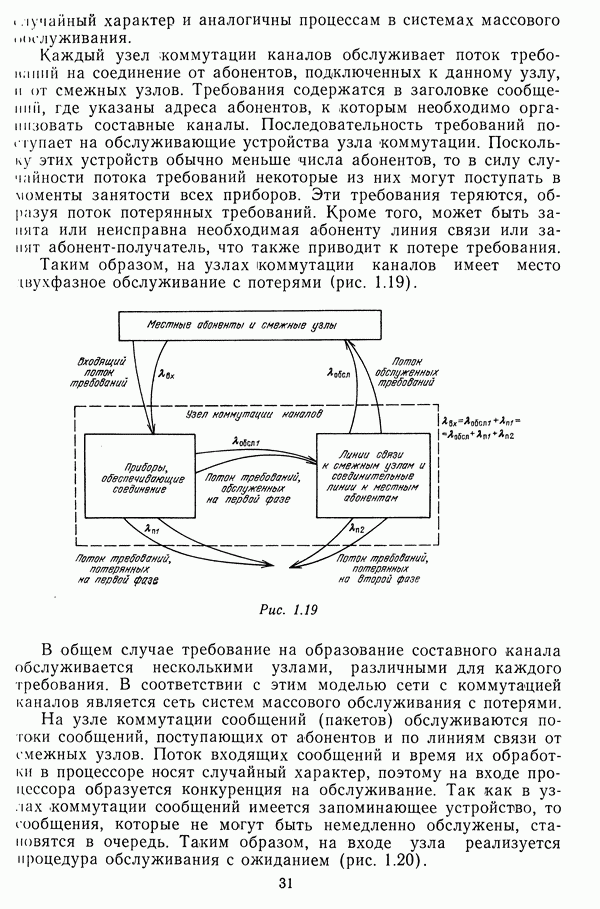
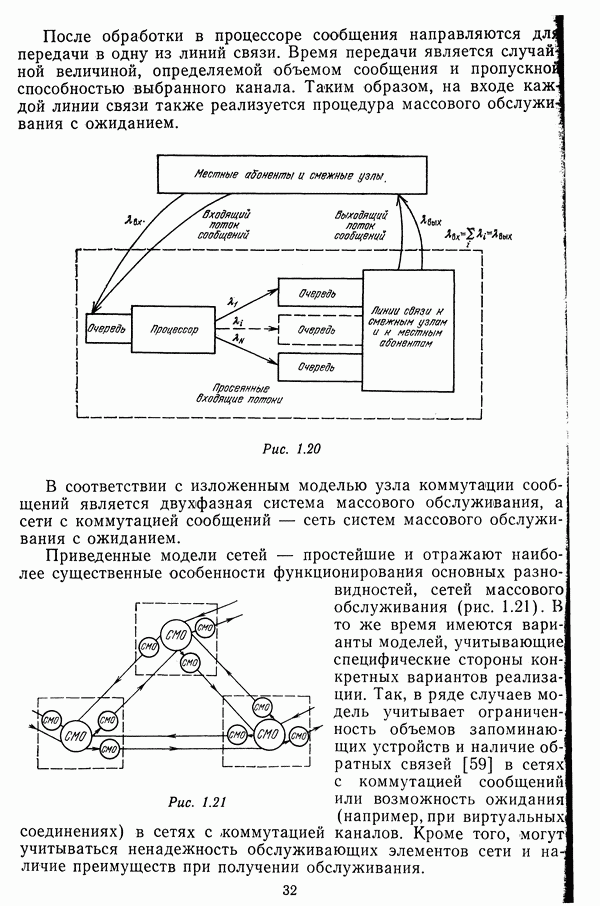
- Матрицы маршрутов
- 1.4. МОДЕЛИРОВАНИЕ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- Математические модели, используемые при расчете сетей
- Потоки в сетях передачи данных
- ГЛАВА 2. ПРИНЦИПЫ ФУНКЦИОНИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.1. СТРУКТУРА ФУНКЦИОНАЛЬНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.2. ФОРМАЛИЗАЦИЯ СООБЩЕНИИ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 2.3. АДРЕСОВАНИЕ СООБЩЕНИЙ
- 2.4. ПРОЦЕДУРЫ ВЫБОРА МАРШРУТОВ
- 2.5. РЕГУЛИРОВАНИЕ ПОТОКОВ СООБЩЕНИЙ ПО ПРИОРИТЕТАМ
- 2.6. УПРАВЛЕНИЕ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- Глава 3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ МАРШРУТИЗАЦИИ И УПРАВЛЕНИЯ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 3.2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПОИСКОВЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.4. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КВАЗИСЛУЧАИНЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.5. ФИЗИЧЕСКИЕ ВЕРСИИ ВЕСОВ ЭЛЕМЕНТОВ СЕТИ
- 3.6. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УПРАВЛЕНИЯ ВНЕШНИМИ ПОТОКАМИ СООБЩЕНИЙ
- Глава 4. ВОПРОСЫ ПРОЕКТИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 4.1. ЗАДАЧИ СИСТЕМНОГО ПРОЕКТИРОВАНИЯ СЕТЕЙ
- 4.2. РАЗМЕЩЕНИЕ УЗЛОВ КОММУТАЦИИ
- Оптимизация числа узлов и их размещения при независимом положении абонентов
- Размещение узлов для связи с мобильными абонентами
- Размещение центра управления сетью
- 4.3. СИНТЕЗ СТРУКТУРЫ СЕТИ
- Синтез структуры сети минимальной стоимости при заданной связности
- 4.4. РАСЧЕТ МОЩНОСТИ ЛИНИИ СВЯЗИ СЕТИ
- Оптимизация мощности линий связи при произвольном виде функций затрат
- Методика выбора каналов передачи данных для линий связи с заданной мощностью
- 4.5. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ЖИВУЧЕСТИ ЭЛЕМЕНТОВ СЕТИ
- 4.6. ВЫБОР ПАРАМЕТРОВ НАДЕЖНОСТИ ЭЛЕМЕНТОВ СЕТИ
- Методы вычисления вероятности связности сети
- Выбор параметров надежности центров коммутации
- Аналитическая оптимизация внутренних показателей надежности элементов сети
- Оптимизация внутренних показателей надежности при произвольном виде функций затрат
- СПИСОК ЛИТЕРАТУРЫ