3.3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПОИСКОВЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ

Поисковые процедуры выбора маршрутов или процедуры, допускающие альтернативу [9, 12], требуют наличия на узлах коммутации информации о нескольких маршрутах к узлам-получателям. В соответствии с этим математическое обеспечение таких процедур должно содержать программы вычисления не векторов,

а матриц маршрутов. Ниже излагаются два наиболее известных метода решения данной задачи: метод кназимппорои и метод обмена минимальными векторами весов.

Метод квазиминоров [28] позволяет вычислить аккордные матрицы маршрутов для выбранной пары узлов. Вычисление осуществляется разложением квазиминора соответствующего элемента матрицы весов. Предварительно элементы, соответствующие несмежным парам узлов, обнуляются.

Квазиминором элемента матрицы размерности называется определитель особого рода матрицы размерности получаемой из вычеркиванием строки и столбца. Квазиминор обозначается и может быть представлен разложением вида

Здесь — квазиминор матрицы размерности полученной из вычеркиванием строки и столбца, т. е.

Таким образом, на первом шаге производится разложение по элементам строки матрицы весов — номер узла, от которого строятся маршруты), в результате чего определяются первые компоненты всех маршрутов. Заметим, что каждый квазиминор, образованный на первом шаге, определяет все маршруты от одного из смежных с узлов к узлу

На втором шаге разложения по элементам строки матрицы весов — номер одного из узлов, смежного с определяются вторые компоненты всех маршрутов, включающих в качестве первых компонент узел Каждый полученный на этом шаге квазиминор определяет все маршруты от одного из узлов, являющегося смежным с у до узла

Разложение завершается по мере получения квазиминоров, определяющих последние элементы маршрутов, т. е. узлы, смежные с . В результате полного разложения квазиминор

где маршрут; — множество маршрутов из в у Полученное разложение определяет состав каждого из маршрутов. Для построения аккордной матрицы необходимо вычислить веса этих маршрутов и упорядочить их в соответствии с принятым критерием.

Особенностью метода квазиминоров является возможность получения информации о маршрутах от выбранного узла. В силу этого он может быть использован совместно с маршрутным методом адресования.

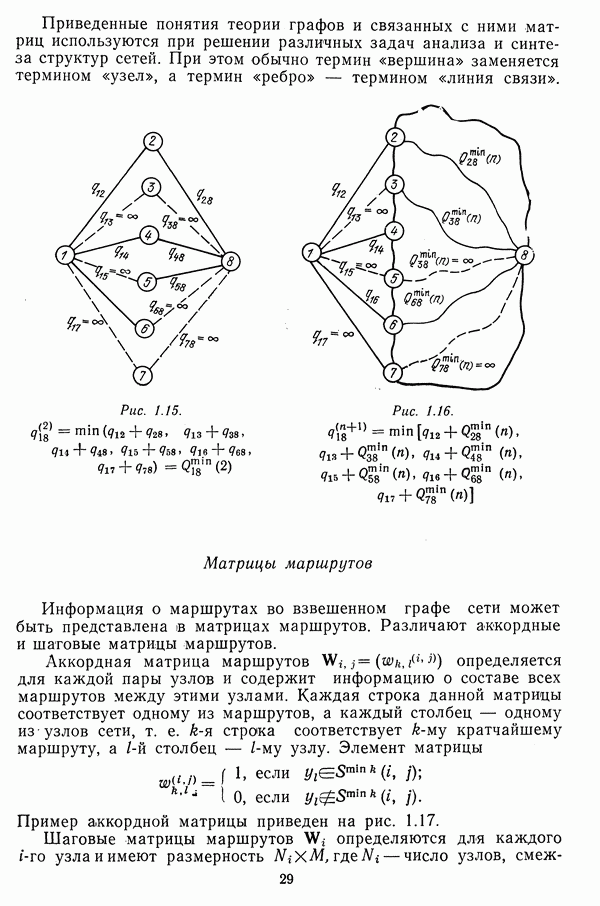
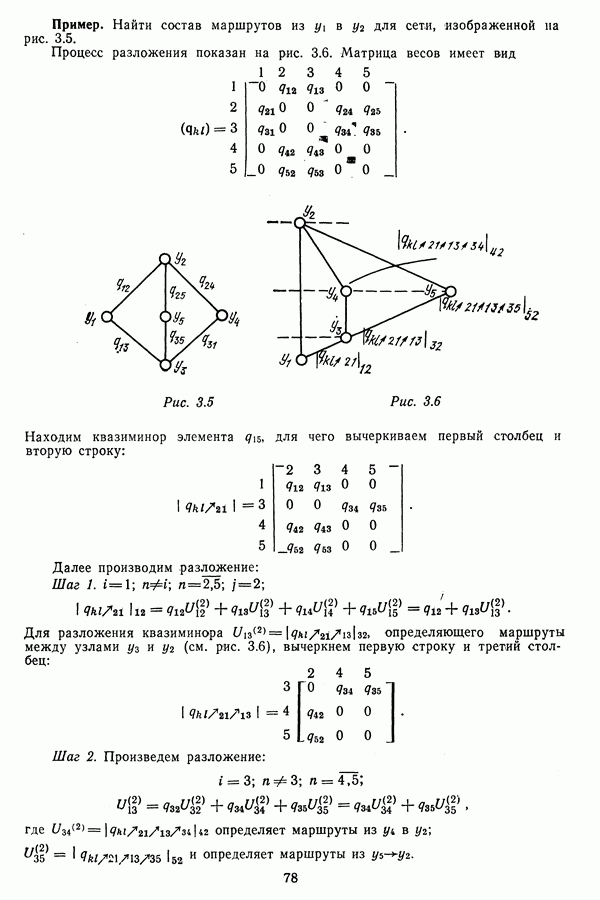
Пример. Найти состав маршрутов из для сети, изображенной на рис. 3.5.

Процесс разложения показан на рис. 3.6. Матрица весов имеет вид

Рис. 5.5

Рис. 5.5

Находим квазиминор элемента для чего вычеркиваем первый столбец и вторую строку:

Далее производим разложение:

Шаг 3.

Для разложения квазиминора определяющего маршруты между узлами (см. ряс. 3.6), вычеркнем первую строку и третий столбец:

Шаг 2. Произведем разложение:

где определяет маршруты из и определяет маршруты из

Шаг 3. Произведем разложение

Для имеем

Произведя обратную подстановку, получим

Таким образом, разложение квазиминора содержит информацию о составе всех маршрутов между соответствующей парой узлов.

Метод обмена минимальными векторами весов в отечественной литературе известен под названием метода рельефов и описан главным образом применительно к сетям с коммутацией каналов и единичными весами линий связи [6].

Практически метод заключается в построении для каждого узла специальной матрицы весов маршрутов ко всем остальным узлам сети. Данная матрица для узла имеет число строк равное числу линий связи, инцидентных и число столбцов, равное числу узлов сети.

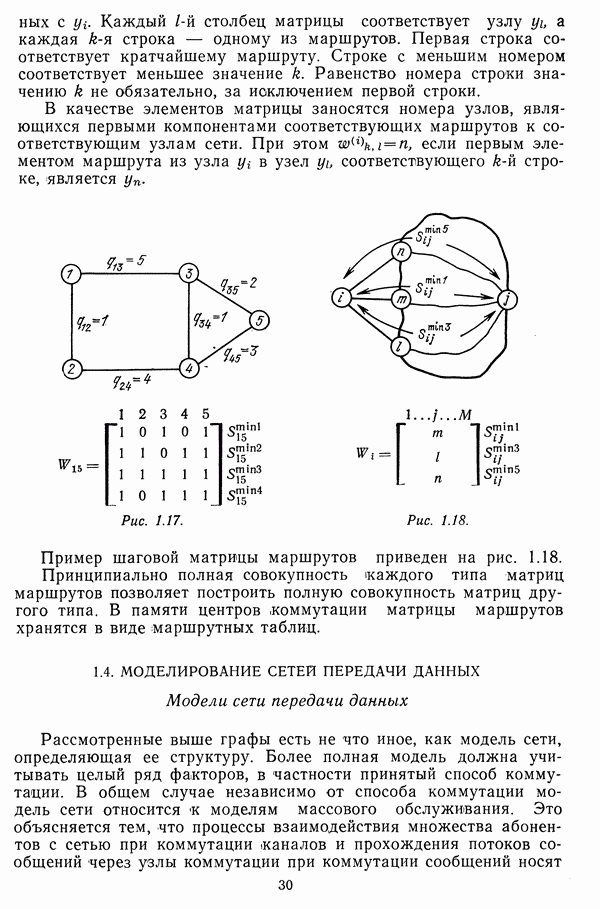
В дальнейшем будем пользоваться термином «матрица рельефов» и обозначать ее следующим образом:

где — «вес маршрута из если в качестве первого элемента этого маршрута используются линия связи и узел (рис. 3.7).

Каждой строке присваивается индекс одного из смежных узлов. Формирование матриц рельефов производится по следующему алгоритму.

Шаг 0. Ввод исходных данных и задание начальных значений переменным: матрицам рельефов

и минимальным векторам .

Шаг 1. Вычисление минимальных векторов:

Шаг 2. Сравнение . Если то процесс формирования закончен и алгоритм останавливается. Если то Далее переход к шагу 3.

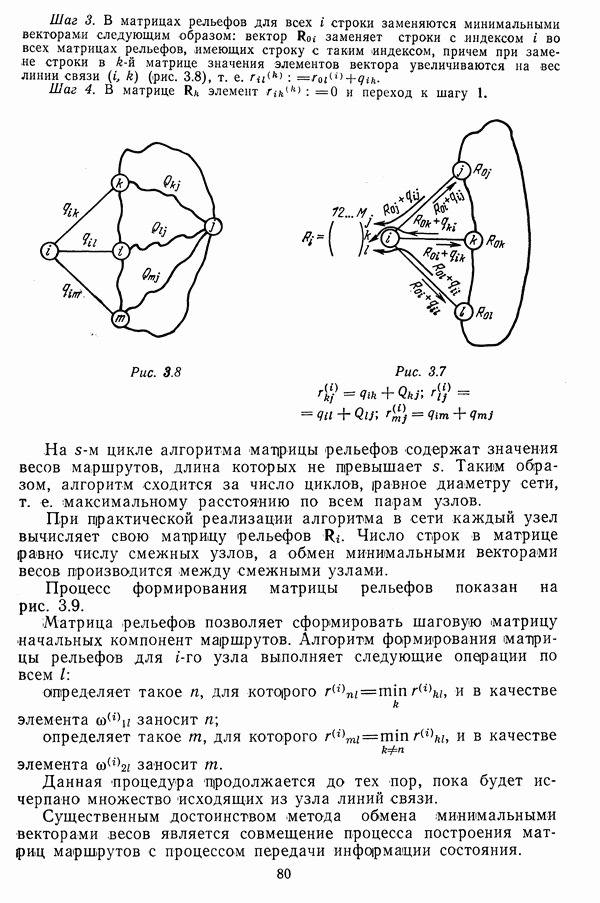
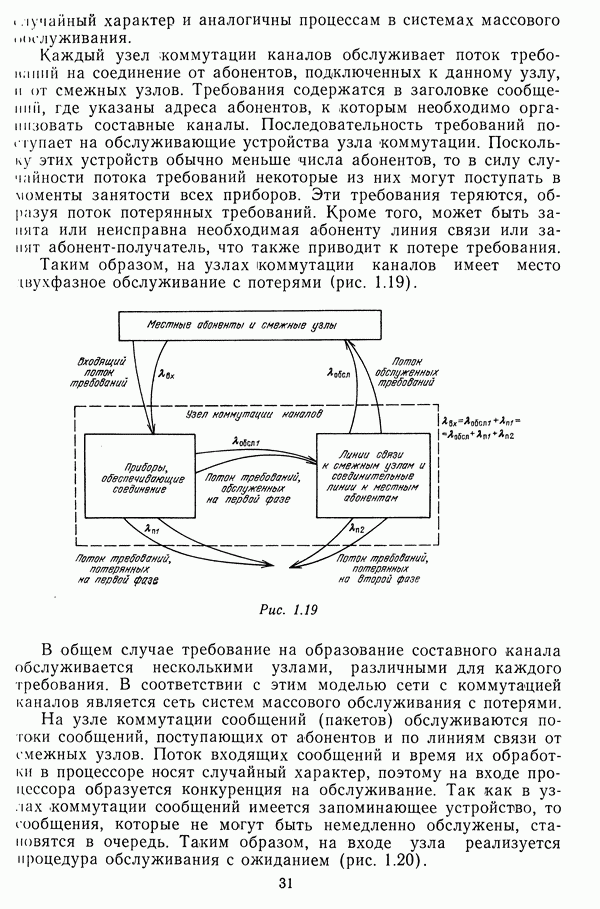
Шаг 3. В матрицах рельефов для всех строки заменяются минимальными векторами следующим образом: вектор заменяет строки с индексом во всех матрицах рельефов, имеющих строку с таким индексом, причем при замене строки в матрице значения элементов вектора увеличиваются на вес линии связи () (рис. 3.8), т. е.

Шаг 4. В матрице элемент и переход к шагу 1.

Рис. 3.8

Рис. 3.7

На цикле алгоритма матрицы рельефов содержат значения весов маршрутов, длина которых не превышает Таким образом, алгоритм сходится за число циклов, равное диаметру сети, т. е. максимальному расстоянию по всем парам узлов.

При практической реализации алгоритма в сети каждый узел вычисляет свою матрицу рельефов . Число строк в матрице равно числу смежных узлов, а обмен минимальными векторами весов производится между смежными узлами.

Процесс формирования матрицы рельефов показан на рис. 3.9.

Матрица рельефов позволяет сформировать шаговую матрицу начальных компонент маршрутов. Алгоритм формирования матрицы рельефов для узла выполняет следующие операции по всем :

определяет такое , для которого и в качестве элемента заносит

определяет такое для которого и в качестве элемента заносит .

Данная процедура продолжается до тех пор, пока будет исчерпано множество исходящих из узла линий связи.

Существенным достоинством метода обмена минимальными векторами весов является совмещение процесса построения матриц маршрутов с процессом передачи информации состояния.

Рис. 3.9

Рис. 3.10

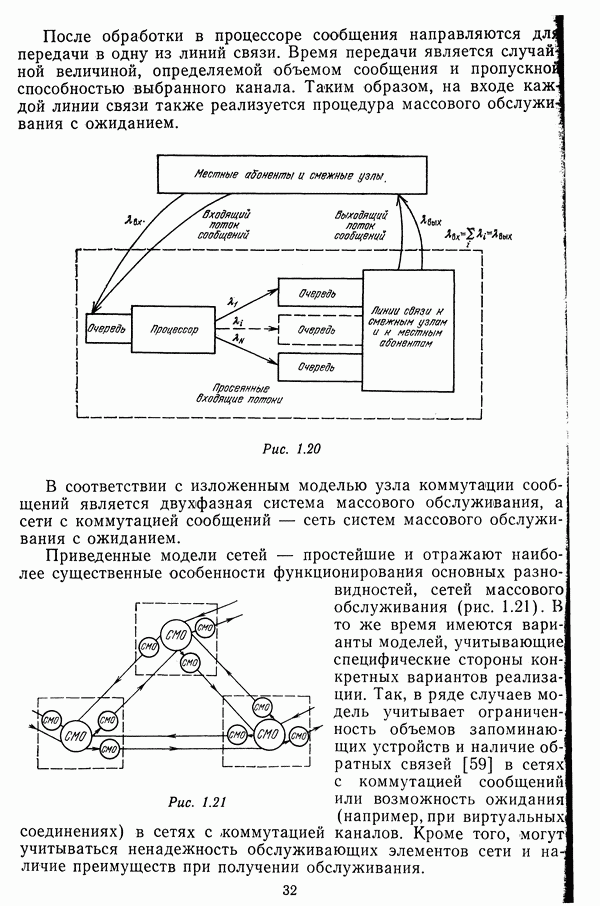
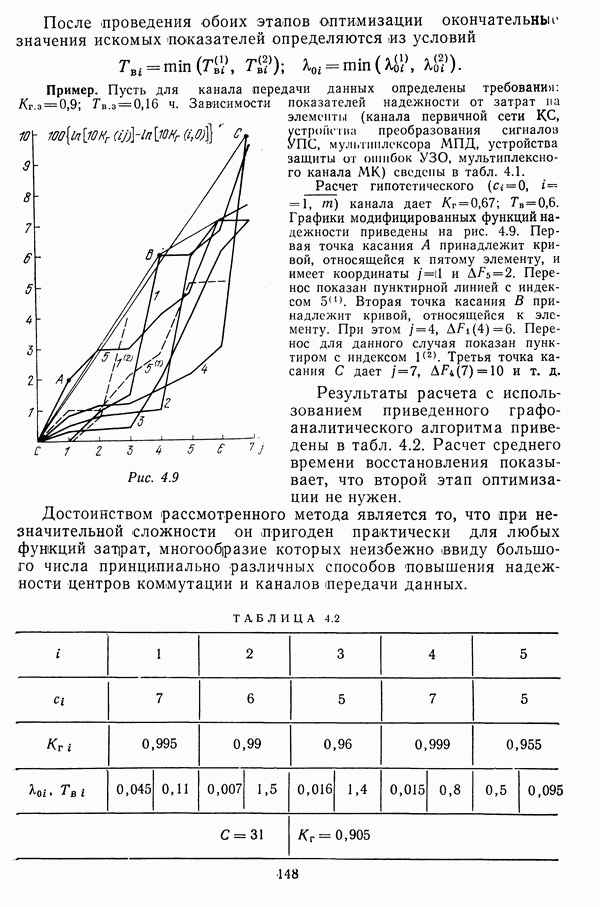
Пример. Для сети, имеющей структуру, показанную на рис. 3.10, и единичные веса линий связи, построить шаговые матрицы начальных компонент маршрутов. Вместо будем заносить «-».

(см. скан)

(кликните для просмотра скана)

(2,5)

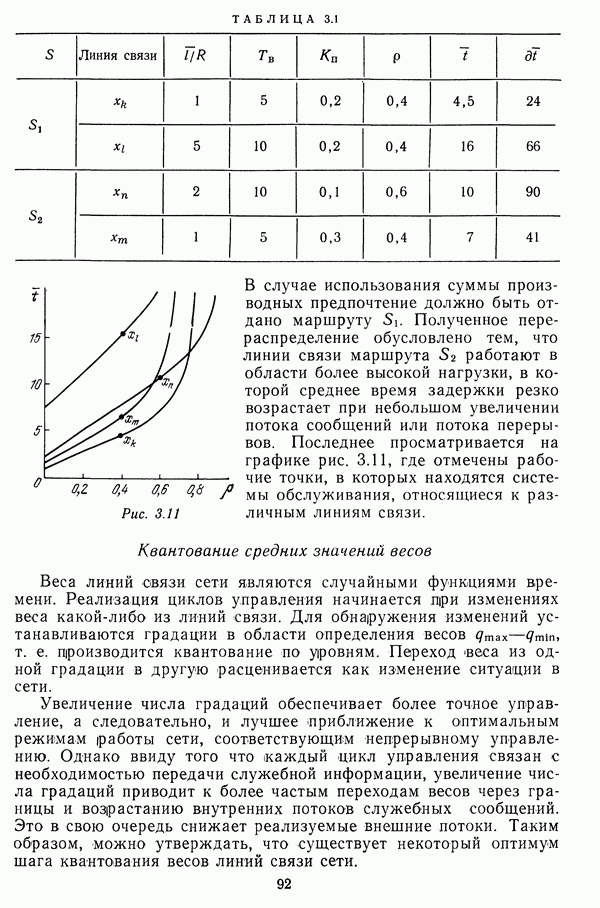
Номера, указанные в скобках, соответствуют начальным компонентам маршрутов с одинаковыми весами. Для упорядочивания таких маршрутов должен быть введен дополнительный критерий.