1.3. ПРЕДСТАВЛЕНИЕ СТРУКТУР СЕТЕЙ

Структуры сетей и элементы теории графов

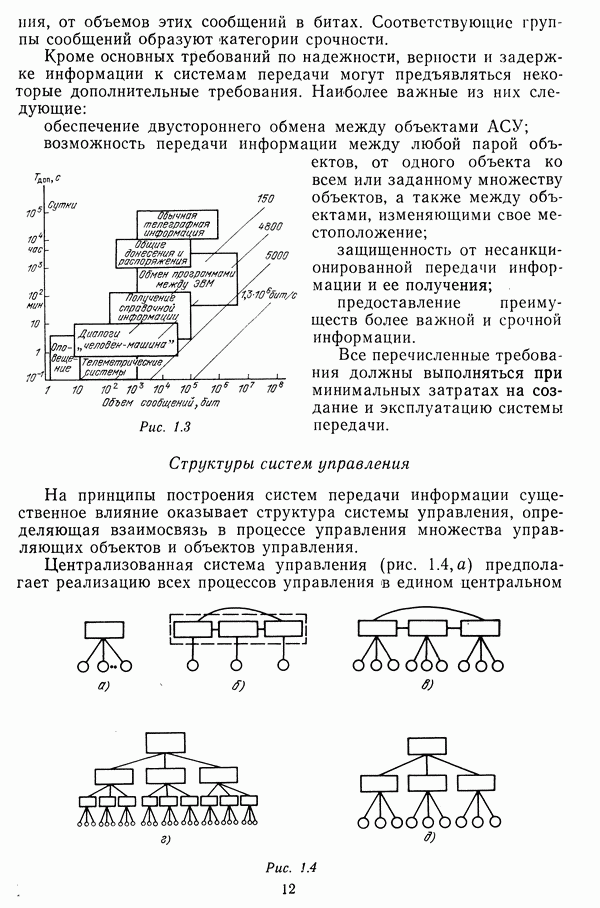
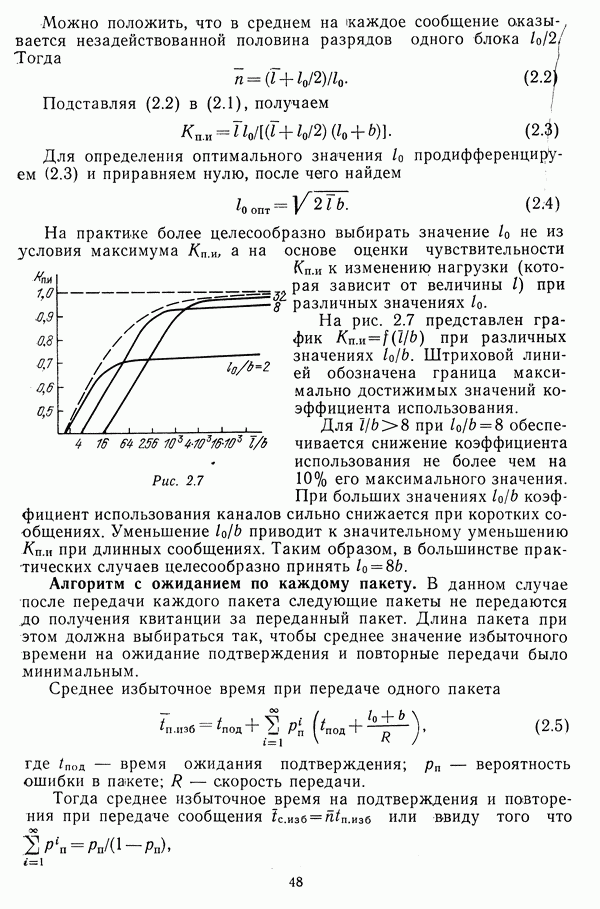
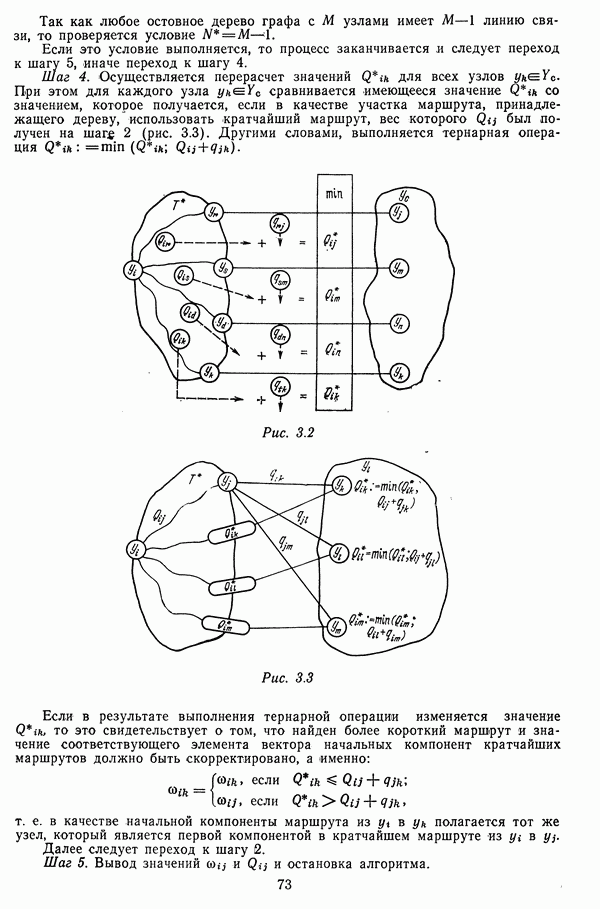
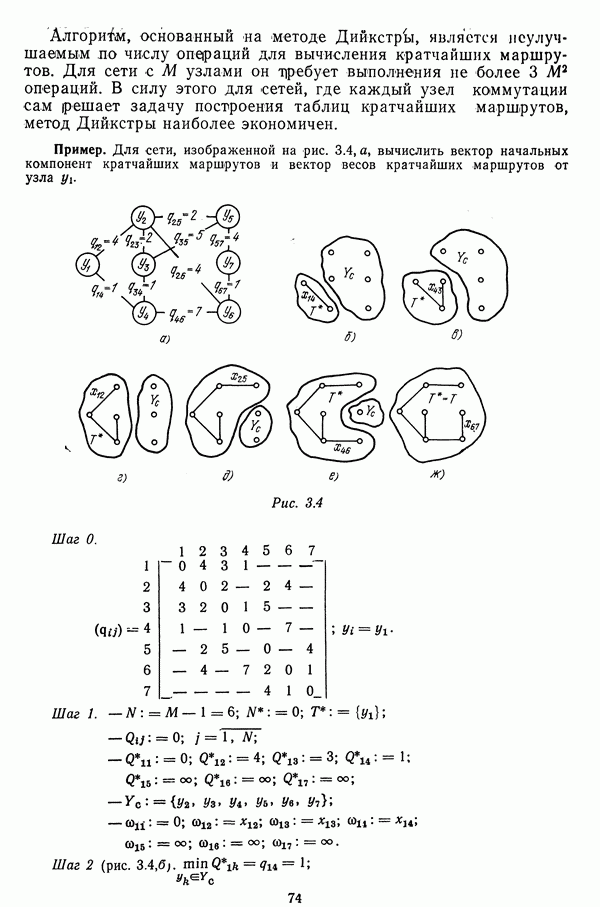
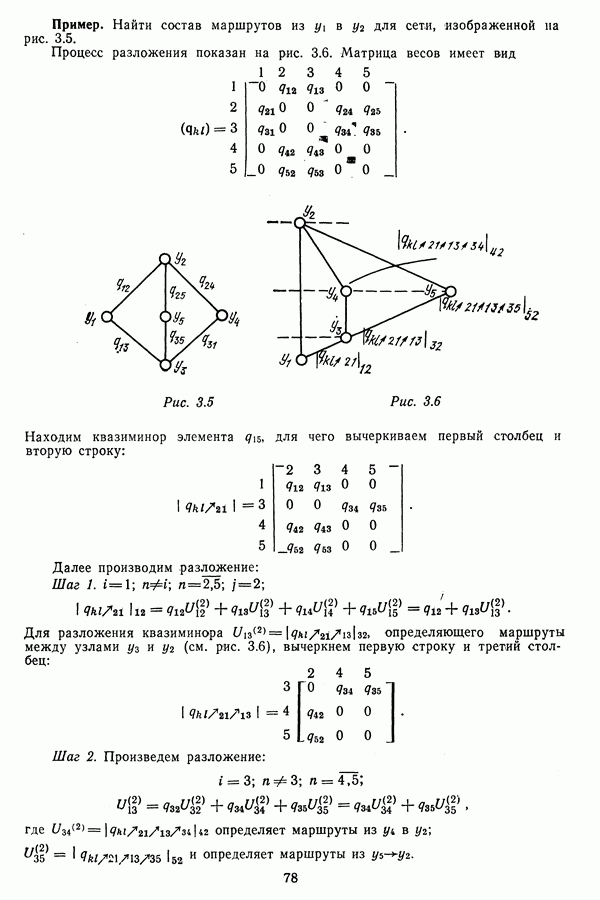
Одной из характеристик сети является ее структура, которая определяет взаимное соединение узлов и линий связи независимо от их фактического расположения на местности. Структура сети может соответствовать системе управления, в интересах которой она строится, или выбираться независимо от нее.

Существует большое число структур сетей, которые объединяют заданное множество узлов, однако среди них можно выделить три типа: древовидные, полносвязная и рекуррентные.

К древовидным структурам относятся все структуры, включающие при М узлах линию связи. Характерный пример древовидной структуры приведен на рис. 1.10, а. Частными видами древовидных структур являются структуры типа «звезда» и линейная.

Рис. 1.10

В линейных структурах (рис. 1.10, б) все узлы, кроме концевых, выполняют коммутационные функции. Структура типа «звезда» (рис. 1.10, в) используется при соответствии сети централизованной системе управления. В этом случае в центральном узле располагаются ЭВМ и банки данных, а на периферийных узлах — абонентские пункты. Центральный узел выполняет только коммутационные функции.

Полносвязная структура — это структура, в которой каждая пара узлов соединена линией связи (рис. 1.10, г). Для построения такой структуры необходимо иметь линий связи.

К рекуррентным относятся структуры с повторяющимися фрагментами простейшего вида.

Наиболее распространенными являются структуры типа решетка (рис. 1.10, д), соты (рис. 1.10, ж) и иерархическая древовидная с одинаковым коэффициентом ветвления (рис. 1.10, е).

Реальные сети, как правило, имеют смешанные (распределенные) структуры. Однако эти структуры обычно могут быть сведены к перечисленным видам либо путем выделения фрагментов, либо путем незначительных упрощений. Примеры распределенных структур приведены на рис. 1.10, з.

При описании сетей широко используются методы теории графов. Введем наиболее часто встречающиеся определения и понятия, связанные с сетевыми приложениями графов.

Граф состоит из конечного непустого множества вершин У, содержащего М вершин, и заданного множества X, содержащего неупорядоченных пар различных вершин из У. (Каждую пару вершин в множестве X называют «ребром графа . Граф называется помеченным, если его вершины и ребра имеют некоторые отличные друг от друга индексы.

Если существует ребро то говорят, что вершины смежны. Ребро является инцидентным для вершин

При наличии в графе ориентированных ребер, помеченных стрелками, граф называется ориентированным.

Подграфом графа называется граф для которого В случае, когда подграф называется остовным.

Рис. 1.11

Рис. 1.12

Одна и та же структура сети может быть изображена различными изоморфными графами. Два графа называются изоморфными, если между их множествами вершин существует взаимно-однозначное соответствие, сохраняющее смежность. На рис. 1.11 графы изоморфны, если есть соответствие

Наиболее важными понятиями, относящимися к сетям, являются понятия маршрутов и связности графов.

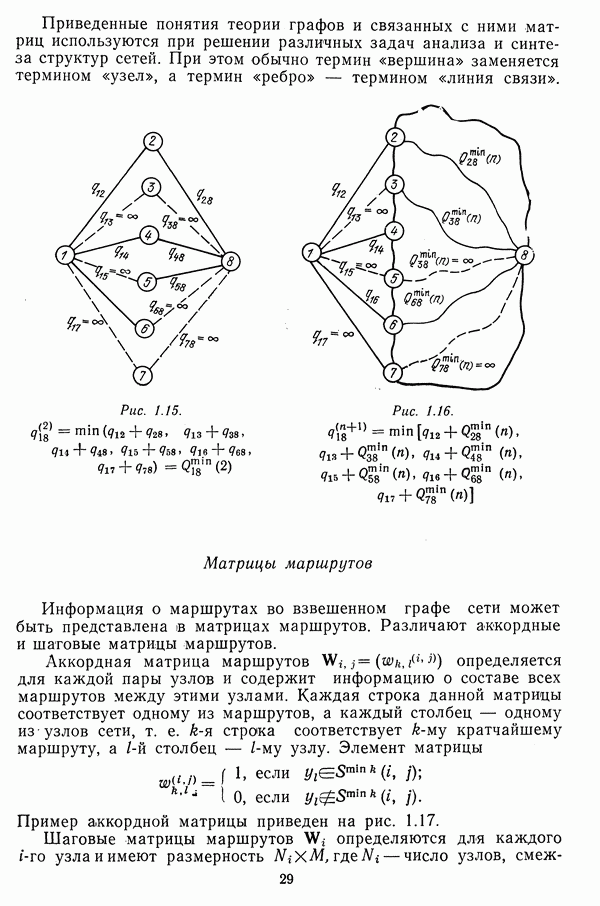
Маршрутом в графе называется чередующаяся последовательность вершин и ребер. Эта последовательность начинается и кончается вершиной, и каждое ребро последовательности инцидентно двум вершинам. На рис. 1.12 одним из маршрутов между вершинами является .

Два любых маршрута между узлами независимы по ребрам, если они не имеют общих ребер, и независимы по вершинам, если они не содержат общих вершин.

Рис. 1.13

Открытый маршрут называется простой цепью, если все его вершины различны. Замкнутая цепь называется циклом. В графе на рис. 1.13 маршрут является простой цепью, а — простым циклом.

Граф называется связным, если любая пара вершин его соединена простой цепью.

Длиною маршрута в графе называется число входящих в него (ребер. Длина кратчайшей простой цепи между двумя вершинами графа есть расстояние между этими вершинами, обозначаемое Минимальное расстояние графа называется его диаметром

С каждой вершиной графа связано число — степень вершины, равное числу инцидентных ребер

При граф является однородным степени Величина

называется средней степенью узлов сети, где — целая часть величины Если то вершина концевая.

Связный граф, включающий М вершин и ребер, называется остовным деревом . Связный граф, каждые две вершины которого соединены ребром, является полносвязным и при М вершинах содержит линий связи. Число помеченных деревьев с М вершинами равно

Существует только одна полносвязная вершина.

На рис. 1.13 приведены одно из деревьев и полный граф. Характерной чертой деревьев является отсутствие в них циклов. Для связного графа существует понятие разреза или сечения.

Совокупность ребер, удаление которых приводит к несвязному графу, называется реберным сечением.

Рис. 1.14

Совокупность вершин, удаление которых приводит к несвязному графу, называется вершинным сечением (при удалении вершины удаляются все инцидентные ребра). Если сечение определено относительно связности двух вершин то его обозначают -сечением. Если множество ребер сечения не включает подмножество, также являющееся сечением, то такое сечение называется простым.

Минимальное число ребер по всем -сечениям, обозначаемое называется реберной связностью а минимальное число вершин по всем вершинным -сечениям называется вершинной связностью Реберная связность для графа в целом определяется следующим образом:

Граф называется -реберно связным, если . Аналогично граф является -вершинно связным, если

Для графа на рис. 1.14 , так как при удалении вершин образуются два несвязных подграфа: Реберная связность в данном случае равна так как вершину можно изолировать, изъяв ребра и .

- Если граф Г рассматривать как совокупность некоторого дерева Т и множества ребер то любое простое сечение образуется из одного ребра, входящего в дерево, и остальных ребер из множества X.