| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Оптимизация внутренних показателей надежности при произвольном виде функций затрат
Изложенный в предыдущем разделе метод оптимизации внутренних показателей надежности применим только в частных случаях, когда функции затрат удается аппроксимировать аналитически выпуклыми зависимостями. В общем случае эти зависимости не являются строго выпуклыми, поскольку надежность может быть повышена за счет как небольших усовершенствований, так и принципиальных изменений, обеспечивающих при определенных затратах резкое возрастание надежности элементов (переход на новую элементарную базу, существенное упрощение схем или программ, изменение технологии производства, введение модульности, систем контроля и резервирования).
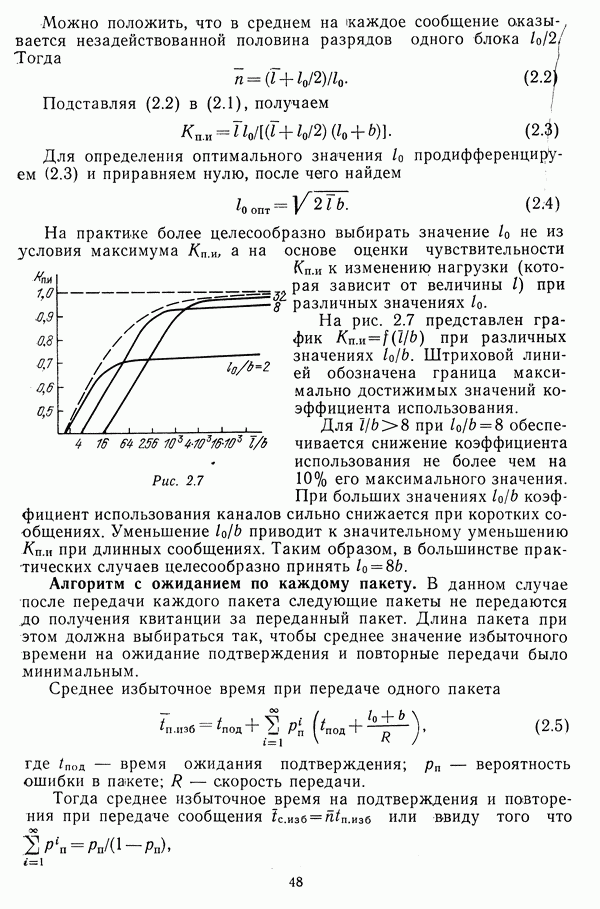
Для оптимизации внутренних показателей надежности центров коммутации и каналов ПД при функциях затрат произвольного вида может быть использован численный метод, не налагающий ограничений на эти функции, кроме сепарабельности. Выражение для коэффициента готовности системы имеет вид

или после преобразования к сепарабельной форме

где  — интенсивность отказов и средняя длительность восстановления
— интенсивность отказов и средняя длительность восстановления  элемента при затратах
элемента при затратах  Нулевым затратам поставим в соответствие показатели гипотетической системы.
Нулевым затратам поставим в соответствие показатели гипотетической системы.
Поскольку при каждом варианте затрат средства могут быть направлены как на повышение безотказности, так и на сокращение длительности восстановления, то общая формулировка задачи будет следующей: найти такое распределение средств на повышение надежности, при котором обеспечивается

при ограничении 
В силу принципа двойственности эта задача эквивалентна (4.77). Для ее решения может быть использован алгоритм, в основу которого положен метод выпуклых оболочек [2]. Ниже, не эстаппвливаясь на теоретических особенностях, которые достаточно подробно изложены в первоисточнике, приводится схема расчета, ориентированная на решение задачи оптимизации надежности.
Первый этап расчета заключается в составлении таблицы исходных данных. В таблице число строк соответствует области
определения функции затрат и значению единицы затрат, а число столбцов равно удвоенному числу элементов системы. Для обеспечения достаточной точности решения единицу затрат наиболее целесообразно выбирать из условий

где  — минимально необходимые затраты для повышения надежности
— минимально необходимые затраты для повышения надежности  элемента по безотказности и восстанавливаемости на
элемента по безотказности и восстанавливаемости на  соответственно и находятся из уравнений (4.94);
соответственно и находятся из уравнений (4.94);  — значения допустимой погрешности, определяемые верностью исходных данных.
— значения допустимой погрешности, определяемые верностью исходных данных.
Каждому элементу в таблице соответствуют два столбца. В первый заносятся интенсивности отказов, а во второй — средние длительности восстановления при различных затратах.
Второй этап расчета сводится  графическому представлению зависимостей коэффициентов готовности элементов от затрат. С этой целью строится система координат, по оси абсцисс которой откладываются единицы затрат, а по оси ординат — значения
графическому представлению зависимостей коэффициентов готовности элементов от затрат. С этой целью строится система координат, по оси абсцисс которой откладываются единицы затрат, а по оси ординат — значения  По данным таблицы на систему координат наносятся модифицированные для удобства расчетов путем введения множителей функции
По данным таблицы на систему координат наносятся модифицированные для удобства расчетов путем введения множителей функции

В результате образуется семейство неубывающих ломаных кривых.
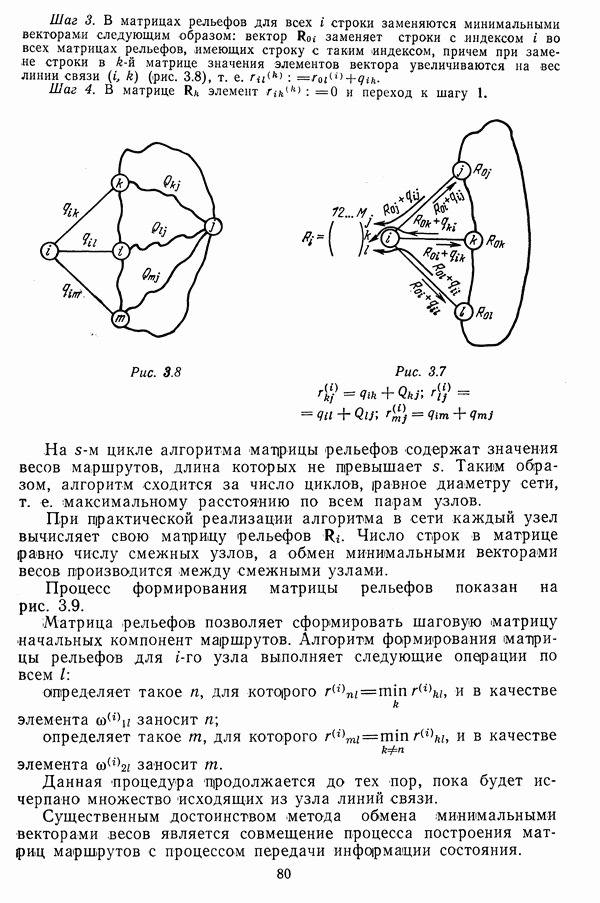
На третьем этапе производятся вычисления согласно следующему алгоритму.
Шаг 0. Обнулить величины: 
Шаг 1. Из начала координат провести касательную к семейству кривых.
Шаг 2. В соответствии с точкой касания определить:
а) номер кривой, к которой проведена касательная I (номер элемента, по которому осуществляется оптимизация на данном шаге);
б) координаты точки касания, соответствующие приращению модифицированной функции  средствам, выделенным на данном шаге.
средствам, выделенным на данном шаге.
Шаг 3. Вычислить текущие значения общих затрат и модифицированной функции системы по  элементу
элементу 
Шаг 4. Вычислить текущие значения общих затрат и модифицированной функции системы: 
Шаг 5. Проверить условия:

Нарушение первого условия говорит о том, что достигнут максимально возможный при затратах  коэффициент готовности системы. Нарушение второго условия означает, что заданный коэффициент готовности достигнут при минимальных затратах. В этих случаях расчет останавливается и выводятся результаты, т. е. значения
коэффициент готовности системы. Нарушение второго условия означает, что заданный коэффициент готовности достигнут при минимальных затратах. В этих случаях расчет останавливается и выводятся результаты, т. е. значения  по которым определяются окончательные показатели надежности элементов. Если
по которым определяются окончательные показатели надежности элементов. Если  то следует
то следует
выделить  единиц средств на повышение восстанавливаемости, в противном сщчае те же сродства целесообразнее использовать для увеличения безотказности
единиц средств на повышение восстанавливаемости, в противном сщчае те же сродства целесообразнее использовать для увеличения безотказности  элемента. Если не нарушено ни одно из условий, следует перейти к следующему шагу.
элемента. Если не нарушено ни одно из условий, следует перейти к следующему шагу.  Точку касания перенести в начало координат таким образом, чтобы
Точку касания перенести в начало координат таким образом, чтобы  кривая с номером
кривая с номером  переместилась параллельно самой себе. Перейти к шагу 1.
переместилась параллельно самой себе. Перейти к шагу 1.
По окончании процесса вычислений необходимо проверить выполнение ограничений по  Если последнее не выполняется, то следует повторить оптимизацию относительно показателей восстанавливаемости. Окончательными в соответствии с методом частной оптимизации должны приниматься более жесткие результаты.
Если последнее не выполняется, то следует повторить оптимизацию относительно показателей восстанавливаемости. Окончательными в соответствии с методом частной оптимизации должны приниматься более жесткие результаты.
Задача оптимизации относительно длительности восстановления формулируется следующим образом: найти значения  при которых обеспечиваются
при которых обеспечиваются

и ограничение 
В силу принципа двойственности эта задача имеет то же решение, что и задача (4.77) при втором ограничении.
При использовании метода выпуклых оболочек в данном случае по оси ординат откладываются значения

Графоаналитический алгоритм расчета соответствует изложенному выше, за исключением условия окончания процесса оптимизации, которое запишется следующим образом:

ТАБЛИЦА 4.1

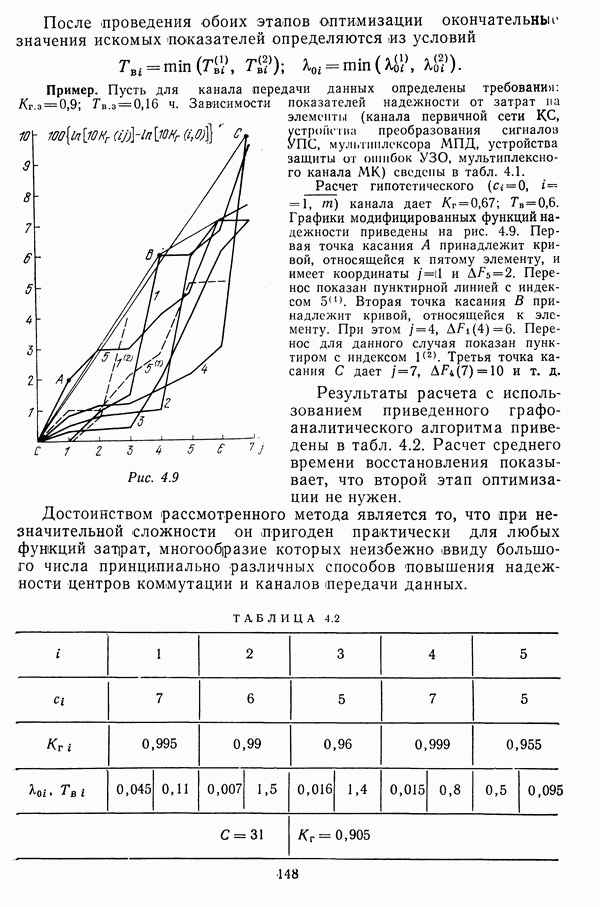
После проведения обоих этапов оптимизации окончательные значения искомых показателей определяются из условий

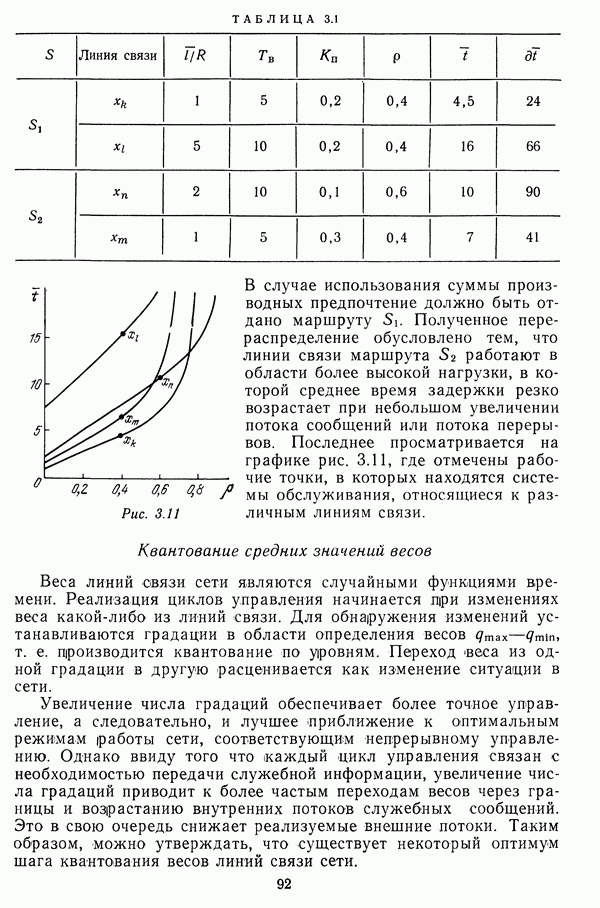
Пример. Пусть для канала передачи данных определены требования:  Зависимости показателей надежности от затрат на элементы (канала первичной сети КС, устройства преобразования сигналов
Зависимости показателей надежности от затрат на элементы (канала первичной сети КС, устройства преобразования сигналов  мультиплексора
мультиплексора  устройства защиты от ошибок
устройства защиты от ошибок  мультиплексного канала
мультиплексного канала  сведены в табл. 4.1.
сведены в табл. 4.1.
Расчет гипотетического  канала дает
канала дает  Графики модифицированных функций надежности приведены на рис. 4.9. Первая точка касания А принадлежит кривой, относящейся к пятому элементу, и имеет координаты
Графики модифицированных функций надежности приведены на рис. 4.9. Первая точка касания А принадлежит кривой, относящейся к пятому элементу, и имеет координаты  Перенос показан пунктирной линией с индексом
Перенос показан пунктирной линией с индексом  Вторая точка касания В принадлежит кривой, относящейся к элементу. При этом
Вторая точка касания В принадлежит кривой, относящейся к элементу. При этом  Перенос для данного случая показан пунктиром с индексом
Перенос для данного случая показан пунктиром с индексом  Третья точка касания С дает
Третья точка касания С дает 

Рис. 4.9
Результаты расчета с использованием приведенного графоаналитического алгоритма приведены в табл. 4.2. Расчет среднего времени восстановления показывает, что второй этап оптимизации не нужен.
Достоинством рассмотренного метода является то, что при незначительной сложности он (Пригоден практически для любых функций затрат, многообразие которых неизбежно ввиду большого числа принципиально различных способов повышения надежности центров коммутации и каналов передачи данных.
ТАБЛИЦА 4.2 (см. скан)
Размерность задачи при использовании графо-аналитического алгоритма по должна превышать десяти (десять элементов, десять значении затрат), что вполне достаточно для рассматриваемых тпмои систем. Число выполняемых три этом операций не превышает 100. Отметим, что сплошной перебор в задаче такой размерности потребовал бы просмотра 10! вариантов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
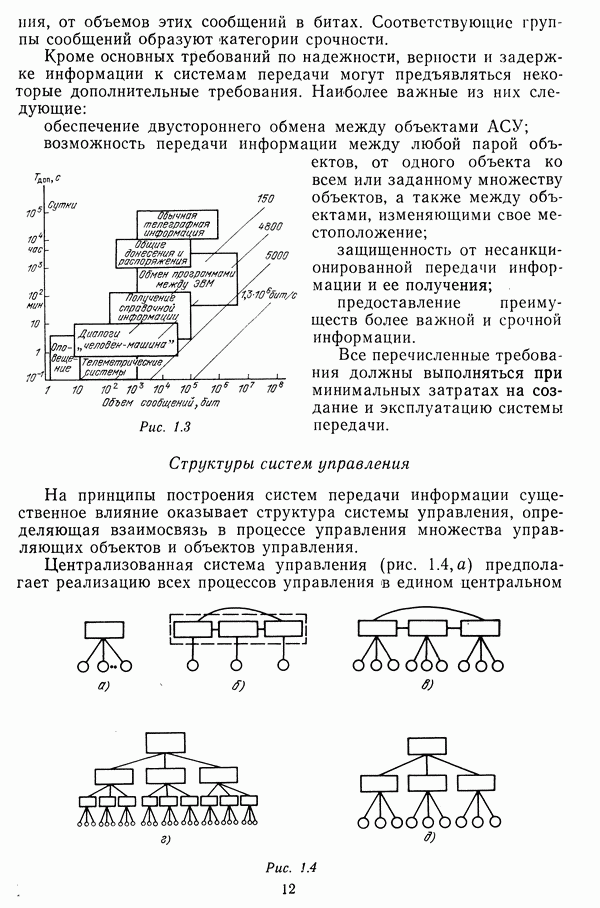
- Глава 1 ОБЩАЯ ХАРАКТЕРИСТИКА СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 1.1. СЕТЬ СВЯЗИ КАК ПОДСИСТЕМА СИСТЕМЫ УПРАВЛЕНИЯ
- 1.2. ПРИНЦИПЫ ПОСТРОЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 1.3. ПРЕДСТАВЛЕНИЕ СТРУКТУР СЕТЕЙ
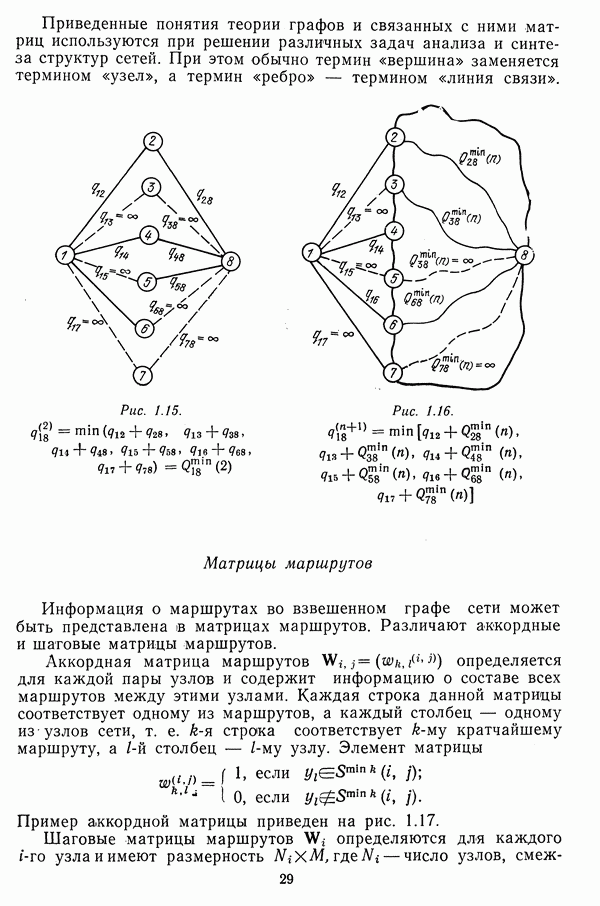
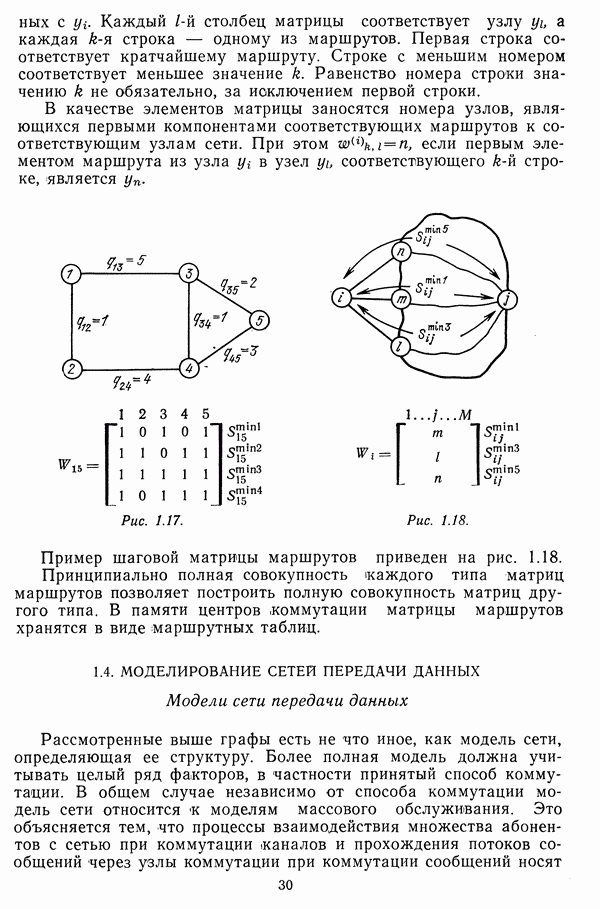
- Кратчайшие маршруты во взвешенных графах
- Матрицы, определяющие структуру сетей
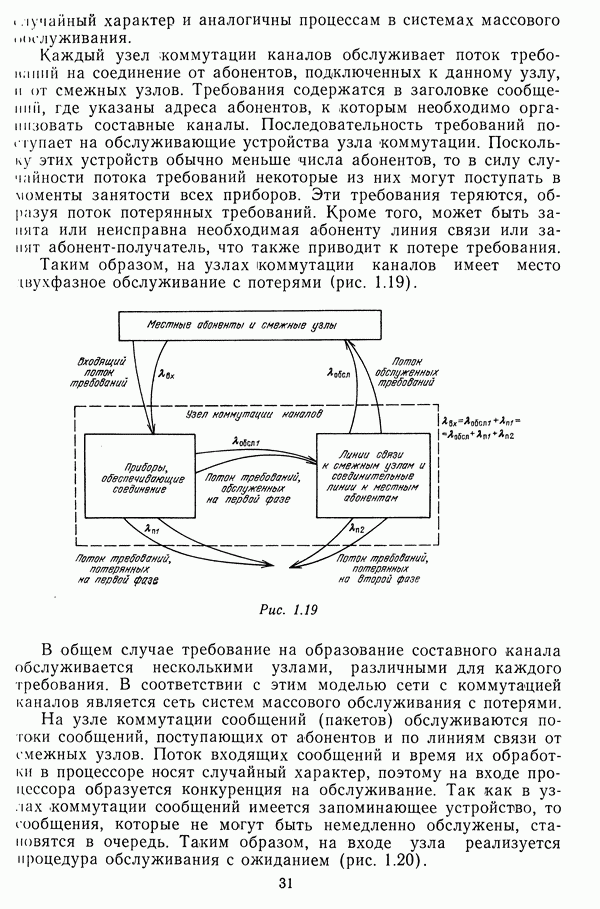
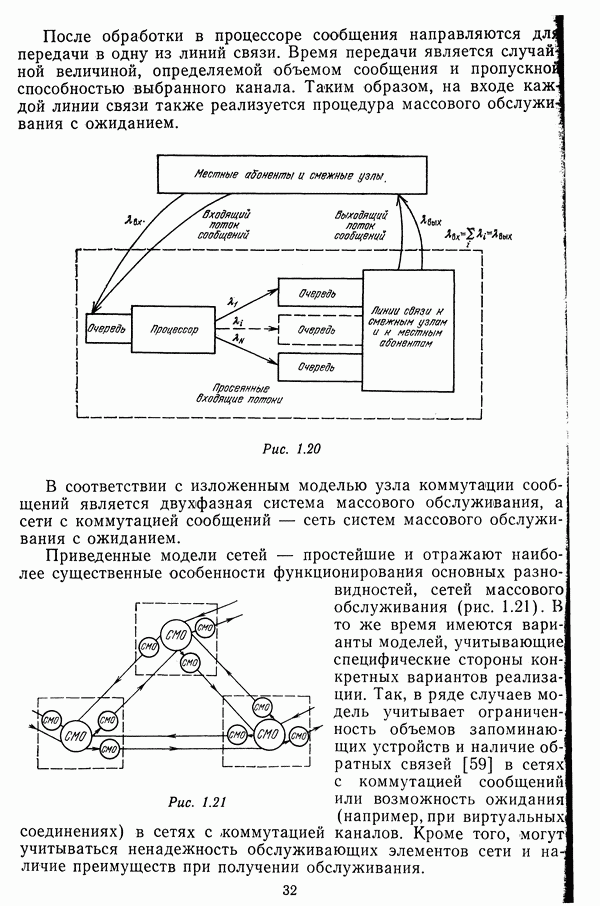
- Матрицы маршрутов
- 1.4. МОДЕЛИРОВАНИЕ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- Математические модели, используемые при расчете сетей
- Потоки в сетях передачи данных
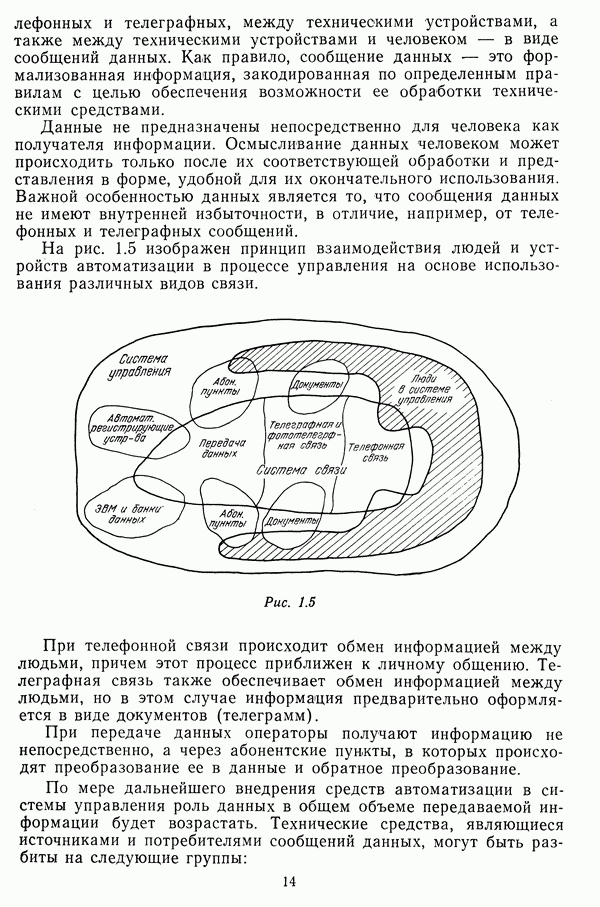
- ГЛАВА 2. ПРИНЦИПЫ ФУНКЦИОНИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.1. СТРУКТУРА ФУНКЦИОНАЛЬНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ СЕТЕЙ ПЕРЕДАЧИ ДАННЫХ
- 2.2. ФОРМАЛИЗАЦИЯ СООБЩЕНИИ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 2.3. АДРЕСОВАНИЕ СООБЩЕНИЙ
- 2.4. ПРОЦЕДУРЫ ВЫБОРА МАРШРУТОВ
- 2.5. РЕГУЛИРОВАНИЕ ПОТОКОВ СООБЩЕНИЙ ПО ПРИОРИТЕТАМ
- 2.6. УПРАВЛЕНИЕ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- Глава 3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ МАРШРУТИЗАЦИИ И УПРАВЛЕНИЯ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ
- 3.2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПОИСКОВЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.4. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КВАЗИСЛУЧАИНЫХ ПРОЦЕДУР ВЫБОРА МАРШРУТОВ
- 3.5. ФИЗИЧЕСКИЕ ВЕРСИИ ВЕСОВ ЭЛЕМЕНТОВ СЕТИ
- 3.6. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УПРАВЛЕНИЯ ВНЕШНИМИ ПОТОКАМИ СООБЩЕНИЙ
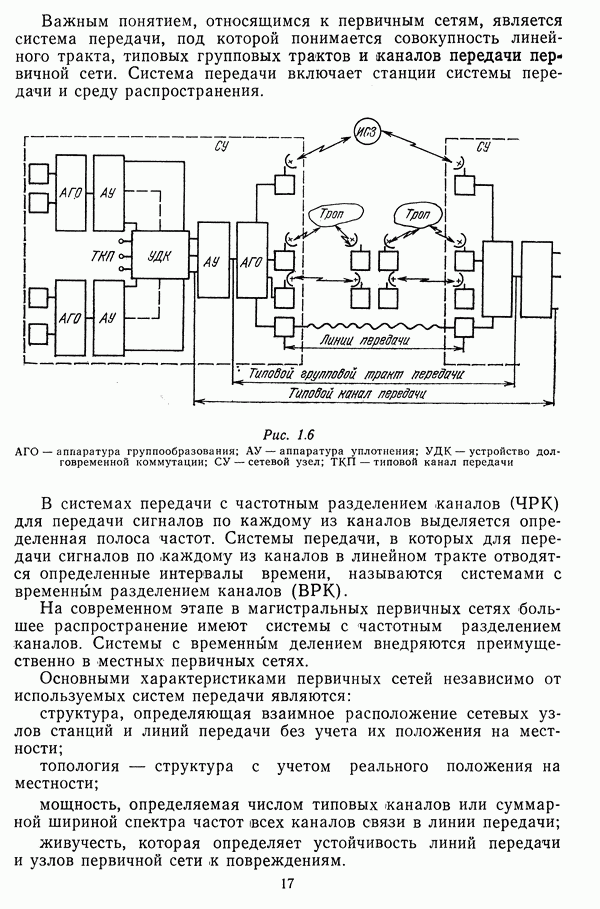
- Глава 4. ВОПРОСЫ ПРОЕКТИРОВАНИЯ СЕТЕЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АСУ
- 4.1. ЗАДАЧИ СИСТЕМНОГО ПРОЕКТИРОВАНИЯ СЕТЕЙ
- 4.2. РАЗМЕЩЕНИЕ УЗЛОВ КОММУТАЦИИ
- Оптимизация числа узлов и их размещения при независимом положении абонентов
- Размещение узлов для связи с мобильными абонентами
- Размещение центра управления сетью
- 4.3. СИНТЕЗ СТРУКТУРЫ СЕТИ
- Синтез структуры сети минимальной стоимости при заданной связности
- 4.4. РАСЧЕТ МОЩНОСТИ ЛИНИИ СВЯЗИ СЕТИ
- Оптимизация мощности линий связи при произвольном виде функций затрат
- Методика выбора каналов передачи данных для линий связи с заданной мощностью
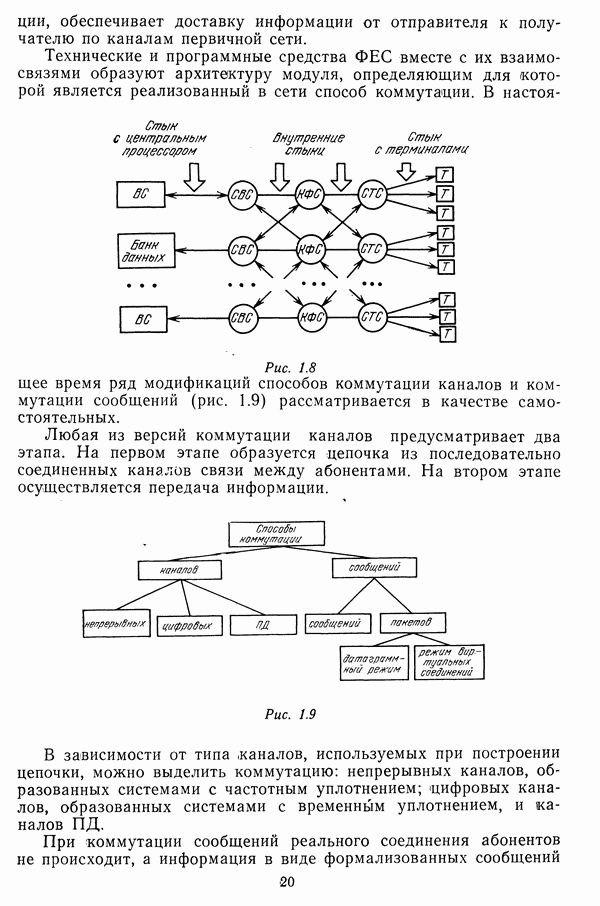
- 4.5. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ЖИВУЧЕСТИ ЭЛЕМЕНТОВ СЕТИ
- 4.6. ВЫБОР ПАРАМЕТРОВ НАДЕЖНОСТИ ЭЛЕМЕНТОВ СЕТИ
- Методы вычисления вероятности связности сети
- Выбор параметров надежности центров коммутации
- Аналитическая оптимизация внутренних показателей надежности элементов сети
- Оптимизация внутренних показателей надежности при произвольном виде функций затрат
- СПИСОК ЛИТЕРАТУРЫ